Article contents
Erdős–Ko–Rado for Random Hypergraphs: Asymptotics and Stability
Published online by Cambridge University Press: 29 March 2017
Abstract
We investigate the asymptotic version of the Erdős–Ko–Rado theorem for the random k-uniform hypergraph 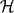 $\mathcal{H}$ k (n, p). For 2⩽k(n) ⩽ n/2, let
$\mathcal{H}$ k (n, p). For 2⩽k(n) ⩽ n/2, let 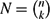 $N=\binom{n}k$ and
$N=\binom{n}k$ and 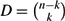 $D=\binom{n-k}k$ . We show that with probability tending to 1 as n → ∞, the largest intersecting subhypergraph of
$D=\binom{n-k}k$ . We show that with probability tending to 1 as n → ∞, the largest intersecting subhypergraph of 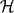 $\mathcal{H}$ has size
$\mathcal{H}$ has size 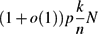 $$(1+o(1))p\ffrac kn N$$
$$(1+o(1))p\ffrac kn N$$ 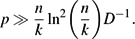 $$p\gg \ffrac nk\ln^2\biggl(\ffrac nk\biggr)D^{-1}.$$
$$p\gg \ffrac nk\ln^2\biggl(\ffrac nk\biggr)D^{-1}.$$
A different behaviour occurs when k = o(n). In this case, the lower bound on p is almost optimal. Further, for the small interval D −1 ≪ p ⩽ (n/k)1−ϵ D −1, the largest intersecting subhypergraph of  $\mathcal{H}$ k (n, p) has size Θ(ln(pD)ND −1), provided that
$\mathcal{H}$ k (n, p) has size Θ(ln(pD)ND −1), provided that 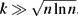 $k \gg \sqrt{n \ln n}$ .
$k \gg \sqrt{n \ln n}$ .
Together with previous work of Balogh, Bohman and Mubayi, these results settle the asymptotic size of the largest intersecting family in 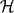 $\mathcal{H}$ k , for essentially all values of p and k.
$\mathcal{H}$ k , for essentially all values of p and k.
Information
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2017
References
- 2
- Cited by

