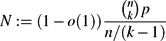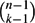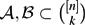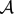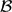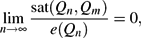Contents
Paper
A Rainbow r-Partite Version of the Erdős–Ko–Rado Theorem
- Part of:
-
- Published online by Cambridge University Press:
- 23 January 2017, pp. 321-337
-
- Article
- Export citation
Convex Polygons in Geometric Triangulations†
- Part of:
-
- Published online by Cambridge University Press:
- 30 May 2017, pp. 641-659
-
- Article
- Export citation
Diameter of the Stochastic Mean-Field Model of Distance
- Part of:
-
- Published online by Cambridge University Press:
- 07 August 2017, pp. 797-825
-
- Article
- Export citation
A Bound on the Number of Edges in Graphs Without an Even Cycle
- Part of:
-
- Published online by Cambridge University Press:
- 07 April 2016, pp. 1-15
-
- Article
- Export citation
Triangles in Cartesian Squares of Quasirandom Groups
- Part of:
-
- Published online by Cambridge University Press:
- 25 August 2016, pp. 161-182
-
- Article
- Export citation
On Regularity Lemmas and their Algorithmic Applications
-
- Published online by Cambridge University Press:
- 28 March 2017, pp. 481-505
-
- Article
- Export citation
Maximal Steiner Trees in the Stochastic Mean-Field Model of Distance
- Part of:
-
- Published online by Cambridge University Press:
- 27 July 2017, pp. 826-838
-
- Article
- Export citation
A Stability Result for Families with Fixed Diameter
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2017, pp. 506-516
-
- Article
- Export citation
On the Widom–Rowlinson Occupancy Fraction in Regular Graphs
- Part of:
-
- Published online by Cambridge University Press:
- 09 August 2016, pp. 183-194
-
- Article
- Export citation
Monotonicity of Avoidance Coupling on KN
- Part of:
-
- Published online by Cambridge University Press:
- 03 June 2016, pp. 16-23
-
- Article
- Export citation
Critical Window for Connectivity in the Configuration Model
- Part of:
-
- Published online by Cambridge University Press:
- 29 May 2017, pp. 660-680
-
- Article
- Export citation
Planting Colourings Silently
- Part of:
-
- Published online by Cambridge University Press:
- 07 December 2016, pp. 338-366
-
- Article
- Export citation
Comparing Graphs of Different Sizes
- Part of:
-
- Published online by Cambridge University Press:
- 02 May 2017, pp. 681-696
-
- Article
- Export citation
Stability and Turán Numbers of a Class of Hypergraphs via Lagrangians
- Part of:
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. 367-405
-
- Article
- Export citation
Packing Loose Hamilton Cycles
-
- Published online by Cambridge University Press:
- 01 August 2017, pp. 839-849
-
- Article
- Export citation
Uniform s-Cross-Intersecting Families
-
- Published online by Cambridge University Press:
- 28 March 2017, pp. 517-524
-
- Article
- Export citation
Patterns in Random Permutations Avoiding the Pattern 132
-
- Published online by Cambridge University Press:
- 18 May 2016, pp. 24-51
-
- Article
- Export citation
A Sequence of Triangle-Free Pseudorandom Graphs
-
- Published online by Cambridge University Press:
- 13 September 2016, pp. 195-200
-
- Article
- Export citation
The Minimum Number of Triangular Edges and a Symmetrization Method for Multiple Graphs
-
- Published online by Cambridge University Press:
- 23 January 2017, pp. 525-535
-
- Article
- Export citation
Saturated Subgraphs of the Hypercube
- Part of:
-
- Published online by Cambridge University Press:
- 19 September 2016, pp. 52-67
-
- Article
- Export citation