Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Samotij, Wojciech
and
Sudakov, Benny
2015.
On the number of monotone sequences.
Journal of Combinatorial Theory, Series B,
Vol. 115,
Issue. ,
p.
132.
Balogh, József
Hu, Ping
Lidický, Bernard
and
Pfender, Florian
2016.
Maximum density of induced 5-cycle is achieved by an iterated blow-up of 5-cycle.
European Journal of Combinatorics,
Vol. 52,
Issue. ,
p.
47.
SAMOTIJ, WOJCIECH
and
SUDAKOV, BENNY
2016.
The number of additive triples in subsets of abelian groups.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 160,
Issue. 3,
p.
495.
Alon, Noga
Naves, Humberto
and
Sudakov, Benny
2016.
On the Maximum Quartet Distance between Phylogenetic Trees.
SIAM Journal on Discrete Mathematics,
Vol. 30,
Issue. 2,
p.
718.
Balogh, József
Hu, Ping
Lidický, Bernard
Pfender, Florian
Volec, Jan
and
Young, Michael
2017.
Rainbow triangles in three-colored graphs.
Journal of Combinatorial Theory, Series B,
Vol. 126,
Issue. ,
p.
83.
Gethner, Ellen
Hogben, Leslie
Lidický, Bernard
Pfender, Florian
Ruiz, Amanda
and
Young, Michael
2017.
On Crossing Numbers of Complete Tripartite and Balanced Complete Multipartite Graphs.
Journal of Graph Theory,
Vol. 84,
Issue. 4,
p.
552.
Nagami Coregliano, Leonardo
2018.
Quasi‐carousel tournaments.
Journal of Graph Theory,
Vol. 88,
Issue. 1,
p.
192.
KRÁL', DANIEL
LIDICKÝ, BERNARD
MARTINS, TAÍSA L.
and
PEHOVA, YANITSA
2019.
Decomposing Graphs into Edges and Triangles.
Combinatorics, Probability and Computing,
Vol. 28,
Issue. 3,
p.
465.
Grzesik, Andrzej
Hu, Ping
and
Volec, Jan
2019.
Minimum number of edges that occur in odd cycles.
Journal of Combinatorial Theory, Series B,
Vol. 137,
Issue. ,
p.
65.
Even-Zohar, Chaim
2020.
Patterns in Random Permutations.
Combinatorica,
Vol. 40,
Issue. 6,
p.
775.
Choi, Ilkyoo
Lidický, Bernard
and
Pfender, Florian
2020.
Inducibility of directed paths.
Discrete Mathematics,
Vol. 343,
Issue. 10,
p.
112015.
Lidický, Bernard
and
Pfender, Florian
2021.
Semidefinite Programming and Ramsey Numbers.
SIAM Journal on Discrete Mathematics,
Vol. 35,
Issue. 4,
p.
2328.
Balogh, József
Clemen, Felix Christian
and
Lidický, Bernard
2022.
Maximum number of almost similar triangles in the plane.
Computational Geometry,
Vol. 105-106,
Issue. ,
p.
101880.
Bożyk, Łukasz
Grzesik, Andrzej
and
Kielak, Bartłomiej
2022.
On the inducibility of oriented graphs on four vertices.
Discrete Mathematics,
Vol. 345,
Issue. 7,
p.
112874.
Balogh, József
Clemen, Felix Christian
and
Lidický, Bernard
2022.
Solving Turán's tetrahedron problem for the ℓ2$\ell _2$‐norm.
Journal of the London Mathematical Society,
Vol. 106,
Issue. 1,
p.
60.
Balogh, József
Lidický, Bernard
Norin, Sergey
Pfender, Florian
Salazar, Gelasio
and
Spiro, Sam
2023.
Crossing numbers of complete bipartite graphs.
Procedia Computer Science,
Vol. 223,
Issue. ,
p.
78.
Garbe, Frederik
Kral, Daniel
Malekshahian, Alexandru
and
Penaguiao, Raul
2023.
The dimension of the feasible region of pattern densities.
p.
471.
Emrah Amrahov, Sahin
Ar, Yilmaz
Tugrul, Bulent
Akay, Bekir Emirhan
and
Kartli, Nermin
2024.
A new approach to Mergesort algorithm: Divide smart and conquer.
Future Generation Computer Systems,
Vol. 157,
Issue. ,
p.
330.
Král’, Daniel
Lamaison, Ander
Prorok, Magdalena
and
Shu, Xichao
2025.
The Dimension of the Region of Feasible Tournament Profiles.
SIAM Journal on Discrete Mathematics,
Vol. 39,
Issue. 2,
p.
1335.
GARBE, FREDERIK
KRÁL’, DANIEL
MALEKSHAHIAN, ALEXANDRU
and
PENAGUIAO, RAUL
2025.
The dimension of the feasible region of pattern densities.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 178,
Issue. 1,
p.
1.
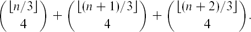 \begin{equation*}\binom{\lfloor{n/3}\rfloor}{4} + \binom{\lfloor{(n+1)/3}\rfloor}{4} + \binom{\lfloor{(n+2)/3}\rfloor}{4}.\end{equation*}
\begin{equation*}\binom{\lfloor{n/3}\rfloor}{4} + \binom{\lfloor{(n+1)/3}\rfloor}{4} + \binom{\lfloor{(n+2)/3}\rfloor}{4}.\end{equation*}
