Article contents
Parking on a Random Tree
Published online by Cambridge University Press: 23 October 2018
Abstract
Consider a uniform random rooted labelled tree on n vertices. We imagine that each node of the tree has space for a single car to park. A number m ≤ n of cars arrive one by one, each at a node chosen independently and uniformly at random. If a car arrives at a space which is already occupied, it follows the unique path towards the root until it encounters an empty space, in which case it parks there; if there is no empty space, it leaves the tree. Consider m = ⌊α n⌋ and let An,α denote the event that all ⌊α n⌋ cars find spaces in the tree. Lackner and Panholzer proved (via analytic combinatorics methods) that there is a phase transition in this model. Then if α ≤ 1/2, we have 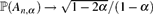 $\mathbb{P}({A_{n,\alpha}}) \to {\sqrt{1-2\alpha}}/{(1-\alpha})$, whereas if α > 1/2 we have
$\mathbb{P}({A_{n,\alpha}}) \to {\sqrt{1-2\alpha}}/{(1-\alpha})$, whereas if α > 1/2 we have 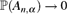 $\mathbb{P}({A_{n,\alpha}}) \to 0$. We give a probabilistic explanation for this phenomenon, and an alternative proof via the objective method. Along the way, we consider the following variant of the problem: take the tree to be the family tree of a Galton–Watson branching process with Poisson(1) offspring distribution, and let an independent Poisson(α) number of cars arrive at each vertex. Let X be the number of cars which visit the root of the tree. We show that
$\mathbb{P}({A_{n,\alpha}}) \to 0$. We give a probabilistic explanation for this phenomenon, and an alternative proof via the objective method. Along the way, we consider the following variant of the problem: take the tree to be the family tree of a Galton–Watson branching process with Poisson(1) offspring distribution, and let an independent Poisson(α) number of cars arrive at each vertex. Let X be the number of cars which visit the root of the tree. We show that 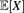 $\mathbb{E}{[X]}$ undergoes a discontinuous phase transition, which turns out to be a generic phenomenon for arbitrary offspring distributions of mean at least 1 for the tree and arbitrary arrival distributions.
$\mathbb{E}{[X]}$ undergoes a discontinuous phase transition, which turns out to be a generic phenomenon for arbitrary offspring distributions of mean at least 1 for the tree and arbitrary arrival distributions.
MSC classification
Information
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2018
Footnotes
Research supported by EPSRC Fellowship EP/N004833/1.
References
- 19
- Cited by

