Contents
Research Article
Point Selections and Weak ε-Nets for Convex Hulls
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 189-200
-
- Article
- Export citation
On the Diameter of Random Cayley Graphs of the Symmetric Group
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 201-208
-
- Article
- Export citation
A Characterisation of Strict Matching Matroids
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 209-217
-
- Article
- Export citation
Duality for Random Sequential Adsorption on a Lattice†
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 219-222
-
- Article
- Export citation
Cycles in a Uniform Graph Process†
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 223-239
-
- Article
- Export citation
Complete Subgraphs of r-partite Graphs
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 241-250
-
- Article
- Export citation
Maximum Waiting Times are Asymptotically Independent
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 251-264
-
- Article
- Export citation
The Strongly Connected Components of 1-in, 1-out
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 265-274
-
- Article
- Export citation
Duality in Polymatroids and Set Functions
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 275-280
-
- Article
- Export citation
Front matter
CPC volume 1 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
CPC volume 1 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. b1-b6
-
- Article
-
- You have access
- Export citation
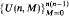 in which the minimum degree of
in which the minimum degree of 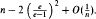 .
.