Contents
Paper
Sums of Dilates
-
- Published online by Cambridge University Press:
- 01 September 2008, pp. 627-639
-
- Article
- Export citation
Generating All Sets With Bounded Unions
-
- Published online by Cambridge University Press:
- 01 September 2008, pp. 641-660
-
- Article
- Export citation
Subtree Sizes in Recursive Trees and Binary Search Trees: Berry–Esseen Bounds and Poisson Approximations
-
- Published online by Cambridge University Press:
- 01 September 2008, pp. 661-680
-
- Article
- Export citation
Projecting Difference Sets on the Positive Orthant
-
- Published online by Cambridge University Press:
- 01 September 2008, pp. 681-688
-
- Article
- Export citation
A Dirac-Type Result on Hamilton Cycles in Oriented Graphs
-
- Published online by Cambridge University Press:
- 01 September 2008, pp. 689-709
-
- Article
- Export citation
Growth of the Number of Spanning Trees of the Erdős–Rényi Giant Component
-
- Published online by Cambridge University Press:
- 01 September 2008, pp. 711-726
-
- Article
- Export citation


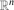 , write
, write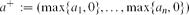
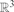 , and that |(
, and that |(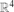 such that |
such that |