Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Rabideau, Michelle
2018.
F-polynomial formula from continued fractions.
Journal of Algebra,
Vol. 509,
Issue. ,
p.
467.
Schiffler, Ralf
2018.
Homological Methods, Representation Theory, and Cluster Algebras.
p.
65.
Lee, Kyungyong
and
Schiffler, Ralf
2019.
Cluster algebras and Jones polynomials.
Selecta Mathematica,
Vol. 25,
Issue. 4,
Henke, Niklas
and
Papathanasiou, Georgios
2020.
How tropical are seven- and eight-particle amplitudes?.
Journal of High Energy Physics,
Vol. 2020,
Issue. 8,
Reading, Nathan
2020.
A combinatorial approach to scattering diagrams.
Algebraic Combinatorics,
Vol. 3,
Issue. 3,
p.
603.
Nagai, Wataru
and
Terashima, Yuji
2020.
Cluster variables, ancestral triangles and Alexander polynomials.
Advances in Mathematics,
Vol. 363,
Issue. ,
p.
106965.
Rabideau, Michelle
and
Schiffler, Ralf
2020.
Continued fractions and orderings on the Markov numbers.
Advances in Mathematics,
Vol. 370,
Issue. ,
p.
107231.
Çanakçı, İlke
and
Schiffler, Ralf
2020.
Snake graphs and continued fractions.
European Journal of Combinatorics,
Vol. 86,
Issue. ,
p.
103081.
Çanakçı, İlke
and
Lampe, Philipp
2020.
An expansion formula for type A and Kronecker quantum cluster algebras.
Journal of Combinatorial Theory, Series A,
Vol. 171,
Issue. ,
p.
105132.
Gyoda, Yasuaki
2021.
Relation Between f-Vectors and d-Vectors in Cluster Algebras of Finite Type or Rank 2.
Annals of Combinatorics,
Vol. 25,
Issue. 3,
p.
573.
Çanakçı, İlke
and
Schroll, Sibylle
2021.
Lattice bijections for string modules, snake graphs and the weak Bruhat order.
Advances in Applied Mathematics,
Vol. 126,
Issue. ,
p.
102094.
Henke, Niklas
and
Papathanasiou, Georgios
2021.
Singularities of eight- and nine-particle amplitudes from cluster algebras and tropical geometry.
Journal of High Energy Physics,
Vol. 2021,
Issue. 10,
Espinosa, Pedro Fernando Fernández
González, Javier Fernando
Herrán, Juan Pablo
Cañadas, Agustín Moreno
and
Ramírez, José Luis
2022.
On some relationships between snake graphs and Brauer configuration algebras.
Algebra and Discrete Mathematics,
Vol. 33,
Issue. 2,
p.
29.
Bailey, Rachel
and
Gunawan, Emily
2022.
Cluster Algebras and Binary Subwords.
Order,
Vol. 39,
Issue. 1,
p.
55.
Papathanasiou, Georgios
2022.
The SAGEX review on scattering amplitudes Chapter 5: Analytic bootstraps for scattering amplitudes and beyond.
Journal of Physics A: Mathematical and Theoretical,
Vol. 55,
Issue. 44,
p.
443006.
Cañadas, Agustín Moreno
Espinosa, Pedro Fernando Fernández
and
Muñetón, Natalia Agudelo
2022.
Brauer configuration algebras defined by snake graphs and Kronecker modules.
Electronic Research Archive,
Vol. 30,
Issue. 8,
p.
3087.
Bazier-Matte, Véronique
and
Schiffler, Ralf
2022.
Knot theory and cluster algebras.
Advances in Mathematics,
Vol. 408,
Issue. ,
p.
108609.
Ovenhouse, Nicholas
2023.
q-Rationals and Finite Schubert Varieties.
Comptes Rendus. Mathématique,
Vol. 361,
Issue. G4,
p.
807.
Lee, Kyungyong
Li, Li
Rabideau, Michelle
and
Schiffler, Ralf
2023.
On the ordering of the Markov numbers.
Advances in Applied Mathematics,
Vol. 143,
Issue. ,
p.
102453.
Cañadas, Agustín Moreno
Fernández Espinosa, Pedro Fernando
and
Ballester-Bolinches, Adolfo
2023.
Solutions of the Yang–Baxter Equation and Automaticity Related to Kronecker Modules.
Computation,
Vol. 11,
Issue. 3,
p.
43.
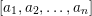 $[a_{1},a_{2},\ldots ,a_{n}]$ we associate a snake graph
$[a_{1},a_{2},\ldots ,a_{n}]$ we associate a snake graph 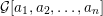 ${\mathcal{G}}[a_{1},a_{2},\ldots ,a_{n}]$ such that the continued fraction is the quotient of the number of perfect matchings of
${\mathcal{G}}[a_{1},a_{2},\ldots ,a_{n}]$ such that the continued fraction is the quotient of the number of perfect matchings of 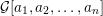 ${\mathcal{G}}[a_{1},a_{2},\ldots ,a_{n}]$ and
${\mathcal{G}}[a_{1},a_{2},\ldots ,a_{n}]$ and 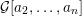 ${\mathcal{G}}[a_{2},\ldots ,a_{n}]$ . We also show that snake graphs are in bijection with continued fractions. We then apply this connection between cluster algebras and continued fractions in two directions. First we use results from snake graph calculus to obtain new identities for the continuants of continued fractions. Then we apply the machinery of continued fractions to cluster algebras and obtain explicit direct formulas for quotients of elements of the cluster algebra as continued fractions of Laurent polynomials in the initial variables. Building on this formula, and using classical methods for infinite periodic continued fractions, we also study the asymptotic behavior of quotients of elements of the cluster algebra.
${\mathcal{G}}[a_{2},\ldots ,a_{n}]$ . We also show that snake graphs are in bijection with continued fractions. We then apply this connection between cluster algebras and continued fractions in two directions. First we use results from snake graph calculus to obtain new identities for the continuants of continued fractions. Then we apply the machinery of continued fractions to cluster algebras and obtain explicit direct formulas for quotients of elements of the cluster algebra as continued fractions of Laurent polynomials in the initial variables. Building on this formula, and using classical methods for infinite periodic continued fractions, we also study the asymptotic behavior of quotients of elements of the cluster algebra.
