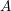Hostname: page-component-76c49bb84f-t6sgf Total loading time: 0 Render date: 2025-07-10T05:40:52.323Z Has data issue: false hasContentIssue false
  • English
  • Français

Counting Higgs bundles and type $A$ quiver bundles

Part of: Representation theory of rings and algebras Families, fibrations

Published online by Cambridge University Press:  27 February 2020

Sergey Mozgovoy  and
Olivier Schiffmann
Sergey Mozgovoy
Affiliation:
School of Mathematics, Trinity College, Dublin 2, Ireland email mozgovoy@maths.tcd.ie
Olivier Schiffmann
Affiliation:
Institut de Mathématiques d’Orsay, bât. 307, Faculté des Sciences d’Orsay, 91405Orsay Cedex, France email Olivier.Schiffmann@math.u-psud.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a closed formula counting semistable twisted (or meromorphic) Higgs bundles of fixed rank and degree over a smooth projective curve of genus 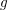$g$ defined over a finite field, when the twisting line bundle degree is at least 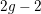$2g-2$ (this includes the case of usual Higgs bundles). This yields a closed expression for the Donaldson–Thomas invariants of the moduli spaces of twisted Higgs bundles. We similarly deal with twisted quiver sheaves of type 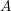$A$ (finite or affine), obtaining in particular a Harder–Narasimhan-type formula counting semistable 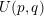$U(p,q)$-Higgs bundles over a smooth projective curve defined over a finite field.

Keywords

semistable Higgs bundlesDonaldson–Thomas invariantsquiver bundles

MSC classification

Primary: 14D20: Algebraic moduli problems, moduli of vector bundles 16G20: Representations of quivers and partially ordered sets

Information

Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 4 , April 2020 , pp. 744 - 769
Copyright
© The Authors 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

OS is partially supported by ANR grant 13-BS01-0001-01.

References

Chaudouard, P.-H., Sur le comptage des fibrés de Hitchin, Astérisque 369 (2015), 223–284.Google Scholar
Chaudouard, P.-H. and Laumon, G., Sur le comptage des fibrés de Hitchin nilpotents, J. Inst. Math. Jussieu 15 (2016), 91–164.CrossRefGoogle Scholar
Chuang, W.-y., Diaconescu, D.-E. and Pan, G., Wallcrossing and cohomology of the moduli space of Hitchin pairs, Commun. Number Theory Phys. 5 (2011), 1–56.CrossRefGoogle Scholar
García-Prada, O. and Heinloth, J., The y-genus of the moduli space of PGLn-Higgs bundles on a curve (for degree coprime to n), Duke Math. J. 162 (2013), 2731–2749.CrossRefGoogle Scholar
García-Prada, O., Heinloth, J. and Schmitt, A., On the motives of moduli of chains and Higgs bundles, J. Eur. Math. Soc. (JEMS) 16 (2014), 2617–2668.CrossRefGoogle Scholar
Gothen, P. B., The Betti numbers of the moduli space of stable rank 3 Higgs bundles on a Riemann surface, Internat. J. Math. 5 (1994), 861–875.CrossRefGoogle Scholar
Gothen, P. B., Hitchin pairs for non-compact real Lie groups, Trav. Math. 24 (2016), 183–200. Special issue based on School GEOQUANT at the ICMAT Madrid, Spain, September 2015.Google Scholar
Gothen, P. B. and King, A. D., Homological algebra of twisted quiver bundles, J. Lond. Math. Soc. (2) 71 (2005), 85–99.CrossRefGoogle Scholar
Hausel, T., Mirror symmetry and Langlands duality in the non-abelian Hodge theory of a curve, in Geometric methods in algebra and number theory, Progress in Mathematics, vol. 235 (Birkhäuser, Boston, MA, 2005), 193–217.CrossRefGoogle Scholar
Hausel, T. and Rodriguez-Villegas, F., Mixed Hodge polynomials of character varieties, Invent. Math. 174 (2008), 555–624; with an appendix by Nicholas M. Katz.CrossRefGoogle Scholar
Hitchin, N. J., The self-duality equations on a Riemann surface, Proc. Lond. Math. Soc. (3) 55 (1987), 59–126.CrossRefGoogle Scholar
Laumon, G. and Rapoport, M., The Langlands lemma and the Betti numbers of stacks of G-bundles on a curve, Internat. J. Math. 7 (1996), 29–45.CrossRefGoogle Scholar
Macdonald, I. G., Symmetric functions and Hall polynomials, Oxford Mathematical Monographs, second edition (Clarendon Press, Oxford, 1995); with contributions by A. Zelevinsky.Google Scholar
Mellit, A., Poincaré polynomials of moduli spaces of Higgs bundles and character varieties (no punctures), Invent. Math., to appear. Preprint (2017), arXiv:1707.04214.Google Scholar
Mozgovoy, S., A computational criterion for the Kac conjecture, J. Algebra 318 (2007), 669–679.CrossRefGoogle Scholar
Mozgovoy, S., Poincaré polynomials of moduli spaces of stable bundles over curves, Manuscripta Math. 131 (2010), 63–86.CrossRefGoogle Scholar
Mozgovoy, S., Motivic Donaldson–Thomas invariants and McKay correspondence, Preprint (2011), arXiv:1107.6044.Google Scholar
Mozgovoy, S., Solutions of the motivic ADHM recursion formula, Int. Math. Res. Not. IMRN 2012 (2012), 4218–4244.CrossRefGoogle Scholar
Mozgovoy, S. and Reineke, M., Moduli spaces of stable pairs and non-abelian zeta functions of curves via wall-crossing, J. Éc. Polytech. Math. 1 (2014), 117–146.CrossRefGoogle Scholar
Reineke, M., The Harder–Narasimhan system in quantum groups and cohomology of quiver moduli, Invent. Math. 152 (2003), 349–368.CrossRefGoogle Scholar
Reineke, M., Counting rational points of quiver moduli, Int. Math. Res. Not. IMRN 2006 (2006), 70456.Google Scholar
Schiffmann, O., Lectures on Hall algebras, in Geometric methods in representation theory. II, Sḿinaire et Congrès, vol. 24 (Société Mathématique de France, Paris, 2012).Google Scholar
Schiffmann, O., Indecomposable vector bundles and stable Higgs bundles over smooth projective curves, Ann. of Math. (2) 183 (2016), 297–362.CrossRefGoogle Scholar
Zagier, D., Elementary aspects of the Verlinde formula and of the Harder–Narasimhan–Atiyah–Bott formula, in Proceedings of the Hirzebruch 65 Conference on Algebraic Geometry (Ramat Gan), Israel Mathematical Conference Proceedings, vol. 9 (Bar-Ilan University, 1996), 445–462.Google Scholar