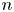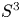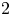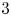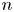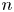1. Introduction
Question Let ![]() $M$ be a compact topological
$M$ be a compact topological ![]() $4$-manifold and let
$4$-manifold and let ![]() $x \in \pi _2(M)$. Can
$x \in \pi _2(M)$. Can ![]() $x$ be represented by a locally flat embedded
$x$ be represented by a locally flat embedded ![]() $2$-sphere?
$2$-sphere?
Versions of this fundamental question have been studied by many authors, such as [Reference Kervaire and MilnorKM61, Reference TristramTri69, Reference RohlinRoh71, Reference Hsiang and SzczarbaHS71]. The seminal work of Freedman and Quinn [Reference FreedmanFre82, Reference Freedman and QuinnFQ90] provided new tools with which to approach this problem. In independent work of Lee and Wilczyński [Reference Lee and WilczyńskiLW90, Theorem 1.1] and Hambleton and Kreck [Reference Hambleton and KreckHK93, Theorem 4.5], the methods of topological surgery theory were applied to provide a complete answer for simply connected, closed 4-manifolds, in the presence of a natural fundamental group restriction. That is, they classified when an element of the second homotopy group of such a 4-manifold can be represented by a locally flat embedded sphere whose complement has abelian fundamental group. Lee and Wilczyński [Reference Lee and WilczyńskiLW97] later generalised their theorem to apply to simply connected, compact ![]() $4$-manifolds with homology sphere boundary. In this article, we expand our understanding to another general class of 4-manifolds with boundary.
$4$-manifolds with homology sphere boundary. In this article, we expand our understanding to another general class of 4-manifolds with boundary.
Our main result is an answer to the sphere embedding question for ![]() $4$-manifolds called knot traces, with
$4$-manifolds called knot traces, with ![]() $x$ a generator of the second homotopy group. Let
$x$ a generator of the second homotopy group. Let ![]() $\nu K$ be an open tubular neighbourhood of a knot
$\nu K$ be an open tubular neighbourhood of a knot ![]() $K$ in
$K$ in ![]() $S^{3}$ and let
$S^{3}$ and let ![]() $n$ be an integer. The
$n$ be an integer. The ![]() $n$-framed knot trace
$n$-framed knot trace ![]() $X_n(K)$ is the smooth 4-manifold obtained by attaching a 2-handle
$X_n(K)$ is the smooth 4-manifold obtained by attaching a 2-handle ![]() $D^{2}\times D^{2}$ to the 4-ball along
$D^{2}\times D^{2}$ to the 4-ball along ![]() $\nu K\subset S^{3}$, using framing coefficient
$\nu K\subset S^{3}$, using framing coefficient ![]() $n$ and smoothing corners. The boundary of
$n$ and smoothing corners. The boundary of ![]() $X_n(K)$ is the
$X_n(K)$ is the ![]() $n$–framed surgery
$n$–framed surgery ![]() $S_n^{3}(K) := (S^{3} {{\smallsetminus }} \nu K) \cup D^{2} \times S^{1}$, where
$S_n^{3}(K) := (S^{3} {{\smallsetminus }} \nu K) \cup D^{2} \times S^{1}$, where ![]() $\partial D^{2} \times \{1\}$ is attached to the
$\partial D^{2} \times \{1\}$ is attached to the ![]() $n$-framed longitude of
$n$-framed longitude of ![]() $K$.
$K$.
Theorem 1.1 Let ![]() $K$ be a knot in
$K$ be a knot in ![]() $S^{3}$ and let
$S^{3}$ and let ![]() $n$ be an integer. A generator of
$n$ be an integer. A generator of ![]() $\pi _2(X_n(K))$ can be represented by a locally flat embedded
$\pi _2(X_n(K))$ can be represented by a locally flat embedded ![]() $2$-sphere whose complement has abelian fundamental group if and only if:
$2$-sphere whose complement has abelian fundamental group if and only if:
(i)
 $H_1(S_n^{3}(K);\mathbb {Z}[\mathbb {Z}/n])=0$; or equivalently for
$H_1(S_n^{3}(K);\mathbb {Z}[\mathbb {Z}/n])=0$; or equivalently for  $n \neq 0$,
$n \neq 0$,  $\prod _{\{\xi \mid \xi ^{n}=1\} }\Delta _K(\xi ) =1$;
$\prod _{\{\xi \mid \xi ^{n}=1\} }\Delta _K(\xi ) =1$;(ii)
 $\operatorname {Arf}(K)=0$; and
$\operatorname {Arf}(K)=0$; and(iii)
 $\sigma _K(\xi ) =0$ for every
$\sigma _K(\xi ) =0$ for every  $\xi \in S^{1}$ such that
$\xi \in S^{1}$ such that  $\xi ^{n}=1$.
$\xi ^{n}=1$.
The theorem is stated in terms of some well-known knot invariants that arise from a Seifert matrix ![]() $V$ for
$V$ for ![]() $K$. The Alexander polynomial
$K$. The Alexander polynomial ![]() $\Delta _K(t) \in \mathbb {Z}[t,t^{-1}]$ can be most quickly defined as
$\Delta _K(t) \in \mathbb {Z}[t,t^{-1}]$ can be most quickly defined as ![]() $\det (tV-V^{T})$. Then the Arf invariant of
$\det (tV-V^{T})$. Then the Arf invariant of ![]() $K$ in
$K$ in ![]() $\mathbb {Z}/2$ is
$\mathbb {Z}/2$ is ![]() $0$ if
$0$ if ![]() $\Delta _K(-1) \equiv \pm 1 \mod {8}$ and is
$\Delta _K(-1) \equiv \pm 1 \mod {8}$ and is ![]() $1$ if
$1$ if ![]() $\Delta _K(-1) \equiv \pm 3 \mod {8}$. Finally the Tristram–Levine signature, for
$\Delta _K(-1) \equiv \pm 3 \mod {8}$. Finally the Tristram–Levine signature, for ![]() $\xi \in S^{1} \subseteq \mathbb {C}$, is the signature of the Hermitian matrix
$\xi \in S^{1} \subseteq \mathbb {C}$, is the signature of the Hermitian matrix ![]() $(1-\xi )V + (1-\overline {\xi })V^{T}$. These invariants are independent of the choice of Seifert surface and Seifert matrix, and they are straightforward to compute from a knot diagram.
$(1-\xi )V + (1-\overline {\xi })V^{T}$. These invariants are independent of the choice of Seifert surface and Seifert matrix, and they are straightforward to compute from a knot diagram.
For certain choices of ![]() $n$, there are logical dependencies among the conditions (i), (ii), and (iii) above. When
$n$, there are logical dependencies among the conditions (i), (ii), and (iii) above. When ![]() $n=0$, condition (i) states that
$n=0$, condition (i) states that ![]() $H_1(S^{3}_0(K); \mathbb {Z}[\mathbb {Z}])=0$, which is equivalent to
$H_1(S^{3}_0(K); \mathbb {Z}[\mathbb {Z}])=0$, which is equivalent to ![]() $\Delta _K(t)=1$, which in turn implies both conditions (ii) and (iii). When
$\Delta _K(t)=1$, which in turn implies both conditions (ii) and (iii). When ![]() $n=\pm 1$, conditions (i) and (iii) are automatically satisfied.
$n=\pm 1$, conditions (i) and (iii) are automatically satisfied.
When ![]() $n \neq 0$, condition (i) is equivalent to the condition that
$n \neq 0$, condition (i) is equivalent to the condition that ![]() $\Sigma _{|n|}(K)$, the
$\Sigma _{|n|}(K)$, the ![]() $n$-fold cyclic branched cover of
$n$-fold cyclic branched cover of ![]() $S^{3}$ with branching set
$S^{3}$ with branching set ![]() $K$, is an integral homology sphere. This is due to the classical formula
$K$, is an integral homology sphere. This is due to the classical formula ![]() $|H_1(\Sigma _{|n|}(K);\mathbb {Z})| = \prod _{\{\xi \mid \xi ^{n}=1\} }\Delta _K(\xi )$ due to [Reference GoeritzGoe34, Reference FoxFox56]. When
$|H_1(\Sigma _{|n|}(K);\mathbb {Z})| = \prod _{\{\xi \mid \xi ^{n}=1\} }\Delta _K(\xi )$ due to [Reference GoeritzGoe34, Reference FoxFox56]. When ![]() $n \neq 0$ is even, condition (i) implies condition (ii), as follows. The expression
$n \neq 0$ is even, condition (i) implies condition (ii), as follows. The expression ![]() $\prod _{\{\xi \mid \xi ^{n}=1\} }\Delta _K(\xi )$ equals the resultant
$\prod _{\{\xi \mid \xi ^{n}=1\} }\Delta _K(\xi )$ equals the resultant ![]() $\operatorname {Res}(\Delta _K(t), t^{n}-1) \in \mathbb {Z}$. Whenever
$\operatorname {Res}(\Delta _K(t), t^{n}-1) \in \mathbb {Z}$. Whenever ![]() $m$ divides
$m$ divides ![]() $n$,
$n$, ![]() $t^{m}-1$ divides
$t^{m}-1$ divides ![]() $t^{n}-1$, and so by the characterising properties of resultants we have
$t^{n}-1$, and so by the characterising properties of resultants we have
Since ![]() $\operatorname {Arf}(K)=1$ implies that
$\operatorname {Arf}(K)=1$ implies that ![]() $\operatorname {Res}(\Delta _K(t), t^{2}-1) = \Delta _K(-1) \neq 1$, it follows that
$\operatorname {Res}(\Delta _K(t), t^{2}-1) = \Delta _K(-1) \neq 1$, it follows that ![]() $\operatorname {Arf}(K)=1$ further implies that
$\operatorname {Arf}(K)=1$ further implies that ![]() $\operatorname {Res}(\Delta _K(t), t^{n}-1)= \prod _{\{\xi \mid \xi ^{n}=1\} }\Delta _K(\xi )$ is not equal to 1 for
$\operatorname {Res}(\Delta _K(t), t^{n}-1)= \prod _{\{\xi \mid \xi ^{n}=1\} }\Delta _K(\xi )$ is not equal to 1 for ![]() $n$ even.
$n$ even.
Throughout the paper we will assume knots are oriented in order to make various constructions in the standard way. However, none of the conditions (i), (ii), or (iii) depends on a given orientation for the knot, and so the characterisation provided by Theorem 1.1 is independent of this choice.
The remainder of the introduction proceeds as follows. In § 1.1, we discuss the applications of Theorem 1.1 to the study of whether a knot is shake slice. In § 1.2 we give a quick proof of the main theorem for the case ![]() $n=0$, and then some further results that we have obtained when
$n=0$, and then some further results that we have obtained when ![]() $n=\pm 1$. In § 1.3 we outline the topological surgery theory strategy we use to prove our main result.
$n=\pm 1$. In § 1.3 we outline the topological surgery theory strategy we use to prove our main result.
1.1 Shake slice knots
The embedding question for a generator of the second homotopy group of a knot trace is of interest via the lens of knot theory.
Definition 1.2 A knot ![]() $K$ is
$K$ is ![]() $n$-shake slice if a generator of
$n$-shake slice if a generator of ![]() $\pi _2(X_n(K)) \cong \mathbb {Z}$ can be realised by a locally flat embedded 2-sphere
$\pi _2(X_n(K)) \cong \mathbb {Z}$ can be realised by a locally flat embedded 2-sphere ![]() $S$. We say a knot
$S$. We say a knot ![]() $K$ is
$K$ is ![]() $\mathbb {Z}/n$-shake slice if in addition
$\mathbb {Z}/n$-shake slice if in addition ![]() $\pi _1(X_n(K) {{\smallsetminus }}S) \cong \mathbb {Z}/n$.
$\pi _1(X_n(K) {{\smallsetminus }}S) \cong \mathbb {Z}/n$.
For every ![]() $n \in \mathbb {Z}$, the fundamental group of the complement of an embedded sphere generating
$n \in \mathbb {Z}$, the fundamental group of the complement of an embedded sphere generating ![]() $\pi _2(X_n(K))$ abelianises to
$\pi _2(X_n(K))$ abelianises to ![]() $\mathbb {Z}/n$, so our condition that
$\mathbb {Z}/n$, so our condition that ![]() $\pi _1(X_n(K)) \cong \mathbb {Z}/n$ is just a more specific way to express the abelian condition on the fundamental group.
$\pi _1(X_n(K)) \cong \mathbb {Z}/n$ is just a more specific way to express the abelian condition on the fundamental group.
Theorem 1.1 can be viewed as a characterisation of when a knot ![]() $K$ is
$K$ is ![]() $\mathbb {Z}/n$-shake slice. Although the term ‘
$\mathbb {Z}/n$-shake slice. Although the term ‘![]() $n$-shake slice’ was not coined until much later, classical obstructions to being
$n$-shake slice’ was not coined until much later, classical obstructions to being ![]() $n$-shake slice were already obtained in the 1960s. In the course of proving Theorem 1.1 we obtained several new proofs of these classical results. Robertello [Reference RobertelloRob65] showed that the Arf invariant obstructs
$n$-shake slice were already obtained in the 1960s. In the course of proving Theorem 1.1 we obtained several new proofs of these classical results. Robertello [Reference RobertelloRob65] showed that the Arf invariant obstructs ![]() $K$ from being
$K$ from being ![]() $n$-shake slice, for every
$n$-shake slice, for every ![]() $n$. We give a new proof of Robertello's result in Proposition 6.5 for all
$n$. We give a new proof of Robertello's result in Proposition 6.5 for all ![]() $n$, and we outline a second new proof in Remark 4.7 for even
$n$, and we outline a second new proof in Remark 4.7 for even ![]() $n$. Both proofs are different from Robertello's. Saeki [Reference SaekiSae92] has yet another proof in the smooth category that uses the Casson invariant.
$n$. Both proofs are different from Robertello's. Saeki [Reference SaekiSae92] has yet another proof in the smooth category that uses the Casson invariant.
Tristram [Reference TristramTri69] showed that the signatures ![]() $\sigma _K(\xi _p^{m})$, for
$\sigma _K(\xi _p^{m})$, for ![]() $p$ a prime power dividing
$p$ a prime power dividing ![]() $n$, obstruct
$n$, obstruct ![]() $K$ being
$K$ being ![]() $n$-shake slice. We provide a different proof in § 3 that also explains Tristram's theorem in the context of our results. Our proof is similar to that sketched by Saeki in [Reference SaekiSae92, Theorem 3.4].
$n$-shake slice. We provide a different proof in § 3 that also explains Tristram's theorem in the context of our results. Our proof is similar to that sketched by Saeki in [Reference SaekiSae92, Theorem 3.4].
For ![]() $n=0$, it remains unknown in both the smooth and topological categories whether every
$n=0$, it remains unknown in both the smooth and topological categories whether every ![]() $0$-shake slice knot is slice. An immediate consequence of our theorem is that a knot is
$0$-shake slice knot is slice. An immediate consequence of our theorem is that a knot is ![]() $\mathbb {Z}$-shake slice if and only if it is
$\mathbb {Z}$-shake slice if and only if it is ![]() $\mathbb {Z}$-slice: both correspond to Alexander polynomial one.
$\mathbb {Z}$-slice: both correspond to Alexander polynomial one.
Now we describe some further consequences of Theorem 1.1 that are proved as corollaries in § 2. First, we provide new examples of the difference between the smooth and topological categories. Recall that a knot is smoothly ![]() $n$-shake slice if a generator of
$n$-shake slice if a generator of ![]() $\pi _2(X_n(K)) \cong \mathbb {Z}$ can be realised by a smoothly embedded 2-sphere
$\pi _2(X_n(K)) \cong \mathbb {Z}$ can be realised by a smoothly embedded 2-sphere ![]() $S$.
$S$.
Corollary 2.3 For every ![]() $n>0$ there exist infinitely many knots that are
$n>0$ there exist infinitely many knots that are ![]() $n$-shake slice but neither smoothly
$n$-shake slice but neither smoothly ![]() $n$-shake slice nor
$n$-shake slice nor ![]() $($topologically
$($topologically![]() $)$ slice. These knots may be chosen to be distinct in concordance.
$)$ slice. These knots may be chosen to be distinct in concordance.
We then show that being ![]() $n$-shake slice for infinitely many
$n$-shake slice for infinitely many ![]() $n \in \mathbb {Z}$ does not imply slice.
$n \in \mathbb {Z}$ does not imply slice.
Corollary 2.4 There exist infinitely many non-slice knots, each of which is ![]() $n$-shake slice for infinitely many
$n$-shake slice for infinitely many ![]() $n \in \mathbb {Z}$. Moreover, these knots may be chosen to be distinct in concordance.
$n \in \mathbb {Z}$. Moreover, these knots may be chosen to be distinct in concordance.
A question of Hedden [Max16] asks whether the concordance class of a knot must be determined by the infinite tuple of homology cobordism classes ![]() $(S^{3}_{p/q}(K))_{p/q \in \mathbb {Q}}$. We provide evidence for a negative answer to this question as follows, in what we believe is the first example of non-concordant knots with the property that infinitely many of their integer surgeries are homology cobordant.
$(S^{3}_{p/q}(K))_{p/q \in \mathbb {Q}}$. We provide evidence for a negative answer to this question as follows, in what we believe is the first example of non-concordant knots with the property that infinitely many of their integer surgeries are homology cobordant.
Corollary 2.5 There exist infinitely many knots ![]() $\{K_i\}$, mutually distinct in concordance, and an infinite family of integers
$\{K_i\}$, mutually distinct in concordance, and an infinite family of integers ![]() $\{n_j\}$ such that
$\{n_j\}$ such that ![]() $S^{3}_{n_j}(K_i)$ is homology cobordant to
$S^{3}_{n_j}(K_i)$ is homology cobordant to ![]() $S^{3}_{n_j}(U)$ for all
$S^{3}_{n_j}(U)$ for all ![]() $i, j\in \mathbb {Z}$.
$i, j\in \mathbb {Z}$.
We remark that ![]() $0$ is not an element of our family of integers
$0$ is not an element of our family of integers ![]() $\{n_j\}$:
$\{n_j\}$: ![]() $S^{3}_0(K)$ is homology cobordant to
$S^{3}_0(K)$ is homology cobordant to ![]() $S^{3}_0(U)$ if and only if
$S^{3}_0(U)$ if and only if ![]() $K$ is slice in an integral homology 4-ball (which, incidentally, implies that
$K$ is slice in an integral homology 4-ball (which, incidentally, implies that ![]() $S^{3}_n(K)$ is homology cobordant to
$S^{3}_n(K)$ is homology cobordant to ![]() $S^{3}_n(U)$ for all
$S^{3}_n(U)$ for all ![]() $n \in \mathbb {Z}$). It is currently an open question in both categories whether there exists a non-slice knot that is slice in a homology ball.
$n \in \mathbb {Z}$). It is currently an open question in both categories whether there exists a non-slice knot that is slice in a homology ball.
We then show that, for most ![]() $m$ and
$m$ and ![]() $n$, the
$n$, the ![]() $m$-shake slice and
$m$-shake slice and ![]() $n$-shake slice conditions are independent.
$n$-shake slice conditions are independent.
Corollary 2.8 If ![]() $m$ does not divide
$m$ does not divide ![]() $n$ then there exist infinitely many knots which are
$n$ then there exist infinitely many knots which are ![]() $n$-shake slice but not
$n$-shake slice but not ![]() $m$-shake slice. These knots may be chosen to be distinct in concordance.
$m$-shake slice. These knots may be chosen to be distinct in concordance.
The difference between ![]() $n$-shake slice and
$n$-shake slice and ![]() $\mathbb {Z}/n$-shake slice can also be investigated using Theorem 1.1. For composite
$\mathbb {Z}/n$-shake slice can also be investigated using Theorem 1.1. For composite ![]() $n$ the theorem says there are extra signatures away from the prime power divisors of
$n$ the theorem says there are extra signatures away from the prime power divisors of ![]() $n$ whose vanishing is necessary for an
$n$ whose vanishing is necessary for an ![]() $n$-shake slice knot to be moreover
$n$-shake slice knot to be moreover ![]() $\mathbb {Z}/n$-shake slice; cf. [Reference SaekiSae92, Proposition 3.7]. Consider that every slice knot is
$\mathbb {Z}/n$-shake slice; cf. [Reference SaekiSae92, Proposition 3.7]. Consider that every slice knot is ![]() $n$-shake slice for all
$n$-shake slice for all ![]() $n$, but according to Cha and Livingston [Reference Cha and LivingstonCL04], for any choice of composite
$n$, but according to Cha and Livingston [Reference Cha and LivingstonCL04], for any choice of composite ![]() $n$ and root of unity
$n$ and root of unity ![]() $\xi _n$, there exist slice knots
$\xi _n$, there exist slice knots ![]() $K$ with
$K$ with ![]() $\sigma _K(\xi _n)\neq 0$. We will prove that examples of this sort are not peculiar to composite
$\sigma _K(\xi _n)\neq 0$. We will prove that examples of this sort are not peculiar to composite ![]() $n$.
$n$.
Corollary 2.10 For all ![]() $n \neq \pm 1$, there exists a slice, and therefore
$n \neq \pm 1$, there exists a slice, and therefore ![]() $n$-shake slice, knot that is not
$n$-shake slice, knot that is not ![]() $\mathbb {Z}/n$-shake slice.
$\mathbb {Z}/n$-shake slice.
1.2 The cases  $n=0$ and
$n=0$ and  $n=\pm 1$
$n=\pm 1$
The cases ![]() $n=0$ and
$n=0$ and ![]() $n=\pm 1$ for Theorem 1.1 are special, in that they can be proved relatively quickly by appealing directly to results of Freedman and Quinn. We provide a quick proof for
$n=\pm 1$ for Theorem 1.1 are special, in that they can be proved relatively quickly by appealing directly to results of Freedman and Quinn. We provide a quick proof for ![]() $n=0$ now. Recall that when
$n=0$ now. Recall that when ![]() $n=0$ the three conditions in Theorem 1.1 reduce to
$n=0$ the three conditions in Theorem 1.1 reduce to ![]() $\Delta _K(t)=1$.
$\Delta _K(t)=1$.
Example 1.3 (The case ![]() $n=0$)
$n=0$)
First assume a generator of ![]() $\pi _2(X_0(K))$ is represented by an embedded sphere whose complement has fundamental group
$\pi _2(X_0(K))$ is represented by an embedded sphere whose complement has fundamental group ![]() $\mathbb {Z}$. Since
$\mathbb {Z}$. Since ![]() $n=0$, the normal bundle of this sphere is trivial. Perform surgery on
$n=0$, the normal bundle of this sphere is trivial. Perform surgery on ![]() $X_0(K)$ along this 2-sphere to obtain a pair
$X_0(K)$ along this 2-sphere to obtain a pair ![]() $(V, S_0^{3}(K))$ where
$(V, S_0^{3}(K))$ where ![]() $\pi _2(V)=0$, and
$\pi _2(V)=0$, and ![]() $\pi _1(V)\cong \mathbb {Z}$, generated by a meridian of
$\pi _1(V)\cong \mathbb {Z}$, generated by a meridian of ![]() $K$. Now attach a 2-handle to a meridian in the boundary. The cocore of the 2-handle is a slice disc
$K$. Now attach a 2-handle to a meridian in the boundary. The cocore of the 2-handle is a slice disc ![]() $D'$ for
$D'$ for ![]() $K$ in a homotopy 4-ball
$K$ in a homotopy 4-ball ![]() $B'$ such that
$B'$ such that ![]() $\pi _1(B' \smallsetminus D') \cong \mathbb {Z}$. Hence
$\pi _1(B' \smallsetminus D') \cong \mathbb {Z}$. Hence ![]() $\Delta _K(t)=1$.
$\Delta _K(t)=1$.
Now assume ![]() $\Delta _K(t)=1$. By [Reference FreedmanFre84, Theorem 7] and [Reference Freedman and QuinnFQ90, 11.7B] (see also [Reference Garoufalidis and TeichnerGT04, Appendix]),
$\Delta _K(t)=1$. By [Reference FreedmanFre84, Theorem 7] and [Reference Freedman and QuinnFQ90, 11.7B] (see also [Reference Garoufalidis and TeichnerGT04, Appendix]), ![]() $K$ has a slice disc
$K$ has a slice disc ![]() $D$ in
$D$ in ![]() $D^{4}$ with
$D^{4}$ with ![]() $\pi _1(D^{4} \smallsetminus D) \cong \mathbb {Z}$. Cap this disc off with the core of the 2-handle to obtain the desired sphere in
$\pi _1(D^{4} \smallsetminus D) \cong \mathbb {Z}$. Cap this disc off with the core of the 2-handle to obtain the desired sphere in ![]() $X_0(K)$. This completes the proof of Theorem 1.1 for
$X_0(K)$. This completes the proof of Theorem 1.1 for ![]() $n=0$.
$n=0$.
To see a similarly quick proof for ![]() $n=\pm 1$, the reader is invited to skip ahead to Example 8.1. In this case, we rely on the result of Freedman that as
$n=\pm 1$, the reader is invited to skip ahead to Example 8.1. In this case, we rely on the result of Freedman that as ![]() $S^{3}_{\pm 1}(K)$ is an integer homology sphere, it must bound a contractible 4-manifold. When
$S^{3}_{\pm 1}(K)$ is an integer homology sphere, it must bound a contractible 4-manifold. When ![]() $n=\pm 1$ we have obtained a wholly different proof of Theorem 1.1 using Seifert surface constructions. These methods, detailed in § 8, lead to the two results described next.
$n=\pm 1$ we have obtained a wholly different proof of Theorem 1.1 using Seifert surface constructions. These methods, detailed in § 8, lead to the two results described next.
For each ![]() $n$, one can measure how far a knot
$n$, one can measure how far a knot ![]() $K$ is from being
$K$ is from being ![]() $n$-shake slice by considering the minimal genus of a locally flat embedded surface generating
$n$-shake slice by considering the minimal genus of a locally flat embedded surface generating ![]() $H_2(X_n(K))$. This minimum is called the (topological)
$H_2(X_n(K))$. This minimum is called the (topological) ![]() $n$-shake genus
$n$-shake genus ![]() $g_{\operatorname {sh}}^{n}(K)$. For
$g_{\operatorname {sh}}^{n}(K)$. For ![]() $n=1$ we have a precise understanding of this invariant.
$n=1$ we have a precise understanding of this invariant.
Proposition 8.7 For every knot ![]() $K$ there exists a locally flat embedded torus in
$K$ there exists a locally flat embedded torus in ![]() $X_1(K)$ that generates
$X_1(K)$ that generates ![]() $H_2(X_1(K))$ and has simply connected complement. In particular,
$H_2(X_1(K))$ and has simply connected complement. In particular,
Now for a slice knot ![]() $K$, and for each
$K$, and for each ![]() $n$, a slice disc capped off by the core of the 2-handle in
$n$, a slice disc capped off by the core of the 2-handle in ![]() $X_n(K)$ geometrically intersects the cocore once. This suggests a way to measure of how far an
$X_n(K)$ geometrically intersects the cocore once. This suggests a way to measure of how far an ![]() $n$-shake slice knot
$n$-shake slice knot ![]() $K$ is from being slice, by taking the minimum over all embedded spheres
$K$ is from being slice, by taking the minimum over all embedded spheres ![]() $S$ generating
$S$ generating ![]() $\pi _2(X_n(K))$ of the geometric intersection number of
$\pi _2(X_n(K))$ of the geometric intersection number of ![]() $S$ with the cocore of the 2-handle of
$S$ with the cocore of the 2-handle of ![]() $X_n(K)$. We call this minimum the
$X_n(K)$. We call this minimum the ![]() $n$-shaking number of
$n$-shaking number of ![]() $K$.
$K$.
Since the algebraic intersection of ![]() $S$ with the cocore of the 2-handle of
$S$ with the cocore of the 2-handle of ![]() $X_n(K)$ is algebraically one, the shaking number measures the difference between geometric and algebraic intersection numbers. For closed surfaces, this difference was investigated in [Reference Morgan and SzabóMS99, Reference StrleStr03, Reference HorvatHor15, Reference SunukjianSun10].
$X_n(K)$ is algebraically one, the shaking number measures the difference between geometric and algebraic intersection numbers. For closed surfaces, this difference was investigated in [Reference Morgan and SzabóMS99, Reference StrleStr03, Reference HorvatHor15, Reference SunukjianSun10].
For a knot ![]() $K$,
$K$, ![]() ${g^{\operatorname {top}}_4}(K)$ denotes the (topological) 4-genus or slice genus, the minimal genus among compact, oriented, locally flat surfaces in
${g^{\operatorname {top}}_4}(K)$ denotes the (topological) 4-genus or slice genus, the minimal genus among compact, oriented, locally flat surfaces in ![]() $D^{4}$ with boundary
$D^{4}$ with boundary ![]() $K$. The (topological)
$K$. The (topological) ![]() $\mathbb {Z}$-slice genus
$\mathbb {Z}$-slice genus ![]() ${g_4^{\mathbb {Z}}}(K)$ is the minimal genus among such surfaces whose complement has infinite cyclic fundamental group. Computable upper bounds for
${g_4^{\mathbb {Z}}}(K)$ is the minimal genus among such surfaces whose complement has infinite cyclic fundamental group. Computable upper bounds for ![]() ${g_4^{\mathbb {Z}}}(K)$ are discussed in [Reference Feller and LewarkFL18], and include
${g_4^{\mathbb {Z}}}(K)$ are discussed in [Reference Feller and LewarkFL18], and include ![]() $2{g_4^{\mathbb {Z}}}(K) \leq \deg (\Delta _K)$ [Reference FellerFel16]. For
$2{g_4^{\mathbb {Z}}}(K) \leq \deg (\Delta _K)$ [Reference FellerFel16]. For ![]() $n=1$, as well as proving again that a knot with vanishing
$n=1$, as well as proving again that a knot with vanishing ![]() $\operatorname {Arf}$ invariant is
$\operatorname {Arf}$ invariant is ![]() $1$-shake slice, the Seifert surface method provides explicit upper bounds on the
$1$-shake slice, the Seifert surface method provides explicit upper bounds on the ![]() $1$-shaking number.
$1$-shaking number.
Proposition 8.8 For a knot ![]() $K$ with
$K$ with ![]() $\operatorname {Arf}(K)=0$ we have
$\operatorname {Arf}(K)=0$ we have
In particular, for each integer ![]() $k \geq 0$ there exists a
$k \geq 0$ there exists a ![]() $1$-shake slice knot
$1$-shake slice knot ![]() $K_k$ such that the
$K_k$ such that the ![]() $1$-shaking number of
$1$-shaking number of ![]() $K_k$ is exactly
$K_k$ is exactly ![]() $2k+1$.
$2k+1$.
Note that for every ![]() $n$, the
$n$, the ![]() $n$-shaking number is always odd since the algebraic intersection of the generator of
$n$-shaking number is always odd since the algebraic intersection of the generator of ![]() $\pi _2(X_n(K))$ with the cocore of the 2-handle is
$\pi _2(X_n(K))$ with the cocore of the 2-handle is ![]() $1$. Thus this is a complete realisation result for
$1$. Thus this is a complete realisation result for ![]() $1$-shaking numbers.
$1$-shaking numbers.
1.3 Proof outline
Having already proved Theorem 1.1 for the case of ![]() $n=0$ above, we now restrict to
$n=0$ above, we now restrict to ![]() $n\neq 0$. The components of the ‘only if’ direction are proven respectively in Proposition 3.3, Proposition 6.5, and Proposition 3.5. As mentioned previously, with different approaches Proposition 6.5 is due to Robertello [Reference RobertelloRob65] and Proposition 3.5 is due to Tristram [Reference TristramTri69] (see also [Reference SaekiSae92]).
$n\neq 0$. The components of the ‘only if’ direction are proven respectively in Proposition 3.3, Proposition 6.5, and Proposition 3.5. As mentioned previously, with different approaches Proposition 6.5 is due to Robertello [Reference RobertelloRob65] and Proposition 3.5 is due to Tristram [Reference TristramTri69] (see also [Reference SaekiSae92]).
Now we will outline the proof of the ‘if’ direction. Given a group ![]() $\pi$ and closed
$\pi$ and closed ![]() $3$-manifolds
$3$-manifolds ![]() $M_1$ and
$M_1$ and ![]() $M_2$, together with homomorphisms
$M_2$, together with homomorphisms ![]() $\varphi _i\colon \pi _1(M_i)\to \pi$, we say a cobordism
$\varphi _i\colon \pi _1(M_i)\to \pi$, we say a cobordism ![]() $W$ from
$W$ from ![]() $M_1$ to
$M_1$ to ![]() $M_2$ is over
$M_2$ is over ![]() $\pi$ if
$\pi$ if ![]() $W$ is equipped with a map
$W$ is equipped with a map ![]() $\pi _1(W)\to \pi$ restricting to the given homomorphisms on the boundary.
$\pi _1(W)\to \pi$ restricting to the given homomorphisms on the boundary.
The key idea of our proof is that for a fixed knot ![]() $K$, a generator of
$K$, a generator of ![]() $\pi _2(X_n(K))$ can be represented by a locally flat embedded 2-sphere
$\pi _2(X_n(K))$ can be represented by a locally flat embedded 2-sphere ![]() $S$ with
$S$ with ![]() $\pi _1(X_n(K) {{\smallsetminus }}S) \cong \mathbb {Z}/n$ if and only if there exists a homology cobordism
$\pi _1(X_n(K) {{\smallsetminus }}S) \cong \mathbb {Z}/n$ if and only if there exists a homology cobordism ![]() $V$ from
$V$ from ![]() $S^{3}_n(K)$ to the lens space
$S^{3}_n(K)$ to the lens space ![]() $L(n,1)$ over
$L(n,1)$ over ![]() $\mathbb {Z}/n$, extending standard maps
$\mathbb {Z}/n$, extending standard maps ![]() $\pi _1(S^{3}_n(K))\to \mathbb {Z}/n$ and
$\pi _1(S^{3}_n(K))\to \mathbb {Z}/n$ and ![]() $\pi _1(L(n,1))\to \mathbb {Z}/n$, such that
$\pi _1(L(n,1))\to \mathbb {Z}/n$, such that ![]() $\pi _1(V) \cong \mathbb {Z}/n$ and
$\pi _1(V) \cong \mathbb {Z}/n$ and ![]() $V \cup _{L(n,1)} D_n$ is homeomorphic to
$V \cup _{L(n,1)} D_n$ is homeomorphic to ![]() $X_n(K)$, where
$X_n(K)$, where ![]() $D_n$ denotes the
$D_n$ denotes the ![]() $D^{2}$-bundle over
$D^{2}$-bundle over ![]() $S^{2}$ with euler number
$S^{2}$ with euler number ![]() $n$.
$n$.
The proof of the ‘if’ direction involves constructing such a cobordism ![]() $V$ when the list of invariants in Theorem 1.1 vanish. Here is an outline.
$V$ when the list of invariants in Theorem 1.1 vanish. Here is an outline.
(1) Show there exists a cobordism
 $W$ between
$W$ between  $S^{3}_n(K)$ and the lens space
$S^{3}_n(K)$ and the lens space  $L(n,1)$ and a map
$L(n,1)$ and a map  $W \to L(n,1)\times [0,1]$ that restricts to a degree-one normal map (Definition 4.2)
$W \to L(n,1)\times [0,1]$ that restricts to a degree-one normal map (Definition 4.2)  $f\colon S^{3}_n(K) \to L(n,1) \times \{0\}$ and the identity map
$f\colon S^{3}_n(K) \to L(n,1) \times \{0\}$ and the identity map  $L(n,1) \to L(n,1) \times \{1\}$ (see § 4). This uses the assumption that
$L(n,1) \to L(n,1) \times \{1\}$ (see § 4). This uses the assumption that  $\operatorname {Arf}(K)=0$ when
$\operatorname {Arf}(K)=0$ when  $n$ is even and no assumptions when
$n$ is even and no assumptions when  $n$ is odd.
$n$ is odd.(2) Use the computation of the simple surgery obstruction groups
 $L_4^{s}(\mathbb {Z}[\mathbb {Z}/n])$ in terms of multisignatures to show that we can replace
$L_4^{s}(\mathbb {Z}[\mathbb {Z}/n])$ in terms of multisignatures to show that we can replace  $W$ with a homology cobordism
$W$ with a homology cobordism  $V$ between
$V$ between  $S^{3}_n(K)$ and
$S^{3}_n(K)$ and  $L(n,1)$ over
$L(n,1)$ over  $\mathbb {Z}/n$, with
$\mathbb {Z}/n$, with  $V$ homotopy equivalent to
$V$ homotopy equivalent to  $L(n,1) \times I$ (see § 5). This uses the assumptions that
$L(n,1) \times I$ (see § 5). This uses the assumptions that  $H_1(S_n^{3}(K);\mathbb {Z}[\mathbb {Z}/n])=0$ and
$H_1(S_n^{3}(K);\mathbb {Z}[\mathbb {Z}/n])=0$ and  $\sigma _K(\xi _n^{m}) =0$ for all
$\sigma _K(\xi _n^{m}) =0$ for all  $m$.
$m$.(3) Let
 $X:= V \cup _{L(n,1)} D_n$. Note that a generator for
$X:= V \cup _{L(n,1)} D_n$. Note that a generator for  $\pi _2(X)$ is represented by an embedded sphere in
$\pi _2(X)$ is represented by an embedded sphere in  $D_n$. Use Boyer's classification (Theorem 7.1) to conclude that
$D_n$. Use Boyer's classification (Theorem 7.1) to conclude that  $X$ is homeomorphic to
$X$ is homeomorphic to  $X_n(K)$ (see § 6). This uses the assumption that
$X_n(K)$ (see § 6). This uses the assumption that  $\operatorname {Arf}(K)=0$ when
$\operatorname {Arf}(K)=0$ when  $n$ is odd and no additional assumptions when
$n$ is odd and no additional assumptions when  $n$ is even. More precisely, according to the classification,
$n$ is even. More precisely, according to the classification,  $X$ is homeomorphic to
$X$ is homeomorphic to  $X_n(K)$ automatically when
$X_n(K)$ automatically when  $n$ is even, and if and only if
$n$ is even, and if and only if  $\operatorname {ks}(X)=\operatorname {ks}(X_n(K))=0$ when
$\operatorname {ks}(X)=\operatorname {ks}(X_n(K))=0$ when  $n$ is odd; the latter equality follows since
$n$ is odd; the latter equality follows since  $X_n(K)$ is smooth. We show in Proposition 6.8 that
$X_n(K)$ is smooth. We show in Proposition 6.8 that  $\operatorname {Arf}(K)=\operatorname {ks}(X)$.
$\operatorname {Arf}(K)=\operatorname {ks}(X)$.
An interesting aspect of the proof (of both the ‘if’ and ‘only if’ directions) of Theorem 1.1 is that the Arf invariant appears in different places for ![]() $n$ odd and
$n$ odd and ![]() $n$ even. However, in each case its vanishing is required.
$n$ even. However, in each case its vanishing is required.
Recent work of Kim and Ruberman [Reference Kim and RubermanKR20] uses similar techniques to prove the existence of topological spines in certain 4-manifolds. Their argument is in some ways structurally quite similar to ours, since both works follow a surgery theoretic strategy. There is no overlap between our results: every knot trace ![]() $X_n(K)$ admits a PL-spine consisting of the cone on
$X_n(K)$ admits a PL-spine consisting of the cone on ![]() $K$ union the core of the attached 2-handle, as is crucially used in [Reference Kim and RubermanKR20]. Moreover, there is a key difference: Kim and Ruberman have flexibility in their choice of a second 3-manifold, whereas we have a fixed choice of
$K$ union the core of the attached 2-handle, as is crucially used in [Reference Kim and RubermanKR20]. Moreover, there is a key difference: Kim and Ruberman have flexibility in their choice of a second 3-manifold, whereas we have a fixed choice of ![]() $S^{3}_n(K)$ and
$S^{3}_n(K)$ and ![]() $L(n,1)$.
$L(n,1)$.
2. Corollaries to Theorem 1.1
Before embarking on the main work of proving Theorem 1.1, we use it to prove several knot theoretic corollaries. For a knot ![]() $K$ in
$K$ in ![]() $S^{3}$, let
$S^{3}$, let ![]() $C_{n,1}(K)$ denote the
$C_{n,1}(K)$ denote the ![]() $(n,1)$-cable of
$(n,1)$-cable of ![]() $K$.
$K$.
Corollary 2.1 Let ![]() $K$ be any knot and let
$K$ be any knot and let ![]() $n$ be an integer. Suppose that
$n$ be an integer. Suppose that ![]() $n$ is even or
$n$ is even or ![]() ${\operatorname {Arf}(K)=0}$. Then
${\operatorname {Arf}(K)=0}$. Then ![]() $C_{n,1}(K)$ is
$C_{n,1}(K)$ is ![]() $\mathbb {Z}/n$-shake slice.
$\mathbb {Z}/n$-shake slice.
Proof. We use the formulae for the Alexander polynomial and signatures of a satellite knot, due respectively to Seifert [Reference SeifertSei50] and Litherland [Reference LitherlandLit79], to verify the conditions of Theorem 1.1 for ![]() $C_{n,1}(K)$.
$C_{n,1}(K)$.
Since ![]() $C_{n,1}(U)=U$ we have
$C_{n,1}(U)=U$ we have ![]() $\Delta _{C_{n,1}(K)}(t)= \Delta _K(t^{n})$ and
$\Delta _{C_{n,1}(K)}(t)= \Delta _K(t^{n})$ and ![]() $\sigma _{C_{n,1}(K)}(\omega )= \sigma _K(\omega ^{n})$ for all
$\sigma _{C_{n,1}(K)}(\omega )= \sigma _K(\omega ^{n})$ for all ![]() $\omega \in S^{1}$. Letting
$\omega \in S^{1}$. Letting ![]() $\omega _n$ denote a primitive
$\omega _n$ denote a primitive ![]() $n$th root of unity, we therefore have for
$n$th root of unity, we therefore have for ![]() $1 \leq k \leq n$ that
$1 \leq k \leq n$ that
We have that
 \[ \prod_{k=1}^{n} \Delta_{C_{n,1}(K)}(\omega_n)= \prod_{k=1}^{n} \Delta_{K}(\omega_n^{n}) =1. \]
\[ \prod_{k=1}^{n} \Delta_{C_{n,1}(K)}(\omega_n)= \prod_{k=1}^{n} \Delta_{K}(\omega_n^{n}) =1. \]
Levine [Reference LevineLev66, Proposition 3.4] showed that ![]() $\operatorname {Arf}(J)=0$ if and only if
$\operatorname {Arf}(J)=0$ if and only if ![]() $\Delta _J(-1)\equiv \pm 1\ {\rm mod}\ 8$, and so since
$\Delta _J(-1)\equiv \pm 1\ {\rm mod}\ 8$, and so since
 \[ \Delta_{C_{n,1}(K)}({-}1)= \Delta_{K}(({-}1)^{n})= \begin{cases} \Delta_K({-}1) & n \text{ odd}, \\ 1 & n \text{ even} \end{cases} \]
\[ \Delta_{C_{n,1}(K)}({-}1)= \Delta_{K}(({-}1)^{n})= \begin{cases} \Delta_K({-}1) & n \text{ odd}, \\ 1 & n \text{ even} \end{cases} \]
we obtain as desired that ![]() $\operatorname {Arf}(C_{n,1}(K))=0$.
$\operatorname {Arf}(C_{n,1}(K))=0$.
Remark 2.2 Gordon [Reference GordonGor83] observed that for any knot ![]() $K$
$K$
This gives a slightly more direct argument that ![]() $C_{n,1}(K)$ is
$C_{n,1}(K)$ is ![]() $\mathbb {Z}/n$-shake slice whenever
$\mathbb {Z}/n$-shake slice whenever ![]() $n$ is even or
$n$ is even or ![]() $\operatorname {Arf}(K)=0$, as follows. Let
$\operatorname {Arf}(K)=0$, as follows. Let ![]() $C$ be the contractible 4-manifold with boundary
$C$ be the contractible 4-manifold with boundary ![]() $S^{3}_{1/n}(K)$ guaranteed by [Reference FreedmanFre82, Theorem 1.4
$S^{3}_{1/n}(K)$ guaranteed by [Reference FreedmanFre82, Theorem 1.4![]() $'$], and define
$'$], and define ![]() $V$ to be the boundary connected sum of
$V$ to be the boundary connected sum of ![]() $L(n,1) \times I$ and
$L(n,1) \times I$ and ![]() $C$. The manifold
$C$. The manifold ![]() $V$ is now a homology cobordism from
$V$ is now a homology cobordism from ![]() $S^{3}_n(C_{n,1}(K))$ to
$S^{3}_n(C_{n,1}(K))$ to ![]() $L(n,1)$ that is homotopy equivalent to
$L(n,1)$ that is homotopy equivalent to ![]() $L(n,1) \times I$. This allows one to skip the work of §§ 4 and 5 constructing a homology cobordism and go straight to proving that
$L(n,1) \times I$. This allows one to skip the work of §§ 4 and 5 constructing a homology cobordism and go straight to proving that ![]() $V \cup D_n$ is homeomorphic to
$V \cup D_n$ is homeomorphic to ![]() $X_n(C_{n,1}(K))$ using the results we prove in § 6 and Boyer's classification (Theorem 7.1), which when
$X_n(C_{n,1}(K))$ using the results we prove in § 6 and Boyer's classification (Theorem 7.1), which when ![]() $n$ is odd requires
$n$ is odd requires ![]() $\operatorname {Arf}(C_{n,1}(K))= \operatorname {Arf}(K)=0$.
$\operatorname {Arf}(C_{n,1}(K))= \operatorname {Arf}(K)=0$.
We can use Corollary 2.1 to obtain many new examples of ![]() $n$-shake slice knots.
$n$-shake slice knots.
Corollary 2.3 For every ![]() $n \neq 0$ there exist infinitely many topological concordance classes of knots that are
$n \neq 0$ there exist infinitely many topological concordance classes of knots that are ![]() $n$-shake slice but not smoothly
$n$-shake slice but not smoothly ![]() $n$-shake slice.
$n$-shake slice.
Proof. In both the smooth and topological categories a knot ![]() $K$ is
$K$ is ![]() $n$-shake slice if and only if
$n$-shake slice if and only if ![]() $-K$ is
$-K$ is ![]() $(-n)$-shake slice. So it suffices to show the
$(-n)$-shake slice. So it suffices to show the ![]() $n>0$ case as follows.
$n>0$ case as follows.
We can use the description of ![]() $S^{3}_n(C_{n,1}(K))$ from Remark 2.2 to show that
$S^{3}_n(C_{n,1}(K))$ from Remark 2.2 to show that ![]() $C_{n,1}(K)$ is often not smoothly
$C_{n,1}(K)$ is often not smoothly ![]() $n$-shake slice. Given an integer homology sphere
$n$-shake slice. Given an integer homology sphere ![]() $Y$, Ozsváth and Szabó associate a so-called
$Y$, Ozsváth and Szabó associate a so-called ![]() $d$-invariant
$d$-invariant ![]() $d(Y) \in \mathbb {Q}$, with the property that
$d(Y) \in \mathbb {Q}$, with the property that ![]() $d(Y)=0$ if
$d(Y)=0$ if ![]() $Y$ bounds a rational homology ball [Reference Ozsváth and SzabóOS03a]. We show that if
$Y$ bounds a rational homology ball [Reference Ozsváth and SzabóOS03a]. We show that if ![]() $C_{n,1}(K)$ is smoothly
$C_{n,1}(K)$ is smoothly ![]() $n$-shake slice for some
$n$-shake slice for some ![]() $n>0$, then
$n>0$, then ![]() ${d(S^{3}_{1}(K))=0}$ as follows.
${d(S^{3}_{1}(K))=0}$ as follows.
Suppose that ![]() $C_{n,1}(K)$ is smoothly
$C_{n,1}(K)$ is smoothly ![]() $n$-shake slice via a sphere
$n$-shake slice via a sphere ![]() $S$ in
$S$ in ![]() $X_n(J)$. The exterior of
$X_n(J)$. The exterior of ![]() $S$ can be quickly confirmed to be a smooth homology cobordism between
$S$ can be quickly confirmed to be a smooth homology cobordism between ![]() $S^{3}_n(J)$ and
$S^{3}_n(J)$ and ![]() $L(n,1)$; see Lemma 3.1. Therefore
$L(n,1)$; see Lemma 3.1. Therefore ![]() $S^{3}_n(C_{n,1}(K))= L(n,1)\, \#\, S^{3}_{1/n}(K)$ and
$S^{3}_n(C_{n,1}(K))= L(n,1)\, \#\, S^{3}_{1/n}(K)$ and ![]() $S^{3}_n(U)= L(n,1)$ are homology cobordant via some smooth
$S^{3}_n(U)= L(n,1)$ are homology cobordant via some smooth ![]() $W$. By summing
$W$. By summing ![]() $W$ with
$W$ with ![]() $-L(n,1) \times I$ along
$-L(n,1) \times I$ along ![]() $D^{4} \times I \subset W$, we further obtain that
$D^{4} \times I \subset W$, we further obtain that ![]() $S^{3}_{1/n}(K)$ is smoothly rationally homology cobordant to
$S^{3}_{1/n}(K)$ is smoothly rationally homology cobordant to ![]() $S^{3}$. Therefore,
$S^{3}$. Therefore, ![]() $d(S^{3}_{1/n}(K))= d(S^{3})=0$. Furthermore, since
$d(S^{3}_{1/n}(K))= d(S^{3})=0$. Furthermore, since ![]() $n >0$ we have
$n >0$ we have ![]() $d(S^{3}_{1/n}(K))= d(S^{3}_1(K))$ by [Reference Ni and WuNW15, Proposition 1.6].
$d(S^{3}_{1/n}(K))= d(S^{3}_1(K))$ by [Reference Ni and WuNW15, Proposition 1.6].
Now for each ![]() $j \in \mathbb {N}$ let
$j \in \mathbb {N}$ let ![]() $K_j:= T_{2,8j+1}$. Note that since
$K_j:= T_{2,8j+1}$. Note that since ![]() $K_j$ is alternating and the ordinary signature
$K_j$ is alternating and the ordinary signature ![]() $\sigma _{K_j}(-1) <0$, [Reference Ozsváth and SzabóOS03b, Corollary 1.5] implies that
$\sigma _{K_j}(-1) <0$, [Reference Ozsváth and SzabóOS03b, Corollary 1.5] implies that ![]() $d(S^{3}_1(K)) \neq 0$. So
$d(S^{3}_1(K)) \neq 0$. So ![]() $C_{n,1}(K_j)$ is not smoothly
$C_{n,1}(K_j)$ is not smoothly ![]() $n$-shake slice, despite being
$n$-shake slice, despite being ![]() $\mathbb {Z}/n$-shake slice by Corollary 2.1. One can use Litherland's satellite formula [Reference LitherlandLit79] to compute that the first jump of the Tristram–Levine signature function of
$\mathbb {Z}/n$-shake slice by Corollary 2.1. One can use Litherland's satellite formula [Reference LitherlandLit79] to compute that the first jump of the Tristram–Levine signature function of ![]() $C_{n,1}(K_j)$ occurs at
$C_{n,1}(K_j)$ occurs at ![]() $e^{2 \pi i \theta _j}$, where
$e^{2 \pi i \theta _j}$, where ![]() $\theta _j= {1}/{2n(8j+1)}$. Therefore the knots
$\theta _j= {1}/{2n(8j+1)}$. Therefore the knots ![]() $C_{n,1}(K_j)$ are distinct in concordance.
$C_{n,1}(K_j)$ are distinct in concordance.
In another direction, we are able to show that there exist non-slice knots which are nevertheless ![]() $n$-shake slice for infinitely many
$n$-shake slice for infinitely many ![]() $n \in \mathbb {Z}$. It is presently unknown in either category whether
$n \in \mathbb {Z}$. It is presently unknown in either category whether ![]() $0$-shake slice implies slice, and so the question of whether being
$0$-shake slice implies slice, and so the question of whether being ![]() $n$-shake slice for all
$n$-shake slice for all ![]() $n \in \mathbb {Z}$ implies slice appears both interesting and difficult.
$n \in \mathbb {Z}$ implies slice appears both interesting and difficult.
Corollary 2.4 There exist knots that are ![]() $\mathbb {Z}/n$-shake slice for every prime power
$\mathbb {Z}/n$-shake slice for every prime power ![]() $n \in \mathbb {Z}$, but are not slice. Moreover, these knots may be chosen to represent infinitely many concordance classes.
$n \in \mathbb {Z}$, but are not slice. Moreover, these knots may be chosen to represent infinitely many concordance classes.
Proof. Let ![]() $J$ be a knot with Alexander polynomial equal to the
$J$ be a knot with Alexander polynomial equal to the ![]() $m\textrm {th}$ cyclotomic polynomial, where
$m\textrm {th}$ cyclotomic polynomial, where ![]() $m$ is divisible by at least 3 distinct primes. Since
$m$ is divisible by at least 3 distinct primes. Since ![]() $J \#-J$ does not have trivial Alexander polynomial, there exist infinitely many non-concordant knots sharing its Seifert form [Reference KimKim05]. We show that any such knot
$J \#-J$ does not have trivial Alexander polynomial, there exist infinitely many non-concordant knots sharing its Seifert form [Reference KimKim05]. We show that any such knot ![]() $K$ is
$K$ is ![]() $\mathbb {Z}/n$-shake slice for all prime powers
$\mathbb {Z}/n$-shake slice for all prime powers ![]() $n$.
$n$.
By [Reference LivingstonLiv02], we have ![]() $|H_1(\Sigma _{|n|}(J))|=1$, so condition (i) of Theorem 1.1 follows immediately:
$|H_1(\Sigma _{|n|}(J))|=1$, so condition (i) of Theorem 1.1 follows immediately:
For conditions (ii) and (iii), observe that since ![]() $K$ shares a Seifert form with the knot
$K$ shares a Seifert form with the knot ![]() $J \#-J$, we have that
$J \#-J$, we have that ![]() $\operatorname {Arf}(K)=0$ and for every
$\operatorname {Arf}(K)=0$ and for every ![]() $\omega \in S^{1}$ we have
$\omega \in S^{1}$ we have
We remark that it is open whether there is a smoothly non-slice knot that is smoothly ![]() $n$-shake slice for infinitely many
$n$-shake slice for infinitely many ![]() $n$. The smooth analogue of the next result is also open.
$n$. The smooth analogue of the next result is also open.
Corollary 2.5 There exist infinitely many knots ![]() $\{K_i\}$, mutually distinct in concordance, and an infinite family of integers
$\{K_i\}$, mutually distinct in concordance, and an infinite family of integers ![]() $\{n_j\}$ such that
$\{n_j\}$ such that ![]() $S^{3}_{n_j}(K_i)$ is homology cobordant to
$S^{3}_{n_j}(K_i)$ is homology cobordant to ![]() $S^{3}_{n_j}(U)$ for all
$S^{3}_{n_j}(U)$ for all ![]() $i, j\in \mathbb {N}$.
$i, j\in \mathbb {N}$.
We are also able to show that homology cobordism of the ![]() $n$-surgeries is often not enough to determine that a knot is
$n$-surgeries is often not enough to determine that a knot is ![]() $n$-shake slice, as follows.
$n$-shake slice, as follows.
Corollary 2.6 For each odd ![]() $n \in \mathbb {N}$, there exists
$n \in \mathbb {N}$, there exists ![]() $K$ such that
$K$ such that ![]() $S^{3}_n(K)$ and
$S^{3}_n(K)$ and ![]() $S^{3}_n(U)$ are topologically homology cobordant but
$S^{3}_n(U)$ are topologically homology cobordant but ![]() $K$ is not
$K$ is not ![]() $n$-shake slice. In fact, for each odd
$n$-shake slice. In fact, for each odd ![]() $n$ there exist knots representing infinitely many concordance classes that satisfy this.
$n$ there exist knots representing infinitely many concordance classes that satisfy this.
Proof. By the proof of Theorem 1.1, if ![]() $n$ is odd and
$n$ is odd and ![]() $K$ is a knot with
$K$ is a knot with ![]() $\prod _{\{\xi \mid \xi ^{n}=1\} }\Delta _K(\xi ) =1$ and
$\prod _{\{\xi \mid \xi ^{n}=1\} }\Delta _K(\xi ) =1$ and ![]() $\sigma _K(\xi )=0$ for all
$\sigma _K(\xi )=0$ for all ![]() $n$th roots of unity
$n$th roots of unity ![]() $\xi$, then
$\xi$, then ![]() $S^{3}_n(K)$ and
$S^{3}_n(K)$ and ![]() $S^{3}_n(U)= L(n,1)$ are homology cobordant. As discussed in the proof of Corollary 2.3, for every knot
$S^{3}_n(U)= L(n,1)$ are homology cobordant. As discussed in the proof of Corollary 2.3, for every knot ![]() $J$ the knot
$J$ the knot ![]() $K= C_{n,1}(J)$ satisfies these conditions. However, if
$K= C_{n,1}(J)$ satisfies these conditions. However, if ![]() $\operatorname {Arf}(J) \neq 0$, then since
$\operatorname {Arf}(J) \neq 0$, then since ![]() $\operatorname {Arf}(K)= \operatorname {Arf}(J)$ we obtain that
$\operatorname {Arf}(K)= \operatorname {Arf}(J)$ we obtain that ![]() $C_{n,1}(J)$ is not
$C_{n,1}(J)$ is not ![]() $n$-shake slice (or even, for the cognoscenti,
$n$-shake slice (or even, for the cognoscenti, ![]() $n$-shake concordant to the unknot). Therefore the set
$n$-shake concordant to the unknot). Therefore the set ![]() $\{C_{n,1}(T_{2, 8j+3}\}_{j\geq 1}$ is an infinite collection of such knots, all distinguished in concordance by the first jump of their Tristram–Levine signature functions, which occur at
$\{C_{n,1}(T_{2, 8j+3}\}_{j\geq 1}$ is an infinite collection of such knots, all distinguished in concordance by the first jump of their Tristram–Levine signature functions, which occur at ![]() $e^{2 \pi i y_j}$, where
$e^{2 \pi i y_j}$, where ![]() $y_j= {1}/{2n(8j +3)}$.
$y_j= {1}/{2n(8j +3)}$.
We remark that in the examples of Corollary 2.6, ![]() $S^{3}_n(K)$ and
$S^{3}_n(K)$ and ![]() $S^{3}_n(U)$ are homology cobordant not just with integer coefficients, but also with
$S^{3}_n(U)$ are homology cobordant not just with integer coefficients, but also with ![]() $\mathbb {Z}[\mathbb {Z}/n]$-coefficients.
$\mathbb {Z}[\mathbb {Z}/n]$-coefficients.
We also compare the difference between ![]() $m$-shake slice and
$m$-shake slice and ![]() $n$-shake slice for
$n$-shake slice for ![]() $m\neq n$.
$m\neq n$.
Corollary 2.7 If ![]() $m \mid n$ and
$m \mid n$ and ![]() $K$ is
$K$ is ![]() $\mathbb {Z}/n$-shake slice, then
$\mathbb {Z}/n$-shake slice, then ![]() $K$ is
$K$ is ![]() $\mathbb {Z}/m$-shake slice.
$\mathbb {Z}/m$-shake slice.
Proof. First, note that if ![]() $n=0$ and
$n=0$ and ![]() $K$ is
$K$ is ![]() $\mathbb {Z}/n$-shake slice then
$\mathbb {Z}/n$-shake slice then ![]() $\Delta _K(t)=1$, and so the conditions (i), (ii), and (iii) of Theorem 1.1 are satisfied for all
$\Delta _K(t)=1$, and so the conditions (i), (ii), and (iii) of Theorem 1.1 are satisfied for all ![]() $m \in \mathbb {Z}$.
$m \in \mathbb {Z}$.
So assume ![]() $n \neq 0$. Since
$n \neq 0$. Since ![]() $\prod _{\{\xi \mid \xi ^{m}=1\} }\Delta _K(\xi )$ divides
$\prod _{\{\xi \mid \xi ^{m}=1\} }\Delta _K(\xi )$ divides ![]() $\prod _{\{\xi \mid \xi ^{n}=1\} }\Delta _K(\xi )$ and both are integers, if the criterion (i) holds for
$\prod _{\{\xi \mid \xi ^{n}=1\} }\Delta _K(\xi )$ and both are integers, if the criterion (i) holds for ![]() $n$, then it also holds for
$n$, then it also holds for ![]() $m$. The signature and Arf invariant conditions are immediate.
$m$. The signature and Arf invariant conditions are immediate.
Corollary 2.8 If ![]() $m$ does not divide
$m$ does not divide ![]() $n$ then there exist infinitely many knots that are
$n$ then there exist infinitely many knots that are ![]() $n$-shake slice but not
$n$-shake slice but not ![]() $m$-shake slice. These knots may be chosen to be distinct in concordance.
$m$-shake slice. These knots may be chosen to be distinct in concordance.
Proof. Let ![]() $q$ be a prime power which divides
$q$ be a prime power which divides ![]() $m$ but not
$m$ but not ![]() $n$. Let
$n$. Let ![]() $K$ be any knot with
$K$ be any knot with ![]() $\operatorname {Arf}(K)=0$ and
$\operatorname {Arf}(K)=0$ and ![]() $\sigma _{K}(e^{2 \pi ik/q}) \neq 0$ for all
$\sigma _{K}(e^{2 \pi ik/q}) \neq 0$ for all ![]() $k=1, \dots , q-1$. Such knots are easy to find, for example by taking
$k=1, \dots , q-1$. Such knots are easy to find, for example by taking ![]() $K=T_{2, 8N+1}$ for sufficiently large
$K=T_{2, 8N+1}$ for sufficiently large ![]() $N$. Now let
$N$. Now let ![]() $J=C_{n,1}(K)$, and note that since
$J=C_{n,1}(K)$, and note that since ![]() $\operatorname {Arf}(K)=0$ Corollary 2.1 tells us that
$\operatorname {Arf}(K)=0$ Corollary 2.1 tells us that ![]() $J$ is
$J$ is ![]() $n$-shake slice. However,
$n$-shake slice. However, ![]() $\sigma _{C_{n,1}(K)}(e^{2 \pi i/q})= \sigma _{K}(e^{2 \pi in/q}) \neq 0$, since
$\sigma _{C_{n,1}(K)}(e^{2 \pi i/q})= \sigma _{K}(e^{2 \pi in/q}) \neq 0$, since ![]() $q$ does not divide
$q$ does not divide ![]() $n$. So
$n$. So ![]() $J$ is not
$J$ is not ![]() $m$-shake slice.
$m$-shake slice.
We can obtain ![]() $\{J_j\}_{j \in \mathbb {N}}$ representing infinitely many concordance classes of
$\{J_j\}_{j \in \mathbb {N}}$ representing infinitely many concordance classes of ![]() $n$-shake but not
$n$-shake but not ![]() $m$-shake slice knots by letting
$m$-shake slice knots by letting ![]() $J_j=C_{n,1}(T_{2,8(N+j)+1})$ for sufficiently large
$J_j=C_{n,1}(T_{2,8(N+j)+1})$ for sufficiently large ![]() $N$. As in the proof of Corollary 2.3, these knots are distinguished in concordance by the first jump of the Tristram–Levine signature, which occurs for
$N$. As in the proof of Corollary 2.3, these knots are distinguished in concordance by the first jump of the Tristram–Levine signature, which occurs for ![]() $J_j$ at
$J_j$ at ![]() $e^{2 \pi i x_j}$, where
$e^{2 \pi i x_j}$, where ![]() $x_j= {1}/{2n(8(N+j)+1)}$.
$x_j= {1}/{2n(8(N+j)+1)}$.
Remark 2.9 For many pairs ![]() $(n,m)$ such that
$(n,m)$ such that ![]() $m$ does not divide
$m$ does not divide ![]() $n$, one can also find examples of
$n$, one can also find examples of ![]() $n$-shake slice knots which are not
$n$-shake slice knots which are not ![]() $m$-shake slice by considering certain linear combinations of
$m$-shake slice by considering certain linear combinations of ![]() $(2,2k+1)$ torus knots. For example, one can verify that
$(2,2k+1)$ torus knots. For example, one can verify that ![]() $K_n:=6T_{2,4n+1} \# - 4T_{2, 6n+1}$ satisfies the conditions of Theorem 1.1 for
$K_n:=6T_{2,4n+1} \# - 4T_{2, 6n+1}$ satisfies the conditions of Theorem 1.1 for ![]() $n$, and hence is
$n$, and hence is ![]() $\mathbb {Z}/n$-shake slice. Additionally, computation of Tristram–Levine signatures shows that if
$\mathbb {Z}/n$-shake slice. Additionally, computation of Tristram–Levine signatures shows that if ![]() $m$ does not divide
$m$ does not divide ![]() $2n$, then
$2n$, then ![]() $K_n$ is not
$K_n$ is not ![]() $m$-shake slice.
$m$-shake slice.
Finally, we show in almost all cases that ![]() $\mathbb {Z}/n$-shake slice is a strictly stronger condition than
$\mathbb {Z}/n$-shake slice is a strictly stronger condition than ![]() $n$-shake slice.
$n$-shake slice.
Corollary 2.10 A knot is ![]() $(\pm 1)$-shake slice if and only if it is
$(\pm 1)$-shake slice if and only if it is ![]() $\mathbb {Z}/1$-shake slice. For all other
$\mathbb {Z}/1$-shake slice. For all other ![]() $n$ there exists a slice, and therefore
$n$ there exists a slice, and therefore ![]() $n$-shake slice, knot that is not
$n$-shake slice, knot that is not ![]() $\mathbb {Z}/n$-shake slice.
$\mathbb {Z}/n$-shake slice.
Proof. The ‘if’ direction of the first sentence is obvious. For the other direction, observe that an embedded sphere ![]() $S$ representing a generator of
$S$ representing a generator of ![]() $\pi _2(X_{\pm 1}(K))$ has a normal bundle
$\pi _2(X_{\pm 1}(K))$ has a normal bundle ![]() $\nu S$ with euler number
$\nu S$ with euler number ![]() $\pm 1$ (see Lemma 6.1). Since
$\pm 1$ (see Lemma 6.1). Since ![]() $\nu S \to S$ is a homotopy equivalence,
$\nu S \to S$ is a homotopy equivalence, ![]() $\nu S$ is simply connected. Since the euler number is
$\nu S$ is simply connected. Since the euler number is ![]() $\pm 1$,
$\pm 1$, ![]() $\partial (D\nu S) \cong S^{3}$, where
$\partial (D\nu S) \cong S^{3}$, where ![]() $D\nu S$ denotes the disc bundle of the normal bundle. We know that
$D\nu S$ denotes the disc bundle of the normal bundle. We know that ![]() $X_{\pm 1}(K)$ is simply connected. Apply the Seifert–Van Kampen theorem to the decomposition
$X_{\pm 1}(K)$ is simply connected. Apply the Seifert–Van Kampen theorem to the decomposition
to deduce that ![]() $\pi _1(X_{\pm 1}(K) {{\smallsetminus }}D\nu S) \cong \pi _1(X_{\pm 1}(K) {{\smallsetminus }}S) \cong \{1\} \cong \mathbb {Z}/1$. This proves the reverse direction.
$\pi _1(X_{\pm 1}(K) {{\smallsetminus }}D\nu S) \cong \pi _1(X_{\pm 1}(K) {{\smallsetminus }}S) \cong \{1\} \cong \mathbb {Z}/1$. This proves the reverse direction.
For the second sentence, the knot ![]() $K=4_1 \# 4_1$ is slice and hence
$K=4_1 \# 4_1$ is slice and hence ![]() $n$-shake slice for all
$n$-shake slice for all ![]() $n$. But
$n$. But ![]() $K$ has
$K$ has ![]() $|H_1(\Sigma _n(K))| \neq 1$ for all
$|H_1(\Sigma _n(K))| \neq 1$ for all ![]() $n>1$, and hence is not
$n>1$, and hence is not ![]() $\mathbb {Z}/n$-shake slice for
$\mathbb {Z}/n$-shake slice for ![]() $|n|>1$ by condition (iii) of Theorem 1.1. Recall that when
$|n|>1$ by condition (iii) of Theorem 1.1. Recall that when ![]() $n=0$, the conditions of Theorem 1.1 reduce to triviality of the Alexander polynomial. But since
$n=0$, the conditions of Theorem 1.1 reduce to triviality of the Alexander polynomial. But since ![]() $\Delta _K(t)=(t^{2}-3t+1)^{2}$, this knot
$\Delta _K(t)=(t^{2}-3t+1)^{2}$, this knot ![]() $K$ is not
$K$ is not ![]() $\mathbb {Z}/0$-shake slice either.
$\mathbb {Z}/0$-shake slice either.
When ![]() $n=\pm 1$, the conditions (i) and (iii) of Theorem 1.1 are automatically satisfied, so Corollary 2.10 immediately gives the following.
$n=\pm 1$, the conditions (i) and (iii) of Theorem 1.1 are automatically satisfied, so Corollary 2.10 immediately gives the following.
Corollary 2.11 A knot ![]() $K$ is
$K$ is ![]() $(\pm 1)$-shake slice if and only if it is
$(\pm 1)$-shake slice if and only if it is ![]() $\mathbb {Z}/ (\pm 1)$-shake slice if and only if
$\mathbb {Z}/ (\pm 1)$-shake slice if and only if ![]() $\operatorname {Arf}(K)=0$.
$\operatorname {Arf}(K)=0$.
If a knot is ![]() $n$-shake slice, then it has vanishing Arf invariant [Reference RobertelloRob65], so Corollary 2.11 immediately gives the following.
$n$-shake slice, then it has vanishing Arf invariant [Reference RobertelloRob65], so Corollary 2.11 immediately gives the following.
Corollary 2.12 If a knot ![]() $K$ is
$K$ is ![]() $n$-shake slice for some integer
$n$-shake slice for some integer ![]() $n$, then it is
$n$, then it is ![]() $(\pm 1)$-shake slice.
$(\pm 1)$-shake slice.
Changing the orientation on an ![]() $n$-trace
$n$-trace ![]() $X_n(K)$ results in the trace
$X_n(K)$ results in the trace ![]() $X_{-n}(-K)$, and so
$X_{-n}(-K)$, and so ![]() $K$ is
$K$ is ![]() $n$-shake slice if and only if
$n$-shake slice if and only if ![]() $-K$ is
$-K$ is ![]() $(-n)$-shake slice. Surprisingly, the conditions in Theorem 1.1 show that an even stronger symmetry holds, as in the following corollary.
$(-n)$-shake slice. Surprisingly, the conditions in Theorem 1.1 show that an even stronger symmetry holds, as in the following corollary.
Corollary 2.13 A knot ![]() $K$ is
$K$ is ![]() $\mathbb {Z}/n$-shake slice if and only if it is
$\mathbb {Z}/n$-shake slice if and only if it is ![]() $\mathbb {Z}/(-n)$-shake slice.
$\mathbb {Z}/(-n)$-shake slice.
Here of course ![]() $\mathbb {Z}/n \cong \mathbb {Z}/(-n)$, but the 4-manifolds
$\mathbb {Z}/n \cong \mathbb {Z}/(-n)$, but the 4-manifolds ![]() $X_n(K)$ and
$X_n(K)$ and ![]() $X_{-n}(K)$ are generally different. In particular, we know of no reason to believe that a knot is
$X_{-n}(K)$ are generally different. In particular, we know of no reason to believe that a knot is ![]() $n$-shake slice if and only if it is
$n$-shake slice if and only if it is ![]() $(-n)$-shake slice.
$(-n)$-shake slice.
For any ![]() $n$, it remains unknown in both the smooth and topological category whether
$n$, it remains unknown in both the smooth and topological category whether ![]() $n$-shake slice knots have
$n$-shake slice knots have ![]() $n$-shake slice connected sum. As the invariants involved in conditions (i), (ii), and (iii) of Theorem 1.1 are all additive under connected sum we have the following immediate corollary.
$n$-shake slice connected sum. As the invariants involved in conditions (i), (ii), and (iii) of Theorem 1.1 are all additive under connected sum we have the following immediate corollary.
Corollary 2.14 If ![]() $K$ and
$K$ and ![]() $J$ are
$J$ are ![]() $\mathbb {Z}/n$-shake slice, then so is
$\mathbb {Z}/n$-shake slice, then so is ![]() $K \#J$.
$K \#J$.
3. Obstructions to  $\mathbb {Z}/n$-shake sliceness
$\mathbb {Z}/n$-shake sliceness
In this section we prove that the conditions listed in Theorem 1.1 on the knot signatures and the Alexander polynomial are indeed necessary conditions for a knot to be ![]() $\mathbb {Z}/n$-shake slice. Some of these results have been shown by Tristram [Reference TristramTri69] and Saeki [Reference SaekiSae92]; we include our own proofs for completeness, for the convenience of the reader, and to introduce the identification of certain Atiyah–Singer/Casson–Gordon signatures with Tristram–Levine knot signatures that will be needed later on. As stated in the conventions section, we henceforth assume that
$\mathbb {Z}/n$-shake slice. Some of these results have been shown by Tristram [Reference TristramTri69] and Saeki [Reference SaekiSae92]; we include our own proofs for completeness, for the convenience of the reader, and to introduce the identification of certain Atiyah–Singer/Casson–Gordon signatures with Tristram–Levine knot signatures that will be needed later on. As stated in the conventions section, we henceforth assume that ![]() $n>0$.
$n>0$.
Lemma 3.1 If a knot ![]() $K$ is
$K$ is ![]() $n$-shake slice via an embedded sphere
$n$-shake slice via an embedded sphere ![]() $S$ in
$S$ in ![]() $X_n(K)$ then
$X_n(K)$ then ![]() $W:= X_n(K) \smallsetminus \nu (S)$ is a homology cobordism from
$W:= X_n(K) \smallsetminus \nu (S)$ is a homology cobordism from ![]() $S^{3}_n(K)$ to
$S^{3}_n(K)$ to ![]() $L(n,1)$. If
$L(n,1)$. If ![]() $K$ is further
$K$ is further ![]() $\mathbb {Z}/n$-shake slice via
$\mathbb {Z}/n$-shake slice via ![]() $S$, then
$S$, then ![]() $\pi _1(W) \cong \mathbb {Z}/n$.
$\pi _1(W) \cong \mathbb {Z}/n$.
Proof. The first statement follows from computation using the Mayer–Vietoris sequence for ![]() $X_n(K)= W \cup \nu (S)$. The second statement is immediate from the definition.
$X_n(K)= W \cup \nu (S)$. The second statement is immediate from the definition.
Remark 3.2 In this section, we only use the hypothesis that the manifolds ![]() $S^{3}_n(K)$ and
$S^{3}_n(K)$ and ![]() $L(n,1)$ are homology cobordant via a homology cobordism
$L(n,1)$ are homology cobordant via a homology cobordism ![]() $W$ with
$W$ with ![]() $\pi _1(W) \cong \mathbb {Z}/n$. This hypothesis is sufficient to establish conditions (i) and (iii) of Theorem 1.1 However, one cannot make this weaker assumption, at least when
$\pi _1(W) \cong \mathbb {Z}/n$. This hypothesis is sufficient to establish conditions (i) and (iii) of Theorem 1.1 However, one cannot make this weaker assumption, at least when ![]() $n$ is odd, if we wish to conclude that
$n$ is odd, if we wish to conclude that ![]() $\operatorname {Arf}(K)=0$. In particular, for every knot
$\operatorname {Arf}(K)=0$. In particular, for every knot ![]() $K$ we know that
$K$ we know that ![]() $S^{3}_1(K)$ is homology cobordant to
$S^{3}_1(K)$ is homology cobordant to ![]() $L(1,1)=S^{3}$ by a simply connected cobordism [Reference FreedmanFre82, Theorem 1.4
$L(1,1)=S^{3}$ by a simply connected cobordism [Reference FreedmanFre82, Theorem 1.4![]() $'$] (see also [Reference Freedman and QuinnFQ90, 9.3C]), but of course some knots have Arf invariant 1. On the other hand, the existence of a smooth homology cobordism would be enough to imply that
$'$] (see also [Reference Freedman and QuinnFQ90, 9.3C]), but of course some knots have Arf invariant 1. On the other hand, the existence of a smooth homology cobordism would be enough to imply that ![]() $\operatorname {Arf}(K)=0$ [Reference SaekiSae92].
$\operatorname {Arf}(K)=0$ [Reference SaekiSae92].
Proposition 3.3 Let ![]() $K$ be a knot such that
$K$ be a knot such that ![]() $S^{3}_n(K)$ and
$S^{3}_n(K)$ and ![]() $L(n,1)$ are homology cobordant via a homology cobordism
$L(n,1)$ are homology cobordant via a homology cobordism ![]() $W$ with
$W$ with ![]() $\pi _1(W) \cong \mathbb {Z}/n$. Then
$\pi _1(W) \cong \mathbb {Z}/n$. Then ![]() $H_1(S^{3}_n(K); \mathbb {Z}[\mathbb {Z}/n])=0= H_1(\Sigma _n(K);\mathbb {Z})$.
$H_1(S^{3}_n(K); \mathbb {Z}[\mathbb {Z}/n])=0= H_1(\Sigma _n(K);\mathbb {Z})$.
Proof. We will show that the ![]() $n$-sheeted cyclic cover
$n$-sheeted cyclic cover ![]() $Y_n:=(S^{3}_n(K))_n$ of
$Y_n:=(S^{3}_n(K))_n$ of ![]() $S^{3}_n(K)$ has trivial integral homology. Since
$S^{3}_n(K)$ has trivial integral homology. Since ![]() $H_1(Y_n;\mathbb {Z})=0$ implies that
$H_1(Y_n;\mathbb {Z})=0$ implies that ![]() $H_1(S^{3}_n(K); \mathbb {Z}[\mathbb {Z}/n])=0$, this will imply the first part of our desired result. By the universal coefficient theorem, it suffices to show that
$H_1(S^{3}_n(K); \mathbb {Z}[\mathbb {Z}/n])=0$, this will imply the first part of our desired result. By the universal coefficient theorem, it suffices to show that ![]() $H_1(Y_n ;\mathbb {F}_p)=0$ for all primes
$H_1(Y_n ;\mathbb {F}_p)=0$ for all primes ![]() $p$.
$p$.
Let ![]() $p$ be a prime. For each
$p$ be a prime. For each ![]() $k \in \mathbb {N}$ and space
$k \in \mathbb {N}$ and space ![]() $X$, let
$X$, let ![]() $b_k^{p}(X)$ denote the dimension of
$b_k^{p}(X)$ denote the dimension of ![]() $H_k(X; \mathbb {F}_p)$ as a
$H_k(X; \mathbb {F}_p)$ as a ![]() $\mathbb {F}_p$-vector space. Let
$\mathbb {F}_p$-vector space. Let ![]() $\widetilde {W}$ be the
$\widetilde {W}$ be the ![]() $\mathbb {Z}/n$-cover of
$\mathbb {Z}/n$-cover of ![]() $W$, and observe that since
$W$, and observe that since ![]() $\widetilde {W}$ is simply connected we have
$\widetilde {W}$ is simply connected we have ![]() $H_1(\widetilde {W}; \mathbb {F}_p)=0$. It follows that
$H_1(\widetilde {W}; \mathbb {F}_p)=0$. It follows that
Here the first equality holds since ![]() $W$ has the same Euler characteristic as a closed 3-manifold. By considering the long exact sequence of the pair
$W$ has the same Euler characteristic as a closed 3-manifold. By considering the long exact sequence of the pair ![]() $(W, \partial W)$, we obtain that
$(W, \partial W)$, we obtain that
and hence that ![]() $b_2^{p}(\widetilde {W})=0$. It then follows from the same long exact sequence that
$b_2^{p}(\widetilde {W})=0$. It then follows from the same long exact sequence that ![]() $b_1^{p}(\partial \widetilde {W})= b_1^{p}( Y_n \sqcup S^{3})=0$, and so we have established the first claim.
$b_1^{p}(\partial \widetilde {W})= b_1^{p}( Y_n \sqcup S^{3})=0$, and so we have established the first claim.
Let ![]() $E(K)$ denote the exterior of the knot
$E(K)$ denote the exterior of the knot ![]() $K$ in
$K$ in ![]() $S^{3}$ and
$S^{3}$ and ![]() $\mu _K$ and
$\mu _K$ and ![]() $\lambda _K$ denote the meridian and longitude respectively. By definition the manifold
$\lambda _K$ denote the meridian and longitude respectively. By definition the manifold ![]() $S^{3}_n(K)= E(K) \cup (S^{1} \times D^{2})$, where
$S^{3}_n(K)= E(K) \cup (S^{1} \times D^{2})$, where ![]() $\{\operatorname {pt}\} \times \partial D^{2}$ is identified with
$\{\operatorname {pt}\} \times \partial D^{2}$ is identified with ![]() $n \mu _K + \lambda _K$ and
$n \mu _K + \lambda _K$ and ![]() $S^{1} \times \{\operatorname {pt}\}$ with
$S^{1} \times \{\operatorname {pt}\}$ with ![]() $\lambda _K$. Therefore, we have that
$\lambda _K$. Therefore, we have that
where ![]() $\{\operatorname {pt}\} \times \partial D^{2}$ is identified with
$\{\operatorname {pt}\} \times \partial D^{2}$ is identified with ![]() $\widetilde {\mu _K^{n}}+ \widetilde{\lambda }_K$ and
$\widetilde {\mu _K^{n}}+ \widetilde{\lambda }_K$ and ![]() $S^{1} \times \{\operatorname {pt}\}$ with
$S^{1} \times \{\operatorname {pt}\}$ with ![]() $\widetilde{\lambda }_K$, where
$\widetilde{\lambda }_K$, where ![]() $\widetilde{\cdot }$ denotes a lift to the
$\widetilde{\cdot }$ denotes a lift to the ![]() $n$-fold cover
$n$-fold cover ![]() $E_n(K)\to E(K)$.
$E_n(K)\to E(K)$.
We also have that
where ![]() $\{\operatorname {pt}\} \times \partial D^{2}$ is identified with
$\{\operatorname {pt}\} \times \partial D^{2}$ is identified with ![]() $\widetilde {\mu _K^{n}}$ and
$\widetilde {\mu _K^{n}}$ and ![]() $S^{1} \times \{\operatorname {pt}\}$ with
$S^{1} \times \{\operatorname {pt}\}$ with ![]() $\widetilde{\lambda }_K$. Since
$\widetilde{\lambda }_K$. Since ![]() $\widetilde{\lambda }_K$ is null-homologous in
$\widetilde{\lambda }_K$ is null-homologous in ![]() $E_n(K)$, we see that
$E_n(K)$, we see that ![]() $H_1(\Sigma _n(K))$ and
$H_1(\Sigma _n(K))$ and ![]() $H_1(Y_n)$ are isomorphic quotients of
$H_1(Y_n)$ are isomorphic quotients of ![]() $H_1(E_n(K))$.
$H_1(E_n(K))$.
We extract the next statement from the proof of Proposition 3.3 for later use.
Corollary 3.4 Let ![]() $K$ be a knot such that
$K$ be a knot such that ![]() $S^{3}_n(K)$ and
$S^{3}_n(K)$ and ![]() $L(n,1)$ are homology cobordant via a homology cobordism
$L(n,1)$ are homology cobordant via a homology cobordism ![]() $W$ with
$W$ with ![]() $\pi _1(W) \cong \mathbb {Z}/n$ and let
$\pi _1(W) \cong \mathbb {Z}/n$ and let ![]() $\widetilde {W}$ denote the
$\widetilde {W}$ denote the ![]() $\mathbb {Z}/n$-cover of
$\mathbb {Z}/n$-cover of ![]() $W$. Then
$W$. Then ![]() $H_2(\widetilde {W};\mathbb {F}_p)=0$ for every prime
$H_2(\widetilde {W};\mathbb {F}_p)=0$ for every prime ![]() $p$.
$p$.
We would now like to prove the following. Note that the first statement implies that if a knot ![]() $K$ is
$K$ is ![]() $n$-shake slice then
$n$-shake slice then ![]() $\sigma _{\omega }(K)=0$ for every
$\sigma _{\omega }(K)=0$ for every ![]() $q\textrm {th}$ root of unity
$q\textrm {th}$ root of unity ![]() $\omega$, where
$\omega$, where ![]() $q$ is a prime power dividing
$q$ is a prime power dividing ![]() $n$. This was originally proved using different methods by Tristram [Reference TristramTri69].
$n$. This was originally proved using different methods by Tristram [Reference TristramTri69].
Proposition 3.5 [Reference TristramTri69]
Let ![]() $K$ be a knot such that
$K$ be a knot such that ![]() $S^{3}_n(K)$ and
$S^{3}_n(K)$ and ![]() $L(n,1)$ are homology cobordant via a homology cobordism
$L(n,1)$ are homology cobordant via a homology cobordism ![]() $W$. Then
$W$. Then ![]() $\sigma _{\omega }(K)=0$ for every
$\sigma _{\omega }(K)=0$ for every ![]() $q{th}$ root of unity
$q{th}$ root of unity ![]() $\omega$, where
$\omega$, where ![]() $q$ is a prime power dividing
$q$ is a prime power dividing ![]() $n$. If
$n$. If ![]() $\pi _1(W) \cong \mathbb {Z}/n$, then
$\pi _1(W) \cong \mathbb {Z}/n$, then ![]() $\sigma _{\omega }(K)=0$ for every
$\sigma _{\omega }(K)=0$ for every ![]() $n{th}$ root of unity
$n{th}$ root of unity ![]() $\omega$.
$\omega$.
Our strategy in proving Proposition 3.5 will be to relate the Tristram–Levine signature of ![]() $K$ at the
$K$ at the ![]() $n\textrm {th}$ roots of unity to the Atiyah–Singer/Casson–Gordon signatures [Reference Atiyah and SingerAS68, Reference Casson and GordonCG78] of the 3-manifold
$n\textrm {th}$ roots of unity to the Atiyah–Singer/Casson–Gordon signatures [Reference Atiyah and SingerAS68, Reference Casson and GordonCG78] of the 3-manifold ![]() $S^{3}_n(K)$. We will then use the
$S^{3}_n(K)$. We will then use the ![]() $n$-fold cyclic cover of the hypothesised homology cobordism
$n$-fold cyclic cover of the hypothesised homology cobordism ![]() $W$ between
$W$ between ![]() $S^{3}_n(K)$ and
$S^{3}_n(K)$ and ![]() $L(n,1)$, capped off in a certain nice way, to compute these Casson–Gordon signatures. We therefore recall the definition of the Casson–Gordon signatures of a 3-manifold, as given in [Reference Casson and GordonCG78]. For every
$L(n,1)$, capped off in a certain nice way, to compute these Casson–Gordon signatures. We therefore recall the definition of the Casson–Gordon signatures of a 3-manifold, as given in [Reference Casson and GordonCG78]. For every ![]() $n \in \mathbb {N}$ we think of the cyclic group
$n \in \mathbb {N}$ we think of the cyclic group ![]() $\mathbb {Z}/n$ as coming with a canonical multiplicative generator
$\mathbb {Z}/n$ as coming with a canonical multiplicative generator ![]() $t$.
$t$.
To a closed oriented 3-manifold ![]() $Y$ and a map
$Y$ and a map ![]() $\phi \colon H_1(Y) \to \mathbb {Z}/n$, we wish to associate
$\phi \colon H_1(Y) \to \mathbb {Z}/n$, we wish to associate ![]() $\sigma _k(Y, \phi ) \in \mathbb {Q}$ for
$\sigma _k(Y, \phi ) \in \mathbb {Q}$ for ![]() $k=1, \dots , n-1$. Let
$k=1, \dots , n-1$. Let ![]() $\widetilde{Y} \to Y$ be the covering induced by
$\widetilde{Y} \to Y$ be the covering induced by ![]() $\phi$, and note that there is a canonical covering transformation
$\phi$, and note that there is a canonical covering transformation ![]() $\tau$ of
$\tau$ of ![]() $\widetilde{Y}$ corresponding to
$\widetilde{Y}$ corresponding to ![]() $t \in \mathbb {Z}/n$.
$t \in \mathbb {Z}/n$.
Now suppose there exists a ![]() $\mathbb {Z}/n$ branched covering of 4-manifolds
$\mathbb {Z}/n$ branched covering of 4-manifolds ![]() $\widetilde{Z} \to Z$, branched over a surface
$\widetilde{Z} \to Z$, branched over a surface ![]() $F$ contained in the interior of
$F$ contained in the interior of ![]() $Z$, and such that
$Z$, and such that ![]() $\partial (\widetilde{Z} \to Z)=(\widetilde{Y} \to Y)$. Suppose in addition that the covering transformation
$\partial (\widetilde{Z} \to Z)=(\widetilde{Y} \to Y)$. Suppose in addition that the covering transformation ![]() $\widetilde{\tau }\colon \widetilde{Z}\to \widetilde{Z}$ that induces rotation through
$\widetilde{\tau }\colon \widetilde{Z}\to \widetilde{Z}$ that induces rotation through ![]() $2 \pi /n$ on the fibres of the normal bundle of
$2 \pi /n$ on the fibres of the normal bundle of ![]() $\widetilde{F}$ is such that it restricts on
$\widetilde{F}$ is such that it restricts on ![]() $\widetilde{Y}$ to
$\widetilde{Y}$ to ![]() $\tau$. An explicit construction as given, for example, in the proof of [Reference Casson and GordonCG78, Lemma 3.1], shows that such a branched cover does always exist. Then
$\tau$. An explicit construction as given, for example, in the proof of [Reference Casson and GordonCG78, Lemma 3.1], shows that such a branched cover does always exist. Then ![]() $H_2(\widetilde{Z};\mathbb {C})$ decomposes as
$H_2(\widetilde{Z};\mathbb {C})$ decomposes as ![]() $\bigoplus _{k=0}^{n-1} V_k$, where
$\bigoplus _{k=0}^{n-1} V_k$, where ![]() $V_k$ is the
$V_k$ is the ![]() $\xi _n^{k}$-eigenspace of the
$\xi _n^{k}$-eigenspace of the ![]() $\widetilde{\tau }$-induced action on second homology, and as before
$\widetilde{\tau }$-induced action on second homology, and as before ![]() $\xi _n := e^{2 \pi i/n}$. Let
$\xi _n := e^{2 \pi i/n}$. Let ![]() $\sigma _k(\widetilde{Z})$ denote the signature of the intersection form of
$\sigma _k(\widetilde{Z})$ denote the signature of the intersection form of ![]() $\widetilde{Z}$ restricted to
$\widetilde{Z}$ restricted to ![]() $V_k$. Define, for
$V_k$. Define, for ![]() $k=1, \dots , n-1$, the signature defect
$k=1, \dots , n-1$, the signature defect
Casson and Gordon [Reference Casson and GordonCG78] used the Atiyah–Singer ![]() $G$-signature theorem [Reference Atiyah and SingerAS68] to show that
$G$-signature theorem [Reference Atiyah and SingerAS68] to show that ![]() $\sigma _k(Y, \phi )$ is an invariant of the pair
$\sigma _k(Y, \phi )$ is an invariant of the pair ![]() $(Y,\phi )$ for each
$(Y,\phi )$ for each ![]() $0< k< n$.
$0< k< n$.
Proposition 3.7 Let ![]() $K$ be a knot and
$K$ be a knot and ![]() $W$ be a cobordism between
$W$ be a cobordism between ![]() $S^{3}_n(K)$ and
$S^{3}_n(K)$ and ![]() $L(n,1)$ over
$L(n,1)$ over ![]() $\mathbb {Z}/n$. Let
$\mathbb {Z}/n$. Let ![]() $\xi _n=e^{2 \pi i/n}$ and
$\xi _n=e^{2 \pi i/n}$ and ![]() $1 \leq k \leq n-1$. Then
$1 \leq k \leq n-1$. Then
where ![]() $\sigma _k(\widetilde {W})$ is the signature of the intersection form of the
$\sigma _k(\widetilde {W})$ is the signature of the intersection form of the ![]() $\mathbb {Z}/n$-cover of
$\mathbb {Z}/n$-cover of ![]() $W$ induced by the map
$W$ induced by the map ![]() $H_1(W) \to \mathbb {Z}/n$ when restricted to the
$H_1(W) \to \mathbb {Z}/n$ when restricted to the ![]() $\xi _n^{k}$-eigenspace of the action of the generator of the group of deck transformations on
$\xi _n^{k}$-eigenspace of the action of the generator of the group of deck transformations on ![]() $H_2(\widetilde {W}, \mathbb {C})$.
$H_2(\widetilde {W}, \mathbb {C})$.
Proof. Our proof follows from computing ![]() $\sigma _k(S^{3}_n(K), \phi )$, where
$\sigma _k(S^{3}_n(K), \phi )$, where ![]() $\phi \colon H_1(S^{3}_n(K)) \to \mathbb {Z}/n$ is the canonical map sending the meridian
$\phi \colon H_1(S^{3}_n(K)) \to \mathbb {Z}/n$ is the canonical map sending the meridian ![]() $\mu _K$ to
$\mu _K$ to ![]() $1 \in \mathbb {Z}/n$, in two different ways.
$1 \in \mathbb {Z}/n$, in two different ways.
First, observe that in this setting the surgery formula of [Reference Casson and GordonCG78, Lemma 3.1] is particularly simple and reduces to
Second, let ![]() $\widetilde {W} \to W$ be the
$\widetilde {W} \to W$ be the ![]() $n$-fold cyclic cover. We have that
$n$-fold cyclic cover. We have that
Now let ![]() $X_n(U)$ denote the
$X_n(U)$ denote the ![]() $n$-trace of the unknot, i.e. the disc bundle
$n$-trace of the unknot, i.e. the disc bundle ![]() $D_n$ over
$D_n$ over ![]() $S^{2}$ with euler number
$S^{2}$ with euler number ![]() $n$. Let
$n$. Let ![]() $S$ be the
$S$ be the ![]() $n$-framed embedded 2-sphere in
$n$-framed embedded 2-sphere in ![]() $X_n(U)$. There is an
$X_n(U)$. There is an ![]() $n$-fold cyclic branched cover
$n$-fold cyclic branched cover ![]() $\widetilde{X}_S$ of
$\widetilde{X}_S$ of ![]() $X_n(U)$ along
$X_n(U)$ along ![]() $S$, which restricts on the boundary to the same (unbranched) cover
$S$, which restricts on the boundary to the same (unbranched) cover ![]() $S^{3} \to L(n,1)$ we saw above. Note that
$S^{3} \to L(n,1)$ we saw above. Note that ![]() $\widetilde{X}_S$ is a punctured
$\widetilde{X}_S$ is a punctured ![]() $\mathbb {CP}^{2}$.
$\mathbb {CP}^{2}$.
We can therefore use ![]() $Z:= W \cup _{L(n,1)} X_n(U)$ and
$Z:= W \cup _{L(n,1)} X_n(U)$ and ![]() $\widetilde{Z}= \widetilde {W} \cup _{S^{3}} \widetilde{X}_S$ to compute
$\widetilde{Z}= \widetilde {W} \cup _{S^{3}} \widetilde{X}_S$ to compute ![]() $\sigma _k(S^{3}_n(K), \phi )$ using (3.6). Note that
$\sigma _k(S^{3}_n(K), \phi )$ using (3.6). Note that ![]() $H_2(\widetilde{Z}) \cong H_2(\widetilde {W}) \oplus \mathbb {Z}$, where the generator of the
$H_2(\widetilde{Z}) \cong H_2(\widetilde {W}) \oplus \mathbb {Z}$, where the generator of the ![]() $\mathbb {Z}$ summand is represented by the lift of
$\mathbb {Z}$ summand is represented by the lift of ![]() $S$ and hence has self-intersection
$S$ and hence has self-intersection ![]() $+1$, intersects trivially with all elements of
$+1$, intersects trivially with all elements of ![]() $H_2(\widetilde {W})$, and is preserved under the action of the covering transformation so lies in the
$H_2(\widetilde {W})$, and is preserved under the action of the covering transformation so lies in the ![]() $1$-eigenspace. Consequently, for
$1$-eigenspace. Consequently, for ![]() $0< k< n$ we have
$0< k< n$ we have ![]() $\sigma _k(\widetilde{Z})=\sigma _k(\widetilde {W})$ and hence
$\sigma _k(\widetilde{Z})=\sigma _k(\widetilde {W})$ and hence
 \begin{align} \sigma_k(S^{3}_n(K), \phi)&= \sigma(Z)- \sigma_k(\widetilde{Z}) - \frac{2 ([S] \cdot [S]) k(n-k)}{n^{2}} \nonumber\\ &= (\sigma(W)+1)- \sigma_k(\widetilde {W}) - \frac{2nk(n-k)}{n^{2}}. \end{align}
\begin{align} \sigma_k(S^{3}_n(K), \phi)&= \sigma(Z)- \sigma_k(\widetilde{Z}) - \frac{2 ([S] \cdot [S]) k(n-k)}{n^{2}} \nonumber\\ &= (\sigma(W)+1)- \sigma_k(\widetilde {W}) - \frac{2nk(n-k)}{n^{2}}. \end{align} Since ![]() $\sigma _k(S^{3}_n(K), \phi )$ is well defined, by comparing the formulae of (3.8) and (3.9) we obtain as desired that
$\sigma _k(S^{3}_n(K), \phi )$ is well defined, by comparing the formulae of (3.8) and (3.9) we obtain as desired that
Versions of the next lemma have appeared in many places, the earliest of which we know of is [Reference LevineLev94, Lemma I.4.3 and II.3.2]. See also [Reference Cochran, Orr and TeichnerCOT03, Proposition 2.10].
Lemma 3.10 Let ![]() $i \colon X \to Y$ be a map of
$i \colon X \to Y$ be a map of ![]() $($spaces homotopy equivalent to
$($spaces homotopy equivalent to![]() $)$ finite CW complexes that induces isomorphisms
$)$ finite CW complexes that induces isomorphisms ![]() $i_* \colon H_k(X; \mathbb {Z}) \to H_k(Y;\mathbb {Z})$ for all
$i_* \colon H_k(X; \mathbb {Z}) \to H_k(Y;\mathbb {Z})$ for all ![]() $k$. Suppose
$k$. Suppose ![]() $\varepsilon \colon H_1(Y;\mathbb {Z}) \to \mathbb {Z}/{q}$ is a surjective map inducing
$\varepsilon \colon H_1(Y;\mathbb {Z}) \to \mathbb {Z}/{q}$ is a surjective map inducing ![]() $\mathbb {Z}/q$-covers
$\mathbb {Z}/q$-covers ![]() $\widetilde{Y} \to Y$ and
$\widetilde{Y} \to Y$ and ![]() $\widetilde{X} \to X$.
$\widetilde{X} \to X$.
If ![]() $q$ is a prime power, then the induced map
$q$ is a prime power, then the induced map
is an isomorphism for all ![]() $k$.
$k$.
Proof. Let ![]() $\alpha \colon H_1(Y) \to \operatorname {GL}_q(\mathbb {Q})$ be the map obtained by composing
$\alpha \colon H_1(Y) \to \operatorname {GL}_q(\mathbb {Q})$ be the map obtained by composing ![]() $\varepsilon$ with the regular representation
$\varepsilon$ with the regular representation
 \begin{align*} \mathbb{Z}/q &\to \operatorname{GL}_q(\mathbb{Q}) \\ k &\mapsto \left[ \begin{array}{ccccc} 0 & 1 & 0 & \dots & 0 \\ 0 & 0 & 1 & \dots & 0 \\ \vdots & \vdots & \ddots & \ddots & \vdots \\ 0 & 0 & 0 & \dots & 1 \\ 1 & 0 & 0 & \dots & 0 \end{array} \right]^{k}. \end{align*}
\begin{align*} \mathbb{Z}/q &\to \operatorname{GL}_q(\mathbb{Q}) \\ k &\mapsto \left[ \begin{array}{ccccc} 0 & 1 & 0 & \dots & 0 \\ 0 & 0 & 1 & \dots & 0 \\ \vdots & \vdots & \ddots & \ddots & \vdots \\ 0 & 0 & 0 & \dots & 1 \\ 1 & 0 & 0 & \dots & 0 \end{array} \right]^{k}. \end{align*} As usual, this regular representation endows ![]() $\mathbb {Q}^{q}$ with the structure of a free
$\mathbb {Q}^{q}$ with the structure of a free ![]() $\mathbb {Q}[\mathbb {Z}/q]$-module of rank one.
$\mathbb {Q}[\mathbb {Z}/q]$-module of rank one.
From the work of Friedl and Powell [Reference Friedl and PowellFP12, Proposition 4.1] (applied with, in their notation, ![]() $H=\{1\}$) we have that
$H=\{1\}$) we have that
is an isomorphism. Then for ![]() $Z\in \{X,Y\}$, we have natural identifications
$Z\in \{X,Y\}$, we have natural identifications
and the desired result follows.
Proof of Proposition 3.5. Let ![]() $\widetilde {W}$ denote the
$\widetilde {W}$ denote the ![]() $\mathbb {Z}/n$ cover of
$\mathbb {Z}/n$ cover of ![]() $W$. Note that since
$W$. Note that since ![]() $W$ is a homology cobordism between
$W$ is a homology cobordism between ![]() $S^{3}_n(K)$ and
$S^{3}_n(K)$ and ![]() $L(n,1)$ we have that
$L(n,1)$ we have that ![]() $H_2(W)=0$ and so certainly
$H_2(W)=0$ and so certainly ![]() $\sigma (W)=0$.
$\sigma (W)=0$.
The case when ![]() $\pi _1(W)\cong \mathbb {Z}/n$ follows quickly: Corollary 3.4 tells us that
$\pi _1(W)\cong \mathbb {Z}/n$ follows quickly: Corollary 3.4 tells us that ![]() $H_2(\widetilde {W}; \mathbb {F}_p)=0$ for all primes
$H_2(\widetilde {W}; \mathbb {F}_p)=0$ for all primes ![]() $p$, and hence that
$p$, and hence that ![]() $H_2(\widetilde {W}; \mathbb {Z})=0$ and so
$H_2(\widetilde {W}; \mathbb {Z})=0$ and so ![]() $H_2(\widetilde {W}; \mathbb {C})=0$. Therefore, by Proposition 3.7 we have for
$H_2(\widetilde {W}; \mathbb {C})=0$. Therefore, by Proposition 3.7 we have for ![]() $k=1, \ldots , n-1$ that
$k=1, \ldots , n-1$ that
So we now assume only that ![]() $W$ is a homology cobordism, with no condition on the fundamental group. Let
$W$ is a homology cobordism, with no condition on the fundamental group. Let ![]() $q$ be a prime power dividing
$q$ be a prime power dividing ![]() $n$, and let
$n$, and let ![]() $1 \leq k \leq q-1$ be relatively prime to
$1 \leq k \leq q-1$ be relatively prime to ![]() $q$. Let
$q$. Let ![]() $\phi \colon H_1(S^{3}_n(K)) \to \mathbb {Z}/q$ be the map sending the class
$\phi \colon H_1(S^{3}_n(K)) \to \mathbb {Z}/q$ be the map sending the class ![]() $[\mu _K]$ of the meridian of
$[\mu _K]$ of the meridian of ![]() $K$ to
$K$ to ![]() $+1 \in \mathbb {Z}/q$. We now argue exactly as in the proof of Proposition 3.7 to show that
$+1 \in \mathbb {Z}/q$. We now argue exactly as in the proof of Proposition 3.7 to show that
and hence, since ![]() $H_2(W; \mathbb {Q})=0$, that
$H_2(W; \mathbb {Q})=0$, that
But by Lemma 3.10, since the inclusion induced map
is an isomorphism and ![]() $q$ is a prime power, we have that
$q$ is a prime power, we have that
is also an isomorphism. But since ![]() $\widetilde {L(n,1)}$ is itself a lens space (or
$\widetilde {L(n,1)}$ is itself a lens space (or ![]() $S^{3}$ if
$S^{3}$ if ![]() $n=q$), we have that
$n=q$), we have that ![]() $H_2(\widetilde {L(n,1)}; \mathbb {Q})=0$ and so
$H_2(\widetilde {L(n,1)}; \mathbb {Q})=0$ and so ![]() $H_2(\widetilde {W}; \mathbb {Q})=0$ as well. Thus the
$H_2(\widetilde {W}; \mathbb {Q})=0$ as well. Thus the ![]() $\xi _n^{k}$-eigenspace
$\xi _n^{k}$-eigenspace ![]() $V_k=0$, and so as desired
$V_k=0$, and so as desired
4. Setting up the surgery problem
We will use surgery theory to construct the exterior of the desired embedded sphere in an ![]() $n$-trace. We will eventually apply surgery in the topological category, but our initial input manifolds will be smooth. We thus now recall the input to a surgery problem in the smooth category. There is an analogous theory in the topological category, and we will discuss this below at the point when it becomes necessary.
$n$-trace. We will eventually apply surgery in the topological category, but our initial input manifolds will be smooth. We thus now recall the input to a surgery problem in the smooth category. There is an analogous theory in the topological category, and we will discuss this below at the point when it becomes necessary.
Definition 4.1 Given a smooth ![]() $m$-manifold
$m$-manifold ![]() $X$, the tangent bundle is classified up to isomorphism by a homotopy class of maps
$X$, the tangent bundle is classified up to isomorphism by a homotopy class of maps ![]() $\tau _X\colon X\to \operatorname {BO}(m)\subset \operatorname {BO}$. The unique stable bundle
$\tau _X\colon X\to \operatorname {BO}(m)\subset \operatorname {BO}$. The unique stable bundle ![]() $\nu _X\colon X\to \operatorname {BO}$ such that
$\nu _X\colon X\to \operatorname {BO}$ such that ![]() $\tau _X\oplus \nu _X\colon X\to \operatorname {BO}$ is null-homotopic is called the stable normal bundle of
$\tau _X\oplus \nu _X\colon X\to \operatorname {BO}$ is null-homotopic is called the stable normal bundle of ![]() $X$. The manifold
$X$. The manifold ![]() $X$ can be stably framed if
$X$ can be stably framed if ![]() $\nu _X$ is null-homotopic, and a choice of null homotopy is called a stable framing. A choice of stable framing for
$\nu _X$ is null-homotopic, and a choice of null homotopy is called a stable framing. A choice of stable framing for ![]() $X$ is determined by a choice of stable trivialisation of the tangent bundle,that is, a choice of
$X$ is determined by a choice of stable trivialisation of the tangent bundle,that is, a choice of ![]() $k$ and vector bundle isomorphism
$k$ and vector bundle isomorphism ![]() $TX\oplus \underline {\mathbb {R}}^{k}\cong \underline {\mathbb {R}}^{m+k}$.
$TX\oplus \underline {\mathbb {R}}^{k}\cong \underline {\mathbb {R}}^{m+k}$.
Recall that an oriented ![]() $m$-manifold
$m$-manifold ![]() $X$ with (possibly empty) boundary has a fundamental class, denoted
$X$ with (possibly empty) boundary has a fundamental class, denoted ![]() $[X,\partial X]\in H_m(X,\partial X;\mathbb {Z})$, capping with which induces (twisted) Poincaré–Lefschetz duality isomorphisms
$[X,\partial X]\in H_m(X,\partial X;\mathbb {Z})$, capping with which induces (twisted) Poincaré–Lefschetz duality isomorphisms ![]() $H^{m-k}(X,\partial X;\mathbb {Z}[\pi _1(X)]) \xrightarrow {\cong } H_{k}(X;\mathbb {Z}[\pi _1(X)])$ and
$H^{m-k}(X,\partial X;\mathbb {Z}[\pi _1(X)]) \xrightarrow {\cong } H_{k}(X;\mathbb {Z}[\pi _1(X)])$ and ![]() $H^{m-k}(X;\mathbb {Z}[\pi _1(X)]) \xrightarrow {\cong } H_{k}(X,\partial X;\mathbb {Z}[\pi _1(X)])$ for every
$H^{m-k}(X;\mathbb {Z}[\pi _1(X)]) \xrightarrow {\cong } H_{k}(X,\partial X;\mathbb {Z}[\pi _1(X)])$ for every ![]() $k$.
$k$.
Definition 4.2 A map ![]() $(f,\partial f)\colon (X,\partial X)\to (Y,\partial Y)$ of smooth oriented
$(f,\partial f)\colon (X,\partial X)\to (Y,\partial Y)$ of smooth oriented ![]() $m$-manifolds with (possibly empty) boundary is called degree one if
$m$-manifolds with (possibly empty) boundary is called degree one if ![]() $f_*([X, \partial X])=[Y,\partial Y]$. Given a degree-one map
$f_*([X, \partial X])=[Y,\partial Y]$. Given a degree-one map ![]() $f$, a normal structure is an isomorphism of stable bundles
$f$, a normal structure is an isomorphism of stable bundles ![]() $\nu _X\simeq \nu _Y\circ f$. A degree-one map with choice of normal structure is called a degree-one normal map. We will often write
$\nu _X\simeq \nu _Y\circ f$. A degree-one map with choice of normal structure is called a degree-one normal map. We will often write ![]() $(X,f)$ for the data of a degree-one normal map (suppressing the choice of stable bundle isomorphism).
$(X,f)$ for the data of a degree-one normal map (suppressing the choice of stable bundle isomorphism).
For a topological space ![]() $Y$, a bordism
$Y$, a bordism ![]() $Z$ between closed
$Z$ between closed ![]() $m$-manifolds
$m$-manifolds ![]() $X$ and
$X$ and ![]() $X'$ is over Y if there is a proper map
$X'$ is over Y if there is a proper map ![]() $F\colon Z\to Y\times I$ such that
$F\colon Z\to Y\times I$ such that ![]() $F(X)\subset Y\times \{0\}$ and
$F(X)\subset Y\times \{0\}$ and ![]() $F(X')\subset Y\times \{1\}$. If
$F(X')\subset Y\times \{1\}$. If ![]() $Y$ and
$Y$ and ![]() $Z$ are smooth oriented
$Z$ are smooth oriented ![]() $m$-manifolds and the map
$m$-manifolds and the map ![]() $F$ is a degree-one normal map, then we call
$F$ is a degree-one normal map, then we call ![]() $(Z,F)$ a degree-one normal bordism from
$(Z,F)$ a degree-one normal bordism from ![]() $(X,F|_X)$ to
$(X,F|_X)$ to ![]() $(X',F|_{X'})$.
$(X',F|_{X'})$.
Remark 4.3 Given a degree-one map ![]() $(f,\partial f)\colon (X,\partial X)\to (Y,\partial Y)$, if
$(f,\partial f)\colon (X,\partial X)\to (Y,\partial Y)$, if ![]() $\nu _Y$ is null-homotopic, then so is
$\nu _Y$ is null-homotopic, then so is ![]() $\nu _Y\circ f$. So
$\nu _Y\circ f$. So ![]() $f$ admits a normal structure if and only if
$f$ admits a normal structure if and only if ![]() $X$ can be stably framed.
$X$ can be stably framed.
Furthermore, we will sometimes be interested in picking a normal structure on ![]() $f$ that is compatible with a given one on
$f$ that is compatible with a given one on ![]() $\partial f$. To understand this, suppose we are given a choice of stable framing on
$\partial f$. To understand this, suppose we are given a choice of stable framing on ![]() $Y$. This induces a choice of stable framing on
$Y$. This induces a choice of stable framing on ![]() $\partial Y$. Suppose we have a degree-one map
$\partial Y$. Suppose we have a degree-one map ![]() $\partial f\colon \partial X\to \partial Y$. A choice of normal structure on
$\partial f\colon \partial X\to \partial Y$. A choice of normal structure on ![]() $\partial f$ is equivalent to a choice of stable framing on
$\partial f$ is equivalent to a choice of stable framing on ![]() $\partial X$. Suppose such a choice has been made. Then a degree-one map
$\partial X$. Suppose such a choice has been made. Then a degree-one map ![]() $(f,\partial f)\colon (X,\partial X)\to (Y,\partial Y)$ admits a normal structure inducing the given one on the boundary if and only if
$(f,\partial f)\colon (X,\partial X)\to (Y,\partial Y)$ admits a normal structure inducing the given one on the boundary if and only if ![]() $X$ can be stably framed compatibly with
$X$ can be stably framed compatibly with ![]() $\partial X$.
$\partial X$.
Note that the lens space ![]() $L(n,1)$ is diffeomorphic to the result of
$L(n,1)$ is diffeomorphic to the result of ![]() $n$-surgery along the unknot. In our applications, the target manifold for the map in the surgery problem will be either
$n$-surgery along the unknot. In our applications, the target manifold for the map in the surgery problem will be either ![]() $(L(n,1),\varnothing )$ or
$(L(n,1),\varnothing )$ or ![]() $(L(n,1) \times I,L(n,1) \times \{0,1\})$. The tangent bundles of
$(L(n,1) \times I,L(n,1) \times \{0,1\})$. The tangent bundles of ![]() $L(n,1)$ and of
$L(n,1)$ and of ![]() $L(n,1) \times I$ are trivial, so in particular these manifolds can be stably framed. Choose once and for all a stable framing for
$L(n,1) \times I$ are trivial, so in particular these manifolds can be stably framed. Choose once and for all a stable framing for ![]() $L(n,1)$, and hence one for
$L(n,1)$, and hence one for ![]() $L(n,1) \times I$.
$L(n,1) \times I$.
Lemma 4.4 For any knot ![]() $K$, there exists a degree-one normal map
$K$, there exists a degree-one normal map ![]() $f \colon S_n^{3}(K) \to L(n,1)$ that is a
$f \colon S_n^{3}(K) \to L(n,1)$ that is a ![]() $\mathbb {Z}$-homology equivalence and that extends to a homotopy equivalence
$\mathbb {Z}$-homology equivalence and that extends to a homotopy equivalence ![]() $\bar {f}\colon X_n(K) \to D_n$, where
$\bar {f}\colon X_n(K) \to D_n$, where ![]() $D_n$ is the
$D_n$ is the ![]() $D^{2}$-bundle over
$D^{2}$-bundle over ![]() $S^{2}$ with euler number
$S^{2}$ with euler number ![]() $n$. Additionally, one can arrange that the cocore of the
$n$. Additionally, one can arrange that the cocore of the ![]() $2$-handle of
$2$-handle of ![]() $X_n(K)$ maps to the cocore of the
$X_n(K)$ maps to the cocore of the ![]() $2$-handle in the standard handle decomposition for
$2$-handle in the standard handle decomposition for ![]() $D_n$.
$D_n$.
Proof. There is a standard degree-one map from ![]() $E(K) \to E(U)$ that realises the homology equivalence
$E(K) \to E(U)$ that realises the homology equivalence ![]() $E(K)\to S^{1}$ and is the identity map on the boundary; see e.g. [Reference Miller and PowellMP19, Construction 7.1] for the details. As submanifolds of
$E(K)\to S^{1}$ and is the identity map on the boundary; see e.g. [Reference Miller and PowellMP19, Construction 7.1] for the details. As submanifolds of ![]() $S^{3}$, both
$S^{3}$, both ![]() $E(K)$ and
$E(K)$ and ![]() $E(U)$ have stably trivial tangent bundles and can thus be stably framed. So this degree-one map can be given a choice of normal structure by Remark 4.3. Now extend this degree-one normal map to the Dehn filling.
$E(U)$ have stably trivial tangent bundles and can thus be stably framed. So this degree-one map can be given a choice of normal structure by Remark 4.3. Now extend this degree-one normal map to the Dehn filling.
We construct the homotopy equivalence ![]() $\bar {f}$. By construction,
$\bar {f}$. By construction, ![]() $f\colon S^{3}_n(K)\rightarrow S^{3}_n(U)=L(n,1)$ sends a meridian of
$f\colon S^{3}_n(K)\rightarrow S^{3}_n(U)=L(n,1)$ sends a meridian of ![]() $K$ to a meridian of the unknot
$K$ to a meridian of the unknot ![]() $U$. We also have a handle decomposition of
$U$. We also have a handle decomposition of ![]() $X_n(K)$ relative to its boundary consisting of a
$X_n(K)$ relative to its boundary consisting of a ![]() $2$-handle, attached along a meridian of
$2$-handle, attached along a meridian of ![]() $K$, and a
$K$, and a ![]() $4$-handle. Define
$4$-handle. Define ![]() $\bar {f}\colon X_n(K)\to X_n(U)=D_n$ by mapping the
$\bar {f}\colon X_n(K)\to X_n(U)=D_n$ by mapping the ![]() $2$-handles and the
$2$-handles and the ![]() $4$-handles homeomorphically to each other. To do this, first note that the attaching circle of the 2-handle of
$4$-handles homeomorphically to each other. To do this, first note that the attaching circle of the 2-handle of ![]() $X_n(U)$ is a meridian of
$X_n(U)$ is a meridian of ![]() $U$, so the attaching circle of the 2-handle of
$U$, so the attaching circle of the 2-handle of ![]() $X_n(K)$ is sent to the attaching circle of the 2-handle of
$X_n(K)$ is sent to the attaching circle of the 2-handle of ![]() $X_n(U)$. Also the framings agree, so we can extend over the 2-handle. Then note that attaching the 2-handles undoes the Dehn surgeries, converting both
$X_n(U)$. Also the framings agree, so we can extend over the 2-handle. Then note that attaching the 2-handles undoes the Dehn surgeries, converting both ![]() $S^{3}_n(K)$ and
$S^{3}_n(K)$ and ![]() $S^{3}_n(U)$ to
$S^{3}_n(U)$ to ![]() $S^{3}$. The 4-handles are attached to these copies of
$S^{3}$. The 4-handles are attached to these copies of ![]() $S^{3}$. Since every orientation-preserving homeomorphism of
$S^{3}$. Since every orientation-preserving homeomorphism of ![]() $S^{3}$ is isotopic to the identity, we may extend the map over the 4-handles. Observe that
$S^{3}$ is isotopic to the identity, we may extend the map over the 4-handles. Observe that ![]() $\bar {f}$ is a homotopy equivalence by Whitehead's theorem.
$\bar {f}$ is a homotopy equivalence by Whitehead's theorem.
Recall the Whitehead group ![]() $\operatorname {Wh}(\mathbb {Z}/n)$ is a certain quotient of the algebraic
$\operatorname {Wh}(\mathbb {Z}/n)$ is a certain quotient of the algebraic ![]() $K$-group
$K$-group ![]() $K_1(\mathbb {Z}[\mathbb {Z}/n])$. When
$K_1(\mathbb {Z}[\mathbb {Z}/n])$. When ![]() $H_1(S^{3}_n(K);\mathbb {Z}[\mathbb {Z}/n])=0$, a map
$H_1(S^{3}_n(K);\mathbb {Z}[\mathbb {Z}/n])=0$, a map ![]() $f$ as in Lemma 4.4 induces a chain homotopy equivalence
$f$ as in Lemma 4.4 induces a chain homotopy equivalence ![]() $\widetilde{f}_*\colon C_*(S^{3}_n(K);\mathbb {Z}[\mathbb {Z}/n])\to C_*(L(n,1);\mathbb {Z}[\mathbb {Z}/n])$ and thus determines a
$\widetilde{f}_*\colon C_*(S^{3}_n(K);\mathbb {Z}[\mathbb {Z}/n])\to C_*(L(n,1);\mathbb {Z}[\mathbb {Z}/n])$ and thus determines a ![]() $\mathbb {Z}[\mathbb {Z}/n]$-coefficient Whitehead torsion
$\mathbb {Z}[\mathbb {Z}/n]$-coefficient Whitehead torsion ![]() $\tau (f):=\tau (\widetilde{f}_*) \in \operatorname {Wh}(\mathbb {Z}/n)$. We will need the following technical lemma later.
$\tau (f):=\tau (\widetilde{f}_*) \in \operatorname {Wh}(\mathbb {Z}/n)$. We will need the following technical lemma later.
Lemma 4.5 If the knot ![]() $K$ satisfies
$K$ satisfies ![]() $H_1(S^{3}_n(K);\mathbb {Z}[\mathbb {Z}/n])=0$, then a map
$H_1(S^{3}_n(K);\mathbb {Z}[\mathbb {Z}/n])=0$, then a map ![]() $f$ as in Lemma 4.4 has trivial
$f$ as in Lemma 4.4 has trivial ![]() $\mathbb {Z}[\mathbb {Z}/n]$-coefficient Whitehead torsion
$\mathbb {Z}[\mathbb {Z}/n]$-coefficient Whitehead torsion ![]() $\tau (f)=1\in \operatorname {Wh}(\mathbb {Z}/n)$.
$\tau (f)=1\in \operatorname {Wh}(\mathbb {Z}/n)$.
Proof. Fix a cell complex ![]() $A\cong S^{1}\times S^{1}$ and extend it to a cell complex
$A\cong S^{1}\times S^{1}$ and extend it to a cell complex ![]() $B\cong S^{1}\times D^{2}$. Denote by
$B\cong S^{1}\times D^{2}$. Denote by ![]() $Y(K)$ and
$Y(K)$ and ![]() $Y(U)$ any fixed choice of cell structures for
$Y(U)$ any fixed choice of cell structures for ![]() $E(K)$ and
$E(K)$ and ![]() $E(U)$ (we will make quite specific choices later). For each of
$E(U)$ (we will make quite specific choices later). For each of ![]() $J=U, K$, let
$J=U, K$, let ![]() $M(J)$ denote the cell complex obtained as the mapping cylinder of a map
$M(J)$ denote the cell complex obtained as the mapping cylinder of a map ![]() $A\to Y(J)$ which is a cellular approximation to the inclusion
$A\to Y(J)$ which is a cellular approximation to the inclusion ![]() $S^{1}\times S^{1}\to E(J)$.
$S^{1}\times S^{1}\to E(J)$.
Each of these spaces has a ![]() $\mathbb {Z}/n$ cover, determined by
$\mathbb {Z}/n$ cover, determined by ![]() $\pi _1(L(n,1))\cong \mathbb {Z}/n$ and composing with, where appropriate, the map
$\pi _1(L(n,1))\cong \mathbb {Z}/n$ and composing with, where appropriate, the map ![]() $f$. Choose a lift of the cell structure on
$f$. Choose a lift of the cell structure on ![]() $A$ to the
$A$ to the ![]() $\mathbb {Z}/n$ cover, and denote this by
$\mathbb {Z}/n$ cover, and denote this by ![]() $\widetilde{A}$. Extend this lift to
$\widetilde{A}$. Extend this lift to ![]() $B$,
$B$, ![]() $M(J)$ and
$M(J)$ and ![]() $M(U)$ and write
$M(U)$ and write ![]() $\widetilde{B}$,
$\widetilde{B}$, ![]() $\widetilde {M(J)}$ and
$\widetilde {M(J)}$ and ![]() $\widetilde {M(U)}$ for the corresponding covering spaces. Write
$\widetilde {M(U)}$ for the corresponding covering spaces. Write ![]() $\widetilde{f}$ for a lift of
$\widetilde{f}$ for a lift of ![]() $f$ to the
$f$ to the ![]() $\mathbb {Z}/n$ covers.
$\mathbb {Z}/n$ covers.

In this diagram we use cellular chain complexes and ![]() $\mathscr {C}$ denotes taking an algebraic mapping cone. Strictly, we have replaced the maps
$\mathscr {C}$ denotes taking an algebraic mapping cone. Strictly, we have replaced the maps ![]() $\widetilde{f}$ and
$\widetilde{f}$ and ![]() $\widetilde{f}|_{\widetilde {M(K)}}$ by cellular approximations. This is thus a diagram in the category of finite, finitely generated, based
$\widetilde{f}|_{\widetilde {M(K)}}$ by cellular approximations. This is thus a diagram in the category of finite, finitely generated, based ![]() $\mathbb {Z}[\mathbb {Z}/n]$-coefficient chain complexes. All complexes in the lower sequence are acyclic so by the multiplicativity of torsion under such exact sequences, and the fact that the identity map has vanishing torsion, we obtain
$\mathbb {Z}[\mathbb {Z}/n]$-coefficient chain complexes. All complexes in the lower sequence are acyclic so by the multiplicativity of torsion under such exact sequences, and the fact that the identity map has vanishing torsion, we obtain ![]() $\tau (f)=\tau (\widetilde{f}_*)=\tau ((\widetilde{f}|_{\widetilde {M(K)}})_*)\in \operatorname {Wh}(\mathbb {Z}/n)$.
$\tau (f)=\tau (\widetilde{f}_*)=\tau ((\widetilde{f}|_{\widetilde {M(K)}})_*)\in \operatorname {Wh}(\mathbb {Z}/n)$.
We now choose convenient cell structures for ![]() $E(K)$ and
$E(K)$ and ![]() $E(U)$. Let
$E(U)$. Let ![]() $Y(K)$ and
$Y(K)$ and ![]() $Y(U)$ be the cell structures associated to Wirtinger presentations of the respective knot groups (see e.g. proof of [Reference TuraevTur01, Theorem 16.5]), where for
$Y(U)$ be the cell structures associated to Wirtinger presentations of the respective knot groups (see e.g. proof of [Reference TuraevTur01, Theorem 16.5]), where for ![]() $K$ we choose an arbitrary such presentation and for
$K$ we choose an arbitrary such presentation and for ![]() $U$ we choose the presentation of
$U$ we choose the presentation of ![]() $\mathbb {Z}$ with no relations. By [Reference TuraevTur01, Lemma 8.4], the Whitehead torsions
$\mathbb {Z}$ with no relations. By [Reference TuraevTur01, Lemma 8.4], the Whitehead torsions ![]() $\tau (M(J),Y(J))=1$ for each of
$\tau (M(J),Y(J))=1$ for each of ![]() $J=K,U$, so we have that
$J=K,U$, so we have that ![]() $\tau ((\widetilde{f}|_{\widetilde {M(K)}})_*)$ may be computed by a cellular map
$\tau ((\widetilde{f}|_{\widetilde {M(K)}})_*)$ may be computed by a cellular map ![]() $F\colon \widetilde {Y(K)}\to \widetilde {Y(U)}$ representing
$F\colon \widetilde {Y(K)}\to \widetilde {Y(U)}$ representing ![]() $\widetilde{f}|_{\widetilde {E(K)}}$. This map is given by
$\widetilde{f}|_{\widetilde {E(K)}}$. This map is given by

where we are writing ![]() $\mathbb {Z}[\mathbb {Z}/n]=\mathbb {Z}[t, t^{-1}]/(t^{n}-1)$,
$\mathbb {Z}[\mathbb {Z}/n]=\mathbb {Z}[t, t^{-1}]/(t^{n}-1)$, ![]() $m+1$ is the number of generators in the Wirtinger presentation for
$m+1$ is the number of generators in the Wirtinger presentation for ![]() $\pi _1(K)$, and
$\pi _1(K)$, and ![]() $\partial _2(t)$ is determined by the relations in that presentation. Up to basis change, and a simple homotopy equivalence, the algebraic mapping cone
$\partial _2(t)$ is determined by the relations in that presentation. Up to basis change, and a simple homotopy equivalence, the algebraic mapping cone ![]() $\mathscr {C}(F)$ is
$\mathscr {C}(F)$ is
where ![]() $\partial '_2(t)$ is the effect of deleting a row from the matrix
$\partial '_2(t)$ is the effect of deleting a row from the matrix ![]() $\partial _2(t)$, after the basis change. We then compute that
$\partial _2(t)$, after the basis change. We then compute that ![]() $\tau ((\widetilde{f}|_{\widetilde {M(K)}})_*)=\tau (F)=\big [ \partial '_2(t)\big ]\in \operatorname {Wh}(\mathbb {Z}/n)$.
$\tau ((\widetilde{f}|_{\widetilde {M(K)}})_*)=\tau (F)=\big [ \partial '_2(t)\big ]\in \operatorname {Wh}(\mathbb {Z}/n)$.
When ![]() $G$ is an abelian group, the determinant map
$G$ is an abelian group, the determinant map ![]() $\det \colon K_1(\mathbb {Z}[G])\to (\mathbb {Z}[G])^{\times }$ is a split surjection (see e.g. [Reference MilnorMil66, p. 359]), and for any finite cyclic
$\det \colon K_1(\mathbb {Z}[G])\to (\mathbb {Z}[G])^{\times }$ is a split surjection (see e.g. [Reference MilnorMil66, p. 359]), and for any finite cyclic ![]() $G$ the kernel of this map vanishes [Reference OliverOli88, Theorem 5.6]. So the determinant gives an isomorphism
$G$ the kernel of this map vanishes [Reference OliverOli88, Theorem 5.6]. So the determinant gives an isomorphism ![]() $K_1(\mathbb {Z}[\mathbb {Z}/n])\cong (\mathbb {Z}[\mathbb {Z}/n])^{\times }$. The matrix
$K_1(\mathbb {Z}[\mathbb {Z}/n])\cong (\mathbb {Z}[\mathbb {Z}/n])^{\times }$. The matrix ![]() $\partial _2'(t)$ is a presentation matrix for the Alexander module of
$\partial _2'(t)$ is a presentation matrix for the Alexander module of ![]() $K$ when considered over the ring
$K$ when considered over the ring ![]() $\mathbb {Z}[t,t^{-1}]$. From this, and using the left regular representation of
$\mathbb {Z}[t,t^{-1}]$. From this, and using the left regular representation of ![]() $\mathbb {Z}[\mathbb {Z}/n]$, we may consider
$\mathbb {Z}[\mathbb {Z}/n]$, we may consider ![]() $\partial '_2$ as an
$\partial '_2$ as an ![]() $mn\times mn$ matrix over
$mn\times mn$ matrix over ![]() $\mathbb {Z}$, such that the absolute value of the determinant
$\mathbb {Z}$, such that the absolute value of the determinant ![]() $|{\det (\partial '_2)}|$ is the order of the first homology of the
$|{\det (\partial '_2)}|$ is the order of the first homology of the ![]() $n$-fold branched cover
$n$-fold branched cover ![]() $H_1(\Sigma _n(K);\mathbb {Z})$. This, in turn, is the order of
$H_1(\Sigma _n(K);\mathbb {Z})$. This, in turn, is the order of ![]() $H_1(S^{3}_n(K);\mathbb {Z}[\mathbb {Z}/n])$, which we have assumed to be
$H_1(S^{3}_n(K);\mathbb {Z}[\mathbb {Z}/n])$, which we have assumed to be ![]() $1$. Thus, as an element of
$1$. Thus, as an element of ![]() $K_1(\mathbb {Z}[\mathbb {Z}/n])\cong (\mathbb {Z}[\mathbb {Z}/n])^{\times }$, we have that
$K_1(\mathbb {Z}[\mathbb {Z}/n])\cong (\mathbb {Z}[\mathbb {Z}/n])^{\times }$, we have that ![]() $\tau (F)=\det (\partial '_2(t))=\pm 1$, under this isomorphism. Finally, both
$\tau (F)=\det (\partial '_2(t))=\pm 1$, under this isomorphism. Finally, both ![]() $+1$ and
$+1$ and ![]() $-1$ become the trivial element on passage to the Whitehead group
$-1$ become the trivial element on passage to the Whitehead group ![]() $\operatorname {Wh}(\mathbb {Z}/n)$, so we obtain the desired result.
$\operatorname {Wh}(\mathbb {Z}/n)$, so we obtain the desired result.
Lemma 4.6 When ![]() $\operatorname {Arf}(K)=0$, there exists a degree-one normal map
$\operatorname {Arf}(K)=0$, there exists a degree-one normal map ![]() $(S_n^{3}(K),f)$ satisfying the conditions of Lemma 4.4, and that is degree-one normal bordant over
$(S_n^{3}(K),f)$ satisfying the conditions of Lemma 4.4, and that is degree-one normal bordant over ![]() $L(n,1)$ to the identity map
$L(n,1)$ to the identity map ![]() $(L(n,1),\operatorname {Id})$.
$(L(n,1),\operatorname {Id})$.
Proof. Write ![]() $f \colon S_n^{3}(K) \to L(n,1)$ for the degree-one normal map obtained in Lemma 4.4. By Remark 4.3, if we can show there is a degree-one map
$f \colon S_n^{3}(K) \to L(n,1)$ for the degree-one normal map obtained in Lemma 4.4. By Remark 4.3, if we can show there is a degree-one map ![]() $F\colon W\to L(n,1)\times I$ describing a stably framed cobordism over
$F\colon W\to L(n,1)\times I$ describing a stably framed cobordism over ![]() $L(n,1)$ from
$L(n,1)$ from ![]() $(S_n^{3}(K),f)$ to
$(S_n^{3}(K),f)$ to ![]() $(L(n,1),\operatorname {Id})$, we will be done. (Note, we may change the choice of stable framing on
$(L(n,1),\operatorname {Id})$, we will be done. (Note, we may change the choice of stable framing on ![]() $S_n^{3}(K)$ during the course of the proof.)
$S_n^{3}(K)$ during the course of the proof.)
Consider the closed 3-manifold
glueing so that the result is homeomorphic to the 0-framed surgery ![]() $S^{3}_0(K)$, but we decompose it in this way for later. Choose a framing of the tangent bundle of
$S^{3}_0(K)$, but we decompose it in this way for later. Choose a framing of the tangent bundle of ![]() $N_K$ that is a product framing on
$N_K$ that is a product framing on ![]() $S^{1} \times S^{1} \times I$. This determines an element of
$S^{1} \times S^{1} \times I$. This determines an element of ![]() $[N_K,g]\in \Omega _3^{\operatorname {fr}}(S^{1} \times D^{2}\times I)$, where the map
$[N_K,g]\in \Omega _3^{\operatorname {fr}}(S^{1} \times D^{2}\times I)$, where the map ![]() $g\colon N_K\to S^{1} \times D^{2} \times I = E(U) \times I$ has image
$g\colon N_K\to S^{1} \times D^{2} \times I = E(U) \times I$ has image
and is obtained by glueing together the standard degree-one map ![]() $E(K) \to E(U) = S^{1} \times D^{2}$, the identity on
$E(K) \to E(U) = S^{1} \times D^{2}$, the identity on ![]() $S^{1} \times S^{1} \times I$, and the canonical identification
$S^{1} \times S^{1} \times I$, and the canonical identification ![]() $E(U) \to S^{1} \times D^{2}$.
$E(U) \to S^{1} \times D^{2}$.
We have ![]() $\Omega _3^{\operatorname {fr}}(S^{1} \times D^{2}\times I) \cong \Omega ^{\operatorname {fr}}_3(S^{1})$. The map from
$\Omega _3^{\operatorname {fr}}(S^{1} \times D^{2}\times I) \cong \Omega ^{\operatorname {fr}}_3(S^{1})$. The map from ![]() $S^{1}$ to a point induces a split short exact sequence
$S^{1}$ to a point induces a split short exact sequence ![]() $0\to \widetilde{\Omega }_3^{\operatorname {fr}}(S^{1})\to \Omega ^{\operatorname {fr}}_3(S^{1})\to \Omega ^{\operatorname {fr}}_3\to 0$. Thus
$0\to \widetilde{\Omega }_3^{\operatorname {fr}}(S^{1})\to \Omega ^{\operatorname {fr}}_3(S^{1})\to \Omega ^{\operatorname {fr}}_3\to 0$. Thus ![]() $\Omega ^{\operatorname {fr}}_3(S^{1})\cong \Omega ^{\operatorname {fr}}_3\oplus \Omega ^{\operatorname {fr}}_2$, where we have used the isomorphism
$\Omega ^{\operatorname {fr}}_3(S^{1})\cong \Omega ^{\operatorname {fr}}_3\oplus \Omega ^{\operatorname {fr}}_2$, where we have used the isomorphism ![]() $\widetilde{\Omega }^{\operatorname {fr}}_3(S^{1})\cong \widetilde{\Omega }^{\operatorname {fr}}_2(S^{0})\cong \Omega ^{\operatorname {fr}}_2$, coming from the fact that
$\widetilde{\Omega }^{\operatorname {fr}}_3(S^{1})\cong \widetilde{\Omega }^{\operatorname {fr}}_2(S^{0})\cong \Omega ^{\operatorname {fr}}_2$, coming from the fact that ![]() $\Omega _*^{\operatorname {fr}}(-)$ is a generalised homology theory and thus satisfies the suspension axiom. Under this isomorphism, the projection of
$\Omega _*^{\operatorname {fr}}(-)$ is a generalised homology theory and thus satisfies the suspension axiom. Under this isomorphism, the projection of ![]() $[N_K,g]$ to
$[N_K,g]$ to ![]() $\Omega _3^{\operatorname {fr}}\cong \mathbb {Z}/24$ is given by the framed bordism class of
$\Omega _3^{\operatorname {fr}}\cong \mathbb {Z}/24$ is given by the framed bordism class of ![]() $N_K$. Since any element in
$N_K$. Since any element in ![]() $\Omega _3^{\operatorname {fr}}\cong \mathbb {Z}/24$ can be realised by a suitable framing on
$\Omega _3^{\operatorname {fr}}\cong \mathbb {Z}/24$ can be realised by a suitable framing on ![]() $S^{3}$, the framing of
$S^{3}$, the framing of ![]() $N_K$ can be modified in a small neighbourhood until the element in
$N_K$ can be modified in a small neighbourhood until the element in ![]() $\Omega _3^{\operatorname {fr}}\cong \mathbb {Z}/24$ vanishes; see e.g. [Reference Cha and PowellCP14, p. 13] for details.
$\Omega _3^{\operatorname {fr}}\cong \mathbb {Z}/24$ vanishes; see e.g. [Reference Cha and PowellCP14, p. 13] for details.
The map from ![]() $\Omega _2^{\operatorname {fr}}\cong \widetilde{\Omega }_2^{\operatorname {fr}}(S^{0})\cong \widetilde{\Omega }_3^{\operatorname {fr}}(S^{1})\to \Omega _3(S^{1})$ is given by applying the reduced suspension, sending the class of
$\Omega _2^{\operatorname {fr}}\cong \widetilde{\Omega }_2^{\operatorname {fr}}(S^{0})\cong \widetilde{\Omega }_3^{\operatorname {fr}}(S^{1})\to \Omega _3(S^{1})$ is given by applying the reduced suspension, sending the class of ![]() $f\colon F^{2}\to \operatorname {pt}$ to
$f\colon F^{2}\to \operatorname {pt}$ to ![]() $f\times \operatorname {Id}\colon F\times S^{1}\to S^{1}$ in
$f\times \operatorname {Id}\colon F\times S^{1}\to S^{1}$ in ![]() $\Omega _3(S^{1})$, and framing
$\Omega _3(S^{1})$, and framing ![]() $F\times S^{1}$ via the product framing with the trivial framing on
$F\times S^{1}$ via the product framing with the trivial framing on ![]() $S^{1}$. Under the projection
$S^{1}$. Under the projection ![]() $\Omega _3(S^{1})\to \Omega _2^{\operatorname {fr}}$, the class
$\Omega _3(S^{1})\to \Omega _2^{\operatorname {fr}}$, the class ![]() $[N_K,g]$ is thus mapped to a framed surface
$[N_K,g]$ is thus mapped to a framed surface ![]() $F$ given by taking the transverse preimage of a regular point in
$F$ given by taking the transverse preimage of a regular point in ![]() $S^{1}$ under
$S^{1}$ under ![]() $g$. Recall that
$g$. Recall that ![]() $g$ was obtained using the standard degree-one normal maps
$g$ was obtained using the standard degree-one normal maps ![]() $E(K)\to E(U)$ and
$E(K)\to E(U)$ and ![]() $E(U)\to E(U)$. Under these, generic transverse point preimages are Seifert surfaces,
$E(U)\to E(U)$. Under these, generic transverse point preimages are Seifert surfaces, ![]() $F_K$ and
$F_K$ and ![]() $F_U$, respectively for the knots
$F_U$, respectively for the knots ![]() $K$ and
$K$ and ![]() $U$. Thus the projection to
$U$. Thus the projection to ![]() $\Omega _2^{\operatorname {fr}}$ is the Arf invariant of the framed surface
$\Omega _2^{\operatorname {fr}}$ is the Arf invariant of the framed surface ![]() $F=F_K \cup (\{\operatorname {pt}\} \times S^{1} )\cup - F_U$. Since we assumed that
$F=F_K \cup (\{\operatorname {pt}\} \times S^{1} )\cup - F_U$. Since we assumed that ![]() $\operatorname {Arf}(K)=0$ this component already vanishes in
$\operatorname {Arf}(K)=0$ this component already vanishes in ![]() $\Omega ^{\operatorname {fr}}_2$. So overall we obtain
$\Omega ^{\operatorname {fr}}_2$. So overall we obtain ![]() $[N_K,g]=0\in \Omega _3^{\operatorname {fr}}(S^{1} \times D^{2}\times I)$
$[N_K,g]=0\in \Omega _3^{\operatorname {fr}}(S^{1} \times D^{2}\times I)$
Write ![]() $W'$ for a framed null bordism of
$W'$ for a framed null bordism of ![]() $(N_K,g)$ over
$(N_K,g)$ over ![]() $S^{1} \times D^{2}\times I$. Now attach
$S^{1} \times D^{2}\times I$. Now attach ![]() $D^{2}\times S^{1} \times I$ to
$D^{2}\times S^{1} \times I$ to ![]() $S^{1} \times S^{1} \times I$ such that
$S^{1} \times S^{1} \times I$ such that ![]() $D^{2}\times S^{1} \times \{t\}$ attaches to
$D^{2}\times S^{1} \times \{t\}$ attaches to ![]() $S^{1} \times S^{1} \times \{t\}$ with the
$S^{1} \times S^{1} \times \{t\}$ with the ![]() $n$-framing, and similarly attach the
$n$-framing, and similarly attach the ![]() $n$-framed
$n$-framed ![]() $D^{2}\times S^{1} \times I$ to the codomain
$D^{2}\times S^{1} \times I$ to the codomain ![]() $S^{1}\times D^{2} \times I$. This yields a map
$S^{1}\times D^{2} \times I$. This yields a map ![]() $F\colon W\to L(n,1)\times I$ that describes a framed cobordism from
$F\colon W\to L(n,1)\times I$ that describes a framed cobordism from ![]() $(S_n^{3}(K),f)$ to
$(S_n^{3}(K),f)$ to ![]() $(L(n,1),\operatorname {Id})$, over
$(L(n,1),\operatorname {Id})$, over ![]() $L(n,1)$. To see that the cobordism is framed, note that we can glue the two framings together along the product framing on both pieces
$L(n,1)$. To see that the cobordism is framed, note that we can glue the two framings together along the product framing on both pieces ![]() $W'$ and
$W'$ and ![]() $D^{2} \times S^{1} \times I$.
$D^{2} \times S^{1} \times I$.
We finally also note that the map ![]() $F\colon W\to L(n,1)$ is degree one. This can be computed by considering the naturality of the long exact sequences in homology of the pairs
$F\colon W\to L(n,1)$ is degree one. This can be computed by considering the naturality of the long exact sequences in homology of the pairs ![]() $(W,\partial W)$ and
$(W,\partial W)$ and ![]() $(L(n,1) \times I,L(n,1) \times \{0,1\})$, and the fact that both components of
$(L(n,1) \times I,L(n,1) \times \{0,1\})$, and the fact that both components of ![]() $\partial F$ are already known to be degree one.
$\partial F$ are already known to be degree one.
Remark 4.7 For even ![]() $n$, there is a sequence of group homomorphisms
$n$, there is a sequence of group homomorphisms
given from left to right by: the inclusion of ![]() $L(n,1)$ as the
$L(n,1)$ as the ![]() $3$-skeleton, the surjective group homomorphism
$3$-skeleton, the surjective group homomorphism ![]() $\mathbb {Z}/n\to \mathbb {Z}/2$, and the forgetful map.
$\mathbb {Z}/n\to \mathbb {Z}/2$, and the forgetful map.
An argument similar to that of [Reference Hambleton and SuHS13, Lemma 4.2] can be made to determine that ![]() $\Omega _3^{\operatorname {Spin}}(B(\mathbb {Z}/2))\cong \Omega _2^{\operatorname {Pin}^{-}}\cong \mathbb {Z}/8$. This argument would take us too far afield here, but we allow ourselves to consider the consequences. Under this isomorphism, the element of
$\Omega _3^{\operatorname {Spin}}(B(\mathbb {Z}/2))\cong \Omega _2^{\operatorname {Pin}^{-}}\cong \mathbb {Z}/8$. This argument would take us too far afield here, but we allow ourselves to consider the consequences. Under this isomorphism, the element of ![]() $\mathbb {Z}/8$ is detected by the Brown invariant of a
$\mathbb {Z}/8$ is detected by the Brown invariant of a ![]() $\operatorname {Pin}^{-}$ structure on the surface in
$\operatorname {Pin}^{-}$ structure on the surface in ![]() $M$ that is the transverse preimage of
$M$ that is the transverse preimage of ![]() $\mathbb {RP}^{2} \subseteq \mathbb {RP}^{3}$, the
$\mathbb {RP}^{2} \subseteq \mathbb {RP}^{3}$, the ![]() $3$-skeleton of
$3$-skeleton of ![]() $B(\mathbb {Z}/2)$. Let
$B(\mathbb {Z}/2)$. Let ![]() $(M,f)\in \Omega _3^{\operatorname {Spin}}(B(\mathbb {Z}/2))$ with
$(M,f)\in \Omega _3^{\operatorname {Spin}}(B(\mathbb {Z}/2))$ with ![]() $f^{-1}(\mathbb {RP}^{2})=N\subset M$. The
$f^{-1}(\mathbb {RP}^{2})=N\subset M$. The ![]() $\operatorname {Pin}^{-}$ structure on
$\operatorname {Pin}^{-}$ structure on ![]() $N$ gives a
$N$ gives a ![]() $\mathbb {Z}/4$ enhancement of the
$\mathbb {Z}/4$ enhancement of the ![]() $\mathbb {Z}/2$ intersection form on
$\mathbb {Z}/2$ intersection form on ![]() $N$, which counts the number of half twists modulo 4 of the bands. If the surface
$N$, which counts the number of half twists modulo 4 of the bands. If the surface ![]() $N$ is orientable, then the enhancement lies in
$N$ is orientable, then the enhancement lies in ![]() $2\mathbb {Z}/4$ and the Brown invariant lies in
$2\mathbb {Z}/4$ and the Brown invariant lies in ![]() $4\mathbb {Z}/8\cong \mathbb {Z}/2$, computing the Arf invariant of the surface
$4\mathbb {Z}/8\cong \mathbb {Z}/2$, computing the Arf invariant of the surface ![]() $N$ with respect to the
$N$ with respect to the ![]() $\operatorname {Spin}$ structure on
$\operatorname {Spin}$ structure on ![]() $N$ pulled back from
$N$ pulled back from ![]() $M$ [Reference Kirby and TaylorKT90, § 3].
$M$ [Reference Kirby and TaylorKT90, § 3].
In our case, the map ![]() $f$ is the one from Lemma 4.4, and is constructed as a Pontryagin–Thom collapse on a normal neighbourhood of a Seifert surface, followed by the extension to the Dehn filling. Thus in this case, the surface
$f$ is the one from Lemma 4.4, and is constructed as a Pontryagin–Thom collapse on a normal neighbourhood of a Seifert surface, followed by the extension to the Dehn filling. Thus in this case, the surface ![]() $N=f^{-1}(\mathbb {RP}^{2})\subset S^{3}_n(K)$ is represented by a capped off Seifert surface for
$N=f^{-1}(\mathbb {RP}^{2})\subset S^{3}_n(K)$ is represented by a capped off Seifert surface for ![]() $K$. This shows that the obstruction to vanishing of
$K$. This shows that the obstruction to vanishing of ![]() $(S^{3}_n(K),f)\in \Omega _3^{\operatorname {Spin}}(B(\mathbb {Z}/2))$ is given by the Arf invariant of the knot.
$(S^{3}_n(K),f)\in \Omega _3^{\operatorname {Spin}}(B(\mathbb {Z}/2))$ is given by the Arf invariant of the knot.
For even ![]() $n$, Remark 4.7 shows that the bordism of Lemma 4.6 cannot exist unless
$n$, Remark 4.7 shows that the bordism of Lemma 4.6 cannot exist unless ![]() $\operatorname {Arf}(K)=0$. This is not so for
$\operatorname {Arf}(K)=0$. This is not so for ![]() $n$ odd, and to demonstrate this we now include an alternative existence proof for degree one normal bordism, with no Arf invariant assumption, when
$n$ odd, and to demonstrate this we now include an alternative existence proof for degree one normal bordism, with no Arf invariant assumption, when ![]() $n$ is odd.
$n$ is odd.
Lemma 4.8 For ![]() $n$ odd, there exists a degree-one normal map
$n$ odd, there exists a degree-one normal map ![]() $(S_n^{3}(K),f)$ that satisfies the conditions of Lemma 4.4 and is degree-one normal bordant over
$(S_n^{3}(K),f)$ that satisfies the conditions of Lemma 4.4 and is degree-one normal bordant over ![]() $L(n,1)$ to the identity map
$L(n,1)$ to the identity map ![]() $(L(n,1),\operatorname {Id})$.
$(L(n,1),\operatorname {Id})$.
Proof. Write ![]() $f \colon S_n^{3}(K) \to L(n,1)$ for the degree-one normal map obtained in Lemma 4.4. Again, by Remark 4.3, the objective is to show there is a degree-one map
$f \colon S_n^{3}(K) \to L(n,1)$ for the degree-one normal map obtained in Lemma 4.4. Again, by Remark 4.3, the objective is to show there is a degree-one map ![]() $F\colon W\to L(n,1)\times I$ describing a stably framed cobordism over
$F\colon W\to L(n,1)\times I$ describing a stably framed cobordism over ![]() $L(n,1)$ from
$L(n,1)$ from ![]() $(S_n^{3}(K),f)$ to
$(S_n^{3}(K),f)$ to ![]() $(L(n,1),\operatorname {Id})$.
$(L(n,1),\operatorname {Id})$.
We show that there is a choice of stable framing for ![]() $S_n^{3}(K)$ such that
$S_n^{3}(K)$ such that ![]() $[S_n^{3}(K),f] - [L(n,1),\operatorname {Id}] =0 \in \Omega ^{\operatorname {fr}}_3(L(n,1))$.
$[S_n^{3}(K),f] - [L(n,1),\operatorname {Id}] =0 \in \Omega ^{\operatorname {fr}}_3(L(n,1))$.
Consider the Atiyah–Hirzebruch spectral sequence for ![]() $\Omega _*^{\operatorname {fr}}(-)$, with
$\Omega _*^{\operatorname {fr}}(-)$, with ![]() $E^{2}$ page
$E^{2}$ page ![]() $E^{2}_{p,q}= H_p(L(n,1);\Omega ^{\operatorname {fr}}_q)$ and converging to
$E^{2}_{p,q}= H_p(L(n,1);\Omega ^{\operatorname {fr}}_q)$ and converging to ![]() $\Omega _{p+q}^{\operatorname {fr}}(L(n,1))$. By inspection of the differentials, this sequence collapses already at the
$\Omega _{p+q}^{\operatorname {fr}}(L(n,1))$. By inspection of the differentials, this sequence collapses already at the ![]() $E^{2}$ page, so the groups
$E^{2}$ page, so the groups ![]() $H_p(L(n,1);\Omega ^{\operatorname {fr}}_q)$ form iterated graded quotients for a filtration of
$H_p(L(n,1);\Omega ^{\operatorname {fr}}_q)$ form iterated graded quotients for a filtration of ![]() $\Omega ^{\operatorname {fr}}_3(L(n,1))$. We note that by the Pontryagin–Thom theorem, we have
$\Omega ^{\operatorname {fr}}_3(L(n,1))$. We note that by the Pontryagin–Thom theorem, we have ![]() $\Omega _q^{\operatorname {fr}}= \mathbb {Z},\mathbb {Z}/2,\mathbb {Z}/2,\mathbb {Z}/24$ when
$\Omega _q^{\operatorname {fr}}= \mathbb {Z},\mathbb {Z}/2,\mathbb {Z}/2,\mathbb {Z}/24$ when ![]() $q=0,1,2,3$ respectively.
$q=0,1,2,3$ respectively.
We analyse the groups on the ![]() $E^{2}$ page in turn by considering the CW decomposition of
$E^{2}$ page in turn by considering the CW decomposition of ![]() $L(n,1)$ with a single
$L(n,1)$ with a single ![]() $p$-cell
$p$-cell ![]() $e^{p}$ for each of
$e^{p}$ for each of ![]() $p=0,1,2,3$ and recalling that the
$p=0,1,2,3$ and recalling that the ![]() $E^{1}$ page is given by
$E^{1}$ page is given by
where ![]() $X^{(p)}$ denotes the
$X^{(p)}$ denotes the ![]() $p$-skeleton of
$p$-skeleton of ![]() $L(n,1)$. The groups on the
$L(n,1)$. The groups on the ![]() $E^{2}$ page can be considered as a sequence of obstructions to finding a framed null-bordism of
$E^{2}$ page can be considered as a sequence of obstructions to finding a framed null-bordism of ![]() $S^{3}_n(K)\sqcup -L(n,1)$ over
$S^{3}_n(K)\sqcup -L(n,1)$ over ![]() $L(n,1)$ so we analyse these obstructions in turn.
$L(n,1)$ so we analyse these obstructions in turn.
At ![]() $q=0$, a representative class for
$q=0$, a representative class for ![]() $[S_n^{3}(K),f] - [L(n,1),\operatorname {Id}]\in \Omega _3^{\operatorname {fr}}(L(n,1))$ is given by a cycle in
$[S_n^{3}(K),f] - [L(n,1),\operatorname {Id}]\in \Omega _3^{\operatorname {fr}}(L(n,1))$ is given by a cycle in ![]() $E^{1}_{3,0}=\Omega ^{\operatorname {fr}}_3(X^{(3)},X^{(2)})$. The resulting class in
$E^{1}_{3,0}=\Omega ^{\operatorname {fr}}_3(X^{(3)},X^{(2)})$. The resulting class in ![]() $E^{2}$ vanishes if we can do surgery on the disjoint union
$E^{2}$ vanishes if we can do surgery on the disjoint union ![]() $S_n^{3}(K)\sqcup - L(n,1)$ in a way that respects the degree-one normal maps to
$S_n^{3}(K)\sqcup - L(n,1)$ in a way that respects the degree-one normal maps to ![]() $L(n,1)$ and such that the effect of surgery maps to the
$L(n,1)$ and such that the effect of surgery maps to the ![]() $2$-skeleton of
$2$-skeleton of ![]() $L(n,1)$. In other words we seek to compatibly stably frame the connected sum
$L(n,1)$. In other words we seek to compatibly stably frame the connected sum ![]() $S_n^{3}(K)\#(- L(n,1))$. The obstruction to doing this is the difference of
$S_n^{3}(K)\#(- L(n,1))$. The obstruction to doing this is the difference of ![]() $f_*[S_n^{3}(K)]-\operatorname {Id}_*[L(n,1)]\in H_3(L(n,1);\Omega _0^{\operatorname {fr}})$, which vanishes because the maps
$f_*[S_n^{3}(K)]-\operatorname {Id}_*[L(n,1)]\in H_3(L(n,1);\Omega _0^{\operatorname {fr}})$, which vanishes because the maps ![]() $f$ and
$f$ and ![]() $\operatorname {Id}$ are degree one.
$\operatorname {Id}$ are degree one.
Next, for ![]() $q=1$ and
$q=1$ and ![]() $q=2$ homology computations using that
$q=2$ homology computations using that ![]() $n$ is odd show that both
$n$ is odd show that both ![]() $H_2(L(n,1);\Omega ^{\operatorname {fr}}_1) = 0$ and
$H_2(L(n,1);\Omega ^{\operatorname {fr}}_1) = 0$ and ![]() $H_1(L(n,1);\Omega ^{\operatorname {fr}}_2)=0$, so there is no obstruction here. Thus we may assume we have done surgery on
$H_1(L(n,1);\Omega ^{\operatorname {fr}}_2)=0$, so there is no obstruction here. Thus we may assume we have done surgery on ![]() $S_n^{3}(K)\sqcup (-L(n,1))$ over
$S_n^{3}(K)\sqcup (-L(n,1))$ over ![]() $L(n,1)$ to obtain some closed, connected
$L(n,1)$ to obtain some closed, connected ![]() $Y$ together with a degree-one normal map
$Y$ together with a degree-one normal map ![]() $g\colon Y\to L(n,1)$, where the map
$g\colon Y\to L(n,1)$, where the map ![]() $g\colon Y\to L(n,1)$ has codomain the
$g\colon Y\to L(n,1)$ has codomain the ![]() $0$-skeleton, and
$0$-skeleton, and ![]() $[Y,g]=[S_3(K),f)]-[L(n,1),\operatorname {Id}]\in \Omega _3^{\operatorname {fr}}(L(n,1))$.
$[Y,g]=[S_3(K),f)]-[L(n,1),\operatorname {Id}]\in \Omega _3^{\operatorname {fr}}(L(n,1))$.
Finally, for ![]() $q=3$, the last
$q=3$, the last ![]() $E^{2}$ page obstruction is given by a class in
$E^{2}$ page obstruction is given by a class in ![]() $E^{1}_{0,3}=\Omega _3^{\operatorname {fr}}(X^{(0)},\emptyset )$ which is equal to
$E^{1}_{0,3}=\Omega _3^{\operatorname {fr}}(X^{(0)},\emptyset )$ which is equal to ![]() $[Y]\in \Omega _3^{\operatorname {fr}}\cong \mathbb {Z}/24$. By framed bordism invariance, this is equal to
$[Y]\in \Omega _3^{\operatorname {fr}}\cong \mathbb {Z}/24$. By framed bordism invariance, this is equal to ![]() $[S_n^{3}(K)]-[L(n,1)]\in H_0(L(n,1);\Omega ^{\operatorname {fr}}_3)\cong \Omega _3^{\operatorname {fr}}\cong \mathbb {Z}/24$. Similarly to the proof of Lemma 4.6, the framing near a point in
$[S_n^{3}(K)]-[L(n,1)]\in H_0(L(n,1);\Omega ^{\operatorname {fr}}_3)\cong \Omega _3^{\operatorname {fr}}\cong \mathbb {Z}/24$. Similarly to the proof of Lemma 4.6, the framing near a point in ![]() $S_n^{3}(K)$ may be modified in a small neighbourhood to force vanishing of this obstruction.
$S_n^{3}(K)$ may be modified in a small neighbourhood to force vanishing of this obstruction.
As the various representative elements of ![]() $[S_n^{3}(K),f] - [L(n,1),\operatorname {Id}]\in \Omega _3^{\operatorname {fr}}(L(n,1))$ can be made to vanish on the
$[S_n^{3}(K),f] - [L(n,1),\operatorname {Id}]\in \Omega _3^{\operatorname {fr}}(L(n,1))$ can be made to vanish on the ![]() $E_2$ page, this class vanishes in
$E_2$ page, this class vanishes in ![]() $\Omega ^{\operatorname {fr}}_3(L(n,1))$, and we obtain the required bordism. Similarly to the proof of Lemma 4.6, this bordism over
$\Omega ^{\operatorname {fr}}_3(L(n,1))$, and we obtain the required bordism. Similarly to the proof of Lemma 4.6, this bordism over ![]() $L(n,1)$ is seen to be a degree one normal bordism.
$L(n,1)$ is seen to be a degree one normal bordism.
From this point onwards we require the definition of a degree-one normal map in the topological category. The necessary definitions are identical to those in Definitions 4.1 and 4.2, except now we use the topological stable normal bundle, which is a topological ![]() $\mathbb {R}^{\infty }$-bundle classified by a map into the classifying space
$\mathbb {R}^{\infty }$-bundle classified by a map into the classifying space ![]() $\operatorname {BTOP}$; see e.g. [Reference Friedl, Nagel, Orson and PowellFNOP19, Definition 7.12]. There is a forgetful map
$\operatorname {BTOP}$; see e.g. [Reference Friedl, Nagel, Orson and PowellFNOP19, Definition 7.12]. There is a forgetful map ![]() $\operatorname {BO}\to \operatorname {BTOP}$, under which the stable normal vector bundle of a smooth manifold is sent to the stable topological normal bundle of the underlying topological manifold. The results derived so far in this section thus descend to statements in the topological category.
$\operatorname {BO}\to \operatorname {BTOP}$, under which the stable normal vector bundle of a smooth manifold is sent to the stable topological normal bundle of the underlying topological manifold. The results derived so far in this section thus descend to statements in the topological category.
Proposition 4.9 Let ![]() $K$ be a knot, and let
$K$ be a knot, and let ![]() $n$ be odd. There is a degree-one normal bordism
$n$ be odd. There is a degree-one normal bordism ![]() $F\colon W\to L(n,1)\times I$ from the map
$F\colon W\to L(n,1)\times I$ from the map ![]() $f\colon S_n^{3}(K) \to L(n,1)$ of Lemma 4.4 to
$f\colon S_n^{3}(K) \to L(n,1)$ of Lemma 4.4 to ![]() $\operatorname {Id} \colon L(n,1)\to L(n,1)$, such that
$\operatorname {Id} \colon L(n,1)\to L(n,1)$, such that ![]() $\pi _1(W)\cong \mathbb {Z}/n$ and
$\pi _1(W)\cong \mathbb {Z}/n$ and ![]() $\sigma (W)=0$. The same is true for
$\sigma (W)=0$. The same is true for ![]() $n$ even when
$n$ even when ![]() $\operatorname {Arf}(K)=0$.
$\operatorname {Arf}(K)=0$.
Proof. When ![]() $n$ is odd, we use Lemma 4.8, and when
$n$ is odd, we use Lemma 4.8, and when ![]() $n$ is even we use Lemma 4.6, to obtain a (smooth) degree-one normal bordism
$n$ is even we use Lemma 4.6, to obtain a (smooth) degree-one normal bordism ![]() $W$. Now perform (smooth) 1-surgeries on the interior of
$W$. Now perform (smooth) 1-surgeries on the interior of ![]() $W$ to modify the fundamental group to
$W$ to modify the fundamental group to ![]() $\mathbb {Z}/n$ while still retaining a degree-one normal map. We abuse notation and continue to write
$\mathbb {Z}/n$ while still retaining a degree-one normal map. We abuse notation and continue to write ![]() $F\colon W\to L(n,1)\times I$ for this degree-one map, so that now
$F\colon W\to L(n,1)\times I$ for this degree-one map, so that now ![]() $\pi _1(W) \cong \mathbb {Z}/n$. Next take connected sums with the degree-one normal map
$\pi _1(W) \cong \mathbb {Z}/n$. Next take connected sums with the degree-one normal map ![]() $E_8\to S^{4}$ (or the oppositely oriented version
$E_8\to S^{4}$ (or the oppositely oriented version ![]() $-E_8\to S^{4}$), in order to kill the signature of
$-E_8\to S^{4}$), in order to kill the signature of ![]() $W$. Here
$W$. Here ![]() $E_8$ denotes the
$E_8$ denotes the ![]() $E_8$ manifold, that is, a closed, simply connected topological
$E_8$ manifold, that is, a closed, simply connected topological ![]() $4$-manifold with intersection form given by the
$4$-manifold with intersection form given by the ![]() $E_8$ matrix. The result may no longer be smooth, but now has all the desired properties.
$E_8$ matrix. The result may no longer be smooth, but now has all the desired properties.
The objective is now to perform 2-surgeries on ![]() $W$, so that after the surgeries the map
$W$, so that after the surgeries the map ![]() $W\to L(n,1)\times I$ is a homotopy equivalence. This will imply that
$W\to L(n,1)\times I$ is a homotopy equivalence. This will imply that ![]() $W$ is a
$W$ is a ![]() $\mathbb {Z}[\mathbb {Z}/n]$-coefficient homology bordism from
$\mathbb {Z}[\mathbb {Z}/n]$-coefficient homology bordism from ![]() $S_n^{3}(K)$ to
$S_n^{3}(K)$ to ![]() $L(n,1)$. To analyse whether this is possible, we proceed as in [Reference WallWal99, § 5]. Since
$L(n,1)$. To analyse whether this is possible, we proceed as in [Reference WallWal99, § 5]. Since ![]() $H_2(L(n,1) \times I;\mathbb {Z}[\mathbb {Z}/n]) =0$, the surgery kernel module (see [Reference WallWal99, § 5]) is equal to
$H_2(L(n,1) \times I;\mathbb {Z}[\mathbb {Z}/n]) =0$, the surgery kernel module (see [Reference WallWal99, § 5]) is equal to ![]() $H_2(W;\mathbb {Z}[\mathbb {Z}/n])$ and the middle-dimensional
$H_2(W;\mathbb {Z}[\mathbb {Z}/n])$ and the middle-dimensional ![]() $\mathbb {Z}[\mathbb {Z}/n]$-coefficient intersection pairing
$\mathbb {Z}[\mathbb {Z}/n]$-coefficient intersection pairing
is equal to the surgery kernel pairing. This intersection form, together with the Wall self-intersection form ![]() $\mu$, determine a quadratic form
$\mu$, determine a quadratic form ![]() $(H_2(W;\mathbb {Z}[\mathbb {Z}/n]),\lambda ,\mu )$ over
$(H_2(W;\mathbb {Z}[\mathbb {Z}/n]),\lambda ,\mu )$ over ![]() $\mathbb {Z}[\mathbb {Z}/n]$. In the next lemma we confirm this quadratic form gives a well-defined element in a surgery obstruction group. The obstruction group is analysed in the next section of the article.
$\mathbb {Z}[\mathbb {Z}/n]$. In the next lemma we confirm this quadratic form gives a well-defined element in a surgery obstruction group. The obstruction group is analysed in the next section of the article.
Lemma 4.10 Let ![]() $K\subset S^{3}$ be a knot satisfying
$K\subset S^{3}$ be a knot satisfying ![]() $H_1(S_n^{3}(K);\mathbb {Z}[\mathbb {Z}/n]) = 0$ and suppose there is a degree-one normal bordism
$H_1(S_n^{3}(K);\mathbb {Z}[\mathbb {Z}/n]) = 0$ and suppose there is a degree-one normal bordism ![]() $(W,F)$ as in Proposition 4.9. Then the quadratic form
$(W,F)$ as in Proposition 4.9. Then the quadratic form ![]() $(H_2(W;\mathbb {Z}[\mathbb {Z}/n]),\lambda ,\mu )$ is non-singular and simple, thus it determines a well-defined surgery obstruction in the group
$(H_2(W;\mathbb {Z}[\mathbb {Z}/n]),\lambda ,\mu )$ is non-singular and simple, thus it determines a well-defined surgery obstruction in the group ![]() $L_4^{s}(\mathbb {Z}[\mathbb {Z}/n])$.
$L_4^{s}(\mathbb {Z}[\mathbb {Z}/n])$.
Proof. The quadratic form is non-singular because ![]() $H_1(S_n^{3}(K);\mathbb {Z}[\mathbb {Z}/n]) = 0$, by assumption. We claim this quadratic form is moreover simple (with respect to some stable
$H_1(S_n^{3}(K);\mathbb {Z}[\mathbb {Z}/n]) = 0$, by assumption. We claim this quadratic form is moreover simple (with respect to some stable ![]() $\mathbb {Z}[\mathbb {Z}/n]$ basis). Indeed, the manifold with boundary
$\mathbb {Z}[\mathbb {Z}/n]$ basis). Indeed, the manifold with boundary ![]() $(W,S_n^{3}(K)\sqcup -L(n,1))$ is a simple Poincaré pair [Reference Kirby and SiebenmannKS77, Essay III, Theorem 5.13], so it remains to check that the
$(W,S_n^{3}(K)\sqcup -L(n,1))$ is a simple Poincaré pair [Reference Kirby and SiebenmannKS77, Essay III, Theorem 5.13], so it remains to check that the ![]() $\mathbb {Z}[\mathbb {Z}/n]$-homology equivalence on the boundary
$\mathbb {Z}[\mathbb {Z}/n]$-homology equivalence on the boundary
has vanishing Whitehead torsion. But the identity map has vanishing Whitehead torsion, and so does ![]() $f$ by Lemma 4.5.
$f$ by Lemma 4.5.
5. The surgery obstruction
For all ![]() $n$, the surgery obstruction group
$n$, the surgery obstruction group ![]() $L_4^{s}(\mathbb {Z}[\mathbb {Z}/n])$ has been computed and is given by a collection of signatures known as the multisignature. In this section we describe the multisignature and then relate it to Tristram–Levine signatures of a knot in the case of interest to us.
$L_4^{s}(\mathbb {Z}[\mathbb {Z}/n])$ has been computed and is given by a collection of signatures known as the multisignature. In this section we describe the multisignature and then relate it to Tristram–Levine signatures of a knot in the case of interest to us.
5.1 The multisignature for a general finite group
We first recall some representation theory. Let ![]() $\pi$ be any finite group and let
$\pi$ be any finite group and let ![]() $\mathbb {C}\pi$ be the complex group ring. The elements of the representation ring
$\mathbb {C}\pi$ be the complex group ring. The elements of the representation ring ![]() $R_\mathbb {C}\pi$ are formal additive differences of finitely generated
$R_\mathbb {C}\pi$ are formal additive differences of finitely generated ![]() $\mathbb {C}\pi$-modules. The product structure is given by tensor product; we note the formal addition also agrees with the direct sum of modules.
$\mathbb {C}\pi$-modules. The product structure is given by tensor product; we note the formal addition also agrees with the direct sum of modules.
Given a finitely generated ![]() $\mathbb {C}\pi$-module
$\mathbb {C}\pi$-module ![]() $V$, we obtain the underlying complex vector space, denoted
$V$, we obtain the underlying complex vector space, denoted ![]() $V_\mathbb {C}$, by forgetting the
$V_\mathbb {C}$, by forgetting the ![]() $\pi$ action. For example, the rank
$\pi$ action. For example, the rank ![]() $1$ free module
$1$ free module ![]() $V = \mathbb {C}\pi$ has underlying
$V = \mathbb {C}\pi$ has underlying ![]() $|\pi |$-dimensional complex vector space, which has a natural basis given by the group elements of
$|\pi |$-dimensional complex vector space, which has a natural basis given by the group elements of ![]() $\pi$. We are emphasising the distinction between
$\pi$. We are emphasising the distinction between ![]() $V$ and
$V$ and ![]() $V_\mathbb {C}$ to avoid confusion between rank and dimension, and to increase clarity in later proofs. A
$V_\mathbb {C}$ to avoid confusion between rank and dimension, and to increase clarity in later proofs. A ![]() $\mathbb {C}\pi$-module
$\mathbb {C}\pi$-module ![]() $V$ determines a
$V$ determines a ![]() $\mathbb {C}\pi$-module structure on the complex conjugate vector space
$\mathbb {C}\pi$-module structure on the complex conjugate vector space ![]() $\overline {V_\mathbb {C}}$, and this is called the complex conjugate representation. Those
$\overline {V_\mathbb {C}}$, and this is called the complex conjugate representation. Those ![]() $\mathbb {C}\pi$-modules that are isomorphic to their own complex conjugate representation form a subring
$\mathbb {C}\pi$-modules that are isomorphic to their own complex conjugate representation form a subring ![]() $R_\mathbb {C}^{+}\pi \subset R_\mathbb {C}\pi$ called the purely real representation ring. Given a
$R_\mathbb {C}^{+}\pi \subset R_\mathbb {C}\pi$ called the purely real representation ring. Given a ![]() $\mathbb {C}\pi$-module
$\mathbb {C}\pi$-module ![]() $V$, the character is
$V$, the character is ![]() $\chi _V\colon \pi \to \mathbb {C}$, where
$\chi _V\colon \pi \to \mathbb {C}$, where ![]() $\chi _V(g)$ is the trace of the endomorphism of
$\chi _V(g)$ is the trace of the endomorphism of ![]() $V$ given by
$V$ given by ![]() $g$.
$g$.
Now let ![]() $\lambda \colon V\times V\to \mathbb {C}\pi$ be a hermitian form on a finitely generated
$\lambda \colon V\times V\to \mathbb {C}\pi$ be a hermitian form on a finitely generated ![]() $\mathbb {C}\pi$-module
$\mathbb {C}\pi$-module ![]() $V$. The form
$V$. The form ![]() $(V,\lambda )$ determines a
$(V,\lambda )$ determines a ![]() $\pi$-equivariant hermitian form
$\pi$-equivariant hermitian form ![]() $(V_\mathbb {C},\lambda _\mathbb {C})$ over
$(V_\mathbb {C},\lambda _\mathbb {C})$ over ![]() $\mathbb {C}$, where
$\mathbb {C}$, where
and where ‘trace’ denotes taking the coefficient of the neutral element ![]() $e\in \pi$. We may take
$e\in \pi$. We may take ![]() $V^{+}$ and
$V^{+}$ and ![]() $V^{-}$, the maximal positive definite and negative definite subspaces with respect to
$V^{-}$, the maximal positive definite and negative definite subspaces with respect to ![]() $\lambda _\mathbb {C}$. These subspaces are moreover
$\lambda _\mathbb {C}$. These subspaces are moreover ![]() $\pi$-invariant and hence are themselves
$\pi$-invariant and hence are themselves ![]() $\mathbb {C}\pi$-modules. We define the representation-valued multisignature:
$\mathbb {C}\pi$-modules. We define the representation-valued multisignature:
Given a non-singular hermitian form ![]() $(V,\lambda )$ representing an element of
$(V,\lambda )$ representing an element of ![]() $L_4^{s}(\mathbb {Z}[\pi ])$, we may complexify to obtain a hermitian form over
$L_4^{s}(\mathbb {Z}[\pi ])$, we may complexify to obtain a hermitian form over ![]() $\mathbb {C}\pi$, and then take the representation-valued multisignature. This determines a group homomorphism
$\mathbb {C}\pi$, and then take the representation-valued multisignature. This determines a group homomorphism
Taking characters determines an injective ring homomorphism ![]() $R_\mathbb {C}\pi \to \operatorname {Hom}^{\text {class}}(\pi ,\mathbb {C})$, where the latter denotes the ring of
$R_\mathbb {C}\pi \to \operatorname {Hom}^{\text {class}}(\pi ,\mathbb {C})$, where the latter denotes the ring of ![]() $\mathbb {Z}$-linear combinations of complex-valued functions on
$\mathbb {Z}$-linear combinations of complex-valued functions on ![]() $\pi$ that are constant on conjugacy classes of
$\pi$ that are constant on conjugacy classes of ![]() $\pi$. We call the image of
$\pi$. We call the image of ![]() $\text {mult}(V,\lambda )$ under this homomorphism the character-valued multisignature.
$\text {mult}(V,\lambda )$ under this homomorphism the character-valued multisignature.
5.2 The multisignature for a finite cyclic group
We now restrict our attention to ![]() $\pi =\mathbb {Z}/n$ and choose a generator
$\pi =\mathbb {Z}/n$ and choose a generator ![]() $t$, obtaining an isomorphism
$t$, obtaining an isomorphism ![]() $\mathbb {C}[\mathbb {Z}/n]\cong \mathbb {C}[t]/(t^{n}-1)$. Let
$\mathbb {C}[\mathbb {Z}/n]\cong \mathbb {C}[t]/(t^{n}-1)$. Let ![]() $\chi$ represent the character of the irreducible
$\chi$ represent the character of the irreducible ![]() $\mathbb {C}[t]/(t^{n}-1)$-module
$\mathbb {C}[t]/(t^{n}-1)$-module ![]() $\mathbb {C}$, where
$\mathbb {C}$, where ![]() $t$ acts by
$t$ acts by ![]() $\exp (2\pi i/n)$. The characters for the irreducible
$\exp (2\pi i/n)$. The characters for the irreducible ![]() $\mathbb {C}[\mathbb {Z}/n]$-modules are then
$\mathbb {C}[\mathbb {Z}/n]$-modules are then ![]() $\chi ^{0}, \chi ^{1}, \chi ^{2}, \dots ,\chi ^{n-1}$, and the ring of complex class functions for
$\chi ^{0}, \chi ^{1}, \chi ^{2}, \dots ,\chi ^{n-1}$, and the ring of complex class functions for ![]() $\mathbb {Z}/n$ is well known to be isomorphic to
$\mathbb {Z}/n$ is well known to be isomorphic to ![]() $\mathbb {Z}[\chi ]/(1+\chi +\chi ^{2}+\dots +\chi ^{n-1})$.
$\mathbb {Z}[\chi ]/(1+\chi +\chi ^{2}+\dots +\chi ^{n-1})$.
Proposition 5.1 Let ![]() $(V,\lambda )$ be a hermitian form over
$(V,\lambda )$ be a hermitian form over ![]() $\mathbb {C}[\mathbb {Z}/n]$, with associated
$\mathbb {C}[\mathbb {Z}/n]$, with associated ![]() $\pi$-equivariant complex hermitian form
$\pi$-equivariant complex hermitian form ![]() $(V_\mathbb {C},\lambda _\mathbb {C})$. The coefficient
$(V_\mathbb {C},\lambda _\mathbb {C})$. The coefficient ![]() $\alpha _k$ of the character-valued multisignature
$\alpha _k$ of the character-valued multisignature
is equal to the ordinary signature of the restriction of ![]() $\lambda _\mathbb {C}$ to the
$\lambda _\mathbb {C}$ to the ![]() $\exp (2\pi ik/n)$-eigenspace of the action of
$\exp (2\pi ik/n)$-eigenspace of the action of ![]() $t$ on
$t$ on ![]() $V_\mathbb {C}$.
$V_\mathbb {C}$.
Proof. Recall the positive and negative definite ![]() $\mathbb {C}[\mathbb {Z}/n]$-modules
$\mathbb {C}[\mathbb {Z}/n]$-modules ![]() $V^{+}$ and
$V^{+}$ and ![]() $V^{-}$. There is then a decomposition into irreducible components
$V^{-}$. There is then a decomposition into irreducible components ![]() $V^{\pm }\cong \bigoplus _{k=0}^{n-1}V^{\pm }_k$, where
$V^{\pm }\cong \bigoplus _{k=0}^{n-1}V^{\pm }_k$, where ![]() $V^{\pm }_k$ denotes the component that corresponds to the character
$V^{\pm }_k$ denotes the component that corresponds to the character ![]() $\chi ^{k}$. The representation-valued multisignature then decomposes as
$\chi ^{k}$. The representation-valued multisignature then decomposes as
 \[ \text{mult}(V,\lambda)=V^{+}-V^{-}=\sum_{k=0}^{n-1}(V^{+}_k-V^{-}_k)\in R_\mathbb{C}(\mathbb{Z}/n). \]
\[ \text{mult}(V,\lambda)=V^{+}-V^{-}=\sum_{k=0}^{n-1}(V^{+}_k-V^{-}_k)\in R_\mathbb{C}(\mathbb{Z}/n). \]
Taking characters, we see that ![]() $\alpha _k=\dim _\mathbb {C}(V_k^{+})-\dim _\mathbb {C}(V_k^{-})$. In other words,
$\alpha _k=\dim _\mathbb {C}(V_k^{+})-\dim _\mathbb {C}(V_k^{-})$. In other words, ![]() $\alpha _k$ is the ordinary signature of the restriction of
$\alpha _k$ is the ordinary signature of the restriction of ![]() $\lambda _\mathbb {C}$ to
$\lambda _\mathbb {C}$ to ![]() $V_k=V_k^{+}\oplus V_k^{-}$. Note that, viewing
$V_k=V_k^{+}\oplus V_k^{-}$. Note that, viewing ![]() $V_k$ as a complex vector subspace
$V_k$ as a complex vector subspace ![]() $V_k\subset V_\mathbb {C}$, it is the
$V_k\subset V_\mathbb {C}$, it is the ![]() $\exp (2\pi i k/n)$-eigenspace of the action of the generator
$\exp (2\pi i k/n)$-eigenspace of the action of the generator ![]() $t\in \mathbb {Z}/n$ on
$t\in \mathbb {Z}/n$ on ![]() $V_\mathbb {C}$.
$V_\mathbb {C}$.
Example 5.2 Suppose ![]() $(V,\lambda )$ as in Proposition 5.1 and
$(V,\lambda )$ as in Proposition 5.1 and ![]() $A(t)$ is a hermitian matrix over
$A(t)$ is a hermitian matrix over ![]() $\mathbb {C}[\mathbb {Z}/n]\cong \mathbb {C}[t]/(t^{n}-1)$ representing
$\mathbb {C}[\mathbb {Z}/n]\cong \mathbb {C}[t]/(t^{n}-1)$ representing ![]() $(V,\lambda )$. Then the signature of
$(V,\lambda )$. Then the signature of ![]() $\lambda _\mathbb {C}$ restricted to
$\lambda _\mathbb {C}$ restricted to ![]() $V_k$ is given by the signature of the complex hermitian matrix
$V_k$ is given by the signature of the complex hermitian matrix ![]() $A(\exp (2\pi ik/n))$.
$A(\exp (2\pi ik/n))$.
Example 5.3 Let ![]() $W$ be a compact oriented
$W$ be a compact oriented ![]() $4$-manifold with a homomorphism
$4$-manifold with a homomorphism ![]() $\phi \colon \pi _1(W)\to \mathbb {Z}/n$. This determines an
$\phi \colon \pi _1(W)\to \mathbb {Z}/n$. This determines an ![]() $n$-fold cyclic cover
$n$-fold cyclic cover ![]() $\widetilde {W}\to W$ with covering transformation
$\widetilde {W}\to W$ with covering transformation ![]() $\tau \colon \widetilde {W}\to \widetilde {W}$. The complex vector space
$\tau \colon \widetilde {W}\to \widetilde {W}$. The complex vector space ![]() $V_\mathbb {C}:=H_2(\widetilde {W};\mathbb {C})$ has an action of
$V_\mathbb {C}:=H_2(\widetilde {W};\mathbb {C})$ has an action of ![]() $\mathbb {Z}/n$ generated by
$\mathbb {Z}/n$ generated by ![]() $\tau _*=t$, and the middle-dimensional intersection pairing
$\tau _*=t$, and the middle-dimensional intersection pairing ![]() $\lambda _\mathbb {C}$ of
$\lambda _\mathbb {C}$ of ![]() $\widetilde {W}$ is equivariant with respect to this. Thus
$\widetilde {W}$ is equivariant with respect to this. Thus ![]() $(W,\phi )$ determines a multisignature via
$(W,\phi )$ determines a multisignature via ![]() $(V_\mathbb {C},\lambda _\mathbb {C})$. The coefficients of this multisignature may be computed using Proposition 5.1 and Example 5.2.
$(V_\mathbb {C},\lambda _\mathbb {C})$. The coefficients of this multisignature may be computed using Proposition 5.1 and Example 5.2.
For odd ![]() $n$, the next result is due to Wall [Reference WallWal99, Theorem 13A.4(ii)] and independently to Bak [Reference BakBak78]. For
$n$, the next result is due to Wall [Reference WallWal99, Theorem 13A.4(ii)] and independently to Bak [Reference BakBak78]. For ![]() $n$ a power of 2, it was explicitly derived in [Reference WallWal76, Corollary 3.3.3] and the techniques for the general even
$n$ a power of 2, it was explicitly derived in [Reference WallWal76, Corollary 3.3.3] and the techniques for the general even ![]() $n$ case were outlined. This general even
$n$ case were outlined. This general even ![]() $n$ case is stated in [Reference Hambleton and TaylorHT00, p. 3] and implicitly calculated there.
$n$ case is stated in [Reference Hambleton and TaylorHT00, p. 3] and implicitly calculated there.
Theorem 5.4 [Reference Hambleton and TaylorHT00, §§ 10, 12]
For ![]() $n$ any positive integer, the group homomorphism
$n$ any positive integer, the group homomorphism
determined by the character-valued multisignature factors through the purely real representations ![]() $R^{+}_\mathbb {C}(\mathbb {Z}/n)\subset R_\mathbb {C}(\mathbb {Z}/n)$. There is moreover an isomorphism
$R^{+}_\mathbb {C}(\mathbb {Z}/n)\subset R_\mathbb {C}(\mathbb {Z}/n)$. There is moreover an isomorphism
 \[ L_4^{s}(\mathbb{Z}[\mathbb{Z}/n]) \cong \left\{\begin{array}{@{}ll} 4\mathbb{Z}^{(n-1)/2}\oplus 8\mathbb{Z} & n\text{ odd,}\\ 4\mathbb{Z}^{(n-2)/2}\oplus 8\mathbb{Z}\oplus 8\mathbb{Z} & n\text{ even,}\end{array}\right. \]
\[ L_4^{s}(\mathbb{Z}[\mathbb{Z}/n]) \cong \left\{\begin{array}{@{}ll} 4\mathbb{Z}^{(n-1)/2}\oplus 8\mathbb{Z} & n\text{ odd,}\\ 4\mathbb{Z}^{(n-2)/2}\oplus 8\mathbb{Z}\oplus 8\mathbb{Z} & n\text{ even,}\end{array}\right. \]given by the function
 \[ (V,\lambda)\mapsto \left\{\begin{array}{@{}ll} (\alpha_1,\alpha_2\dots,\alpha_{(n-1)/2},\alpha_0) & n\text{ odd,}\\ (\alpha_1,\alpha_2\dots,\alpha_{(n-2)/2}, \alpha_{n/2},\alpha_0) & n\text{ even.}\end{array}\right. \]
\[ (V,\lambda)\mapsto \left\{\begin{array}{@{}ll} (\alpha_1,\alpha_2\dots,\alpha_{(n-1)/2},\alpha_0) & n\text{ odd,}\\ (\alpha_1,\alpha_2\dots,\alpha_{(n-2)/2}, \alpha_{n/2},\alpha_0) & n\text{ even.}\end{array}\right. \]
where ![]() $\alpha _k$ is the coefficient of
$\alpha _k$ is the coefficient of ![]() $\chi ^{k}$ in
$\chi ^{k}$ in ![]() $\operatorname {mult}(V,\lambda )$.
$\operatorname {mult}(V,\lambda )$.
Remark 5.5 The reader may be wondering why only half the character coefficients of ![]() $\operatorname {mult}(V,\lambda )$ appear in the above isomorphism. It is a consequence of the fact that the character-valued multisignature factors through
$\operatorname {mult}(V,\lambda )$ appear in the above isomorphism. It is a consequence of the fact that the character-valued multisignature factors through ![]() $\mathbb {R}_\mathbb {C}^{+}(\mathbb {Z}/n)$ that the complex irreducible representations will appear as conjugate pairs in
$\mathbb {R}_\mathbb {C}^{+}(\mathbb {Z}/n)$ that the complex irreducible representations will appear as conjugate pairs in ![]() $\operatorname {mult}(V,\lambda )$:
$\operatorname {mult}(V,\lambda )$:
 \[ \text{mult}(V,\lambda)=\left\{\begin{array}{@{}ll} \alpha_0\cdot\chi^{0} + \sum_{k=0}^{(n-1)/2}\,\alpha_k(\chi^{k}+\chi^{{-}k}) & n\text{ odd,}\\ \alpha_0\cdot\chi^{0} + \alpha_{n/2}\cdot\chi^{n/2}+ \sum_{k=0}^{(n-2)/2}\,\alpha_k(\chi^{k}+\chi^{{-}k}) & n\text{ even.}\end{array}\right. \]
\[ \text{mult}(V,\lambda)=\left\{\begin{array}{@{}ll} \alpha_0\cdot\chi^{0} + \sum_{k=0}^{(n-1)/2}\,\alpha_k(\chi^{k}+\chi^{{-}k}) & n\text{ odd,}\\ \alpha_0\cdot\chi^{0} + \alpha_{n/2}\cdot\chi^{n/2}+ \sum_{k=0}^{(n-2)/2}\,\alpha_k(\chi^{k}+\chi^{{-}k}) & n\text{ even.}\end{array}\right. \]
In other words, for all ![]() $k$ we have that
$k$ we have that ![]() $\alpha _k=\alpha _{-k}$.
$\alpha _k=\alpha _{-k}$.
5.3 The multisignature as Tristram–Levine signatures
For this section, let ![]() $K$ be a knot and let
$K$ be a knot and let ![]() $W$ be a bordism from
$W$ be a bordism from ![]() $S_n^{3}(K)$ to
$S_n^{3}(K)$ to ![]() $L(n,1)$ over the group
$L(n,1)$ over the group ![]() $\mathbb {Z}/n$. Such a bordism in particular has a multisignature as in Example 5.3. Now we relate the Tristram–Levine signatures of
$\mathbb {Z}/n$. Such a bordism in particular has a multisignature as in Example 5.3. Now we relate the Tristram–Levine signatures of ![]() $K$ to the multisignature of
$K$ to the multisignature of ![]() $W$.
$W$.
Lemma 5.6 Let ![]() $K$ be a knot and let
$K$ be a knot and let ![]() $W$ be a cobordism from
$W$ be a cobordism from ![]() $S_n^{3}(K)$ to
$S_n^{3}(K)$ to ![]() $L(n,1)$ over the group
$L(n,1)$ over the group ![]() $\mathbb {Z}/n$. Assume that
$\mathbb {Z}/n$. Assume that ![]() $\sigma (W)=0$. When
$\sigma (W)=0$. When ![]() $0< k< n$, the coefficient
$0< k< n$, the coefficient ![]() $\alpha _k\in \mathbb {Z}$ of the multisignature of
$\alpha _k\in \mathbb {Z}$ of the multisignature of ![]() $W$ at
$W$ at ![]() $\chi ^{k}$ coincides with the Tristram–Levine signature of
$\chi ^{k}$ coincides with the Tristram–Levine signature of ![]() $K$ at
$K$ at ![]() $\xi _n^{k}$, where
$\xi _n^{k}$, where ![]() $\xi _n=\exp (2\pi i /n)$.
$\xi _n=\exp (2\pi i /n)$.
Proof. Noting that by hypothesis ![]() $\sigma (W)=0$, we have by Proposition 3.7 that
$\sigma (W)=0$, we have by Proposition 3.7 that
Proposition 5.1 tells us that ![]() $\sigma _k(\widetilde {W})$ is the coefficient of the character
$\sigma _k(\widetilde {W})$ is the coefficient of the character ![]() $\chi ^{k}$ in the multisignature as claimed.
$\chi ^{k}$ in the multisignature as claimed.
We summarise the results in the previous three sections for our purposes.
Proposition 5.7 Let ![]() $K$ be a knot and let
$K$ be a knot and let ![]() $f\colon S_n^{3}(K)\to L(n,1)$ be a degree-one normal map. Suppose
$f\colon S_n^{3}(K)\to L(n,1)$ be a degree-one normal map. Suppose ![]() $W$ is a degree-one normal bordism from
$W$ is a degree-one normal bordism from ![]() $(S_n^{3}(K),f)$ to
$(S_n^{3}(K),f)$ to ![]() $(L(n,1),\operatorname {Id})$ with
$(L(n,1),\operatorname {Id})$ with ![]() $\sigma (W)=0$. Then the associated surgery obstruction
$\sigma (W)=0$. Then the associated surgery obstruction
is trivial if and only
 \[ \sigma_{\xi_n^{k}}(K)=0\text{ for every }\left\{\begin{array}{@{}ll}k=1,\dots, (n-1)/2 & n\text{ odd,}\\ k=1,\dots, n/2 & n\text{ even,}\end{array}\right. \]
\[ \sigma_{\xi_n^{k}}(K)=0\text{ for every }\left\{\begin{array}{@{}ll}k=1,\dots, (n-1)/2 & n\text{ odd,}\\ k=1,\dots, n/2 & n\text{ even,}\end{array}\right. \]
where ![]() $\sigma _{\xi _n^{k}}(K)$ denotes the Tristram–Levine signature of
$\sigma _{\xi _n^{k}}(K)$ denotes the Tristram–Levine signature of ![]() $K$ at
$K$ at ![]() $\xi _n^{k}$, for
$\xi _n^{k}$, for ![]() $\xi _n=\exp (2\pi i /n)$.
$\xi _n=\exp (2\pi i /n)$.
Proof. By Theorem 5.4, a class in ![]() $L_4^{s}(\mathbb {Z}[\mathbb {Z}/n])$ vanishes if and only if there is vanishing of the associated multisignature coefficients:
$L_4^{s}(\mathbb {Z}[\mathbb {Z}/n])$ vanishes if and only if there is vanishing of the associated multisignature coefficients:
The coefficient ![]() $\alpha _0$ corresponds to the trivial character and thus corresponds to the eigenspace of the
$\alpha _0$ corresponds to the trivial character and thus corresponds to the eigenspace of the ![]() $t$ action on
$t$ action on ![]() $(H_2(W;\mathbb {Z}[\mathbb {Z}/n])$ with eigenvalue 1. The signature of the
$(H_2(W;\mathbb {Z}[\mathbb {Z}/n])$ with eigenvalue 1. The signature of the ![]() $\mathbb {Z}[\mathbb {Z}/n]$-coefficient intersection form of
$\mathbb {Z}[\mathbb {Z}/n]$-coefficient intersection form of ![]() $W$ restricted to this component is then just the ordinary signature of
$W$ restricted to this component is then just the ordinary signature of ![]() $W$, whose vanishing is in the hypotheses.
$W$, whose vanishing is in the hypotheses.
For ![]() $k\neq 0$, the coefficient
$k\neq 0$, the coefficient ![]() $\alpha _k$ is equal to
$\alpha _k$ is equal to ![]() $\sigma _{\xi _n^{k}}(K)$, by Lemma 5.6.
$\sigma _{\xi _n^{k}}(K)$, by Lemma 5.6.
Proposition 5.8 For odd ![]() $n$, suppose that
$n$, suppose that ![]() $H_1(S_n^{3}(K);\mathbb {Z}[\mathbb {Z}/n])=\{0\}$ and
$H_1(S_n^{3}(K);\mathbb {Z}[\mathbb {Z}/n])=\{0\}$ and ![]() $\sigma _{\xi _n^{k}}(K) = 0$ for all
$\sigma _{\xi _n^{k}}(K) = 0$ for all ![]() $0< k< n$, and
$0< k< n$, and ![]() $\xi _n$ a primitive
$\xi _n$ a primitive ![]() $n$th root of unity. Then
$n$th root of unity. Then ![]() $S_n^{3}(K)$ is homology cobordant to
$S_n^{3}(K)$ is homology cobordant to ![]() $L(n,1)$ via a cobordism
$L(n,1)$ via a cobordism ![]() $V$ homotopy equivalent to
$V$ homotopy equivalent to ![]() $L(n,1) \times I$, via a homotopy equivalence restricting to the identity map on
$L(n,1) \times I$, via a homotopy equivalence restricting to the identity map on ![]() $L(n,1)$ and the standard degree one collapse map on
$L(n,1)$ and the standard degree one collapse map on ![]() $S^{3}_n(K)$. The same is true for even
$S^{3}_n(K)$. The same is true for even ![]() $n$ when
$n$ when ![]() $\operatorname {Arf}(K)=0$.
$\operatorname {Arf}(K)=0$.
In fact, Propositions 3.5 and 3.3 show that this is an ‘if and only if’.
Proof. Lemma 4.4 shows how to construct the degree-one normal collapse map ![]() $f\colon S_n^{3}(K)\to L(n,1)$. In Proposition 4.9, with the assumption that
$f\colon S_n^{3}(K)\to L(n,1)$. In Proposition 4.9, with the assumption that ![]() $\operatorname {Arf}(K)=0$ when
$\operatorname {Arf}(K)=0$ when ![]() $n$ even, we further constructed a degree-one normal bordism
$n$ even, we further constructed a degree-one normal bordism ![]() $W$ over
$W$ over ![]() $L(n,1)$ from
$L(n,1)$ from ![]() $(S_n^{3}(K),f)$ to
$(S_n^{3}(K),f)$ to ![]() $(L(n,1),\operatorname {Id})$, such that
$(L(n,1),\operatorname {Id})$, such that ![]() $\pi _1(W)\cong \mathbb {Z}/n$, and
$\pi _1(W)\cong \mathbb {Z}/n$, and ![]() $\sigma (W)=0$.
$\sigma (W)=0$.
By the discussion at the end of § 4, using the fact that ![]() $H_1(S_n^{3}(K);\mathbb {Z}[\mathbb {Z}/n])=\{0\}$, the obstruction to performing further surgeries on
$H_1(S_n^{3}(K);\mathbb {Z}[\mathbb {Z}/n])=\{0\}$, the obstruction to performing further surgeries on ![]() $W$ to improve it to be homotopy equivalent to
$W$ to improve it to be homotopy equivalent to ![]() $L(n,1)$ lies in the group
$L(n,1)$ lies in the group ![]() $L_4^{s}(\mathbb {Z}[\mathbb {Z}/n])$.
$L_4^{s}(\mathbb {Z}[\mathbb {Z}/n])$.
The vanishing of the surgery obstruction from Proposition 5.7 and the fact that ![]() $\mathbb {Z}/n$ is a good group implies that we can perform surgery on the interior of
$\mathbb {Z}/n$ is a good group implies that we can perform surgery on the interior of ![]() $W$ to obtain a cobordism
$W$ to obtain a cobordism ![]() $V$ that is homotopy equivalent to
$V$ that is homotopy equivalent to ![]() $L(n,1)$ [Reference Freedman and QuinnFQ90, Chapter 11]. In particular,
$L(n,1)$ [Reference Freedman and QuinnFQ90, Chapter 11]. In particular, ![]() $V$ is a
$V$ is a ![]() $\mathbb {Z}[\mathbb {Z}/n]$-homology cobordism from
$\mathbb {Z}[\mathbb {Z}/n]$-homology cobordism from ![]() $S_n^{3}(K)$ to
$S_n^{3}(K)$ to ![]() $L(n,1)$.
$L(n,1)$.
6. The Arf and  $\tau$ invariants
$\tau$ invariants
6.1 The  $\tau$ invariant
$\tau$ invariant
Recall that a locally flat sphere in a topological ![]() $4$-manifold
$4$-manifold ![]() $M$ is said to be generically immersed if all its self-intersections are transverse double points. A locally flat union of discs in
$M$ is said to be generically immersed if all its self-intersections are transverse double points. A locally flat union of discs in ![]() $M$ is said to be generically immersed if its self-intersections are transverse double points and if the boundaries are mutually disjoint and embedded.
$M$ is said to be generically immersed if its self-intersections are transverse double points and if the boundaries are mutually disjoint and embedded.
We refer the reader to [Reference Freedman and QuinnFQ90, Chapter 1] for standard notions such as the intersection and self-intersection numbers ![]() $\lambda$ and
$\lambda$ and ![]() $\mu$ for generically immersed spheres in an ambient topological
$\mu$ for generically immersed spheres in an ambient topological ![]() $4$-manifold. We will use the following lemma.
$4$-manifold. We will use the following lemma.
Lemma 6.1 [Reference Freedman and QuinnFQ90, p. 22]
For a generically immersed sphere ![]() $S$ in a topological
$S$ in a topological ![]() $4$-manifold, we have that
$4$-manifold, we have that
where the last term denotes the euler number of the normal bundle ![]() $\nu S$ of
$\nu S$ of ![]() $S$.
$S$.
We also use the fact that a locally flat submanifold of a topological ![]() $4$-manifold has a linear normal bundle, as well as notions of topological transversality, immersions, and so on, for which we refer the reader to [Reference Freedman and QuinnFQ90].
$4$-manifold has a linear normal bundle, as well as notions of topological transversality, immersions, and so on, for which we refer the reader to [Reference Freedman and QuinnFQ90].
The key tool in this section is the ![]() $\tau$ invariant of a generically immersed sphere with vanishing self-intersection number in a topological
$\tau$ invariant of a generically immersed sphere with vanishing self-intersection number in a topological ![]() $4$-manifold. This was originally defined by [Reference MatsumotoMat78] and [Reference Freedman and KirbyFK78], and then significantly generalised by Schneiderman and Teichner [Reference Schneiderman and TeichnerST01]. We define
$4$-manifold. This was originally defined by [Reference MatsumotoMat78] and [Reference Freedman and KirbyFK78], and then significantly generalised by Schneiderman and Teichner [Reference Schneiderman and TeichnerST01]. We define ![]() $\tau$ in our setting, referring the reader to [Reference Schneiderman and TeichnerST01] for a more general definition.
$\tau$ in our setting, referring the reader to [Reference Schneiderman and TeichnerST01] for a more general definition.
Definition 6.2 A generically immersed sphere ![]() $S$ in a topological
$S$ in a topological ![]() $4$-manifold
$4$-manifold ![]() $M$ is said to be
$M$ is said to be ![]() $s$-characteristic, or spherically characteristic, if
$s$-characteristic, or spherically characteristic, if ![]() $S\cdot R\equiv R\cdot R\mod {2}$ for every immersed sphere
$S\cdot R\equiv R\cdot R\mod {2}$ for every immersed sphere ![]() $R$ in
$R$ in ![]() $M$.
$M$.
Proposition 6.3 [Reference Schneiderman and TeichnerST01, Theorem 1, Remark 5]
Let ![]() $M$ be a simply connected topological
$M$ be a simply connected topological ![]() $4$-manifold and suppose that
$4$-manifold and suppose that ![]() $S$ is a generically immersed
$S$ is a generically immersed ![]() $s$-characteristic
$s$-characteristic ![]() $2$-sphere in
$2$-sphere in ![]() $M$ with
$M$ with ![]() $\mu (S)=0$. Consider the quantity
$\mu (S)=0$. Consider the quantity
where ![]() $\{W_i\}$ is a set of framed, generically immersed Whitney discs in
$\{W_i\}$ is a set of framed, generically immersed Whitney discs in ![]() $M$, pairing the self-intersection points of
$M$, pairing the self-intersection points of ![]() $S$, and such that each
$S$, and such that each ![]() $W_i$ intersects
$W_i$ intersects ![]() $S$ transversely in double points in the interior of
$S$ transversely in double points in the interior of ![]() $\{\mathring {W_i}\}$. Such a family of Whitney discs exists since
$\{\mathring {W_i}\}$. Such a family of Whitney discs exists since ![]() $\mu (S)=0$.
$\mu (S)=0$.
The value of ![]() $\tau (S,\{W_i\})\in \mathbb {Z}/2$ does not depend on choices of pairing of double points, Whitney arcs, or Whitney discs.
$\tau (S,\{W_i\})\in \mathbb {Z}/2$ does not depend on choices of pairing of double points, Whitney arcs, or Whitney discs.
Consequently we write ![]() $\tau (S) \in \mathbb {Z}/2$, dropping the discs
$\tau (S) \in \mathbb {Z}/2$, dropping the discs ![]() $\{W_i\}$ from the notation. When we judge that the manifold
$\{W_i\}$ from the notation. When we judge that the manifold ![]() $M$ is not immediately clear from the context, we use the notation
$M$ is not immediately clear from the context, we use the notation ![]() $\tau _M(S)$ instead of
$\tau _M(S)$ instead of ![]() $\tau (S)$.
$\tau (S)$.
Indeed, ![]() $\tau (S)$ is an invariant of the homotopy class
$\tau (S)$ is an invariant of the homotopy class ![]() $[S]\in \pi _2(M)$, as follows. Each class in
$[S]\in \pi _2(M)$, as follows. Each class in ![]() $\pi _2(M)$ can be represented by a generic immersion of a sphere
$\pi _2(M)$ can be represented by a generic immersion of a sphere ![]() $S$ in
$S$ in ![]() $M$ by [Reference Freedman and QuinnFQ90, Immersion lemma, p. 13]. Perform local cusp moves to ensure that
$M$ by [Reference Freedman and QuinnFQ90, Immersion lemma, p. 13]. Perform local cusp moves to ensure that ![]() $\mu (S)=0$ and then compute
$\mu (S)=0$ and then compute ![]() $\tau (S)$. Representatives of a given homotopy class with vanishing self-intersection number are regularly homotopic [Reference Freedman and QuinnFQ90, Proposition 1.7], where by definition, a regular homotopy in the topological category is a concatenation of finger moves and (embedded) Whitney moves. (If
$\tau (S)$. Representatives of a given homotopy class with vanishing self-intersection number are regularly homotopic [Reference Freedman and QuinnFQ90, Proposition 1.7], where by definition, a regular homotopy in the topological category is a concatenation of finger moves and (embedded) Whitney moves. (If ![]() $M$ admits a smooth structure, a generic regular homotopy can be decomposed into a sequence of such moves, and every regular homotopy can be perturbed to such a homotopy [Reference Golubitsky and GuilleminGG73, § III.3].) It is clear that either such move preserves
$M$ admits a smooth structure, a generic regular homotopy can be decomposed into a sequence of such moves, and every regular homotopy can be perturbed to such a homotopy [Reference Golubitsky and GuilleminGG73, § III.3].) It is clear that either such move preserves ![]() $\tau (S)$. Consequently, the invariant
$\tau (S)$. Consequently, the invariant ![]() $\tau$ is well defined on homotopy classes, and we sometimes use the notation
$\tau$ is well defined on homotopy classes, and we sometimes use the notation ![]() $\tau (x)$ for an
$\tau (x)$ for an ![]() $s$-characteristic class
$s$-characteristic class ![]() $x\in \pi _2(M)$ for a simply connected topological
$x\in \pi _2(M)$ for a simply connected topological ![]() $4$-manifold
$4$-manifold ![]() $M$.
$M$.
In particular, if such an ![]() $x\in \pi _2(M)$ is represented by a locally flat, embedded sphere, then
$x\in \pi _2(M)$ is represented by a locally flat, embedded sphere, then ![]() $\tau (x)=0$, and thus
$\tau (x)=0$, and thus ![]() $\tau$ gives an obstruction for a homotopy class to contain a locally flat embedding. Observe that
$\tau$ gives an obstruction for a homotopy class to contain a locally flat embedding. Observe that ![]() $\tau$ does not see the orientation of a sphere, that is,
$\tau$ does not see the orientation of a sphere, that is, ![]() $\tau (x)=\tau (-x)$ for an
$\tau (x)=\tau (-x)$ for an ![]() $s$-characteristic class
$s$-characteristic class ![]() $x\in \pi _2(M)$ in a simply connected topological
$x\in \pi _2(M)$ in a simply connected topological ![]() $4$-manifold
$4$-manifold ![]() $M$.
$M$.
Next we recall a well-known formulation of the Arf invariant of a knot.
Proposition 6.4 ([Reference MatsumotoMat78, Reference Freedman and KirbyFK78] and [Reference Conant, Schneiderman and TeichnerCST14, Lemma 10])
Let ![]() $K$ be a knot in
$K$ be a knot in ![]() $S^{3}$ bounding a generically immersed disc
$S^{3}$ bounding a generically immersed disc ![]() $\Delta$ in
$\Delta$ in ![]() $D^{4}$ with
$D^{4}$ with ![]() $\mu (\Delta )=0$. Since
$\mu (\Delta )=0$. Since ![]() $\mu (\Delta )=0$, there exists a collection
$\mu (\Delta )=0$, there exists a collection ![]() $\{W_i\}$ of framed, generically immersed Whitney discs pairing up the self-intersections of
$\{W_i\}$ of framed, generically immersed Whitney discs pairing up the self-intersections of ![]() $\Delta$ and intersecting
$\Delta$ and intersecting ![]() $\Delta$ in transverse double points in the interior of
$\Delta$ in transverse double points in the interior of ![]() $\{\mathring {W_i}\}$. Then
$\{\mathring {W_i}\}$. Then
For a sketch of a proof, see [Reference Conant, Schneiderman and TeichnerCST14, Lemma 10]. We give a brief outline here for the convenience of the reader. The Arf invariant of a knot ![]() $K$ is equal to
$K$ is equal to ![]() $\sum _i \operatorname {lk}(a_i,a_i^{+})\operatorname {lk}(b_i,b_i^{+})\mod {2}$ where
$\sum _i \operatorname {lk}(a_i,a_i^{+})\operatorname {lk}(b_i,b_i^{+})\mod {2}$ where ![]() $\{a_i,b_i\}$ is a symplectic basis for the first homology of some Seifert surface
$\{a_i,b_i\}$ is a symplectic basis for the first homology of some Seifert surface ![]() $F$ of
$F$ of ![]() $K$, represented by simple closed curves with
$K$, represented by simple closed curves with ![]() $|a_i \pitchfork b_j| = \delta _{ij}$ [Reference LickorishLic93, § 10, p. 105]. Given such a surface
$|a_i \pitchfork b_j| = \delta _{ij}$ [Reference LickorishLic93, § 10, p. 105]. Given such a surface ![]() $F$ and curves
$F$ and curves ![]() $\{a_i,b_i\}$, construct an immersed disc bounded by
$\{a_i,b_i\}$, construct an immersed disc bounded by ![]() $K$ by pushing the interior of
$K$ by pushing the interior of ![]() $F$ into
$F$ into ![]() $D^{4}$ and surgering along correctly framed immersed discs bounded by the curves
$D^{4}$ and surgering along correctly framed immersed discs bounded by the curves ![]() $\{a_i\}$ (correct framing can be arranged by boundary twisting). Construct Whitney discs for the self-intersections using the immersed discs bounded by the
$\{a_i\}$ (correct framing can be arranged by boundary twisting). Construct Whitney discs for the self-intersections using the immersed discs bounded by the ![]() $\{b_i\}$. Then all intersections are created in pairs, except for the
$\{b_i\}$. Then all intersections are created in pairs, except for the ![]() $\sum \operatorname {lk}(a_i,a_i^{+})\operatorname {lk}(b_i,b_i^{+})$ intersections created when adjusting the framings of the discs bounded by
$\sum \operatorname {lk}(a_i,a_i^{+})\operatorname {lk}(b_i,b_i^{+})$ intersections created when adjusting the framings of the discs bounded by ![]() $\{a_i,b_i\}$. This equals the Arf invariant of
$\{a_i,b_i\}$. This equals the Arf invariant of ![]() $K$ via the Seifert form definition.
$K$ via the Seifert form definition.
That the count in Proposition 6.4 is well defined follows from glueing together two generically immersed discs bounded by ![]() $K$, producing an
$K$, producing an ![]() $s$-characteristic generically immersed sphere in
$s$-characteristic generically immersed sphere in ![]() $S^{4}$ with vanishing
$S^{4}$ with vanishing ![]() $\tau$ (since
$\tau$ (since ![]() $\pi _2(S^{4})=0$).
$\pi _2(S^{4})=0$).
The next lemma shows, in particular, that knots with Arf invariant ![]() $1$ are not
$1$ are not ![]() $n$-shake slice. This was shown by Robertello [Reference RobertelloRob65] using a different proof.
$n$-shake slice. This was shown by Robertello [Reference RobertelloRob65] using a different proof.
Proposition 6.5 [Reference RobertelloRob65]
Let ![]() $n$ be an integer. Let
$n$ be an integer. Let ![]() $S$ be an immersed sphere representing a generator of
$S$ be an immersed sphere representing a generator of ![]() $\pi _2(X_n(K))\cong \mathbb {Z}$ for a knot
$\pi _2(X_n(K))\cong \mathbb {Z}$ for a knot ![]() $K$ with
$K$ with ![]() $\mu (S)=0$. Then
$\mu (S)=0$. Then ![]() $\tau (S) =\operatorname {Arf}(K)$.
$\tau (S) =\operatorname {Arf}(K)$.
Proof. Given any null homotopy of ![]() $K$ in
$K$ in ![]() $D^{4}$, the union with the core of the
$D^{4}$, the union with the core of the ![]() $2$-handle of
$2$-handle of ![]() $X_n(K)$ is a sphere
$X_n(K)$ is a sphere ![]() $S$ generating
$S$ generating ![]() $\pi _2(X_n(K))$ but it might not have vanishing self-intersection number. However,
$\pi _2(X_n(K))$ but it might not have vanishing self-intersection number. However, ![]() $n=\lambda (S,S)=2\mu (S) + e(\nu S)$, since
$n=\lambda (S,S)=2\mu (S) + e(\nu S)$, since ![]() $X_n(K)$ is simply connected (see Lemma 6.1). Adding a local cusp to
$X_n(K)$ is simply connected (see Lemma 6.1). Adding a local cusp to ![]() $S$ changes
$S$ changes ![]() $\mu (S)$ by
$\mu (S)$ by ![]() $\pm 1$ and the euler number
$\pm 1$ and the euler number ![]() $e(\nu S)$ by
$e(\nu S)$ by ![]() $\mp 2$, but does not change the homotopy class of
$\mp 2$, but does not change the homotopy class of ![]() $S$. Add local cusps as necessary to produce a sphere
$S$. Add local cusps as necessary to produce a sphere ![]() $S_K$, also generating
$S_K$, also generating ![]() $\pi _2(X_n(K))$, with
$\pi _2(X_n(K))$, with ![]() $\mu (S_K)=0$ and
$\mu (S_K)=0$ and ![]() $e(S_K)=\lambda (S_K,S_K)=n$. Perform the local cusps inside
$e(S_K)=\lambda (S_K,S_K)=n$. Perform the local cusps inside ![]() $D^{4}$, so
$D^{4}$, so ![]() $S_K$ still intersects the 2-handle of
$S_K$ still intersects the 2-handle of ![]() $X_n(K)$ only in the core.
$X_n(K)$ only in the core.
Next, we claim that ![]() $S_K$ is
$S_K$ is ![]() $s$-characteristic. To see this, let
$s$-characteristic. To see this, let ![]() $R$ be an immersed sphere in
$R$ be an immersed sphere in ![]() $X_n(K)$. Then since
$X_n(K)$. Then since ![]() $S_K$ generates
$S_K$ generates ![]() $\pi _2(X_n(K)) \cong \mathbb {Z}$ there is some
$\pi _2(X_n(K)) \cong \mathbb {Z}$ there is some ![]() $a \in \mathbb {Z}$ such that
$a \in \mathbb {Z}$ such that ![]() $R$ has homotopy class
$R$ has homotopy class ![]() $a[S_K]$. Then
$a[S_K]$. Then ![]() $S_K\cdot R = an$ and
$S_K\cdot R = an$ and ![]() $R\cdot R = a^{2} n$, which have the same parity. So
$R\cdot R = a^{2} n$, which have the same parity. So ![]() $S_K$ is indeed
$S_K$ is indeed ![]() $s$-characteristic.
$s$-characteristic.
By definition, ![]() $\tau (S_K)$ is computed as
$\tau (S_K)$ is computed as
where ![]() $\{W_i\}$ is some collection of framed, generically immersed Whitney discs pairing up all the self-intersections of
$\{W_i\}$ is some collection of framed, generically immersed Whitney discs pairing up all the self-intersections of ![]() $S_K$ and intersecting
$S_K$ and intersecting ![]() $S_K$ in transverse double points in the interior of the
$S_K$ in transverse double points in the interior of the ![]() $\{W_i\}$. Since the self-intersections of
$\{W_i\}$. Since the self-intersections of ![]() $S_K$ lie in the
$S_K$ lie in the ![]() $0$-handle
$0$-handle ![]() $D^{4}$ of
$D^{4}$ of ![]() $X_n(K)$, we may and shall assume that the discs
$X_n(K)$, we may and shall assume that the discs ![]() $\{W_i\}$ also lie in
$\{W_i\}$ also lie in ![]() $D^{4}$. In that case, the value of
$D^{4}$. In that case, the value of ![]() $\tau (S_K)$ is computed purely in
$\tau (S_K)$ is computed purely in ![]() $D^{4}$ and equals
$D^{4}$ and equals ![]() $\operatorname {Arf}(K)$ by Proposition 6.4.
$\operatorname {Arf}(K)$ by Proposition 6.4.
Recall that by Freedman's classification [Reference FreedmanFre82] of closed, simply connected ![]() $4$-manifolds, there exists a closed topological 4-manifold homotopy equivalent but not homeomorphic to
$4$-manifolds, there exists a closed topological 4-manifold homotopy equivalent but not homeomorphic to ![]() $\mathbb {CP}^{2}$, known as the Chern manifold, and denoted
$\mathbb {CP}^{2}$, known as the Chern manifold, and denoted ![]() $*\mathbb {CP}^{2}$. To build
$*\mathbb {CP}^{2}$. To build ![]() $*\mathbb {CP}^{2}$, attach a
$*\mathbb {CP}^{2}$, attach a ![]() $2$-handle to
$2$-handle to ![]() $D^{4}$ along a
$D^{4}$ along a ![]() $+1$-framed knot
$+1$-framed knot ![]() $J$ in
$J$ in ![]() $S^{3} = \partial D^{4}$ with
$S^{3} = \partial D^{4}$ with ![]() $\operatorname {Arf}(J)=1$, such as the figure eight knot, and cap off the boundary, which is a homology 3-sphere, with a contractible
$\operatorname {Arf}(J)=1$, such as the figure eight knot, and cap off the boundary, which is a homology 3-sphere, with a contractible ![]() $4$-manifold
$4$-manifold ![]() $C$, which can be found by [Reference FreedmanFre82, Theorem 1.4
$C$, which can be found by [Reference FreedmanFre82, Theorem 1.4![]() $'$], [Reference Freedman and QuinnFQ90, 9.3C].
$'$], [Reference Freedman and QuinnFQ90, 9.3C].
The next lemma shows how to use the ![]() $\tau$ invariant to distinguish between the manifolds
$\tau$ invariant to distinguish between the manifolds ![]() $\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$ and
$\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$ and ![]() $*\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$.
$*\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$.
Lemma 6.6 Let ![]() $x$,
$x$, ![]() $*x$, and
$*x$, and ![]() $\bar {x}$ denote generators of, respectively,
$\bar {x}$ denote generators of, respectively, ![]() $\pi _2(\mathbb {CP}^{2})\cong \pi _2(*\mathbb {CP}^{2})\cong \pi _2(\overline {\mathbb {CP}^{2}})\cong \mathbb {Z}$. Then
$\pi _2(\mathbb {CP}^{2})\cong \pi _2(*\mathbb {CP}^{2})\cong \pi _2(\overline {\mathbb {CP}^{2}})\cong \mathbb {Z}$. Then ![]() $x+\bar {x}$ and
$x+\bar {x}$ and ![]() $*x+\bar {x}$ are
$*x+\bar {x}$ are ![]() $s$-characteristic classes in
$s$-characteristic classes in ![]() $\pi _2(\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}})$ and
$\pi _2(\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}})$ and ![]() $\pi _2(*\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}})$ respectively. Moreover,
$\pi _2(*\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}})$ respectively. Moreover, ![]() $\tau (x+\bar {x})=0$ while
$\tau (x+\bar {x})=0$ while ![]() $\tau (*x+\bar {x})=1$.
$\tau (*x+\bar {x})=1$.
Proof. Let ![]() $S$ denote the sphere
$S$ denote the sphere ![]() $\mathbb {CP}^{1}\subset \mathbb {CP}^{2}\subset \mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$ and let
$\mathbb {CP}^{1}\subset \mathbb {CP}^{2}\subset \mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$ and let ![]() $\bar {S}$ denote the sphere
$\bar {S}$ denote the sphere ![]() $\overline {\mathbb {CP}^{1}}\subset \overline {\mathbb {CP}^{2}}\subset \mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$. Then without loss of generality,
$\overline {\mathbb {CP}^{1}}\subset \overline {\mathbb {CP}^{2}}\subset \mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$. Then without loss of generality, ![]() $x=[S]$ and
$x=[S]$ and ![]() $\bar {x}=[\bar {S}]$.
$\bar {x}=[\bar {S}]$.
First we consider ![]() $\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$. The pair
$\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$. The pair ![]() $\{x,\bar {x}\}$ generates
$\{x,\bar {x}\}$ generates ![]() $\pi _2(\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}})$. Then
$\pi _2(\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}})$. Then
Thus, ![]() $x+\bar {x}$ is
$x+\bar {x}$ is ![]() $s$-characteristic in
$s$-characteristic in ![]() $\pi _2(\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}})$. Then
$\pi _2(\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}})$. Then ![]() $\tau (x+\bar {x})=0$ since the class
$\tau (x+\bar {x})=0$ since the class ![]() $x+\bar {x}$ can be represented by an embedded sphere in
$x+\bar {x}$ can be represented by an embedded sphere in ![]() $\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$ produced by tubing
$\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$ produced by tubing ![]() $S$ and
$S$ and ![]() $\bar {S}$ together.
$\bar {S}$ together.
As described above, ![]() $*\mathbb {CP}^{2}$ is built by capping off the surgery trace
$*\mathbb {CP}^{2}$ is built by capping off the surgery trace ![]() $X_1(J)$ of some knot
$X_1(J)$ of some knot ![]() $J$ with
$J$ with ![]() $\operatorname {Arf}(J)=1$ by a contractible
$\operatorname {Arf}(J)=1$ by a contractible ![]() $4$-manifold. Inclusion induces an isomorphism
$4$-manifold. Inclusion induces an isomorphism ![]() $\pi _2(X_1(J))\cong \pi _2(*\mathbb {CP}^{2})$, and, as before, the generator is
$\pi _2(X_1(J))\cong \pi _2(*\mathbb {CP}^{2})$, and, as before, the generator is ![]() $s$-characteristic. By Proposition 6.5, the image of
$s$-characteristic. By Proposition 6.5, the image of ![]() $*x$ in
$*x$ in ![]() $X_1(J)$ can be represented by a sphere
$X_1(J)$ can be represented by a sphere ![]() $*S\subset X_1(J)$ with trivial self-intersection number and self-intersections paired by a family of Whitney discs
$*S\subset X_1(J)$ with trivial self-intersection number and self-intersections paired by a family of Whitney discs ![]() $\{W_i\}$ so that
$\{W_i\}$ so that ![]() $\sum *S\cdot \mathring {W}_i \mod 2 =\operatorname {Arf}(J)=1$. Since
$\sum *S\cdot \mathring {W}_i \mod 2 =\operatorname {Arf}(J)=1$. Since ![]() $X_1(J)\subset *\mathbb {CP}^{2}$, both
$X_1(J)\subset *\mathbb {CP}^{2}$, both ![]() $*S$ and the same Whitney discs are contained within
$*S$ and the same Whitney discs are contained within ![]() $*\mathbb {CP}^{2}$.
$*\mathbb {CP}^{2}$.
The pair ![]() $\{*x, \bar {x}\}$ generates
$\{*x, \bar {x}\}$ generates ![]() $\pi _2(*\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}})$ and the corresponding intersection form is
$\pi _2(*\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}})$ and the corresponding intersection form is ![]() $[+1]\oplus [-1]$. The same calculation as above shows that
$[+1]\oplus [-1]$. The same calculation as above shows that ![]() $*x+\bar {x}$ is
$*x+\bar {x}$ is ![]() $s$-characteristic in
$s$-characteristic in ![]() $\pi _2(*\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}})$.
$\pi _2(*\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}})$.
Now, to compute ![]() $\tau (*x+\bar {x})$, we tube together
$\tau (*x+\bar {x})$, we tube together ![]() $*S$ and
$*S$ and ![]() $\bar {S}$ in
$\bar {S}$ in ![]() $*\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$. Call the result
$*\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$. Call the result ![]() $*S+ \bar {S}$. Since
$*S+ \bar {S}$. Since ![]() $\bar {S}$ is embedded and
$\bar {S}$ is embedded and ![]() $S$ and
$S$ and ![]() $*S$ are disjoint, the discs
$*S$ are disjoint, the discs ![]() $\{W_i\}$ from above form a complete set of Whitney discs for the self-intersections of
$\{W_i\}$ from above form a complete set of Whitney discs for the self-intersections of ![]() $*S+\bar {S}$. Moreover, the discs
$*S+\bar {S}$. Moreover, the discs ![]() $\{W_i\}$ do not intersect
$\{W_i\}$ do not intersect ![]() $\bar {S}$. It follows that
$\bar {S}$. It follows that ![]() $\tau (*x+\bar {x})=\operatorname {Arf}(J) = 1$.
$\tau (*x+\bar {x})=\operatorname {Arf}(J) = 1$.
6.2 Equating the Arf and Kirby–Siebenmann invariants
Now we bring in the ingredients from the previous two sections. Our aim is to apply the ![]() $\tau$ invariant to prove that
$\tau$ invariant to prove that ![]() $\operatorname {Arf}(K)$ computes the Kirby–Siebenmann invariant of a certain
$\operatorname {Arf}(K)$ computes the Kirby–Siebenmann invariant of a certain ![]() $4$-manifold.
$4$-manifold.
Recall that we built a homology cobordism ![]() $V$ between
$V$ between ![]() $S^{3}_n(K)$ and the lens space
$S^{3}_n(K)$ and the lens space ![]() $L(n,1)$ in Proposition 5.8. The following technical lemma will be used below to show that the union of
$L(n,1)$ in Proposition 5.8. The following technical lemma will be used below to show that the union of ![]() $V$ and
$V$ and ![]() $D_n$, the
$D_n$, the ![]() $D^{2}$-bundle over
$D^{2}$-bundle over ![]() $S^{2}$ with euler number
$S^{2}$ with euler number ![]() $n$ is homeomorphic to
$n$ is homeomorphic to ![]() $\mathbb {CP}^{2} \# \overline {\mathbb {CP}^{2}}$ when
$\mathbb {CP}^{2} \# \overline {\mathbb {CP}^{2}}$ when ![]() $n$ is odd and
$n$ is odd and ![]() $\operatorname {Arf}(K)=0$.
$\operatorname {Arf}(K)=0$.
Lemma 6.7 Let ![]() $n$ be an odd integer. Let
$n$ be an odd integer. Let ![]() $D_n$ denote the
$D_n$ denote the ![]() $D^{2}$-bundle over
$D^{2}$-bundle over ![]() $S^{2}$ with euler number
$S^{2}$ with euler number ![]() $n$. Suppose that
$n$. Suppose that ![]() $S_n^{3}(K)$ is homology cobordant to
$S_n^{3}(K)$ is homology cobordant to ![]() $L(n,1)$ via a cobordism
$L(n,1)$ via a cobordism ![]() $V$ which is homotopy equivalent to
$V$ which is homotopy equivalent to ![]() $L(n,1)\times I$ via a homotopy equivalence
$L(n,1)\times I$ via a homotopy equivalence ![]() $h$ restricting to the identity on
$h$ restricting to the identity on ![]() $L(n,1)$ and the map
$L(n,1)$ and the map ![]() $f$ on
$f$ on ![]() $S_n^{3}(K)$ from Lemma 4.4. Let
$S_n^{3}(K)$ from Lemma 4.4. Let ![]() $Z$ denote the space
$Z$ denote the space ![]() $-X_n(K)\cup _{S_n^{3}(K)} V\cup _{L(n,1)} D_n$.
$-X_n(K)\cup _{S_n^{3}(K)} V\cup _{L(n,1)} D_n$.
If ![]() $\operatorname {Arf}(K)=0$ then
$\operatorname {Arf}(K)=0$ then ![]() $Z$ is homeomorphic to
$Z$ is homeomorphic to ![]() $\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$. If
$\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$. If ![]() $\operatorname {Arf}(K)=1$ then
$\operatorname {Arf}(K)=1$ then ![]() $Z$ is homeomorphic to
$Z$ is homeomorphic to ![]() $*\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$.
$*\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$.
Proof. Recall from Lemma 4.4 that the map ![]() $f\colon S_n^{3}(K)\to L(n,1)$ extends to a homotopy equivalence
$f\colon S_n^{3}(K)\to L(n,1)$ extends to a homotopy equivalence ![]() $\bar {f}\colon X_n(K)\to D_n$ (this is merely the collapse map). Observe that
$\bar {f}\colon X_n(K)\to D_n$ (this is merely the collapse map). Observe that ![]() $D_n\cup _{L(n,1)} L(n,1)\times I \cup _{L(n,1)} D_n$ is an alternate decomposition of the double of
$D_n\cup _{L(n,1)} L(n,1)\times I \cup _{L(n,1)} D_n$ is an alternate decomposition of the double of ![]() $D_n$, which is homeomorphic to
$D_n$, which is homeomorphic to ![]() $S^{2}\widetilde {\times } S^{2}$ since
$S^{2}\widetilde {\times } S^{2}$ since ![]() $n$ is odd.
$n$ is odd.
Now we define a function ![]() $G\colon Z\to S^{2}\widetilde{\times } S^{2}$.
$G\colon Z\to S^{2}\widetilde{\times } S^{2}$.

We now show that ![]() $G$ is a homotopy equivalence. Note that
$G$ is a homotopy equivalence. Note that ![]() $Z$ is constructed from
$Z$ is constructed from ![]() $V\cup D_n$ by adding a
$V\cup D_n$ by adding a ![]() $2$-handle and then a
$2$-handle and then a ![]() $4$-handle, namely, the handles constituting
$4$-handle, namely, the handles constituting ![]() $X_n(K)$ turned upside down. It is then easy to compute using the Seifert-van Kampen theorem and the Mayer–Vietoris sequence that
$X_n(K)$ turned upside down. It is then easy to compute using the Seifert-van Kampen theorem and the Mayer–Vietoris sequence that ![]() $\pi _1(Z)=1$,
$\pi _1(Z)=1$, ![]() $H_2(Z)\cong \mathbb {Z}\oplus \mathbb {Z}$,
$H_2(Z)\cong \mathbb {Z}\oplus \mathbb {Z}$, ![]() $H_4(Z)=\mathbb {Z}$. All other reduced homology groups vanish. Thus,
$H_4(Z)=\mathbb {Z}$. All other reduced homology groups vanish. Thus, ![]() $Z$ has the same homology groups as
$Z$ has the same homology groups as ![]() $S^{2}\widetilde{\times } S^{2}$. Note further that
$S^{2}\widetilde{\times } S^{2}$. Note further that ![]() $H_2(Z)$ is generated by
$H_2(Z)$ is generated by ![]() $[S]$ and
$[S]$ and ![]() $[\Delta ]$, where
$[\Delta ]$, where ![]() $S$ is the base sphere of
$S$ is the base sphere of ![]() $D_n$ and
$D_n$ and ![]() $\Delta$ is represented by the union of the cocore of the
$\Delta$ is represented by the union of the cocore of the ![]() $2$-handle of
$2$-handle of ![]() $X_n(K)$ and some null-homology for the meridian
$X_n(K)$ and some null-homology for the meridian ![]() $\mu _K$ of
$\mu _K$ of ![]() $K$ in the surgery diagram for
$K$ in the surgery diagram for ![]() $S_n^{3}(K)$ in
$S_n^{3}(K)$ in ![]() $V\cup D_n$. We will choose a specific
$V\cup D_n$. We will choose a specific ![]() $\Delta$ presently.
$\Delta$ presently.
We know that ![]() $H_2(S^{2}\widetilde{\times } S^{2})\cong \mathbb {Z}\oplus \mathbb {Z}$. Consider again the decomposition
$H_2(S^{2}\widetilde{\times } S^{2})\cong \mathbb {Z}\oplus \mathbb {Z}$. Consider again the decomposition
Let ![]() $C$ denote the cocore of the
$C$ denote the cocore of the ![]() $2$-handle of
$2$-handle of ![]() $D_n$. The boundary is the meridian
$D_n$. The boundary is the meridian ![]() $\mu _{U}$ of the unknot
$\mu _{U}$ of the unknot ![]() $U$ in the surgery diagram for
$U$ in the surgery diagram for ![]() $L(n,1)$ as the boundary of
$L(n,1)$ as the boundary of ![]() $D_n$. We see that
$D_n$. We see that ![]() $H_2(S^{2}\widetilde{\times } S^{2})$ is generated by
$H_2(S^{2}\widetilde{\times } S^{2})$ is generated by ![]() $S$, the base sphere of
$S$, the base sphere of ![]() $D_n$, and
$D_n$, and ![]() $\Delta _0:= -C\cup \mu _{U}\times I\cup C$. Note that
$\Delta _0:= -C\cup \mu _{U}\times I\cup C$. Note that ![]() $\Delta _0\cdot \Delta _0=0$. Now define
$\Delta _0\cdot \Delta _0=0$. Now define ![]() $\Delta :=G^{-1}(\Delta _0)$. By construction,
$\Delta :=G^{-1}(\Delta _0)$. By construction, ![]() $f^{-1}(\mu _{U})=\mu _K$. Moreover,
$f^{-1}(\mu _{U})=\mu _K$. Moreover, ![]() $\overline {f}^{-1}(C)$ is a cocore of the
$\overline {f}^{-1}(C)$ is a cocore of the ![]() $2$-handle of
$2$-handle of ![]() $X_n(K)$ by Lemma 4.4. Thus
$X_n(K)$ by Lemma 4.4. Thus ![]() $G^{-1}(\mu _{U}\times I\cup C)$ is a null-homology for
$G^{-1}(\mu _{U}\times I\cup C)$ is a null-homology for ![]() $\mu _K\subset S_n^{3}(K)$ in
$\mu _K\subset S_n^{3}(K)$ in ![]() $V\cup D_n$ and
$V\cup D_n$ and ![]() $\Delta$ has the form promised in the previous paragraph. Consequently,
$\Delta$ has the form promised in the previous paragraph. Consequently, ![]() $H_2(Z)\cong \mathbb {Z}\oplus \mathbb {Z}$ is generated by
$H_2(Z)\cong \mathbb {Z}\oplus \mathbb {Z}$ is generated by ![]() $\{S,\Delta \}$ and
$\{S,\Delta \}$ and ![]() $H_2(S^{2}\widetilde{\times } S^{2})\cong \mathbb {Z}\oplus \mathbb {Z}$ is generated by
$H_2(S^{2}\widetilde{\times } S^{2})\cong \mathbb {Z}\oplus \mathbb {Z}$ is generated by ![]() $\{S,\Delta _0\}$. By construction,
$\{S,\Delta _0\}$. By construction, ![]() $G(S)=S$ and
$G(S)=S$ and ![]() $G(\Delta )=\Delta _0$. The map
$G(\Delta )=\Delta _0$. The map ![]() $G$ also induces an isomorphism
$G$ also induces an isomorphism ![]() $H_4(Z) \to H_4(S^{2}\widetilde{\times } S^{2})$, which follows from a calculation using naturality of the Mayer–Vietoris sequences corresponding to the decompositions of
$H_4(Z) \to H_4(S^{2}\widetilde{\times } S^{2})$, which follows from a calculation using naturality of the Mayer–Vietoris sequences corresponding to the decompositions of ![]() $Z$ and
$Z$ and ![]() $S^{2}\widetilde{\times } S^{2}$ in the definition of
$S^{2}\widetilde{\times } S^{2}$ in the definition of ![]() $G$ above. Thus we have shown that
$G$ above. Thus we have shown that ![]() $G$ induces isomorphisms on the homology groups of
$G$ induces isomorphisms on the homology groups of ![]() $Z$ and
$Z$ and ![]() $S^{2}\widetilde{\times } S^{2}$. Since
$S^{2}\widetilde{\times } S^{2}$. Since ![]() $Z$ and
$Z$ and ![]() $S^{2}\widetilde{\times } S^{2}$ are simply connected, this completes the proof that
$S^{2}\widetilde{\times } S^{2}$ are simply connected, this completes the proof that ![]() $G$ is a homotopy equivalence by Whitehead's theorem and the fact that any
$G$ is a homotopy equivalence by Whitehead's theorem and the fact that any ![]() $4$-manifold is homotopy equivalent to a cell complex. Moreover, since
$4$-manifold is homotopy equivalent to a cell complex. Moreover, since ![]() $G$ is a homotopy equivalence,
$G$ is a homotopy equivalence, ![]() $\Delta \cdot \Delta =\Delta _0\cdot \Delta _0=0$.
$\Delta \cdot \Delta =\Delta _0\cdot \Delta _0=0$.
From now on we work only within the space ![]() $Z$. Note that
$Z$. Note that ![]() $Z$ is a closed, simply connected, topological
$Z$ is a closed, simply connected, topological ![]() $4$-manifold with intersection form
$4$-manifold with intersection form ![]() $[+1]\oplus [-1]$. By the classification of such
$[+1]\oplus [-1]$. By the classification of such ![]() $4$-manifolds [Reference FreedmanFre82],
$4$-manifolds [Reference FreedmanFre82], ![]() $Z$ is homeomorphic to either
$Z$ is homeomorphic to either ![]() $\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$ or
$\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$ or ![]() $*\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$. The remainder of the proof will use Lemma 6.6 to determine the homeomorphism type of
$*\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$. The remainder of the proof will use Lemma 6.6 to determine the homeomorphism type of ![]() $Z$. To do this we need to find elements of
$Z$. To do this we need to find elements of ![]() $\pi _2(Z)$ with self-intersection
$\pi _2(Z)$ with self-intersection ![]() $\pm 1$.
$\pm 1$.
Let ![]() $S'$ denote an immersed sphere within
$S'$ denote an immersed sphere within ![]() $-X_n(K)\subset Z$ representing a generator of
$-X_n(K)\subset Z$ representing a generator of ![]() $\pi _2(-X_n(K))$. We know that
$\pi _2(-X_n(K))$. We know that ![]() $S'\cdot S'=-n$ within
$S'\cdot S'=-n$ within ![]() $Z$. Here the sign has changed since
$Z$. Here the sign has changed since ![]() $Z$ contains the oriented manifold
$Z$ contains the oriented manifold ![]() $-X_n(K)$ rather than
$-X_n(K)$ rather than ![]() $X_n(K)$. The pair
$X_n(K)$. The pair ![]() $\{[S],[\Delta ]\}$ is a basis for
$\{[S],[\Delta ]\}$ is a basis for ![]() $H_2(Z)$ and we calculate that
$H_2(Z)$ and we calculate that ![]() $[S']=[S]-n[\Delta ]$. Here we have also used the facts that
$[S']=[S]-n[\Delta ]$. Here we have also used the facts that ![]() $S'\cdot \Delta =1$,
$S'\cdot \Delta =1$, ![]() $S\cdot \Delta =1$, and
$S\cdot \Delta =1$, and ![]() $S\cdot S=n$. Add local cusps to arrange that
$S\cdot S=n$. Add local cusps to arrange that ![]() $\mu (S')=0$ and thus
$\mu (S')=0$ and thus ![]() $S'\cdot S'=e(S')=-n$.
$S'\cdot S'=e(S')=-n$.
Next we seek the classes in ![]() $H_2(Z)\cong \pi _2(Z)$ with self-intersection
$H_2(Z)\cong \pi _2(Z)$ with self-intersection ![]() $\pm 1$. Since
$\pm 1$. Since ![]() $n$ is odd, it can be represented as
$n$ is odd, it can be represented as ![]() $n=2k+1$ for some integer
$n=2k+1$ for some integer ![]() $k$. Straightforward algebra implies that
$k$. Straightforward algebra implies that ![]() $[S]-k[\Delta ]=[S']+(k+1)[\Delta ]$ is the unique class, up to sign, with self-intersection
$[S]-k[\Delta ]=[S']+(k+1)[\Delta ]$ is the unique class, up to sign, with self-intersection ![]() $+1$ and that
$+1$ and that ![]() $[S']+k[\Delta ]=[S]-(k+1)[\Delta ]$ is the unique class, up to sign, that has self-intersection
$[S']+k[\Delta ]=[S]-(k+1)[\Delta ]$ is the unique class, up to sign, that has self-intersection ![]() $-1$. That is,
$-1$. That is,
and so ![]() $b \in \mathbb {Z}$ only if
$b \in \mathbb {Z}$ only if ![]() $a=\pm 1$.
$a=\pm 1$.
Our goal is to compute the ![]() $\tau$ invariant of the sum of these classes, since this determines the homeomorphism type of
$\tau$ invariant of the sum of these classes, since this determines the homeomorphism type of ![]() $Z$ by Lemma 6.6. We must first check that the sum is
$Z$ by Lemma 6.6. We must first check that the sum is ![]() $s$-characteristic. This is virtually the same computation as in Lemma 6.6. We compute the sum
$s$-characteristic. This is virtually the same computation as in Lemma 6.6. We compute the sum ![]() $([S]-k[\Delta ])+([S']+k[\Delta ])=[S]+[S']$. Let
$([S]-k[\Delta ])+([S']+k[\Delta ])=[S]+[S']$. Let ![]() $a[S]+b[\Delta ]$ be any class in
$a[S]+b[\Delta ]$ be any class in ![]() $\pi _2(Z)$. Then
$\pi _2(Z)$. Then ![]() $([S]+[S'])\cdot (a[S]+b[\Delta ])\equiv a \mod {2}$ and
$([S]+[S'])\cdot (a[S]+b[\Delta ])\equiv a \mod {2}$ and ![]() $(a[S]+b[\Delta ])\cdot {(a[S]+b[\Delta ])}\equiv a^{2} \mod {2}$. Since
$(a[S]+b[\Delta ])\cdot {(a[S]+b[\Delta ])}\equiv a^{2} \mod {2}$. Since ![]() ${a\equiv a^{2}\mod {2}}$, this shows that
${a\equiv a^{2}\mod {2}}$, this shows that ![]() $[S]+[S']$ is
$[S]+[S']$ is ![]() $s$-characteristic.
$s$-characteristic.
Finally, we compute ![]() $\tau (([S]-k[\Delta ])+([S']+k[\Delta ]))=\tau ([S]+[S'])$. Represent the class
$\tau (([S]-k[\Delta ])+([S']+k[\Delta ]))=\tau ([S]+[S'])$. Represent the class ![]() $[S]+[S']$ by a sphere
$[S]+[S']$ by a sphere ![]() $\Sigma$ obtained by tubing together
$\Sigma$ obtained by tubing together ![]() $S$ and
$S$ and ![]() $S'$. Observe that
$S'$. Observe that ![]() $\mu (\Sigma )=0$ since
$\mu (\Sigma )=0$ since ![]() $\mu (S')=\mu (S)=\lambda (S,S')=0$.
$\mu (S')=\mu (S)=\lambda (S,S')=0$.
In order to compute ![]() $\tau (\Sigma )$, pair up the self-intersections of
$\tau (\Sigma )$, pair up the self-intersections of ![]() $\Sigma$ by framed, generically immersed Whitney discs with pairwise disjoint and embedded boundaries. All the self-intersections of
$\Sigma$ by framed, generically immersed Whitney discs with pairwise disjoint and embedded boundaries. All the self-intersections of ![]() $\Sigma$ arise from self-intersections of
$\Sigma$ arise from self-intersections of ![]() $S'$ since
$S'$ since ![]() $S$ is embedded and
$S$ is embedded and ![]() $S$ and
$S$ and ![]() $S'$ are disjoint. We have Whitney discs
$S'$ are disjoint. We have Whitney discs ![]() $\{W_i\}$ for the self-intersections of
$\{W_i\}$ for the self-intersections of ![]() $S'$ within
$S'$ within ![]() $D^{4}\subset -X_n(K)$ and by Proposition 6.5, we know that
$D^{4}\subset -X_n(K)$ and by Proposition 6.5, we know that ![]() $\operatorname {Arf}(K)=\sum _i S'\cdot \mathring {W_i}\mod {2}$. Then
$\operatorname {Arf}(K)=\sum _i S'\cdot \mathring {W_i}\mod {2}$. Then ![]() $\tau (\Sigma )=\operatorname {Arf}(K)$ and by Lemma 6.6,
$\tau (\Sigma )=\operatorname {Arf}(K)$ and by Lemma 6.6, ![]() $Z$ is homeomorphic to
$Z$ is homeomorphic to ![]() $\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$ if
$\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$ if ![]() $\operatorname {Arf}(K)=0$ and to
$\operatorname {Arf}(K)=0$ and to ![]() $*\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$ if
$*\mathbb {CP}^{2}\#\overline {\mathbb {CP}^{2}}$ if ![]() $\operatorname {Arf}(K)=1$. This completes the proof.
$\operatorname {Arf}(K)=1$. This completes the proof.
Proposition 6.8 Let ![]() $n$ be odd. Let
$n$ be odd. Let ![]() $D_n$ denote the
$D_n$ denote the ![]() $D^{2}$-bundle over
$D^{2}$-bundle over ![]() $S^{2}$ with euler number
$S^{2}$ with euler number ![]() $n$. Suppose that
$n$. Suppose that ![]() $S_n^{3}(K)$ is homology cobordant to
$S_n^{3}(K)$ is homology cobordant to ![]() $L(n,1)$ via a cobordism
$L(n,1)$ via a cobordism ![]() $V$ which is homotopy equivalent to
$V$ which is homotopy equivalent to ![]() $L(n,1)\times I$ via a homotopy equivalence
$L(n,1)\times I$ via a homotopy equivalence ![]() $h$ that restricts to the identity on
$h$ that restricts to the identity on ![]() $L(n,1)$ and to the degree-one normal map
$L(n,1)$ and to the degree-one normal map ![]() $j$ on
$j$ on ![]() $S_n^{3}(K)$ from Lemma 4.4. Let
$S_n^{3}(K)$ from Lemma 4.4. Let ![]() $X$ be the union of
$X$ be the union of ![]() $V$ and
$V$ and ![]() $D_n$. Then
$D_n$. Then ![]() $\operatorname {Arf}(K) = \operatorname {ks}(X)$.
$\operatorname {Arf}(K) = \operatorname {ks}(X)$.
Proof. Consider the union ![]() $Z:= -X_n(K)\cup X$. Since
$Z:= -X_n(K)\cup X$. Since ![]() $\operatorname {ks}(X_n(K))=0$, we have that
$\operatorname {ks}(X_n(K))=0$, we have that ![]() $\operatorname {ks}(Z) = \operatorname {ks}(X)$ by additivity of the Kirby–Siebenmann invariant [Reference Friedl, Nagel, Orson and PowellFNOP19, Theorem 8.2]. From Lemma 6.7, we know that if
$\operatorname {ks}(Z) = \operatorname {ks}(X)$ by additivity of the Kirby–Siebenmann invariant [Reference Friedl, Nagel, Orson and PowellFNOP19, Theorem 8.2]. From Lemma 6.7, we know that if ![]() $\operatorname {Arf}(K)=0$, then
$\operatorname {Arf}(K)=0$, then ![]() $Z$ is homeomorphic to
$Z$ is homeomorphic to ![]() $\mathbb {CP}^{2} \# \overline {\mathbb {CP}^{2}}$, which is smooth and thus
$\mathbb {CP}^{2} \# \overline {\mathbb {CP}^{2}}$, which is smooth and thus ![]() $\operatorname {ks}(Z)=0$. If
$\operatorname {ks}(Z)=0$. If ![]() $\operatorname {Arf}(K)=1$, we saw that
$\operatorname {Arf}(K)=1$, we saw that ![]() $Z$ is homeomorphic to
$Z$ is homeomorphic to ![]() $*\mathbb {CP}^{2} \# \overline {\mathbb {CP}^{2}}$ and we have that
$*\mathbb {CP}^{2} \# \overline {\mathbb {CP}^{2}}$ and we have that ![]() $\operatorname {ks}(*\mathbb {CP}^{2} \# \overline {\mathbb {CP}^{2}})=\operatorname {ks}(*\mathbb {CP}^{2})+\operatorname {ks}(\overline {\mathbb {CP}^{2}})=1$ since the Kirby–Siebenmann invariant is additive under connected sum. This completes the proof.
$\operatorname {ks}(*\mathbb {CP}^{2} \# \overline {\mathbb {CP}^{2}})=\operatorname {ks}(*\mathbb {CP}^{2})+\operatorname {ks}(\overline {\mathbb {CP}^{2}})=1$ since the Kirby–Siebenmann invariant is additive under connected sum. This completes the proof.
7. Proof of Theorem 1.1
In order to prove Theorem 1.1, we need the following result of Boyer.
Theorem 7.1 [Reference BoyerBoy86, Theorems 0.1 and 0.7; Proposition 0.8(i)]
For ![]() $i=1,2$, let
$i=1,2$, let ![]() $V_i$ be a compact, simply connected, oriented, topological 4-manifold with boundary a rational homology 3-sphere.
$V_i$ be a compact, simply connected, oriented, topological 4-manifold with boundary a rational homology 3-sphere.
An orientation preserving homeomorphism ![]() $f\colon \partial V_1\to \partial V_2$ extends to an orientation preserving homeomorphism
$f\colon \partial V_1\to \partial V_2$ extends to an orientation preserving homeomorphism ![]() $F \colon V_1 \to V_2$ if and only if the following two conditions hold.
$F \colon V_1 \to V_2$ if and only if the following two conditions hold.
(1) There exists an isomorphism
 $\Lambda \colon H_2(V_1) \to H_2(V_2)$, inducing an isometry of intersection forms such that the following diagram commutes:
where
$\Lambda \colon H_2(V_1) \to H_2(V_2)$, inducing an isometry of intersection forms such that the following diagram commutes:
where
 $\Lambda ^{*}$ indicates the
$\Lambda ^{*}$ indicates the  $\operatorname {Hom}$-dual of
$\operatorname {Hom}$-dual of  $\Lambda$, together with the implicit use of the identifications
$\Lambda$, together with the implicit use of the identifications  $H_2(V_i,\partial V_i)\cong H^{2}(V_i)\cong \operatorname {Hom}(H_2(V_i),\mathbb {Z})$, coming from Poincaré–Lefschetz duality, and the universal coefficient theorem respectively.
$H_2(V_i,\partial V_i)\cong H^{2}(V_i)\cong \operatorname {Hom}(H_2(V_i),\mathbb {Z})$, coming from Poincaré–Lefschetz duality, and the universal coefficient theorem respectively.(2) Either the intersection form on
 $H_2(V_1)$ is even or
$H_2(V_1)$ is even or  $\operatorname {ks}(V_1)= \operatorname {ks}(V_2)$.
$\operatorname {ks}(V_1)= \operatorname {ks}(V_2)$.
In our applications, the homeomorphism ![]() $f$ we propose to extend will be the identity map. We remark that when using this theorem, the specific homeomorphism
$f$ we propose to extend will be the identity map. We remark that when using this theorem, the specific homeomorphism ![]() $f$, or more precisely the induced map
$f$, or more precisely the induced map ![]() $f_*$, is highly significant. We illustrate this with an example.
$f_*$, is highly significant. We illustrate this with an example.
Example 7.2 A construction of Brakes gives examples of knots ![]() $K, J \subset S^{3}$ with homeomorphic
$K, J \subset S^{3}$ with homeomorphic ![]() $n$-surgeries but with non-homeomorphic
$n$-surgeries but with non-homeomorphic ![]() $n$-traces, as follows. By [Reference BrakesBra80, Example 3], for any two distinct integers
$n$-traces, as follows. By [Reference BrakesBra80, Example 3], for any two distinct integers ![]() $a$ and
$a$ and ![]() $b$ with
$b$ with ![]() $|a|, |b| > 1$, the knots
$|a|, |b| > 1$, the knots ![]() $K_{a,b}:= C_{a, ab^{2}+1}(T_{b,b+1})$ and
$K_{a,b}:= C_{a, ab^{2}+1}(T_{b,b+1})$ and ![]() $K_{b,a}:= C_{b, a^{2}b+1}(T_{a,a+1})$ have homeomorphic
$K_{b,a}:= C_{b, a^{2}b+1}(T_{a,a+1})$ have homeomorphic ![]() $(a^{2}b^{2}-1)$-surgeries. Brakes’ homeomorphism induces a map on the first homology groups of the boundary, which are isomorphic to
$(a^{2}b^{2}-1)$-surgeries. Brakes’ homeomorphism induces a map on the first homology groups of the boundary, which are isomorphic to ![]() $\mathbb {Z}/ (a^{2}b^{2}-1)$ that is given by
$\mathbb {Z}/ (a^{2}b^{2}-1)$ that is given by ![]() $[\mu (K_{a,b})] \mapsto ab [\mu (K_{b,a})]$. Theorem 7.1 immediately implies that this homeomorphism of the boundaries does not extend to the traces. We now argue that no homeomorphism of the boundaries can extend to the traces by computing certain Tristram–Levine signatures of the knots.
$[\mu (K_{a,b})] \mapsto ab [\mu (K_{b,a})]$. Theorem 7.1 immediately implies that this homeomorphism of the boundaries does not extend to the traces. We now argue that no homeomorphism of the boundaries can extend to the traces by computing certain Tristram–Levine signatures of the knots.
It is straightforward to verify that Theorem 7.1 implies that if ![]() $f \colon S^{3}_n(K) \to S^{3}_n(J)$ is a homeomorphism which extends to a homeomorphism of the
$f \colon S^{3}_n(K) \to S^{3}_n(J)$ is a homeomorphism which extends to a homeomorphism of the ![]() $n$-traces, then
$n$-traces, then ![]() $f_*([\mu _K])= \pm [\mu _J] \in H_1(S^{3}_n(J))$. An argument as in Proposition 3.7 then shows that if
$f_*([\mu _K])= \pm [\mu _J] \in H_1(S^{3}_n(J))$. An argument as in Proposition 3.7 then shows that if ![]() $K$ and
$K$ and ![]() $J$ have homeomorphic
$J$ have homeomorphic ![]() $n$-traces then
$n$-traces then ![]() $\sigma _{\xi }(K)= \sigma _{\xi }(J)$ for every
$\sigma _{\xi }(K)= \sigma _{\xi }(J)$ for every ![]() $n$th root of unity
$n$th root of unity ![]() $\xi$. However, a straightforward computation using Litherland's formula for the signatures of a satellite knot and the well-known formula for the signatures of a torus knot [Reference LitherlandLit79] shows that
$\xi$. However, a straightforward computation using Litherland's formula for the signatures of a satellite knot and the well-known formula for the signatures of a torus knot [Reference LitherlandLit79] shows that
and hence ![]() $K_{3,5}= C_{3, 76}(T_{5,6})$ and
$K_{3,5}= C_{3, 76}(T_{5,6})$ and ![]() $K_{5,3}= C_{5, 46}(T_{3,4})$ do not have homeomorphic
$K_{5,3}= C_{5, 46}(T_{3,4})$ do not have homeomorphic ![]() $224$-traces despite having homeomorphic 224-surgeries. We remark to those interested in shake concordance that this example shows that even homeomorphism of the
$224$-traces despite having homeomorphic 224-surgeries. We remark to those interested in shake concordance that this example shows that even homeomorphism of the ![]() $n$-surgery is not enough to imply
$n$-surgery is not enough to imply ![]() $n$-shake concordance for general
$n$-shake concordance for general ![]() $n \in \mathbb {Z}$.
$n \in \mathbb {Z}$.
After this brief interlude, we prove the main theorem.
Proof of Theorem 1.1. Suppose that the generator of ![]() $\pi _2(X_n(K))$ can be represented by a locally flat embedded sphere
$\pi _2(X_n(K))$ can be represented by a locally flat embedded sphere ![]() $S$ such that
$S$ such that ![]() $\pi _1(X_n(K){{\smallsetminus }}S)\cong \mathbb {Z}/n$. Then Propositions 3.3 and 3.5 establish conditions (i) and (iii) respectively, using Lemma 3.1. Condition (ii) is established in Proposition 6.5 for all
$\pi _1(X_n(K){{\smallsetminus }}S)\cong \mathbb {Z}/n$. Then Propositions 3.3 and 3.5 establish conditions (i) and (iii) respectively, using Lemma 3.1. Condition (ii) is established in Proposition 6.5 for all ![]() $n$, and another proof is outlined in Remark 4.7 for even
$n$, and another proof is outlined in Remark 4.7 for even ![]() $n$.
$n$.
Now consider the converse. Using conditions (i) and (iii), Proposition 5.8 constructs a homology cobordism ![]() $V$ between
$V$ between ![]() $S^{3}_n(K)$ and
$S^{3}_n(K)$ and ![]() $L(n,1)$ along with a homotopy equivalence to
$L(n,1)$ along with a homotopy equivalence to ![]() $L(n,1)\times I$ restricting to the identity map on
$L(n,1)\times I$ restricting to the identity map on ![]() $L(n,1)$ and the standard degree-one collapse map on
$L(n,1)$ and the standard degree-one collapse map on ![]() $S^{3}_n(K)$. Let
$S^{3}_n(K)$. Let ![]() $X$ denote the union of
$X$ denote the union of ![]() $V$ and the disc bundle
$V$ and the disc bundle ![]() $D_n$ over
$D_n$ over ![]() $S^{2}$ with Euler number
$S^{2}$ with Euler number ![]() $n$. Note that
$n$. Note that ![]() $\pi _1(X)=\{1\}$,
$\pi _1(X)=\{1\}$, ![]() $\pi _2(X)=\mathbb {Z}$, and the intersection form is
$\pi _2(X)=\mathbb {Z}$, and the intersection form is ![]() $[n]$, which presents the linking form
$[n]$, which presents the linking form ![]() $[1/n]$ on
$[1/n]$ on ![]() $S_n^{3}(K)$.
$S_n^{3}(K)$.
Suppose ![]() $n$ is even. Then Boyer's classification (Theorem 7.1) implies that
$n$ is even. Then Boyer's classification (Theorem 7.1) implies that ![]() $X \cong X_n(K)$, extending the identity map on the boundary. Suppose
$X \cong X_n(K)$, extending the identity map on the boundary. Suppose ![]() $n$ is odd. By Proposition 6.8,
$n$ is odd. By Proposition 6.8, ![]() $\operatorname {Arf}(K)=0$ implies that
$\operatorname {Arf}(K)=0$ implies that ![]() $\operatorname {ks}(X)=0$, which implies by Boyer's classification (Theorem 7.1) that
$\operatorname {ks}(X)=0$, which implies by Boyer's classification (Theorem 7.1) that ![]() $X \cong X_n(K)$, extending the identity map on the boundary. In either case, the image of the zero section of
$X \cong X_n(K)$, extending the identity map on the boundary. In either case, the image of the zero section of ![]() $D_n$ in
$D_n$ in ![]() $X_n(K)$ gives rise to a locally flat embedded sphere in
$X_n(K)$ gives rise to a locally flat embedded sphere in ![]() $X_n(K)$ representing a generator of
$X_n(K)$ representing a generator of ![]() $\pi _2(X_n(K))$.
$\pi _2(X_n(K))$.
8.  $\pm 1$-shake sliceness
$\pm 1$-shake sliceness
Recall that when ![]() $n=\pm 1$, the three conditions of Theorem 1.1 reduce to
$n=\pm 1$, the three conditions of Theorem 1.1 reduce to ![]() $\operatorname {Arf}(K)=0$. As noted in the introduction, there is a quick proof that if
$\operatorname {Arf}(K)=0$. As noted in the introduction, there is a quick proof that if ![]() $\operatorname {Arf}(K)=0$ then
$\operatorname {Arf}(K)=0$ then ![]() $K$ is
$K$ is ![]() $1$-shake slice.
$1$-shake slice.
Example 8.1 (The ‘if’ direction when ![]() $n=1$)
$n=1$)
Let ![]() $K$ be a knot with
$K$ be a knot with ![]() $\operatorname {Arf}(K)=0$. Since
$\operatorname {Arf}(K)=0$. Since ![]() $S^{3}_{ 1}(K)$ is a homology sphere, it bounds a contractible 4-manifold
$S^{3}_{ 1}(K)$ is a homology sphere, it bounds a contractible 4-manifold ![]() $C$, by [Reference FreedmanFre82, Theorem 1.4
$C$, by [Reference FreedmanFre82, Theorem 1.4![]() $'$] (see also [Reference Freedman and QuinnFQ90, 9.3C]). By removing a small ball from
$'$] (see also [Reference Freedman and QuinnFQ90, 9.3C]). By removing a small ball from ![]() $C$ we obtain a simply connected homology cobordism
$C$ we obtain a simply connected homology cobordism ![]() $V$ from
$V$ from ![]() $S^{3}_{1}(K)$ to
$S^{3}_{1}(K)$ to ![]() $S^{3}=S^{3}_{1}(U)$. Define
$S^{3}=S^{3}_{1}(U)$. Define ![]() $X:= V \cup _{S^{3}} X_{1}(U) \cong C \# \mathbb {CP}^{2}$, and observe that
$X:= V \cup _{S^{3}} X_{1}(U) \cong C \# \mathbb {CP}^{2}$, and observe that ![]() $X$ is a simply connected
$X$ is a simply connected ![]() $4$-manifold with boundary
$4$-manifold with boundary ![]() $S^{3}_{\pm 1}(K)$ and intersection form
$S^{3}_{\pm 1}(K)$ and intersection form ![]() $[ 1 ]$. By Boyer's classification (Theorem 7.1), the manifold
$[ 1 ]$. By Boyer's classification (Theorem 7.1), the manifold ![]() $X$ is homeomorphic to
$X$ is homeomorphic to ![]() $X_{1}(K)$ if and only if the Kirby–Siebenmann invariant
$X_{1}(K)$ if and only if the Kirby–Siebenmann invariant ![]() $\operatorname {ks}(X)=\operatorname {ks}(X_{1}(K))=0$.
$\operatorname {ks}(X)=\operatorname {ks}(X_{1}(K))=0$.
Since the Kirby–Siebenmann invariant is additive under connected sum [Reference Friedl, Nagel, Orson and PowellFNOP19, Theorem 8.2] and ![]() $\mathbb {CP}^{2}$ is smooth, we have
$\mathbb {CP}^{2}$ is smooth, we have ![]() $\operatorname {ks}(X)=\operatorname {ks}(C)+\operatorname {ks}(\mathbb {CP}^{2}) = \operatorname {ks}(C)$. Moreover
$\operatorname {ks}(X)=\operatorname {ks}(C)+\operatorname {ks}(\mathbb {CP}^{2}) = \operatorname {ks}(C)$. Moreover ![]() $C$ is contractible and hence is a topological spin manifold. By [Reference Freedman and QuinnFQ90, p. 165] and [Reference González-AcuñaGon70],
$C$ is contractible and hence is a topological spin manifold. By [Reference Freedman and QuinnFQ90, p. 165] and [Reference González-AcuñaGon70], ![]() $\operatorname {ks}(C)=\mu (S^{3}_1(K))=\operatorname {Arf}(K)=0$, where
$\operatorname {ks}(C)=\mu (S^{3}_1(K))=\operatorname {Arf}(K)=0$, where ![]() $\mu (S^{3}_1(K))$ is the Rochlin invariant of the homology sphere
$\mu (S^{3}_1(K))$ is the Rochlin invariant of the homology sphere ![]() $S^{3}_1(K)$. Thus we have a homeomorphism
$S^{3}_1(K)$. Thus we have a homeomorphism ![]() $X \to X_1(K)$ and the image of
$X \to X_1(K)$ and the image of ![]() $\mathbb {CP}^{1} \subset \mathbb {CP}^{2}$ is an embedded sphere with simply connected complement representing the generator of
$\mathbb {CP}^{1} \subset \mathbb {CP}^{2}$ is an embedded sphere with simply connected complement representing the generator of ![]() $\pi _2(X_1(K))$.
$\pi _2(X_1(K))$.
8.1 A Seifert surface approach
Now we describe yet another proof that, if ![]() $\operatorname {Arf}(K)=0$, then
$\operatorname {Arf}(K)=0$, then ![]() $K$ is
$K$ is ![]() $1$-shake slice. This proof is Seifert surface based and has the advantage that we control the number of intersections of the resulting 2-sphere with the cocore of the 2-handle, yielding an upper bound on the
$1$-shake slice. This proof is Seifert surface based and has the advantage that we control the number of intersections of the resulting 2-sphere with the cocore of the 2-handle, yielding an upper bound on the ![]() $1$-shaking number of knots. A similar proof for Theorem 1.1 when
$1$-shaking number of knots. A similar proof for Theorem 1.1 when ![]() $|n|\geq 2$, including similar control on the
$|n|\geq 2$, including similar control on the ![]() $n$-shaking number of
$n$-shaking number of ![]() $\mathbb {Z}/n$-shake slice knots, seems possible in principle, but we have not managed to find it yet.
$\mathbb {Z}/n$-shake slice knots, seems possible in principle, but we have not managed to find it yet.
Definition 8.2 A ![]() $(2k+1)$-component
$(2k+1)$-component ![]() $n$-shaking of a knot
$n$-shaking of a knot ![]() $K$ is a link
$K$ is a link ![]() $S_{2k+1, n}(K)$ obtained by taking
$S_{2k+1, n}(K)$ obtained by taking ![]() $2k+1$ push-offs with respect to the
$2k+1$ push-offs with respect to the ![]() $n$-framing, oriented so that
$n$-framing, oriented so that ![]() $k+1$ push-offs are oriented the same as
$k+1$ push-offs are oriented the same as ![]() $K$, and
$K$, and ![]() $k$ push-offs are oriented in the opposite direction.
$k$ push-offs are oriented in the opposite direction.
The link ![]() $S_{2k+1, n}(K)$ is the (untwisted) satellite link with companion
$S_{2k+1, n}(K)$ is the (untwisted) satellite link with companion ![]() $K$ and pattern
$K$ and pattern ![]() $S_{2k+1, n}$ as in Figure 1. It is determined up to isotopy by
$S_{2k+1, n}$ as in Figure 1. It is determined up to isotopy by ![]() $K$,
$K$, ![]() $n$, and
$n$, and ![]() $k$.
$k$.

Figure 1. The pattern ![]() $S_{3, 1}$.
$S_{3, 1}$.
Now we explain the well-known relationship between the existence of an embedded sphere in the ![]() $n$-trace
$n$-trace ![]() $X_n(K)$ and shakings
$X_n(K)$ and shakings ![]() $S_{2k+1,n}(K)$. Recall that a link
$S_{2k+1,n}(K)$. Recall that a link ![]() $L$ is weakly slice if
$L$ is weakly slice if ![]() $L$ bounds a locally flat planar surface in
$L$ bounds a locally flat planar surface in ![]() $D^{4}$.
$D^{4}$.
Lemma 8.3 Let ![]() $K$ be an oriented knot. There exists a surface of genus
$K$ be an oriented knot. There exists a surface of genus ![]() $g$ that represents the generator of
$g$ that represents the generator of ![]() $H_2(X_n(K); \mathbb {Z})$ if and only if, for some
$H_2(X_n(K); \mathbb {Z})$ if and only if, for some ![]() $k \geq 0$, the shaking
$k \geq 0$, the shaking ![]() $S_{2k+1,n}(K) \subset S^{3}$ bounds a surface of genus
$S_{2k+1,n}(K) \subset S^{3}$ bounds a surface of genus ![]() $g$ in
$g$ in ![]() $D^{4}$. Consequently,
$D^{4}$. Consequently, ![]() $K$ is
$K$ is ![]() $n$-shake slice if and only if
$n$-shake slice if and only if ![]() $K$ admits a weakly slice
$K$ admits a weakly slice ![]() $n$-shaking
$n$-shaking ![]() $S_{2k+1,n}(K)$ for some
$S_{2k+1,n}(K)$ for some ![]() $k \in \mathbb {Z}$.
$k \in \mathbb {Z}$.
Proof. The if direction follows from the observation that any filling surface in ![]() $D^{4}$ for the shaking
$D^{4}$ for the shaking ![]() $S_{2k+1,n}(K)$ can be capped of with
$S_{2k+1,n}(K)$ can be capped of with ![]() $2k+1$ parallel copies of the two-handle to produce a surface that represents the generator of
$2k+1$ parallel copies of the two-handle to produce a surface that represents the generator of ![]() $H_2(X_n(K); \mathbb {Z})$.
$H_2(X_n(K); \mathbb {Z})$.
For the only if direction, let ![]() $F$ be a surface of genus
$F$ be a surface of genus ![]() $g$ that represents the generator of
$g$ that represents the generator of ![]() $H_2(X_n(K); \mathbb {Z})$. Isotope
$H_2(X_n(K); \mathbb {Z})$. Isotope ![]() $F$ so that it is transverse to the cocore of the
$F$ so that it is transverse to the cocore of the ![]() $2$–handle. Cut
$2$–handle. Cut ![]() $X_n(K)$ along the cocore
$X_n(K)$ along the cocore ![]() $C$ to obtain back
$C$ to obtain back ![]() $D^{4}$. This punctures
$D^{4}$. This punctures ![]() $F$ to a surface
$F$ to a surface ![]() $F'$. The surface
$F'$. The surface ![]() $F'$ has the same genus as
$F'$ has the same genus as ![]() $F$ and is bounded by the shaking
$F$ and is bounded by the shaking ![]() $S_{2k+1,n}(K)$, where
$S_{2k+1,n}(K)$, where ![]() $2k+1$ is the geometric intersection number of
$2k+1$ is the geometric intersection number of ![]() $F$ with the cocore
$F$ with the cocore ![]() $C$.
$C$.
For ![]() $1$-shakings, we provide the following explicit variant of our main result Theorem 1.1. Recall that the
$1$-shakings, we provide the following explicit variant of our main result Theorem 1.1. Recall that the ![]() $($topological
$($topological ![]() $)$
$)$ ![]() $\mathbb {Z}$–slice genus
$\mathbb {Z}$–slice genus ![]() ${g_4^{\mathbb {Z}}}(L)$ of a link
${g_4^{\mathbb {Z}}}(L)$ of a link ![]() $L$ is the smallest genus among
$L$ is the smallest genus among ![]() $\mathbb {Z}$-slice surfaces for
$\mathbb {Z}$-slice surfaces for ![]() $L$. Here, a
$L$. Here, a ![]() $\mathbb {Z}$–slice surface for
$\mathbb {Z}$–slice surface for ![]() $L$ is a properly, locally flatly embedded, compact, connected, and orientable surface in
$L$ is a properly, locally flatly embedded, compact, connected, and orientable surface in ![]() $D^{4}$ with boundary
$D^{4}$ with boundary ![]() $L$ and infinite cyclic fundamental group of the complement. For knots, the topological
$L$ and infinite cyclic fundamental group of the complement. For knots, the topological ![]() $\mathbb {Z}$-slice genus equals the algebraic genus
$\mathbb {Z}$-slice genus equals the algebraic genus ![]() ${g_{\operatorname {alg}}}$ [Reference Feller and LewarkFL19], which is a quantity depending only on the
${g_{\operatorname {alg}}}$ [Reference Feller and LewarkFL19], which is a quantity depending only on the ![]() $S$-equivalence class of the Seifert form of knots and that in particular satisfies
$S$-equivalence class of the Seifert form of knots and that in particular satisfies ![]() ${g_4^{\mathbb {Z}}}(K)={g_{\operatorname {alg}}}(K)\leq \deg (\Delta _K)/2\leq g_3(K)$. Here
${g_4^{\mathbb {Z}}}(K)={g_{\operatorname {alg}}}(K)\leq \deg (\Delta _K)/2\leq g_3(K)$. Here ![]() $g_3$ denotes the 3-genus.
$g_3$ denotes the 3-genus.
For our purposes, it will suffice to define ![]() ${g_{\operatorname {alg}}}(K)$ to be the minimal
${g_{\operatorname {alg}}}(K)$ to be the minimal ![]() $g$ such that there exists a Seifert surface
$g$ such that there exists a Seifert surface ![]() $S$ for
$S$ for ![]() $K$ and a basis for
$K$ and a basis for ![]() $H_1(S)$ with respect to which the Seifert form is given by
$H_1(S)$ with respect to which the Seifert form is given by ![]() $\big [\begin {smallmatrix}A & B \\ B^{T} & C \end {smallmatrix}\big ]$, where
$\big [\begin {smallmatrix}A & B \\ B^{T} & C \end {smallmatrix}\big ]$, where ![]() $C$ is a
$C$ is a ![]() $2g \times 2g$ matrix and
$2g \times 2g$ matrix and ![]() $A$ is Alexander trivial, i.e.
$A$ is Alexander trivial, i.e. ![]() $\det (tA-A^{T})$ is some power of
$\det (tA-A^{T})$ is some power of ![]() $t$. From this definition, one can see that
$t$. From this definition, one can see that ![]() ${g_{\operatorname {alg}}}(K)$ gives a lower bound on the topological
${g_{\operatorname {alg}}}(K)$ gives a lower bound on the topological ![]() $\mathbb {Z}$-slice genus of
$\mathbb {Z}$-slice genus of ![]() $K$:
$K$: ![]() $A$ corresponds to a subsurface
$A$ corresponds to a subsurface ![]() $S_A$ of
$S_A$ of ![]() $S$ with boundary
$S$ with boundary ![]() $\partial S_A= J_A$, where
$\partial S_A= J_A$, where ![]() $J_A$ has trivial Alexander polynomial, and so surgering
$J_A$ has trivial Alexander polynomial, and so surgering ![]() $S$ along
$S$ along ![]() $J_A$ gives a
$J_A$ gives a ![]() $\mathbb {Z}$-slice surface for
$\mathbb {Z}$-slice surface for ![]() $K$ of genus
$K$ of genus ![]() $g$. See [Reference Feller and LewarkFL18] for details on
$g$. See [Reference Feller and LewarkFL18] for details on ![]() ${g_{\operatorname {alg}}}$.
${g_{\operatorname {alg}}}$.
Proposition 8.4 Let ![]() $K$ be a knot with algebraic genus
$K$ be a knot with algebraic genus ![]() ${g_{\operatorname {alg}}}(K)$. Suppose
${g_{\operatorname {alg}}}(K)$. Suppose ![]() ${g_{\operatorname {alg}}}(K)\geq h > 0$. Then there exists a
${g_{\operatorname {alg}}}(K)\geq h > 0$. Then there exists a ![]() $\mathbb {Z}$-slice surface with genus
$\mathbb {Z}$-slice surface with genus ![]() $h$ for the
$h$ for the ![]() $1$-shaking of
$1$-shaking of ![]() $K$ with
$K$ with ![]() $2(g_{\rm alg}(K) - h) + 1$-components. If
$2(g_{\rm alg}(K) - h) + 1$-components. If ![]() $K$ has trivial Arf invariant, then the statement also holds for
$K$ has trivial Arf invariant, then the statement also holds for ![]() $h=0$, i.e. there exists a
$h=0$, i.e. there exists a ![]() $\mathbb {Z}$-slice genus
$\mathbb {Z}$-slice genus ![]() $0$ surface for a
$0$ surface for a ![]() $2g_{\rm alg}(K) + 1$-component
$2g_{\rm alg}(K) + 1$-component ![]() $1$-shaking of
$1$-shaking of ![]() $K$.
$K$.
Let ![]() $K$ be a knot satisfying the assumptions of Proposition 8.4. Thus, we obtain a
$K$ be a knot satisfying the assumptions of Proposition 8.4. Thus, we obtain a ![]() $\mathbb {Z}$-slice surface
$\mathbb {Z}$-slice surface ![]() $S$ with boundary a
$S$ with boundary a ![]() $1$–shaking of
$1$–shaking of ![]() $K$ and genus
$K$ and genus ![]() $h$. Now cap off
$h$. Now cap off ![]() $S$ with parallel copies of the core of the
$S$ with parallel copies of the core of the ![]() $2$-handle of
$2$-handle of ![]() $X_1(K)$ to obtain a closed
$X_1(K)$ to obtain a closed ![]() $\mathbb {Z}$-slice surface of genus
$\mathbb {Z}$-slice surface of genus ![]() $h$ in
$h$ in ![]() $X_1(K)$, which represents a generator of
$X_1(K)$, which represents a generator of ![]() $H_2(X_1(K);\mathbb {Z})$. We have shown the following corollary.
$H_2(X_1(K);\mathbb {Z})$. We have shown the following corollary.
Corollary 8.5 For a knot ![]() $K$ with
$K$ with ![]() ${g_{\operatorname {alg}}}(K)\geq h>0$, the generator of
${g_{\operatorname {alg}}}(K)\geq h>0$, the generator of ![]() $H_2(X_1(K);\mathbb {Z})$ can be represented by a locally flat genus
$H_2(X_1(K);\mathbb {Z})$ can be represented by a locally flat genus ![]() $h$ surface whose complement is simply connected and that has geometric intersection number
$h$ surface whose complement is simply connected and that has geometric intersection number ![]() $2({g_{\operatorname {alg}}}(K) -h)+1$ with the cocore of the 2-handle. If
$2({g_{\operatorname {alg}}}(K) -h)+1$ with the cocore of the 2-handle. If ![]() $K$ has trivial Arf invariant, then the statement also holds for
$K$ has trivial Arf invariant, then the statement also holds for ![]() $h=0$.
$h=0$.
Proposition 8.4 and Corollary 8.5 give an explicit bound on the genus and the number of points of intersection with the cocore of the 2-handle in terms of ![]() ${g_{\operatorname {alg}}}(K)$, a quantity accessible in terms of Seifert matrices, and which is bounded above by the 3-genus. In particular, this together with the next remark yield Propositions 8.7 and 8.8 from the introduction.
${g_{\operatorname {alg}}}(K)$, a quantity accessible in terms of Seifert matrices, and which is bounded above by the 3-genus. In particular, this together with the next remark yield Propositions 8.7 and 8.8 from the introduction.
Remark 8.6 For a locally flat genus ![]() $g$ surface
$g$ surface ![]() $F$ that represents a generator of
$F$ that represents a generator of ![]() $H_2(X_n(K);\mathbb {Z})$ and that intersects the cocore of the 2-handle transversely
$H_2(X_n(K);\mathbb {Z})$ and that intersects the cocore of the 2-handle transversely ![]() $2k+1$ times, one has
$2k+1$ times, one has ![]() ${g^{\operatorname {top}}_4}(K)\leq g+k$. Here
${g^{\operatorname {top}}_4}(K)\leq g+k$. Here ![]() ${g^{\operatorname {top}}_4}(K)$ denotes the (topological) slice genus of a knot
${g^{\operatorname {top}}_4}(K)$ denotes the (topological) slice genus of a knot ![]() $K$.
$K$.
Indeed, as in the proof of Lemma 8.3, we find a locally flat connected surface in ![]() $D^{4}$ with genus
$D^{4}$ with genus ![]() $g$ and boundary the shaking
$g$ and boundary the shaking ![]() $L=S_{2k+1,n}(K)$. Since
$L=S_{2k+1,n}(K)$. Since ![]() $2k$ saddle/band moves turn
$2k$ saddle/band moves turn ![]() $L$ into
$L$ into ![]() $K$, we find a genus
$K$, we find a genus ![]() $g+k$ locally flat surface in
$g+k$ locally flat surface in ![]() $D^{4}$ with boundary
$D^{4}$ with boundary ![]() $K$. Hence
$K$. Hence ![]() ${g^{\operatorname {top}}_4}(K)\leq g+k$.
${g^{\operatorname {top}}_4}(K)\leq g+k$.
Proposition 8.7 For every knot ![]() $K$ there exists a locally flat embedded torus in
$K$ there exists a locally flat embedded torus in ![]() $X_1(K)$ that generates
$X_1(K)$ that generates ![]() $H_2(X_1(K))$ and has simply connected complement. In particular,
$H_2(X_1(K))$ and has simply connected complement. In particular,
Proof. For knots with Arf invariant ![]() $1$, setting
$1$, setting ![]() $h=1$ in Corollary 8.5 provides a locally flat torus with simply connected complement representing a generator of
$h=1$ in Corollary 8.5 provides a locally flat torus with simply connected complement representing a generator of ![]() $H_2(X_1(K);\mathbb {Z})$. For knots with Arf invariant
$H_2(X_1(K);\mathbb {Z})$. For knots with Arf invariant ![]() $0$, we even find a locally flat sphere whose complement is simply connected by setting
$0$, we even find a locally flat sphere whose complement is simply connected by setting ![]() $h=0$ in Corollary 8.5.
$h=0$ in Corollary 8.5.
Proposition 8.8 For a knot ![]() $K$ with
$K$ with ![]() $\operatorname {Arf}(K)=0$ we have
$\operatorname {Arf}(K)=0$ we have
In particular, for each integer ![]() $k \geq 0$ there exists a
$k \geq 0$ there exists a ![]() $1$-shake slice knot
$1$-shake slice knot ![]() $K_k$ such that the
$K_k$ such that the ![]() $1$-shaking number of
$1$-shaking number of ![]() $K_k$ is exactly
$K_k$ is exactly ![]() $2k+1$.
$2k+1$.
Proof. Corollary 8.5 gives a sphere that has geometric intersection number ![]() $2({g_{\operatorname {alg}}}(K))+1$ with the cocore of the 2-handle. Hence the
$2({g_{\operatorname {alg}}}(K))+1$ with the cocore of the 2-handle. Hence the ![]() $1$-shake slice number of knots with Arf invariant
$1$-shake slice number of knots with Arf invariant ![]() $0$ is less than or equal to
$0$ is less than or equal to ![]() $2{g_{\operatorname {alg}}}(K)+1$. We already know that
$2{g_{\operatorname {alg}}}(K)+1$. We already know that ![]() ${g_4^{\mathbb {Z}}}(K) = {g_{\operatorname {alg}}}(K) \leq g_3(K)$ from [Reference Feller and LewarkFL19]. To obtain the first inequality, note that for any 2-sphere that realises the
${g_4^{\mathbb {Z}}}(K) = {g_{\operatorname {alg}}}(K) \leq g_3(K)$ from [Reference Feller and LewarkFL19]. To obtain the first inequality, note that for any 2-sphere that realises the ![]() $1$-shake slice number
$1$-shake slice number ![]() $2k+1$, we have
$2k+1$, we have ![]() ${g^{\operatorname {top}}_4}(K)\leq 0+ k = k$ by Remark 8.6.
${g^{\operatorname {top}}_4}(K)\leq 0+ k = k$ by Remark 8.6.
For the second sentence, take ![]() $K_k$ to be an Arf invariant 0 knot with
$K_k$ to be an Arf invariant 0 knot with ![]() ${g^{\operatorname {top}}_4(K)=g_3(K)=k}$. For example, let
${g^{\operatorname {top}}_4(K)=g_3(K)=k}$. For example, let ![]() $K_k$ be the
$K_k$ be the ![]() $k$-fold connected sum of
$k$-fold connected sum of ![]() $5_2$, the twist knot with
$5_2$, the twist knot with ![]() $5$ crossings. This satisfies
$5$ crossings. This satisfies ![]() $|\sigma (K)|=2g_3(K)=2$, and thus
$|\sigma (K)|=2g_3(K)=2$, and thus ![]() ${g^{\operatorname {top}}_4}(K)=g_3(K)=1$ by the Murasugi–Tristram inequality relating the signature and the slice genus.
${g^{\operatorname {top}}_4}(K)=g_3(K)=1$ by the Murasugi–Tristram inequality relating the signature and the slice genus.
Next we describe a Seifert surface (and the corresponding Seifert matrix) for ![]() $S_{2k+1,n}(K)$. For this, one could iterate a construction of Tristram [Reference TristramTri69, Definition 3.1] and extract the Seifert form from his proof of signature invariance [Reference TristramTri69, Theorem 3.2], but, for the convenience of the reader, we give an argument in Lemma 8.9 below. Although, we will only need the case
$S_{2k+1,n}(K)$. For this, one could iterate a construction of Tristram [Reference TristramTri69, Definition 3.1] and extract the Seifert form from his proof of signature invariance [Reference TristramTri69, Theorem 3.2], but, for the convenience of the reader, we give an argument in Lemma 8.9 below. Although, we will only need the case ![]() $n=1$ here, we give the general statement for future reference.
$n=1$ here, we give the general statement for future reference.
For any ![]() $k$ and
$k$ and ![]() $n$,
$n$, ![]() $S_{2k+1,n}$ is a winding number
$S_{2k+1,n}$ is a winding number ![]() $1$ pattern, and so we can construct a Seifert surface
$1$ pattern, and so we can construct a Seifert surface ![]() $F_{2k+1,n}$ for
$F_{2k+1,n}$ for ![]() $S_{2k+1,n}(K)$ as the union of two pieces. The first is a surface in the solid torus identified with
$S_{2k+1,n}(K)$ as the union of two pieces. The first is a surface in the solid torus identified with ![]() $\nu (K)$, and illustrated in Figure 2. The second is a Seifert surface for
$\nu (K)$, and illustrated in Figure 2. The second is a Seifert surface for ![]() $K$ outside a tubular neighbourhood
$K$ outside a tubular neighbourhood ![]() $\nu K$.
$\nu K$.

Figure 2. The portion of the Seifert surface ![]() $F_{2k+1,n}$ contained in
$F_{2k+1,n}$ contained in ![]() $\nu (K)$, drawn for
$\nu (K)$, drawn for ![]() $n = 2$ and
$n = 2$ and ![]() $k=3$. Each
$k=3$. Each ![]() $+1$-box denotes a positive full twist on
$+1$-box denotes a positive full twist on ![]() $2k$ strands. The left and right edges of the figure are identified. The figure also shows curves,
$2k$ strands. The left and right edges of the figure are identified. The figure also shows curves, ![]() $\alpha _j^{i}$ and
$\alpha _j^{i}$ and ![]() $\beta _j^{i}$, on the Seifert surface forming part of a generating set for
$\beta _j^{i}$, on the Seifert surface forming part of a generating set for ![]() $H_1(F_{2k+1,n};\mathbb {Z})$. The dashed line on the top is glued to a Seifert surface for
$H_1(F_{2k+1,n};\mathbb {Z})$. The dashed line on the top is glued to a Seifert surface for ![]() $K$.
$K$.
Let ![]() $Z_n \in \operatorname {GL}(n,\mathbb {Z})$ be the permutation matrix corresponding to the cyclic permutation
$Z_n \in \operatorname {GL}(n,\mathbb {Z})$ be the permutation matrix corresponding to the cyclic permutation ![]() $\sigma = (1 \ldots n)$, with entries are given by
$\sigma = (1 \ldots n)$, with entries are given by ![]() $(Z_n)_{i,j}=\delta _{i, \sigma (j)}$. That is,
$(Z_n)_{i,j}=\delta _{i, \sigma (j)}$. That is,
 \[ Z_n = \begin{pmatrix} 0 & 0 & \ldots & 0 & 1\\ 1 & 0 & \ldots & 0 & 0\\ 0 & 1 & \ldots & 0 & 0\\ \vdots & & \ddots & & \vdots\\ 0 & 0 & \ldots & 1 & 0 \end{pmatrix}. \]
\[ Z_n = \begin{pmatrix} 0 & 0 & \ldots & 0 & 1\\ 1 & 0 & \ldots & 0 & 0\\ 0 & 1 & \ldots & 0 & 0\\ \vdots & & \ddots & & \vdots\\ 0 & 0 & \ldots & 1 & 0 \end{pmatrix}. \]Lemma 8.9 Let ![]() $V$ be a Seifert matrix for the knot
$V$ be a Seifert matrix for the knot ![]() $K$. The Seifert surface
$K$. The Seifert surface ![]() $F_{2k+1,n}$ for the
$F_{2k+1,n}$ for the ![]() $(2k+1)$-component
$(2k+1)$-component ![]() $n$-shaking of
$n$-shaking of ![]() $K$ depicted in Figure 2 has Seifert form given by the matrix
$K$ depicted in Figure 2 has Seifert form given by the matrix
 \begin{equation} V\oplus \bigoplus_{j=1}^{k} \begin{pmatrix} 0 & \operatorname{Id}_n \\ Z_n & 0 \end{pmatrix}. \end{equation}
\begin{equation} V\oplus \bigoplus_{j=1}^{k} \begin{pmatrix} 0 & \operatorname{Id}_n \\ Z_n & 0 \end{pmatrix}. \end{equation}Proof. The Seifert surface ![]() $F_{2k+1,n}$ agrees with a Seifert surface
$F_{2k+1,n}$ agrees with a Seifert surface ![]() $S$ for
$S$ for ![]() $K$ outside a tubular neighbourhood
$K$ outside a tubular neighbourhood ![]() $\nu K$. We compute the Seifert form
$\nu K$. We compute the Seifert form ![]() $(x,y) \mapsto \operatorname {lk}(x, y^{+})$ of
$(x,y) \mapsto \operatorname {lk}(x, y^{+})$ of ![]() $F_{2k+1,n}$. The generators of
$F_{2k+1,n}$. The generators of ![]() $H_1(F_{2k+1,n}; \mathbb {Z})$ are given by the generators
$H_1(F_{2k+1,n}; \mathbb {Z})$ are given by the generators ![]() $v_i$ of
$v_i$ of ![]() $S$, and the additional generators
$S$, and the additional generators ![]() $\alpha _i^{j}$ and
$\alpha _i^{j}$ and ![]() $\beta _i^{j}$, depicted in Figure 2, where
$\beta _i^{j}$, depicted in Figure 2, where ![]() $i = 0, \ldots , n-1$ and
$i = 0, \ldots , n-1$ and ![]() $j=1, \ldots , k$.
$j=1, \ldots , k$.
Denote the span ![]() $\langle v_1, \ldots , v_{2g} \rangle$ by
$\langle v_1, \ldots , v_{2g} \rangle$ by ![]() $C$, where
$C$, where ![]() $g$ is the genus of the Seifert surface of
$g$ is the genus of the Seifert surface of ![]() $K$ used to construct
$K$ used to construct ![]() $F_{2k+1,n}$. Also, for each
$F_{2k+1,n}$. Also, for each ![]() $j=1, \dots , k$ denote the span
$j=1, \dots , k$ denote the span ![]() $\langle \alpha _i^{j}, \beta _i^{j}\,|\, i = 0, \ldots , n-1\rangle$ by
$\langle \alpha _i^{j}, \beta _i^{j}\,|\, i = 0, \ldots , n-1\rangle$ by ![]() $D_j$. We say that two, possibly non-distinct curves
$D_j$. We say that two, possibly non-distinct curves ![]() $\gamma _1$ and
$\gamma _1$ and ![]() $\gamma _2$ are orthogonal if
$\gamma _2$ are orthogonal if ![]() $\operatorname {lk}(\gamma _1, \gamma _2^{+})= 0= \operatorname {lk}(\gamma _1^{+}, \gamma _2)$.
$\operatorname {lk}(\gamma _1, \gamma _2^{+})= 0= \operatorname {lk}(\gamma _1^{+}, \gamma _2)$.
Examination of ![]() $F_{2k+1,n}$ gives us the following vanishing linking numbers.
$F_{2k+1,n}$ gives us the following vanishing linking numbers.
(1) For any
 $i,j,k$ the curve
$i,j,k$ the curve  $v_k$ is orthogonal to
$v_k$ is orthogonal to  $\alpha ^{j}_i$ and
$\alpha ^{j}_i$ and  $\beta ^{j}_i$ since there exists a 3-ball containing each
$\beta ^{j}_i$ since there exists a 3-ball containing each  $\alpha ^{j}_i$ or
$\alpha ^{j}_i$ or  $\beta ^{j}_i$ which is disjoint from the surface
$\beta ^{j}_i$ which is disjoint from the surface  $S$.
$S$.(2) For any
 $i, i', j, j'$ we have that
$i, i', j, j'$ we have that  $\beta ^{j}_i$ and
$\beta ^{j}_i$ and  $\beta ^{j'}_{i'}$ are orthogonal.
$\beta ^{j'}_{i'}$ are orthogonal.(3) For
 $i \neq i'$ and arbitrary
$i \neq i'$ and arbitrary  $j, j'$ we have that
$j, j'$ we have that  $\alpha ^{j}_i$ and
$\alpha ^{j}_i$ and  $\alpha ^{j'}_{i'}$ are orthogonal.
$\alpha ^{j'}_{i'}$ are orthogonal.(4) For arbitrary
 $i$,
$i$,  $j$ we have that
$j$ we have that  $\operatorname {lk}( \alpha ^{j}_i, (\alpha ^{j}_i)^{+})=0$ i.e.
$\operatorname {lk}( \alpha ^{j}_i, (\alpha ^{j}_i)^{+})=0$ i.e.  $\alpha ^{j}_i$ is self-orthogonal.
$\alpha ^{j}_i$ is self-orthogonal.(5) For arbitrary
 $i, j, j'$ we have that
$i, j, j'$ we have that  $\alpha ^{j}_i$ and
$\alpha ^{j}_i$ and  ${\alpha ^{j'}_{i}}$ are orthogonal, since
${\alpha ^{j'}_{i}}$ are orthogonal, since  ${\alpha ^{j}_i}^{+}$ is isotopic to any
${\alpha ^{j}_i}^{+}$ is isotopic to any  ${\alpha ^{j'}_{i}}^{+}$ in
${\alpha ^{j'}_{i}}^{+}$ in  $S^{3} {{\smallsetminus }} \alpha ^{j}_i$ and the self-linking of
$S^{3} {{\smallsetminus }} \alpha ^{j}_i$ and the self-linking of  $\alpha ^{j}_i$ vanishes.
$\alpha ^{j}_i$ vanishes.(6) For
 $j \neq j'$ and arbitrary
$j \neq j'$ and arbitrary  $i, i'$ we have
$i, i'$ we have  $\operatorname {lk}\big (\alpha ^{j}_i, {\beta ^{j'}_{i'}}^{+}\big ) = \operatorname {lk}\big (\beta ^{j}_i, {\alpha ^{j'}_{i'}}^{+}\big ) =0$.
$\operatorname {lk}\big (\alpha ^{j}_i, {\beta ^{j'}_{i'}}^{+}\big ) = \operatorname {lk}\big (\beta ^{j}_i, {\alpha ^{j'}_{i'}}^{+}\big ) =0$.
In particular, we have that the first homology splits as an orthogonal sum
 \[ H_1(F_{2k+1,n};\mathbb{Z}) = C \oplus \bigoplus_{j=1}^{k} D_j, \]
\[ H_1(F_{2k+1,n};\mathbb{Z}) = C \oplus \bigoplus_{j=1}^{k} D_j, \]
where the Seifert form on ![]() $C$ is given by the Seifert matrix
$C$ is given by the Seifert matrix ![]() $V$ of
$V$ of ![]() $K$ with respect to the basis
$K$ with respect to the basis ![]() $v_1, \ldots , v_{2g}$.
$v_1, \ldots , v_{2g}$.
What remains is to compute the Seifert form on ![]() $D_j$. Fix a
$D_j$. Fix a ![]() $j$, and from now on suppress the index
$j$, and from now on suppress the index ![]() $j$ from the notation. Recalling that
$j$ from the notation. Recalling that ![]() $\sigma$ is the cyclic permutation
$\sigma$ is the cyclic permutation ![]() $(1 \ldots n)$, we compute
$(1 \ldots n)$, we compute
 \[ \operatorname{lk}(\alpha_i, \beta_{i'}^{+}) = \begin{cases} 1 & i = i',\\ 0 & \text{otherwise} \end{cases} \quad\text{and}\quad \operatorname{lk}(\beta_{i},\alpha_{i'}^{+}) = \begin{cases} 1 & i' = i+1 = \sigma(i),\\ 0 & \text{otherwise.} \end{cases} \]
\[ \operatorname{lk}(\alpha_i, \beta_{i'}^{+}) = \begin{cases} 1 & i = i',\\ 0 & \text{otherwise} \end{cases} \quad\text{and}\quad \operatorname{lk}(\beta_{i},\alpha_{i'}^{+}) = \begin{cases} 1 & i' = i+1 = \sigma(i),\\ 0 & \text{otherwise.} \end{cases} \]
This shows that the Seifert form for ![]() $F_{2k+1,n}$ is indeed represented by the matrix in the statement of the lemma.
$F_{2k+1,n}$ is indeed represented by the matrix in the statement of the lemma.
Proof of Proposition 8.4. The case ![]() $g_{\rm alg}(K)=0$ follows from the result of Freedman and Quinn that
$g_{\rm alg}(K)=0$ follows from the result of Freedman and Quinn that ![]() $\Delta _K(t)=1$ if and only if
$\Delta _K(t)=1$ if and only if ![]() $K$ is the boundary of a
$K$ is the boundary of a ![]() $\mathbb {Z}$-slice disc [Reference FreedmanFre84, Theorem 7], [Reference Freedman and QuinnFQ90, 11.7B], since, by definition, a knot
$\mathbb {Z}$-slice disc [Reference FreedmanFre84, Theorem 7], [Reference Freedman and QuinnFQ90, 11.7B], since, by definition, a knot ![]() $K$ has algebraic genus
$K$ has algebraic genus ![]() $0$ if and only if
$0$ if and only if ![]() $\Delta _K(t)=1$. So, we consider the case
$\Delta _K(t)=1$. So, we consider the case ![]() $g:=g_{\rm alg}(K)>0$.
$g:=g_{\rm alg}(K)>0$.
Let ![]() $V$ be a
$V$ be a ![]() $2m\times 2m$ Seifert matrix of
$2m\times 2m$ Seifert matrix of ![]() $K$ that realises the algebraic genus of
$K$ that realises the algebraic genus of ![]() $K$ in the following way: the top left square block
$K$ in the following way: the top left square block ![]() $P$ of
$P$ of ![]() $V$ of size
$V$ of size ![]() $2(m-g)\times 2(m-g)$ is Alexander trivial, that is
$2(m-g)\times 2(m-g)$ is Alexander trivial, that is ![]() $\det (tP-P^{T})=t^{m-g}$. Additionally, arrange that the anti-symmetrisation of
$\det (tP-P^{T})=t^{m-g}$. Additionally, arrange that the anti-symmetrisation of ![]() $V$ is a direct sum of
$V$ is a direct sum of ![]() $P-P^{T}$ and the standard
$P-P^{T}$ and the standard ![]() $2g\times 2g$ symplectic form. Denoting the lower right
$2g\times 2g$ symplectic form. Denoting the lower right ![]() $2g\times 2g$ square block of
$2g\times 2g$ square block of ![]() $V$ by
$V$ by ![]() $B$, the latter amounts to requiring that
$B$, the latter amounts to requiring that
where ![]() $A$ is a
$A$ is a ![]() $g\times g$ matrix and
$g\times g$ matrix and ![]() $S$ is a
$S$ is a ![]() $g\times g$ symmetric matrix.
$g\times g$ symmetric matrix.
By applying a base change that preserves the intersection form ![]() $B-B^{T}$, we can and do arrange for the first
$B-B^{T}$, we can and do arrange for the first ![]() $g-h$ diagonal entries of
$g-h$ diagonal entries of ![]() $S$ to be even. To see this, note that one easily arranges for all but at most one diagonal entries of
$S$ to be even. To see this, note that one easily arranges for all but at most one diagonal entries of ![]() $S$ to be even, and one may further arrange for the last entry to be even if and only if the Arf invariant is trivial. This can be checked using the formula for the Arf invariant in terms of a symplectic basis [Reference LickorishLic93, § 10, p. 105] and is only needed in the case that
$S$ to be even, and one may further arrange for the last entry to be even if and only if the Arf invariant is trivial. This can be checked using the formula for the Arf invariant in terms of a symplectic basis [Reference LickorishLic93, § 10, p. 105] and is only needed in the case that ![]() $h=0$.
$h=0$.
Let ![]() $L$ be the
$L$ be the ![]() $2(g-h)+1$-component
$2(g-h)+1$-component ![]() $1$-shaking of
$1$-shaking of ![]() $K$. With everything set up as above, we now look at the
$K$. With everything set up as above, we now look at the ![]() $2(m+g-h)$-Seifert matrix
$2(m+g-h)$-Seifert matrix ![]() $M$ of
$M$ of ![]() $L$ given by
$L$ given by ![]() $V\oplus \bigoplus _{j=1}^{g-h} \big (\begin {smallmatrix} 0 & 1 \\ 1 & 0 \end {smallmatrix}\big )$ by (8.10). To establish that
$V\oplus \bigoplus _{j=1}^{g-h} \big (\begin {smallmatrix} 0 & 1 \\ 1 & 0 \end {smallmatrix}\big )$ by (8.10). To establish that ![]() $L$ admits a
$L$ admits a ![]() $\mathbb {Z}$-slice surface of genus
$\mathbb {Z}$-slice surface of genus ![]() $h$, it suffices to find a
$h$, it suffices to find a ![]() $2(m-h)\times 2(m-h)$ Alexander trivial subblock of
$2(m-h)\times 2(m-h)$ Alexander trivial subblock of ![]() $M$ by [Reference Feller and LewarkFL18, Theorem 1].
$M$ by [Reference Feller and LewarkFL18, Theorem 1].
For this, perform the base change corresponding to adding the basis element ![]() $e_{2m+2l-1}$ to the basis element
$e_{2m+2l-1}$ to the basis element ![]() $e_{2(m-g)+l}$ for each
$e_{2(m-g)+l}$ for each ![]() $l=1,\ldots , g-h$. This corresponds to changing both entries
$l=1,\ldots , g-h$. This corresponds to changing both entries ![]() $M_{2(m-g)+l,2(m+l)}$ and
$M_{2(m-g)+l,2(m+l)}$ and ![]() $M_{2(m+l),2(m-g)+l}$ from
$M_{2(m+l),2(m-g)+l}$ from ![]() $0$ to
$0$ to ![]() $1$. The result is the following Seifert matrix for
$1$. The result is the following Seifert matrix for ![]() $L$, which we again denote by
$L$, which we again denote by ![]() $M$.
$M$.

By adding multiples of the ![]() $(2m+2l)^{th}$ basis element appropriately to the first
$(2m+2l)^{th}$ basis element appropriately to the first ![]() $2m-h$ basis elements, for
$2m-h$ basis elements, for ![]() $l=1,\dots , g-h$, we can arrange that the first
$l=1,\dots , g-h$, we can arrange that the first ![]() $g-h$ rows and columns of
$g-h$ rows and columns of ![]() $C$,
$C$, ![]() $A$, and
$A$, and ![]() $S$ become
$S$ become ![]() $0$, while no other entries in the first
$0$, while no other entries in the first ![]() $2m-h$ rows and columns of
$2m-h$ rows and columns of ![]() $M$ are modified. This is possible since
$M$ are modified. This is possible since ![]() $S$ is symmetric and its first
$S$ is symmetric and its first ![]() $g-h$ diagonal entries are even. We keep referring to the resulting matrix by
$g-h$ diagonal entries are even. We keep referring to the resulting matrix by ![]() $M$ and conclude the proof by noting that the sub-block
$M$ and conclude the proof by noting that the sub-block ![]() $M_\text {sub}$ of
$M_\text {sub}$ of ![]() $M$ corresponding to the sub-basis
$M$ corresponding to the sub-basis
is Alexander trivial.
In other words, the block ![]() $M_\text {sub}$ is the
$M_\text {sub}$ is the ![]() $2(m-h)\times 2(m-h)$–matrix that is obtained from
$2(m-h)\times 2(m-h)$–matrix that is obtained from ![]() $M$ by deleting the rows and columns
$M$ by deleting the rows and columns ![]() $2(m-g)+g-h+1$ through
$2(m-g)+g-h+1$ through ![]() $2m-g$ and deleting all rows and columns with index
$2m-g$ and deleting all rows and columns with index ![]() $2m-h+1$ or larger. This submatrix is of the form
$2m-h+1$ or larger. This submatrix is of the form
 \[ M_\text{sub}=\begin{pmatrix} P & 0 & * \\ 0 & 0 & \operatorname{Id}_{g-h}\\ * & 0 & * \end{pmatrix}, \]
\[ M_\text{sub}=\begin{pmatrix} P & 0 & * \\ 0 & 0 & \operatorname{Id}_{g-h}\\ * & 0 & * \end{pmatrix}, \]
and so satisfies ![]() $\det (tM_\text {sub}-M_\text {sub}^{T})=\det (tP-P^{T})t^{g-h}=t^{m-h}$.
$\det (tM_\text {sub}-M_\text {sub}^{T})=\det (tP-P^{T})t^{g-h}=t^{m-h}$.
Acknowledgements
We are grateful to Peter Teichner for explaining a proof of the ![]() $n=\pm 1$ case to us in 2016, and to Danny Ruberman and Fico González-Acuña for interesting discussions. This project started during the ‘Workshop on 4-manifolds’ at the Max Planck Institute for Mathematics in Bonn in the autumn of 2019, and we thank the organisers of this workshop and the MPIM. ANM is supported by NSF DMS-1902880. PF and MN gratefully acknowledge support by the SNSF Grant 181199.
$n=\pm 1$ case to us in 2016, and to Danny Ruberman and Fico González-Acuña for interesting discussions. This project started during the ‘Workshop on 4-manifolds’ at the Max Planck Institute for Mathematics in Bonn in the autumn of 2019, and we thank the organisers of this workshop and the MPIM. ANM is supported by NSF DMS-1902880. PF and MN gratefully acknowledge support by the SNSF Grant 181199.