Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Genestier, Alain
and
Lysenko, Sergey
2012.
Geometric Weil representation in characteristic two.
Journal of the Institute of Mathematics of Jussieu,
Vol. 11,
Issue. 2,
p.
221.
Farang-Hariri, Banafsheh
2012.
La fonctorialité dʼArthur–Langlands locale géométrique et la correspondance de Howe au niveau Iwahori.
Comptes Rendus. Mathématique,
Vol. 350,
Issue. 17-18,
p.
813.
Shin, Sug Woo
2012.
Abelian varieties and Weil representations.
Algebra & Number Theory,
Vol. 6,
Issue. 8,
p.
1719.
Farang-Hariri, Banafsheh
2013.
Geometric local theta correspondence for dual reductive pairs of type II at the Iwahori level.
Representation Theory of the American Mathematical Society,
Vol. 17,
Issue. 21,
p.
610.
Thomas, Teruji
2013.
Weil representation and transfer factor.
Algebra & Number Theory,
Vol. 7,
Issue. 7,
p.
1535.
Farang-Hariri, Banafsheh
2016.
GEOMETRIC TAMELY RAMIFIED LOCAL THETA CORRESPONDENCE IN THE FRAMEWORK OF THE GEOMETRIC LANGLANDS PROGRAM.
Journal of the Institute of Mathematics of Jussieu,
Vol. 15,
Issue. 3,
p.
625.
Lysenko, Sergey
2020.
Geometric Waldspurger periods II.
Representation Theory of the American Mathematical Society,
Vol. 24,
Issue. 9,
p.
235.

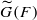 . This is a category of certain perverse sheaves on some stack, on which
. This is a category of certain perverse sheaves on some stack, on which 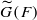 acts by functors. This construction will be used by Lysenko (in [
acts by functors. This construction will be used by Lysenko (in [