Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-21T13:42:36.587Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher symmetries of powers of the Laplacian and rings of differential operators

Part of: Partial differential equations on manifolds; differential operators Lie algebras and Lie superalgebras Rings and algebras arising under various constructions Classical field theories Classical differential geometry

Published online by Cambridge University Press:  08 March 2017

T. Levasseur  and
J. T. Stafford
T. Levasseur
Affiliation:
Laboratoire de Mathématiques de Bretagne Atlantique, CNRS - UMR6205, Université de Brest, 29238 Brest cedex 3, France email Thierry.Levasseur@univ-brest.fr
J. T. Stafford
Affiliation:
School of Mathematics, Alan Turing Building, The University of Manchester, Oxford Road, Manchester M13 9PL, UK email Toby.Stafford@manchester.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the interplay between the minimal representations of the orthogonal Lie algebra 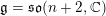$\mathfrak{g}=\mathfrak{so}(n+2,\mathbb{C})$ and the algebra of symmetries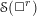$\mathscr{S}(\Box ^{r})$ of powers of the Laplacian $\Box$ on 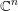$\mathbb{C}^{n}$. The connection is made through the construction of a highest-weight representation of 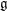$\mathfrak{g}$ via the ring of differential operators 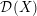${\mathcal{D}}(X)$ on the singular scheme 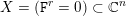$X=(\mathtt{F}^{r}=0)\subset \mathbb{C}^{n}$, for 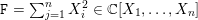$\mathtt{F}=\sum _{j=1}^{n}X_{i}^{2}\in \mathbb{C}[X_{1},\ldots ,X_{n}]$. In particular, we prove that 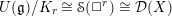$U(\mathfrak{g})/K_{r}\cong \mathscr{S}(\Box ^{r})\cong {\mathcal{D}}(X)$ for a certain primitive ideal 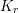$K_{r}$. Interestingly, if (and only if) $n$ is even with 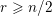$r\geqslant n/2$, then both 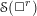$\mathscr{S}(\Box ^{r})$ and its natural module 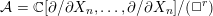${\mathcal{A}}=\mathbb{C}[\unicode[STIX]{x2202}/\unicode[STIX]{x2202}X_{n},\ldots ,\unicode[STIX]{x2202}/\unicode[STIX]{x2202}X_{n}]/(\Box ^{r})$ have a finite-dimensional factor. The same holds for the 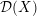${\mathcal{D}}(X)$-module 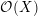${\mathcal{O}}(X)$. We also study higher-dimensional analogues 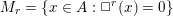$M_{r}=\{x\in A:\Box ^{r}(x)=0\}$ of the module of harmonic elements in 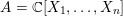$A=\mathbb{C}[X_{1},\ldots ,X_{n}]$ and of the space of ‘harmonic densities’. In both cases we obtain a minimal 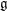$\mathfrak{g}$-representation that is closely related to the 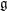$\mathfrak{g}$-modules 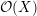${\mathcal{O}}(X)$ and 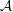${\mathcal{A}}$. Essentially all these results have real analogues, with the Laplacian replaced by the d’Alembertian 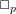$\Box _{p}$ on the pseudo-Euclidean space 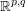$\mathbb{R}^{p,q}$ and with 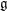$\mathfrak{g}$ replaced by the real Lie algebra 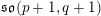$\mathfrak{so}(p+1,q+1)$.

Keywords

higher symmetriesLaplacianrings of differential operatorsharmonic polynomialsprimitive idealsscalar singletonsconformal geometry

MSC classification

Primary: 16S32: Rings of differential operators 58J70: Invariance and symmetry properties 17B08: Coadjoint orbits; nilpotent varieties 17B81: Applications to physics 53A30: Conformal differential geometry 70S10: Symmetries and conservation laws
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 4 , April 2017 , pp. 678 - 716
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bagrov, V. G. and Gitman, D. M., Exact solutions of relativistic wave equations, Mathematics and its Applications (Soviet Series), vol. 39 (Kluwer, Dordrecht, 1990).Google Scholar
Bagrov, V. G., Samsonov, B. F., Shapovalov, A. V. and Shirokov, A. V., Identities on solutions of the wave equation in the enveloping algebra of the conformal group , Teoret. Mat. Fiz. 83 (1990), 14–22; Engl. transl. in Theoret. Math. Phys. 83 (1990), 347–353.Google Scholar
Bekaert, X., Comments on higher-spin symmetries , Int. J. Geom. Methods Mod. Phys. 6 (2009), 285–342.Google Scholar
Bekaert, X., Singletons and their maximal symmetry algebras , in 6th Mathematical physics meeting: summer school and conference on modern mathematical physics 2010 (Institute of Physics, Belgrade, 2012).Google Scholar
Bekaert, X., The many faces of singletons , Physics AUC 21 (2011), 154–170; special issue.Google Scholar
Bekaert, X. and Grigoriev, M., Higher order singletons, partially massless fields and their boundary values in the ambient approach , Nuclear Phys. B 876 (2013), 667–714.Google Scholar
Bernstein, J. N., Gelfand, I. M. and Gelfand, S. I., Differential operators on the cubic cone , Russian Math. Surveys 27 (1972), 466–488.CrossRefGoogle Scholar
Binegar, B. and Zierau, R., Unitarization of a singular representation of SO(p, q) , Commun. Math. Phys. 138 (1991), 245–258.CrossRefGoogle Scholar
Bourbaki, N., Algèbre: Chapitre 8 (Hermann, Paris, 1973).Google Scholar
Bourbaki, N., Groupes et Algèbres de Lie: Chapitres 4, 5, 6 (Masson, Paris, 1981).Google Scholar
Bourbaki, N., Groupes et Algèbres de Lie: Chapitres 7, 8 (Hermann, Paris, 1990).Google Scholar
Boyer, C. P., Kalnins, E. G. and Miller, W. Jr., Symmetry and separation of variables for the Helmholtz and Laplacian equations , Nagoya Math. J. 60 (1976), 35–80.Google Scholar
Dietrich, H., Faccin, P. and de Graaf, W., Computing with real Lie algebras: real forms, Cartan decompositions and Cartan subalgebras , J. Symbolic Comput. 56 (2013), 27–45.Google Scholar
Dirac, P. A. M., The electron wave equation in de-Sitter space , Ann. of Math. (2) 36 (1935), 657–669.Google Scholar
Dirac, P. A. M., Wave equations in conformal space , Ann. of Math. (2) 37 (1936), 429–442.Google Scholar
Eastwood, M. G., Higher symmetries of the Laplacian , Ann. of Math. (2) 161 (2005), 1645–1665.CrossRefGoogle Scholar
Eastwood, M. G. and Graham, C. R., Invariants of conformal densities , Duke Math. J. 63 (1991), 633–671.Google Scholar
Eastwood, M. G. and Leistner, T., Higher symmetries of the square of the Laplacian , in Symmetries and overdetermined systems of partial differential equations, The IMA Volumes in Mathematics and its Applications, vol. 144 (Springer, New York, 2008), 319–338.CrossRefGoogle Scholar
Eastwood, M. G., Somberg, P. and Souček, V., The uniqueness of the Joseph ideal for the classical groups, Preprint (2005), arXiv:math/0512296.Google Scholar
Goodman, R. and Wallach, N. R., Representations and invariants of the classical groups (Cambridge University Press, Cambridge, 1998).Google Scholar
Gover, A. R. and Šilhan, J., Higher symmetries of the conformal powers of the Laplacian on conformally flat manifolds , J. Math. Phys. 53 (2012), article no. 032301; arXiv:0911.5265.Google Scholar
Graham, C. R., Jenne, R., Mason, L. J. and Sparling, G. A., Conformally invariant powers of the Laplacian, I: Existence , J. Lond. Math. Soc. (2) 46 (1992), 557–565.Google Scholar
Grothendieck, A., Éléments de Géométrie Algébrique IV , Publ. Math. Inst. Hautes Études Sci. 20 (1967), 5–259.Google Scholar
Helgason, S., Differential geometry, Lie groups, and symmetric spaces, Graduate Studies in Mathematics, vol. 34 (American Mathematical Society, Providence, RI, 2001).CrossRefGoogle Scholar
Howe, R., Dual pairs in physics: harmonic oscillators, photons, electrons, and singletons , Lectures in Applied Mathematics, vol. 21 (American Mathematical Society, Providence, RI, 1985), 179–207.Google Scholar
Howe, R., Remarks on classical invariant theory , Trans. Amer. Math. Soc. 313 (1989), 539–570.Google Scholar
Hunziker, M., Sepanski, M. R. and Stanke, R. J., The minimal representation of the conformal group and classical solutions to the wave equation , J. Lie Theory 22 (2012), 301–360.Google Scholar
Jantzen, J. C., Einhüllende Algebren halbeinfacher Lie-Algebren (Springer, Berlin, 1983).Google Scholar
Joseph, A., The minimal orbit in a simple Lie algbera and its associated ideal , Ann. Sci. Éc. Norm. Supér. (4) 9 (1976), 1–29.Google Scholar
Joseph, A., Kostant’s problem, Goldie rank and the Gelfand–Kirillov conjecture , Invent. Math. 56 (1980), 191–213.Google Scholar
Joseph, A., On the associated variety of a primitive ideal , J. Algebra 93 (1985), 509–523.Google Scholar
Joseph, A., A surjectivity theorem for rigid highest weight modules , Invent. Math. 92 (1988), 567–596.Google Scholar
Joseph, A., Rings which are modules in the Bernstein–Gelfand–Gelfand 𝓞 category , J. Algebra 113 (1988), 110–126.Google Scholar
Joseph, A. and Stafford, J. T., Modules of k-finite vectors over semi-simple Lie algebras , Proc. Lond. Math. Soc. (3) 49 (1984), 361–384.Google Scholar
Kobayashi, T. and Mano, G., The Schrödinger model for the minimal representation of the indefinite orthogonal group O (p, q) , Mem. Amer. Math. Soc. 213 (2011), no. 1000.Google Scholar
Kobayashi, T. and Ørsted, B., Analysis on the minimal representation of O(p, q) III. Ultrahyperbolic equations on ℝ p-1, q-1 , Adv. Math. 180 (2003), 551–595.Google Scholar
Levasseur, T., La dimension de Krull de U (sl(3)) , J. Algebra 102 (1986), 39–59.Google Scholar
Levasseur, T., Smith, S. P. and Stafford, J. T., The minimal nilpotent orbit, the Joseph ideal, and differential operators , J. Algebra 116 (1988), 480–501.Google Scholar
Levasseur, T. and Stafford, J. T., Rings of differential operators on classical rings of invariants , Mem. Amer. Math. Soc. 412 (1989), no. 412.Google Scholar
Matsumura, H., Commutative algebra, Mathematics Lecture Notes Series, vol. 56, second edition (W. A. Benjamin, Reading, MA, 1980).Google Scholar
Maury, G. and Renaud, J., Ordres maximaux au sens de K. Asano, Lecture Notes in Mathematics, vol. 341 (Springer, Berlin, 1973).Google Scholar
McConnell, J. C. and Robson, J. C., Noncommutative noetherian rings, Graduate Texts in Mathematics, vol. 30 (American Mathematical Society, Providence, RI, 2000).Google Scholar
Michel, J.-P., Higher symmetries of the Laplacian via quantization , Ann. Inst. Fourier 64 (2014), 1581–1609.CrossRefGoogle Scholar
Miller, W. Jr., Symmetry and separation of variables, Encyclopedia of Mathematics and its Applications, vol. 4 (Addison-Wesley, Reading, MA, 1977).Google Scholar
Musson, I., Rings of differential operators and zero divisors , J. Algebra 125 (1989), 489–501.Google Scholar
Shapovalov, A. V. and Shirokov, I. V., On the symmetry algebra of a linear differential equation , Teoret. Mat. Fiz. 92 (1992), 3–12; Engl. transl. in Theoret. Math. Phys. 92 (1993), 697–703.Google Scholar
Smith, S. P. and Stafford, J. T., Differential operators on an affine curve , Proc. Lond. Math. Soc. (3) 56 (1988), 229–259.CrossRefGoogle Scholar
Somberg, P., Deformations of quadratic algebras, the Joseph ideal for classical Lie algebras, and special tensors , in Symmetries and overdetermined systems of partial differential equations, The IMA Volumes in Mathematics and its Applications, vol. 144 (Springer, New York, 2008), 527–536.Google Scholar
Vassiliev, M. A., Nonlinear equations for symmetric massless higher spin fields in (A)dS(d) , Phys. Lett. B567 (2003), 139–151.Google Scholar