No CrossRef data available.
Article contents
Isometric actions on Lp-spaces: dependence on the value of p
Part of:
Ergodic theory
Selfadjoint operator algebras
Lie groups
Special aspects of infinite or finite groups
Linear function spaces and their duals
Published online by Cambridge University Press: 26 May 2023
Abstract
Answering a question by Chatterji–Druţu–Haglund, we prove that, for every locally compact group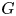 
$G$, there exists a critical constant 
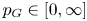$p_G \in [0,\infty ]$ such that 
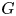$G$ admits a continuous affine isometric action on an 
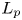$L_p$ space (
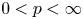$0< p<\infty$) with unbounded orbits if and only if 
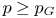$p \geq p_G$. A similar result holds for the existence of proper continuous affine isometric actions on 
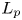$L_p$ spaces. Using a representation of cohomology by harmonic cocycles, we also show that such unbounded orbits cannot occur when the linear part comes from a measure-preserving action, or more generally a state-preserving action on a von Neumann algebra and 
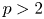$p>2$. We also prove the stability of this critical constant 
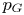$p_G$ under 
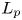$L_p$ measure equivalence, answering a question of Fisher.
Keywords
MSC classification
Primary:
22E41: Continuous cohomology
20F65: Geometric group theory
37A40: Nonsingular (and infinite-measure preserving) transformations
46E30: Spaces of measurable functions ($L^p$-spaces, Orlicz spaces, Köthe function spaces, Lorentz spaces, rearrangement invariant spaces, ideal spaces, etc.)
46L52: Noncommutative function spaces
Information
- Type
- Research Article
- Information
- Copyright
- © 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
Arano, Y., Isono, Y. and Marrakchi, A., Ergodic theory of affine isometric actions on Hilbert spaces, Geom. Funct. Anal. 31 (2021), 1013–1094.10.1007/s00039-021-00584-2CrossRefGoogle Scholar
Bader, U., Furman, A., Gelander, T. and Monod, N., Property (T) and rigidity for actions on Banach spaces, Acta Math. 198 (2007), 57–105.10.1007/s11511-007-0013-0CrossRefGoogle Scholar
Bader, U., Furman, A. and Sauer, R., Integrable measure equivalence and rigidity of hyperbolic lattices, Invent. Math. 194 (2013), 313–379.10.1007/s00222-012-0445-9CrossRefGoogle Scholar
Bader, U., Gelander, T. and Monod, N., A fixed point theorem for 
$L^1$ spaces, Invent. Math. 189 (2012), 143–148.10.1007/s00222-011-0363-2CrossRefGoogle Scholar
$L^1$ spaces, Invent. Math. 189 (2012), 143–148.10.1007/s00222-011-0363-2CrossRefGoogle ScholarBourdon, M. and Pajot, H., Cohomologie $l_p$ et espaces de Besov, J. Reine Angew. Math. 558 (2003), 85–108.Google Scholar
$l_p$ et espaces de Besov, J. Reine Angew. Math. 558 (2003), 85–108.Google ScholarChatterji, I., Druţu, C. and Haglund, F., Kazhdan and Haagerup properties from the median viewpoint, Adv. Math. 225 (2010), 882–921.10.1016/j.aim.2010.03.012CrossRefGoogle Scholar
Cherix, P.-A., Cowling, M., Jolissaint, P., Julg, P. and Valette, A., Groups with the Haagerup property, Progress in Mathematics, vol. 197 (Birkhäuser, Basel, 2001).Google Scholar
Czuroń, A., Property $F\ell _q$ implies property $F\ell _p$ for $1< p< q<\infty$, Adv. Math. 307 (2017), 715–726.10.1016/j.aim.2016.11.025CrossRefGoogle Scholar
$F\ell _q$ implies property 
$F\ell _p$ for 
$1< p< q<\infty$, Adv. Math. 307 (2017), 715–726.10.1016/j.aim.2016.11.025CrossRefGoogle ScholarCzuroń, A. and Kalantar, M., On fixed point property for $l_p$-representations of Kazhdan groups, Preprint (2020), arXiv:2007.15168.Google Scholar
$l_p$-representations of Kazhdan groups, Preprint (2020), arXiv:2007.15168.Google ScholarDe Cornulier, Y., Tessera, R. and Valette, A., Isometric group actions on Banach spaces and representations vanishing at infinity, Transform. Groups 13 (2008), 125–147.10.1007/s00031-008-9006-0CrossRefGoogle Scholar
Druţu, C. and Kapovich, M., Geometric group theory, American Mathematical Society Colloquium Publications, vol. 63 (American Mathematical Society, Providence, RI, 2018), with an appendix by Bogdan Nica.10.1090/coll/063CrossRefGoogle Scholar
Druţu, C. and Mackay, J. M., Random groups, random graphs and eigenvalues of $p$-Laplacians, Adv. Math. 341 (2019), 188–254.10.1016/j.aim.2018.10.035CrossRefGoogle Scholar
$p$-Laplacians, Adv. Math. 341 (2019), 188–254.10.1016/j.aim.2018.10.035CrossRefGoogle ScholarDruţu, C. and Nowak, P. W., Kazhdan projections, random walks and ergodic theorems, J. Reine Angew. Math. 754 (2019), 49–86.10.1515/crelle-2017-0002CrossRefGoogle Scholar
Fisher, D. and Margulis, G., Almost isometric actions, property (T), and local rigidity, Invent. Math. 162 (2005), 19–80.10.1007/s00222-004-0437-5CrossRefGoogle Scholar
Furman, A., Orbit equivalence rigidity, Ann. of Math. (2) 150 (1999), 1083–1108.10.2307/121063CrossRefGoogle Scholar
Gromov, M., Asymptotic invariants of infinite groups, in Geometric group theory, Vol. 2, London Mathematical Society Lecture Note Series, vol. 182 (Cambridge University Press, Cambridge, 1993), 1–295.Google Scholar
Haagerup, U., Lp-spaces associated with an arbitrary von Neumann algebra, in Algèbres d'opérateurs et leurs applications en physique mathématique, Colloques Internationaux du CNRS, vol. 274 (CNRS, Paris, 1979), 175–184.Google Scholar
Lavy, O. and Olivier, B., Fixed-point spectrum for group actions by affine isometries on $L_p$-spaces, Ann. Inst. Fourier (Grenoble) 71 (2021), 1–26.10.5802/aif.3348CrossRefGoogle Scholar
$L_p$-spaces, Ann. Inst. Fourier (Grenoble) 71 (2021), 1–26.10.5802/aif.3348CrossRefGoogle Scholarde Laat, T. and de la Salle, M., Banach space actions and L2-spectral gap, Anal. PDE 14 (2021), 45–76.10.2140/apde.2021.14.45CrossRefGoogle Scholar
Marrakchi, A., Spectral gap characterization of full type III factors, J. Reine Angew. Math. 753 (2019), 193–210.10.1515/crelle-2016-0071CrossRefGoogle Scholar
Megrelishvili, M., Reflexively representable but not Hilbert representable compact flows and semitopological semigroups, Colloq. Math. 110 (2008), 383–407.10.4064/cm110-2-5CrossRefGoogle Scholar
Mendel, M. and Naor, A., Euclidean quotients of finite metric spaces, Adv. Math. 189 (2004), 451–494.10.1016/j.aim.2003.12.001CrossRefGoogle Scholar
Naor, A. and Peres, Y., $L_p$ compression, traveling salesmen, and stable walks, Duke Math. J. 157 (2011), 53–108.10.1215/00127094-2011-002CrossRefGoogle Scholar
$L_p$ compression, traveling salesmen, and stable walks, Duke Math. J. 157 (2011), 53–108.10.1215/00127094-2011-002CrossRefGoogle ScholarNica, B., Proper isometric actions of hyperbolic groups on $L^p$-spaces, Compos. Math. 149 (2013), 773–792.10.1112/S0010437X12000693CrossRefGoogle Scholar
$L^p$-spaces, Compos. Math. 149 (2013), 773–792.10.1112/S0010437X12000693CrossRefGoogle ScholarNowak, P. W., Group actions on Banach spaces and a geometric characterization of a-T-menability, Topology Appl. 153 (2006), 3409–3412.10.1016/j.topol.2006.03.001CrossRefGoogle Scholar
Nowak, P. W., Group actions on Banach spaces, in Handbook of group actions. Vol. II, Advanced Lectures in Mathematics (ALM), vol. 32 (International Press, Somerville, MA, 2015), 121–149.Google Scholar
Olivier, B., Kazhdan's property $(T)$ with respect to non-commutative $L_p$-spaces, Proc. Amer. Math. Soc. 140 (2012), 4259–4269.10.1090/S0002-9939-2012-11481-9CrossRefGoogle Scholar
$(T)$ with respect to non-commutative 
$L_p$-spaces, Proc. Amer. Math. Soc. 140 (2012), 4259–4269.10.1090/S0002-9939-2012-11481-9CrossRefGoogle ScholarOppenhein, I., Garland's method with Banach coefficients, Preprint (2020), arXiv:2009.01234.Google Scholar
Pansu, P., Cohomologie $L^p$ des variétés à courbure négative, cas du degré $1$. Rend. Sem. Mat. Univ. Politec. Torino, Special Issue (1989), 95–120.Google Scholar
$L^p$ des variétés à courbure négative, cas du degré 
$1$. Rend. Sem. Mat. Univ. Politec. Torino, Special Issue (1989), 95–120.Google Scholarde la Salle, M., A local characterization of Kazhdan projections and applications, Comment. Math. Helv. 94 (2019), 623–660.10.4171/CMH/469CrossRefGoogle Scholar
Takesaki, M., Theory of operator algebras II, Encyclopaedia of Mathematical Sciences, vol. 125 (Springer, Berlin, 2003).Google Scholar
Tzafriri, L., Remarks on contractive projections in $L_{p}$-spaces, Israel J. Math. 7 (1969), 9–15.10.1007/BF02771741CrossRefGoogle Scholar
$L_{p}$-spaces, Israel J. Math. 7 (1969), 9–15.10.1007/BF02771741CrossRefGoogle ScholarYeadon, J., Isometries of noncommutative $L^{p}$-spaces, Math. Proc. Cambridge Philos. Soc. 90 (1981), 41–50.10.1017/S0305004100058515CrossRefGoogle Scholar
$L^{p}$-spaces, Math. Proc. Cambridge Philos. Soc. 90 (1981), 41–50.10.1017/S0305004100058515CrossRefGoogle ScholarYu, G., Hyperbolic groups admit proper affine isometric actions on $l^p$-spaces, Geom. Funct. Anal. 15 (2005), 1144–1151.10.1007/s00039-005-0533-8CrossRefGoogle Scholar
$l^p$-spaces, Geom. Funct. Anal. 15 (2005), 1144–1151.10.1007/s00039-005-0533-8CrossRefGoogle Scholar