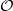Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Weidner, Jan
2014.
Grassmannians and Koszul duality.
Mathematische Zeitschrift,
Vol. 278,
Issue. 3-4,
p.
1033.
Achar, Pramod
Henderson, Anthony
and
Riche, Simon
2015.
Geometric Satake, Springer correspondence, and small representations II.
Representation Theory of the American Mathematical Society,
Vol. 19,
Issue. 6,
p.
94.
Rottmaier, Michael
and
Soergel, Wolfgang
2015.
Unicity of graded covers of the category $\mathcal{O}$ of Bernstein–Gelfand–Gelfand.
Arkiv för Matematik,
Vol. 53,
Issue. 2,
p.
383.
Achar, Pramod N.
2015.
Representations of Reductive Groups.
Vol. 312,
Issue. ,
p.
11.
Achar, Pramod N.
and
Riche, Simon
2016.
Modular perverse sheaves on flag varieties, II: Koszul duality and formality.
Duke Mathematical Journal,
Vol. 165,
Issue. 1,
Achar, Pramod
and
Riche, Simon
2017.
Modular perverse sheaves on flag varieties III: Positivity conditions.
Transactions of the American Mathematical Society,
Vol. 370,
Issue. 1,
p.
447.
Kalck, Martin
and
Yang, Dong
2018.
Derived categories of graded gentle one-cycle algebras.
Journal of Pure and Applied Algebra,
Vol. 222,
Issue. 10,
p.
3005.
Bezrukavnikov, Roman
Gaitsgory, Dennis
Mirković, Ivan
Riche, Simon
and
Rider, Laura
2019.
An Iwahori-Whittaker model for the Satake category.
Journal de l’École polytechnique — Mathématiques,
Vol. 6,
Issue. ,
p.
707.
Eberhardt, Jens Niklas
and
Kelly, Shane
2019.
Mixed motives and geometric representation theory in equal characteristic.
Selecta Mathematica,
Vol. 25,
Issue. 2,
Elias, Ben
Makisumi, Shotaro
Thiel, Ulrich
and
Williamson, Geordie
2020.
Introduction to Soergel Bimodules.
Vol. 5,
Issue. ,
p.
513.
Bezrukavnikov, Roman
and
Riche, Simon
2022.
Representation Theory and Algebraic Geometry.
p.
267.
Lam, Thomas
and
Speyer, David E.
2022.
Cohomology of cluster varieties, I: Locally acyclic case.
Algebra & Number Theory,
Vol. 16,
Issue. 1,
p.
179.
Antor, Jonas
2024.
Formality in the Deligne-Langlands Correspondence.
International Mathematics Research Notices,
Vol. 2024,
Issue. 7,
p.
6043.
Galashin, Pavel
and
Lam, Thomas
2024.
Positroids, knots, and q,t-Catalan numbers.
Duke Mathematical Journal,
Vol. 173,
Issue. 11,
Lam, Thomas
and
Templier, Nicolas
2024.
The mirror conjecture for minuscule flag varieties.
Duke Mathematical Journal,
Vol. 173,
Issue. 1,
Hone, Chris
and
Williamson, Geordie
2025.
Geometric Extensions.
International Mathematics Research Notices,
Vol. 2025,
Issue. 11,