Article contents
On the family of affine threefolds 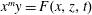 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}x^m y= F(x, z, t)$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}x^m y= F(x, z, t)$
Published online by Cambridge University Press: 09 June 2014
Abstract
Let 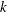 $k$ be a field and
$k$ be a field and 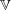 $\mathbb{V}$ the affine threefold in
$\mathbb{V}$ the affine threefold in 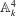 $\mathbb{A}^4_k$ defined by
$\mathbb{A}^4_k$ defined by 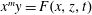 $x^m y=F(x, z, t)$,
$x^m y=F(x, z, t)$, 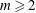 $m \ge 2$. In this paper, we show that
$m \ge 2$. In this paper, we show that 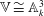 $\mathbb{V} \cong \mathbb{A}^3_k$ if and only if
$\mathbb{V} \cong \mathbb{A}^3_k$ if and only if 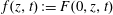 $f(z, t): = F(0, z, t)$ is a coordinate of
$f(z, t): = F(0, z, t)$ is a coordinate of 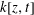 $k[z, t]$. In particular, when
$k[z, t]$. In particular, when 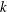 $k$ is a field of positive characteristic and
$k$ is a field of positive characteristic and 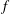 $f$ defines a non-trivial line in the affine plane
$f$ defines a non-trivial line in the affine plane 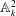 $\mathbb{A}^2_k$ (we shall call such a
$\mathbb{A}^2_k$ (we shall call such a 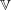 $\mathbb{V}$ as an Asanuma threefold), then
$\mathbb{V}$ as an Asanuma threefold), then 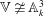 $\mathbb{V}\ncong \mathbb{A}^3_k$ although
$\mathbb{V}\ncong \mathbb{A}^3_k$ although 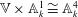 $\mathbb{V} \times \mathbb{A}^1_k \cong \mathbb{A}^4_k$, thereby providing a family of counter-examples to Zariski’s cancellation conjecture for the affine 3-space in positive characteristic. Our main result also proves a special case of the embedding conjecture of Abhyankar–Sathaye in arbitrary characteristic.
$\mathbb{V} \times \mathbb{A}^1_k \cong \mathbb{A}^4_k$, thereby providing a family of counter-examples to Zariski’s cancellation conjecture for the affine 3-space in positive characteristic. Our main result also proves a special case of the embedding conjecture of Abhyankar–Sathaye in arbitrary characteristic.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- © The Author 2014
References
- 18
- Cited by

