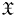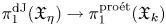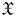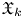1. Introduction
Throughout the following we fix a non-archimedean field ![]() $K$ with valuation ring
$K$ with valuation ring ![]() $\mathcal {O}_K$, residue field
$\mathcal {O}_K$, residue field ![]() $k$, and a pseudo-uniformizer
$k$, and a pseudo-uniformizer ![]() $\varpi$. Let
$\varpi$. Let ![]() $X$ be a proper scheme over
$X$ be a proper scheme over ![]() $\mathcal {O}_K$ with generic fiber
$\mathcal {O}_K$ with generic fiber ![]() $X_K$ and special fiber
$X_K$ and special fiber ![]() $X_k$. In [Reference GrothendieckGro71, Exp. X], Grothendieck constructed a continuous homomorphism
$X_k$. In [Reference GrothendieckGro71, Exp. X], Grothendieck constructed a continuous homomorphism
between the étale fundamental groups, called the specialization map. This map is moreover surjective if ![]() $X$ is normal or if
$X$ is normal or if ![]() $X_k$ is reduced (see [Reference RaynaudRay70, § 6] for other criteria). Translated in terms of coverings, the existence of the specialization map amounts to the fact that the pullback functor
$X_k$ is reduced (see [Reference RaynaudRay70, § 6] for other criteria). Translated in terms of coverings, the existence of the specialization map amounts to the fact that the pullback functor ![]() $\operatorname {\mathbf {F\acute {E}t}}_X \to \operatorname {\mathbf {F\acute {E}t}}_{X_k}$ between the corresponding categories of finite étale coverings is an equivalence, so that by composing its inverse with the restriction functor
$\operatorname {\mathbf {F\acute {E}t}}_X \to \operatorname {\mathbf {F\acute {E}t}}_{X_k}$ between the corresponding categories of finite étale coverings is an equivalence, so that by composing its inverse with the restriction functor ![]() $\operatorname {\mathbf {F\acute {E}t}}_{X}\to \operatorname {\mathbf {F\acute {E}t}}_{X_K}$ we obtain a functor
$\operatorname {\mathbf {F\acute {E}t}}_{X}\to \operatorname {\mathbf {F\acute {E}t}}_{X_K}$ we obtain a functor
Surjectivity of the specialization map then corresponds to the statement that ![]() $u$ maps connected coverings to connected coverings.
$u$ maps connected coverings to connected coverings.
In cases of geometric interest, such as semistable reduction, the special fiber ![]() $X_k$ will often not be normal. For such schemes, the pro-étale fundamental group introduced by Bhatt and Scholze [Reference Bhatt and ScholzeBS15] contains more refined information than the étale fundamental group. The corresponding notion of a covering space, a geometric covering, is an étale morphism which satisfies the valuative criterion of properness. As connected geometric coverings may have infinite degree and may not admit Galois closures, the pro-étale fundamental group is not pro-finite (or even pro-discrete) in general, but is a Noohi topological group (see [Reference Bhatt and ScholzeBS15]). As it turns out though, there is no specialization map for the pro-étale fundamental group fitting inside the following commutative square.
$X_k$ will often not be normal. For such schemes, the pro-étale fundamental group introduced by Bhatt and Scholze [Reference Bhatt and ScholzeBS15] contains more refined information than the étale fundamental group. The corresponding notion of a covering space, a geometric covering, is an étale morphism which satisfies the valuative criterion of properness. As connected geometric coverings may have infinite degree and may not admit Galois closures, the pro-étale fundamental group is not pro-finite (or even pro-discrete) in general, but is a Noohi topological group (see [Reference Bhatt and ScholzeBS15]). As it turns out though, there is no specialization map for the pro-étale fundamental group fitting inside the following commutative square.

Example 1.1 (Tate elliptic curve)
Suppose that ![]() $K$ is algebraically closed of characteristic zero and let
$K$ is algebraically closed of characteristic zero and let ![]() $X\subseteq \mathbf {P}^{2}_{\mathcal {O}_K}$ be a cubic hypersurface whose generic fiber
$X\subseteq \mathbf {P}^{2}_{\mathcal {O}_K}$ be a cubic hypersurface whose generic fiber ![]() $X_\eta$ is smooth and whose special fiber
$X_\eta$ is smooth and whose special fiber ![]() $X_k$ is nodal. Then
$X_k$ is nodal. Then ![]() $X_k$ is isomorphic to
$X_k$ is isomorphic to ![]() $\mathbf {P}^{1}_k$ with
$\mathbf {P}^{1}_k$ with ![]() $0$ and
$0$ and ![]() $\infty$ identified, and has a (unique) geometric covering
$\infty$ identified, and has a (unique) geometric covering ![]() $Y\to X_k$ with Galois group
$Y\to X_k$ with Galois group ![]() $\mathbf {Z}$. Explicitly
$\mathbf {Z}$. Explicitly ![]() $Y$ is given by an infinite chain of copies of
$Y$ is given by an infinite chain of copies of ![]() $\mathbf {P}^{1}_k$ glued along the poles. In this case, the diagram of fundamental groups as above would have to be of the form
$\mathbf {P}^{1}_k$ glued along the poles. In this case, the diagram of fundamental groups as above would have to be of the form

where there is no homomorphism making the square commute.
To clarify the issue, it is useful to note that Grothendieck's specialization map may be understood in terms of a more general specialization map involving formal schemes and rigid spaces. Namely, for any formal scheme ![]() $\mathfrak {X}$ locally of finite type over
$\mathfrak {X}$ locally of finite type over ![]() $\mathcal {O}_K$ there is an equivalence
$\mathcal {O}_K$ there is an equivalence ![]() $\operatorname {\mathbf {\acute {E}t}}_{\mathfrak {X}_k}{\buildrel \sim \over \longrightarrow} \operatorname {\mathbf {\acute {E}t}}_{\mathfrak {X}}$ and, thus, one is able to form the functors
$\operatorname {\mathbf {\acute {E}t}}_{\mathfrak {X}_k}{\buildrel \sim \over \longrightarrow} \operatorname {\mathbf {\acute {E}t}}_{\mathfrak {X}}$ and, thus, one is able to form the functors
where ![]() $\mathfrak {X}_\eta$ is the rigid generic fiber in the sense of Raynaud, a rigid
$\mathfrak {X}_\eta$ is the rigid generic fiber in the sense of Raynaud, a rigid ![]() $K$-space (see our notation and conventions section for a precise definition). Consequently, we have a formal version of the specialization map
$K$-space (see our notation and conventions section for a precise definition). Consequently, we have a formal version of the specialization map ![]() $\pi^{{\unicode{x00E9}}{\text{t}}}_1(\mathfrak {X}_\eta, \overline {x}) \to \pi ^{{\unicode{x00E9}}{\text{t}}}_1(\mathfrak {X}_k, \overline {y})$. To obtain Grothendieck's specialization map, one uses Grothendieck's existence theorem to show that if
$\pi^{{\unicode{x00E9}}{\text{t}}}_1(\mathfrak {X}_\eta, \overline {x}) \to \pi ^{{\unicode{x00E9}}{\text{t}}}_1(\mathfrak {X}_k, \overline {y})$. To obtain Grothendieck's specialization map, one uses Grothendieck's existence theorem to show that if ![]() $X$ is a proper
$X$ is a proper ![]() $\mathcal {O}_K$-scheme and
$\mathcal {O}_K$-scheme and ![]() $\mathfrak {X}=\widehat {X}$ (the
$\mathfrak {X}=\widehat {X}$ (the ![]() $\varpi$-adic completion of
$\varpi$-adic completion of ![]() $X$), then all finite étale covers of
$X$), then all finite étale covers of ![]() $\mathfrak {X}$ and
$\mathfrak {X}$ and ![]() $\mathfrak {X}_\eta =X_K^{\mathrm {an}}$ are algebraizable (i.e. that
$\mathfrak {X}_\eta =X_K^{\mathrm {an}}$ are algebraizable (i.e. that ![]() $\operatorname {\mathbf {F\acute {E}t}}_{\mathfrak {X}}\simeq \operatorname {\mathbf {F\acute {E}t}}_X$ and
$\operatorname {\mathbf {F\acute {E}t}}_{\mathfrak {X}}\simeq \operatorname {\mathbf {F\acute {E}t}}_X$ and ![]() $\operatorname {\mathbf {F\acute {E}t}}_{\mathfrak {X}_\eta }\simeq \operatorname {\mathbf {F\acute {E}t}}_{X_K}$). In contrast, in Example 1.1, if
$\operatorname {\mathbf {F\acute {E}t}}_{\mathfrak {X}_\eta }\simeq \operatorname {\mathbf {F\acute {E}t}}_{X_K}$). In contrast, in Example 1.1, if ![]() $\mathfrak {Y}\to \mathfrak {X}$ is the unique étale lifting of
$\mathfrak {Y}\to \mathfrak {X}$ is the unique étale lifting of ![]() $Y\to X_k$, then the rigid generic fiber
$Y\to X_k$, then the rigid generic fiber ![]() $u(Y)=\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$ is the Tate uniformization
$u(Y)=\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$ is the Tate uniformization ![]() $\mathbf {G}_m^{\rm an}\to X_\eta ^{\rm an}$, which is patently non-algebraizable.
$\mathbf {G}_m^{\rm an}\to X_\eta ^{\rm an}$, which is patently non-algebraizable.
To accommodate coverings of ![]() $\mathfrak {X}_\eta$ arising from geometric coverings of
$\mathfrak {X}_\eta$ arising from geometric coverings of ![]() $\mathfrak {X}_k$, one needs a suitably general class of covering spaces in non-archimedean geometry. In the seminal paper [Reference de JongdJ95b] de Jong explored a class of morphisms, which we call de Jong covering spaces, defined as maps
$\mathfrak {X}_k$, one needs a suitably general class of covering spaces in non-archimedean geometry. In the seminal paper [Reference de JongdJ95b] de Jong explored a class of morphisms, which we call de Jong covering spaces, defined as maps ![]() $Y\to X$ of rigid
$Y\to X$ of rigid ![]() $K$-spaces such that for any point
$K$-spaces such that for any point ![]() $x$ of
$x$ of ![]() $X$ there exists an overconvergent (i.e. Berkovich) open neighborhood
$X$ there exists an overconvergent (i.e. Berkovich) open neighborhood ![]() $U$ such that
$U$ such that ![]() $Y_U$ is a disjoint union of finite étale coverings of
$Y_U$ is a disjoint union of finite étale coverings of ![]() $U$. This class of covering spaces contains finite étale coverings as well as more exotic examples, such as Tate's uniformization of elliptic curves and period mappings for certain Rapoport–Zink spaces. In [Reference de JongdJ95b] it is shown that the category of de Jong covering spaces is sufficiently rich as to support a version of Galois theory and, thus, gives rise to a fundamental group which we call the de Jong fundamental group and denote
$U$. This class of covering spaces contains finite étale coverings as well as more exotic examples, such as Tate's uniformization of elliptic curves and period mappings for certain Rapoport–Zink spaces. In [Reference de JongdJ95b] it is shown that the category of de Jong covering spaces is sufficiently rich as to support a version of Galois theory and, thus, gives rise to a fundamental group which we call the de Jong fundamental group and denote ![]() $\pi _1^{\mathrm {dJ}}(X,\overline {x})$.
$\pi _1^{\mathrm {dJ}}(X,\overline {x})$.
Our first main result is then the following.
Theorem 1.2 (See Theorem 3.7)
Let ![]() $\mathfrak {X}$ be a quasi-paracompact formal scheme locally of finite type over
$\mathfrak {X}$ be a quasi-paracompact formal scheme locally of finite type over ![]() $\mathcal {O}_K$, and let
$\mathcal {O}_K$, and let ![]() $Y\to \mathfrak {X}_k$ be a geometric covering. Then the induced étale morphism
$Y\to \mathfrak {X}_k$ be a geometric covering. Then the induced étale morphism ![]() $u(Y)\to \mathfrak {X}_\eta$ is a de Jong covering space.
$u(Y)\to \mathfrak {X}_\eta$ is a de Jong covering space.
This result is somewhat surprising, because it implies that ![]() $u(Y)$ is a disjoint union of finite étale coverings locally in a fairly coarse topology of
$u(Y)$ is a disjoint union of finite étale coverings locally in a fairly coarse topology of ![]() $\mathfrak {X}_\eta$ despite the fact that
$\mathfrak {X}_\eta$ despite the fact that ![]() $Y$ does not even necessarily split into finite étale coverings étale locally on
$Y$ does not even necessarily split into finite étale coverings étale locally on ![]() $\mathfrak {X}_k$ (see Remark 3.10). To address this apparent discrepancy, we first establish a criterion for the generic fiber of a morphism of formal schemes to be a de Jong covering space. Namely, for a map of formal schemes
$\mathfrak {X}_k$ (see Remark 3.10). To address this apparent discrepancy, we first establish a criterion for the generic fiber of a morphism of formal schemes to be a de Jong covering space. Namely, for a map of formal schemes ![]() $\mathfrak {Y}\to \mathfrak {X}$ such that
$\mathfrak {Y}\to \mathfrak {X}$ such that ![]() $\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$ is étale, if its restriction to every irreducible component of
$\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$ is étale, if its restriction to every irreducible component of ![]() $\mathfrak {X}_k$ is the disjoint union of finite morphisms, then
$\mathfrak {X}_k$ is the disjoint union of finite morphisms, then ![]() $\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$ is a de Jong covering space (Proposition 3.5). In the second step, we reduce to the situation where this criterion applies using a delicate blowup procedure (see Proposition 3.13) and the fact that geometric coverings of a normal scheme are disjoint unions of finite étale coverings.
$\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$ is a de Jong covering space (Proposition 3.5). In the second step, we reduce to the situation where this criterion applies using a delicate blowup procedure (see Proposition 3.13) and the fact that geometric coverings of a normal scheme are disjoint unions of finite étale coverings.
In Corollary 3.9, we strengthen the link between de Jong covering spaces and geometric coverings by establishing a converse of Theorem 1.2. For an étale map of formal schemes, its generic fiber is a de Jong covering if and only if its special fiber is a geometric covering, and both are equivalent to the generic fiber being partially proper.
As a formal consequence of Theorem 1.2 we obtain the specialization homomorphism: assuming that ![]() $\mathfrak {X}_\eta$ and
$\mathfrak {X}_\eta$ and ![]() $\mathfrak {X}_k$ are both connected, for a compatible choice of geometric points
$\mathfrak {X}_k$ are both connected, for a compatible choice of geometric points ![]() $\overline {x}$ of
$\overline {x}$ of ![]() $\mathfrak {X}_\eta$ and
$\mathfrak {X}_\eta$ and ![]() $\overline {y}$ of
$\overline {y}$ of ![]() $\mathfrak {X}_k$ (see the discussion following the statement of Theorem 3.7), there is a continuous homomorphism
$\mathfrak {X}_k$ (see the discussion following the statement of Theorem 3.7), there is a continuous homomorphism
fitting inside the following commutative diagram.

As in the finite étale setting, we provide criteria for this homomorphism to have dense image (because the groups are no longer compact, density is not equivalent to surjectivity, and checking the latter could be more challenging). To this end, in Appendix A we define a property of formal schemes ![]() $\mathfrak {X}$ over
$\mathfrak {X}$ over ![]() $\mathcal {O}_K$ that we call
$\mathcal {O}_K$ that we call ![]() $\eta$-normal. In essence this means that
$\eta$-normal. In essence this means that ![]() $\mathfrak {X}$ is ‘integrally closed in
$\mathfrak {X}$ is ‘integrally closed in ![]() $\mathfrak {X}_\eta$’, and covers the cases when
$\mathfrak {X}_\eta$’, and covers the cases when ![]() $\mathfrak {X}$ is normal or
$\mathfrak {X}$ is normal or ![]() $\mathfrak {X}_k$ is reduced. We also show a version of Serre's criterion for
$\mathfrak {X}_k$ is reduced. We also show a version of Serre's criterion for ![]() $\eta$-normality (see Theorem A.15).
$\eta$-normality (see Theorem A.15).
We then have the following density result.
Proposition 1.3 (See Corollary 3.8)
In the situation of Theorem 1.2, suppose that ![]() $\mathfrak {X}$ is
$\mathfrak {X}$ is ![]() $\eta$-normal. Then the specialization map
$\eta$-normal. Then the specialization map ![]() $\pi _1^{\mathrm {dJ}}(\mathfrak {X}_\eta, \overline {x})\to \pi ^{{\textrm{pro}}\unicode{x00E9}{\textrm{t}}}_1(\mathfrak {X}_k,\overline {y})$ has dense image.
$\pi _1^{\mathrm {dJ}}(\mathfrak {X}_\eta, \overline {x})\to \pi ^{{\textrm{pro}}\unicode{x00E9}{\textrm{t}}}_1(\mathfrak {X}_k,\overline {y})$ has dense image.
The criterion for being a de Jong covering space used in the proof of Theorem 1.2 can be useful even in the presence of ramification. In our second main result, we apply it to study covering spaces which are tame in the sense introduced by Hübner [Reference HübnerHüb21]. We warn the reader that these coverings are only ‘tame along the special fiber’, so to speak (for example, an Artin–Schreier covering of ![]() $\mathbf {A}^{1}_{\mathbf {F}_p}$ induces a tame covering of the affinoid unit disc over
$\mathbf {A}^{1}_{\mathbf {F}_p}$ induces a tame covering of the affinoid unit disc over ![]() $\mathbf {Q}_p$). In [Reference Achinger, Lara and YoucisALY21b], we studied the question whether de Jong coverings of a rigid
$\mathbf {Q}_p$). In [Reference Achinger, Lara and YoucisALY21b], we studied the question whether de Jong coverings of a rigid ![]() $K$-space satisfy admissible or étale descent, and gave a negative answer by constructing a covering of an annulus in positive characteristic which is not a de Jong covering, but which becomes a de Jong covering space on a non-overconvergent open cover of the base. However, the construction relied on wild ramification phenomena, and it seems natural to expect that such behavior is avoided under a tameness assumption.
$K$-space satisfy admissible or étale descent, and gave a negative answer by constructing a covering of an annulus in positive characteristic which is not a de Jong covering, but which becomes a de Jong covering space on a non-overconvergent open cover of the base. However, the construction relied on wild ramification phenomena, and it seems natural to expect that such behavior is avoided under a tameness assumption.
In order to state the result, we need to introduce some terminology used in [Reference Achinger, Lara and YoucisALY21b]. Let us call a morphism of rigid ![]() $K$-spaces
$K$-spaces ![]() $Y\to X$ an
$Y\to X$ an ![]() ${\textit{adm}}$-covering space (respectively, an
${\textit{adm}}$-covering space (respectively, an ![]() ${\unicode{x00E9}}{\text{t}}$-covering space) if there exists an open (respectively, étale) cover
${\unicode{x00E9}}{\text{t}}$-covering space) if there exists an open (respectively, étale) cover ![]() $\{U_i\to X\}$ such that
$\{U_i\to X\}$ such that ![]() $Y_{U_i}\to U_i$ is the disjoint union of finite étale coverings of
$Y_{U_i}\to U_i$ is the disjoint union of finite étale coverings of ![]() $U_i$ for all
$U_i$ for all ![]() $i$.
$i$.
Theorem 1.4 (See Theorem 4.14 and Corollary 4.16)
Suppose that ![]() $K$ is discretely valued. Let
$K$ is discretely valued. Let ![]() $X$ be a smooth quasi-paracompact and quasi-separated rigid
$X$ be a smooth quasi-paracompact and quasi-separated rigid ![]() $K$-space, and suppose that generalized strictly semistable (gss) formal models of
$K$-space, and suppose that generalized strictly semistable (gss) formal models of ![]() $X$ are cofinal (see Definition 4.12). Then, every tame
$X$ are cofinal (see Definition 4.12). Then, every tame ![]() ${\unicode{x00E9}}{\text{t}}$-covering space of
${\unicode{x00E9}}{\text{t}}$-covering space of ![]() $X$ is a de Jong covering.
$X$ is a de Jong covering.
In other words, tame de Jong coverings can be glued in the étale topology. The assumption on gss formal models is a technical condition that is automatically satisfied if ![]() $K$ is of equal characteristic zero (see [Reference TemkinTem12]) and conjecturally satisfied in general. Moreover, because tameness is automatic when
$K$ is of equal characteristic zero (see [Reference TemkinTem12]) and conjecturally satisfied in general. Moreover, because tameness is automatic when ![]() $K$ has equal characteristic zero, we obtain the following unconditional corollary.
$K$ has equal characteristic zero, we obtain the following unconditional corollary.
Corollary 1.5 (See Corollary 4.17)
Let ![]() $K$ be a discretely valued non-archimedean field of equal characteristic zero. Then, for any smooth quasi-paracompact and quasi-separated rigid
$K$ be a discretely valued non-archimedean field of equal characteristic zero. Then, for any smooth quasi-paracompact and quasi-separated rigid ![]() $K$-space
$K$-space ![]() $X$, the notions of de Jong, adm-covering spaces, and
$X$, the notions of de Jong, adm-covering spaces, and ![]() ${\unicode{x00E9}}{\text{t}}$-covering spaces coincide.
${\unicode{x00E9}}{\text{t}}$-covering spaces coincide.
As stated previously, the proof of Theorem 1.4 contains in its kernel the same technique used in the proof of Theorem 1.2. Suppose for simplicity that ![]() $Y\to X$ is a tame étale map which splits into the disjoint union of finite étale coverings on an open covering of
$Y\to X$ is a tame étale map which splits into the disjoint union of finite étale coverings on an open covering of ![]() $X$. If
$X$. If ![]() $\mathfrak {X}$ is a gss formal model of
$\mathfrak {X}$ is a gss formal model of ![]() $X$ such that this open covering of
$X$ such that this open covering of ![]() $X$ extends to an open covering of
$X$ extends to an open covering of ![]() $\mathfrak {X}$, we show using (a logarithmic version of) Abhyankar's lemma the existence of a formal model
$\mathfrak {X}$, we show using (a logarithmic version of) Abhyankar's lemma the existence of a formal model ![]() $\mathfrak {Y}\to \mathfrak {X}$ which is Kummer étale. Using some basic toric geometry we show that
$\mathfrak {Y}\to \mathfrak {X}$ which is Kummer étale. Using some basic toric geometry we show that ![]() $\mathfrak {Y}\to \mathfrak {X}$ satisfies the criterion of Proposition 3.5, and deduce that
$\mathfrak {Y}\to \mathfrak {X}$ satisfies the criterion of Proposition 3.5, and deduce that ![]() $\mathfrak {Y}_\eta =Y$ is a de Jong covering space of
$\mathfrak {Y}_\eta =Y$ is a de Jong covering space of ![]() $\mathfrak {X}_\eta =X$ as desired. To extend this result from
$\mathfrak {X}_\eta =X$ as desired. To extend this result from ![]() $\mathrm {adm}$-covering spaces to
$\mathrm {adm}$-covering spaces to ![]() ${\unicode{x00E9}}{\text{t}}$-covering spaces we apply an étale bootstrap argument in the sense of [Reference Achinger, Lara and YoucisALY21a, § 3.7] (see Corollary 4.16).
${\unicode{x00E9}}{\text{t}}$-covering spaces we apply an étale bootstrap argument in the sense of [Reference Achinger, Lara and YoucisALY21a, § 3.7] (see Corollary 4.16).
It seems believable that the smoothness and semistability assumptions in Theorem 1.4 are not necessary, but the authors were unable to remove them. In a different direction, the link with logarithmic geometry used in the proof strongly suggests the existence of a specialization map to a logarithmic variant of the pro-étale fundamental group of the special fiber of a semistable model, and we would expect such a map to be an isomorphism. Finally, in the companion paper [Reference Achinger, Lara and YoucisALY21a], the authors have developed the notion of a ‘geometric covering’ of a rigid space which provides a generalization of ![]() ${\unicode{x00E9}}{\text{t}}$-covering spaces. A natural question is whether in the setting of Corollary 1.5 every such tame geometric covering must be a de Jong covering space.
${\unicode{x00E9}}{\text{t}}$-covering spaces. A natural question is whether in the setting of Corollary 1.5 every such tame geometric covering must be a de Jong covering space.
Notation and conventions
Throughout this paper, we use the following notation and terminology.
– By a non-archimedean field
 $K$ we mean a field complete with respect to a rank-one valuation
$K$ we mean a field complete with respect to a rank-one valuation  $|\cdot |\colon K\to [0, \infty )$.
$|\cdot |\colon K\to [0, \infty )$.– For a Huber ring
 $A$ we denote by
$A$ we denote by  $A^{\circ }$ the subring of powerbounded elements and by
$A^{\circ }$ the subring of powerbounded elements and by  $A^{{\circ \circ }}$ the set of topologically nilpotent elements. We abbreviate
$A^{{\circ \circ }}$ the set of topologically nilpotent elements. We abbreviate  $\operatorname {Spa}(A,A^{\circ })$ to
$\operatorname {Spa}(A,A^{\circ })$ to  $\operatorname {Spa}(A)$.
$\operatorname {Spa}(A)$.– By a rigid
 $K$-space we mean an adic space locally of finite type over
$K$-space we mean an adic space locally of finite type over  $\operatorname {Spa}(K)$. Our conventions and notation concerning adic spaces is as in [Reference Achinger, Lara and YoucisALY21a, §§ 2–3]. We denote by
$\operatorname {Spa}(K)$. Our conventions and notation concerning adic spaces is as in [Reference Achinger, Lara and YoucisALY21a, §§ 2–3]. We denote by  $\operatorname {\mathbf {Rig}}_K$ the category of rigid
$\operatorname {\mathbf {Rig}}_K$ the category of rigid  $K$-spaces, and by
$K$-spaces, and by  $\operatorname {\mathbf {Rig}}^{\rm qcqs}_K$ the full subcategory consisting of quasi-compact and quasi-separated rigid
$\operatorname {\mathbf {Rig}}^{\rm qcqs}_K$ the full subcategory consisting of quasi-compact and quasi-separated rigid  $K$-spaces.
$K$-spaces.– A topological space
 $X$ is quasi-paracompact [Reference BoschBos14, Definition 8.2/12] if it admits an open cover
$X$ is quasi-paracompact [Reference BoschBos14, Definition 8.2/12] if it admits an open cover  $X=\bigcup U_i$ by quasi-compact opens such that each
$X=\bigcup U_i$ by quasi-compact opens such that each  $U_i$ intersects only finitely many other
$U_i$ intersects only finitely many other  $U_j$.
$U_j$.– An open subset
 $U$ of a rigid
$U$ of a rigid  $K$-space
$K$-space  $X$ is overconvergent if it is stable under specialization or, equivalently, if the inclusion
$X$ is overconvergent if it is stable under specialization or, equivalently, if the inclusion  $U\hookrightarrow X$ is partially proper [Reference Achinger, Lara and YoucisALY21a, Proposition 3.3.3].
$U\hookrightarrow X$ is partially proper [Reference Achinger, Lara and YoucisALY21a, Proposition 3.3.3].– By a maximal point of a rigid
 $K$-space
$K$-space  $X$ we mean a point which is maximal with respect to the generalization relation. By [Reference HuberHub96, Lemma 1.1.10] this is equivalent to the corresponding valuation being rank
$X$ we mean a point which is maximal with respect to the generalization relation. By [Reference HuberHub96, Lemma 1.1.10] this is equivalent to the corresponding valuation being rank  $1$.
$1$.– Let
 $X$ be an adic space, formal scheme, or scheme. By
$X$ be an adic space, formal scheme, or scheme. By  $\operatorname {\mathbf {\acute {E}t}}_X$ (respectively,
$\operatorname {\mathbf {\acute {E}t}}_X$ (respectively,  $\operatorname {\mathbf {F\acute {E}t}}_X$) we mean the category of objects étale (respectively, finite étale) over
$\operatorname {\mathbf {F\acute {E}t}}_X$) we mean the category of objects étale (respectively, finite étale) over  $X$.
$X$.– Closed subsets of (formal) schemes are implicitly treated as schemes endowed with the reduced scheme structure.
– We consistently use the term cover as in ‘open cover’ and covering as in ‘covering space’.
2. Rigid generic fibers of formal schemes
In this section, we review the theory of formal schemes and their rigid generic fibers. As before, we fix a non-archimedean field ![]() $K$ with ring of integers
$K$ with ring of integers ![]() $\mathcal {O}_K$, residue field
$\mathcal {O}_K$, residue field ![]() $k$, and a pseudo-uniformizer
$k$, and a pseudo-uniformizer ![]() $\varpi$. We will need to work with certain non-adic formal schemes over
$\varpi$. We will need to work with certain non-adic formal schemes over ![]() $\mathcal {O}_K$, such as
$\mathcal {O}_K$, such as ![]() $\operatorname {Spf}(\mathcal {O}_K[\kern-1pt[ x ]\kern-1pt] )$; for such formal schemes the rigid generic fiber has been constructed by Berthelot [Reference BerthelotBer96b] (see also de Jong [Reference de JongdJ95a, § 7]) in case
$\operatorname {Spf}(\mathcal {O}_K[\kern-1pt[ x ]\kern-1pt] )$; for such formal schemes the rigid generic fiber has been constructed by Berthelot [Reference BerthelotBer96b] (see also de Jong [Reference de JongdJ95a, § 7]) in case ![]() $K$ is discretely valued. For an extension to
$K$ is discretely valued. For an extension to ![]() $K$ arbitrary, we use the approach of Fujiwara and Kato [Reference Fujiwara and KatoFK18, Chapter II, § 9.6] (see also Scholze and Weinstein [Reference Scholze and WeinsteinSW13] for an alternative definition).
$K$ arbitrary, we use the approach of Fujiwara and Kato [Reference Fujiwara and KatoFK18, Chapter II, § 9.6] (see also Scholze and Weinstein [Reference Scholze and WeinsteinSW13] for an alternative definition).
2.1 Formal schemes
We refer to [Reference Fujiwara and KatoFK18, Chapter I] for the basic terminology regarding formal schemes. We only consider formal schemes which are locally of the form ![]() $\operatorname {Spf}(A)$ where
$\operatorname {Spf}(A)$ where ![]() $A$ has the
$A$ has the ![]() $I$-adic topology for a finitely generated ideal
$I$-adic topology for a finitely generated ideal ![]() $I$, and is
$I$, and is ![]() $I$-adically complete and separated. By an ideal of definition of
$I$-adically complete and separated. By an ideal of definition of ![]() $A$ we shall always mean a finitely generated ideal of definition. Recall that a continuous homomorphism of such algebras
$A$ we shall always mean a finitely generated ideal of definition. Recall that a continuous homomorphism of such algebras ![]() $A\to B$ is adic if
$A\to B$ is adic if ![]() $I\cdot B$ is an ideal of definition of
$I\cdot B$ is an ideal of definition of ![]() $B$ for some (equivalently, every) ideal of definition
$B$ for some (equivalently, every) ideal of definition ![]() $I$ of
$I$ of ![]() $A$, and a map of formal schemes
$A$, and a map of formal schemes ![]() $\mathfrak {Y}\to \mathfrak {X}$ is adic if it is locally of the form
$\mathfrak {Y}\to \mathfrak {X}$ is adic if it is locally of the form ![]() $\operatorname {Spf}(B)\to \operatorname {Spf}(A)$ for an adic homomorphism
$\operatorname {Spf}(B)\to \operatorname {Spf}(A)$ for an adic homomorphism ![]() $A\to B$.
$A\to B$.
We first discuss a hypothesis on formal schemes over ![]() $\mathcal {O}_K$ that is more flexible than locally topologically of finite type (in the discrete case such objects were considered in [Reference BerkovichBer96a, § 1] under the terminology ‘special’).
$\mathcal {O}_K$ that is more flexible than locally topologically of finite type (in the discrete case such objects were considered in [Reference BerkovichBer96a, § 1] under the terminology ‘special’).
Proposition 2.1 Let ![]() $A$ be a topological
$A$ be a topological ![]() $\mathcal {O}_K$-algebra which is complete and separated with respect to a finitely generated ideal. The following conditions are then equivalent.
$\mathcal {O}_K$-algebra which is complete and separated with respect to a finitely generated ideal. The following conditions are then equivalent.
(a) For every (equivalently, any) pseudo-uniformizer
 $\varpi$ of
$\varpi$ of  $\mathcal {O}_K$ and ideal of definition
$\mathcal {O}_K$ and ideal of definition  $I\subseteq A$ such that
$I\subseteq A$ such that  $\varpi A\subseteq I$, the ring
$\varpi A\subseteq I$, the ring  $A/I$ is a finitely generated
$A/I$ is a finitely generated  $\mathcal {O}_K/\varpi$-algebra.
$\mathcal {O}_K/\varpi$-algebra.(b) There is a continuous and adic
 $\mathcal {O}_K$-algebra surjection
for some
$\mathcal {O}_K$-algebra surjection
for some \[ \psi\colon P:= \mathcal{O}_K\langle x_1, \ldots, x_n\rangle [\kern-1pt[ y_1, \ldots, y_m]\kern-1pt] \to A \]
\[ \psi\colon P:= \mathcal{O}_K\langle x_1, \ldots, x_n\rangle [\kern-1pt[ y_1, \ldots, y_m]\kern-1pt] \to A \] $n, m\geqslant 0$. (Here,
$n, m\geqslant 0$. (Here,  $P$ is the completion of
$P$ is the completion of  $\mathcal {O}_K[x_1, \ldots, x_n, y_1, \ldots, y_m]$ with respect to the idealFootnote 1
$\mathcal {O}_K[x_1, \ldots, x_n, y_1, \ldots, y_m]$ with respect to the idealFootnote 1  $(\varpi, y_1, \ldots, y_m)$.)
$(\varpi, y_1, \ldots, y_m)$.)
Proof. Suppose that ![]() $A/I$ is finitely generated over
$A/I$ is finitely generated over ![]() $\mathcal {O}_K/\varpi$ and choose a surjection
$\mathcal {O}_K/\varpi$ and choose a surjection
Write ![]() $I = (f_1, \ldots, f_m, \varpi )$, and let
$I = (f_1, \ldots, f_m, \varpi )$, and let ![]() $\psi \colon P \to A$ be the unique continuous
$\psi \colon P \to A$ be the unique continuous ![]() $\mathcal {O}_K$-algebra homomorphism sending
$\mathcal {O}_K$-algebra homomorphism sending ![]() $x_i$ to prescribed lifts of
$x_i$ to prescribed lifts of ![]() $\varphi (x_i)$ and with
$\varphi (x_i)$ and with ![]() $\psi (y_i)=f_i$. Such a homomorphism exists because each
$\psi (y_i)=f_i$. Such a homomorphism exists because each ![]() $f_i$ is topologically nilpotent. As
$f_i$ is topologically nilpotent. As ![]() $P$ is by definition the
$P$ is by definition the ![]() $(y_1, \ldots, y_m, \varpi )$-adic completion of
$(y_1, \ldots, y_m, \varpi )$-adic completion of ![]() $\mathcal {O}_K[x_1, \ldots, x_n, y_1, \ldots, y_m]$, the map
$\mathcal {O}_K[x_1, \ldots, x_n, y_1, \ldots, y_m]$, the map ![]() $\psi$ is adic. Therefore, by [Reference Fujiwara and KatoFK18, Chapter I, Proposition 4.3.6] the map
$\psi$ is adic. Therefore, by [Reference Fujiwara and KatoFK18, Chapter I, Proposition 4.3.6] the map ![]() $\psi$ is surjective, and hence condition (b) is satisfied.
$\psi$ is surjective, and hence condition (b) is satisfied.
For the other direction, note that there exists a ![]() $k\geqslant 1$ such that
$k\geqslant 1$ such that ![]() $(\psi (y_1^{k}), \ldots, \psi (y_m^{k}), \varpi ) \subseteq I$. Then
$(\psi (y_1^{k}), \ldots, \psi (y_m^{k}), \varpi ) \subseteq I$. Then ![]() $P/(\psi (y_1^{k}), \ldots, \psi (y_m^{k}), \varpi )\simeq (\mathcal {O}_K/\varpi )[x_1,\ldots,x_n,y_1,\ldots,y_m]/(y_1^{k},\ldots,y_m^{k})$ is a finitely generated
$P/(\psi (y_1^{k}), \ldots, \psi (y_m^{k}), \varpi )\simeq (\mathcal {O}_K/\varpi )[x_1,\ldots,x_n,y_1,\ldots,y_m]/(y_1^{k},\ldots,y_m^{k})$ is a finitely generated ![]() $\mathcal {O}_K/\varpi$-algebra, and hence so is its quotient
$\mathcal {O}_K/\varpi$-algebra, and hence so is its quotient ![]() $A/I$.
$A/I$.
Definition 2.2 (See [Reference Fujiwara and KatoFK18, Chapter II, Definition 9.6.5])
Let ![]() $A$ be a topological
$A$ be a topological ![]() $\mathcal {O}_K$-algebra which is complete and separated with respect to a finitely generated ideal.
$\mathcal {O}_K$-algebra which is complete and separated with respect to a finitely generated ideal.
(a) We say that
 $A$ is topologically formally of finite type if it satisfies any of the equivalent conditions of Proposition 2.1, topologically of finite type if it is formally topologically of finite type and adic over
$A$ is topologically formally of finite type if it satisfies any of the equivalent conditions of Proposition 2.1, topologically of finite type if it is formally topologically of finite type and adic over  $\mathcal {O}_K$ (equivalently, an adic quotient of
$\mathcal {O}_K$ (equivalently, an adic quotient of  $\mathcal {O}_K\langle x_1, \ldots, x_n\rangle$ for some
$\mathcal {O}_K\langle x_1, \ldots, x_n\rangle$ for some  $n\geqslant 0$), and admissible if it is topologically of finite type and flat (equivalently, torsion free) over
$n\geqslant 0$), and admissible if it is topologically of finite type and flat (equivalently, torsion free) over  $\mathcal {O}_K$.
$\mathcal {O}_K$.(b) We say that a formal scheme
 $\mathfrak {X}$ over
$\mathfrak {X}$ over  $\mathcal {O}_K$ is locally formally of finite type (respectively, locally of finite type, respectively, admissible) if for all affine open covers
$\mathcal {O}_K$ is locally formally of finite type (respectively, locally of finite type, respectively, admissible) if for all affine open covers  $\{\operatorname {Spf}(A_i)\}$ (equivalently, for a single such open cover) each
$\{\operatorname {Spf}(A_i)\}$ (equivalently, for a single such open cover) each  $A_i$ is topologically formally of finite type (respectively, topologically of finite type, respectively, admissible).
$A_i$ is topologically formally of finite type (respectively, topologically of finite type, respectively, admissible).(c) We say that a formal scheme
 $\mathfrak {X}$ over
$\mathfrak {X}$ over  $\mathcal {O}_K$ is (formally) of finite type if it is locally (formally) of finite type and quasi-compact.
$\mathcal {O}_K$ is (formally) of finite type if it is locally (formally) of finite type and quasi-compact.
We denote the category of formal schemes locally formally of finite type (respectively, locally of finite type, respectively, of finite type) over ![]() $\mathcal {O}_K$ by
$\mathcal {O}_K$ by ![]() $\operatorname {\mathbf {F Sch}}_{\mathcal {O}_K}^{\rm lfft}$ (respectively,
$\operatorname {\mathbf {F Sch}}_{\mathcal {O}_K}^{\rm lfft}$ (respectively, ![]() $\operatorname {\mathbf {FSch}}_{\mathcal {O}_K}^{\rm lft}$, respectively,
$\operatorname {\mathbf {FSch}}_{\mathcal {O}_K}^{\rm lft}$, respectively, ![]() $\operatorname {\mathbf {FSch}}_{\mathcal {O}_K}^{\rm ft}$). The notions of (locally) formally of finite type, (locally) of finite type, and admissible are preserved under base change along
$\operatorname {\mathbf {FSch}}_{\mathcal {O}_K}^{\rm ft}$). The notions of (locally) formally of finite type, (locally) of finite type, and admissible are preserved under base change along ![]() $\mathcal {O}_K\to \mathcal {O}_{K'}$ for
$\mathcal {O}_K\to \mathcal {O}_{K'}$ for ![]() $K'$ a non-archimedean extension of
$K'$ a non-archimedean extension of ![]() $K$.
$K$.
2.1 Admissible ideals
For a formal scheme ![]() $\mathfrak {X}$ we say that an ideal sheaf
$\mathfrak {X}$ we say that an ideal sheaf ![]() $\mathcal {I}\subseteq \mathcal {O}_\mathfrak {X}$ is an ideal sheaf of definition if it is adically quasi-coherent (see [Reference Fujiwara and KatoFK18, Chapter I, Definition 3.1.3]) and if for all affine open formal subschemes
$\mathcal {I}\subseteq \mathcal {O}_\mathfrak {X}$ is an ideal sheaf of definition if it is adically quasi-coherent (see [Reference Fujiwara and KatoFK18, Chapter I, Definition 3.1.3]) and if for all affine open formal subschemes ![]() $U$ we have that
$U$ we have that ![]() $\mathcal {I}(U)$ is an ideal of definition of
$\mathcal {I}(U)$ is an ideal of definition of ![]() $\mathcal {O}_{\mathfrak {X}}(U)$. If
$\mathcal {O}_{\mathfrak {X}}(U)$. If ![]() $\mathfrak {X}$ is quasi-compact and quasi-separated, then the set of ideal sheaves of definition is cofiltering, and in particular non-empty (cf. [Reference Fujiwara and KatoFK18, Chapter I, Corollary 3.7.12]). We say that an ideal sheaf
$\mathfrak {X}$ is quasi-compact and quasi-separated, then the set of ideal sheaves of definition is cofiltering, and in particular non-empty (cf. [Reference Fujiwara and KatoFK18, Chapter I, Corollary 3.7.12]). We say that an ideal sheaf ![]() $\mathcal {J}\subseteq \mathcal {O}_\mathfrak {X}$ is admissible if it is adically quasi-coherent, of finite type, and open (i.e. locally contains an ideal of definition). For an admissible ideal sheaf
$\mathcal {J}\subseteq \mathcal {O}_\mathfrak {X}$ is admissible if it is adically quasi-coherent, of finite type, and open (i.e. locally contains an ideal of definition). For an admissible ideal sheaf ![]() $\mathcal {J}$ we denote by
$\mathcal {J}$ we denote by ![]() $\mathfrak {X}(\mathcal {J})$ the scheme cut out by
$\mathfrak {X}(\mathcal {J})$ the scheme cut out by ![]() $\mathcal {J}$.
$\mathcal {J}$.
2.1 Admissible blowups
Let ![]() $\mathfrak {X}$ be a formal scheme and
$\mathfrak {X}$ be a formal scheme and ![]() $\mathcal {J}$ an admissible ideal sheaf of
$\mathcal {J}$ an admissible ideal sheaf of ![]() $\mathfrak {X}$. There then exists a final object amongst morphisms
$\mathfrak {X}$. There then exists a final object amongst morphisms ![]() $\pi \colon \mathfrak {X}'\to \mathfrak {X}$ which are adic, proper, and satisfy
$\pi \colon \mathfrak {X}'\to \mathfrak {X}$ which are adic, proper, and satisfy ![]() $\mathcal {J}\mathcal {O}_{\mathfrak {X}'}$ is invertible. We call this universal object the admissible blowup of
$\mathcal {J}\mathcal {O}_{\mathfrak {X}'}$ is invertible. We call this universal object the admissible blowup of ![]() $\mathfrak {X}$ relative to
$\mathfrak {X}$ relative to ![]() $\mathcal {J}$ and denote it by
$\mathcal {J}$ and denote it by ![]() $\pi _\mathcal {J}\colon \mathfrak {X}_\mathcal {J}\to \mathfrak {X}$. We call the subscheme cut out by
$\pi _\mathcal {J}\colon \mathfrak {X}_\mathcal {J}\to \mathfrak {X}$. We call the subscheme cut out by ![]() $\mathcal {J}$ the center of the admissible blowup
$\mathcal {J}$ the center of the admissible blowup ![]() $\mathfrak {X}'\to \mathfrak {X}$. One can give an explicit description of this admissible blowup as in classical algebraic geometry (cf. [Reference Fujiwara and KatoFK18, Chapter II, §§ 1.1.(a) and 1.1.(b)]). As admissible blowups are finite type and do not introduce torsion for an ideal of definition (see [Reference Fujiwara and KatoFK18, Chapter II, Corollary 1.1.6] for this latter claim), one sees that the properties defined in Definition 2.2(bc) are stable under admissible blowups.
$\mathfrak {X}'\to \mathfrak {X}$. One can give an explicit description of this admissible blowup as in classical algebraic geometry (cf. [Reference Fujiwara and KatoFK18, Chapter II, §§ 1.1.(a) and 1.1.(b)]). As admissible blowups are finite type and do not introduce torsion for an ideal of definition (see [Reference Fujiwara and KatoFK18, Chapter II, Corollary 1.1.6] for this latter claim), one sees that the properties defined in Definition 2.2(bc) are stable under admissible blowups.
2.1 Strict transform
If ![]() $\mathfrak {X}_\mathcal {J}\to \mathfrak {X}$ is an admissible blowup and
$\mathfrak {X}_\mathcal {J}\to \mathfrak {X}$ is an admissible blowup and ![]() $\mathfrak {Y}\to \mathfrak {X}$ an adic morphism, then the map
$\mathfrak {Y}\to \mathfrak {X}$ an adic morphism, then the map ![]() $\mathfrak {Y}_{\mathfrak {X}_\mathcal {J}}\to \mathfrak {Y}$ will, in general, not be an admissible blowup. That said, one can show (see [Reference Fujiwara and KatoFK18, Chapter II, § 1.2]) that the
$\mathfrak {Y}_{\mathfrak {X}_\mathcal {J}}\to \mathfrak {Y}$ will, in general, not be an admissible blowup. That said, one can show (see [Reference Fujiwara and KatoFK18, Chapter II, § 1.2]) that the ![]() $\mathcal {J}$-torsion ideal sheaf
$\mathcal {J}$-torsion ideal sheaf ![]() $\mathcal {K}=\mathcal {O}_{\mathfrak {Y}_{\mathfrak {X}_\mathcal {J}},\mathcal {J}\text {-tors}}$ is of finite type. One then considers the closed formal subscheme
$\mathcal {K}=\mathcal {O}_{\mathfrak {Y}_{\mathfrak {X}_\mathcal {J}},\mathcal {J}\text {-tors}}$ is of finite type. One then considers the closed formal subscheme ![]() $\mathfrak {Y}'$ of
$\mathfrak {Y}'$ of ![]() $\mathfrak {Y}_{\mathfrak {X}_{\mathcal {J}}}$ cut out by
$\mathfrak {Y}_{\mathfrak {X}_{\mathcal {J}}}$ cut out by ![]() $\mathcal {K}$ which is called the strict transform of
$\mathcal {K}$ which is called the strict transform of ![]() $\mathfrak {Y}\to \mathfrak {X}$ along
$\mathfrak {Y}\to \mathfrak {X}$ along ![]() $\mathfrak {X}_\mathcal {J}\to \mathfrak {X}$. The map
$\mathfrak {X}_\mathcal {J}\to \mathfrak {X}$. The map ![]() $\mathfrak {Y}'\to \mathfrak {Y}$ is isomorphic to the admissible blowup
$\mathfrak {Y}'\to \mathfrak {Y}$ is isomorphic to the admissible blowup ![]() $\mathfrak {Y}_{\mathcal {J}\mathcal {O}_{\mathfrak {Y}}}$ (see [Reference Fujiwara and KatoFK18, Chapter II, Proposition 1.2.9]).
$\mathfrak {Y}_{\mathcal {J}\mathcal {O}_{\mathfrak {Y}}}$ (see [Reference Fujiwara and KatoFK18, Chapter II, Proposition 1.2.9]).
2.1 Underlying reduced subscheme
For a formal scheme ![]() $\mathfrak {X}$ there exists a unique ideal sheaf
$\mathfrak {X}$ there exists a unique ideal sheaf ![]() $\mathcal {O}_\mathfrak {X}^{{\circ \circ }}\subseteq \mathcal {O}_\mathfrak {X}$ such that
$\mathcal {O}_\mathfrak {X}^{{\circ \circ }}\subseteq \mathcal {O}_\mathfrak {X}$ such that ![]() $\mathcal {O}_\mathfrak {X}^{{\circ \circ }}(\operatorname {Spf}(A))=A^{{\circ \circ }}$ for all affine open
$\mathcal {O}_\mathfrak {X}^{{\circ \circ }}(\operatorname {Spf}(A))=A^{{\circ \circ }}$ for all affine open ![]() $\operatorname {Spf}(A)\subseteq \mathfrak {X}$. We call
$\operatorname {Spf}(A)\subseteq \mathfrak {X}$. We call ![]() $\mathcal {O}_\mathfrak {X}^{{\circ \circ }}$ the ideal sheaf of topologically nilpotent elements. The pair
$\mathcal {O}_\mathfrak {X}^{{\circ \circ }}$ the ideal sheaf of topologically nilpotent elements. The pair ![]() $\underline {\mathfrak {X}}:=(\mathfrak {X},\mathcal {O}_\mathfrak {X}/\mathcal {O}_\mathfrak {X}^{{\circ \circ }})$ defines a closed subscheme of
$\underline {\mathfrak {X}}:=(\mathfrak {X},\mathcal {O}_\mathfrak {X}/\mathcal {O}_\mathfrak {X}^{{\circ \circ }})$ defines a closed subscheme of ![]() $\mathfrak {X}$ called the underlying reduced subscheme of
$\mathfrak {X}$ called the underlying reduced subscheme of ![]() $\mathfrak {X}$. For any ideal sheaf of definition
$\mathfrak {X}$. For any ideal sheaf of definition ![]() $\mathcal {I}$ of
$\mathcal {I}$ of ![]() $\mathfrak {X}$ the map
$\mathfrak {X}$ the map ![]() $\underline {\mathfrak {X}}\to \mathfrak {X}$ factorizes through
$\underline {\mathfrak {X}}\to \mathfrak {X}$ factorizes through ![]() $\mathfrak {X}(\mathcal {I})$ and identifies
$\mathfrak {X}(\mathcal {I})$ and identifies ![]() $\underline {\mathfrak {X}}$ with the underlying reduced subscheme of
$\underline {\mathfrak {X}}$ with the underlying reduced subscheme of ![]() $\mathfrak {X}(\mathcal {I})$.
$\mathfrak {X}(\mathcal {I})$.
2.1 Completions
Let ![]() $\mathfrak {X}$ be a formal scheme and let
$\mathfrak {X}$ be a formal scheme and let ![]() $\mathcal {J}\subseteq \mathcal {O}_\mathfrak {X}$ be an admissible ideal sheaf. Consider the colimitFootnote 2
$\mathcal {J}\subseteq \mathcal {O}_\mathfrak {X}$ be an admissible ideal sheaf. Consider the colimitFootnote 2 ![]() $\mathfrak {X}(\mathcal {J}^{\infty })=\varinjlim \mathfrak {X}(\mathcal {J}^{n})$ of locally ringed spaces. Let us note that the underlying topological space of
$\mathfrak {X}(\mathcal {J}^{\infty })=\varinjlim \mathfrak {X}(\mathcal {J}^{n})$ of locally ringed spaces. Let us note that the underlying topological space of ![]() $\mathfrak {X}(\mathcal {J}^{n})$ is independent of
$\mathfrak {X}(\mathcal {J}^{n})$ is independent of ![]() $n\geqslant 1$. Let us call it
$n\geqslant 1$. Let us call it ![]() $X$. We then consider the sheaves
$X$. We then consider the sheaves ![]() $\mathcal {O}_{\mathfrak {X}(\mathcal {J}^{n})}$ on
$\mathcal {O}_{\mathfrak {X}(\mathcal {J}^{n})}$ on ![]() $X$ for all
$X$ for all ![]() $n$. We have obvious surjections
$n$. We have obvious surjections ![]() $\mathcal {O}_{\mathfrak {X}(\mathcal {J}^{i})}\to \mathcal {O}_{\mathfrak {X}(\mathcal {J}^{j})}$ for
$\mathcal {O}_{\mathfrak {X}(\mathcal {J}^{i})}\to \mathcal {O}_{\mathfrak {X}(\mathcal {J}^{j})}$ for ![]() $i\geqslant j\geqslant 1$. Using [Reference Fujiwara and KatoFK18, Chapter I, Proposition 1.4.2] one shows that
$i\geqslant j\geqslant 1$. Using [Reference Fujiwara and KatoFK18, Chapter I, Proposition 1.4.2] one shows that ![]() $\mathfrak {X}(\mathcal {J}^{\infty })$ is a formal scheme. If
$\mathfrak {X}(\mathcal {J}^{\infty })$ is a formal scheme. If ![]() $\mathfrak {X}=\operatorname {Spf}(A)$ and
$\mathfrak {X}=\operatorname {Spf}(A)$ and ![]() $J\subseteq A$ is the ideal corresponding to
$J\subseteq A$ is the ideal corresponding to ![]() $\mathcal {J}$, then
$\mathcal {J}$, then ![]() $\mathfrak {X}(\mathcal {J}^{\infty })$ is in fact equal to
$\mathfrak {X}(\mathcal {J}^{\infty })$ is in fact equal to ![]() $\operatorname {Spf}(B)$ with
$\operatorname {Spf}(B)$ with ![]() $B$ the
$B$ the ![]() $J$-adic completion of
$J$-adic completion of ![]() $A$.
$A$.
The proof of the following representability result is left to the reader.
Proposition 2.3 Let ![]() $\mathfrak {X}$ be a formal scheme such that
$\mathfrak {X}$ be a formal scheme such that ![]() $\underline {\mathfrak {X}}$ is locally Noetherian. Then, for any closed subset
$\underline {\mathfrak {X}}$ is locally Noetherian. Then, for any closed subset ![]() $Z$ of
$Z$ of ![]() $|\mathfrak {X}|$ the functor
$|\mathfrak {X}|$ the functor
is representable. Moreover, if ![]() $|\mathfrak {X}(\mathcal {J})|=Z$ for an admissible ideal sheaf
$|\mathfrak {X}(\mathcal {J})|=Z$ for an admissible ideal sheaf ![]() $\mathcal {J}\subseteq \mathcal {O}_\mathfrak {X}$, then it is represented by
$\mathcal {J}\subseteq \mathcal {O}_\mathfrak {X}$, then it is represented by ![]() $\mathfrak {X}(\mathcal {J}^{\infty })$.
$\mathfrak {X}(\mathcal {J}^{\infty })$.
We call the formal scheme ![]() $\widehat {\mathfrak {X}}_Z$ the completion of
$\widehat {\mathfrak {X}}_Z$ the completion of ![]() $\mathfrak {X}$ along
$\mathfrak {X}$ along ![]() $Z$. It is clear that if
$Z$. It is clear that if ![]() $\mathfrak {U}$ is an open formal subscheme of
$\mathfrak {U}$ is an open formal subscheme of ![]() $\mathfrak {X}$, then
$\mathfrak {X}$, then ![]() $\widehat {\mathfrak {U}}_{U\cap Z}$ is the preimage of
$\widehat {\mathfrak {U}}_{U\cap Z}$ is the preimage of ![]() $\mathfrak {U}$ in
$\mathfrak {U}$ in ![]() $\widehat {\mathfrak {X}}_Z$. By reducing to the affine case using [Reference Fujiwara and KatoFK18, Chapter I, Proposition 3.7.11] one can show that if
$\widehat {\mathfrak {X}}_Z$. By reducing to the affine case using [Reference Fujiwara and KatoFK18, Chapter I, Proposition 3.7.11] one can show that if ![]() $\mathfrak {X}$ is moreover quasi-compact and quasi-separated, then every closed subset
$\mathfrak {X}$ is moreover quasi-compact and quasi-separated, then every closed subset ![]() $Z$ is of the form
$Z$ is of the form ![]() $|\mathfrak {X}(\mathcal {J})|$ for some admissible ideal sheaf
$|\mathfrak {X}(\mathcal {J})|$ for some admissible ideal sheaf ![]() $\mathcal {J}\subseteq \mathcal {O}_{\mathfrak {X}}$.
$\mathcal {J}\subseteq \mathcal {O}_{\mathfrak {X}}$.
The following result will play an important role in the proof of Proposition 3.5. In its statement, we use the notion of adically locally of finite presentation as in [Reference Fujiwara and KatoFK18, Chapter I, Definition 5.3.1]. Note that by [Reference Fujiwara and KatoFK18, Chapter I, Corollary 2.2.4] and [Reference Fujiwara and KatoFK18, Chapter 0, Corollary 9.2.9] this condition is automatic for a morphism of admissible formal schemes over ![]() $\mathcal {O}_K$.
$\mathcal {O}_K$.
Proposition 2.4 Let ![]() $\mathfrak {Y}\to \mathfrak {X}$ be a morphism adically locally of finite presentation of formal schemes and assume that the underlying reduced scheme
$\mathfrak {Y}\to \mathfrak {X}$ be a morphism adically locally of finite presentation of formal schemes and assume that the underlying reduced scheme ![]() $\underline {\mathfrak {X}}$ of
$\underline {\mathfrak {X}}$ of ![]() $\mathfrak {X}$ is locally Noetherian. Let
$\mathfrak {X}$ is locally Noetherian. Let ![]() $Z$ be a closed subset of
$Z$ be a closed subset of ![]() $\mathfrak {X}$ and
$\mathfrak {X}$ and ![]() $\mathcal {Z}$ any closed subscheme of
$\mathcal {Z}$ any closed subscheme of ![]() $\mathfrak {X}$ with
$\mathfrak {X}$ with ![]() $|\mathcal {Z}|=Z$. Then if
$|\mathcal {Z}|=Z$. Then if ![]() $\mathfrak {Y}_\mathcal {Z}\to \mathcal {Z}$ is finite (respectively, a disjoint union of finite morphisms), then the same is true for
$\mathfrak {Y}_\mathcal {Z}\to \mathcal {Z}$ is finite (respectively, a disjoint union of finite morphisms), then the same is true for ![]() $\mathfrak {Y}_{\widehat {\mathfrak {X}}_Z}\to \widehat {\mathfrak {X}}_Z$.
$\mathfrak {Y}_{\widehat {\mathfrak {X}}_Z}\to \widehat {\mathfrak {X}}_Z$.
Proof. Suppose first that the map is finite. Without loss of generality, we may assume that ![]() $\mathcal {Z}=Z$ with the reduced scheme structure. By working locally on the target, we may assume that
$\mathcal {Z}=Z$ with the reduced scheme structure. By working locally on the target, we may assume that ![]() $\mathfrak {X}=\operatorname {Spf}(A)$ and that
$\mathfrak {X}=\operatorname {Spf}(A)$ and that ![]() $Z_\mathrm {red}=\operatorname {Spec}(A/J)_\mathrm {red}$ for some admissible ideal
$Z_\mathrm {red}=\operatorname {Spec}(A/J)_\mathrm {red}$ for some admissible ideal ![]() $J$ of
$J$ of ![]() $A$. Set
$A$. Set ![]() $T=\operatorname {Spec}(A/J)$. Note then that
$T=\operatorname {Spec}(A/J)$. Note then that ![]() $\mathfrak {Y}_T\to T$ is, by assumption, a morphism of schemes locally of finite presentation. By assumption, we have that the pullback of this map along
$\mathfrak {Y}_T\to T$ is, by assumption, a morphism of schemes locally of finite presentation. By assumption, we have that the pullback of this map along ![]() $T_\mathrm {red}\to T$ is finite, and thus it is itself finite by [SP21, Tag 0BPG]. By [Reference Fujiwara and KatoFK18, Chapter I, Proposition 4.2.3] to verify
$T_\mathrm {red}\to T$ is finite, and thus it is itself finite by [SP21, Tag 0BPG]. By [Reference Fujiwara and KatoFK18, Chapter I, Proposition 4.2.3] to verify ![]() $\mathfrak {Y}_{\widehat {\mathfrak {X}}_Z}\to \widehat {\mathfrak {X}}_Z$ is finite, it suffices to check this after base change along
$\mathfrak {Y}_{\widehat {\mathfrak {X}}_Z}\to \widehat {\mathfrak {X}}_Z$ is finite, it suffices to check this after base change along ![]() $T\to \widehat {\mathfrak {X}}_Z$ from where the claim follows. The second claim is clear by the previous discussion because
$T\to \widehat {\mathfrak {X}}_Z$ from where the claim follows. The second claim is clear by the previous discussion because ![]() $\mathfrak {Y}_{Z_\mathrm {red}}\to \mathfrak {Y}_{\widehat {\mathfrak {X}}_{Z}}$ is a homeomorphism, and so if
$\mathfrak {Y}_{Z_\mathrm {red}}\to \mathfrak {Y}_{\widehat {\mathfrak {X}}_{Z}}$ is a homeomorphism, and so if ![]() $\mathfrak {Y}_{Z_\mathrm {red}}$ is a disjoint union of clopen subsets finite over
$\mathfrak {Y}_{Z_\mathrm {red}}$ is a disjoint union of clopen subsets finite over ![]() $Z_\mathrm {red}$, then
$Z_\mathrm {red}$, then ![]() $\mathfrak {Y}_{\widehat {\mathfrak {X}}_Z}$ is a disjoint union of clopen subsets which, by the above, must be finite over
$\mathfrak {Y}_{\widehat {\mathfrak {X}}_Z}$ is a disjoint union of clopen subsets which, by the above, must be finite over ![]() $\widehat {\mathfrak {X}}_Z$.
$\widehat {\mathfrak {X}}_Z$.
2.2 Generic fibers of formal schemes
In this subsection we discuss the notion of the rigid generic fiber of a formal scheme locally formally of finite type over ![]() $\mathcal {O}_K$, which is a rigid
$\mathcal {O}_K$, which is a rigid ![]() $K$-space. We then note several properties of the generic fiber construction.
$K$-space. We then note several properties of the generic fiber construction.
We first recall Raynaud's equivalence as developed by Fujiwara–Kato in [Reference Fujiwara and KatoFK18], which, in particular, gives the construction for formal schemes locally of finite type over ![]() $\mathcal {O}_K$. Let
$\mathcal {O}_K$. Let ![]() $A$ be a topologically finite type
$A$ be a topologically finite type ![]() $\mathcal {O}_K$-algebra. The algebra
$\mathcal {O}_K$-algebra. The algebra ![]() $A_K = A[{1}/{\pi }]$ is then an affinoid
$A_K = A[{1}/{\pi }]$ is then an affinoid ![]() $K$-algebra, i.e. an algebra topologically of finite type over
$K$-algebra, i.e. an algebra topologically of finite type over ![]() $K$. The subring
$K$. The subring ![]() $A^{\circ }_K\subseteq A_K$ of powerbounded elements coincides with the integral closure of (the image of)
$A^{\circ }_K\subseteq A_K$ of powerbounded elements coincides with the integral closure of (the image of) ![]() $A$ in
$A$ in ![]() $A_K$ (see [Reference Fujiwara and KatoFK18, Chapter II, Corollary A.4.10]). Combining [Reference Fujiwara and KatoFK18, Chapter II] and [Reference Fujiwara and KatoFK18, Chapter II, Theorem A.5.1], there exists a unique functor
$A_K$ (see [Reference Fujiwara and KatoFK18, Chapter II, Corollary A.4.10]). Combining [Reference Fujiwara and KatoFK18, Chapter II] and [Reference Fujiwara and KatoFK18, Chapter II, Theorem A.5.1], there exists a unique functor
such that ![]() $\operatorname {Spf}(A)_\eta = \operatorname {Spa}(A_K)$ for every topologically finite type
$\operatorname {Spf}(A)_\eta = \operatorname {Spa}(A_K)$ for every topologically finite type ![]() $\mathcal {O}_K$-algebra
$\mathcal {O}_K$-algebra ![]() $A$, and which respects open immersions and open covers. This functor naturally extends to a functor
$A$, and which respects open immersions and open covers. This functor naturally extends to a functor
and for ![]() $\mathfrak {X}$ locally of finite type over
$\mathfrak {X}$ locally of finite type over ![]() $\mathcal {O}_K$, the rigid
$\mathcal {O}_K$, the rigid ![]() $K$-space
$K$-space ![]() $\mathfrak {X}_\eta$ is called the rigid generic fiber of
$\mathfrak {X}_\eta$ is called the rigid generic fiber of ![]() $\mathfrak {X}$. Furthermore,
$\mathfrak {X}$. Furthermore, ![]() $(-)_\eta$ sends the class
$(-)_\eta$ sends the class ![]() $W$ of admissible blowups to isomorphisms and induces equivalences of categories
$W$ of admissible blowups to isomorphisms and induces equivalences of categories
Here ![]() $\operatorname {\mathbf {FSch}}^{\rm adm,qc}_{\mathcal {O}_K}$ consists of quasi-compact admissible formal schemes over
$\operatorname {\mathbf {FSch}}^{\rm adm,qc}_{\mathcal {O}_K}$ consists of quasi-compact admissible formal schemes over ![]() $\mathcal {O}_K$, and
$\mathcal {O}_K$, and ![]() $(-)[W^{-1}]$ denotes the localization with respect to
$(-)[W^{-1}]$ denotes the localization with respect to ![]() $W$, i.e. the category obtained by formally inverting all admissible blowups. By a formal model of a rigid
$W$, i.e. the category obtained by formally inverting all admissible blowups. By a formal model of a rigid ![]() $K$-space
$K$-space ![]() $X$ we shall mean a formal scheme
$X$ we shall mean a formal scheme ![]() $\mathfrak {X}$ locally of finite type over
$\mathfrak {X}$ locally of finite type over ![]() $\mathcal {O}_K$ together with an isomorphism
$\mathcal {O}_K$ together with an isomorphism ![]() $\mathfrak {X}_\eta \simeq X$. By [Reference Fujiwara and KatoFK18, Chapter II, Proposition 2.1.10], for any quasi-compact and quasi-separated rigid
$\mathfrak {X}_\eta \simeq X$. By [Reference Fujiwara and KatoFK18, Chapter II, Proposition 2.1.10], for any quasi-compact and quasi-separated rigid ![]() $K$-space, the category of admissible formal models of
$K$-space, the category of admissible formal models of ![]() $X$ is (equivalent to) a cofiltering poset.
$X$ is (equivalent to) a cofiltering poset.
If ![]() $X$ is a quasi-compact and quasi-separated rigid
$X$ is a quasi-compact and quasi-separated rigid ![]() $K$-space, then the construction of the rigid generic fiber allows one to identify the locally topologically ringed space
$K$-space, then the construction of the rigid generic fiber allows one to identify the locally topologically ringed space ![]() $(X,\mathcal {O}_X^{+})$ as
$(X,\mathcal {O}_X^{+})$ as ![]() $\varprojlim \, (\mathfrak {X},\mathcal {O}_\mathfrak {X})$ where
$\varprojlim \, (\mathfrak {X},\mathcal {O}_\mathfrak {X})$ where ![]() $\mathfrak {X}$ runs over admissible formal models of
$\mathfrak {X}$ runs over admissible formal models of ![]() $X$. In particular, for each admissible formal model
$X$. In particular, for each admissible formal model ![]() $\mathfrak {X}$ of
$\mathfrak {X}$ of ![]() $X$ we have a morphism of locally topologically ringed spaces
$X$ we have a morphism of locally topologically ringed spaces
called the specialization map for ![]() $\mathfrak {X}$. For
$\mathfrak {X}$. For ![]() $\mathfrak {X}=\operatorname {Spf}(A)$ affine, the underlying map of topological spaces sends a valuation
$\mathfrak {X}=\operatorname {Spf}(A)$ affine, the underlying map of topological spaces sends a valuation ![]() $\nu \colon A_K\to \Gamma \cup \{0\}$ to the (open) prime ideal
$\nu \colon A_K\to \Gamma \cup \{0\}$ to the (open) prime ideal ![]() $\{x\in A: \nu (x)<1\}$ and the map on global sections is the natural map
$\{x\in A: \nu (x)<1\}$ and the map on global sections is the natural map ![]() $\mathcal {O}_\mathfrak {X}(\mathfrak {X})=A\to A_K^{\circ } =\mathcal {O}_X(X)^{+}$.
$\mathcal {O}_\mathfrak {X}(\mathfrak {X})=A\to A_K^{\circ } =\mathcal {O}_X(X)^{+}$.
As ![]() $|\mathfrak {X}|=|\mathfrak {X}_k|$ we shall often implicitly treat the specialization map
$|\mathfrak {X}|=|\mathfrak {X}_k|$ we shall often implicitly treat the specialization map ![]() $\operatorname {sp}_\mathfrak {X}$ as a map of topological spaces
$\operatorname {sp}_\mathfrak {X}$ as a map of topological spaces ![]() $|X|\to |\mathfrak {X}_k|$. This map is continuous, quasi-compact, closed, and surjective (see [Reference Fujiwara and KatoFK18, Chapter II, Theorem 3.1.2] and [Reference Fujiwara and KatoFK18, Chapter II, Proposition 3.1.5]). If
$|X|\to |\mathfrak {X}_k|$. This map is continuous, quasi-compact, closed, and surjective (see [Reference Fujiwara and KatoFK18, Chapter II, Theorem 3.1.2] and [Reference Fujiwara and KatoFK18, Chapter II, Proposition 3.1.5]). If ![]() $\varphi \colon \mathfrak {X}'\to \mathfrak {X}$ is a morphism in
$\varphi \colon \mathfrak {X}'\to \mathfrak {X}$ is a morphism in ![]() $\operatorname {\mathbf {FSch}}_{\mathcal {O}_K}^{\mathrm {ft}}$ then the diagram
$\operatorname {\mathbf {FSch}}_{\mathcal {O}_K}^{\mathrm {ft}}$ then the diagram

commutes. Moreover, for any open subset ![]() $\mathfrak {U}$ of
$\mathfrak {U}$ of ![]() $\mathfrak {X}$ the induced map
$\mathfrak {X}$ the induced map ![]() $\mathfrak {U}_\eta \to \mathfrak {X}_\eta$ is an open immersion with image
$\mathfrak {U}_\eta \to \mathfrak {X}_\eta$ is an open immersion with image ![]() $\operatorname {sp}_\mathfrak {X}^{-1}(\mathfrak {U})$ (see [Reference Fujiwara and KatoFK18, Chapter II, Proposition 3.1.3]). It follows that the definition of the specialization map may be extended to formal schemes
$\operatorname {sp}_\mathfrak {X}^{-1}(\mathfrak {U})$ (see [Reference Fujiwara and KatoFK18, Chapter II, Proposition 3.1.3]). It follows that the definition of the specialization map may be extended to formal schemes ![]() $\mathfrak {X}$ locally of finite type over
$\mathfrak {X}$ locally of finite type over ![]() $\mathcal {O}_K$, and that this extension enjoys also the property of being continuous, quasi-compact, closed, and surjective if
$\mathcal {O}_K$, and that this extension enjoys also the property of being continuous, quasi-compact, closed, and surjective if ![]() $\mathfrak {X}$ is admissible.
$\mathfrak {X}$ is admissible.
In order to extend the definition of the rigid generic fiber to the category ![]() $\operatorname {\mathbf {FSch}}^{\rm lfft}_{\mathcal {O}_K}$, we need the following result.
$\operatorname {\mathbf {FSch}}^{\rm lfft}_{\mathcal {O}_K}$, we need the following result.
Proposition 2.5 (See [Reference Fujiwara and KatoFK18, Chapter II, § 9.6.(b)])
Let ![]() $\mathfrak {X}$ be a formal scheme locally formally of finite type over
$\mathfrak {X}$ be a formal scheme locally formally of finite type over ![]() $\mathcal {O}_K$. Then, the functor
$\mathcal {O}_K$. Then, the functor
where ![]() $\mathfrak {Z}$ runs over the admissible formal models of
$\mathfrak {Z}$ runs over the admissible formal models of ![]() $Z$, is representable by a rigid
$Z$, is representable by a rigid ![]() $K$-space
$K$-space ![]() $\mathfrak {X}_\eta$.
$\mathfrak {X}_\eta$.
We call ![]() $\mathfrak {X}_\eta$ the rigid generic fiber of
$\mathfrak {X}_\eta$ the rigid generic fiber of ![]() $\mathfrak {X}$. If
$\mathfrak {X}$. If ![]() $\mathfrak {X}$ is locally of finite type over
$\mathfrak {X}$ is locally of finite type over ![]() $\mathcal {O}_K$, this agrees with the previous definition of
$\mathcal {O}_K$, this agrees with the previous definition of ![]() $\mathfrak {X}_\eta$. The association
$\mathfrak {X}_\eta$. The association ![]() $\mathfrak {X}\mapsto \mathfrak {X}_\eta$ is functorial in
$\mathfrak {X}\mapsto \mathfrak {X}_\eta$ is functorial in ![]() $\mathfrak {X}$ and commutes with finite limits and disjoint unions. Moreover, it sends admissible blowups to isomorphisms.
$\mathfrak {X}$ and commutes with finite limits and disjoint unions. Moreover, it sends admissible blowups to isomorphisms.
The following construction makes the rigid generic fiber more explicit in the affine case.
Construction 2.6 (The rigid generic fiber of an affine formal scheme)
Let ![]() $\mathfrak {X}=\operatorname {Spf}(B)$ for a topologically formally of finite type
$\mathfrak {X}=\operatorname {Spf}(B)$ for a topologically formally of finite type ![]() $\mathcal {O}_K$-algebra
$\mathcal {O}_K$-algebra ![]() $B$, and let
$B$, and let ![]() $J=(b_1,\ldots,b_m)$ be an ideal of definition of
$J=(b_1,\ldots,b_m)$ be an ideal of definition of ![]() $B$. We denote by
$B$. We denote by ![]() $B[ {J}/{\varpi }]$ the affine blowup algebra [SP21, Tag 052Q], i.e. the image of
$B[ {J}/{\varpi }]$ the affine blowup algebra [SP21, Tag 052Q], i.e. the image of ![]() $B[x_1, \ldots, x_m]/(\pi x_i - b_i)$ in
$B[x_1, \ldots, x_m]/(\pi x_i - b_i)$ in ![]() $B[ {1}/{\varpi }]$; it is independent of the choice of generators of
$B[ {1}/{\varpi }]$; it is independent of the choice of generators of ![]() $J$. Let
$J$. Let ![]() $B\langle {J}/{\varpi }\rangle$ be the
$B\langle {J}/{\varpi }\rangle$ be the ![]() $J$-adic completion of
$J$-adic completion of ![]() $B[ {J}/\varpi ]$, which is an admissible
$B[ {J}/\varpi ]$, which is an admissible ![]() $\mathcal {O}_K$-algebra on which the
$\mathcal {O}_K$-algebra on which the ![]() $J$-adic topology coincides with the
$J$-adic topology coincides with the ![]() $\varpi$-adic topology. The map
$\varpi$-adic topology. The map ![]() $B\to B\langle J/ \varpi \rangle$ is continuous, and the morphism
$B\to B\langle J/ \varpi \rangle$ is continuous, and the morphism ![]() $\operatorname {Spf}(B\langle {J}/{\varpi }\rangle )\to \operatorname {Spf}(B)$ induces a map
$\operatorname {Spf}(B\langle {J}/{\varpi }\rangle )\to \operatorname {Spf}(B)$ induces a map ![]() $\operatorname {Spf}(B\langle J/ \varpi \rangle )_\eta \to \operatorname {Spf}(B)_\eta$ of rigid
$\operatorname {Spf}(B\langle J/ \varpi \rangle )_\eta \to \operatorname {Spf}(B)_\eta$ of rigid ![]() $K$-spaces. Writing
$K$-spaces. Writing ![]() $B(J) = B\langle {J}/{\varpi }\rangle [ {1}/{\varpi }]$, we have
$B(J) = B\langle {J}/{\varpi }\rangle [ {1}/{\varpi }]$, we have ![]() $\operatorname {Spf}(B\langle {J}/{\varpi } \rangle )_\eta = \operatorname {Spa}(B(J))$.Footnote 3
$\operatorname {Spf}(B\langle {J}/{\varpi } \rangle )_\eta = \operatorname {Spa}(B(J))$.Footnote 3
For ![]() $J'\subseteq J$, we have an inclusion
$J'\subseteq J$, we have an inclusion ![]() $B[ {J'}/{\varpi }]\subseteq B[ {J}/{\varpi }]$ and consequently a morphism
$B[ {J'}/{\varpi }]\subseteq B[ {J}/{\varpi }]$ and consequently a morphism ![]() $\operatorname {Spf}(B[ {J}/{\varpi }])\to \operatorname {Spf}(B[ {J'}/{\varpi }])$ over
$\operatorname {Spf}(B[ {J}/{\varpi }])\to \operatorname {Spf}(B[ {J'}/{\varpi }])$ over ![]() $\operatorname {Spf}(B)$. The induced morphism
$\operatorname {Spf}(B)$. The induced morphism ![]() $\operatorname {Spa}(B(J))\to \operatorname {Spa}(B(J'))$ is an isomorphism onto a rational open domain of
$\operatorname {Spa}(B(J))\to \operatorname {Spa}(B(J'))$ is an isomorphism onto a rational open domain of ![]() $\operatorname {Spa}(B(J'))$. Thus, the inductive system
$\operatorname {Spa}(B(J'))$. Thus, the inductive system ![]() $\{\operatorname {Spa}(B(J))\}$ indexed by all finitely generated ideals of definition of
$\{\operatorname {Spa}(B(J))\}$ indexed by all finitely generated ideals of definition of ![]() $B$ gives a well-defined adic space
$B$ gives a well-defined adic space ![]() $\varinjlim _J \operatorname {Spa}(B(J))$. As this system admits compatible maps to
$\varinjlim _J \operatorname {Spa}(B(J))$. As this system admits compatible maps to ![]() $\mathfrak {X}_\eta$, we obtain a morphism of rigid
$\mathfrak {X}_\eta$, we obtain a morphism of rigid ![]() $K$-spaces
$K$-spaces
One then has the following concrete description of the generic fiber ![]() $\mathfrak {X}_\eta$.
$\mathfrak {X}_\eta$.
Lemma 2.7 (See [Reference Fujiwara and KatoFK18, Chapter II, Remark 9.6.3])
With notation as in Construction 2.6 the map (2.2.2) is an isomorphism.
Let us note that for any given ideal of definition ![]() $J_0$ of
$J_0$ of ![]() $B$, the set
$B$, the set ![]() $\{J_0^{n}\}$ is cofinal in the set of all ideals of definition of
$\{J_0^{n}\}$ is cofinal in the set of all ideals of definition of ![]() $B$. In particular, in Lemma 2.7 we may replace
$B$. In particular, in Lemma 2.7 we may replace ![]() $\varinjlim _J \operatorname {Spa}(B(J))$ with
$\varinjlim _J \operatorname {Spa}(B(J))$ with ![]() $\varinjlim _n \operatorname {Spa}(B(J_0^{n}))$. We often do this without comment in the following.
$\varinjlim _n \operatorname {Spa}(B(J_0^{n}))$. We often do this without comment in the following.
With this, we can give a more concrete description of the functor of points of the generic fiber in the situation dictated in Construction 2.6. It will enable us to show easily that an étale morphism of formal schemes induces an étale morphism on rigid generic fibers.
Construction 2.8 Let ![]() $\mathfrak {X}=\operatorname {Spf}(B)$ and
$\mathfrak {X}=\operatorname {Spf}(B)$ and ![]() $\mathfrak {X}'=\operatorname {Spf}(B')$ be affine objects of
$\mathfrak {X}'=\operatorname {Spf}(B')$ be affine objects of ![]() $\operatorname {\mathbf {FSch}}^{\mathrm {lfft}}_{\mathcal {O}_K}$ and let
$\operatorname {\mathbf {FSch}}^{\mathrm {lfft}}_{\mathcal {O}_K}$ and let ![]() $\mathfrak {X}'\to \mathfrak {X}$ be a morphism over
$\mathfrak {X}'\to \mathfrak {X}$ be a morphism over ![]() $\mathcal {O}_K$. Let
$\mathcal {O}_K$. Let ![]() $J$ be an ideal of definition of
$J$ be an ideal of definition of ![]() $B$ and let
$B$ and let ![]() $J'$ be an ideal of definition of
$J'$ be an ideal of definition of ![]() $B'$ such that
$B'$ such that ![]() $JB\subseteq J'$ (which exists because
$JB\subseteq J'$ (which exists because ![]() $B\to B'$ is continuous). It is then easy to see that the morphism
$B\to B'$ is continuous). It is then easy to see that the morphism ![]() $\mathfrak {X}'_\eta \to \mathfrak {X}_\eta$ maps
$\mathfrak {X}'_\eta \to \mathfrak {X}_\eta$ maps ![]() $\operatorname {Spa}(B'((J')^{n}))$ into
$\operatorname {Spa}(B'((J')^{n}))$ into ![]() $\operatorname {Spa}(B(J^{n}))$ for all
$\operatorname {Spa}(B(J^{n}))$ for all ![]() $n$.
$n$.
Let ![]() $(R,R^{+})$ be a Huber
$(R,R^{+})$ be a Huber ![]() $(K,\mathcal {O}_K)$-algebra. Then, any morphism
$(K,\mathcal {O}_K)$-algebra. Then, any morphism ![]() $\operatorname {Spa}(R,R^{+})\to \mathfrak {X}_\eta$ of adic spaces over
$\operatorname {Spa}(R,R^{+})\to \mathfrak {X}_\eta$ of adic spaces over ![]() $(K,\mathcal {O}_K)$ must factorize through
$(K,\mathcal {O}_K)$ must factorize through ![]() $\operatorname {Spa}(B(J^{n}))$ for some
$\operatorname {Spa}(B(J^{n}))$ for some ![]() $n$ and, thus, defines a map of Huber pairs
$n$ and, thus, defines a map of Huber pairs ![]() $(B(J^{n}),B(J^{n})^{\circ })\to (R,R^{+})$ which, in turn, defines a continuous map
$(B(J^{n}),B(J^{n})^{\circ })\to (R,R^{+})$ which, in turn, defines a continuous map ![]() $B\to R^{+}$ of
$B\to R^{+}$ of ![]() $\mathcal {O}_K$-algebras independent of the choice of
$\mathcal {O}_K$-algebras independent of the choice of ![]() $n$. Moreover, this map must send
$n$. Moreover, this map must send ![]() $\varpi$ to an element of
$\varpi$ to an element of ![]() $R^{\times }$. Note that one has a natural map
$R^{\times }$. Note that one has a natural map
Indeed, any map ![]() $\operatorname {Spa}(R,R^{+})\to \mathfrak {X}'_\eta$ must factorize through
$\operatorname {Spa}(R,R^{+})\to \mathfrak {X}'_\eta$ must factorize through ![]() $\operatorname {Spa}(B'((J')^{m}))$ for some
$\operatorname {Spa}(B'((J')^{m}))$ for some ![]() $m\geqslant n$ and so defines a map of Huber pairs
$m\geqslant n$ and so defines a map of Huber pairs ![]() $(B'((J')^{m}),B'((J')^{m})^{\circ })\to (R,R^{+})$. This then defines a continuous map
$(B'((J')^{m}),B'((J')^{m})^{\circ })\to (R,R^{+})$. This then defines a continuous map ![]() $B'\to R^{+}$ of
$B'\to R^{+}$ of ![]() $B$-algebras which is independent of
$B$-algebras which is independent of ![]() $m$.
$m$.
Lemma 2.9 With notation as in Construction 2.8, the map
is a functorial bijection. Moreover,
as ![]() $R_0$ runs over the open and bounded
$R_0$ runs over the open and bounded ![]() $B$-subalgebras of
$B$-subalgebras of ![]() $R^{+}$.Footnote 4
$R^{+}$.Footnote 4
With this, we can prove the following.
Proposition 2.10 Let ![]() $f\colon \mathfrak {X}'\to \mathfrak {X}$ be an étale (respectively, finite) morphism in
$f\colon \mathfrak {X}'\to \mathfrak {X}$ be an étale (respectively, finite) morphism in ![]() $\operatorname {\mathbf {FSch}}^{\mathrm {lfft}}_{\mathcal {O}_K}$. Then,
$\operatorname {\mathbf {FSch}}^{\mathrm {lfft}}_{\mathcal {O}_K}$. Then, ![]() $f_\eta \colon \mathfrak {X}'_\eta \to \mathfrak {X}_\eta$ is étale (respectively, finite).
$f_\eta \colon \mathfrak {X}'_\eta \to \mathfrak {X}_\eta$ is étale (respectively, finite).
Proof. We may assume that ![]() $\mathfrak {X}=\operatorname {Spa}(B)$ and
$\mathfrak {X}=\operatorname {Spa}(B)$ and ![]() $\mathfrak {X}'=\operatorname {Spa}(B')$. Suppose first that
$\mathfrak {X}'=\operatorname {Spa}(B')$. Suppose first that ![]() $\mathfrak {X}'\to \mathfrak {X}$ is étale. We deduce from Lemma 2.9 that for any Huber
$\mathfrak {X}'\to \mathfrak {X}$ is étale. We deduce from Lemma 2.9 that for any Huber ![]() $(K,\mathcal {O}_K)$-algebra
$(K,\mathcal {O}_K)$-algebra ![]() $(R,R^{+})$ and square-zero ideal
$(R,R^{+})$ and square-zero ideal ![]() $N$ of
$N$ of ![]() $R$ one has a commutative square
$R$ one has a commutative square

where the horizontal maps are bijections. However, the right vertical arrow is a bijection because ![]() $\mathfrak {X}'\to \mathfrak {X}$ is étale and, thus, the left vertical arrow must also be a bijection. As
$\mathfrak {X}'\to \mathfrak {X}$ is étale and, thus, the left vertical arrow must also be a bijection. As ![]() $f_\eta \colon \mathfrak {X}'_\eta \to \mathfrak {X}_\eta$ is locally of finite type (because both are locally of finite type over
$f_\eta \colon \mathfrak {X}'_\eta \to \mathfrak {X}_\eta$ is locally of finite type (because both are locally of finite type over ![]() $\operatorname {Spa}(K)$) we deduce that
$\operatorname {Spa}(K)$) we deduce that ![]() $f_\eta$ is étale as desired.
$f_\eta$ is étale as desired.
Now suppose that ![]() $f$ is finite, and let
$f$ is finite, and let ![]() $J$ be an ideal of definition of
$J$ be an ideal of definition of ![]() $B$. As
$B$. As ![]() $f$ is adic, the ideal
$f$ is adic, the ideal ![]() $J'=J B'$ is an ideal of definition of
$J'=J B'$ is an ideal of definition of ![]() $B'$. As
$B'$. As ![]() $B \to B'$ is finite,
$B \to B'$ is finite, ![]() $B'\langle {(J')^{n}}/{\varpi }\rangle = B\langle {J^{n}}/{\varpi }\rangle \otimes _B B'$ and it follows that
$B'\langle {(J')^{n}}/{\varpi }\rangle = B\langle {J^{n}}/{\varpi }\rangle \otimes _B B'$ and it follows that ![]() $B'((J')^{n}) = B(J^{n})\otimes _B B'$. Since
$B'((J')^{n}) = B(J^{n})\otimes _B B'$. Since ![]() $\mathfrak {X}'_\eta \to \mathfrak {X}_\eta$ is the colimit of the maps
$\mathfrak {X}'_\eta \to \mathfrak {X}_\eta$ is the colimit of the maps ![]() $\operatorname {Spa}(B'((J')^{n})) \to \operatorname {Spa}(B(J^{n}))$, which are finite by [Reference HuberHub96, Lemma 1.4.5 iv)], it follows that this map is finite, as desired.
$\operatorname {Spa}(B'((J')^{n})) \to \operatorname {Spa}(B(J^{n}))$, which are finite by [Reference HuberHub96, Lemma 1.4.5 iv)], it follows that this map is finite, as desired.
We end this subsection by showing that the generic fiber preserves the partial properness of the special fiber.Footnote 5 Recall here that a morphism of schemes is called partially proper if it is locally of finite type, quasi-separated, and satisfies the valuative criterion for properness (see [SP21, Tag 03IX]). A morphism of rigid ![]() $K$-spaces is called partially proper if it is separated and universally specializing (see [Reference HuberHub96, Definition 1.3.3]).
$K$-spaces is called partially proper if it is separated and universally specializing (see [Reference HuberHub96, Definition 1.3.3]).
Lemma 2.11 Let ![]() $\mathfrak {Y}\to \mathfrak {X}$ be a morphism of admissible formal schemes over
$\mathfrak {Y}\to \mathfrak {X}$ be a morphism of admissible formal schemes over ![]() $\mathcal {O}_K$, and assume that
$\mathcal {O}_K$, and assume that ![]() $\mathfrak {X}$ is quasi-paracompact. If
$\mathfrak {X}$ is quasi-paracompact. If ![]() $\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$ is partially proper, then so is
$\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$ is partially proper, then so is ![]() $\mathfrak {Y}_k\to \mathfrak {X}_k$.
$\mathfrak {Y}_k\to \mathfrak {X}_k$.
Before proving the lemma, we recall some facts about taut spaces. A locally spectral topological space ![]() $X$ is taut if it is quasi-separated and the closure of every quasi-compact open is quasi-compact [Reference HuberHub96, Definition 5.1.2]. It is easy to check that a locally topologically Noetherian space is taut if and only if its irreducible components are quasi-compact. Moreover, if
$X$ is taut if it is quasi-separated and the closure of every quasi-compact open is quasi-compact [Reference HuberHub96, Definition 5.1.2]. It is easy to check that a locally topologically Noetherian space is taut if and only if its irreducible components are quasi-compact. Moreover, if ![]() $X$ is quasi-paracompact and quasi-separated, then
$X$ is quasi-paracompact and quasi-separated, then ![]() $X$ is taut by [Reference HuberHub96, Lemma 5.1.3(ii)]. If
$X$ is taut by [Reference HuberHub96, Lemma 5.1.3(ii)]. If ![]() $Y\to X$ is a partially proper morphism of rigid
$Y\to X$ is a partially proper morphism of rigid ![]() $K$-spaces and
$K$-spaces and ![]() $X$ is taut, then so is
$X$ is taut, then so is ![]() $Y$, by [Reference HuberHub96, Lemma 5.1.4]. Finally, for an admissible formal scheme
$Y$, by [Reference HuberHub96, Lemma 5.1.4]. Finally, for an admissible formal scheme ![]() $\mathfrak {Y}$ over
$\mathfrak {Y}$ over ![]() $\mathcal {O}_K$, because the specialization map
$\mathcal {O}_K$, because the specialization map ![]() $\operatorname {sp}_{\mathfrak {Y}}$ is closed, quasi-compact, and surjective, we deduce that
$\operatorname {sp}_{\mathfrak {Y}}$ is closed, quasi-compact, and surjective, we deduce that ![]() $\mathfrak {Y}_\eta$ is taut if and only if
$\mathfrak {Y}_\eta$ is taut if and only if ![]() $\mathfrak {Y}_k$ is taut.
$\mathfrak {Y}_k$ is taut.
Lemma 2.12 Let ![]() $f\colon Y\to X$ be a separated morphism of schemes locally of finite type over
$f\colon Y\to X$ be a separated morphism of schemes locally of finite type over ![]() $k$ where
$k$ where ![]() $Y$ is taut. Then
$Y$ is taut. Then ![]() $f$ is partially proper if and only if the maps
$f$ is partially proper if and only if the maps
are specializing for all ![]() $n\geqslant 0$.
$n\geqslant 0$.
Proof. The only if direction is clear, because a partially proper map is specializing and being partially proper is stable under base change. To prove the converse, we first claim that ![]() $f$ is partially proper if and only if for all irreducible components
$f$ is partially proper if and only if for all irreducible components ![]() $Z$ of
$Z$ of ![]() $Y$ the map
$Y$ the map ![]() $Z\to X$ is proper. As
$Z\to X$ is proper. As ![]() $Z$ is quasi-compact, evidently if
$Z$ is quasi-compact, evidently if ![]() $Y\to X$ is partially proper, then
$Y\to X$ is partially proper, then ![]() $Z\to X$ is partially proper and, thus, proper (see [SP21, Tag 0BX5]). The converse is clear by thinking about the valuative criterion of properness for
$Z\to X$ is partially proper and, thus, proper (see [SP21, Tag 0BX5]). The converse is clear by thinking about the valuative criterion of properness for ![]() $Y\to X$ because for any valuation ring
$Y\to X$ because for any valuation ring ![]() $V$ with fraction field
$V$ with fraction field ![]() $K$, a map
$K$, a map ![]() $\operatorname {Spec}(K)\to Y$ must factorize through a unique irreducible component of
$\operatorname {Spec}(K)\to Y$ must factorize through a unique irreducible component of ![]() $Y$.
$Y$.
From the above we see that it suffices to show that ![]() $Z\to X$ is proper for all irreducible components
$Z\to X$ is proper for all irreducible components ![]() $Z$ of
$Z$ of ![]() $Y$. However, because
$Y$. However, because ![]() $Z\to X$ is of finite type, by [SP21, Tag 0205] it suffices to show that
$Z\to X$ is of finite type, by [SP21, Tag 0205] it suffices to show that ![]() $Z\times \mathbf {A}^{n}_k \to X\times \mathbf {A}^{n}_k$ is specializing for all
$Z\times \mathbf {A}^{n}_k \to X\times \mathbf {A}^{n}_k$ is specializing for all ![]() $n\geqslant 0$. Since
$n\geqslant 0$. Since ![]() $Z$ is a closed subscheme of
$Z$ is a closed subscheme of ![]() $Y$, a moment's thought reveals that this is implied by the fact that the maps
$Y$, a moment's thought reveals that this is implied by the fact that the maps ![]() $f_n$ are specializing for all
$f_n$ are specializing for all ![]() $n\geqslant 0$.
$n\geqslant 0$.
Proof Proof of Lemma 2.11
As ![]() $f_\eta$ is separated, so is
$f_\eta$ is separated, so is ![]() $f_k$, by [Reference Bosch and LütkebohmertBL93, Proposition 4.7]. As
$f_k$, by [Reference Bosch and LütkebohmertBL93, Proposition 4.7]. As ![]() $\mathfrak {X}_\eta$ is quasi-paracompact and quasi-separated, it is taut, and hence so is
$\mathfrak {X}_\eta$ is quasi-paracompact and quasi-separated, it is taut, and hence so is ![]() $\mathfrak {Y}_\eta$ and therefore also
$\mathfrak {Y}_\eta$ and therefore also ![]() $\mathfrak {Y}_k$. By Lemma 2.12, it suffices to show that
$\mathfrak {Y}_k$. By Lemma 2.12, it suffices to show that ![]() $\mathfrak {Y}_k\times \mathbf {A}^{n}_k\to \mathfrak {X}_k\times \mathbf {A}^{n}_k$ is specializing for all
$\mathfrak {Y}_k\times \mathbf {A}^{n}_k\to \mathfrak {X}_k\times \mathbf {A}^{n}_k$ is specializing for all ![]() $n\geqslant 0$. Replacing
$n\geqslant 0$. Replacing ![]() $f\colon \mathfrak {Y}\to \mathfrak {X}$ with
$f\colon \mathfrak {Y}\to \mathfrak {X}$ with ![]() $\mathfrak {Y}\times \widehat {\mathbf {A}}^{n}_{\mathcal {O}_K}\to \mathfrak {X}\times \widehat {\mathbf {A}}^{n}_{\mathcal {O}_K}$, we are reduced to showing that
$\mathfrak {Y}\times \widehat {\mathbf {A}}^{n}_{\mathcal {O}_K}\to \mathfrak {X}\times \widehat {\mathbf {A}}^{n}_{\mathcal {O}_K}$, we are reduced to showing that ![]() $f_k$ itself is specializing. We have the following commutative square of topological spaces.
$f_k$ itself is specializing. We have the following commutative square of topological spaces.

Here, the horizontal arrows are specializing (because they are closed) and surjective. If the left arrow is specializing, then so is the diagonal composition, and then it is straightforward to check that the right arrow must be specializing as well.
2.3 Tube open subsets
Let ![]() $\mathfrak {X}$ be a formal scheme of finite type over
$\mathfrak {X}$ be a formal scheme of finite type over ![]() $\mathcal {O}_K$ and let
$\mathcal {O}_K$ and let ![]() $Z\subseteq |\mathfrak {X}|$ be a closed subset. We then define the tube open subset of
$Z\subseteq |\mathfrak {X}|$ be a closed subset. We then define the tube open subset of ![]() $\mathfrak {X}_\eta$ associated with
$\mathfrak {X}_\eta$ associated with ![]() $Z$, denoted
$Z$, denoted ![]() $T(\mathfrak {X}\,|\,Z)$, to be the open subset
$T(\mathfrak {X}\,|\,Z)$, to be the open subset ![]() $\operatorname {sp}_\mathfrak {X}^{-1}(Z)^{\circ }$, i.e. the topological interior of
$\operatorname {sp}_\mathfrak {X}^{-1}(Z)^{\circ }$, i.e. the topological interior of ![]() $\operatorname {sp}_\mathfrak {X}^{-1}(Z)$. With the notation
$\operatorname {sp}_\mathfrak {X}^{-1}(Z)$. With the notation ![]() $]Z[$, such opens were first considered by Berthelot in the context of rigid cohomology [Reference BerthelotBer96b]. The following topological properties of tube open subsets of
$]Z[$, such opens were first considered by Berthelot in the context of rigid cohomology [Reference BerthelotBer96b]. The following topological properties of tube open subsets of ![]() $\mathfrak {X}_\eta$ are important for the proof of Theorem 3.7.
$\mathfrak {X}_\eta$ are important for the proof of Theorem 3.7.
Proposition 2.13 Let notation be as before.
(i) The tube open subset
 $T(\mathfrak {X}|Z)$ is an overconvergent open subset.
$T(\mathfrak {X}|Z)$ is an overconvergent open subset.(ii) The tube open subset
 $T(\mathfrak {X}|Z)$ contains every maximal point of
$T(\mathfrak {X}|Z)$ contains every maximal point of  $\operatorname {sp}_\mathfrak {X}^{-1}(Z)$.
$\operatorname {sp}_\mathfrak {X}^{-1}(Z)$.(iii) For any cover
 $\{Z_i\}$ of
$\{Z_i\}$ of  $|\mathfrak {X}|$ by closed subsets, the set of corresponding tube open subsets
$|\mathfrak {X}|$ by closed subsets, the set of corresponding tube open subsets  $\{T(\mathfrak {X}\,|\,Z_i)\}$ forms an overconvergent open cover of
$\{T(\mathfrak {X}\,|\,Z_i)\}$ forms an overconvergent open cover of  $\mathfrak {X}_\eta$.
$\mathfrak {X}_\eta$.
Proof. The proof of the first statement follows by combining [Reference Fujiwara and KatoFK18, Chapter 0, Proposition 2.3.15] and [Reference Fujiwara and KatoFK18, Chapter II, Proposition 4.2.5]. The second statement follows by combining [Reference Fujiwara and KatoFK18, Chapter II, Proposition 4.2.9] and [Reference Fujiwara and KatoFK18, Chapter II, Proposition 4.2.10 (2)]. The final statement is clear because ![]() $\bigcup _i T(\mathfrak {X}\,|\,Z_i)$ is an overconvergent open subset of
$\bigcup _i T(\mathfrak {X}\,|\,Z_i)$ is an overconvergent open subset of ![]() $\mathfrak {X}_\eta$ by the first statement, but also clearly contains every maximal point by the second statement, and thus must be all of
$\mathfrak {X}_\eta$ by the first statement, but also clearly contains every maximal point by the second statement, and thus must be all of ![]() $\mathfrak {X}_\eta$ as desired.
$\mathfrak {X}_\eta$ as desired.
We now relate the tube open subset ![]() $T(\mathfrak {X}\,|\,Z)$ with the generic fiber
$T(\mathfrak {X}\,|\,Z)$ with the generic fiber ![]() $(\widehat {\mathfrak {X}}_{Z})_\eta$ of the formal completion of
$(\widehat {\mathfrak {X}}_{Z})_\eta$ of the formal completion of ![]() $\mathfrak {X}$ along
$\mathfrak {X}$ along ![]() $Z$.
$Z$.
Proposition 2.14 Let ![]() $\mathfrak {X}$ be a formal scheme of finite type over
$\mathfrak {X}$ be a formal scheme of finite type over ![]() $\mathcal {O}_K$ and let
$\mathcal {O}_K$ and let ![]() $Z\subseteq |\mathfrak {X}|$ be a closed subset. The map of rigid
$Z\subseteq |\mathfrak {X}|$ be a closed subset. The map of rigid ![]() $K$-spaces
$K$-spaces ![]() $(\widehat {\mathfrak {X}}_Z)_\eta \to \mathfrak {X}_\eta$ induced by
$(\widehat {\mathfrak {X}}_Z)_\eta \to \mathfrak {X}_\eta$ induced by ![]() $\widehat {\mathfrak {X}}_Z\to \mathfrak {X}$ is an open immersion with image
$\widehat {\mathfrak {X}}_Z\to \mathfrak {X}$ is an open immersion with image ![]() $T(\mathfrak {X}\,|\,Z)$.
$T(\mathfrak {X}\,|\,Z)$.
Proof. Let us first verify that ![]() $(\widehat {\mathfrak {X}}_Z)_\eta \to \mathfrak {X}_\eta$ is an open immersion. By working on an affine open cover we may assume that
$(\widehat {\mathfrak {X}}_Z)_\eta \to \mathfrak {X}_\eta$ is an open immersion. By working on an affine open cover we may assume that ![]() $\mathfrak {X}=\operatorname {Spf}(A)$ and that
$\mathfrak {X}=\operatorname {Spf}(A)$ and that ![]() $J$ is an admissible ideal of
$J$ is an admissible ideal of ![]() $A$ such that
$A$ such that ![]() $\underline {\operatorname {Spf}(A/J)}=Z$. However, we know that
$\underline {\operatorname {Spf}(A/J)}=Z$. However, we know that ![]() $\widehat {\mathfrak {X}}_Z=\operatorname {Spf}(B)$ where
$\widehat {\mathfrak {X}}_Z=\operatorname {Spf}(B)$ where ![]() $B$ is the
$B$ is the ![]() $J$-adic completion of
$J$-adic completion of ![]() $A$. One can then directly check that, in the notation of Construction 2.6 that each
$A$. One can then directly check that, in the notation of Construction 2.6 that each ![]() $(B(J^{n}),B(J^{n})^{+})$ is a rational localization of
$(B(J^{n}),B(J^{n})^{+})$ is a rational localization of ![]() $(A_K, A_K^{\circ })$ and, thus, we see from Lemma 2.7 that the map
$(A_K, A_K^{\circ })$ and, thus, we see from Lemma 2.7 that the map ![]() $\mathfrak {X}_\eta \to \operatorname {Spa}(A_K)=\operatorname {Spf}(A)_\eta$ is an open immersion.
$\mathfrak {X}_\eta \to \operatorname {Spa}(A_K)=\operatorname {Spf}(A)_\eta$ is an open immersion.
Thus, to show our desired claim it suffices to show that for any quasi-compact and quasi-separated open subset ![]() $U$ of
$U$ of ![]() $\mathfrak {X}_\eta$ that the map
$\mathfrak {X}_\eta$ that the map ![]() $j\colon U\to \mathfrak {X}_\eta$ factorizes through
$j\colon U\to \mathfrak {X}_\eta$ factorizes through ![]() $T(\mathfrak {X}\,|\,Z)$ if and only if it factorizes through
$T(\mathfrak {X}\,|\,Z)$ if and only if it factorizes through ![]() $(\widehat {\mathfrak {X}}_Z)_\eta$. However,
$(\widehat {\mathfrak {X}}_Z)_\eta$. However, ![]() $j$ factorizes through
$j$ factorizes through ![]() $T(\mathfrak {X}\,|\,Z)$ if and only if there exists a morphism of admissible formal schemes
$T(\mathfrak {X}\,|\,Z)$ if and only if there exists a morphism of admissible formal schemes ![]() $\mathfrak {j}\colon \mathfrak {U}\to \mathfrak {X}$ such that
$\mathfrak {j}\colon \mathfrak {U}\to \mathfrak {X}$ such that ![]() $j=\mathfrak {j}_\eta$ and
$j=\mathfrak {j}_\eta$ and ![]() $\mathfrak {j}(|\mathfrak {U}|)\subseteq Z$. However, by combining Propositions 2.3 and 2.5 this is also precisely the condition for
$\mathfrak {j}(|\mathfrak {U}|)\subseteq Z$. However, by combining Propositions 2.3 and 2.5 this is also precisely the condition for ![]() $j$ to factorize through
$j$ to factorize through ![]() $(\widehat {\mathfrak {X}}_Z)_\eta$.
$(\widehat {\mathfrak {X}}_Z)_\eta$.
3. The specialization map
In this section we produce the specialization map from the de Jong fundamental group of the rigid generic fiber of a formal scheme to the pro-étale fundamental group of its special fiber.
3.1 Geometric coverings
We briefly recall the theory of the pro-étale fundamental group [Reference Bhatt and ScholzeBS15, § 7], which is based on the following notion of a covering space.
Definition 3.1 (See [Reference Bhatt and ScholzeBS15, Definition 7.3.1(3)])
Let ![]() $X$ be a locally topologically Noetherian scheme. A morphism of schemes
$X$ be a locally topologically Noetherian scheme. A morphism of schemes ![]() $Y\to X$ is a geometric covering if it is étale and satisfies the valuative criterion of properness (see [SP21, Tag 03IX]) or equivalently if it is étale and partially proper (see [Reference Bhatt and ScholzeBS15, Remark 7.3.3]). We denote by
$Y\to X$ is a geometric covering if it is étale and satisfies the valuative criterion of properness (see [SP21, Tag 03IX]) or equivalently if it is étale and partially proper (see [Reference Bhatt and ScholzeBS15, Remark 7.3.3]). We denote by ![]() $\operatorname {\mathbf {Cov}}_X$ the category of geometric coverings of
$\operatorname {\mathbf {Cov}}_X$ the category of geometric coverings of ![]() $X$, treated as a full subcategory of
$X$, treated as a full subcategory of ![]() $\operatorname {\mathbf {\acute {E}t}}_X$.
$\operatorname {\mathbf {\acute {E}t}}_X$.
The following lemma plays a pivotal role in the construction of the specialization map.
Lemma 3.2 (See [Reference Bhatt and ScholzeBS15, Lemma 7.4.10] and its proof)
Let ![]() $X$ be a locally topologically Noetherian scheme. If
$X$ be a locally topologically Noetherian scheme. If ![]() $X$ is geometrically unibranch ([SP21, Tag 0BQ2], e.g. normal), then every geometric covering of
$X$ is geometrically unibranch ([SP21, Tag 0BQ2], e.g. normal), then every geometric covering of ![]() $X$ is the disjoint union of finite étale coverings of
$X$ is the disjoint union of finite étale coverings of ![]() $X$.
$X$.
By [Reference Bhatt and ScholzeBS15, Lemma 7.4.1], for a connected and locally topologically Noetherian scheme ![]() $X$ with a geometric point
$X$ with a geometric point ![]() $\overline {x}$, the pair
$\overline {x}$, the pair ![]() $(\operatorname {\mathbf {Cov}}_X,F_{\overline {x}})$ where
$(\operatorname {\mathbf {Cov}}_X,F_{\overline {x}})$ where ![]() $F_{\overline {x}}\colon \operatorname {\mathbf {Cov}}_X\to \operatorname {\mathbf {Set}}$ is the fiber functor at
$F_{\overline {x}}\colon \operatorname {\mathbf {Cov}}_X\to \operatorname {\mathbf {Set}}$ is the fiber functor at ![]() $\overline {x}$, is a tame infinite Galois category (see [Reference Bhatt and ScholzeBS15, § 7.2]). Following [Reference Bhatt and ScholzeBS15, Definition 7.4.2] we denote the fundamental group of
$\overline {x}$, is a tame infinite Galois category (see [Reference Bhatt and ScholzeBS15, § 7.2]). Following [Reference Bhatt and ScholzeBS15, Definition 7.4.2] we denote the fundamental group of ![]() $(\operatorname {\mathbf {Cov}}_X,F_{\overline {x}})$ by
$(\operatorname {\mathbf {Cov}}_X,F_{\overline {x}})$ by ![]() $\pi _1^{{\textrm{pro}}\unicode{x00E9}{\textrm{t}}}(X,\overline {x})$ and call it the pro-étale fundamental group of
$\pi _1^{{\textrm{pro}}\unicode{x00E9}{\textrm{t}}}(X,\overline {x})$ and call it the pro-étale fundamental group of ![]() $X$. By definition, it is a Noohi topological group (see [Reference Bhatt and ScholzeBS15, § 7.1]) for which the induced functor
$X$. By definition, it is a Noohi topological group (see [Reference Bhatt and ScholzeBS15, § 7.1]) for which the induced functor
is an equivalence, where the target is the category of (discrete) sets with a continuous action of ![]() $\pi _1^{{\textrm{pro}}\unicode{x00E9}{\textrm{t}}}(X, \overline {x})$.
$\pi _1^{{\textrm{pro}}\unicode{x00E9}{\textrm{t}}}(X, \overline {x})$.
3.2 Coverings of rigid-analytic spaces
Next, we recall various notions of ‘covering spaces’ of a rigid space, as defined in [Reference Achinger, Lara and YoucisALY21b]. Here, we only use de Jong covering spaces, whereas the more general ![]() $\mathrm {adm}$-covering spaces and
$\mathrm {adm}$-covering spaces and ![]() ${\unicode{x00E9}}{\text{t}}$-covering spaces are needed in the next section.
${\unicode{x00E9}}{\text{t}}$-covering spaces are needed in the next section.
Let ![]() $X$ be a rigid
$X$ be a rigid ![]() $K$-space, and let
$K$-space, and let ![]() $\tau \in \{\mathrm {oc},\mathrm {adm},{\unicode{x00E9}}{\text{t}}\}$. By a
$\tau \in \{\mathrm {oc},\mathrm {adm},{\unicode{x00E9}}{\text{t}}\}$. By a ![]() $\tau$-cover of
$\tau$-cover of ![]() $X$ we shall mean a surjective morphism
$X$ we shall mean a surjective morphism ![]() $U\to X$ such that:
$U\to X$ such that:
(i) if
 $\tau =\mathrm {oc}$, then
$\tau =\mathrm {oc}$, then  $U\to X$ is the disjoint union of overconvergent open immersions into
$U\to X$ is the disjoint union of overconvergent open immersions into  $X$;
$X$;(ii) if
 $\tau =\mathrm {adm}$, then
$\tau =\mathrm {adm}$, then  $U\to X$ is the disjoint union of open immersions into
$U\to X$ is the disjoint union of open immersions into  $X$;
$X$;(iii) if
 $\tau ={\unicode{x00E9}}{\text{t}}$, then
$\tau ={\unicode{x00E9}}{\text{t}}$, then  $U\to X$ is étale.
$U\to X$ is étale.
Definition 3.3 Let ![]() $X$ be a rigid
$X$ be a rigid ![]() $K$-space, and let
$K$-space, and let ![]() $\tau \in \{\mathrm {oc},\mathrm {adm},{\unicode{x00E9}}{\text{t}}\}$. By a
$\tau \in \{\mathrm {oc},\mathrm {adm},{\unicode{x00E9}}{\text{t}}\}$. By a ![]() $\tau$-covering space of
$\tau$-covering space of ![]() $X$ we mean a morphism
$X$ we mean a morphism ![]() $Y\to X$ for which there exists a
$Y\to X$ for which there exists a ![]() $\tau$-cover
$\tau$-cover ![]() $U\to X$ such that
$U\to X$ such that ![]() $Y_U\to U$ is the disjoint union of finite étale coverings of
$Y_U\to U$ is the disjoint union of finite étale coverings of ![]() $U$. We denote by
$U$. We denote by ![]() $\operatorname {\mathbf {Cov}}_X^{\tau }$ the full subcategory of
$\operatorname {\mathbf {Cov}}_X^{\tau }$ the full subcategory of ![]() $\operatorname {\mathbf {\acute {E}t}}_X$ consisting of
$\operatorname {\mathbf {\acute {E}t}}_X$ consisting of ![]() $\tau$-covering spaces, and by
$\tau$-covering spaces, and by ![]() $\operatorname {\mathbf {UCov}}_X^{\tau }$ the full subcategory of
$\operatorname {\mathbf {UCov}}_X^{\tau }$ the full subcategory of ![]() $\operatorname {\mathbf {\acute {E}t}}_X$ consisting of arbitrary disjoint unions of objects of
$\operatorname {\mathbf {\acute {E}t}}_X$ consisting of arbitrary disjoint unions of objects of ![]() $\operatorname {\mathbf {Cov}}_X^{\tau }$.
$\operatorname {\mathbf {Cov}}_X^{\tau }$.
Remark 3.4 It is not difficult to see, and already pointed out by de Jong, that de Jong covering spaces are not closed under disjoint unions. Let us indicate an example for ![]() $\mathrm {adm}$-covering spaces, using a variant of the construction in [Reference Achinger, Lara and YoucisALY21b, § 2] (see also Example 4.7). Let
$\mathrm {adm}$-covering spaces, using a variant of the construction in [Reference Achinger, Lara and YoucisALY21b, § 2] (see also Example 4.7). Let ![]() $X$ be the annulus
$X$ be the annulus ![]() $\{1\leq |x|\leq |\varpi |^{-1}\}\subseteq \mathbf {A}^{1, {\rm an}}_K$ where
$\{1\leq |x|\leq |\varpi |^{-1}\}\subseteq \mathbf {A}^{1, {\rm an}}_K$ where ![]() $K$ is of equal characteristic
$K$ is of equal characteristic ![]() $p$. For
$p$. For ![]() $n\geq 1$, let
$n\geq 1$, let ![]() $U_n^{-}$ be the subannulus
$U_n^{-}$ be the subannulus ![]() $\{1\leq |x|\leq |\varpi |^{-1/n}\}$ and let
$\{1\leq |x|\leq |\varpi |^{-1/n}\}$ and let ![]() $U_n^{+} = \{|\varpi |^{-1/n}\leq |x|\leq |\varpi |^{-1}\}$. For each
$U_n^{+} = \{|\varpi |^{-1/n}\leq |x|\leq |\varpi |^{-1}\}$. For each ![]() $n$, we perform a construction analogous to that of [Reference Achinger, Lara and YoucisALY21b, § 2] using the affinoid cover
$n$, we perform a construction analogous to that of [Reference Achinger, Lara and YoucisALY21b, § 2] using the affinoid cover ![]() $X=U_n^{-}\cup U_n^{+}$, obtaining an
$X=U_n^{-}\cup U_n^{+}$, obtaining an ![]() $\mathrm {adm}$-cover
$\mathrm {adm}$-cover ![]() $Y_n\to X$ which is the disjoint union of finite étale coverings on
$Y_n\to X$ which is the disjoint union of finite étale coverings on ![]() $U_n^{\pm }$. Then
$U_n^{\pm }$. Then ![]() $Y=\coprod _{n\geq 1} Y_n\to X$ is not an
$Y=\coprod _{n\geq 1} Y_n\to X$ is not an ![]() $\mathrm {adm}$-covering space, as the type
$\mathrm {adm}$-covering space, as the type ![]() $5$ point
$5$ point ![]() $\eta _+$ in the closure of the Gauss point
$\eta _+$ in the closure of the Gauss point ![]() $\eta$ of the circle
$\eta$ of the circle ![]() $C=\{|x|=1\}$ does not have a required neighborhood. We leave the details to the reader.
$C=\{|x|=1\}$ does not have a required neighborhood. We leave the details to the reader.
When ![]() $X$ is a taut rigid
$X$ is a taut rigid ![]() $K$-space (see [Reference HuberHub96, Definition 5.1.2]), then
$K$-space (see [Reference HuberHub96, Definition 5.1.2]), then ![]() $\operatorname {\mathbf {Cov}}_X^{\mathrm {oc}}$ is naturally equivalent (via the functor in [Reference HuberHub96, § 8.3]) to the category of étale covering spaces of the associated Berkovich space
$\operatorname {\mathbf {Cov}}_X^{\mathrm {oc}}$ is naturally equivalent (via the functor in [Reference HuberHub96, § 8.3]) to the category of étale covering spaces of the associated Berkovich space ![]() $X^{\mathrm {Berk}}$ considered in [Reference de JongdJ95b]. Thus, we refer to
$X^{\mathrm {Berk}}$ considered in [Reference de JongdJ95b]. Thus, we refer to ![]() $\text {oc}$-covering spaces as de Jong covering spaces.
$\text {oc}$-covering spaces as de Jong covering spaces.
For a geometric point ![]() $\overline {x}$ let
$\overline {x}$ let ![]() $F_{\overline {x}}\colon \operatorname {\mathbf {\acute {E}t}}_X\to \operatorname {\mathbf {Set}}$ be the fiber functor
$F_{\overline {x}}\colon \operatorname {\mathbf {\acute {E}t}}_X\to \operatorname {\mathbf {Set}}$ be the fiber functor ![]() $F_{\overline {x}}(Y)=\pi _0(Y_{\overline {x}})$. For a connected rigid
$F_{\overline {x}}(Y)=\pi _0(Y_{\overline {x}})$. For a connected rigid ![]() $K$-space
$K$-space ![]() $X$ and
$X$ and ![]() $\tau =\mathrm {oc}$, de Jong essentially showed that the pair
$\tau =\mathrm {oc}$, de Jong essentially showed that the pair ![]() $(\operatorname {\mathbf {UCov}}^{\mathrm {oc}}_X,F_{\overline {x}})$ is a tame infinite Galois category (see [Reference de JongdJ95b, Theorem 2.9]). More generally, for a connected rigid
$(\operatorname {\mathbf {UCov}}^{\mathrm {oc}}_X,F_{\overline {x}})$ is a tame infinite Galois category (see [Reference de JongdJ95b, Theorem 2.9]). More generally, for a connected rigid ![]() $K$-space
$K$-space ![]() $X$ one knows from [Reference Achinger, Lara and YoucisALY21b, Theorem 2] that the pair
$X$ one knows from [Reference Achinger, Lara and YoucisALY21b, Theorem 2] that the pair ![]() $(\operatorname {\mathbf {UCov}}^{\tau }_X,F_{\overline {x}})$ is a tame infinite Galois category for each
$(\operatorname {\mathbf {UCov}}^{\tau }_X,F_{\overline {x}})$ is a tame infinite Galois category for each ![]() $\tau \in \{\mathrm {oc},\mathrm {adm},{\unicode{x00E9}}{\text{t}}\}$. In particular, we have an equivalence of categories
$\tau \in \{\mathrm {oc},\mathrm {adm},{\unicode{x00E9}}{\text{t}}\}$. In particular, we have an equivalence of categories
We denote the fundamental group of ![]() $(\operatorname {\mathbf {UCov}}^{\mathrm {oc}}_X,F_{\overline {x}})$ by
$(\operatorname {\mathbf {UCov}}^{\mathrm {oc}}_X,F_{\overline {x}})$ by ![]() $\pi _1^{\mathrm {dJ}}(X,\overline {x})$ and call it the de Jong fundamental group.
$\pi _1^{\mathrm {dJ}}(X,\overline {x})$ and call it the de Jong fundamental group.
One of the upshots of the material discussed and developed in § 2 is the ability to prove the following criterion for when the rigid generic fiber of an étale map of formal schemes is a de Jong covering space.
Proposition 3.5 (Overconvergence criterion)
Let ![]() $\mathfrak {Y}\to \mathfrak {X}$ be a morphism of admissible formal schemes over
$\mathfrak {Y}\to \mathfrak {X}$ be a morphism of admissible formal schemes over ![]() $\mathcal {O}_K$ with
$\mathcal {O}_K$ with ![]() $\mathfrak {X}$ quasi-compact and such that
$\mathfrak {X}$ quasi-compact and such that ![]() $\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$ is étale. Suppose that for each irreducible component
$\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$ is étale. Suppose that for each irreducible component ![]() $Z$ of
$Z$ of ![]() $\mathfrak {X}_k$ one has that
$\mathfrak {X}_k$ one has that ![]() $\mathfrak {Y}_Z$ is a disjoint union of finite
$\mathfrak {Y}_Z$ is a disjoint union of finite ![]() $Z$-schemes. Then,
$Z$-schemes. Then, ![]() $\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$ is a de Jong covering space.
$\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$ is a de Jong covering space.
Proof. Let ![]() $Z_1, \ldots, Z_r$ be the irreducible components of
$Z_1, \ldots, Z_r$ be the irreducible components of ![]() $\mathfrak {X}_k$ and let
$\mathfrak {X}_k$ and let ![]() $\widehat {\mathfrak {X}}_i$ for
$\widehat {\mathfrak {X}}_i$ for ![]() $i=1, \ldots, r$ be the formal completion of
$i=1, \ldots, r$ be the formal completion of ![]() $\mathfrak {X}$ along
$\mathfrak {X}$ along ![]() $Z_i$. As the pullback of
$Z_i$. As the pullback of ![]() $\mathfrak {Y}_{\widehat {\mathfrak {X}}_i}\to \widehat {\mathfrak {X}}_i$ to
$\mathfrak {Y}_{\widehat {\mathfrak {X}}_i}\to \widehat {\mathfrak {X}}_i$ to ![]() $Z_i$ is the disjoint union of finite maps, we know by Proposition 2.4 that the same holds for
$Z_i$ is the disjoint union of finite maps, we know by Proposition 2.4 that the same holds for ![]() $\mathfrak {Y}_{\widehat {\mathfrak {X}}_i}\to \widehat {\mathfrak {X}}_i$. We deduce from Propositions 2.10 and 2.14 that the pullback of
$\mathfrak {Y}_{\widehat {\mathfrak {X}}_i}\to \widehat {\mathfrak {X}}_i$. We deduce from Propositions 2.10 and 2.14 that the pullback of ![]() $\mathfrak {Y}_\eta$ to
$\mathfrak {Y}_\eta$ to ![]() $T(\mathfrak {X}\,|\,Z_i)$ is the disjoint union of finite étale coverings (étale by our assumption on
$T(\mathfrak {X}\,|\,Z_i)$ is the disjoint union of finite étale coverings (étale by our assumption on ![]() $\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$) for all
$\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$) for all ![]() $i$. As
$i$. As ![]() $\{T(\mathfrak {X}\,|\,Z_i)\}$ is an overconvergent open cover of
$\{T(\mathfrak {X}\,|\,Z_i)\}$ is an overconvergent open cover of ![]() $\mathfrak {X}_\eta$ by Proposition 2.13 we are done.
$\mathfrak {X}_\eta$ by Proposition 2.13 we are done.
3.3 The étale site of a formal scheme
We now recall the topological invariance of the étale site of a formal scheme.
Proposition 3.6 Let ![]() $\mathfrak {X}'\to \mathfrak {X}$ be a universal homeomorphism of formal schemes. Then, the induced functor
$\mathfrak {X}'\to \mathfrak {X}$ be a universal homeomorphism of formal schemes. Then, the induced functor ![]() $\operatorname {\mathbf {\acute {E}t}}_\mathfrak {X}\to \operatorname {\mathbf {\acute {E}t}}_{\mathfrak {X}'}$ is an equivalence. In particular, the functor
$\operatorname {\mathbf {\acute {E}t}}_\mathfrak {X}\to \operatorname {\mathbf {\acute {E}t}}_{\mathfrak {X}'}$ is an equivalence. In particular, the functor ![]() $\operatorname {\mathbf {\acute {E}t}}_{\mathfrak {X}}\to \operatorname {\mathbf {\acute {E}t}}_{\underline {\mathfrak {X}}}$ is an equivalence, and if
$\operatorname {\mathbf {\acute {E}t}}_{\mathfrak {X}}\to \operatorname {\mathbf {\acute {E}t}}_{\underline {\mathfrak {X}}}$ is an equivalence, and if ![]() $\mathfrak {X}$ is an adic formal scheme over
$\mathfrak {X}$ is an adic formal scheme over ![]() $\mathcal {O}_K$, then
$\mathcal {O}_K$, then ![]() $\operatorname {\mathbf {\acute {E}t}}_{\mathfrak {X}}\to \operatorname {\mathbf {\acute {E}t}}_{\mathfrak {X}_k}$ is an equivalence.
$\operatorname {\mathbf {\acute {E}t}}_{\mathfrak {X}}\to \operatorname {\mathbf {\acute {E}t}}_{\mathfrak {X}_k}$ is an equivalence.
Proof. Note that because ![]() $\mathfrak {X}'\to \mathfrak {X}$ is a universal homeomorphism, so then is the morphism of schemes
$\mathfrak {X}'\to \mathfrak {X}$ is a universal homeomorphism, so then is the morphism of schemes ![]() $\underline {\mathfrak {X}}'\to \underline {\mathfrak {X}}$. Thus, the induced morphism
$\underline {\mathfrak {X}}'\to \underline {\mathfrak {X}}$. Thus, the induced morphism ![]() $\operatorname {\mathbf {\acute {E}t}}_{\underline {\mathfrak {X}}}\to \operatorname {\mathbf {\acute {E}t}}_{\underline {\mathfrak {X}}'}$ is an equivalence by [SP21, Tag 04DZ]. This clearly then reduces us to showing that, in general, the map
$\operatorname {\mathbf {\acute {E}t}}_{\underline {\mathfrak {X}}}\to \operatorname {\mathbf {\acute {E}t}}_{\underline {\mathfrak {X}}'}$ is an equivalence by [SP21, Tag 04DZ]. This clearly then reduces us to showing that, in general, the map ![]() $\operatorname {\mathbf {\acute {E}t}}_{\mathfrak {X}}\to \operatorname {\mathbf {\acute {E}t}}_{\underline {\mathfrak {X}}}$ is an equivalence. This assertion is clearly local on
$\operatorname {\mathbf {\acute {E}t}}_{\mathfrak {X}}\to \operatorname {\mathbf {\acute {E}t}}_{\underline {\mathfrak {X}}}$ is an equivalence. This assertion is clearly local on ![]() $\mathfrak {X}$ and so we may assume without loss of generality that
$\mathfrak {X}$ and so we may assume without loss of generality that ![]() $\mathfrak {X}$ is quasi-compact and quasi-separated and, hence, has an ideal sheaf of definition
$\mathfrak {X}$ is quasi-compact and quasi-separated and, hence, has an ideal sheaf of definition ![]() $\mathcal {I}$. As the map of schemes
$\mathcal {I}$. As the map of schemes ![]() $\underline {\mathfrak {X}}\to \mathfrak {X}(\mathcal {I})$ induces an equivalence on étale sites by [SP21, Tag 04DZ] we are reduced to showing that the map
$\underline {\mathfrak {X}}\to \mathfrak {X}(\mathcal {I})$ induces an equivalence on étale sites by [SP21, Tag 04DZ] we are reduced to showing that the map ![]() $\operatorname {\mathbf {\acute {E}t}}_\mathfrak {X}\to \operatorname {\mathbf {\acute {E}t}}_{\mathfrak {X}(\mathcal {I})}$ is an equivalence. However, this follows by combining [SP21, Tag 04DZ] and [Reference Fujiwara and KatoFK18, Chapter I, Proposition 1.4.2] because
$\operatorname {\mathbf {\acute {E}t}}_\mathfrak {X}\to \operatorname {\mathbf {\acute {E}t}}_{\mathfrak {X}(\mathcal {I})}$ is an equivalence. However, this follows by combining [SP21, Tag 04DZ] and [Reference Fujiwara and KatoFK18, Chapter I, Proposition 1.4.2] because ![]() $\mathfrak {X}=\varinjlim \mathfrak {X}(\mathcal {I}^{n})$ and each
$\mathfrak {X}=\varinjlim \mathfrak {X}(\mathcal {I}^{n})$ and each ![]() $\mathfrak {X}(\mathcal {I}^{n})\to \mathfrak {X}(\mathcal {I}^{n+1})$ is a thickening of schemes.
$\mathfrak {X}(\mathcal {I}^{n})\to \mathfrak {X}(\mathcal {I}^{n+1})$ is a thickening of schemes.
3.4 Statement of the main result
Let ![]() $\mathfrak {X}$ be a formal scheme locally of finite type over
$\mathfrak {X}$ be a formal scheme locally of finite type over ![]() $\mathcal {O}_K$ and let
$\mathcal {O}_K$ and let ![]() $X=\mathfrak {X}_\eta$ be its rigid generic fiber. We have the functors between the categories of étale objects
$X=\mathfrak {X}_\eta$ be its rigid generic fiber. We have the functors between the categories of étale objects
where ![]() $(-)_\eta$ (respectively,
$(-)_\eta$ (respectively, ![]() $(-)_k$) is the functor which maps
$(-)_k$) is the functor which maps ![]() $\mathfrak {Y}\to \mathfrak {X}$ to
$\mathfrak {Y}\to \mathfrak {X}$ to ![]() $\mathfrak {Y}_{\eta }\to \mathfrak {X}_{\eta }=X$ (respectively,
$\mathfrak {Y}_{\eta }\to \mathfrak {X}_{\eta }=X$ (respectively, ![]() $\mathfrak {Y}_k\to \mathfrak {X}_k$). The functor
$\mathfrak {Y}_k\to \mathfrak {X}_k$). The functor ![]() $(-)_k$ is an equivalence by Proposition 3.6. Let us denote by
$(-)_k$ is an equivalence by Proposition 3.6. Let us denote by
the composition ![]() $u=(-)_\eta \circ (-)_k^{-1}$. The main result of this section can then be stated as follows.
$u=(-)_\eta \circ (-)_k^{-1}$. The main result of this section can then be stated as follows.
Theorem 3.7 Let ![]() $\mathfrak {X}$ be a quasi-paracompact formal scheme locally of finite type over
$\mathfrak {X}$ be a quasi-paracompact formal scheme locally of finite type over ![]() $\mathcal {O}_K$ and let
$\mathcal {O}_K$ and let ![]() $X=\mathfrak {X}_\eta$. Then, the functor
$X=\mathfrak {X}_\eta$. Then, the functor ![]() $u$ maps
$u$ maps ![]() $\operatorname {\mathbf {Cov}}_{\mathfrak {X}_k}$ into
$\operatorname {\mathbf {Cov}}_{\mathfrak {X}_k}$ into ![]() $\operatorname {\mathbf {Cov}}^{\mathrm {oc}}_X$.
$\operatorname {\mathbf {Cov}}^{\mathrm {oc}}_X$.
Let us interpret this result in terms of fundamental groups. To this end, we first need to discuss compatible choices of base points for ![]() $\mathfrak {X}_k$ and
$\mathfrak {X}_k$ and ![]() $X$. Let
$X$. Let ![]() $L$ be an algebraically closed non-archimedean field and let
$L$ be an algebraically closed non-archimedean field and let ![]() $\overline {\xi }\colon \operatorname {Spf}(\mathcal {O}_L)\to \mathfrak {X}$ be a morphism of formal schemes, inducing geometric points
$\overline {\xi }\colon \operatorname {Spf}(\mathcal {O}_L)\to \mathfrak {X}$ be a morphism of formal schemes, inducing geometric points ![]() $\overline {\xi }_\eta \colon \operatorname {Spa}(L)\to X$ and
$\overline {\xi }_\eta \colon \operatorname {Spa}(L)\to X$ and ![]() $\overline {\xi }_0\colon \operatorname {Spec}(\ell )\to \mathfrak {X}_k$, where
$\overline {\xi }_0\colon \operatorname {Spec}(\ell )\to \mathfrak {X}_k$, where ![]() $\ell = \mathcal {O}_L/\mathfrak {m}_L$ is the residue field of
$\ell = \mathcal {O}_L/\mathfrak {m}_L$ is the residue field of ![]() $L$. In this situation, if
$L$. In this situation, if ![]() $\mathfrak {Y}\to \mathfrak {X}$ is an étale morphism, then the induced maps
$\mathfrak {Y}\to \mathfrak {X}$ is an étale morphism, then the induced maps
are bijective. To see this, we may replace ![]() $\mathfrak {X}$ with
$\mathfrak {X}$ with ![]() $\operatorname {Spf}(\mathcal {O}_L)$, and then it suffices to show that every étale morphism
$\operatorname {Spf}(\mathcal {O}_L)$, and then it suffices to show that every étale morphism ![]() $\mathfrak {Y}\to \mathfrak {X}$ is a disjoint union of copies of
$\mathfrak {Y}\to \mathfrak {X}$ is a disjoint union of copies of ![]() $\mathfrak {X}$. This follows from Proposition 3.6 because
$\mathfrak {X}$. This follows from Proposition 3.6 because ![]() $\underline {\mathfrak {X}}=\operatorname {Spec}(\ell )$.
$\underline {\mathfrak {X}}=\operatorname {Spec}(\ell )$.
Corollary 3.8 Let ![]() $\mathfrak {X}$ be a quasi-paracompact formal scheme locally of finite type over
$\mathfrak {X}$ be a quasi-paracompact formal scheme locally of finite type over ![]() $\mathcal {O}_K$ whose special fiber
$\mathcal {O}_K$ whose special fiber ![]() $\mathfrak {X}_k$ and rigid generic fiber
$\mathfrak {X}_k$ and rigid generic fiber ![]() $X=\mathfrak {X}_\eta$ are both connected. Then for a compatible choice of base points as previously discussed, the functor
$X=\mathfrak {X}_\eta$ are both connected. Then for a compatible choice of base points as previously discussed, the functor ![]() $u$ induces a continuous homomorphism of Noohi groups
$u$ induces a continuous homomorphism of Noohi groups
Its image is dense if ![]() $\mathfrak {X}$ is
$\mathfrak {X}$ is ![]() $\eta$-normal (see Appendix A).
$\eta$-normal (see Appendix A).
Proof. Given Theorem 3.7, the existence of the specialization map is immediate from [Reference Bhatt and ScholzeBS15, Theorem 7.2.5 2.], because by the previous discussion there is a natural identification of geometric fibers ![]() $F_{\overline {\xi }_\eta }(u(Y)) \simeq F_{\overline {\xi }_0}(Y)$.
$F_{\overline {\xi }_\eta }(u(Y)) \simeq F_{\overline {\xi }_0}(Y)$.
The only part left to be justified is the claim of dense image. Note that by [Reference LaraLar19, Proposition 2.37.(2)] and the proof of [Reference Achinger, Lara and YoucisALY21a, Proposition 5.4.5] it suffices to show that if ![]() $Y\to \mathfrak {X}_k$ is a connected geometric covering and
$Y\to \mathfrak {X}_k$ is a connected geometric covering and ![]() $\mathfrak {Y}\to \mathfrak {X}$ its unique étale deformation, then
$\mathfrak {Y}\to \mathfrak {X}$ its unique étale deformation, then ![]() $\mathfrak {Y}_\eta =u(Y)$ is connected. However, because
$\mathfrak {Y}_\eta =u(Y)$ is connected. However, because ![]() $\mathfrak {Y}\to \mathfrak {X}$ is étale, the formal scheme
$\mathfrak {Y}\to \mathfrak {X}$ is étale, the formal scheme ![]() $\mathfrak {Y}$ is
$\mathfrak {Y}$ is ![]() $\eta$-normal by Proposition A.16, and we use Lemma A.3 to conclude.
$\eta$-normal by Proposition A.16, and we use Lemma A.3 to conclude.
The natural converse to Theorem 3.7 is relatively straightforward given our setup, and we obtain the following (cf. [Reference Fujiwara and KatoFK18, Chapter II, Theorem 7.5.17]).
Corollary 3.9 Let ![]() $\mathfrak {Y}\to \mathfrak {X}$ be an étale map of admissible formal schemes over
$\mathfrak {Y}\to \mathfrak {X}$ be an étale map of admissible formal schemes over ![]() $\mathcal {O}_K$, with
$\mathcal {O}_K$, with ![]() $\mathfrak {X}$ quasi-paracompact. Then, the following are equivalent:
$\mathfrak {X}$ quasi-paracompact. Then, the following are equivalent:
(a)
 $\mathfrak {Y}_k\to \mathfrak {X}_k$ is a geometric covering;
$\mathfrak {Y}_k\to \mathfrak {X}_k$ is a geometric covering;(b)
 $\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$ is a de Jong covering space;
$\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$ is a de Jong covering space;(c)
 $\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$ is partially proper.
$\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$ is partially proper.
Proof. That part (a) implies part (b) is precisely the content of Theorem 3.7. To see that part (b) implies part (c) is simple because being partially proper is local on the target, and evidently a disjoint union of finite étale coverings is partially proper. That part (c) implies part (a) is then given by Lemma 2.11.
Remark 3.10 The following example shows that geometric coverings might not be the disjoint union of finite étale coverings étale locally on the target, illustrating the essential difficulty behind Theorem 3.7. Let ![]() $k$ be an algebraically closed field, and let
$k$ be an algebraically closed field, and let ![]() $X$ be the nodal curve obtained by gluing two copies
$X$ be the nodal curve obtained by gluing two copies ![]() $X^{+}$,
$X^{+}$, ![]() $X^{-}$ of
$X^{-}$ of ![]() $\mathbf {G}_{m,k}$ at a closed point
$\mathbf {G}_{m,k}$ at a closed point ![]() $x$. For
$x$. For ![]() $n\geqslant 0$, let
$n\geqslant 0$, let ![]() $Y^{\pm }_n\to X^{\pm }$ be the connected cyclic covering of degree equal to the
$Y^{\pm }_n\to X^{\pm }$ be the connected cyclic covering of degree equal to the ![]() $n$th prime number. Let
$n$th prime number. Let ![]() $Y^{+} = \coprod _{n\geqslant 0} Y_n^{+}$ and
$Y^{+} = \coprod _{n\geqslant 0} Y_n^{+}$ and ![]() $Y^{-}=\coprod _{n>0} Y_n^{-}$, and let
$Y^{-}=\coprod _{n>0} Y_n^{-}$, and let ![]() $Y\to X$ be the geometric covering of
$Y\to X$ be the geometric covering of ![]() $X$ with
$X$ with ![]() $Y|_{X^{\pm }}\simeq Y^{\pm }$ obtained by identifying the fibers of
$Y|_{X^{\pm }}\simeq Y^{\pm }$ obtained by identifying the fibers of ![]() $Y^{\pm }$ at
$Y^{\pm }$ at ![]() $x$ as in the following picture.
$x$ as in the following picture.

We sketch the proof that ![]() $Y\to X$ is not the disjoint union of finite étale coverings in any étale neighborhood of
$Y\to X$ is not the disjoint union of finite étale coverings in any étale neighborhood of ![]() $x$. It suffices to observe that for a connected quasi-compact étale neighborhood
$x$. It suffices to observe that for a connected quasi-compact étale neighborhood ![]() $U^{\pm }\to X^{\pm }$ of
$U^{\pm }\to X^{\pm }$ of ![]() $x$, the pull-backs
$x$, the pull-backs ![]() $Y^{\pm }_n\times _{X^{\pm }} U^{\pm }\to U^{\pm }$ are connected for almost all
$Y^{\pm }_n\times _{X^{\pm }} U^{\pm }\to U^{\pm }$ are connected for almost all ![]() $n$. However,
$n$. However, ![]() $U^{\pm }$ is an integral curve, and
$U^{\pm }$ is an integral curve, and ![]() $Y^{\pm }_n\times _{X^{\pm }} U^{\pm }$ will be connected as long as the
$Y^{\pm }_n\times _{X^{\pm }} U^{\pm }$ will be connected as long as the ![]() $n$th prime does not divide the degree of the field extension
$n$th prime does not divide the degree of the field extension ![]() $k(U^{\pm })/k(X^{\pm })$.
$k(U^{\pm })/k(X^{\pm })$.
3.5 The proof
The strategy of proof of Theorem 3.7 is to utilize the overconvergence criterion (Proposition 3.5). In particular, if all of the irreducible components of ![]() $\mathfrak {X}_k$ are normal, then we are done by Lemma 3.2. Of course, this condition on the components of
$\mathfrak {X}_k$ are normal, then we are done by Lemma 3.2. Of course, this condition on the components of ![]() $\mathfrak {X}_k$ will rarely be satisfied for a given formal scheme
$\mathfrak {X}_k$ will rarely be satisfied for a given formal scheme ![]() $\mathfrak {X}$.
$\mathfrak {X}$.
To remedy this we perform a suitable admissible blowup ![]() $\mathfrak {X}'\to \mathfrak {X}$ (Proposition 3.13). Namely, even though the normalization
$\mathfrak {X}'\to \mathfrak {X}$ (Proposition 3.13). Namely, even though the normalization ![]() $n(\mathfrak {X}_k)\to \mathfrak {X}_k$ usually does not extend to a proper birational map to
$n(\mathfrak {X}_k)\to \mathfrak {X}_k$ usually does not extend to a proper birational map to ![]() $\mathfrak {X}$, in most situations it is a blowup, and in any case it is dominated by some blowup
$\mathfrak {X}$, in most situations it is a blowup, and in any case it is dominated by some blowup ![]() $W\to \mathfrak {X}_k$. Then, blowing up the same center on
$W\to \mathfrak {X}_k$. Then, blowing up the same center on ![]() $\mathfrak {X}$ gives an admissible blowup
$\mathfrak {X}$ gives an admissible blowup ![]() $\mathfrak {X}'\to \mathfrak {X}$ such that the strict transform of
$\mathfrak {X}'\to \mathfrak {X}$ such that the strict transform of ![]() $\mathfrak {X}_k$ factors through
$\mathfrak {X}_k$ factors through ![]() $n(\mathfrak {X}_k)$. The restriction of a given geometric covering of
$n(\mathfrak {X}_k)$. The restriction of a given geometric covering of ![]() $\mathfrak {X}_k$ to
$\mathfrak {X}_k$ to ![]() $W\subseteq \mathfrak {X}'_k$ is thus the disjoint union of finite étale maps. However, the irreducible components of
$W\subseteq \mathfrak {X}'_k$ is thus the disjoint union of finite étale maps. However, the irreducible components of ![]() $\mathfrak {X}'_k$ belong to two groups: the strict transforms of the irreducible components of
$\mathfrak {X}'_k$ belong to two groups: the strict transforms of the irreducible components of ![]() $\mathfrak {X}_k$, and those whose image in
$\mathfrak {X}_k$, and those whose image in ![]() $\mathfrak {X}_k$ has positive codimension. We handle the latter in a similar way, and the proof proceeds by induction.
$\mathfrak {X}_k$ has positive codimension. We handle the latter in a similar way, and the proof proceeds by induction.
Lemma 3.11 Let ![]() $\mathfrak {X}$ be a quasi-compact admissible formal scheme over
$\mathfrak {X}$ be a quasi-compact admissible formal scheme over ![]() $\mathcal {O}_K$ and let
$\mathcal {O}_K$ and let ![]() $Z_1, \ldots, Z_r$ be closed integral subschemes of
$Z_1, \ldots, Z_r$ be closed integral subschemes of ![]() $\mathfrak {X}_k$ such that
$\mathfrak {X}_k$ such that ![]() $Z_i\not \subseteq Z_j$ for
$Z_i\not \subseteq Z_j$ for ![]() $i\neq j$. Then there exists an admissible blowup
$i\neq j$. Then there exists an admissible blowup ![]() $\mathfrak {X}'\to \mathfrak {X}$ whose center does not contain any
$\mathfrak {X}'\to \mathfrak {X}$ whose center does not contain any ![]() $Z_i$ and such that the strict transforms
$Z_i$ and such that the strict transforms ![]() $Z'_i\to Z_i$ in
$Z'_i\to Z_i$ in ![]() $\mathfrak {X}'$ are birational and factor through the normalization of
$\mathfrak {X}'$ are birational and factor through the normalization of ![]() $Z_i$ for each
$Z_i$ for each ![]() $i=1, \ldots, r$.
$i=1, \ldots, r$.
Birationality of ![]() $Z'_i\to Z_i$ means that the blowup
$Z'_i\to Z_i$ means that the blowup ![]() $\mathfrak {X}'\to \mathfrak {X}$ is an isomorphism in a neighborhood of the generic point of
$\mathfrak {X}'\to \mathfrak {X}$ is an isomorphism in a neighborhood of the generic point of ![]() $Z_i$.
$Z_i$.
Proof of Lemma 3.11 For every ![]() $i$, there is a non-zero quasi-coherent ideal sheaf
$i$, there is a non-zero quasi-coherent ideal sheaf ![]() $J_i\subseteq \mathcal {O}_{Z_i}$ whose blowup
$J_i\subseteq \mathcal {O}_{Z_i}$ whose blowup ![]() $Z''_i\to Z_i$ factors through the normalization of
$Z''_i\to Z_i$ factors through the normalization of ![]() $Z_i$. Indeed, if
$Z_i$. Indeed, if ![]() $U\subseteq Z_i$ is the normal locus [Reference GrothendieckGro65, Scholie 7.8.3(iv)], then the normalization is a proper map which is an isomorphism over
$U\subseteq Z_i$ is the normal locus [Reference GrothendieckGro65, Scholie 7.8.3(iv)], then the normalization is a proper map which is an isomorphism over ![]() $U$ and, hence, is dominated by a
$U$ and, hence, is dominated by a ![]() $U$-admissible blowup (see [SP21, Tag 080K]) by [Reference Raynaud and GrusonRG71, Première partie, Corollaire 5.7.12] (see also [SP21, Tag 081T]). We also denote by
$U$-admissible blowup (see [SP21, Tag 080K]) by [Reference Raynaud and GrusonRG71, Première partie, Corollaire 5.7.12] (see also [SP21, Tag 081T]). We also denote by ![]() $J_i\subseteq \mathcal {O}_{\mathfrak {X}_k}$ the induced quasi-coherent ideal sheaf. By Lemma 3.12 there exist admissible ideal sheaves
$J_i\subseteq \mathcal {O}_{\mathfrak {X}_k}$ the induced quasi-coherent ideal sheaf. By Lemma 3.12 there exist admissible ideal sheaves ![]() $\mathcal {J}_i\subseteq \mathcal {O}_\mathfrak {X}$ with
$\mathcal {J}_i\subseteq \mathcal {O}_\mathfrak {X}$ with ![]() $\mathcal {J}_i\cdot \mathcal {O}_{\mathfrak {X}_k} = J_i$. If
$\mathcal {J}_i\cdot \mathcal {O}_{\mathfrak {X}_k} = J_i$. If ![]() $\mathfrak {X}'_i\to \mathfrak {X}$ is the admissible blowup of
$\mathfrak {X}'_i\to \mathfrak {X}$ is the admissible blowup of ![]() $\mathcal {J}_i$, then
$\mathcal {J}_i$, then ![]() $Z''_i$ is the strict transform of
$Z''_i$ is the strict transform of ![]() $Z_i$ in
$Z_i$ in ![]() $\mathfrak {X}'_i$.
$\mathfrak {X}'_i$.
Let ![]() $\mathcal {J} = \prod _{i=1}^{r} \mathcal {J}_i$ which is again an admissible ideal sheaf by [Reference Fujiwara and KatoFK18, Chapter I, Proposition 3.7.9], and let
$\mathcal {J} = \prod _{i=1}^{r} \mathcal {J}_i$ which is again an admissible ideal sheaf by [Reference Fujiwara and KatoFK18, Chapter I, Proposition 3.7.9], and let ![]() $\mathfrak {X}'\to \mathfrak {X}$ be the corresponding admissible blowup. As the generic point of
$\mathfrak {X}'\to \mathfrak {X}$ be the corresponding admissible blowup. As the generic point of ![]() $Z_i$ does not belong to any other
$Z_i$ does not belong to any other ![]() $Z_j$, the map
$Z_j$, the map ![]() $\mathfrak {X}'\to \mathfrak {X}$ is an isomorphism generically on
$\mathfrak {X}'\to \mathfrak {X}$ is an isomorphism generically on ![]() $Z_i$ and, in particular, the blowup center
$Z_i$ and, in particular, the blowup center ![]() $V(\mathcal {J})$ does not contain any
$V(\mathcal {J})$ does not contain any ![]() $Z_i$. If
$Z_i$. If ![]() $Z'_i$ is the strict transform of
$Z'_i$ is the strict transform of ![]() $Z_i$ in
$Z_i$ in ![]() $\mathfrak {X}'$, then
$\mathfrak {X}'$, then ![]() $Z'_i\to Z_i$ factors through
$Z'_i\to Z_i$ factors through ![]() $Z''_i\to Z_i$ and, hence, through the normalization of
$Z''_i\to Z_i$ and, hence, through the normalization of ![]() $Z_i$.
$Z_i$.
Lemma 3.12 Let ![]() $\mathfrak {X}$ be a formal scheme of finite type over
$\mathfrak {X}$ be a formal scheme of finite type over ![]() $\mathcal {O}_K$ and let
$\mathcal {O}_K$ and let ![]() $\mathcal {J}\subseteq \mathcal {O}_{\mathfrak {X}_k}$ be a coherent ideal sheaf. Then there exists an admissible ideal sheaf
$\mathcal {J}\subseteq \mathcal {O}_{\mathfrak {X}_k}$ be a coherent ideal sheaf. Then there exists an admissible ideal sheaf ![]() $\mathcal {I}\subseteq \mathcal {O}_{\mathfrak {X}}$ such that
$\mathcal {I}\subseteq \mathcal {O}_{\mathfrak {X}}$ such that ![]() $\mathcal {I}\cdot \mathcal {O}_{\mathfrak {X}_k} = \mathcal {J}$.
$\mathcal {I}\cdot \mathcal {O}_{\mathfrak {X}_k} = \mathcal {J}$.
Proof. We start the proof with an observation. Suppose that ![]() $\mathfrak {X}=\operatorname {Spf}(A)$ and let
$\mathfrak {X}=\operatorname {Spf}(A)$ and let ![]() $J=(a_1, \ldots, a_r)\subseteq A_k$ be the ideal corresponding to
$J=(a_1, \ldots, a_r)\subseteq A_k$ be the ideal corresponding to ![]() $\mathcal {J}$. If
$\mathcal {J}$. If ![]() $a'_i\in A$ are liftings of the
$a'_i\in A$ are liftings of the ![]() $a_i$ and
$a_i$ and ![]() $I' = (a'_1, \ldots, a'_r, \varpi ) \subseteq A$, then
$I' = (a'_1, \ldots, a'_r, \varpi ) \subseteq A$, then ![]() $I'$ is an admissible ideal and
$I'$ is an admissible ideal and ![]() $I'A_k=J$, so in particular the result holds if
$I'A_k=J$, so in particular the result holds if ![]() $\mathfrak {X}$ is affine. Moreover, if
$\mathfrak {X}$ is affine. Moreover, if ![]() $I'=(a'_1, \ldots, a'_r, \varpi )$ and
$I'=(a'_1, \ldots, a'_r, \varpi )$ and ![]() $I''=(b'_1, \ldots, b'_s,\varpi )$ are two admissible ideals of
$I''=(b'_1, \ldots, b'_s,\varpi )$ are two admissible ideals of ![]() $A$ with
$A$ with ![]() $I' A_k = J = I''A_k$, then we can write
$I' A_k = J = I''A_k$, then we can write ![]() $b'_i = \sum _j \alpha _{ij} a'_j + \varpi _i \gamma _i$ with
$b'_i = \sum _j \alpha _{ij} a'_j + \varpi _i \gamma _i$ with ![]() $\alpha _{ij}, \gamma _i\in A$ and
$\alpha _{ij}, \gamma _i\in A$ and ![]() $\varpi _i\in \mathfrak {m}_K$. It follows that if
$\varpi _i\in \mathfrak {m}_K$. It follows that if ![]() $(\varpi,\varpi _1, \ldots, \varpi _s)\mathcal {O}_K = (\varpi ')$, then
$(\varpi,\varpi _1, \ldots, \varpi _s)\mathcal {O}_K = (\varpi ')$, then ![]() $I''\subseteq I'+(\varpi ')$. Swapping the roles of
$I''\subseteq I'+(\varpi ')$. Swapping the roles of ![]() $I'$ and
$I'$ and ![]() $I''$, we obtain
$I''$, we obtain ![]() $I'\subseteq I''+(\varpi '')$ for some pseudo-uniformizer
$I'\subseteq I''+(\varpi '')$ for some pseudo-uniformizer ![]() $\varpi ''$. Taking
$\varpi ''$. Taking ![]() $(\omega )=(\varpi ', \varpi '')$, we see that
$(\omega )=(\varpi ', \varpi '')$, we see that ![]() $I'+(\omega ) = I''+(\omega )$ for a suitably chosen pseudo-uniformizer
$I'+(\omega ) = I''+(\omega )$ for a suitably chosen pseudo-uniformizer ![]() $\omega$.
$\omega$.
For the general case, cover ![]() $\mathfrak {X}$ by finitely many affine opens
$\mathfrak {X}$ by finitely many affine opens ![]() $\mathfrak {U}_i=\operatorname {Spf}(A_i)$ and cover the pairwise intersections
$\mathfrak {U}_i=\operatorname {Spf}(A_i)$ and cover the pairwise intersections ![]() $\mathfrak {U}_i\cap \mathfrak {U}_{i'}$ by finitely many affine opens
$\mathfrak {U}_i\cap \mathfrak {U}_{i'}$ by finitely many affine opens ![]() $\mathfrak {U}_{ii'j}=\operatorname {Spf}(A_{ii'j})$. By the previous paragraph, we can find admissible ideals
$\mathfrak {U}_{ii'j}=\operatorname {Spf}(A_{ii'j})$. By the previous paragraph, we can find admissible ideals ![]() $I'_i\subseteq A_i$ such that
$I'_i\subseteq A_i$ such that ![]() $I'_i(A_i)_k$ is the ideal corresponding to
$I'_i(A_i)_k$ is the ideal corresponding to ![]() $\mathcal {J}|_{(\mathfrak {U}_i)_k}$. Moreover, for each triple
$\mathcal {J}|_{(\mathfrak {U}_i)_k}$. Moreover, for each triple ![]() $(i,i',j)$ there exists a pseudo-uniformizer
$(i,i',j)$ there exists a pseudo-uniformizer ![]() $\omega _{ii'j}$ such that
$\omega _{ii'j}$ such that ![]() $I'_i+(\omega _{ii'j})$ and
$I'_i+(\omega _{ii'j})$ and ![]() $I'_{i'}+(\omega _{ii'j})$ generate the same ideal in
$I'_{i'}+(\omega _{ii'j})$ generate the same ideal in ![]() $A_{ii'j}$. If
$A_{ii'j}$. If ![]() $(\omega )=(\omega _{ii'j})_{(i,i',j)}$, then the admissible ideals
$(\omega )=(\omega _{ii'j})_{(i,i',j)}$, then the admissible ideals ![]() $I_i = I'_i + (\omega ) \subseteq A_i$ glue to give the desired admissible ideal sheaf
$I_i = I'_i + (\omega ) \subseteq A_i$ glue to give the desired admissible ideal sheaf ![]() $\mathcal {I}$.
$\mathcal {I}$.
Next, we show that we may iteratively apply Lemma 3.11 to produce an admissible blowup ![]() $\mathfrak {X}'$ of
$\mathfrak {X}'$ of ![]() $\mathfrak {X}$ whose irreducible components factor through the normalizations of their images in
$\mathfrak {X}$ whose irreducible components factor through the normalizations of their images in ![]() $\mathfrak {X}$.
$\mathfrak {X}$.
Proposition 3.13 Let ![]() $\mathfrak {X}$ be a quasi-compact admissible formal scheme over
$\mathfrak {X}$ be a quasi-compact admissible formal scheme over ![]() $\mathcal {O}_K$. Then there exists an admissible blowup
$\mathcal {O}_K$. Then there exists an admissible blowup ![]() $\mathfrak {X}'\to \mathfrak {X}$ such that for every irreducible component
$\mathfrak {X}'\to \mathfrak {X}$ such that for every irreducible component ![]() $Z'$ of
$Z'$ of ![]() $\mathfrak {X}'_k$ with image
$\mathfrak {X}'_k$ with image ![]() $Z\subseteq \mathfrak {X}_k$, the map
$Z\subseteq \mathfrak {X}_k$, the map ![]() $Z'\to Z$ factors through the normalization of
$Z'\to Z$ factors through the normalization of ![]() $Z$.
$Z$.
Proof. We prove by induction on ![]() $n\geqslant 0$ the following statement: there exists an admissible blowup
$n\geqslant 0$ the following statement: there exists an admissible blowup ![]() $\mathfrak {X}'_n\to \mathfrak {X}$ such that the assertion of the proposition holds for all
$\mathfrak {X}'_n\to \mathfrak {X}$ such that the assertion of the proposition holds for all ![]() $Z'$ such that
$Z'$ such that ![]() $\operatorname {codim} Z\leqslant n$. Here codimension means the Krull dimension of the local ring
$\operatorname {codim} Z\leqslant n$. Here codimension means the Krull dimension of the local ring ![]() $\mathcal {O}_{\mathfrak {X}_k, \eta _Z}$ where
$\mathcal {O}_{\mathfrak {X}_k, \eta _Z}$ where ![]() $\eta _Z$ is the generic point of
$\eta _Z$ is the generic point of ![]() $Z$. This claim for
$Z$. This claim for ![]() $n=\dim \mathfrak {X}_k$ will then imply the required assertion.
$n=\dim \mathfrak {X}_k$ will then imply the required assertion.
Starting with ![]() $n=0$, let
$n=0$, let ![]() $Z_1, \ldots, Z_r$ be the irreducible components of
$Z_1, \ldots, Z_r$ be the irreducible components of ![]() $\mathfrak {X}_k$. Clearly
$\mathfrak {X}_k$. Clearly ![]() $Z_i$ is not contained in
$Z_i$ is not contained in ![]() $Z_j$ for
$Z_j$ for ![]() $i\neq j$. Let
$i\neq j$. Let ![]() $\mathfrak {X}'_0\to \mathfrak {X}$ be the admissible blowup given by Lemma 3.11. This blowup is birational at the generic points of the
$\mathfrak {X}'_0\to \mathfrak {X}$ be the admissible blowup given by Lemma 3.11. This blowup is birational at the generic points of the ![]() $Z_i$, and hence every irreducible component of
$Z_i$, and hence every irreducible component of ![]() $(\mathfrak{X}'_0)_k$ which is not the strict transform of some
$(\mathfrak{X}'_0)_k$ which is not the strict transform of some ![]() $Z_i$ has image of codimension at least one. The claim is thus proved for
$Z_i$ has image of codimension at least one. The claim is thus proved for ![]() $n=0$.
$n=0$.
For the induction step from ![]() $n$ to
$n$ to ![]() $n+1$, suppose that we have constructed
$n+1$, suppose that we have constructed ![]() $\mathfrak {X}'_n\to \mathfrak {X}$ as above. Let
$\mathfrak {X}'_n\to \mathfrak {X}$ as above. Let ![]() $Z'_1, \ldots, Z'_r$ be the irreducible components of
$Z'_1, \ldots, Z'_r$ be the irreducible components of ![]() $(\mathfrak {X}'_{n})_k$ whose images
$(\mathfrak {X}'_{n})_k$ whose images ![]() $Z_1, \ldots, Z_r$ in
$Z_1, \ldots, Z_r$ in ![]() $\mathfrak {X}_k$ have codimension exactly
$\mathfrak {X}_k$ have codimension exactly ![]() $n+1$. Again,
$n+1$. Again, ![]() $Z_i$ does not properly contain another
$Z_i$ does not properly contain another ![]() $Z_j$ (we could have
$Z_j$ (we could have ![]() $Z_i=Z_j$ for some
$Z_i=Z_j$ for some ![]() $i\neq j$). Apply Lemma 3.11 to obtain an admissible blowup
$i\neq j$). Apply Lemma 3.11 to obtain an admissible blowup ![]() $\mathfrak {X}''_n\to \mathfrak {X}$ relative to an admissible ideal sheaf
$\mathfrak {X}''_n\to \mathfrak {X}$ relative to an admissible ideal sheaf ![]() $\mathcal {J}$ with
$\mathcal {J}$ with ![]() $\operatorname {codim} V(J)>n+1$ where
$\operatorname {codim} V(J)>n+1$ where ![]() $J=\mathcal {J}\cdot \mathcal {O}_{\mathfrak {X}_k}$. If
$J=\mathcal {J}\cdot \mathcal {O}_{\mathfrak {X}_k}$. If ![]() $\mathfrak {X}'_n$ is the blowup relative to an admissible ideal sheaf
$\mathfrak {X}'_n$ is the blowup relative to an admissible ideal sheaf ![]() $\mathcal {I}$ and
$\mathcal {I}$ and ![]() $\mathfrak {X}''_n$, let us take
$\mathfrak {X}''_n$, let us take ![]() $\mathfrak {X}'_{n+1}\to \mathfrak {X}$ to be the blowup relative to
$\mathfrak {X}'_{n+1}\to \mathfrak {X}$ to be the blowup relative to ![]() $\mathcal {I}\cdot \mathcal {J}$, which is also the blowup of
$\mathcal {I}\cdot \mathcal {J}$, which is also the blowup of ![]() $\mathfrak {X}'_n$ relative to
$\mathfrak {X}'_n$ relative to ![]() $\mathcal {J}\cdot \mathcal {O}_{\mathfrak {X}'}$.
$\mathcal {J}\cdot \mathcal {O}_{\mathfrak {X}'}$.
We check that ![]() $\mathfrak {X}'_{n+1}\to \mathfrak {X}$ satisfies the assertion for codimension
$\mathfrak {X}'_{n+1}\to \mathfrak {X}$ satisfies the assertion for codimension ![]() $n+1$. Let
$n+1$. Let ![]() $Z''$ be an irreducible component of
$Z''$ be an irreducible component of ![]() $(\mathfrak {X}'_{n+1})_k$, and let
$(\mathfrak {X}'_{n+1})_k$, and let ![]() $Z'$ and
$Z'$ and ![]() $Z$ be its images in
$Z$ be its images in ![]() $(\mathfrak {X}'_n)_k$ and
$(\mathfrak {X}'_n)_k$ and ![]() $\mathfrak {X}_k$, respectively. There are four cases to consider:
$\mathfrak {X}_k$, respectively. There are four cases to consider:
(1)
 $Z'$ is an irreducible component of
$Z'$ is an irreducible component of  $(\mathfrak {X}'_n)_k$ and
$(\mathfrak {X}'_n)_k$ and
(a)
 $\operatorname {codim} Z\leqslant n$,
$\operatorname {codim} Z\leqslant n$,(b)
 $\operatorname {codim} Z = n+1$,
$\operatorname {codim} Z = n+1$,(c)
 $\operatorname {codim} Z > n+1$; or
$\operatorname {codim} Z > n+1$; or
(2)
 $Z'$ is not an irreducible component of
$Z'$ is not an irreducible component of  $(\mathfrak {X}'_n)_k$.
$(\mathfrak {X}'_n)_k$.
In case (1a) we are done by the assumed property of ![]() $\mathfrak {X}'_n$, and in case (1c) there is nothing to show. In case (1b), we have
$\mathfrak {X}'_n$, and in case (1c) there is nothing to show. In case (1b), we have ![]() $Z'=Z'_i$ for some
$Z'=Z'_i$ for some ![]() $i$. As the generic point of
$i$. As the generic point of ![]() $Z=Z_i$ is not in
$Z=Z_i$ is not in ![]() $V(J)$, the generic point of
$V(J)$, the generic point of ![]() $Z'$ is not in
$Z'$ is not in ![]() $V(J\cdot \mathcal {O}_{(\mathfrak {X}'_n)_k})$. As
$V(J\cdot \mathcal {O}_{(\mathfrak {X}'_n)_k})$. As ![]() $\mathfrak {X}'_{n+1}\to \mathfrak {X}'_n$ is the blowup at
$\mathfrak {X}'_{n+1}\to \mathfrak {X}'_n$ is the blowup at ![]() $\mathcal {J}\cdot \mathcal {O}_{\mathfrak {X}'_n}$, it is an isomorphism in a neighborhood of the generic point of
$\mathcal {J}\cdot \mathcal {O}_{\mathfrak {X}'_n}$, it is an isomorphism in a neighborhood of the generic point of ![]() $Z'$, and we conclude that
$Z'$, and we conclude that ![]() $Z''$ is the strict transform of
$Z''$ is the strict transform of ![]() $Z'$ in
$Z'$ in ![]() $\mathfrak {X}'_{n+1}$. That is,
$\mathfrak {X}'_{n+1}$. That is, ![]() $Z'' = \operatorname {Bl}_{\mathcal {J}\cdot \mathcal {O}_{Z'}}(Z')$, and so by functoriality it maps to the strict transform
$Z'' = \operatorname {Bl}_{\mathcal {J}\cdot \mathcal {O}_{Z'}}(Z')$, and so by functoriality it maps to the strict transform ![]() $\operatorname {Bl}_{\mathcal {J}\cdot \mathcal {O}_Z}(Z)$ of
$\operatorname {Bl}_{\mathcal {J}\cdot \mathcal {O}_Z}(Z)$ of ![]() $Z$ in
$Z$ in ![]() $\mathfrak {X}''_n$. By construction, the latter factors through the normalization of
$\mathfrak {X}''_n$. By construction, the latter factors through the normalization of ![]() $Z$, and we are done. See the following diagram.
$Z$, and we are done. See the following diagram.

Finally, in case (2), ![]() $Z''$ is contained in the exceptional locus of
$Z''$ is contained in the exceptional locus of ![]() $\mathfrak {X}'_{n+1}\to \mathfrak {X}'_n$, which is contained in the preimage of
$\mathfrak {X}'_{n+1}\to \mathfrak {X}'_n$, which is contained in the preimage of ![]() $V(\mathcal {J})$ in
$V(\mathcal {J})$ in ![]() $\mathfrak {X}'_n$. Thus
$\mathfrak {X}'_n$. Thus ![]() $Z\subseteq V(J)$ and, hence,
$Z\subseteq V(J)$ and, hence, ![]() $\operatorname {codim} Z\geqslant \operatorname {codim} V(J)> n+1$.
$\operatorname {codim} Z\geqslant \operatorname {codim} V(J)> n+1$.
We are now ready to put the pieces together and present the proof of Theorem 3.7.
Proof of Theorem 3.7 We first reduce to the case ![]() $\mathfrak {X}$ is of finite type. As
$\mathfrak {X}$ is of finite type. As ![]() $\mathfrak {X}$ is quasi-paracompact, its rigid generic fiber
$\mathfrak {X}$ is quasi-paracompact, its rigid generic fiber ![]() $X=\mathfrak {X}_\eta$ is quasi-paracompact and quasi-separated and, hence, taut by [Reference Fujiwara and KatoFK18, Chapter 0, Proposition 2.5.15]. Therefore, for each point
$X=\mathfrak {X}_\eta$ is quasi-paracompact and quasi-separated and, hence, taut by [Reference Fujiwara and KatoFK18, Chapter 0, Proposition 2.5.15]. Therefore, for each point ![]() $x\in X$ there exists a quasi-compact open
$x\in X$ there exists a quasi-compact open ![]() $U_x\in X$ which is an overconvergent neighborhood of
$U_x\in X$ which is an overconvergent neighborhood of ![]() $x$, i.e. it contains an overconvergent open containing
$x$, i.e. it contains an overconvergent open containing ![]() $x$ (see [Reference Achinger, Lara and YoucisALY21a, Proposition 2.3.5]). It then suffices to show that for any geometric covering
$x$ (see [Reference Achinger, Lara and YoucisALY21a, Proposition 2.3.5]). It then suffices to show that for any geometric covering ![]() $Y\to \mathfrak {X}_k$ that
$Y\to \mathfrak {X}_k$ that ![]() $u(Y)$ is a de Jong covering space when restricted to
$u(Y)$ is a de Jong covering space when restricted to ![]() $U_x$. As
$U_x$. As ![]() $U_x$ is quasi-compact, by (the proof of) [Reference BoschBos14, Lemma 8.4/5] there exists an admissible blowup
$U_x$ is quasi-compact, by (the proof of) [Reference BoschBos14, Lemma 8.4/5] there exists an admissible blowup ![]() $\mathfrak {X}'\to \mathfrak {X}$ such that
$\mathfrak {X}'\to \mathfrak {X}$ such that ![]() $U_x=\mathfrak {U}'_\eta$ for an open formal subscheme
$U_x=\mathfrak {U}'_\eta$ for an open formal subscheme ![]() $\mathfrak {U}'\subseteq \mathfrak {X}'$. If the result holds for
$\mathfrak {U}'\subseteq \mathfrak {X}'$. If the result holds for ![]() $\mathfrak {U}'$ (which is of finite type) and the base change
$\mathfrak {U}'$ (which is of finite type) and the base change ![]() $Y' = Y\times _{\mathfrak {X}_k} \mathfrak {U}'_k$ of the given geometric covering
$Y' = Y\times _{\mathfrak {X}_k} \mathfrak {U}'_k$ of the given geometric covering ![]() $Y\to \mathfrak {X}_k$, we deduce that
$Y\to \mathfrak {X}_k$, we deduce that ![]() $\mathfrak {Y}'_\eta \to \mathfrak {U}'_\eta = U_x$ is a de Jong covering, where
$\mathfrak {Y}'_\eta \to \mathfrak {U}'_\eta = U_x$ is a de Jong covering, where ![]() $\mathfrak {Y}'\to \mathfrak {U}'$ is the unique étale lifting of
$\mathfrak {Y}'\to \mathfrak {U}'$ is the unique étale lifting of ![]() $Y'\to \mathfrak {U}'_k$. However,
$Y'\to \mathfrak {U}'_k$. However, ![]() $\mathfrak {Y}'_\eta = u(Y)\times _X U_x$, and we conclude.
$\mathfrak {Y}'_\eta = u(Y)\times _X U_x$, and we conclude.
Suppose now that ![]() $\mathfrak {X}$ is of finite type. Blowing up an ideal sheaf of definition, we may assume that
$\mathfrak {X}$ is of finite type. Blowing up an ideal sheaf of definition, we may assume that ![]() $\mathfrak {X}$ is admissible. Proposition 3.13 yields an admissible blowup
$\mathfrak {X}$ is admissible. Proposition 3.13 yields an admissible blowup ![]() $f\colon \mathfrak {X}'\to \mathfrak {X}$ such that for every irreducible component
$f\colon \mathfrak {X}'\to \mathfrak {X}$ such that for every irreducible component ![]() $Z'$ of
$Z'$ of ![]() $\mathfrak {X}'_k$ the induced map
$\mathfrak {X}'_k$ the induced map ![]() $Z'\to \mathfrak {X}'_k\to \mathfrak {X}_k$ factors through a normal scheme
$Z'\to \mathfrak {X}'_k\to \mathfrak {X}_k$ factors through a normal scheme ![]() $Z$ of finite type over
$Z$ of finite type over ![]() $k$. By Lemma 3.1 we know that
$k$. By Lemma 3.1 we know that ![]() $Y_{Z'}$ is the disjoint union of finite étale coverings of
$Y_{Z'}$ is the disjoint union of finite étale coverings of ![]() $Z'$. As
$Z'$. As ![]() $f_\eta$ is an isomorphism, we may identify
$f_\eta$ is an isomorphism, we may identify ![]() $X'=\mathfrak {X}_{\eta }$ with
$X'=\mathfrak {X}_{\eta }$ with ![]() $X$ and we have the following commutative diagram.
$X$ and we have the following commutative diagram.

By Proposition 3.5, the functor ![]() $u'$ maps the image of
$u'$ maps the image of ![]() $f^{*}\colon \operatorname {\mathbf {Cov}}_{\mathfrak {X}_k}\to \operatorname {\mathbf {Cov}}_{\mathfrak {X}'_k}$ into
$f^{*}\colon \operatorname {\mathbf {Cov}}_{\mathfrak {X}_k}\to \operatorname {\mathbf {Cov}}_{\mathfrak {X}'_k}$ into ![]() $\operatorname {\mathbf {Cov}}^{\mathrm {oc}}_{X'}=\operatorname {\mathbf {Cov}}^{\mathrm {oc}}_X$ and, hence,
$\operatorname {\mathbf {Cov}}^{\mathrm {oc}}_{X'}=\operatorname {\mathbf {Cov}}^{\mathrm {oc}}_X$ and, hence, ![]() $u$ sends
$u$ sends ![]() $\operatorname {\mathbf {Cov}}_{\mathfrak {X}_k}$ into
$\operatorname {\mathbf {Cov}}_{\mathfrak {X}_k}$ into ![]() $\operatorname {\mathbf {Cov}}^{\mathrm {oc}}_X$.
$\operatorname {\mathbf {Cov}}^{\mathrm {oc}}_X$.
Remark 3.14 The authors suspect that the above results hold in a greater generality. Namely, let ![]() $\mathfrak {X}$ be a universally rigid-Noetherian formal scheme (in the sense of [Reference Fujiwara and KatoFK18, Chapter I, Definition 2.1.7]) such that
$\mathfrak {X}$ be a universally rigid-Noetherian formal scheme (in the sense of [Reference Fujiwara and KatoFK18, Chapter I, Definition 2.1.7]) such that ![]() $\underline {\mathfrak {X}}$ is topologically Noetherian and universally Japanese (see [SP21, Tag 032R]). There is then still a functor
$\underline {\mathfrak {X}}$ is topologically Noetherian and universally Japanese (see [SP21, Tag 032R]). There is then still a functor ![]() $\operatorname {\mathbf {\acute {E}t}}_{\underline {\mathfrak {X}}}$ to
$\operatorname {\mathbf {\acute {E}t}}_{\underline {\mathfrak {X}}}$ to ![]() $\operatorname {\mathbf {\acute {E}t}}_{\mathfrak {X}_\mathrm {rig}}$ (where
$\operatorname {\mathbf {\acute {E}t}}_{\mathfrak {X}_\mathrm {rig}}$ (where ![]() $\mathfrak {X}_\mathrm {rig}$ is as in [Reference Fujiwara and KatoFK18, Chapter II]), and the same methods should show that
$\mathfrak {X}_\mathrm {rig}$ is as in [Reference Fujiwara and KatoFK18, Chapter II]), and the same methods should show that ![]() $\operatorname {\mathbf {Cov}}_{\underline {\mathfrak {X}}}$ is mapped into
$\operatorname {\mathbf {Cov}}_{\underline {\mathfrak {X}}}$ is mapped into ![]() $\operatorname {\mathbf {Cov}}^{\mathrm {oc}}_{\mathfrak {X}_\mathrm {rig}}$. However, an interpretation of such a result in terms of fundamental groups is clearly missing, because we do not know if for
$\operatorname {\mathbf {Cov}}^{\mathrm {oc}}_{\mathfrak {X}_\mathrm {rig}}$. However, an interpretation of such a result in terms of fundamental groups is clearly missing, because we do not know if for ![]() $\mathfrak {X}_{\rm rig}$ connected the pair
$\mathfrak {X}_{\rm rig}$ connected the pair ![]() $(\operatorname {\mathbf {Cov}}^{\mathrm {oc}}_{\mathfrak {X}_\mathrm {rig}}, F_{\overline {x}})$ is a tame infinite Galois category in this generality.
$(\operatorname {\mathbf {Cov}}^{\mathrm {oc}}_{\mathfrak {X}_\mathrm {rig}}, F_{\overline {x}})$ is a tame infinite Galois category in this generality.
4. Tame coverings
In this section, we assume that the base non-archimedean field ![]() $K$ is discretely valued and we fix a uniformizer
$K$ is discretely valued and we fix a uniformizer ![]() $\varpi$. We aim to show that, under certain smoothness hypotheses, the notion of tame (see Definition 4.11)
$\varpi$. We aim to show that, under certain smoothness hypotheses, the notion of tame (see Definition 4.11) ![]() ${\unicode{x00E9}}{\text{t}}$-covering spaces,
${\unicode{x00E9}}{\text{t}}$-covering spaces, ![]() $\mathrm {adm}$-covering spaces, and de Jong coverings of a rigid
$\mathrm {adm}$-covering spaces, and de Jong coverings of a rigid ![]() $K$-space all coincide (Theorem 4.14). The method of proof mirrors that of Theorem 3.7. Namely we formulate a simple topological lemma (see Proposition 4.5) which will allow us to apply the overconvergence criterion of Proposition 3.5. We then employ the link between tameness and logarithmic geometry (the logarithmic Abhyankar's lemma, Theorem 4.8) to verify that our topological lemma applies to suitable models of tame covering spaces.
$K$-space all coincide (Theorem 4.14). The method of proof mirrors that of Theorem 3.7. Namely we formulate a simple topological lemma (see Proposition 4.5) which will allow us to apply the overconvergence criterion of Proposition 3.5. We then employ the link between tameness and logarithmic geometry (the logarithmic Abhyankar's lemma, Theorem 4.8) to verify that our topological lemma applies to suitable models of tame covering spaces.
4.1 Preliminaries about finite maps and formal models
The following lemma shows that, as in algebraic geometry (see [SP21, Tag 0BAK]), given a formal scheme ![]() $\mathfrak {X}$ and a finite morphism of rigid
$\mathfrak {X}$ and a finite morphism of rigid ![]() $K$-spaces
$K$-spaces ![]() $Y\to \mathfrak {X}_\eta$, one can ‘normalize
$Y\to \mathfrak {X}_\eta$, one can ‘normalize ![]() $\mathfrak {X}$ in
$\mathfrak {X}$ in ![]() $Y$’, producing a formal model
$Y$’, producing a formal model ![]() $\mathfrak {Y}\to \mathfrak {X}$ which is again a finite morphism. There is a unique such map with the property that
$\mathfrak {Y}\to \mathfrak {X}$ which is again a finite morphism. There is a unique such map with the property that ![]() $\mathfrak {Y}$ is
$\mathfrak {Y}$ is ![]() $\eta$-normal (see Appendix A for the definition and basic properties of
$\eta$-normal (see Appendix A for the definition and basic properties of ![]() $\eta$-normality).
$\eta$-normality).
Lemma 4.1 Let ![]() $\mathfrak {X}$ be an admissible formal scheme over
$\mathfrak {X}$ be an admissible formal scheme over ![]() $\mathcal {O}_K$, let
$\mathcal {O}_K$, let ![]() $X=\mathfrak {X}_\eta$, and let
$X=\mathfrak {X}_\eta$, and let ![]() $f\colon Y\to X$ be a finite morphism with
$f\colon Y\to X$ be a finite morphism with ![]() $Y$ reduced. Then there exists a unique up to unique isomorphism finite morphism of formal schemes
$Y$ reduced. Then there exists a unique up to unique isomorphism finite morphism of formal schemes ![]() $\mathfrak {f}\colon \mathfrak {Y}\to \mathfrak {X}$ with
$\mathfrak {f}\colon \mathfrak {Y}\to \mathfrak {X}$ with ![]() $f=\mathfrak {f}_\eta$ and
$f=\mathfrak {f}_\eta$ and ![]() $\mathfrak {Y}$
$\mathfrak {Y}$ ![]() $\eta$-normal.
$\eta$-normal.
Proof. Suppose that ![]() $\mathfrak {f}\colon \mathfrak {Y}\to \mathfrak {X}$ is a finite map with
$\mathfrak {f}\colon \mathfrak {Y}\to \mathfrak {X}$ is a finite map with ![]() $\mathfrak {f}_\eta = f$ and
$\mathfrak {f}_\eta = f$ and ![]() $\mathfrak {Y}$
$\mathfrak {Y}$ ![]() $\eta$-normal. On the one hand,
$\eta$-normal. On the one hand, ![]() $\operatorname {sp}_{\mathfrak {Y},*}\mathcal {O}_Y^{+} = \mathcal {O}_\mathfrak {Y}$ because
$\operatorname {sp}_{\mathfrak {Y},*}\mathcal {O}_Y^{+} = \mathcal {O}_\mathfrak {Y}$ because ![]() $\mathfrak {Y}$ is
$\mathfrak {Y}$ is ![]() $\eta$-normal. On the other hand,
$\eta$-normal. On the other hand, ![]() $\mathfrak {Y}$ is the relative formal spectrum [Reference Fujiwara and KatoFK18, Chapter I, Proposition 4.2.6] of
$\mathfrak {Y}$ is the relative formal spectrum [Reference Fujiwara and KatoFK18, Chapter I, Proposition 4.2.6] of ![]() $\mathfrak {f}_* \mathcal {O}_\mathfrak {Y} = \mathfrak {f}_* (\operatorname {sp}_{\mathfrak {Y}, *} \mathcal {O}_Y^{+}) = \operatorname {sp}_{\mathfrak {X}, *} (f_*\mathcal {O}^{+}_Y)$. This implies the uniqueness, and that to show existence we need to check that
$\mathfrak {f}_* \mathcal {O}_\mathfrak {Y} = \mathfrak {f}_* (\operatorname {sp}_{\mathfrak {Y}, *} \mathcal {O}_Y^{+}) = \operatorname {sp}_{\mathfrak {X}, *} (f_*\mathcal {O}^{+}_Y)$. This implies the uniqueness, and that to show existence we need to check that ![]() $\operatorname {sp}_{\mathfrak {X}, *} (f_*\mathcal {O}^{+}_Y)$ is an adically quasi-coherent and finitely generated
$\operatorname {sp}_{\mathfrak {X}, *} (f_*\mathcal {O}^{+}_Y)$ is an adically quasi-coherent and finitely generated ![]() $\mathcal {O}_\mathfrak {X}$-algebra. For an affinoid open
$\mathcal {O}_\mathfrak {X}$-algebra. For an affinoid open ![]() $\operatorname {Spf}(A)$ in
$\operatorname {Spf}(A)$ in ![]() $X$, write
$X$, write ![]() $Y\times _X \operatorname {Spa}(A_K) = \operatorname {Spa}(B)$ for a finite and reduced
$Y\times _X \operatorname {Spa}(A_K) = \operatorname {Spa}(B)$ for a finite and reduced ![]() $A_K$-algebra
$A_K$-algebra ![]() $B$. The value of the sheaf in question on
$B$. The value of the sheaf in question on ![]() $\operatorname {Spf}(A)$ is
$\operatorname {Spf}(A)$ is ![]() $B^{\circ }$. Choose a surjection
$B^{\circ }$. Choose a surjection ![]() $\mathcal {O}_K\langle x_1, \ldots, x_n\rangle \to A$. As
$\mathcal {O}_K\langle x_1, \ldots, x_n\rangle \to A$. As ![]() $K$ is discretely valued, by [Reference Bosch, Güntzer and RemmertBGR84, Corollary 6.4.1/6] applied to
$K$ is discretely valued, by [Reference Bosch, Güntzer and RemmertBGR84, Corollary 6.4.1/6] applied to ![]() $K\langle x_1, \ldots, x_n\rangle \to A_K$, the algebra
$K\langle x_1, \ldots, x_n\rangle \to A_K$, the algebra ![]() $A_K^{\circ }$ is finite over
$A_K^{\circ }$ is finite over ![]() $A$, and by the same result applied to
$A$, and by the same result applied to ![]() $A_K\to B$, the algebra
$A_K\to B$, the algebra ![]() $B^{\circ }$ is finite over
$B^{\circ }$ is finite over ![]() $A^\circ_K$ and, hence, also over
$A^\circ_K$ and, hence, also over ![]() $A$. Moreover, the sheaf
$A$. Moreover, the sheaf ![]() $\operatorname {sp}_{\mathfrak {X},*} (f_* \mathcal {O}_Y^{+})$ is adically quasi-coherent because for
$\operatorname {sp}_{\mathfrak {X},*} (f_* \mathcal {O}_Y^{+})$ is adically quasi-coherent because for ![]() $a$ in
$a$ in ![]() $A$ the previous discussion, and the sheaf property for
$A$ the previous discussion, and the sheaf property for ![]() $\mathcal {O}_Y^{+}$, shows that
$\mathcal {O}_Y^{+}$, shows that ![]() $B^{\circ }\otimes _A A\langle a^{-1}\rangle$ is precisely
$B^{\circ }\otimes _A A\langle a^{-1}\rangle$ is precisely ![]() $B^{\circ }\langle a^{-1}\rangle ^{\circ }$.
$B^{\circ }\langle a^{-1}\rangle ^{\circ }$.
The following corollary extends the above result to the case of maps which are locally on the target the disjoint union of finite maps.
Corollary 4.2 Let ![]() $\mathfrak {X}$ be an admissible formal scheme over
$\mathfrak {X}$ be an admissible formal scheme over ![]() $\mathcal {O}_K$, let
$\mathcal {O}_K$, let ![]() $X=\mathfrak {X}_\eta$, and let
$X=\mathfrak {X}_\eta$, and let ![]() $f\colon Y\to X$ be a morphism with
$f\colon Y\to X$ be a morphism with ![]() $Y$ reduced for which there exists an open cover
$Y$ reduced for which there exists an open cover ![]() $\mathfrak {X} = \bigcup _{i\in I} \mathfrak {U}_i$ such that
$\mathfrak {X} = \bigcup _{i\in I} \mathfrak {U}_i$ such that ![]() $Y\times _X \mathfrak {U}_{i,\eta }$ is a disjoint union of finite spaces over
$Y\times _X \mathfrak {U}_{i,\eta }$ is a disjoint union of finite spaces over ![]() $\mathfrak {U}_{i,\eta }$. Then there exists a unique up to unique isomorphism morphism of formal schemes
$\mathfrak {U}_{i,\eta }$. Then there exists a unique up to unique isomorphism morphism of formal schemes ![]() $\mathfrak {f}\colon \mathfrak {Y}\to \mathfrak {X}$ with
$\mathfrak {f}\colon \mathfrak {Y}\to \mathfrak {X}$ with ![]() $f=\mathfrak {f}_\eta$ and
$f=\mathfrak {f}_\eta$ and ![]() $\mathfrak {Y}$
$\mathfrak {Y}$ ![]() $\eta$-normal which locally on
$\eta$-normal which locally on ![]() $\mathfrak {X}$ is the disjoint union of finite formal schemes over
$\mathfrak {X}$ is the disjoint union of finite formal schemes over ![]() $\mathfrak {X}$.
$\mathfrak {X}$.
Proof. Suppose first that ![]() $Y=\coprod _{j\in J} Y_j$ with each
$Y=\coprod _{j\in J} Y_j$ with each ![]() $Y_j$ finite over
$Y_j$ finite over ![]() $X$. In this case, we can apply Lemma 4.1 to each
$X$. In this case, we can apply Lemma 4.1 to each ![]() $Y_j$ and take
$Y_j$ and take ![]() $\mathfrak {Y} = \coprod _{j\in J} \mathfrak {Y}_j$, which clearly satisfies the required property. In particular, this construction does not depend on the way
$\mathfrak {Y} = \coprod _{j\in J} \mathfrak {Y}_j$, which clearly satisfies the required property. In particular, this construction does not depend on the way ![]() $Y$ is presented as a disjoint union of finite
$Y$ is presented as a disjoint union of finite ![]() $X$-spaces, and is compatible with passing to an open formal subscheme of
$X$-spaces, and is compatible with passing to an open formal subscheme of ![]() $\mathfrak {X}$. This implies that in the general case, the formal schemes
$\mathfrak {X}$. This implies that in the general case, the formal schemes ![]() $\mathfrak {V}_i\to \mathfrak {U}_i$ constructed in the first step will glue to provide the desired map
$\mathfrak {V}_i\to \mathfrak {U}_i$ constructed in the first step will glue to provide the desired map ![]() $\mathfrak {Y}\to \mathfrak {X}$.
$\mathfrak {Y}\to \mathfrak {X}$.
We call the model ![]() $\mathfrak {Y}\to \mathfrak {X}$ constructed in Corollary 4.2 the normalization of
$\mathfrak {Y}\to \mathfrak {X}$ constructed in Corollary 4.2 the normalization of ![]() $\mathfrak {X}$ in
$\mathfrak {X}$ in ![]() $Y$.
$Y$.
Remark 4.3 The assertions of Lemma 4.1 and Corollary 4.2 remain valid if ![]() $K$ is stable [Reference Bosch, Güntzer and RemmertBGR84, Definition 3.6.1/1] and with divisible value group (e.g. if
$K$ is stable [Reference Bosch, Güntzer and RemmertBGR84, Definition 3.6.1/1] and with divisible value group (e.g. if ![]() $K$ is algebraically closed). Indeed, under these assumptions the conclusions of [Reference Bosch, Güntzer and RemmertBGR84, Corollary 6.4.1/6] hold (see [Reference Bosch, Güntzer and RemmertBGR84, Corollary 6.4.1/5]).
$K$ is algebraically closed). Indeed, under these assumptions the conclusions of [Reference Bosch, Güntzer and RemmertBGR84, Corollary 6.4.1/6] hold (see [Reference Bosch, Güntzer and RemmertBGR84, Corollary 6.4.1/5]).
The following lemma will help us construct formal models in § 4.4.
Lemma 4.4 Let ![]() $X$ be a quasi-paracompact and quasi-separated rigid space over
$X$ be a quasi-paracompact and quasi-separated rigid space over ![]() $K$, and let
$K$, and let ![]() $X=\bigcup _{i\in I} U_i$ be an open cover. Then there exists an admissible formal model
$X=\bigcup _{i\in I} U_i$ be an open cover. Then there exists an admissible formal model ![]() $\mathfrak {X}$ of
$\mathfrak {X}$ of ![]() $X$ and an open cover
$X$ and an open cover ![]() $\mathfrak {X} = \bigcup _{j\in J} \mathfrak {V}_j$ such that
$\mathfrak {X} = \bigcup _{j\in J} \mathfrak {V}_j$ such that ![]() $\{\mathfrak {V}_{j,\eta }\}_{j\in J}$ refines
$\{\mathfrak {V}_{j,\eta }\}_{j\in J}$ refines ![]() $\{U_i\}_{i\in I}$.
$\{U_i\}_{i\in I}$.
Proof. Refining the given cover, we may assume that the ![]() $U_i$ are quasi-compact. By assumption, there is an open cover
$U_i$ are quasi-compact. By assumption, there is an open cover ![]() $X=\bigcup _{s\in S} X_s$ of finite type (i.e. each member intersects only finitely many others) by quasi-compact opens
$X=\bigcup _{s\in S} X_s$ of finite type (i.e. each member intersects only finitely many others) by quasi-compact opens ![]() $X_s\subseteq X$. As
$X_s\subseteq X$. As ![]() $X_s$ are quasi-compact, for each
$X_s$ are quasi-compact, for each ![]() $s$ there exists a finite subset
$s$ there exists a finite subset ![]() $F_s \subset I$ such that
$F_s \subset I$ such that ![]() $X_s \subset \bigcup _{i \in F_s} U_i$. Now, the open cover
$X_s \subset \bigcup _{i \in F_s} U_i$. Now, the open cover ![]() $\bigcup _{s \in S}\bigcup _{i \in F_s} (U_i \cap X_s)$ is a cover of finite type. Moreover, its members are quasi-compact, as
$\bigcup _{s \in S}\bigcup _{i \in F_s} (U_i \cap X_s)$ is a cover of finite type. Moreover, its members are quasi-compact, as ![]() $X$ was quasi-separated. By [Reference BoschBos14, 8.4/5], there exists a formal model
$X$ was quasi-separated. By [Reference BoschBos14, 8.4/5], there exists a formal model ![]() $\mathfrak {X}$ of
$\mathfrak {X}$ of ![]() $X$ and an open cover
$X$ and an open cover ![]() $\mathfrak {X} = \bigcup _{s \in S}\bigcup _{i \in F_s} \mathfrak {V}_{i,s}$ such that
$\mathfrak {X} = \bigcup _{s \in S}\bigcup _{i \in F_s} \mathfrak {V}_{i,s}$ such that ![]() $(\mathfrak {V}_{i,s})_\eta = U_i \cap X_s$.
$(\mathfrak {V}_{i,s})_\eta = U_i \cap X_s$.
4.2 A special case of the overconvergence criterion
In order to apply our overconvergence criterion (Proposition 3.5) to tame covering spaces, we show the following result.
Proposition 4.5 Let ![]() $\mathfrak {Y}\to \mathfrak {X}$ be a morphism of formal schemes locally of finite type over
$\mathfrak {Y}\to \mathfrak {X}$ be a morphism of formal schemes locally of finite type over ![]() $\mathcal {O}_K$ which locally on
$\mathcal {O}_K$ which locally on ![]() $\mathfrak {X}$ is the disjoint union of finite morphisms. Suppose that for every irreducible component
$\mathfrak {X}$ is the disjoint union of finite morphisms. Suppose that for every irreducible component ![]() $Z$ of
$Z$ of ![]() $\mathfrak {X}_k$, the base change
$\mathfrak {X}_k$, the base change ![]() $\mathfrak {Y}\times _\mathfrak {X} Z$ is locally irreducibleFootnote 6 (e.g.
$\mathfrak {Y}\times _\mathfrak {X} Z$ is locally irreducibleFootnote 6 (e.g. ![]() $(\mathfrak {Y}\times _\mathfrak {X} Z)_{\rm red}$ is normal). Then for all such
$(\mathfrak {Y}\times _\mathfrak {X} Z)_{\rm red}$ is normal). Then for all such ![]() $Z$, the scheme
$Z$, the scheme ![]() $\mathfrak {Y}\times _{\mathfrak {X}} Z$ is a disjoint union of finite
$\mathfrak {Y}\times _{\mathfrak {X}} Z$ is a disjoint union of finite ![]() $Z$-spaces.
$Z$-spaces.
Proof. Let ![]() $T$ be a connected component of
$T$ be a connected component of ![]() $\mathfrak {Y}\times _\mathfrak {X} Z$. By assumption,
$\mathfrak {Y}\times _\mathfrak {X} Z$. By assumption, ![]() $T$ is locally irreducible, and hence irreducible. We show that
$T$ is locally irreducible, and hence irreducible. We show that ![]() $T\to Z$ is a finite morphism, which implies the assertion. If
$T\to Z$ is a finite morphism, which implies the assertion. If ![]() $Z=\bigcup U_i$ is an open cover such that
$Z=\bigcup U_i$ is an open cover such that ![]() $\mathfrak {Y}\times _\mathfrak {X} U_i$ is the disjoint union of finite maps
$\mathfrak {Y}\times _\mathfrak {X} U_i$ is the disjoint union of finite maps ![]() $V_{ij}\to U_i$ with
$V_{ij}\to U_i$ with ![]() $V_{ij}$ connected, then
$V_{ij}$ connected, then ![]() $T\times _Z U_i$ is the disjoint union of some of the
$T\times _Z U_i$ is the disjoint union of some of the ![]() $V_{ij}$. However, because
$V_{ij}$. However, because ![]() $T$ is irreducible, so is the open subset
$T$ is irreducible, so is the open subset ![]() $T\times _Z U_i\subseteq T$. Therefore, we must have
$T\times _Z U_i\subseteq T$. Therefore, we must have ![]() $T\times _Z U_i = V_{ij}$ for some index
$T\times _Z U_i = V_{ij}$ for some index ![]() $j$. Thus,
$j$. Thus, ![]() $T\times _Z U_i\to U_i$ is finite for all
$T\times _Z U_i\to U_i$ is finite for all ![]() $i$ and, hence,
$i$ and, hence, ![]() $T\to Z$ is finite.
$T\to Z$ is finite.
Using Proposition 3.5 we obtain the following corollary.
Corollary 4.6 Let ![]() $\mathfrak {Y}\to \mathfrak {X}$ be a morphism of formal schemes satisfying the assumptions in Proposition 4.5 and such that
$\mathfrak {Y}\to \mathfrak {X}$ be a morphism of formal schemes satisfying the assumptions in Proposition 4.5 and such that ![]() $\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$ is étale. Then,
$\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$ is étale. Then, ![]() $\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$ is a de Jong covering space.
$\mathfrak {Y}_\eta \to \mathfrak {X}_\eta$ is a de Jong covering space.
Example 4.7 In [Reference Achinger, Lara and YoucisALY21b, § 2], we constructed over ![]() $K$ of equal characteristic
$K$ of equal characteristic ![]() $p>0$ an example of an
$p>0$ an example of an ![]() $\mathrm {adm}$-covering space
$\mathrm {adm}$-covering space ![]() $Y\to X$ which is not a de Jong covering space, and it is instructive to see why the above criterion does not apply to it. We recall the setup:
$Y\to X$ which is not a de Jong covering space, and it is instructive to see why the above criterion does not apply to it. We recall the setup: ![]() $X$ is the annulus
$X$ is the annulus ![]() $\{|\varpi |\leqslant |x|\leqslant |\varpi |^{-1}\}$ covered by the two annuli
$\{|\varpi |\leqslant |x|\leqslant |\varpi |^{-1}\}$ covered by the two annuli
intersecting along the unit circle ![]() $U^{+}\cap U^{-}=C=\{|x|=1\}$. The restriction of
$U^{+}\cap U^{-}=C=\{|x|=1\}$. The restriction of ![]() $Y\to X$ to
$Y\to X$ to ![]() $U^{\pm }$ is a disjoint union of well-chosen Artin–Schreier coverings
$U^{\pm }$ is a disjoint union of well-chosen Artin–Schreier coverings ![]() $Y^{\pm }_n$ (
$Y^{\pm }_n$ (![]() $n\in \mathbf {Z}$) which are split over
$n\in \mathbf {Z}$) which are split over ![]() $C$, and
$C$, and ![]() $\coprod _n Y_n^{-}$ and
$\coprod _n Y_n^{-}$ and ![]() $\coprod _n Y^{+}_n$ are identified suitably over
$\coprod _n Y^{+}_n$ are identified suitably over ![]() $C$ in order to make
$C$ in order to make ![]() $Y$ connected.
$Y$ connected.
Construct a formal model ![]() $\mathfrak {X}$ of
$\mathfrak {X}$ of ![]() $X$ by gluing together the formal models
$X$ by gluing together the formal models
of ![]() $U^{+}$ and
$U^{+}$ and ![]() $U^{-}$ along
$U^{-}$ along ![]() $\mathfrak {C} = \operatorname {Spf}(\mathcal {O}_K\langle x^{+},x^{-}\rangle /(x^{+}x^{-} - 1))$ identified with
$\mathfrak {C} = \operatorname {Spf}(\mathcal {O}_K\langle x^{+},x^{-}\rangle /(x^{+}x^{-} - 1))$ identified with ![]() $D(x^{\pm })\subseteq \mathfrak {U}^{\pm }$. (In terms of the coordinate
$D(x^{\pm })\subseteq \mathfrak {U}^{\pm }$. (In terms of the coordinate ![]() $x$, we have
$x$, we have ![]() $x^{+}=1/x$,
$x^{+}=1/x$, ![]() $x^{-}=x$,
$x^{-}=x$, ![]() $y^{+}=\varpi x$,
$y^{+}=\varpi x$, ![]() $y^{-} = \varpi /x$.) The irreducible component
$y^{-} = \varpi /x$.) The irreducible component ![]() $Z$ of
$Z$ of ![]() $\mathfrak {X}_k$ containing
$\mathfrak {X}_k$ containing ![]() $\mathfrak {C}_k \simeq \mathbf {G}_{m,k}$ is isomorphic to
$\mathfrak {C}_k \simeq \mathbf {G}_{m,k}$ is isomorphic to ![]() $\mathbf {P}^{1}_k$. The restriction of the normalization
$\mathbf {P}^{1}_k$. The restriction of the normalization ![]() $\mathfrak {Y}$ of
$\mathfrak {Y}$ of ![]() $\mathfrak {X}$ in
$\mathfrak {X}$ in ![]() $Y\to X$ to
$Y\to X$ to ![]() $Z$ will look like Figure 1: it will consist of infinitely many copies of
$Z$ will look like Figure 1: it will consist of infinitely many copies of ![]() $Z$ glued together in a complicated way over
$Z$ glued together in a complicated way over ![]() $0,\infty \in Z$, and will not be locally irreducible.
$0,\infty \in Z$, and will not be locally irreducible.

Figure 1. Example 4.7 (![]() $p=3$), compare with [Reference Achinger, Lara and YoucisALY21b, Figure 1].
$p=3$), compare with [Reference Achinger, Lara and YoucisALY21b, Figure 1].
4.3 Logarithmic Abhyankar's lemma
The following result describes the local structure of a finite covering of a regular scheme tamely ramified along a strict normal crossings divisor [SP21, Tag 0CBN]. It is a basic consequence of the logarithmic Abhyankar's lemma.
In order to state the result, we first recall some basic terminology from log geometry. For a commutative monoid ![]() $P$ (written additively), we write
$P$ (written additively), we write ![]() $P\to P^{\rm gp}$ for the initial homomorphism into a group. The monoid
$P\to P^{\rm gp}$ for the initial homomorphism into a group. The monoid ![]() $P$ is called integral if
$P$ is called integral if ![]() $P\to P^{\rm gp}$ is injective, fine if it is finitely generated and integral, and saturated if it is integral and for
$P\to P^{\rm gp}$ is injective, fine if it is finitely generated and integral, and saturated if it is integral and for ![]() $x\in P^{\rm gp}$ such that
$x\in P^{\rm gp}$ such that ![]() $nx\in P$ for some
$nx\in P$ for some ![]() $n\geqslant 1$, we have
$n\geqslant 1$, we have ![]() $x\in P$. Finally, a morphism of fine and saturated monoids
$x\in P$. Finally, a morphism of fine and saturated monoids ![]() $\alpha \colon P\to Q$ is called Kummer (see [Reference IllusieIll02, § 1.6]) if it is injective and for every
$\alpha \colon P\to Q$ is called Kummer (see [Reference IllusieIll02, § 1.6]) if it is injective and for every ![]() $x\in Q$ there exists an
$x\in Q$ there exists an ![]() $n\geqslant 1$ such that
$n\geqslant 1$ such that ![]() $nx\in \alpha (P)$. Equivalently,
$nx\in \alpha (P)$. Equivalently, ![]() $P=Q\cap \Lambda$ for a subgroup
$P=Q\cap \Lambda$ for a subgroup ![]() $\Lambda \subseteq Q^{\rm gp}$ of finite index.
$\Lambda \subseteq Q^{\rm gp}$ of finite index.
Recall that if ![]() $D$ is a prime divisor on a scheme
$D$ is a prime divisor on a scheme ![]() $X$ with generic point
$X$ with generic point ![]() $\xi$ such that
$\xi$ such that ![]() $\mathcal {O}_{X, \xi }$ is a discrete valuation ring, we say that an étale morphism
$\mathcal {O}_{X, \xi }$ is a discrete valuation ring, we say that an étale morphism ![]() $V\to X$ is tamely ramified along
$V\to X$ is tamely ramified along ![]() $D$ if
$D$ if ![]() $V\otimes \operatorname {Frac}(\mathcal {O}^{h}_{X, \xi })$ is the disjoint union of spectra of finite extensions of
$V\otimes \operatorname {Frac}(\mathcal {O}^{h}_{X, \xi })$ is the disjoint union of spectra of finite extensions of ![]() $\operatorname {Frac}(\mathcal {O}^{h}_{X, \xi })$ which are tame with respect to the given discrete valuation.
$\operatorname {Frac}(\mathcal {O}^{h}_{X, \xi })$ which are tame with respect to the given discrete valuation.
Theorem 4.8 (See [Reference MochizukiMoc99, Theorem 3.3] and [Reference Gabber and RameroGR04, Theorem 13.3.43])
Let ![]() $R$ be a strictly Henselian regular local ring, and let
$R$ be a strictly Henselian regular local ring, and let ![]() $x_1, \ldots, x_r\in \mathfrak {m}_R$ be elements whose images in
$x_1, \ldots, x_r\in \mathfrak {m}_R$ be elements whose images in ![]() $\mathfrak {m}_R/\mathfrak {m}^{2}_R$ are linearly independent. Let
$\mathfrak {m}_R/\mathfrak {m}^{2}_R$ are linearly independent. Let ![]() $X=\operatorname {Spec}(R)$,
$X=\operatorname {Spec}(R)$, ![]() $D_i=V(x_i)\subseteq X$ (
$D_i=V(x_i)\subseteq X$ (![]() $i=1, \ldots, r$), and
$i=1, \ldots, r$), and ![]() $U=D(x_1\cdots x_r) = X\setminus (D_1 \cup \cdots \cup D_r)$. Let
$U=D(x_1\cdots x_r) = X\setminus (D_1 \cup \cdots \cup D_r)$. Let ![]() $V\to U$ be a connected finite étale covering which is tamely ramified along
$V\to U$ be a connected finite étale covering which is tamely ramified along ![]() $D_1, \ldots, D_r$, and let
$D_1, \ldots, D_r$, and let ![]() $f\colon Y\to X$ be the normalization of
$f\colon Y\to X$ be the normalization of ![]() $X$ in
$X$ in ![]() $V$. Then there exists a Kummer homomorphism
$V$. Then there exists a Kummer homomorphism ![]() $\alpha \colon \mathbf {N}^{r}\to Q$ with
$\alpha \colon \mathbf {N}^{r}\to Q$ with ![]() $Q^{\rm gp}/\mathbf {Z}^{r}$ of order invertible in
$Q^{\rm gp}/\mathbf {Z}^{r}$ of order invertible in ![]() $R$ and an isomorphism of
$R$ and an isomorphism of ![]() $X$-schemes
$X$-schemes
where ![]() $\mathbf {Z}[\mathbf {N}^{r}]\to R$ sends
$\mathbf {Z}[\mathbf {N}^{r}]\to R$ sends ![]() $e_i$ to
$e_i$ to ![]() $x_i$.
$x_i$.
We need the following lemma, which follows from basic facts about log regularity [Reference KatoKat94, Theorems 4.1 and 8.2].
Lemma 4.9 Let ![]() $R$ be a regular local ring, and let
$R$ be a regular local ring, and let ![]() $x_1, \ldots, x_r\in \mathfrak {m}_R$ be elements whose images in
$x_1, \ldots, x_r\in \mathfrak {m}_R$ be elements whose images in ![]() $\mathfrak {m}_R/\mathfrak {m}^{2}_R$ are linearly independent. Let
$\mathfrak {m}_R/\mathfrak {m}^{2}_R$ are linearly independent. Let ![]() $\alpha \colon \mathbf {N}^{r}\to Q$ be a Kummer homomorphism of fine and saturated monoids with
$\alpha \colon \mathbf {N}^{r}\to Q$ be a Kummer homomorphism of fine and saturated monoids with ![]() $Q^{\rm gp}/\mathbf {Z}^{r}$ of order invertible in
$Q^{\rm gp}/\mathbf {Z}^{r}$ of order invertible in ![]() $R$ and let
$R$ and let ![]() $\mathbf {N}^{r}\to R$ send
$\mathbf {N}^{r}\to R$ send ![]() $e_i$ to
$e_i$ to ![]() $x_i$. Then the ring
$x_i$. Then the ring ![]() $R\otimes _{\mathbf {Z}[\mathbf {N}^{r}]} \mathbf {Z}[Q]$ is normal.
$R\otimes _{\mathbf {Z}[\mathbf {N}^{r}]} \mathbf {Z}[Q]$ is normal.
The following corollary is the crux of the argument in this section.
Corollary 4.10 Let ![]() $X$ be a regular scheme and let
$X$ be a regular scheme and let ![]() $D=D_1\cup \cdots \cup D_r$ be a divisor with strict normal crossings. Let
$D=D_1\cup \cdots \cup D_r$ be a divisor with strict normal crossings. Let ![]() $U=X\setminus D$ and let
$U=X\setminus D$ and let ![]() $V\to U$ be a finite étale morphism which is tamely ramified along
$V\to U$ be a finite étale morphism which is tamely ramified along ![]() $D_1, \ldots, D_r$. Let
$D_1, \ldots, D_r$. Let ![]() $Y\to X$ be the normalization of
$Y\to X$ be the normalization of ![]() $X$ in
$X$ in ![]() $V$. Then the schemes
$V$. Then the schemes ![]() $(Y\times _X D_i)_{\rm red}$ are normal for
$(Y\times _X D_i)_{\rm red}$ are normal for ![]() $i=1, \ldots, r$.
$i=1, \ldots, r$.
Proof. Using standard arguments one quickly reduces to the case when ![]() $X$ is strictly local. Write
$X$ is strictly local. Write ![]() $X=\operatorname {Spec}(R)$ and
$X=\operatorname {Spec}(R)$ and ![]() $D_i=V(x_i)$ for some
$D_i=V(x_i)$ for some ![]() $x_i\in R$. Let
$x_i\in R$. Let ![]() $Y\simeq \operatorname {Spec} (R\otimes _{\mathbf {Z}[\mathbf {N}^{r}]} \mathbf {Z}[Q])$ be as in Theorem 4.8. Our goal is to show that the ring
$Y\simeq \operatorname {Spec} (R\otimes _{\mathbf {Z}[\mathbf {N}^{r}]} \mathbf {Z}[Q])$ be as in Theorem 4.8. Our goal is to show that the ring
is normal for ![]() $i=1, \ldots, r$. For notational convenience, we prove this for
$i=1, \ldots, r$. For notational convenience, we prove this for ![]() $i=r$. The ring
$i=r$. The ring ![]() $R'=R/(x_r)$ is again a regular local ring, and
$R'=R/(x_r)$ is again a regular local ring, and ![]() $x_1, \ldots, x_{r-1}$ are elements of the maximal ideal which are linearly independent in
$x_1, \ldots, x_{r-1}$ are elements of the maximal ideal which are linearly independent in ![]() $\mathfrak {m}_{R'}/\mathfrak {m}_{R'}^{2}$. We claim that there exists a Kummer homomorphism of fine and saturated monoids
$\mathfrak {m}_{R'}/\mathfrak {m}_{R'}^{2}$. We claim that there exists a Kummer homomorphism of fine and saturated monoids ![]() $\alpha '\colon \mathbf {N}^{r-1}\to Q'$ with
$\alpha '\colon \mathbf {N}^{r-1}\to Q'$ with ![]() $(Q')^{\rm gp}/\mathbf {Z}^{r-1}$ of order invertible in
$(Q')^{\rm gp}/\mathbf {Z}^{r-1}$ of order invertible in ![]() $R'$ such that
$R'$ such that
The right-hand side of this isomorphism is normal by Lemma 4.9, so the claim implies the required assertion. Note that the left-hand side can also be written as ![]() $(R\otimes _{\mathbf {Z}[\mathbf {N}^{r}]/(e_r)} \mathbf {Z}[Q]/(\alpha (e_r)))_{\rm red}$.
$(R\otimes _{\mathbf {Z}[\mathbf {N}^{r}]/(e_r)} \mathbf {Z}[Q]/(\alpha (e_r)))_{\rm red}$.
Let us first compute ![]() $(\operatorname {Spec}(\mathbf {Z}[Q]/(\alpha (e_r))))_{\rm red}$. To this end, let
$(\operatorname {Spec}(\mathbf {Z}[Q]/(\alpha (e_r))))_{\rm red}$. To this end, let ![]() $\mathbf {N}^{r-1}\subseteq \mathbf {N}^{r}$ be the inclusion omitting the
$\mathbf {N}^{r-1}\subseteq \mathbf {N}^{r}$ be the inclusion omitting the ![]() $r$th factor, let
$r$th factor, let ![]() $Q'\subseteq Q$ consist of elements whose positive multiple lies in
$Q'\subseteq Q$ consist of elements whose positive multiple lies in ![]() $\alpha (\mathbf {N}^{r-1})$, and let
$\alpha (\mathbf {N}^{r-1})$, and let ![]() $\alpha '\colon \mathbf {N}^{r-1}\to Q'$ be the induced map. Every element of
$\alpha '\colon \mathbf {N}^{r-1}\to Q'$ be the induced map. Every element of ![]() $Q\setminus Q'$ has a multiple in the ideal of
$Q\setminus Q'$ has a multiple in the ideal of ![]() $\mathbf {Z}[Q]$ generated by
$\mathbf {Z}[Q]$ generated by ![]() $\alpha (e_r)$. Consequently, the ideal
$\alpha (e_r)$. Consequently, the ideal ![]() $J$ generated by
$J$ generated by ![]() $Q\setminus Q'$ in
$Q\setminus Q'$ in ![]() $\mathbf {Z}[Q]/(\alpha (e_r))$ is nilpotent. As
$\mathbf {Z}[Q]/(\alpha (e_r))$ is nilpotent. As ![]() $\mathbf {Z}[Q]/(\alpha (e_r), J)=\mathbf {Z}[Q]/(J)\simeq \mathbf {Z}[Q']$ is reduced, we have
$\mathbf {Z}[Q]/(\alpha (e_r), J)=\mathbf {Z}[Q]/(J)\simeq \mathbf {Z}[Q']$ is reduced, we have ![]() $(\operatorname {Spec}(\mathbf {Z}[Q]/(\alpha (e_r)))_{\rm red}\simeq \mathbf {Z}[Q']$. Note that
$(\operatorname {Spec}(\mathbf {Z}[Q]/(\alpha (e_r)))_{\rm red}\simeq \mathbf {Z}[Q']$. Note that ![]() $\alpha '\colon \mathbf {N}^{r-1}\to Q'$ is a Kummer homomorphism of fine and saturated monoids, and the order of
$\alpha '\colon \mathbf {N}^{r-1}\to Q'$ is a Kummer homomorphism of fine and saturated monoids, and the order of ![]() $(Q')^{\rm gp}/\mathbf {Z}^{r-1}\subseteq Q^{\rm gp}/\mathbf {Z}^{r}$ is invertible in
$(Q')^{\rm gp}/\mathbf {Z}^{r-1}\subseteq Q^{\rm gp}/\mathbf {Z}^{r}$ is invertible in ![]() $R$.
$R$.
Applying ![]() $R'\otimes _{\mathbf {Z}[\mathbf {N}^{r-1}]}(-)$ to the surjection with nilpotent kernel
$R'\otimes _{\mathbf {Z}[\mathbf {N}^{r-1}]}(-)$ to the surjection with nilpotent kernel ![]() $\mathbf {Z}[Q]/(\alpha (e_r))\to \mathbf {Z}[Q']$ we get a surjection with nilpotent kernel
$\mathbf {Z}[Q]/(\alpha (e_r))\to \mathbf {Z}[Q']$ we get a surjection with nilpotent kernel
The target is reduced (as it is normal) and, hence, it is the reduction of the source.
4.4 Tame coverings
We now begin the setup to the main theorem of this section, which shows that under the additional hypotheses including tameness, every ![]() ${\unicode{x00E9}}{\text{t}}$-covering space is a de Jong covering space. The general definition we use is due to Hübner [Reference HübnerHüb21].Footnote 7
${\unicode{x00E9}}{\text{t}}$-covering space is a de Jong covering space. The general definition we use is due to Hübner [Reference HübnerHüb21].Footnote 7
Definition 4.11 An étale morphism of rigid ![]() $K$-spaces
$K$-spaces ![]() $f\colon Y\to X$ is tame if for every
$f\colon Y\to X$ is tame if for every ![]() $y\in Y$, the corresponding finite extension of valued fields
$y\in Y$, the corresponding finite extension of valued fields ![]() $k(f(x))\subseteq k(y)$ is tame.
$k(f(x))\subseteq k(y)$ is tame.
The second assumption we shall put on the base space is that it has sufficiently many semistable models, as defined in the following. Let us call a formal scheme ![]() $\mathfrak {X}$ locally of finite type over
$\mathfrak {X}$ locally of finite type over ![]() $\mathcal {O}_K$ gss (generalized strictly semistable) if locally
$\mathcal {O}_K$ gss (generalized strictly semistable) if locally ![]() $\mathfrak {X}$ admits an étale map to the formal scheme
$\mathfrak {X}$ admits an étale map to the formal scheme ![]() $\operatorname {Spf}(\mathcal {O}_K\langle x_1, \ldots, x_n\rangle /(x_1^{m_1}\cdots x_n^{m_n} - \varpi ))$ for some
$\operatorname {Spf}(\mathcal {O}_K\langle x_1, \ldots, x_n\rangle /(x_1^{m_1}\cdots x_n^{m_n} - \varpi ))$ for some ![]() $n\geqslant 0$ and
$n\geqslant 0$ and ![]() $m_1, \ldots, m_n\geqslant 0$ not all zero.
$m_1, \ldots, m_n\geqslant 0$ not all zero.
Definition 4.12 Let ![]() $X$ be a smooth quasi-paracompact and quasi-separated rigid
$X$ be a smooth quasi-paracompact and quasi-separated rigid ![]() $K$-space. We say that gss formal models of
$K$-space. We say that gss formal models of ![]() $X$ are cofinal if for every admissible formal model
$X$ are cofinal if for every admissible formal model ![]() $\mathfrak {X}$ of
$\mathfrak {X}$ of ![]() $X$ there exists a finite extension
$X$ there exists a finite extension ![]() $K'$ of
$K'$ of ![]() $K$ with valuation ring
$K$ with valuation ring ![]() $\mathcal {O}_{K'}$, a gss formal model
$\mathcal {O}_{K'}$, a gss formal model ![]() $\mathfrak {X}'$ of
$\mathfrak {X}'$ of ![]() $X_{K'}$ over
$X_{K'}$ over ![]() $\mathcal {O}_{K'}$, and a morphism
$\mathcal {O}_{K'}$, and a morphism
such that ![]() $f_\eta$ is an isomorphism.
$f_\eta$ is an isomorphism.
The cofinality of gss formal models for a smooth quasi-paracompact and quasi-separated rigid ![]() $K$-space condition is satisfied (with
$K$-space condition is satisfied (with ![]() $K'=K$) if
$K'=K$) if ![]() $K$ is of equal characteristic zero (see [Reference TemkinTem12]), or if
$K$ is of equal characteristic zero (see [Reference TemkinTem12]), or if ![]() $X$ is of dimension one. Moreover, it would follow from functorial resolution of singularities for quasi-excellent schemes of dimension
$X$ is of dimension one. Moreover, it would follow from functorial resolution of singularities for quasi-excellent schemes of dimension ![]() $\dim (X)+1$ (again with
$\dim (X)+1$ (again with ![]() $K'=K$).
$K'=K$).
We note that for a gss formal scheme ![]() $\mathfrak {X}$, the complete local rings
$\mathfrak {X}$, the complete local rings ![]() $\widehat {\mathcal {O}}_{\mathfrak {X}, x}$ are regular, and the preimages of the irreducible components of
$\widehat {\mathcal {O}}_{\mathfrak {X}, x}$ are regular, and the preimages of the irreducible components of ![]() $\mathfrak {X}_k$ in
$\mathfrak {X}_k$ in ![]() $\operatorname {Spec}(\widehat {\mathcal {O}}_{\mathfrak {X}, x})$ are of the form
$\operatorname {Spec}(\widehat {\mathcal {O}}_{\mathfrak {X}, x})$ are of the form ![]() $V(x_i)$ for elements
$V(x_i)$ for elements ![]() $x_1, \ldots, x_r\in \mathfrak {m}_x$ which are linearly independent modulo
$x_1, \ldots, x_r\in \mathfrak {m}_x$ which are linearly independent modulo ![]() $\mathfrak {m}^{2}_x$. In particular,
$\mathfrak {m}^{2}_x$. In particular, ![]() $\mathfrak {X}$ is formally normal and, hence,
$\mathfrak {X}$ is formally normal and, hence, ![]() $\eta$-normal by Lemma A.2.
$\eta$-normal by Lemma A.2.
Lemma 4.13 Let ![]() $\mathfrak {X}=\operatorname {Spf}(A)$ be a gss formal scheme over
$\mathfrak {X}=\operatorname {Spf}(A)$ be a gss formal scheme over ![]() $\mathcal {O}_K$ and let
$\mathcal {O}_K$ and let ![]() $f\colon Y\to \mathfrak {X}_\eta = X$ be a finite étale and tame map of rigid
$f\colon Y\to \mathfrak {X}_\eta = X$ be a finite étale and tame map of rigid ![]() $K$-spaces. Then, writing
$K$-spaces. Then, writing ![]() $Y=\operatorname {Spa}(B_K)$, the morphism of schemes
$Y=\operatorname {Spa}(B_K)$, the morphism of schemes ![]() $\operatorname {Spec}(B_K)\to \operatorname {Spec}(A)= \mathfrak{X}$ is tamely ramified along the irreducible components of
$\operatorname {Spec}(B_K)\to \operatorname {Spec}(A)= \mathfrak{X}$ is tamely ramified along the irreducible components of ![]() $\operatorname {Spec}(A_k)$.
$\operatorname {Spec}(A_k)$.
Proof. Let ![]() $\xi _1, \ldots, \xi _r$ be the generic points of the irreducible components of
$\xi _1, \ldots, \xi _r$ be the generic points of the irreducible components of ![]() $\mathfrak {X}_k$. The complete local rings
$\mathfrak {X}_k$. The complete local rings ![]() $V_i=\widehat {\mathcal {O}}_{\mathcal {X}, \xi _i}$ are discrete valuation rings and
$V_i=\widehat {\mathcal {O}}_{\mathcal {X}, \xi _i}$ are discrete valuation rings and ![]() $\varpi$ is in the maximal ideal of
$\varpi$ is in the maximal ideal of ![]() $V_i$. We let
$V_i$. We let ![]() $K_i = V_i[1/\varpi ]=\operatorname {Frac}(V_i)$. We have maps of Huber pairs
$K_i = V_i[1/\varpi ]=\operatorname {Frac}(V_i)$. We have maps of Huber pairs ![]() $(A_K, A)\to (K_i, V_i)$ and pull-back squares as follows.
$(A_K, A)\to (K_i, V_i)$ and pull-back squares as follows.

Thus, the left map is a tame étale map of adic spaces [Reference HübnerHüb21, § 3] and so the map ![]() $\operatorname {Spec}(B_K\otimes _A K_i)\to \operatorname {Spec}(V_i)$ is tamely ramified along the closed point of
$\operatorname {Spec}(B_K\otimes _A K_i)\to \operatorname {Spec}(V_i)$ is tamely ramified along the closed point of ![]() $\operatorname {Spec}(V_i)$. Then the same holds if we replace
$\operatorname {Spec}(V_i)$. Then the same holds if we replace ![]() $V_i$ with the Henselization
$V_i$ with the Henselization ![]() $\mathcal {O}_{\mathcal {X},\xi _i}^{h}$ (because
$\mathcal {O}_{\mathcal {X},\xi _i}^{h}$ (because ![]() $\mathcal {O}_{\mathcal {X},\xi _i}^{h}$ and
$\mathcal {O}_{\mathcal {X},\xi _i}^{h}$ and ![]() $V_i = \widehat {\mathcal {O}}_{\mathcal {X},\xi _i}^{h}$ have the same inertia group) and, hence,
$V_i = \widehat {\mathcal {O}}_{\mathcal {X},\xi _i}^{h}$ have the same inertia group) and, hence, ![]() $\operatorname {Spec}(B_K)\to \operatorname {Spec}(A)$ is tamely ramified at
$\operatorname {Spec}(B_K)\to \operatorname {Spec}(A)$ is tamely ramified at ![]() $\xi _i$.
$\xi _i$.
We now come to our main theorem.
Theorem 4.14 Let ![]() $X$ be a smooth quasi-paracompact and quasi-separated rigid-analytic space and suppose that gss formal models of
$X$ be a smooth quasi-paracompact and quasi-separated rigid-analytic space and suppose that gss formal models of ![]() $X$ are cofinal. Let
$X$ are cofinal. Let ![]() $Y\to X$ be an
$Y\to X$ be an ![]() $\mathrm {adm}$-covering space. If
$\mathrm {adm}$-covering space. If ![]() $Y\to X$ is tame, then it is a de Jong covering space.
$Y\to X$ is tame, then it is a de Jong covering space.
Proof. To show the assertion, it suffices to prove that ![]() $Y_{K'}\to X_{K'}$ is a de Jong covering space for some finite extension
$Y_{K'}\to X_{K'}$ is a de Jong covering space for some finite extension ![]() $K'$ of
$K'$ of ![]() $K$. Indeed, in the case of a separable extension, this follows from [Reference de JongdJ95b, Lemma 2.3], and in the purely inseparable case this is simple because
$K$. Indeed, in the case of a separable extension, this follows from [Reference de JongdJ95b, Lemma 2.3], and in the purely inseparable case this is simple because ![]() $\operatorname {Spa}(K')\to \operatorname {Spa}(K)$ is a universal homeomorphism. By assumption, there exists an open cover
$\operatorname {Spa}(K')\to \operatorname {Spa}(K)$ is a universal homeomorphism. By assumption, there exists an open cover ![]() $X=\bigcup _{i\in I} U_i$ such that
$X=\bigcup _{i\in I} U_i$ such that ![]() $Y|_{U_i}$ is the disjoint union of finite étale covers of
$Y|_{U_i}$ is the disjoint union of finite étale covers of ![]() $U_i$. By Lemma 4.4, we may assume that
$U_i$. By Lemma 4.4, we may assume that ![]() $U_i = \mathfrak {U}_{i,\eta }$ for an open cover
$U_i = \mathfrak {U}_{i,\eta }$ for an open cover ![]() $\mathfrak {X}=\bigcup _{i\in I}\mathfrak {U}_i$ of some admissible formal model
$\mathfrak {X}=\bigcup _{i\in I}\mathfrak {U}_i$ of some admissible formal model ![]() $\mathfrak {X}$ of
$\mathfrak {X}$ of ![]() $X$. Replacing
$X$. Replacing ![]() $K$ with a finite extension and performing an admissible blowup, we may assume that
$K$ with a finite extension and performing an admissible blowup, we may assume that ![]() $\mathfrak {X}$ is gss and, in particular,
$\mathfrak {X}$ is gss and, in particular, ![]() $\eta$-normal.
$\eta$-normal.
Let ![]() $\mathfrak {Y}\to \mathfrak {X}$ be the unique model of
$\mathfrak {Y}\to \mathfrak {X}$ be the unique model of ![]() $Y\to X$ with
$Y\to X$ with ![]() $\mathfrak {Y}$
$\mathfrak {Y}$ ![]() $\eta$-normal and which is locally on
$\eta$-normal and which is locally on ![]() $\mathfrak {X}$ the disjoint union of finite morphisms, provided by Corollary 4.2. Let
$\mathfrak {X}$ the disjoint union of finite morphisms, provided by Corollary 4.2. Let ![]() $D_1, \ldots, D_r$ be the irreducible components of
$D_1, \ldots, D_r$ be the irreducible components of ![]() $(\mathfrak {X}_k)_{\rm red}$. Thanks to Corollary 4.6, it suffices to show that the schemes
$(\mathfrak {X}_k)_{\rm red}$. Thanks to Corollary 4.6, it suffices to show that the schemes ![]() $(\mathfrak {Y}\times _{\mathfrak {X}} D_i)_{\rm red}$ are normal.
$(\mathfrak {Y}\times _{\mathfrak {X}} D_i)_{\rm red}$ are normal.
This assertion being local, we may assume that ![]() $\mathfrak {X}=\operatorname {Spf}(A)$ is affine and that
$\mathfrak {X}=\operatorname {Spf}(A)$ is affine and that ![]() $Y$ is the disjoint union of finite étale covers of
$Y$ is the disjoint union of finite étale covers of ![]() $X=\operatorname {Spa}(A_K)$. Working one connected component of
$X=\operatorname {Spa}(A_K)$. Working one connected component of ![]() $Y$ at a time, we may assume that
$Y$ at a time, we may assume that ![]() $Y\to X$ is finite étale and, therefore,
$Y\to X$ is finite étale and, therefore, ![]() $\mathfrak {Y}=\operatorname {Spf}(B)$ where
$\mathfrak {Y}=\operatorname {Spf}(B)$ where ![]() $B=B_K^{\circ }$,
$B=B_K^{\circ }$, ![]() $A\to B$ is finite, and
$A\to B$ is finite, and ![]() $A_K\to B_K$ is finite étale.
$A_K\to B_K$ is finite étale.
As ![]() $\operatorname {Spf}(A)$ and
$\operatorname {Spf}(A)$ and ![]() $\operatorname {Spec}(A)$ have the same completed local rings at closed points, and the same special fiber, the scheme
$\operatorname {Spec}(A)$ have the same completed local rings at closed points, and the same special fiber, the scheme ![]() $\operatorname {Spec}(A)$ is regular and the divisor
$\operatorname {Spec}(A)$ is regular and the divisor ![]() $V(\varpi )_{\rm red} = D_1\cup \cdots \cup D_r$ has strict normal crossings. By Lemma 4.13, the map of schemes
$V(\varpi )_{\rm red} = D_1\cup \cdots \cup D_r$ has strict normal crossings. By Lemma 4.13, the map of schemes ![]() $\operatorname {Spec}(B_K)\to \operatorname {Spec}(A)$ is tamely ramified along the
$\operatorname {Spec}(B_K)\to \operatorname {Spec}(A)$ is tamely ramified along the ![]() $D_i$. Therefore, by Corollary 4.10, the schemes
$D_i$. Therefore, by Corollary 4.10, the schemes ![]() $T_i=(\operatorname {Spec}(B)\times _{\operatorname {Spec}(A)} D_i)_{\rm red}$ are normal. As the
$T_i=(\operatorname {Spec}(B)\times _{\operatorname {Spec}(A)} D_i)_{\rm red}$ are normal. As the ![]() $D_i$ reside in the special fiber, we have
$D_i$ reside in the special fiber, we have ![]() $T_i = \mathfrak {Y}\times _{\mathfrak {X}} D_i$, and the theorem is proved.
$T_i = \mathfrak {Y}\times _{\mathfrak {X}} D_i$, and the theorem is proved.
Remark 4.15 In the language of logarithmic geometry, the proof of Theorem 4.14 gives the following result. If ![]() $\mathfrak {X}$ is a gss formal scheme over
$\mathfrak {X}$ is a gss formal scheme over ![]() $\mathcal {O}_K$ with rigid generic fiber
$\mathcal {O}_K$ with rigid generic fiber ![]() $X=\mathfrak {X}_\eta$ and if
$X=\mathfrak {X}_\eta$ and if ![]() $Y\to X$ is a tame finite étale covering, then
$Y\to X$ is a tame finite étale covering, then ![]() $Y$ extends uniquely to a Kummer étale morphism
$Y$ extends uniquely to a Kummer étale morphism ![]() $\mathfrak {Y}\to \mathfrak {X}$ where
$\mathfrak {Y}\to \mathfrak {X}$ where ![]() $\mathfrak {Y}$ and
$\mathfrak {Y}$ and ![]() $\mathfrak {X}$ are endowed with the natural log structures induced by
$\mathfrak {X}$ are endowed with the natural log structures induced by ![]() $\mathfrak {Y}_k$ and
$\mathfrak {Y}_k$ and ![]() $\mathfrak {X}_k$. Thus, the category
$\mathfrak {X}_k$. Thus, the category ![]() $\operatorname {\mathbf {F\acute {E}t}}_X$ is equivalent to the category of finite and Kummer étale coverings of
$\operatorname {\mathbf {F\acute {E}t}}_X$ is equivalent to the category of finite and Kummer étale coverings of ![]() $\mathfrak {X}$ treated as a log formal scheme.
$\mathfrak {X}$ treated as a log formal scheme.
We finally extend our result to the full generality by showing that every tame ![]() ${\unicode{x00E9}}{\text{t}}$-covering space is a de Jong covering space. We essentially use a bootstrap argument to reduce to Theorem 4.14.
${\unicode{x00E9}}{\text{t}}$-covering space is a de Jong covering space. We essentially use a bootstrap argument to reduce to Theorem 4.14.
Corollary 4.16 Let ![]() $X$ be a smooth quasi-paracompact and quasi-separated rigid
$X$ be a smooth quasi-paracompact and quasi-separated rigid ![]() $K$-space and suppose that the following conditions hold:
$K$-space and suppose that the following conditions hold:
(i) gss formal models of X are cofinal;
(ii) for every finite étale covering Y of an affinoid open of
 $X$, gss formal models of Y are cofinal.
$X$, gss formal models of Y are cofinal.
Then every tame ét-covering space of ![]() $X$ is a de Jong covering space.
$X$ is a de Jong covering space.
Proof. Let ![]() $Y\to X$ be a tame
$Y\to X$ be a tame ![]() ${\unicode{x00E9}}{\text{t}}$-covering space, and let
${\unicode{x00E9}}{\text{t}}$-covering space, and let ![]() $U\to X$ be an étale cover such that
$U\to X$ be an étale cover such that ![]() $Y_U$ is the disjoint union of finite étale coverings. By [Reference Achinger, Lara and YoucisALY21a, Proposition 3.7.2], the cover
$Y_U$ is the disjoint union of finite étale coverings. By [Reference Achinger, Lara and YoucisALY21a, Proposition 3.7.2], the cover ![]() $\{U\to X\}$ admits as a refinement a cover of the form
$\{U\to X\}$ admits as a refinement a cover of the form ![]() $\{V_{ij}\to X\}_{i\in I,j\in J_i}$ such that for all
$\{V_{ij}\to X\}_{i\in I,j\in J_i}$ such that for all ![]() $i\in I$ and
$i\in I$ and ![]() $j\in J_i$ one has a factorization
$j\in J_i$ one has a factorization
where ![]() $\{U_i\to X\}_{i\in I}$ forms an open cover, the maps
$\{U_i\to X\}_{i\in I}$ forms an open cover, the maps ![]() $W_i\to U_i$ are finite étale, and for every
$W_i\to U_i$ are finite étale, and for every ![]() $i\in I$, the family
$i\in I$, the family ![]() $\{V_{ij}\to W_i\}_{j\in I_j}$ is a finite affinoid open cover. Moreover, refining further we may assume that
$\{V_{ij}\to W_i\}_{j\in I_j}$ is a finite affinoid open cover. Moreover, refining further we may assume that ![]() $\{U_i\to X\}_{i\in I}$ is an affinoid cover of finite type. Now, each
$\{U_i\to X\}_{i\in I}$ is an affinoid cover of finite type. Now, each ![]() $Y_{W_i}\to W_i$ is a tame
$Y_{W_i}\to W_i$ is a tame ![]() $\mathrm {adm}$-covering space, and by assumption (ii) and Theorem 4.14, we see that it is a de Jong covering space. Therefore, by [Reference de JongdJ95b, Lemma 2.3] also each
$\mathrm {adm}$-covering space, and by assumption (ii) and Theorem 4.14, we see that it is a de Jong covering space. Therefore, by [Reference de JongdJ95b, Lemma 2.3] also each ![]() $Y_{U_i}\to U_i$ is a de Jong covering space. Thus,
$Y_{U_i}\to U_i$ is a de Jong covering space. Thus, ![]() $Y\to X$ is an
$Y\to X$ is an ![]() $\mathrm {adm}$-covering space, and we conclude using assumption (i) and Theorem 4.14.
$\mathrm {adm}$-covering space, and we conclude using assumption (i) and Theorem 4.14.
As remarked before all smooth quasi-paracompact and quasi-separated rigid ![]() $K$-varieties, where
$K$-varieties, where ![]() $K$ has equal characteristic zero, have cofinal gss formal models. Moreover, because tameness is automatic when the residue field
$K$ has equal characteristic zero, have cofinal gss formal models. Moreover, because tameness is automatic when the residue field ![]() $k$ is of characteristic zero, we deduce the following result.
$k$ is of characteristic zero, we deduce the following result.
Corollary 4.17 Let ![]() $K$ be a complete discrete valuation field of residue characteristic zero, and let
$K$ be a complete discrete valuation field of residue characteristic zero, and let ![]() $X$ be a smooth quasi-paracompact and quasi-separated rigid-analytic space over
$X$ be a smooth quasi-paracompact and quasi-separated rigid-analytic space over ![]() $K$. Then every ét-covering space of
$K$. Then every ét-covering space of ![]() $X$ is a de Jong covering space.
$X$ is a de Jong covering space.
Acknowledgements
The authors would like to thank Hélène Esnault, Joachim Jelisiejew, and Michael Temkin for helpful conversations. We thank the referee for useful comments and suggestions. A.Y. completed the final editing of this document while a JSPS fellow at the University of Tokyo.
Appendix A.  $\eta$-normality
$\eta$-normality
The rigid generic fiber of a connected admissible formal scheme over ![]() $\mathcal {O}_K$ may be disconnected. In order to control its connectedness, we introduce in this appendix the condition of
$\mathcal {O}_K$ may be disconnected. In order to control its connectedness, we introduce in this appendix the condition of ![]() $\eta$-normality, i.e. being ‘integrally closed in the rigid generic fiber’. To be able to apply it to questions concerning covering spaces, we need to show that if
$\eta$-normality, i.e. being ‘integrally closed in the rigid generic fiber’. To be able to apply it to questions concerning covering spaces, we need to show that if ![]() $\mathfrak {X}'\to \mathfrak {X}$ is étale and
$\mathfrak {X}'\to \mathfrak {X}$ is étale and ![]() $\mathfrak {X}$ is
$\mathfrak {X}$ is ![]() $\eta$-normal, then so is
$\eta$-normal, then so is ![]() $\mathfrak {X}'$ (Proposition A.16). To this end, we provide a version of Serre's criterion ‘normal
$\mathfrak {X}'$ (Proposition A.16). To this end, we provide a version of Serre's criterion ‘normal ![]() $=(S_2)+(R_1)$’ (Proposition A.15). The reader should be aware that many of the proofs in the following are considerably easier in the situation when
$=(S_2)+(R_1)$’ (Proposition A.15). The reader should be aware that many of the proofs in the following are considerably easier in the situation when ![]() $K$ is discretely valued.
$K$ is discretely valued.
A.1 The definition of  $\eta$-normality
$\eta$-normality
We start with a definition of ![]() $\eta$-normality (cf. [Reference de JongdJ95a, Remark 7.4.2]).
$\eta$-normality (cf. [Reference de JongdJ95a, Remark 7.4.2]).
Definition A.1 (Cf. [Reference TemkinTem10, p. 619])
An ![]() $\mathcal {O}_K$-algebra
$\mathcal {O}_K$-algebra ![]() $A$ topologically of finite type over
$A$ topologically of finite type over ![]() $\mathcal {O}_K$ is called
$\mathcal {O}_K$ is called ![]() $\eta$-normal if it is
$\eta$-normal if it is ![]() $\mathcal {O}_K$-torsion free and integrally closed in
$\mathcal {O}_K$-torsion free and integrally closed in ![]() $A_K$. A formal scheme
$A_K$. A formal scheme ![]() $\mathfrak {X}$ locally of finite type over
$\mathfrak {X}$ locally of finite type over ![]() $\mathcal {O}_K$ is called
$\mathcal {O}_K$ is called ![]() $\eta$-normal if for every affine open
$\eta$-normal if for every affine open ![]() $\operatorname {Spf}(A)\subseteq \mathfrak {X}$, the algebra
$\operatorname {Spf}(A)\subseteq \mathfrak {X}$, the algebra ![]() $A$ is
$A$ is ![]() $\eta$-normal.
$\eta$-normal.
In other words, ![]() $A$ is
$A$ is ![]() $\eta$-normal if
$\eta$-normal if ![]() $A=A_K^{\circ }$. In particular,
$A=A_K^{\circ }$. In particular, ![]() $A$ is reduced because if
$A$ is reduced because if ![]() $f$ is nilpotent, then
$f$ is nilpotent, then ![]() $K\cdot f\subseteq A_K^{\circ }$ and
$K\cdot f\subseteq A_K^{\circ }$ and ![]() $A_K^{\circ }$ is not bounded which contradicts that it is equal to
$A_K^{\circ }$ is not bounded which contradicts that it is equal to ![]() $A$. One can rephrase the condition that
$A$. One can rephrase the condition that ![]() $\mathfrak {X}$ is
$\mathfrak {X}$ is ![]() $\eta$-normal by saying that the map of sheaves
$\eta$-normal by saying that the map of sheaves ![]() $\mathcal {O}_\mathfrak {X}\to \operatorname {sp}_{\mathfrak {X},*}\, \mathcal {O}_{\mathfrak {X}_\eta }^{+}$ is an isomorphism. In particular, the property of being
$\mathcal {O}_\mathfrak {X}\to \operatorname {sp}_{\mathfrak {X},*}\, \mathcal {O}_{\mathfrak {X}_\eta }^{+}$ is an isomorphism. In particular, the property of being ![]() $\eta$-normal can be checked on a single affine open cover of
$\eta$-normal can be checked on a single affine open cover of ![]() $\mathfrak {X}$.
$\mathfrak {X}$.
The following lemma gives common conditions which guarantee ![]() $\eta$-normality.
$\eta$-normality.
Lemma A.2 Suppose that one of the following conditions holds:
(a)
 $\mathfrak {X}_k$ is reduced;
$\mathfrak {X}_k$ is reduced;(b)
 $\mathfrak {X}$ is formally normal (i.e.
$\mathfrak {X}$ is formally normal (i.e.  $\mathcal {O}_{\mathfrak {X},x}$ is normal for all
$\mathcal {O}_{\mathfrak {X},x}$ is normal for all  $x$ in
$x$ in  $\mathfrak {X})$.
$\mathfrak {X})$.
Then ![]() $\mathfrak {X}$ is
$\mathfrak {X}$ is ![]() $\eta$-normal.
$\eta$-normal.
Proof. For condition (a) we may assume that ![]() $\mathfrak {X}$ is affine, in which case the claim follows from [Reference Bosch, Lütkebohmert and RaynaudBLR95, Proposition 1.1]. For condition (b) it suffices to show that if
$\mathfrak {X}$ is affine, in which case the claim follows from [Reference Bosch, Lütkebohmert and RaynaudBLR95, Proposition 1.1]. For condition (b) it suffices to show that if ![]() $\operatorname {Spf}(A)$ is formally normal and connected, then
$\operatorname {Spf}(A)$ is formally normal and connected, then ![]() $A$ is a normal domain. As
$A$ is a normal domain. As ![]() $\operatorname {Spec}(A)$ is connected and topologically Noetherian, we know by [SP21, Tag 0357] that it suffices to show that
$\operatorname {Spec}(A)$ is connected and topologically Noetherian, we know by [SP21, Tag 0357] that it suffices to show that ![]() $\operatorname {Spec}(A)$ is a normal scheme. However, by [SP21, Tag 030B] it suffices to show that for every maximal ideal
$\operatorname {Spec}(A)$ is a normal scheme. However, by [SP21, Tag 030B] it suffices to show that for every maximal ideal ![]() $\mathfrak {m}$ of
$\mathfrak {m}$ of ![]() $A$ that
$A$ that ![]() $A_\mathfrak {m}$ is a normal domain. Note though that since
$A_\mathfrak {m}$ is a normal domain. Note though that since ![]() $A$ is
$A$ is ![]() $\varpi$-adically complete, that
$\varpi$-adically complete, that ![]() $\varpi$ is contained in the Jacobson radical of
$\varpi$ is contained in the Jacobson radical of ![]() $A$ (see [Reference Fujiwara and KatoFK18, Chapter 0, Lemma 7.2.13]), and so
$A$ (see [Reference Fujiwara and KatoFK18, Chapter 0, Lemma 7.2.13]), and so ![]() $\mathfrak {m}\supseteq \sqrt {(\varpi )}A=\mathfrak {m}_KA$. Thus, we see that
$\mathfrak {m}\supseteq \sqrt {(\varpi )}A=\mathfrak {m}_KA$. Thus, we see that ![]() $\mathfrak {m}$ corresponds to a point
$\mathfrak {m}$ corresponds to a point ![]() $x$ of
$x$ of ![]() $\operatorname {Spf}(A)$. Moreover, we have a natural map
$\operatorname {Spf}(A)$. Moreover, we have a natural map ![]() $A_\mathfrak {m}\to \mathcal {O}_{\mathfrak {X},x}$ obtained as the colimit of the natural maps
$A_\mathfrak {m}\to \mathcal {O}_{\mathfrak {X},x}$ obtained as the colimit of the natural maps ![]() $A[f^{-1}]\to A\langle f^{-1}\rangle$. By Gabber's theorem (see [Reference BoschBos14, Lemma 8.2/2]) each map
$A[f^{-1}]\to A\langle f^{-1}\rangle$. By Gabber's theorem (see [Reference BoschBos14, Lemma 8.2/2]) each map ![]() $A[f^{-1}]\to A\langle f^{-1}\rangle$ is flat and, thus, is the map
$A[f^{-1}]\to A\langle f^{-1}\rangle$ is flat and, thus, is the map ![]() $A_\mathfrak {m}\to \mathcal {O}_{\mathfrak {X},x}$. This map is local (cf. [Reference BoschBos14, Remark 7.2/1]) and faithfully flat by [SP21, Tag 00HQ]. Thus,
$A_\mathfrak {m}\to \mathcal {O}_{\mathfrak {X},x}$. This map is local (cf. [Reference BoschBos14, Remark 7.2/1]) and faithfully flat by [SP21, Tag 00HQ]. Thus, ![]() $A_\mathfrak {m}$ is normal by [SP21, Tag 033G].
$A_\mathfrak {m}$ is normal by [SP21, Tag 033G].
For us, the main use for ![]() $\eta$-normality is the fact that connectedness is preserved when passing to the rigid generic fiber.
$\eta$-normality is the fact that connectedness is preserved when passing to the rigid generic fiber.
Lemma A.3 Let ![]() $\mathfrak {X}$ be formal scheme locally of finite type over
$\mathfrak {X}$ be formal scheme locally of finite type over ![]() $\mathcal {O}_K$ which is
$\mathcal {O}_K$ which is ![]() $\eta$-normal. If
$\eta$-normal. If ![]() $\mathfrak {X}$ is connected, then so is
$\mathfrak {X}$ is connected, then so is ![]() $\mathfrak {X}_\eta$.
$\mathfrak {X}_\eta$.
Proof. By assumption, the map ![]() $\mathcal {O}_{\mathfrak {X}} \to \operatorname {sp}_{\mathfrak {X},*}\, \mathcal {O}_{\mathfrak {X}_\eta }^{+}$ is an isomorphism. As every idempotent
$\mathcal {O}_{\mathfrak {X}} \to \operatorname {sp}_{\mathfrak {X},*}\, \mathcal {O}_{\mathfrak {X}_\eta }^{+}$ is an isomorphism. As every idempotent ![]() $\Gamma (\mathfrak {X}_\eta, \mathcal {O}_{\mathfrak {X}_\eta })$ belongs to
$\Gamma (\mathfrak {X}_\eta, \mathcal {O}_{\mathfrak {X}_\eta })$ belongs to ![]() $\Gamma (\mathfrak {X}_\eta, \mathcal {O}_{\mathfrak {X}_\eta }^{+})=\Gamma (\mathfrak {X}, \mathcal {O}_{\mathfrak {X}})$, we deduce that
$\Gamma (\mathfrak {X}_\eta, \mathcal {O}_{\mathfrak {X}_\eta }^{+})=\Gamma (\mathfrak {X}, \mathcal {O}_{\mathfrak {X}})$, we deduce that ![]() $\Gamma (\mathfrak {X}_\eta, \mathcal {O}_{\mathfrak {X}_\eta })$ has no non-trivial idempotents, so
$\Gamma (\mathfrak {X}_\eta, \mathcal {O}_{\mathfrak {X}_\eta })$ has no non-trivial idempotents, so ![]() $\mathfrak {X}_\eta$ is connected.
$\mathfrak {X}_\eta$ is connected.
A.2 Conditions  $(S'_1)$ and
$(S'_1)$ and  $(S'_2)$
$(S'_2)$
In the absence of a robust theory of depth and embedded components in the non-Noetherian setting, we use the following condition as a substitute for the condition ![]() $(S_1)$.
$(S_1)$.
Definition A.4 Let ![]() $X$ be a locally topologically Noetherian scheme. We say that
$X$ be a locally topologically Noetherian scheme. We say that ![]() $X$ satisfies condition
$X$ satisfies condition ![]() $(S'_1)$ if every dense open subscheme
$(S'_1)$ if every dense open subscheme ![]() $U\subseteq X$ is schematically dense (i.e.
$U\subseteq X$ is schematically dense (i.e. ![]() $\mathcal {O}_X\to j_* \mathcal {O}_U$ is injective, where
$\mathcal {O}_X\to j_* \mathcal {O}_U$ is injective, where ![]() $j\colon U\to X$ is the inclusion).
$j\colon U\to X$ is the inclusion).
Lemma A.5 Let ![]() $X$ be a locally topologically Noetherian scheme.
$X$ be a locally topologically Noetherian scheme.
(a) If
 $X=\operatorname {Spec}(A)$ is affine, then
$X=\operatorname {Spec}(A)$ is affine, then  $X$ satisfies
$X$ satisfies  $(S_1')$ if and only if every zero divisor of
$(S_1')$ if and only if every zero divisor of  $A$ belongs to at least one minimal prime of
$A$ belongs to at least one minimal prime of  $A$.
$A$.(b) The scheme
 $X$ satisfies condition
$X$ satisfies condition  $(S_1')$ if and only if for one (equivalently, for all) open covers
$(S_1')$ if and only if for one (equivalently, for all) open covers  $\{U_i\}$ of
$\{U_i\}$ of  $X$ each
$X$ each  $U_i$ satisfies condition
$U_i$ satisfies condition  $(S_1')$.
$(S_1')$.(c) If
 $X$ is locally Noetherian, then
$X$ is locally Noetherian, then  $X$ satisfies
$X$ satisfies  $(S'_1)$ if and only if it has no embedded points or, equivalently, if it satisfies condition
$(S'_1)$ if and only if it has no embedded points or, equivalently, if it satisfies condition  $(S_1)$.
$(S_1)$.
Proof. (a) Let us first note that an open of the form ![]() $D(g)$,
$D(g)$, ![]() $g\in A$ is dense in
$g\in A$ is dense in ![]() $X=\operatorname {Spec}(A)$ if and only if
$X=\operatorname {Spec}(A)$ if and only if ![]() $g$ belongs to no minimal prime of
$g$ belongs to no minimal prime of ![]() $A$. To see that
$A$. To see that ![]() $(S'_1)$ implies the given condition, take
$(S'_1)$ implies the given condition, take ![]() $U=D(g)$ and note that the equation
$U=D(g)$ and note that the equation ![]() $gf=0$ implies that
$gf=0$ implies that ![]() $f|_U=0$ and, hence,
$f|_U=0$ and, hence, ![]() $f=0$.
$f=0$.
Conversely, assume the condition holds and let ![]() $U\subseteq X$ be a dense open. We first claim that
$U\subseteq X$ be a dense open. We first claim that ![]() $U$ contains a dense open of the form
$U$ contains a dense open of the form ![]() $D(g)$ for some
$D(g)$ for some ![]() $g\in A$. Indeed, writing
$g\in A$. Indeed, writing ![]() $X\setminus U=V(I)$ for some ideal
$X\setminus U=V(I)$ for some ideal ![]() $I\subseteq A$, and denoting by
$I\subseteq A$, and denoting by ![]() $\mathfrak {p}_1, \ldots, \mathfrak {p}_r$ the minimal primes of
$\mathfrak {p}_1, \ldots, \mathfrak {p}_r$ the minimal primes of ![]() $A$, the condition that
$A$, the condition that ![]() $U$ is dense means that
$U$ is dense means that ![]() $I\not \subseteq \mathfrak {p}_i$ for all
$I\not \subseteq \mathfrak {p}_i$ for all ![]() $i$. By prime avoidance [SP21, Tag 00DS] there exists a
$i$. By prime avoidance [SP21, Tag 00DS] there exists a ![]() $g\in I$ with
$g\in I$ with ![]() $g\notin \mathfrak {p}_i$ for all
$g\notin \mathfrak {p}_i$ for all ![]() $i$. Then
$i$. Then ![]() $D(g)\subseteq U$ and
$D(g)\subseteq U$ and ![]() $D(g)$ is dense. Thus, we may assume that
$D(g)$ is dense. Thus, we may assume that ![]() $U=D(g)$.
$U=D(g)$.
Now, the inclusion ![]() $j\colon U\to X$ is affine and, hence,
$j\colon U\to X$ is affine and, hence, ![]() $\mathcal {O}_X\to j_*\mathcal {O}_U$ is injective if and only if
$\mathcal {O}_X\to j_*\mathcal {O}_U$ is injective if and only if ![]() $A\to A[ {1}/{g}]$ is injective. Its kernel consists of elements
$A\to A[ {1}/{g}]$ is injective. Its kernel consists of elements ![]() $f\in A$ such that
$f\in A$ such that ![]() $g^{n} f =0$ for some
$g^{n} f =0$ for some ![]() $n\geqslant 1$. As the powers
$n\geqslant 1$. As the powers ![]() $g^{n}$ belong to no minimal prime of
$g^{n}$ belong to no minimal prime of ![]() $A$, the given condition implies that
$A$, the given condition implies that ![]() $f=0$.
$f=0$.
(b) If ![]() $X=\bigcup U_i$ and the
$X=\bigcup U_i$ and the ![]() $U_i$ satisfy
$U_i$ satisfy ![]() $(S'_1)$, then so does
$(S'_1)$, then so does ![]() $X$. For the converse, it suffices to show that if
$X$. For the converse, it suffices to show that if ![]() $X$ satisfies
$X$ satisfies ![]() $(S'_1)$, then every open
$(S'_1)$, then every open ![]() $X'\subseteq X$ satisfies
$X'\subseteq X$ satisfies ![]() $(S'_1)$. If
$(S'_1)$. If ![]() $U'\subseteq X'$ is a dense open, then let
$U'\subseteq X'$ is a dense open, then let ![]() $U$ be the union of all opens of
$U$ be the union of all opens of ![]() $X$ whose intersection with
$X$ whose intersection with ![]() $X'$ equals
$X'$ equals ![]() $U'$. Then
$U'$. Then ![]() $U$ is a dense open of
$U$ is a dense open of ![]() $X$, so
$X$, so ![]() $\mathcal {O}_X\to j_*\mathcal {O}_U$ is injective, and so is its restriction to
$\mathcal {O}_X\to j_*\mathcal {O}_U$ is injective, and so is its restriction to ![]() $X'$.
$X'$.
Lemma A.6 Let ![]() $Y\to X$ be an étale morphism of locally topologically Noetherian schemes.Footnote 8 If
$Y\to X$ be an étale morphism of locally topologically Noetherian schemes.Footnote 8 If ![]() $X$ satisfies
$X$ satisfies ![]() $(S_1')$, then so does
$(S_1')$, then so does ![]() $Y$.
$Y$.
Proof. As the condition is local on ![]() $Y$, we may assume that
$Y$, we may assume that ![]() $X$ and
$X$ and ![]() $Y$ are affine and
$Y$ are affine and ![]() $f$ is standard étale, i.e.
$f$ is standard étale, i.e.
where ![]() $f\in A[T]$ is a monic polynomial whose derivative
$f\in A[T]$ is a monic polynomial whose derivative ![]() $f'$ is invertible in
$f'$ is invertible in ![]() $B$ (see [SP21, Tag 02GT]). Let
$B$ (see [SP21, Tag 02GT]). Let ![]() $C=A[T]/(f)$ and let
$C=A[T]/(f)$ and let ![]() $Z=\operatorname {Spec}(C)$, so that
$Z=\operatorname {Spec}(C)$, so that ![]() $Y$ is an open subset of
$Y$ is an open subset of ![]() $Z$. As
$Z$. As ![]() $f$ is monic,
$f$ is monic, ![]() $C$ is a free
$C$ is a free ![]() $A$-module of rank
$A$-module of rank ![]() $\deg (f)$ and, hence, the morphism
$\deg (f)$ and, hence, the morphism ![]() $\varphi \colon Z\to X$ is finite and locally free and therefore locally of finite presentation (see [SP21, Tag 02KB]).
$\varphi \colon Z\to X$ is finite and locally free and therefore locally of finite presentation (see [SP21, Tag 02KB]).
As ![]() $Y$ is an open in
$Y$ is an open in ![]() $Z$, it suffices to show that
$Z$, it suffices to show that ![]() $Z$ satisfies
$Z$ satisfies ![]() $(S_1')$. To this end, suppose that
$(S_1')$. To this end, suppose that ![]() $W\subseteq Z$ is a dense open and
$W\subseteq Z$ is a dense open and ![]() $x\in C$ is an element whose restriction to
$x\in C$ is an element whose restriction to ![]() $W$ is zero. We have to show that
$W$ is zero. We have to show that ![]() $x=0$. Let
$x=0$. Let ![]() $U=X\setminus \varphi (Z\setminus W)$; this is an open subset because
$U=X\setminus \varphi (Z\setminus W)$; this is an open subset because ![]() $\varphi$ is a closed map, and
$\varphi$ is a closed map, and ![]() $\varphi ^{-1}(U)$ is contained in
$\varphi ^{-1}(U)$ is contained in ![]() $W$. We claim that
$W$. We claim that ![]() $\varphi ^{-1}(U)$ is also dense in
$\varphi ^{-1}(U)$ is also dense in ![]() $Z$; otherwise there exists a non-empty open
$Z$; otherwise there exists a non-empty open ![]() $V\subseteq Z$ with
$V\subseteq Z$ with ![]() $\varphi (V)$ contained in
$\varphi (V)$ contained in ![]() $\varphi (Z\setminus W)$. But
$\varphi (Z\setminus W)$. But ![]() $\varphi (V)$ is open (because
$\varphi (V)$ is open (because ![]() $\varphi$ is flat and finitely presented, see [SP21, Tag 01UA]) and so contains a generic point
$\varphi$ is flat and finitely presented, see [SP21, Tag 01UA]) and so contains a generic point ![]() $\xi$. That said, the fiber
$\xi$. That said, the fiber ![]() $\varphi ^{-1}(\xi )$ consists entirely of generic points (cf. [SP21, Tag 0ECG]) which would imply that
$\varphi ^{-1}(\xi )$ consists entirely of generic points (cf. [SP21, Tag 0ECG]) which would imply that ![]() $Z\setminus W$ contains a generic point, which is impossible.
$Z\setminus W$ contains a generic point, which is impossible.
Writing ![]() $x=\sum _{i<\deg (f)} a_i T^{i}$ with
$x=\sum _{i<\deg (f)} a_i T^{i}$ with ![]() $a_i\in A$, if
$a_i\in A$, if ![]() $x$ vanishes on
$x$ vanishes on ![]() $W$, it vanishes on
$W$, it vanishes on ![]() $\varphi ^{-1}(U)$, and then the coefficients
$\varphi ^{-1}(U)$, and then the coefficients ![]() $a_i$ vanish on the dense open
$a_i$ vanish on the dense open ![]() $U\subseteq X$. As
$U\subseteq X$. As ![]() $X$ satisfies
$X$ satisfies ![]() $(S'_1)$, we must have
$(S'_1)$, we must have ![]() $a_i=0$ for all
$a_i=0$ for all ![]() $i$, and hence
$i$, and hence ![]() $x=0$, as desired.
$x=0$, as desired.
Proposition A.7 Let ![]() $A$ be an admissible
$A$ be an admissible ![]() $\mathcal {O}_K$-algebra. Then the following conditions are equivalent:
$\mathcal {O}_K$-algebra. Then the following conditions are equivalent:
(a) for some pseudo-uniformizer
 $\varpi$, the scheme
$\varpi$, the scheme  $\operatorname {Spec}(A/\varpi A)$ satisfies
$\operatorname {Spec}(A/\varpi A)$ satisfies  $(S'_1)$;
$(S'_1)$;(b) for every pseudo-uniformizer
 $\varpi$, the scheme
$\varpi$, the scheme  $\operatorname {Spec}(A/\varpi A)$ satisfies
$\operatorname {Spec}(A/\varpi A)$ satisfies  $(S'_1)$.
$(S'_1)$.
Proof. It suffices to show the following two claims.
(i) If
 $\operatorname {Spec}(A/\varpi ' A)$ and
$\operatorname {Spec}(A/\varpi ' A)$ and  $\operatorname {Spec}(A/\varpi '' A)$ both satisfy
$\operatorname {Spec}(A/\varpi '' A)$ both satisfy  $(S_1')$, then so does
$(S_1')$, then so does  $\operatorname {Spec}(A/\varpi A)$, where
$\operatorname {Spec}(A/\varpi A)$, where  $\varpi = \varpi '\varpi ''$.
$\varpi = \varpi '\varpi ''$.(ii) If
 $\operatorname {Spec}(A/\varpi A)$ satisfies
$\operatorname {Spec}(A/\varpi A)$ satisfies  $(S_1')$ and
$(S_1')$ and  $\varpi '$ divides
$\varpi '$ divides  $\varpi$, then
$\varpi$, then  $\operatorname {Spec}(A/\varpi ' A)$ satisfies
$\operatorname {Spec}(A/\varpi ' A)$ satisfies  $(S_1')$.
$(S_1')$.
For the first claim, suppose that ![]() $g\in A/\varpi A$ belongs to no minimal prime and
$g\in A/\varpi A$ belongs to no minimal prime and ![]() $f\in A/\varpi A$ is such that
$f\in A/\varpi A$ is such that ![]() $gf=0$. Reducing modulo
$gf=0$. Reducing modulo ![]() $\varpi '$ and using the
$\varpi '$ and using the ![]() $(S1')$ property of
$(S1')$ property of ![]() $\operatorname {Spec}(A/\varpi ' A)$, we see that
$\operatorname {Spec}(A/\varpi ' A)$, we see that ![]() $f \in \varpi ' A/\varpi A$, say
$f \in \varpi ' A/\varpi A$, say ![]() $f = \varpi ' f'$. Then
$f = \varpi ' f'$. Then ![]() $\varpi ' f' g = 0$ implies (because
$\varpi ' f' g = 0$ implies (because ![]() $A$ is flat over
$A$ is flat over ![]() $\mathcal {O}_K$) that
$\mathcal {O}_K$) that ![]() $f' g = \varpi '' h$ for some
$f' g = \varpi '' h$ for some ![]() $h$.Footnote 9 Reducing modulo
$h$.Footnote 9 Reducing modulo ![]() $\varpi ''$ we see that
$\varpi ''$ we see that ![]() $f'g=0$ in
$f'g=0$ in ![]() $A/\varpi ''A$ and so using the
$A/\varpi ''A$ and so using the ![]() $(S_1')$ property of
$(S_1')$ property of ![]() $\operatorname {Spec}(A/\varpi '')$, we see that
$\operatorname {Spec}(A/\varpi '')$, we see that ![]() $f'=0$ in
$f'=0$ in ![]() $A/\varpi 'A$ and so
$A/\varpi 'A$ and so ![]() $f' = \varpi '' f''$ in
$f' = \varpi '' f''$ in ![]() $A/\varpi A$, so
$A/\varpi A$, so ![]() $f= \varpi 'f'=\varpi ' \varpi '' f'' = 0$ as desired.
$f= \varpi 'f'=\varpi ' \varpi '' f'' = 0$ as desired.
For the second claim, suppose that ![]() $g'\in A/\varpi ' A$ belongs to no minimal prime and
$g'\in A/\varpi ' A$ belongs to no minimal prime and ![]() $f'\in A/\varpi ' A$ is such that
$f'\in A/\varpi ' A$ is such that ![]() $g'f'=0$. Let
$g'f'=0$. Let ![]() $f$ and
$f$ and ![]() $g$ be lifts to
$g$ be lifts to ![]() $A/\varpi A$, so that
$A/\varpi A$, so that ![]() $gf = \varpi ' h$ for some
$gf = \varpi ' h$ for some ![]() $h$. Write
$h$. Write ![]() $\varpi = \varpi '\varpi ''$, so
$\varpi = \varpi '\varpi ''$, so ![]() $f'' := \varpi '' f$ has the property that
$f'' := \varpi '' f$ has the property that ![]() $gf'' = \varpi ''gf =\varpi ''\varpi ' h =0$. By the
$gf'' = \varpi ''gf =\varpi ''\varpi ' h =0$. By the ![]() $(S_1')$ property of
$(S_1')$ property of ![]() $\operatorname {Spec}(A/\varpi A)$, we thus have
$\operatorname {Spec}(A/\varpi A)$, we thus have ![]() $f''=\varpi ''f =0$. As
$f''=\varpi ''f =0$. As ![]() $A$ is flat over
$A$ is flat over ![]() $\mathcal {O}_K$, we must have
$\mathcal {O}_K$, we must have ![]() $f \in \varpi ' A$, so
$f \in \varpi ' A$, so ![]() $f'=0$.
$f'=0$.
Remark A.8 We do not know if the conditions in Proposition A.7 are further equivalent to the condition that ![]() $\operatorname {Spec}(A_k)$ satisfies
$\operatorname {Spec}(A_k)$ satisfies ![]() $(S'_1)$ (or, equivalently,
$(S'_1)$ (or, equivalently, ![]() $(S_1)$) in the case when
$(S_1)$) in the case when ![]() $K$ is not discretely valued.
$K$ is not discretely valued.
Definition A.9 Let ![]() $\mathfrak {X}$ be a formal scheme locally of finite type over
$\mathfrak {X}$ be a formal scheme locally of finite type over ![]() $\mathcal {O}_K$. We say that
$\mathcal {O}_K$. We say that ![]() $\mathfrak {X}$ satisfies condition
$\mathfrak {X}$ satisfies condition ![]() $(S'_2)$ if it is flat over
$(S'_2)$ if it is flat over ![]() $\mathcal {O}_K$ and for every (equivalently, any) pseudo-uniformizer
$\mathcal {O}_K$ and for every (equivalently, any) pseudo-uniformizer ![]() $\varpi$, the scheme
$\varpi$, the scheme ![]() $\mathfrak {X}\otimes (\mathcal {O}_K/\varpi )$ satisfies condition
$\mathfrak {X}\otimes (\mathcal {O}_K/\varpi )$ satisfies condition ![]() $(S'_1)$.
$(S'_1)$.
The following result follows from Lemma A.6 and [Reference Fujiwara and KatoFK18, Chapter I, Proposition 5.3.11].
Lemma A.10 Let ![]() $\mathfrak {Y}\to \mathfrak {X}$ be an étale morphism of formal schemes locally of finite type over
$\mathfrak {Y}\to \mathfrak {X}$ be an étale morphism of formal schemes locally of finite type over ![]() $\mathcal {O}_K$. If
$\mathcal {O}_K$. If ![]() $\mathfrak {X}$ satisfies
$\mathfrak {X}$ satisfies ![]() $(S'_2)$, then so does
$(S'_2)$, then so does ![]() $\mathfrak {Y}$.
$\mathfrak {Y}$.
A.3 Condition  $(R'_1)$
$(R'_1)$
In our relative situation over ![]() $\mathcal {O}_K$ the replacement for the usual condition
$\mathcal {O}_K$ the replacement for the usual condition ![]() $(R_1)$ for a formal scheme
$(R_1)$ for a formal scheme ![]() $\mathfrak {X}$ is a statement about the local rings of
$\mathfrak {X}$ is a statement about the local rings of ![]() $\mathfrak {X}$ at the generic points
$\mathfrak {X}$ at the generic points ![]() $\zeta$ of
$\zeta$ of ![]() $\mathfrak {X}_k$. As
$\mathfrak {X}_k$. As ![]() $\zeta$ is codimension zero in
$\zeta$ is codimension zero in ![]() $\mathfrak {X}_k$ it is intuitively of codimension one in
$\mathfrak {X}_k$ it is intuitively of codimension one in ![]() $\mathfrak {X}$ and so we would then like to claim that
$\mathfrak {X}$ and so we would then like to claim that ![]() $\mathcal {O}_{\mathfrak {X},\zeta }$ is a discrete valuation ring. As
$\mathcal {O}_{\mathfrak {X},\zeta }$ is a discrete valuation ring. As ![]() $\mathfrak {X}$ is not necessarily Noetherian, we instead require that
$\mathfrak {X}$ is not necessarily Noetherian, we instead require that ![]() $\mathcal {O}_{\mathfrak {X},\zeta }$ is a valuation ring.
$\mathcal {O}_{\mathfrak {X},\zeta }$ is a valuation ring.
To this end, for a formal scheme ![]() $\mathfrak {X}$ locally of finite type over
$\mathfrak {X}$ locally of finite type over ![]() $\mathcal {O}_K$ let us denote by
$\mathcal {O}_K$ let us denote by ![]() $I(\mathfrak {X})$ the set of generic points of the scheme
$I(\mathfrak {X})$ the set of generic points of the scheme ![]() $\mathfrak {X}_k$ or, equivalently, the set of generic points of the locally spectral space
$\mathfrak {X}_k$ or, equivalently, the set of generic points of the locally spectral space ![]() $|\mathfrak {X}|$.
$|\mathfrak {X}|$.
Definition A.11 Let ![]() $\mathfrak {X}$ be an admissible formal scheme over
$\mathfrak {X}$ be an admissible formal scheme over ![]() $\mathcal {O}_K$. We say that
$\mathcal {O}_K$. We say that ![]() $\mathfrak {X}$ satisfies condition
$\mathfrak {X}$ satisfies condition ![]() $(R'_1)$ if for every
$(R'_1)$ if for every ![]() $\zeta$ in
$\zeta$ in ![]() $I(\mathfrak {X})$, the local ring
$I(\mathfrak {X})$, the local ring ![]() $\mathcal {O}_{\mathfrak {X}, \zeta }$ is a valuation ring.
$\mathcal {O}_{\mathfrak {X}, \zeta }$ is a valuation ring.
Assume that ![]() $\mathfrak {X}$ is quasi-compact and set
$\mathfrak {X}$ is quasi-compact and set ![]() $X=\mathfrak {X}_\eta$. It will be useful in the proof of Lemma A.14 and Proposition A.15 to relate the ring
$X=\mathfrak {X}_\eta$. It will be useful in the proof of Lemma A.14 and Proposition A.15 to relate the ring ![]() $\mathcal {O}_{\mathfrak {X},\zeta }$ for
$\mathcal {O}_{\mathfrak {X},\zeta }$ for ![]() $\zeta$ in
$\zeta$ in ![]() $I(\mathfrak {X})$ to local rings of
$I(\mathfrak {X})$ to local rings of ![]() $\mathcal {O}_X^{+}$. To this end, following [Reference Fujiwara and KatoFK18, Chapter II, Definition 11.1.2] let us denote by
$\mathcal {O}_X^{+}$. To this end, following [Reference Fujiwara and KatoFK18, Chapter II, Definition 11.1.2] let us denote by ![]() $D(\mathfrak {X})$ the set of divisorial points of
$D(\mathfrak {X})$ the set of divisorial points of ![]() $X$ which are residually finite over
$X$ which are residually finite over ![]() $\mathfrak {X}$. By [Reference Fujiwara and KatoFK18, Chapter II, Proposition 11.1.3] and [Reference Fujiwara and KatoFK18, Chapter II, Theorem 11.2.1] one has that the set
$\mathfrak {X}$. By [Reference Fujiwara and KatoFK18, Chapter II, Proposition 11.1.3] and [Reference Fujiwara and KatoFK18, Chapter II, Theorem 11.2.1] one has that the set ![]() $D(\mathfrak {X})$ is a finite set of maximal points, and that the equality
$D(\mathfrak {X})$ is a finite set of maximal points, and that the equality
holds. Moreover, one has by [Reference Fujiwara and KatoFK18, Chapter II, Theorem 11.2.1] and [Reference Bosch, Güntzer and RemmertBGR84, Proposition 6.3/3] that
where ![]() $\|\cdot \|_\mathrm {sup}$ is the supremum semi-norm as in [Reference Bosch, Güntzer and RemmertBGR84, § 6.2.1].
$\|\cdot \|_\mathrm {sup}$ is the supremum semi-norm as in [Reference Bosch, Güntzer and RemmertBGR84, § 6.2.1].
Now, for ![]() $x$ in
$x$ in ![]() $D(\mathfrak {X})$ with specialization
$D(\mathfrak {X})$ with specialization ![]() $\zeta =\mathrm {sp}_\mathfrak {X}(x)$ one has a natural map of topological rings
$\zeta =\mathrm {sp}_\mathfrak {X}(x)$ one has a natural map of topological rings ![]() $\mathcal {O}_{\mathfrak {X},\zeta }\to \mathcal {O}_{X,x}^{+}$ (this map exists even if
$\mathcal {O}_{\mathfrak {X},\zeta }\to \mathcal {O}_{X,x}^{+}$ (this map exists even if ![]() $\mathfrak {X}$ is only admissible over
$\mathfrak {X}$ is only admissible over ![]() $\mathcal {O}_K$). Indeed, because
$\mathcal {O}_K$). Indeed, because ![]() $(X,\mathcal {O}_X^{+})$ is isomorphic to the inverse limit
$(X,\mathcal {O}_X^{+})$ is isomorphic to the inverse limit ![]() $\varprojlim (\mathfrak {X}',\mathcal {O}_{\mathfrak {X}'})$ where
$\varprojlim (\mathfrak {X}',\mathcal {O}_{\mathfrak {X}'})$ where ![]() $\mathfrak {X}'$ travels over the admissible blowups of
$\mathfrak {X}'$ travels over the admissible blowups of ![]() $\mathfrak {X}$ one sees that there is a canonical identification
$\mathfrak {X}$ one sees that there is a canonical identification
(see [Reference Fujiwara and KatoFK18, Chapter 0, Proposition 4.1.10]) from where the map ![]() $\mathcal {O}_{\mathfrak {X},\zeta }\to \mathcal {O}_{X,x}^{+}$ is clear. Thus, if
$\mathcal {O}_{\mathfrak {X},\zeta }\to \mathcal {O}_{X,x}^{+}$ is clear. Thus, if ![]() $k(x)^{+}$ denotes the (uncompleted) residue valuation ring, one obtains a map
$k(x)^{+}$ denotes the (uncompleted) residue valuation ring, one obtains a map ![]() $\mathcal {O}_{X,\zeta }\to k(x)^{+}$.
$\mathcal {O}_{X,\zeta }\to k(x)^{+}$.
Lemma A.12 Let ![]() $\mathfrak {X}$ be an admissible formal scheme over
$\mathfrak {X}$ be an admissible formal scheme over ![]() $\mathcal {O}_K$, let
$\mathcal {O}_K$, let ![]() $x\in D(\mathfrak {X})$ with image
$x\in D(\mathfrak {X})$ with image ![]() $\zeta \in I(\mathfrak {X})$. Then, the following are equivalent:
$\zeta \in I(\mathfrak {X})$. Then, the following are equivalent:
(a) the ring
 $\mathcal {O}_{\mathfrak {X},\zeta }$ is a valuation ring;
$\mathcal {O}_{\mathfrak {X},\zeta }$ is a valuation ring;(b) the map
 $\mathcal {O}_{\mathfrak {X},\zeta }\to k(x)^{+}$ is an isomorphism.
$\mathcal {O}_{\mathfrak {X},\zeta }\to k(x)^{+}$ is an isomorphism.
In particular, under these conditions, the ring ![]() $\mathcal {O}_{\mathfrak {X},\zeta }$ is a height one valuation ring which is
$\mathcal {O}_{\mathfrak {X},\zeta }$ is a height one valuation ring which is ![]() $\varpi$-adically separated and Henselian.
$\varpi$-adically separated and Henselian.
Proof. Clearly condition (b) implies condition (a). Moreover, the last statement follows then immediately from the fact that ![]() $x$ is a maximal point and [Reference Fujiwara and KatoFK18, Chapter II, Corollary 3.2.8]. To see that condition (a) implies condition (b), let us begin by observing that for any admissible blowup
$x$ is a maximal point and [Reference Fujiwara and KatoFK18, Chapter II, Corollary 3.2.8]. To see that condition (a) implies condition (b), let us begin by observing that for any admissible blowup ![]() $\mathfrak {X}'$, the map
$\mathfrak {X}'$, the map ![]() $\mathcal {O}_{\mathfrak {X},\zeta }\to \mathcal {O}_{\mathfrak {X}',\zeta '}$ is an isomorphism where
$\mathcal {O}_{\mathfrak {X},\zeta }\to \mathcal {O}_{\mathfrak {X}',\zeta '}$ is an isomorphism where ![]() $\zeta '=\operatorname {sp}_{\mathfrak {X}'}(x)$. Indeed, suppose that
$\zeta '=\operatorname {sp}_{\mathfrak {X}'}(x)$. Indeed, suppose that ![]() $\mathfrak {X}'\to \mathfrak {X}$ is the blowup at an admissible ideal sheaf
$\mathfrak {X}'\to \mathfrak {X}$ is the blowup at an admissible ideal sheaf ![]() $\mathcal {J}$. As
$\mathcal {J}$. As ![]() $\mathcal {J}$ is finitely generated we know that
$\mathcal {J}$ is finitely generated we know that ![]() $\mathcal {J}_\zeta \subseteq \mathcal {O}_{\mathfrak {X},\zeta }$ is a finitely generated ideal which, because
$\mathcal {J}_\zeta \subseteq \mathcal {O}_{\mathfrak {X},\zeta }$ is a finitely generated ideal which, because ![]() $\mathcal {O}_{\mathfrak {X},\zeta }$ is a valuation ring, must be invertible. We may then find an open
$\mathcal {O}_{\mathfrak {X},\zeta }$ is a valuation ring, must be invertible. We may then find an open ![]() $\mathfrak {U}$ of
$\mathfrak {U}$ of ![]() $\mathfrak {X}$ containing
$\mathfrak {X}$ containing ![]() $\zeta$ such that
$\zeta$ such that ![]() $\mathcal {J}|_{\mathfrak {U}}$ is invertible. However,
$\mathcal {J}|_{\mathfrak {U}}$ is invertible. However, ![]() $\mathfrak {X}'_{\mathfrak {U}}\to \mathfrak {U}$ coincides with the blowup of
$\mathfrak {X}'_{\mathfrak {U}}\to \mathfrak {U}$ coincides with the blowup of ![]() $\mathfrak {U}$ along
$\mathfrak {U}$ along ![]() $\mathcal {J}|_\mathfrak {U}$ (see [Reference Fujiwara and KatoFK18, Chapter II, Proposition 1.1.8]) but because
$\mathcal {J}|_\mathfrak {U}$ (see [Reference Fujiwara and KatoFK18, Chapter II, Proposition 1.1.8]) but because ![]() $\mathcal {J}|_\mathfrak {U}$ is invertible this implies that
$\mathcal {J}|_\mathfrak {U}$ is invertible this implies that ![]() $\mathfrak {X}'_\mathfrak {U}\to \mathfrak {U}$ is an isomorphism and so evidently
$\mathfrak {X}'_\mathfrak {U}\to \mathfrak {U}$ is an isomorphism and so evidently ![]() $\mathcal {O}_{\mathfrak {X},\zeta }\to \mathcal {O}_{\mathfrak {X}',\zeta '}$ is an isomorphism as desired.
$\mathcal {O}_{\mathfrak {X},\zeta }\to \mathcal {O}_{\mathfrak {X}',\zeta '}$ is an isomorphism as desired.
Combining this with (A.3.2) we deduce that the map ![]() $\mathcal {O}_{\mathfrak {X},\zeta }\to \mathcal {O}_{X,x}^{+}$ is an isomorphism. To show then that the map
$\mathcal {O}_{\mathfrak {X},\zeta }\to \mathcal {O}_{X,x}^{+}$ is an isomorphism. To show then that the map ![]() $\mathcal {O}_{\mathfrak {X},\zeta }\to k(x)^{+}$ is an isomorphism note that for any admissible blowup
$\mathcal {O}_{\mathfrak {X},\zeta }\to k(x)^{+}$ is an isomorphism note that for any admissible blowup ![]() $\mathfrak {X}'$ of
$\mathfrak {X}'$ of ![]() $\mathfrak {X}$ the map
$\mathfrak {X}$ the map ![]() $\mathcal {O}_{\mathfrak {X},\zeta }\to \mathcal {O}_{\mathfrak {X}',\zeta '}$ is an isomorphism and commutes with the natural maps to
$\mathcal {O}_{\mathfrak {X},\zeta }\to \mathcal {O}_{\mathfrak {X}',\zeta '}$ is an isomorphism and commutes with the natural maps to ![]() $k(x)^{+}$. Thus, we may replace
$k(x)^{+}$. Thus, we may replace ![]() $\mathcal {O}_{\mathfrak {X},\zeta }$ with any
$\mathcal {O}_{\mathfrak {X},\zeta }$ with any ![]() $\mathcal {O}_{\mathfrak {X}',\zeta '}$. However, we in particular may take
$\mathcal {O}_{\mathfrak {X}',\zeta '}$. However, we in particular may take ![]() $\mathfrak {X}'$ as in [Reference Fujiwara and KatoFK18, Chapter II, Proposition 11.2.8]. As the kernel of
$\mathfrak {X}'$ as in [Reference Fujiwara and KatoFK18, Chapter II, Proposition 11.2.8]. As the kernel of ![]() $\mathcal {O}_{\mathfrak {X},\zeta }\simeq \mathcal {O}_{X,x}^{+}\to k(x)^{+}$ is precisely those
$\mathcal {O}_{\mathfrak {X},\zeta }\simeq \mathcal {O}_{X,x}^{+}\to k(x)^{+}$ is precisely those ![]() $f$ with
$f$ with ![]() $|f(x)|=0$ we are done if we can show that for
$|f(x)|=0$ we are done if we can show that for ![]() $f$ in
$f$ in ![]() $\mathcal {O}_{\mathfrak {X},\zeta }$ one has that
$\mathcal {O}_{\mathfrak {X},\zeta }$ one has that ![]() $|f(x)|=0$ implies that
$|f(x)|=0$ implies that ![]() $f=0$. However, we may as well assume that
$f=0$. However, we may as well assume that ![]() $f$ is in
$f$ is in ![]() $\mathcal {O}(\mathfrak {U}_\eta )$ for some affine irreducible neighborhood
$\mathcal {O}(\mathfrak {U}_\eta )$ for some affine irreducible neighborhood ![]() $\mathfrak {U}$ of
$\mathfrak {U}$ of ![]() $\zeta$. However, we then see that by our choice of model
$\zeta$. However, we then see that by our choice of model ![]() $D(\mathfrak {U})=\operatorname {sp}_\mathfrak {X}^{-1}(\zeta )=\{x\}$. Thus, by (A.3.1) we deduce that
$D(\mathfrak {U})=\operatorname {sp}_\mathfrak {X}^{-1}(\zeta )=\{x\}$. Thus, by (A.3.1) we deduce that ![]() $\|f\|_{\mathrm {sup}}=0$ (where this supremum is taken relative to
$\|f\|_{\mathrm {sup}}=0$ (where this supremum is taken relative to ![]() $\mathfrak {U}_\eta$) and, thus, by [Reference BoschBos14, Proposition 3.1/10] we deduce that
$\mathfrak {U}_\eta$) and, thus, by [Reference BoschBos14, Proposition 3.1/10] we deduce that ![]() $f$ is a nilpotent element, and because
$f$ is a nilpotent element, and because ![]() $\mathcal {O}_{\mathfrak {X},\zeta }$ is a domain, has trivial image in
$\mathcal {O}_{\mathfrak {X},\zeta }$ is a domain, has trivial image in ![]() $\mathcal {O}_{\mathfrak {X},\zeta }$.
$\mathcal {O}_{\mathfrak {X},\zeta }$.
We now wish to establish that the ![]() $(R_1')$ condition ascends through étale maps of formal schemes. To do this, we first need the following lemma.
$(R_1')$ condition ascends through étale maps of formal schemes. To do this, we first need the following lemma.
Lemma A.13 Let ![]() $f\colon \operatorname {Spf}(B)\to \operatorname {Spf}(A)$ be a finite étale morphism of admissible formal schemes over
$f\colon \operatorname {Spf}(B)\to \operatorname {Spf}(A)$ be a finite étale morphism of admissible formal schemes over ![]() $\mathcal {O}_K$. Then, the map
$\mathcal {O}_K$. Then, the map ![]() $A\to B$ is finite étale.
$A\to B$ is finite étale.
Proof. We claim that the ring map ![]() $A\to B$ is weakly étale (see [Reference Bhatt and ScholzeBS15, Definition 1.2]). Indeed, we must show that
$A\to B$ is weakly étale (see [Reference Bhatt and ScholzeBS15, Definition 1.2]). Indeed, we must show that ![]() $A\to B$ is flat, and that
$A\to B$ is flat, and that ![]() $B\to B\otimes _A B$ are flat. However, note that because
$B\to B\otimes _A B$ are flat. However, note that because ![]() $A\to B$ is finite,
$A\to B$ is finite, ![]() $B\otimes _A B$ is finite over
$B\otimes _A B$ is finite over ![]() $B$, and so complete. From this and [Reference Fujiwara and KatoFK18, Chapter I, Proposition 4.8.1] we see that it suffices to check that
$B$, and so complete. From this and [Reference Fujiwara and KatoFK18, Chapter I, Proposition 4.8.1] we see that it suffices to check that ![]() $A/\varpi ^{m} A\to B/\varpi ^{m} B$ is weakly étale for all
$A/\varpi ^{m} A\to B/\varpi ^{m} B$ is weakly étale for all ![]() $m\geqslant 0$, but this is clear because this map is étale. Note though that because
$m\geqslant 0$, but this is clear because this map is étale. Note though that because ![]() $A\to B$ is finite,
$A\to B$ is finite, ![]() $B$ is actually finitely presented as an
$B$ is actually finitely presented as an ![]() $A$-module (see [Reference BoschBos14, Theorem 7.2/4]) and so
$A$-module (see [Reference BoschBos14, Theorem 7.2/4]) and so ![]() $A\to B$ is finitely presented (see [SP21, Tag 0D46]). As
$A\to B$ is finitely presented (see [SP21, Tag 0D46]). As ![]() $A\to B$ is both finitely presented and weakly étale, it is étale (see [Reference Bhatt and ScholzeBS15, Theorem 1.3]).
$A\to B$ is both finitely presented and weakly étale, it is étale (see [Reference Bhatt and ScholzeBS15, Theorem 1.3]).
Lemma A.14 Let ![]() $f\colon \mathfrak {Y}\to \mathfrak {X}$ be an étale morphism of admissible formal schemes over
$f\colon \mathfrak {Y}\to \mathfrak {X}$ be an étale morphism of admissible formal schemes over ![]() $\mathcal {O}_K$. If
$\mathcal {O}_K$. If ![]() $\mathfrak {X}$ satisfies
$\mathfrak {X}$ satisfies ![]() $(R'_1)$, then so does
$(R'_1)$, then so does ![]() $\mathfrak {Y}$.
$\mathfrak {Y}$.
Proof. Let ![]() $\xi$ be a generic point of
$\xi$ be a generic point of ![]() $\mathfrak {Y}$ and let
$\mathfrak {Y}$ and let ![]() $\zeta =f(\xi )$. We first show that the map
$\zeta =f(\xi )$. We first show that the map ![]() $\mathcal {O}_{\mathfrak {X},\zeta }\to \mathcal {O}_{\mathfrak {Y},\xi }$ is finite étale. Note that
$\mathcal {O}_{\mathfrak {X},\zeta }\to \mathcal {O}_{\mathfrak {Y},\xi }$ is finite étale. Note that ![]() $\zeta$ is a generic point of
$\zeta$ is a generic point of ![]() $\mathfrak {X}$. Indeed, it suffices to show that
$\mathfrak {X}$. Indeed, it suffices to show that ![]() $f_1(\xi )$ is a generic point where
$f_1(\xi )$ is a generic point where ![]() $f_1$ is the reduction of
$f_1$ is the reduction of ![]() $f$ modulo
$f$ modulo ![]() $(\varpi )$, but this is clear, as
$(\varpi )$, but this is clear, as ![]() $f_1$ is an open morphism of locally topologically Noetherian schemes. Note then, that because
$f_1$ is an open morphism of locally topologically Noetherian schemes. Note then, that because ![]() $f_1$ is an étale morphism of schemes, there exists open neighborhoods
$f_1$ is an étale morphism of schemes, there exists open neighborhoods ![]() $U$ (respectively,
$U$ (respectively, ![]() $V$) of
$V$) of ![]() $\zeta$ (respectively,
$\zeta$ (respectively, ![]() $\xi$) such that
$\xi$) such that ![]() $f(V)\subseteq U$,
$f(V)\subseteq U$, ![]() $f_1|_{V}\colon V\to U$ is finite étale, and
$f_1|_{V}\colon V\to U$ is finite étale, and ![]() $f_1^{-1}(\zeta )\cap V=\{\xi \}$. Indeed, this follows from the fact that the local ring at
$f_1^{-1}(\zeta )\cap V=\{\xi \}$. Indeed, this follows from the fact that the local ring at ![]() $\zeta$ has reduced subscheme which is a field, and so (by [SP21, Tag 04DZ]) all étale algebras are finite product of finite étale algebras. From this and [Reference Fujiwara and KatoFK18, Chapter I, Proposition 4.2.3] we see that we may find affine neighborhoods
$\zeta$ has reduced subscheme which is a field, and so (by [SP21, Tag 04DZ]) all étale algebras are finite product of finite étale algebras. From this and [Reference Fujiwara and KatoFK18, Chapter I, Proposition 4.2.3] we see that we may find affine neighborhoods ![]() $\operatorname {Spf}(A)$ (respectively,
$\operatorname {Spf}(A)$ (respectively, ![]() $\operatorname {Spf}(B)$) of
$\operatorname {Spf}(B)$) of ![]() $\zeta$ (respectively,
$\zeta$ (respectively, ![]() $\xi$) such that
$\xi$) such that ![]() $f(\operatorname {Spf}(B))\subseteq \operatorname {Spf}(A)$ and
$f(\operatorname {Spf}(B))\subseteq \operatorname {Spf}(A)$ and ![]() $f|_{\operatorname {Spf}(B)}\colon \operatorname {Spf}(B)\to \operatorname {Spf}(A)$ is finite étale and
$f|_{\operatorname {Spf}(B)}\colon \operatorname {Spf}(B)\to \operatorname {Spf}(A)$ is finite étale and ![]() $f^{-1}(\zeta )\cap \operatorname {Spf}(B)=\{\xi \}$. Replace
$f^{-1}(\zeta )\cap \operatorname {Spf}(B)=\{\xi \}$. Replace ![]() $f\colon \mathfrak {Y}\to \mathfrak {X}$ by
$f\colon \mathfrak {Y}\to \mathfrak {X}$ by ![]() $f|_{\operatorname {Spf}(B)}$. By Lemma A.13 we then know that
$f|_{\operatorname {Spf}(B)}$. By Lemma A.13 we then know that ![]() $A\to B$ is finite étale. Now, because
$A\to B$ is finite étale. Now, because ![]() $f$ is finite and
$f$ is finite and ![]() $f^{-1}(\zeta )=\{\xi \}$ the neighborhoods of the form
$f^{-1}(\zeta )=\{\xi \}$ the neighborhoods of the form ![]() $f^{-1}(D(f))$ for
$f^{-1}(D(f))$ for ![]() $D(f)$ a neighborhood of
$D(f)$ a neighborhood of ![]() $\zeta$ are cofinal in the neighborhoods of
$\zeta$ are cofinal in the neighborhoods of ![]() $\xi$. Thus,
$\xi$. Thus, ![]() $\mathcal {O}_{\mathfrak {Y},\xi }=\mathcal {O}_{\mathfrak {X},\zeta }\otimes _A B$, and because
$\mathcal {O}_{\mathfrak {Y},\xi }=\mathcal {O}_{\mathfrak {X},\zeta }\otimes _A B$, and because ![]() $A\to B$ is finite étale we deduce that
$A\to B$ is finite étale we deduce that ![]() $\mathcal {O}_{\mathfrak {X},\zeta }\to \mathcal {O}_{\mathfrak {Y},\xi }$ is finite étale as desired. In particular, because
$\mathcal {O}_{\mathfrak {X},\zeta }\to \mathcal {O}_{\mathfrak {Y},\xi }$ is finite étale as desired. In particular, because ![]() $\mathcal {O}_{\mathfrak {X},\zeta }$ is a normal domain, so is
$\mathcal {O}_{\mathfrak {X},\zeta }$ is a normal domain, so is ![]() $\mathcal {O}_{\mathfrak {Y},\xi }$ (see [SP21, Tag 025P]).
$\mathcal {O}_{\mathfrak {Y},\xi }$ (see [SP21, Tag 025P]).
Using [Reference BourbakiBou64, Chapitre VI, § 6, Proposition 6] applied to the map of local rings ![]() $\mathcal {O}_{\mathfrak {X},\zeta }\to \mathcal {O}_{\mathfrak {Y},\xi }$, we deduce that
$\mathcal {O}_{\mathfrak {X},\zeta }\to \mathcal {O}_{\mathfrak {Y},\xi }$, we deduce that ![]() $\mathcal {O}_{\mathfrak {Y},\xi }$ is a valuation ring if
$\mathcal {O}_{\mathfrak {Y},\xi }$ is a valuation ring if ![]() $\mathcal {O}_{\mathfrak {X},\zeta }$ is, as desired.
$\mathcal {O}_{\mathfrak {X},\zeta }$ is, as desired.
A.4 Serre's criterion for  $\eta$-normality
$\eta$-normality
Serre's criterion states that a locally Noetherian scheme is normal if and only if it is both ![]() $(S_2)$ and
$(S_2)$ and ![]() $(R_1)$. In our situation of admissible formal schemes over
$(R_1)$. In our situation of admissible formal schemes over ![]() $\mathcal {O}_K$, we have the following analog (compare with condition
$\mathcal {O}_K$, we have the following analog (compare with condition ![]() $(N)$ in [Reference RaynaudRay70, § 6.1]).
$(N)$ in [Reference RaynaudRay70, § 6.1]).
Proposition A.15 (Serre's criterion for  $\eta$-normality)
$\eta$-normality)
Let ![]() $\mathfrak {X}$ be an admissible formal scheme over
$\mathfrak {X}$ be an admissible formal scheme over ![]() $\mathcal {O}_K$. The following are equivalent:
$\mathcal {O}_K$. The following are equivalent:
(a)
 $\mathfrak {X}$ is
$\mathfrak {X}$ is  $\eta$-normal;
$\eta$-normal;(b)
 $\mathfrak {X}$ satisfies
$\mathfrak {X}$ satisfies  $(S'_2)$ and
$(S'_2)$ and  $(R'_1)$.
$(R'_1)$.
Proof. As being ![]() $\eta$-normal and condition (b) are Zariski local on
$\eta$-normal and condition (b) are Zariski local on ![]() $\mathfrak {X}$, we may assume that
$\mathfrak {X}$, we may assume that ![]() $\mathfrak {X}=\operatorname {Spf}(A)$ where
$\mathfrak {X}=\operatorname {Spf}(A)$ where ![]() $A$ is an admissible
$A$ is an admissible ![]() $\mathcal {O}_K$-algebra. Set
$\mathcal {O}_K$-algebra. Set ![]() $X$ to be
$X$ to be ![]() $\mathfrak {X}_\eta =\operatorname {Spa}(A_K)$.
$\mathfrak {X}_\eta =\operatorname {Spa}(A_K)$.
Suppose first that condition (a) holds. To show condition ![]() $(S'_2)$ it suffices to show that if
$(S'_2)$ it suffices to show that if ![]() $a$ is an element of
$a$ is an element of ![]() $A$ such
$A$ such ![]() $a\in \varpi \mathcal {O}_{\mathfrak {X},\zeta }$ for all
$a\in \varpi \mathcal {O}_{\mathfrak {X},\zeta }$ for all ![]() $\zeta$ in
$\zeta$ in ![]() $I(\mathfrak {X})$, then
$I(\mathfrak {X})$, then ![]() $a\in \varpi A$. Consider
$a\in \varpi A$. Consider ![]() $\varpi ^{-1}a$ as an element of
$\varpi ^{-1}a$ as an element of ![]() $A_K$. Note then that, by assumption, we have that
$A_K$. Note then that, by assumption, we have that ![]() $\varpi ^{-1}a\in \mathcal {O}_{\mathfrak {X},\zeta }\subseteq k(x)^{+}$ for all
$\varpi ^{-1}a\in \mathcal {O}_{\mathfrak {X},\zeta }\subseteq k(x)^{+}$ for all ![]() $x$ in
$x$ in ![]() $D(\mathfrak {X})$. Thus, we see from (A.3.1) and [Reference Bosch, Güntzer and RemmertBGR84, Proposition 6.2.3/1] that
$D(\mathfrak {X})$. Thus, we see from (A.3.1) and [Reference Bosch, Güntzer and RemmertBGR84, Proposition 6.2.3/1] that ![]() $\varpi ^{-1}a$ is in
$\varpi ^{-1}a$ is in ![]() $A_K^{\circ } =A$ as desired.
$A_K^{\circ } =A$ as desired.
To see that ![]() $(R'_1)$ holds, passing to an affine open neighborhood of a given
$(R'_1)$ holds, passing to an affine open neighborhood of a given ![]() $\zeta \in I(\mathfrak {X})$ we may assume that
$\zeta \in I(\mathfrak {X})$ we may assume that ![]() $\mathfrak {X}=\operatorname {Spf}(A)$ and
$\mathfrak {X}=\operatorname {Spf}(A)$ and ![]() $|\mathfrak {X}|$ is irreducible. Moreover, because the equality
$|\mathfrak {X}|$ is irreducible. Moreover, because the equality ![]() $A_K^{\circ }=A$ shows that
$A_K^{\circ }=A$ shows that ![]() $\operatorname {Spec}(\widetilde {A}_K)=\operatorname {Spec}(A_k)_\mathrm {red}$ (where
$\operatorname {Spec}(\widetilde {A}_K)=\operatorname {Spec}(A_k)_\mathrm {red}$ (where ![]() $\widetilde {A}=A_K^{\circ }/A_K^{{\circ \circ }}$ as in [Reference Bosch, Güntzer and RemmertBGR84, § 1.2.5]) we deduce that
$\widetilde {A}=A_K^{\circ }/A_K^{{\circ \circ }}$ as in [Reference Bosch, Güntzer and RemmertBGR84, § 1.2.5]) we deduce that ![]() $\widetilde {A}$ is a domain, and because
$\widetilde {A}$ is a domain, and because ![]() $A$ is moreover reduced, the supremum semi-norm
$A$ is moreover reduced, the supremum semi-norm ![]() $\|\cdot \|_\mathrm {sup}$ is a multiplicative norm by [Reference Bosch, Güntzer and RemmertBGR84, Proposition 6.2.3/5]. This implies that
$\|\cdot \|_\mathrm {sup}$ is a multiplicative norm by [Reference Bosch, Güntzer and RemmertBGR84, Proposition 6.2.3/5]. This implies that ![]() $A$ is a domain; by the same argument, for every
$A$ is a domain; by the same argument, for every ![]() $f\in A$ with
$f\in A$ with ![]() $f(\zeta )\neq 0$, the complete localization
$f(\zeta )\neq 0$, the complete localization ![]() $A\langle f^{-1}\rangle$ is a domain, and passing to the limit also
$A\langle f^{-1}\rangle$ is a domain, and passing to the limit also ![]() $\mathcal {O}_{\mathfrak {X}, \zeta }$ is a domain. To check that
$\mathcal {O}_{\mathfrak {X}, \zeta }$ is a domain. To check that ![]() $\mathcal {O}_{\mathfrak {X}, \zeta }$ is a valuation ring, take a non-zero fraction
$\mathcal {O}_{\mathfrak {X}, \zeta }$ is a valuation ring, take a non-zero fraction ![]() $f/g \in \operatorname {Frac}(\mathcal {O}_{\mathfrak {X}, \zeta })$; shrinking
$f/g \in \operatorname {Frac}(\mathcal {O}_{\mathfrak {X}, \zeta })$; shrinking ![]() $\mathfrak {X}$ further, we may assume
$\mathfrak {X}$ further, we may assume ![]() $f,g\in A$ and
$f,g\in A$ and ![]() $f^{-1}, g^{-1}\in A_K$. For the latter claim, because
$f^{-1}, g^{-1}\in A_K$. For the latter claim, because ![]() $A=A_K^{\circ }$, we can by [Reference Bosch, Güntzer and RemmertBGR84, Proposition 6.2.1/4 (ii)] write
$A=A_K^{\circ }$, we can by [Reference Bosch, Güntzer and RemmertBGR84, Proposition 6.2.1/4 (ii)] write ![]() $f^{n} = \alpha u$,
$f^{n} = \alpha u$, ![]() $g^{m}=\beta v$ where
$g^{m}=\beta v$ where ![]() $\alpha,\beta \in \mathcal {O}_K$ and
$\alpha,\beta \in \mathcal {O}_K$ and ![]() $u, v$ have supremum norm one and, hence, their images in
$u, v$ have supremum norm one and, hence, their images in ![]() $\widetilde {A}$ are non-zero; passing to a smaller affine neighborhood of
$\widetilde {A}$ are non-zero; passing to a smaller affine neighborhood of ![]() $\zeta$, we may assume that
$\zeta$, we may assume that ![]() $u$ and
$u$ and ![]() $v$ are invertible in
$v$ are invertible in ![]() $\widetilde {A}$ and, hence, in
$\widetilde {A}$ and, hence, in ![]() $A$ (because
$A$ (because ![]() $A$ and
$A$ and ![]() $\widetilde {A}$ have the same maximal ideals), so that
$\widetilde {A}$ have the same maximal ideals), so that ![]() $f$ and
$f$ and ![]() $g$ become invertible in
$g$ become invertible in ![]() $A_K$. Then if say
$A_K$. Then if say ![]() $\|f\|_{\rm sup}\leqslant \|g\|_{\rm sup}$, then
$\|f\|_{\rm sup}\leqslant \|g\|_{\rm sup}$, then ![]() $f/g\in A_K$ and
$f/g\in A_K$ and ![]() $\|f/g\|_{\rm sup}\leqslant 1$, so
$\|f/g\|_{\rm sup}\leqslant 1$, so ![]() $f/g \in A_K^{\circ } = A$ and so
$f/g \in A_K^{\circ } = A$ and so ![]() $f/g\in \mathcal {O}_{\mathfrak {X},\zeta }$. Otherwise,
$f/g\in \mathcal {O}_{\mathfrak {X},\zeta }$. Otherwise, ![]() $g/f\in \mathcal {O}_{\mathfrak {X},\zeta }$ by the same argument.
$g/f\in \mathcal {O}_{\mathfrak {X},\zeta }$ by the same argument.
Conversely, suppose that condition (b) holds. On the one hand, again by (A.3.1) we have
where we are implicitly identifying ![]() $a\in A_K$ with its image in
$a\in A_K$ with its image in ![]() $k(x)$. On the other hand, we claim that
$k(x)$. On the other hand, we claim that
where we identify ![]() $a\in A_K$ with its image in
$a\in A_K$ with its image in ![]() $\mathcal {O}_{\mathfrak {X},\zeta }[ {1}/{\varpi }]$. This would imply the required assertion by Lemma A.12 and the
$\mathcal {O}_{\mathfrak {X},\zeta }[ {1}/{\varpi }]$. This would imply the required assertion by Lemma A.12 and the ![]() $(R'_1)$ property.
$(R'_1)$ property.
To show the claim, we note that evidently ![]() $A$ maps into each
$A$ maps into each ![]() $\mathcal {O}_{\mathfrak {X},\zeta }$. Conversely, let
$\mathcal {O}_{\mathfrak {X},\zeta }$. Conversely, let ![]() $a\in A_K$ be an element of the right-hand side, and write
$a\in A_K$ be an element of the right-hand side, and write ![]() $a=\varpi ^{-n}a'$ with
$a=\varpi ^{-n}a'$ with ![]() $a'\in A$ and
$a'\in A$ and ![]() $n\geqslant 0$. By the
$n\geqslant 0$. By the ![]() $(S'_2)$ property of
$(S'_2)$ property of ![]() $\mathfrak {X}$ or, equivalently, the
$\mathfrak {X}$ or, equivalently, the ![]() $(S'_1)$ property of
$(S'_1)$ property of ![]() $\operatorname {Spec}(A/\varpi ^{n})$, our assumption that
$\operatorname {Spec}(A/\varpi ^{n})$, our assumption that ![]() $a'$ lies in
$a'$ lies in ![]() $\varpi ^{n}\mathcal {O}_{\mathfrak {X},\zeta }$ for all
$\varpi ^{n}\mathcal {O}_{\mathfrak {X},\zeta }$ for all ![]() $\zeta$ implies that
$\zeta$ implies that ![]() $a'\in \varpi ^{n} A$ and, hence,
$a'\in \varpi ^{n} A$ and, hence, ![]() $a\in A$ as desired.
$a\in A$ as desired.
Using the criterion of Proposition A.15, Lemmas A.10 and A.14 imply the following result.
Corollary A.16 Let ![]() $\mathfrak {Y}\to \mathfrak {X}$ be an étale morphism of admissible formal schemes over
$\mathfrak {Y}\to \mathfrak {X}$ be an étale morphism of admissible formal schemes over ![]() $\mathcal {O}_K$. If
$\mathcal {O}_K$. If ![]() $\mathfrak {X}$ is
$\mathfrak {X}$ is ![]() $\eta$-normal, then so is
$\eta$-normal, then so is ![]() $\mathfrak {Y}$.
$\mathfrak {Y}$.