Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Francis, John
2013.
The tangent complex and Hochschild cohomology of -rings.
Compositio Mathematica,
Vol. 149,
Issue. 3,
p.
430.
Sati, Hisham
and
Westerland, Craig
2015.
Twisted Morava K-theory and E-theory.
Journal of Topology,
Vol. 8,
Issue. 4,
p.
887.
Muro, Fernando
2020.
Enhanced $$A_{\infty }$$-obstruction theory.
Journal of Homotopy and Related Structures,
Vol. 15,
Issue. 1,
p.
61.
Barthel, Tobias
and
Pstrągowski, Piotr
2025.
MORAVA K-THEORY AND FILTRATIONS BY POWERS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 24,
Issue. 5,
p.
1655.

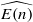 -algebra structures. Here
-algebra structures. Here 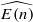 is the
is the 