Hostname: page-component-89b8bd64d-ktprf Total loading time: 0 Render date: 2026-05-07T20:38:03.474Z Has data issue: false hasContentIssue false
  • English
  • Français

Zero cycles with modulus and zero cycles on singular varieties

Part of: $K$-theory in geometry Cycles and subschemes Arithmetic rings and other special rings (Co)homology theory

Published online by Cambridge University Press:  09 October 2017

Federico Binda  and
Amalendu Krishna
Federico Binda
Affiliation:
Fakultät für Mathematik, Universität Regensburg, 93040, Regensburg, Germany email federico.binda@mathematik.uni-regensburg.de
Amalendu Krishna
Affiliation:
School of Mathematics, Tata Institute of Fundamental Research, 1 Homi Bhabha Road, Colaba, Mumbai, India email amal@math.tifr.res.in
Get access Rights & Permissions [Opens in a new window]

Abstract

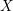Given a smooth variety $X$ and an effective Cartier divisor 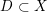$D\subset X$ , we show that the cohomological Chow group of 0-cycles on the double of 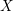$X$ along 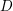$D$ has a canonical decomposition in terms of the Chow group of 0-cycles 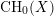$\text{CH}_{0}(X)$ and the Chow group of 0-cycles with modulus 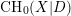$\text{CH}_{0}(X|D)$ on 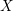$X$ . When 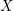$X$ is projective, we construct an Albanese variety with modulus and show that this is the universal regular quotient of 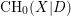$\text{CH}_{0}(X|D)$ . As a consequence of the above decomposition, we prove the Roitman torsion theorem for the 0-cycles with modulus. We show that 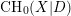$\text{CH}_{0}(X|D)$ is torsion-free and there is an injective cycle class map 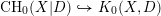$\text{CH}_{0}(X|D){\hookrightarrow}K_{0}(X,D)$ if 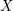$X$ is affine. For a smooth affine surface 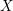$X$ , this is strengthened to show that 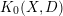$K_{0}(X,D)$ is an extension of 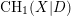$\text{CH}_{1}(X|D)$ by 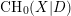$\text{CH}_{0}(X|D)$ .

Keywords

algebraic cyclesChow groupssingular schemescycles with modulus

MSC classification

Primary: 14C25: Algebraic cycles
Secondary: 14F30: $p$-adic cohomology, crystalline cohomology 13F35: Witt vectors and related rings 19E15: Algebraic cycles and motivic cohomology

Information

Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 1 , January 2018 , pp. 120 - 187
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Barbieri-Viale, L., Pedrini, C. and Weibel, C., Roitman’s theorem for singular complex projective surfaces , Duke Math. J. 84 (1996), 155–190.Google Scholar
Bass, H., Algebraic K-theory (W. A. Benjamin, New York, NY, 1968).Google Scholar
Binda, F., Motives and algebraic cycles with moduli conditions, PhD thesis, University of Duisburg-Essen (2016).Google Scholar
Binda, F., Torsion 0-cycles with modulus on affine varieties , J. Pure Appl. Algebra 222 (2018), 61–74.Google Scholar
Binda, F. and Saito, S., Relative cycles with moduli and regulator maps, Preprint (2016),arXiv:1412.0385v2.Google Scholar
Biswas, J. and Srinivas, V., Roitman’s theorem for singular projective varieties , Compos. Math. 119 (1999), 213–237.CrossRefGoogle Scholar
Bloch, S., Algebraic cycles and higher K-theory , Adv. Math. 61 (1986), 267–304.CrossRefGoogle Scholar
Bloch, S., Kas, A. and Lieberman, D., Zero cycles on surfaces with p g = 0 , Compos. Math. 33 (1976), 135–145.Google Scholar
Esnault, H., Srinivas, V. and Viehweg, E., The universal regular quotient of the Chow group of points on projective varieties , Invent. Math. 135 (1999), 595–664.Google Scholar
Esnault, H. and Viehweg, E., Deligne–Beĭlinson cohomology , in Beĭlinson’s conjectures on special values of L-functions, Perspectives in Mathematics, vol. 4 (Academic Press, Boston, MA, 1988), 43–91.CrossRefGoogle Scholar
Friedlander, E. M. and Suslin, A., The spectral sequence relating algebraic K-theory to motivic cohomology , Ann. Sci. Éc. Norm. Supér. (4) 35 (2002), 773–875.Google Scholar
Fulton, W., Intersection theory, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], vol. 2, second edition (Springer, Berlin, 1998).Google Scholar
Geller, S. C. and Weibel, C. A., K 1(A, B, I) , J. Reine Angew. Math. 342 (1983), 12–34.Google Scholar
Görtz, U. and Wedhorn, T., Algebraic geometry I, Schemes, with examples and exercises, Advanced Lectures in Mathematics (Vieweg+Teubner, Wiesbaden, 2010).Google Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York, NY, 1977).Google Scholar
Hartshorne, R., Deformation theory, Graduate Texts in Mathematics, vol. 257 (Springer, New York, NY, 2010).CrossRefGoogle Scholar
Jouanolou, J.-P., Théorèmes de Bertini et applications, Progress in Mathematics, vol. 42 (Birkhäuser Boston, Boston, MA, 1983).Google Scholar
Kai, W., A moving lemma for algebraic cycles with modulus and contravariance, Preprint (2016), arXiv:1507.07619v3.Google Scholar
Kato, K. and Russell, H., Albanese varieties with modulus and Hodge theory , Ann. Inst. Fourier (Grenoble) 62 (2012), 783–806.Google Scholar
Kerz, M. and Saito, S., Chow group of 0-cycles with modulus and higher-dimensional class field theory , Duke Math. J. 165 (2016), 2811–2897.Google Scholar
Kleiman, S. L. and Altman, A. B., Bertini theorems for hypersurface sections containing a subscheme , Comm. Algebra 7 (1979), 775–790.Google Scholar
Krishna, A., Zero cycles on singular surfaces , J. K-Theory 4 (2009), 101–143.Google Scholar
Krishna, A., On 0-cycles with modulus , Algebra Number Theory 9 (2015), 2397–2415.Google Scholar
Krishna, A., Zero cycles on affine varieties, Preprint (2015), arXiv:1511.04221v1.Google Scholar
Krishna, A. and Levine, M., Additive higher Chow groups of schemes , J. Reine Angew. Math. 619 (2008), 75–140.Google Scholar
Krishna, A. and Park, J., A module structure and a vanishing theorem for cycles with modulus , Math. Res. Lett., to appear, Preprint (2014), arXiv:1412.7396v2.Google Scholar
Krishna, A. and Srinivas, V., Zero cycles on singular varieties , in Algebraic cycles and motives, London Mathematical Society Lecture Note Series, vol. 343 (Cambridge University Press, Cambridge, 2007), 264–277.Google Scholar
Levine, M., Bloch’s formula for singular surfaces , Topology 24 (1985), 165–174.Google Scholar
Levine, M., A geometric theory of the Chow ring for singular varieties, unpublished manuscript, 1985.Google Scholar
Levine, M., Zero-cycles and K-theory on singular varieties , in Algebraic geometry: Bowdoin 1985, Brunswick, Maine, 1985, Proceedings of Symposia in Pure Mathematics, vol. 46 (American Mathematical Society, Providence, RI, 1987), 451–462.Google Scholar
Levine, M., Deligne–Beĭlinson cohomology for singular varieties , in Algebraic K-theory, commutative algebra, and algebraic geometry, Santa Margherita Ligure, 1989, Contemporary Mathematics, vol. 126 (American Mathematical Society, Providence, RI, 1992), 113–146.Google Scholar
Levine, M., Bloch’s higher Chow groups revisited , Astérisque 10 (1994), 235–320.Google Scholar
Levine, M. and Weibel, C., Zero cycles and complete intersections on singular varieties , J. Reine Angew. Math. 359 (1985), 106–120.Google Scholar
Mallick, V. M., Roitman’s theorem for singular projective varieties in arbitrary characteristic , J. K-Theory 3 (2009), 501–531.Google Scholar
Milne, J. S., Zero cycles on algebraic varieties in nonzero characteristic: Rojtman’s theorem , Compos. Math. 47 (1982), 271–287.Google Scholar
Milnor, J., Introduction to algebraic K-theory, Annals of Mathematics Studies, vol. 72 (Princeton University Press, Princeton, NJ, 1971).Google Scholar
Park, J., Regulators on additive higher Chow groups , Amer. J. Math. 131 (2009), 257–276.Google Scholar
Pedrini, C. and Weibel, C., Divisibility in the Chow group of zero-cycles on a singular surface , Astérisque 226 (1994), 371–409.Google Scholar
Rojtman, A. A., The torsion of the group of 0-cycles modulo rational equivalence , Ann. of Math. (2) 111 (1980), 553–569.Google Scholar
Rülling, K., The generalized de Rham–Witt complex over a field is a complex of zero-cycles , J. Algebraic Geom. 16 (2007), 109–169.Google Scholar
Rülling, K. and Saito, S., Higher Chow groups with modulus and relative Milnor K-theory , Trans. Amer. Math. Soc., to appear, doi:10.1090/tran/7018.Google Scholar
Russell, H., Albanese varieties with modulus over a perfect field , Algebra Number Theory 7 (2013), 853–892.Google Scholar
Seidenberg, A., The hyperplane sections of normal varieties , Trans. Amer. Math. Soc. 69 (1950), 357–386.Google Scholar
Serre, J.-P., Morphismes universels et differéntielles de troisiéme espéce , Séminaire Claude Chevalley 4(11) (1958–1959).Google Scholar
Serre, J.-P., Algebraic groups and class fields, Graduate Texts in Mathematics, vol. 117 (Springer, New York, NY, 1988).Google Scholar
Srinivas, V., Zero cycles on singular varieties , in The arithmetic and geometry of algebraic cycles, Banff, AB, 1998, NATO Science Series C: Mathematics, Physics and Science, vol. 548 (Kluwer Academic Publishers, Dordrecht, 2000), 347–382.Google Scholar
Srinivas, V., Algebraic K-theory, paperback reprint of the 1996 second edition (Birkhäuser, Boston, MA, 2008).Google Scholar
Suslin, A. and Voevodsky, V., Singular homology of abstract algebraic varieties , Invent. Math. 123 (1996), 61–94.Google Scholar
Voisin, C., Remarks on filtrations on Chow groups and the Bloch conjecture , Ann. Mat. Pura Appl. (4) 183 (2004), 421–438.Google Scholar
Weil, A., Sur les critères d’équivalence en géométrie algébrique , Math. Ann. 128 (1954), 95–127.Google Scholar
Zariski, O., Introduction to the problem of minimal models in the theory of algebraic surfaces, Publications of the Mathematical Society of Japan, vol. 4 (The Mathematical Society of Japan, Tokyo, 1958).Google Scholar