Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
Contents
- Cited by 31
Bias in Regressions With a Lagged Dependent Variable
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 371-386
-
- Article
- Export citation
- Cited by 31
ANALYSIS OF COEXPLOSIVEPROCESSES
-
- Published online by Cambridge University Press:
- 07 October 2009, pp. 882-915
-
- Article
- Export citation
- Cited by 31
IDENTIFICATION OF THE BINARY CHOICE MODEL WITH MISCLASSIFICATION
-
- Published online by Cambridge University Press:
- 01 August 2000, pp. 603-609
-
- Article
- Export citation
- Cited by 31
SIGN-BASED UNIT ROOT TESTS FOR EXPLOSIVE FINANCIAL BUBBLES IN THE PRESENCE OF DETERMINISTICALLY TIME-VARYING VOLATILITY
-
- Published online by Cambridge University Press:
- 29 March 2019, pp. 122-169
-
- Article
- Export citation
- Cited by 31
ESTIMATION OF AND INFERENCE ABOUT THE EXPECTED SHORTFALL FOR TIME SERIES WITH INFINITE VARIANCE
-
- Published online by Cambridge University Press:
- 16 January 2013, pp. 771-807
-
- Article
- Export citation
- Cited by 31
Strong Consistency of Regression Quantiles and Related Empirical Processes
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 191-201
-
- Article
- Export citation
- Cited by 31
ASYMPTOTICALLY EFFICIENT MEDIAN REGRESSION IN THE PRESENCE OF HETEROSKEDASTICITY OF UNKNOWN FORM
-
- Published online by Cambridge University Press:
- 27 July 2001, pp. 765-784
-
- Article
- Export citation
- Cited by 31
ASYMPTOTIC INFERENCE FOR UNIT ROOT PROCESSES WITH GARCH(1,1) ERRORS
-
- Published online by Cambridge University Press:
- 06 June 2003, pp. 541-564
-
- Article
- Export citation
- Cited by 31
Gaussian Estimation of Mixed-OrderContinuous-Time Dynamic Models with UnobservableStochastic Trends from Mixed Stock and FlowData
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 467-505
-
- Article
- Export citation
- Cited by 31
ESTIMATION RISK IN GARCH VaR AND ES ESTIMATES
-
- Published online by Cambridge University Press:
- 23 June 2008, pp. 1404-1424
-
- Article
- Export citation
- Cited by 31
INSTRUMENTAL VARIABLES ESTIMATION WITH PANEL DATA
-
- Published online by Cambridge University Press:
- 19 July 2005, pp. 865-869
-
- Article
- Export citation
- Cited by 30
Problems with the Asymptotic Theory of Maximum Likelihood Estimation in Integrated and Cointegrated Systems
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 888-911
-
- Article
- Export citation
- Cited by 30
TESTING FOR SERIAL CORRELATION OF UNKNOWN FORM USING WAVELET METHODS
-
- Published online by Cambridge University Press:
- 03 March 2001, pp. 386-423
-
- Article
- Export citation
- Cited by 30
A Note on Bootstrapping Generalized Method of Moments Estimators
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 187-197
-
- Article
- Export citation
- Cited by 30
NONPARAMETRIC ESTIMATION OF SECOND-ORDER STOCHASTIC DIFFERENTIAL EQUATIONS
-
- Published online by Cambridge University Press:
- 14 May 2007, pp. 880-898
-
- Article
- Export citation
- Cited by 30
Testing for Unit Roots in Models with Structural Change
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 917-936
-
- Article
- Export citation
- Cited by 30
Noncausality in Continuous Time Models
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 215-256
-
- Article
- Export citation
- Cited by 30
Estimation in Dynamic Linear Regression Models with Infinite Variance Errors
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 570-588
-
- Article
- Export citation
- Cited by 30
NONPARAMETRIC TESTS OF DENSITY RATIO ORDERING
-
- Published online by Cambridge University Press:
- 08 September 2014, pp. 471-492
-
- Article
- Export citation
- Cited by 30
ASYMPTOTIC THEORY FOR EMPIRICAL SIMILARITY MODELS
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 1032-1059
-
- Article
- Export citation
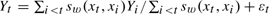 ,
, 