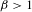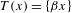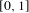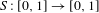Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tavazoei, Mohammad Saleh
2025.
Stabilisation in an infinite time horizon by homomorphically encrypted first-order controllers with regular Pisot poles.
International Journal of Systems Science,
Vol. 56,
Issue. 10,
p.
2221.