Article contents
Bernoulliness of 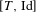 $[T,\text{Id}]$ when
$[T,\text{Id}]$ when  $T$ is an irrational rotation: towards an explicit isomorphism
$T$ is an irrational rotation: towards an explicit isomorphism
Published online by Cambridge University Press: 24 April 2020
Abstract
Let  $\unicode[STIX]{x1D703}$ be an irrational real number. The map
$\unicode[STIX]{x1D703}$ be an irrational real number. The map 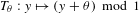 $T_{\unicode[STIX]{x1D703}}:y\mapsto (y+\unicode[STIX]{x1D703})\!\hspace{0.6em}{\rm mod}\hspace{0.2em}1$ from the unit interval
$T_{\unicode[STIX]{x1D703}}:y\mapsto (y+\unicode[STIX]{x1D703})\!\hspace{0.6em}{\rm mod}\hspace{0.2em}1$ from the unit interval 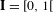 $\mathbf{I}= [\!0,1\![$ (endowed with the Lebesgue measure) to itself is ergodic. In a short paper [Parry, Automorphisms of the Bernoulli endomorphism and a class of skew-products. Ergod. Th. & Dynam. Sys.16 (1996), 519–529] published in 1996, Parry provided an explicit isomorphism between the measure-preserving map
$\mathbf{I}= [\!0,1\![$ (endowed with the Lebesgue measure) to itself is ergodic. In a short paper [Parry, Automorphisms of the Bernoulli endomorphism and a class of skew-products. Ergod. Th. & Dynam. Sys.16 (1996), 519–529] published in 1996, Parry provided an explicit isomorphism between the measure-preserving map 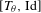 $[T_{\unicode[STIX]{x1D703}},\text{Id}]$ and the unilateral dyadic Bernoulli shift when
$[T_{\unicode[STIX]{x1D703}},\text{Id}]$ and the unilateral dyadic Bernoulli shift when  $\unicode[STIX]{x1D703}$ is extremely well approximated by the rational numbers, namely, if
$\unicode[STIX]{x1D703}$ is extremely well approximated by the rational numbers, namely, if 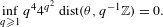 $$\begin{eqnarray}\inf _{q\geq 1}q^{4}4^{q^{2}}~\text{dist}(\unicode[STIX]{x1D703},q^{-1}\mathbb{Z})=0.\end{eqnarray}$$
$$\begin{eqnarray}\inf _{q\geq 1}q^{4}4^{q^{2}}~\text{dist}(\unicode[STIX]{x1D703},q^{-1}\mathbb{Z})=0.\end{eqnarray}$$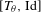 $[T_{\unicode[STIX]{x1D703}},\text{Id}]$ is isomorphic to the unilateral dyadic Bernoulli shift. Their proof is not constructive. In the present paper, we relax notably Parry’s condition on
$[T_{\unicode[STIX]{x1D703}},\text{Id}]$ is isomorphic to the unilateral dyadic Bernoulli shift. Their proof is not constructive. In the present paper, we relax notably Parry’s condition on  $\unicode[STIX]{x1D703}$ : the explicit map provided by Parry’s method is an isomorphism between the map
$\unicode[STIX]{x1D703}$ : the explicit map provided by Parry’s method is an isomorphism between the map 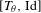 $[T_{\unicode[STIX]{x1D703}},\text{Id}]$ and the unilateral dyadic Bernoulli shift whenever
$[T_{\unicode[STIX]{x1D703}},\text{Id}]$ and the unilateral dyadic Bernoulli shift whenever 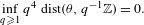 $$\begin{eqnarray}\inf _{q\geq 1}q^{4}~\text{dist}(\unicode[STIX]{x1D703},q^{-1}\mathbb{Z})=0.\end{eqnarray}$$
$$\begin{eqnarray}\inf _{q\geq 1}q^{4}~\text{dist}(\unicode[STIX]{x1D703},q^{-1}\mathbb{Z})=0.\end{eqnarray}$$ $$\begin{eqnarray}\inf _{n\geq 1}q_{n}^{3}~(a_{1}+\cdots +a_{n})~|q_{n}\unicode[STIX]{x1D703}-p_{n}|<+\infty ,\end{eqnarray}$$
$$\begin{eqnarray}\inf _{n\geq 1}q_{n}^{3}~(a_{1}+\cdots +a_{n})~|q_{n}\unicode[STIX]{x1D703}-p_{n}|<+\infty ,\end{eqnarray}$$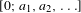 $[0;a_{1},a_{2},\ldots ]$ is the continued fraction expansion and
$[0;a_{1},a_{2},\ldots ]$ is the continued fraction expansion and 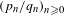 $(p_{n}/q_{n})_{n\geq 0}$ the sequence of convergents of
$(p_{n}/q_{n})_{n\geq 0}$ the sequence of convergents of 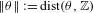 $\Vert \unicode[STIX]{x1D703}\Vert :=\text{dist}(\unicode[STIX]{x1D703},\mathbb{Z})$ . Whether Parry’s map is an isomorphism for every
$\Vert \unicode[STIX]{x1D703}\Vert :=\text{dist}(\unicode[STIX]{x1D703},\mathbb{Z})$ . Whether Parry’s map is an isomorphism for every  $\unicode[STIX]{x1D703}$ or not is still an open question, although we expect a positive answer.
$\unicode[STIX]{x1D703}$ or not is still an open question, although we expect a positive answer.
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s) 2020. Published by Cambridge University Press
References
- 1
- Cited by


