In this paper we consider 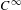$C^{\infty }$-generic families of area-preserving diffeomorphisms of the torus homotopic to the identity and their rotation sets. Let 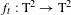$f_{t}:\text{T}^{2}\rightarrow \text{T}^{2}$ be such a family, 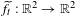$\widetilde{f}_{t}:\mathbb{R}^{2}\rightarrow \mathbb{R}^{2}$ be a fixed family of lifts and 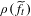$\unicode[STIX]{x1D70C}(\widetilde{f}_{t})$ be their rotation sets, which we assume to have interior for $t$ in a certain open interval $I$. We also assume that some rational point 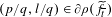$(p/q,l/q)\in \unicode[STIX]{x2202}\unicode[STIX]{x1D70C}(\widetilde{f}_{\overline{t}})$ for a certain parameter 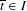$\overline{t}\in I$, and we want to understand the consequences of the following hypothesis: for all 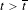$t>\overline{t}$, 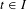$t\in I$, 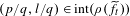$(p/q,l/q)\in \text{int}(\unicode[STIX]{x1D70C}(\widetilde{f}_{t}))$. Under these very natural assumptions, we prove that there exists a 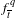$f_{\overline{t}}^{q}$-fixed hyperbolic saddle 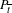$P_{\overline{t}}$ such that its rotation vector is 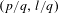$(p/q,l/q)$. We also prove that there exists a sequence 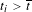$t_{i}>\overline{t}$, 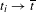$t_{i}\rightarrow \overline{t}$, such that if 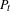$P_{t}$ is the continuation of 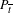$P_{\overline{t}}$ with the parameter, then 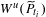$W^{u}(\widetilde{P}_{t_{i}})$ (the unstable manifold) has quadratic tangencies with 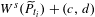$W^{s}(\widetilde{P}_{t_{i}})+(c,d)$ (the stable manifold translated by 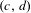$(c,d)$), where 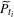$\widetilde{P}_{t_{i}}$ is any lift of 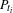$P_{t_{i}}$ to the plane. In other words, 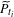$\widetilde{P}_{t_{i}}$ is a fixed point for $(\widetilde{f}_{t_{i}})^{q}-(p,l)$, and 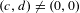$(c,d)\neq (0,0)$ are certain integer vectors such that 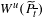$W^{u}(\widetilde{P}_{\overline{t}})$ do not intersect 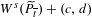$W^{s}(\widetilde{P}_{\overline{t}})+(c,d)$, and these tangencies become transverse as $t$ increases. We also prove that, for 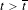$t>\overline{t}$, 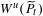$W^{u}(\widetilde{P}_{t})$ has transverse intersections with 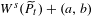$W^{s}(\widetilde{P}_{t})+(a,b)$, for all integer vectors 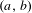$(a,b)$, and thus one may consider that the tangencies above are associated to the birth of the heteroclinic intersections in the plane that do not exist for 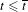$t\leq \overline{t}$.