1 Introduction
A dynamical system is a pair
![]() $(X,f)$
, where X is a compact metric space and
$(X,f)$
, where X is a compact metric space and
![]() $f\colon X\to X$
is a continuous map. A continuum is a compact connected metric space. Throughout this paper, we assume X is a dendrite, that is, a locally connected continuum containing no simple closed curve.
$f\colon X\to X$
is a continuous map. A continuum is a compact connected metric space. Throughout this paper, we assume X is a dendrite, that is, a locally connected continuum containing no simple closed curve.
The main motivation of the paper can be derived from the Möbius disjointness conjecture proposed by Sarnak in 2009 [Reference Kočan, Kornecká-Kurková and Málek23]. By topological arguments, the conjecture was confirmed on various one-dimensional spaces: the interval [Reference Karagulyan14], the circle [Reference Bowen8], topological graphs [Reference Li, Oprocha, Yang and Zeng16], some dendrites [Reference Downarowicz11], etc. However, using ergodic theory, it was proved that if all invariant measures have discrete spectrum, then the conjecture also holds (see e.g. [Reference Huang, Wang and Ye13, Theorem 1.2]). This leads to a natural question, what can be said about the spectrum of measures for zero-entropy maps in the above-mentioned spaces. In [Reference Li, Tu and Ye17], the authors confirmed that, indeed, maps on topological graphs with zero entropy can have only invariant measures with discrete spectrum. This motivated the following open question [Reference Li, Tu and Ye17, Question 1.1].
Question 1.1. Which one-dimensional continua X have the property that every invariant measure of
![]() $(X,f)$
has discrete spectrum, assuming f is a zero-entropy map?
$(X,f)$
has discrete spectrum, assuming f is a zero-entropy map?
Similar questions, however, were stated even before, for example in [Reference Sharkovsky, Kolyada, Sivak and Fedorenko24] from 1982, where the author asked whether every ergodic invariant measure in a mean equicontinuous system has discrete spectrum. The authors of [Reference Li, Tu and Ye17] partially answered this question by showing that the result holds for zero-entropy maps on quasi-graphs X, and it was completely answered in the affirmative in 2015 in [Reference Mai and Shi18]. Let us mention at this point that continua satisfying the condition in Question 1.1 cannot be too complex. It was shown in [Reference Li, Tu and Ye17] that if a dendrite has an uncountable set of endpoints, then it supports a plethora of maps with zero topological entropy possessing invariant measures which do not have discrete spectrum. Then in the realm of dendrites, only those with a countable set of endpoints can be examples in Question 1.1.
In this paper, we study the dynamics of zero-entropy maps on dendrites for which the endpoint set has a countable closure. In §3, we build on results from [Reference Arévalo, Charatonik, Pellicer Covarrubias and Simón3, Reference Askri4] and show that every recurrent point is in fact minimal (Theorem 3.6), which generalizes a well-known property of zero-entropy interval maps. In §4, we use this result together with a characterization of minimal
![]() $\omega $
-limit sets from [Reference Askri4] to show that every invariant measure has discrete spectrum (Theorem 4.3) in the case of these dendrites. Our results almost completely characterize dendrites for which all invariant measures of zero-entropy mappings have discrete spectrum. We leave unsolved the case of dendrites for which the endpoint set is countable but has an uncountable closure. We strongly believe that in the case of these dendrites, the analog of Theorem 3.6 also holds, because all known examples seem to confirm that. Unfortunately, we were not able to find a good argument to justify this statement. Structural properties of (other) one-dimensional continua that may serve as positive examples in Question 1.1 are yet to be understood.
$\omega $
-limit sets from [Reference Askri4] to show that every invariant measure has discrete spectrum (Theorem 4.3) in the case of these dendrites. Our results almost completely characterize dendrites for which all invariant measures of zero-entropy mappings have discrete spectrum. We leave unsolved the case of dendrites for which the endpoint set is countable but has an uncountable closure. We strongly believe that in the case of these dendrites, the analog of Theorem 3.6 also holds, because all known examples seem to confirm that. Unfortunately, we were not able to find a good argument to justify this statement. Structural properties of (other) one-dimensional continua that may serve as positive examples in Question 1.1 are yet to be understood.
2 Preliminaries
Let
![]() $(X,f)$
be a dynamical system and
$(X,f)$
be a dynamical system and
![]() $x\in X$
. The orbit of x, denoted by
$x\in X$
. The orbit of x, denoted by
![]() $\mathrm {Orb}_f(x)$
, is the set
$\mathrm {Orb}_f(x)$
, is the set
![]() $\{f^n(x)\colon n\geq 0\}$
, and the
$\{f^n(x)\colon n\geq 0\}$
, and the
![]() $\omega $
-limit set of x, denoted by
$\omega $
-limit set of x, denoted by
![]() $\omega _f(x)$
, is defined as the intersection
$\omega _f(x)$
, is defined as the intersection
![]() $\bigcap _{n\ge 0} \overline {\{f^m (x)\colon m\ge n\}}$
. It is easy to check that
$\bigcap _{n\ge 0} \overline {\{f^m (x)\colon m\ge n\}}$
. It is easy to check that
![]() $\omega _f(x)$
is closed and strongly f-invariant, that is,
$\omega _f(x)$
is closed and strongly f-invariant, that is,
![]() $f (\omega _f(x))= \omega _f(x)$
. The point x is periodic (
$f (\omega _f(x))= \omega _f(x)$
. The point x is periodic (
![]() $x\in \mathrm {Per}(f)$
) if
$x\in \mathrm {Per}(f)$
) if
![]() $f^p(x) =x$
for some
$f^p(x) =x$
for some
![]() $p\in \mathbb N$
, where the smallest such p is called the period of x. Note that throughout this paper,
$p\in \mathbb N$
, where the smallest such p is called the period of x. Note that throughout this paper,
![]() $\mathbb N$
denotes the set of positive integers. The point x is recurrent (
$\mathbb N$
denotes the set of positive integers. The point x is recurrent (
![]() $x\in \mathrm {Rec}(f)$
) if
$x\in \mathrm {Rec}(f)$
) if
![]() $x\in \omega _f (x)$
. The orbit of a set
$x\in \omega _f (x)$
. The orbit of a set
![]() $A\subset X$
, denoted
$A\subset X$
, denoted
![]() $\mathrm {Orb}_f(A)$
, is the set
$\mathrm {Orb}_f(A)$
, is the set
![]() $\bigcup _{n\geq 0} f^n(A)$
, and A is called invariant if
$\bigcup _{n\geq 0} f^n(A)$
, and A is called invariant if
![]() $f(A)\subseteq A$
. A set M is minimal if it is non-empty, closed, invariant, and does not have a proper subset with these three properties. It can be equivalently characterized by
$f(A)\subseteq A$
. A set M is minimal if it is non-empty, closed, invariant, and does not have a proper subset with these three properties. It can be equivalently characterized by
![]() $M=\omega _f(x)$
for every
$M=\omega _f(x)$
for every
![]() $x\in M$
. A point is minimal if it belongs to a minimal set.
$x\in M$
. A point is minimal if it belongs to a minimal set.
Recall that a dendrite is a locally connected continuum X containing no homeomorphic copy of a circle. A continuous map from a dendrite into itself is called a dendrite map. For any point
![]() $x \in X$
, the order of x, denoted by
$x \in X$
, the order of x, denoted by
![]() $\mathrm {ord}(x)$
, is the number of connected components of
$\mathrm {ord}(x)$
, is the number of connected components of
![]() $X\setminus \{x\}$
. Points of order
$X\setminus \{x\}$
. Points of order
![]() $1$
are called endpoints while points of order at least
$1$
are called endpoints while points of order at least
![]() $3$
are called branch points. By
$3$
are called branch points. By
![]() $E(X)$
and
$E(X)$
and
![]() $B(X)$
we denote the set of endpoints and branch points, respectively. In this paper, we especially focus on dendrites in which
$B(X)$
we denote the set of endpoints and branch points, respectively. In this paper, we especially focus on dendrites in which
![]() $E(X)$
has countable closure. These dendrites are a special case of a tame graph, as introduced in [Reference Askri5]. Note that when
$E(X)$
has countable closure. These dendrites are a special case of a tame graph, as introduced in [Reference Askri5]. Note that when
![]() $\overline {E(X)}$
is countable, so also is
$\overline {E(X)}$
is countable, so also is
![]() $\overline {B(X)\cup E(X)}$
, because
$\overline {B(X)\cup E(X)}$
, because
![]() $B(X)$
is countable in any dendrite and has accumulation points only in
$B(X)$
is countable in any dendrite and has accumulation points only in
![]() $\overline {E(X)}$
.
$\overline {E(X)}$
.
For any two distinct points
![]() $x,y \in X$
, there exists a unique arc
$x,y \in X$
, there exists a unique arc
![]() $[x,y]\subset X$
joining those points. A free arc is an arc containing no branch points. We say that two arcs
$[x,y]\subset X$
joining those points. A free arc is an arc containing no branch points. We say that two arcs
![]() $I, J$
form an arc horseshoe for f if
$I, J$
form an arc horseshoe for f if
![]() $f^n(I) \cap f^m(J)\supset I \cup J$
for some
$f^n(I) \cap f^m(J)\supset I \cup J$
for some
![]() $n,m\in \mathbb {N}$
, where
$n,m\in \mathbb {N}$
, where
![]() $I, J$
are disjoint except possibly at one endpoint. Denote by
$I, J$
are disjoint except possibly at one endpoint. Denote by
![]() $h_{\mathrm {top}}(f)$
the topological entropy of a dendrite map f (for the definition, see [Reference El Abdalaoui, Askri and Marzougui1, Reference Block and Coppel7, Reference Davenport9]). We will frequently use the fact that for dendrite maps, positive topological entropy is implied by the existence of an arc horseshoe [Reference Li, Oprocha and Zhang15].
$h_{\mathrm {top}}(f)$
the topological entropy of a dendrite map f (for the definition, see [Reference El Abdalaoui, Askri and Marzougui1, Reference Block and Coppel7, Reference Davenport9]). We will frequently use the fact that for dendrite maps, positive topological entropy is implied by the existence of an arc horseshoe [Reference Li, Oprocha and Zhang15].
The set of all Borel probability measures over X is denoted by
![]() $M(X)$
, and
$M(X)$
, and
![]() $M_f(X)\subset M(X)$
denotes the set of all elements of
$M_f(X)\subset M(X)$
denotes the set of all elements of
![]() $M(X)$
invariant with respect to the map f. The set of all ergodic measures in
$M(X)$
invariant with respect to the map f. The set of all ergodic measures in
![]() $M_f(X)$
is denoted by
$M_f(X)$
is denoted by
![]() $M_f^e(X)$
. We say that a finite measure
$M_f^e(X)$
. We say that a finite measure
![]() $\mu $
on X is concentrated on
$\mu $
on X is concentrated on
![]() $A\subset X$
if
$A\subset X$
if
![]() $\mu (A)=\mu (X)$
. It is well known that
$\mu (A)=\mu (X)$
. It is well known that
![]() $M(X)$
endowed with the weak-* topology is a compact metric space and that
$M(X)$
endowed with the weak-* topology is a compact metric space and that
![]() $M_f(X)$
is its closed subset. We say that
$M_f(X)$
is its closed subset. We say that
![]() $\mu \in M_f(X)$
has discrete spectrum, if the linear span of the eigenfunctions of
$\mu \in M_f(X)$
has discrete spectrum, if the linear span of the eigenfunctions of
![]() $U_f$
in
$U_f$
in
![]() $L^2_\mu (X)$
is dense in
$L^2_\mu (X)$
is dense in
![]() $L^2_\mu (X)$
, where as usual
$L^2_\mu (X)$
, where as usual
![]() $U_f$
denotes the Koopman operator:
$U_f$
denotes the Koopman operator:
![]() $U_f(\varphi )=\varphi \circ f$
for every
$U_f(\varphi )=\varphi \circ f$
for every
![]() $\varphi \in L^2_\mu (X)$
. We refer the reader to [Reference Dinaburg10, Reference Walters26] for standard monographs on ergodic theory and entropy.
$\varphi \in L^2_\mu (X)$
. We refer the reader to [Reference Dinaburg10, Reference Walters26] for standard monographs on ergodic theory and entropy.
3 Recurrence and minimality in dendrites with
 $\overline {E(X)}$
countable
$\overline {E(X)}$
countable
First we recall the following results by Askri on the structure of minimal
![]() $\omega $
-limit sets in a special class of dendrite maps.
$\omega $
-limit sets in a special class of dendrite maps.
Proposition 3.1. [Reference Askri4, Proposition 3.4]
Let X be a dendrite such that
![]() $E(X)$
is countable and let
$E(X)$
is countable and let
![]() $f\colon X\to X$
be a continuous map with zero topological entropy. If
$f\colon X\to X$
be a continuous map with zero topological entropy. If
![]() $M= \omega _f (x)$
is an infinite minimal
$M= \omega _f (x)$
is an infinite minimal
![]() $\omega $
-limit set for some
$\omega $
-limit set for some
![]() $x\in X$
, then for every
$x\in X$
, then for every
![]() $k\geq 1$
there is an f-periodic subdendrite
$k\geq 1$
there is an f-periodic subdendrite
![]() $D_k$
of X and an integer
$D_k$
of X and an integer
![]() $n_k\geq 2$
with the following properties:
$n_k\geq 2$
with the following properties:
-
(1)
 $D_k$
has period
$D_k$
has period
 $\alpha _k:=n_1 n_2 \ldots n_k$
;
$\alpha _k:=n_1 n_2 \ldots n_k$
; -
(2) for
 $i\neq j\in \{0,\ldots ,\alpha _k-1\}, f^i(D_k)$
and
$i\neq j\in \{0,\ldots ,\alpha _k-1\}, f^i(D_k)$
and
 $ f^j(D_k)$
are either disjoint or intersect at one common point;
$ f^j(D_k)$
are either disjoint or intersect at one common point; -
(3)
 $\bigcup _{k=0}^{n_j-1}f^{k\alpha _{j-1}}(D_j)\subset D_{j-1}$
;
$\bigcup _{k=0}^{n_j-1}f^{k\alpha _{j-1}}(D_j)\subset D_{j-1}$
; -
(4)
 $M \subset \bigcap _{k\geq 0}{\mathrm {Orb}}_f(D_k)$
;
$M \subset \bigcap _{k\geq 0}{\mathrm {Orb}}_f(D_k)$
; -
(5)
 $f(M^k_i) = M^k_{i+1 \mod \alpha _k}$
, where
$f(M^k_i) = M^k_{i+1 \mod \alpha _k}$
, where
 $M^k_i = M\cap f^i(D_k)$
for all k and all
$M^k_i = M\cap f^i(D_k)$
for all k and all
 $0\leq i\leq \alpha _k-1$
.
$0\leq i\leq \alpha _k-1$
.
While equation (5) is not directly stated in [Reference Askri4], it is an obvious consequence of the other statements.
Implicit in Proposition 3.1 is the idea that the minimal set M has an odometer as a factor. Our next lemma shows that when
![]() $E(X)$
has countable closure, the factor map is invertible except on a countable set.
$E(X)$
has countable closure, the factor map is invertible except on a countable set.
Given an increasing sequence
![]() $(\alpha _k)$
with
$(\alpha _k)$
with
![]() $\alpha _k | \alpha _{k+1}$
for all k, we define the group
$\alpha _k | \alpha _{k+1}$
for all k, we define the group
![]() $\Omega =\Omega (\alpha _k)$
of all
$\Omega =\Omega (\alpha _k)$
of all
![]() $\theta \in \prod _{k=0}^\infty \mathbb {Z}/\alpha _k\mathbb {Z}$
, such that
$\theta \in \prod _{k=0}^\infty \mathbb {Z}/\alpha _k\mathbb {Z}$
, such that
![]() $\theta _{k+1}$
is congruent to
$\theta _{k+1}$
is congruent to
![]() $\theta _k$
modulo
$\theta _k$
modulo
![]() $\alpha _k$
for all k, and we let
$\alpha _k$
for all k, and we let
![]() $\tau $
denote the group rotation
$\tau $
denote the group rotation
![]() $\tau (\theta )=\theta +(1,1,1,\ldots )$
. Then
$\tau (\theta )=\theta +(1,1,1,\ldots )$
. Then
![]() $(\Omega ,\tau )$
is called the odometer associated to the sequence
$(\Omega ,\tau )$
is called the odometer associated to the sequence
![]() $(\alpha _k)$
.
$(\alpha _k)$
.
Lemma 3.2. Let
![]() $X,f,M,(D_k),(\alpha _k)$
be as in Proposition 3.1 and suppose that
$X,f,M,(D_k),(\alpha _k)$
be as in Proposition 3.1 and suppose that
![]() $\overline {E(X)}$
is countable. Then the following hold.
$\overline {E(X)}$
is countable. Then the following hold.
-
(1) The sets
 $J_\theta =\bigcap _k f^{\theta _k}(D_k)$
,
$J_\theta =\bigcap _k f^{\theta _k}(D_k)$
,
 $\theta \in \Omega $
, are closed, connected, and pairwise disjoint.
$\theta \in \Omega $
, are closed, connected, and pairwise disjoint. -
(2) There is a factor map
 $\pi :(M,f)\to (\Omega ,\tau )$
which takes the value
$\pi :(M,f)\to (\Omega ,\tau )$
which takes the value
 $\theta $
on
$\theta $
on
 $M\cap J_\theta $
.
$M\cap J_\theta $
. -
(3) Each fiber
 $\pi ^{-1}(\theta )$
,
$\pi ^{-1}(\theta )$
,
 $\theta \in \Omega $
, is countable, and all but countably many of these fibers are singletons.
$\theta \in \Omega $
, is countable, and all but countably many of these fibers are singletons.
Proof. It is clear from Proposition 3.1 that each set
![]() $J_\theta $
is closed, connected, and has non-empty intersection with M. It is also clear that
$J_\theta $
is closed, connected, and has non-empty intersection with M. It is also clear that
![]() $f(J_\theta )=J_{\tau (\theta )}$
. However, because the sets
$f(J_\theta )=J_{\tau (\theta )}$
. However, because the sets
![]() $f^i(D_k)\cap f^j(D_k)$
are allowed to intersect at a point, it is not clear if the sets
$f^i(D_k)\cap f^j(D_k)$
are allowed to intersect at a point, it is not clear if the sets
![]() $J_\theta $
are pairwise disjoint. We prove this fact now. Suppose there are
$J_\theta $
are pairwise disjoint. We prove this fact now. Suppose there are
![]() $\theta \neq \theta '$
with
$\theta \neq \theta '$
with
![]() $J_\theta \cap J_{\theta '}\neq \emptyset $
. Find k minimal such that
$J_\theta \cap J_{\theta '}\neq \emptyset $
. Find k minimal such that
![]() $\theta _k\neq \theta ^{\prime }_k$
. Then clearly
$\theta _k\neq \theta ^{\prime }_k$
. Then clearly
for some single point
![]() $a\in X$
. Taking the image by
$a\in X$
. Taking the image by
![]() $f^{\alpha _k}$
, we have
$f^{\alpha _k}$
, we have
because
![]() $D_k$
is periodic with period
$D_k$
is periodic with period
![]() $\alpha _k$
. This shows that a is periodic with period
$\alpha _k$
. This shows that a is periodic with period
![]() $\alpha _k$
. In particular, it does not belong to the infinite minimal set M. Now for
$\alpha _k$
. In particular, it does not belong to the infinite minimal set M. Now for
![]() $n\in \mathbb {N}$
, let
$n\in \mathbb {N}$
, let
![]() $J_n=J_{\tau ^{n\alpha _k}(\theta )}$
. Then
$J_n=J_{\tau ^{n\alpha _k}(\theta )}$
. Then
![]() $a\in J_n$
and we can choose an additional point
$a\in J_n$
and we can choose an additional point
![]() $m_n \in M \cap J_n$
for all n. Thus the
$m_n \in M \cap J_n$
for all n. Thus the
![]() $J_n$
sets are non-degenerate subdendrites and intersect pairwise only at a. In particular, the sets
$J_n$
sets are non-degenerate subdendrites and intersect pairwise only at a. In particular, the sets
![]() $(a,m_n]$
are pairwise disjoint connected subsets of X, so their diameters must converge to zero (see e.g. [Reference Misiurewicz and Marchioro19, Lemma 2.3]). However, because M is closed, this shows that
$(a,m_n]$
are pairwise disjoint connected subsets of X, so their diameters must converge to zero (see e.g. [Reference Misiurewicz and Marchioro19, Lemma 2.3]). However, because M is closed, this shows that
![]() $a\in M$
, a contradiction.
$a\in M$
, a contradiction.
Now that the sets
![]() $J_\theta $
,
$J_\theta $
,
![]() $\theta \in \Omega $
have been shown to be pairwise disjoint, we see immediately that
$\theta \in \Omega $
have been shown to be pairwise disjoint, we see immediately that
![]() $\pi $
is well defined. It is also easy to see that
$\pi $
is well defined. It is also easy to see that
![]() $\pi $
is continuous and
$\pi $
is continuous and
![]() $\tau \circ \pi = \pi \circ f$
.
$\tau \circ \pi = \pi \circ f$
.
Again, because the sets
![]() $J_\theta $
,
$J_\theta $
,
![]() $\theta \in \Omega $
are pairwise disjoint connected sets in X, only countably many of them can have positive diameter. It follows that
$\theta \in \Omega $
are pairwise disjoint connected sets in X, only countably many of them can have positive diameter. It follows that
![]() $\pi ^{-1}(\theta )$
is a singleton except for countably many
$\pi ^{-1}(\theta )$
is a singleton except for countably many
![]() $\theta $
. It remains to show that
$\theta $
. It remains to show that
![]() $M\cap J_\theta $
is countable when
$M\cap J_\theta $
is countable when
![]() $J_\theta $
is non-degenerate. Because M is minimal and
$J_\theta $
is non-degenerate. Because M is minimal and
![]() $J_\theta $
never returns to itself, we must have
$J_\theta $
never returns to itself, we must have
![]() $M\cap J_\theta \subset \operatorname {\mathrm {Bd}}(J_\theta )$
, where
$M\cap J_\theta \subset \operatorname {\mathrm {Bd}}(J_\theta )$
, where
![]() $\operatorname {\mathrm {Bd}}(J_{\theta })$
stands for the boundary of
$\operatorname {\mathrm {Bd}}(J_{\theta })$
stands for the boundary of
![]() $J_{\theta }$
. However, the boundary in X of the subdendrite
$J_{\theta }$
. However, the boundary in X of the subdendrite
![]() $J_\theta $
is a subset of
$J_\theta $
is a subset of
![]() $E(J_\theta ) \cup B(X) \cup \overline {E(X)}$
, which is countable by the assumption that
$E(J_\theta ) \cup B(X) \cup \overline {E(X)}$
, which is countable by the assumption that
![]() $E(X)$
has countable closure. Here we use the well-known facts that
$E(X)$
has countable closure. Here we use the well-known facts that
![]() $B(X)$
is countable in any dendrite, and the cardinality of the endpoint set of a dendrite cannot increase when we pass to a subdendrite, see e.g. [Reference Naghmouchi21, Reference Scarpellini22].
$B(X)$
is countable in any dendrite, and the cardinality of the endpoint set of a dendrite cannot increase when we pass to a subdendrite, see e.g. [Reference Naghmouchi21, Reference Scarpellini22].
Remark 3.3. We have in fact shown that for a zero entropy map on a dendrite whose endpoint set has countable closure, every minimal subsystem is a regular extension of its maximal equicontinuous factor in the sense defined in [Reference García-Ramos, Jäger and Ye12]. For infinite minimal sets, this is implied by Lemma 3.2(3) and a finite minimal set is just a periodic orbit.
The next lemma strengthens [Reference Askri4, Lemma 3.5] by relaxing the condition that
![]() $E(X)$
be closed.
$E(X)$
be closed.
Lemma 3.4. [Reference Askri4, Lemma 3.5]
Let
![]() $X,f,M,(D_k),(\alpha _k)$
be as in Proposition 3.1 and suppose that
$X,f,M,(D_k),(\alpha _k)$
be as in Proposition 3.1 and suppose that
![]() $\overline {E(X)}$
is countable. Then there is
$\overline {E(X)}$
is countable. Then there is
![]() $N\geq 1$
such that
$N\geq 1$
such that
![]() $\text { for all } k\geq N, f^{i_k}(D_k)$
is a free arc for some
$\text { for all } k\geq N, f^{i_k}(D_k)$
is a free arc for some
![]() $0\leq i_k\leq \alpha _k-1$
.
$0\leq i_k\leq \alpha _k-1$
.
Proof. Using Lemma 3.2, we know that there are uncountably many singleton sets
![]() $J_\theta $
. Now a dendrite whose endpoint set has countable closure is always the union of a countable sequence of free arcs and a countable set, see [Reference Askri5, Theorem 2.2]. It follows that we can find
$J_\theta $
. Now a dendrite whose endpoint set has countable closure is always the union of a countable sequence of free arcs and a countable set, see [Reference Askri5, Theorem 2.2]. It follows that we can find
![]() $\theta $
with the singleton
$\theta $
with the singleton
![]() $J_\theta $
in the interior of a free arc A in X. Because
$J_\theta $
in the interior of a free arc A in X. Because
![]() $J_\theta $
is the nested intersection
$J_\theta $
is the nested intersection
![]() $\bigcap _N f^{\theta _N}(D_N)$
, we can find N large enough that
$\bigcap _N f^{\theta _N}(D_N)$
, we can find N large enough that
![]() $f^{\theta _N}(D_N)$
is contained in A. Then
$f^{\theta _N}(D_N)$
is contained in A. Then
![]() $f^{\theta _k}(D_k)$
is a free arc for all
$f^{\theta _k}(D_k)$
is a free arc for all
![]() $k\geq N$
.
$k\geq N$
.
Our next result is a good first step in showing that recurrent points are minimal. It is a modified version of [Reference Arévalo, Charatonik, Pellicer Covarrubias and Simón3, Theorem 1.1], and the proof closely follows the one from that paper.
Lemma 3.5. Let X be a dendrite with
![]() $\overline {E(X)}$
countable,
$\overline {E(X)}$
countable,
![]() $f:X\to X$
a continuous map with zero topological entropy, and
$f:X\to X$
a continuous map with zero topological entropy, and
![]() $x\in X$
a point which is recurrent but not periodic. Then
$x\in X$
a point which is recurrent but not periodic. Then
![]() $\omega _f(x)$
contains no periodic points.
$\omega _f(x)$
contains no periodic points.
Proof. Throughout the proof, we will use freely the following well-known property of
![]() $\omega $
-limit sets (e.g. [Reference Bartoš, Bobok, Pyrih, Roth and Vejnar6]): if for fixed
$\omega $
-limit sets (e.g. [Reference Bartoš, Bobok, Pyrih, Roth and Vejnar6]): if for fixed
![]() $n\geq 2$
we write
$n\geq 2$
we write
![]() $W_i=\omega _{f^n}(f^i(x))$
for
$W_i=\omega _{f^n}(f^i(x))$
for
![]() $0\leq i<n$
, then
$0\leq i<n$
, then
![]() $\omega _f(x)=\bigcup _{i=0}^{n-1} W_i$
and
$\omega _f(x)=\bigcup _{i=0}^{n-1} W_i$
and
![]() $f(W_i)=W_{i+1 \; (\text {mod }n)}$
. In particular, if
$f(W_i)=W_{i+1 \; (\text {mod }n)}$
. In particular, if
![]() $\omega _f(x)$
is uncountable, then so is each
$\omega _f(x)$
is uncountable, then so is each
![]() $W_i$
, and if
$W_i$
, and if
![]() $\omega _f(x)$
contains a given fixed point, then each
$\omega _f(x)$
contains a given fixed point, then each
![]() $W_i$
contains it as well. We continue to use the notation
$W_i$
contains it as well. We continue to use the notation
![]() $[x,y]$
for the unique arc in X with endpoints
$[x,y]$
for the unique arc in X with endpoints
![]() $x,y\in X$
, and if
$x,y\in X$
, and if
![]() $z\in (x,y)=[x,y]\setminus \{x,y\}$
, we will say for simplicity that z lies between x and y.
$z\in (x,y)=[x,y]\setminus \{x,y\}$
, we will say for simplicity that z lies between x and y.
Now let
![]() $L=\omega _f(x)$
, where x is recurrent but not periodic. Then L is the closure of the orbit of x, and hence it is a perfect uncountable set.
$L=\omega _f(x)$
, where x is recurrent but not periodic. Then L is the closure of the orbit of x, and hence it is a perfect uncountable set.
Step 1: L does not contain a periodic point with a free arc neighborhood in X. Suppose to the contrary that
![]() $a\in L$
,
$a\in L$
,
![]() $f^N(a)=a$
, and some free arc C is a neighborhood of a in X. Then, by the standard properties mentioned above,
$f^N(a)=a$
, and some free arc C is a neighborhood of a in X. Then, by the standard properties mentioned above,
![]() $a\in \omega _{f^N}(f^i(x))$
for some
$a\in \omega _{f^N}(f^i(x))$
for some
![]() $0\leq i<N$
. Replacing f with its iterate and x with its image, we may safely assume that
$0\leq i<N$
. Replacing f with its iterate and x with its image, we may safely assume that
![]() $N=1$
and
$N=1$
and
![]() $i=0$
, that is, a is a fixed point in
$i=0$
, that is, a is a fixed point in
![]() $L=\omega _f(x)$
.
$L=\omega _f(x)$
.
Because periodic points are never isolated in infinite
![]() $\omega $
-limit sets, we know that L accumulates on a from at least one side in the free arc C. So, choose an endpoint b of C such that
$\omega $
-limit sets, we know that L accumulates on a from at least one side in the free arc C. So, choose an endpoint b of C such that
![]() $L\cap [a,b]$
accumulates on a. For convenience, we let C carry its natural order as an arc, oriented in such a way that
$L\cap [a,b]$
accumulates on a. For convenience, we let C carry its natural order as an arc, oriented in such a way that
![]() $a<b$
. Choose five points
$a<b$
. Choose five points
![]() $y_i\in L\cap [a,b]$
with
$y_i\in L\cap [a,b]$
with
![]() $a<y_1<y_2<y_3<y_4<y_5<b$
. Choose three small arc neighborhoods
$a<y_1<y_2<y_3<y_4<y_5<b$
. Choose three small arc neighborhoods
![]() $I_2, I_3, I_4$
containing
$I_2, I_3, I_4$
containing
![]() $y_2,y_3,y_4$
, respectively, and let them be pairwise disjoint and lie between
$y_2,y_3,y_4$
, respectively, and let them be pairwise disjoint and lie between
![]() $y_1$
and
$y_1$
and
![]() $y_5$
. Because the orbit of x visits each of these neighborhoods
$y_5$
. Because the orbit of x visits each of these neighborhoods
![]() $I_i$
infinitely often, there must be points in
$I_i$
infinitely often, there must be points in
![]() $I_2$
and
$I_2$
and
![]() $I_4$
which visit
$I_4$
which visit
![]() $I_3$
, so by [Reference Misiurewicz and Marchioro19, Theorem 2.13], f has a periodic point c between
$I_3$
, so by [Reference Misiurewicz and Marchioro19, Theorem 2.13], f has a periodic point c between
![]() $y_1$
and
$y_1$
and
![]() $y_5$
. Replacing x with a point from its orbit near
$y_5$
. Replacing x with a point from its orbit near
![]() $y_1$
, we may assume that
$y_1$
, we may assume that
![]() $a<x<c<y_5<b$
. Let r be the period of c and put
$a<x<c<y_5<b$
. Let r be the period of c and put
![]() $g=f^r$
. Because a was already fixed for f, we have
$g=f^r$
. Because a was already fixed for f, we have
![]() $a\in \omega _g(x)$
as well. Note that because x is recurrent for f, it is also recurrent for g.
$a\in \omega _g(x)$
as well. Note that because x is recurrent for f, it is also recurrent for g.
Claim. There is an arc I invariant for g with
![]() $[a,x]\subseteq I \subseteq [a,c]$
.
$[a,x]\subseteq I \subseteq [a,c]$
.
Proof of Claim
To prove the claim, put
![]() $I=\overline {\bigcup _{n=0}^{\infty } g^n([a,x])}$
. Because a is fixed and x is recurrent, it suffices to show that
$I=\overline {\bigcup _{n=0}^{\infty } g^n([a,x])}$
. Because a is fixed and x is recurrent, it suffices to show that
![]() $g^n([a,x]) \subseteq [a,c]$
for all n. If this is not true, then there is
$g^n([a,x]) \subseteq [a,c]$
for all n. If this is not true, then there is
![]() $z\in [a,x]$
and
$z\in [a,x]$
and
![]() $n_0 \geq 1$
such that a is between
$n_0 \geq 1$
such that a is between
![]() $g^{n_0}(z)$
and c or c is between
$g^{n_0}(z)$
and c or c is between
![]() $g^{n_0}(z)$
and a. We treat these two cases separately.
$g^{n_0}(z)$
and a. We treat these two cases separately.
Suppose first that a is between
![]() $g^{n_0}(z)$
and c. Then
$g^{n_0}(z)$
and c. Then
![]() $a\in g^{n_0}([z,c])$
, so there is
$a\in g^{n_0}([z,c])$
, so there is
![]() $a_{-1}$
between z and c with
$a_{-1}$
between z and c with
![]() $g^{n_0}(a_{-1})=a$
. Then
$g^{n_0}(a_{-1})=a$
. Then
![]() $f^n(a_{-1})=a$
for all
$f^n(a_{-1})=a$
for all
![]() $n\geq n_0\cdot r$
. Because
$n\geq n_0\cdot r$
. Because
![]() $L\cap [a,b]$
accumulates on a, we can find a point
$L\cap [a,b]$
accumulates on a, we can find a point
![]() $x'\in \mathrm {Orb}_f(x)$
between a and
$x'\in \mathrm {Orb}_f(x)$
between a and
![]() $a_{-1}$
. Because
$a_{-1}$
. Because
![]() $y_5\in \omega _f(x)$
, we can find
$y_5\in \omega _f(x)$
, we can find
![]() $n\geq n_0\cdot r$
such that
$n\geq n_0\cdot r$
such that
![]() $f^n(x')$
is close to
$f^n(x')$
is close to
![]() $y_5$
and
$y_5$
and
![]() $a<x'<a_{-1}<c<f^n(x')$
. Put
$a<x'<a_{-1}<c<f^n(x')$
. Put
![]() $J=[a,x']$
and
$J=[a,x']$
and
![]() $K=[x',a_{-1}]$
. Then
$K=[x',a_{-1}]$
. Then
![]() $f^n(J)\cap f^n(K) \supseteq J\cup K$
, so f possesses an arc horseshoe and thus has positive topological entropy, a contradiction.
$f^n(J)\cap f^n(K) \supseteq J\cup K$
, so f possesses an arc horseshoe and thus has positive topological entropy, a contradiction.
Suppose instead that c is between
![]() $g^{n_0}(z)$
and a. Then
$g^{n_0}(z)$
and a. Then
![]() $c\in g^{n_0}([a,x])$
, so there must be
$c\in g^{n_0}([a,x])$
, so there must be
![]() $c_{-1}$
between a and x with
$c_{-1}$
between a and x with
![]() $g^{n_0}(c_{-1})=c$
. Because
$g^{n_0}(c_{-1})=c$
. Because
![]() $a\in \omega _g(x)$
, we can choose
$a\in \omega _g(x)$
, we can choose
![]() $n>n_0$
with
$n>n_0$
with
![]() $g^n(x)$
close to a so that
$g^n(x)$
close to a so that
![]() $g^n(x)<c_{-1}<x<c$
. Put
$g^n(x)<c_{-1}<x<c$
. Put
![]() $J=[c_{-1},x]$
and
$J=[c_{-1},x]$
and
![]() $K=[x,c]$
. Then again
$K=[x,c]$
. Then again
![]() $g^n(J)\cap g^n(K)\supseteq J\cup K$
, so g has positive topological entropy and so does f, a contradiction. This completes the proof of the claim.
$g^n(J)\cap g^n(K)\supseteq J\cup K$
, so g has positive topological entropy and so does f, a contradiction. This completes the proof of the claim.
Now we may use the claim to finish Step 1. Because x belongs to the closed invariant set I, we have
![]() $\omega _g(x)=\omega _{g|_I}(x)$
. However,
$\omega _g(x)=\omega _{g|_I}(x)$
. However,
![]() $g|_I$
is an interval map, and when an infinite
$g|_I$
is an interval map, and when an infinite
![]() $\omega $
-limit set for an interval map contains a periodic point, the topological entropy must be positive (see [Reference Nadler20]), a contradiction.
$\omega $
-limit set for an interval map contains a periodic point, the topological entropy must be positive (see [Reference Nadler20]), a contradiction.
Step 2: L does not contain any periodic points. Suppose to the contrary that
![]() $a\in L$
is a periodic point. As in Step 1, we may assume that a is fixed. By [Reference Askri5, Theorem 2.2], the dendrite X is the union of a countable sequence of free arcs together with a countable set. In particular, we can find a free arc C not containing a with
$a\in L$
is a periodic point. As in Step 1, we may assume that a is fixed. By [Reference Askri5, Theorem 2.2], the dendrite X is the union of a countable sequence of free arcs together with a countable set. In particular, we can find a free arc C not containing a with
![]() $L\cap C$
uncountable. Write
$L\cap C$
uncountable. Write
![]() $C=[u,v]$
with v between u and a and let
$C=[u,v]$
with v between u and a and let
![]() $<$
denote the order in C with
$<$
denote the order in C with
![]() $u<v$
. Because
$u<v$
. Because
![]() $L\cap C$
is infinite, we may choose four points
$L\cap C$
is infinite, we may choose four points
![]() $x_i\in \mathrm {Orb}_f(x)$
with
$x_i\in \mathrm {Orb}_f(x)$
with
![]() $u<x_1<x_2<x_3<x_4<v$
. As in Step 1, we can use small arc neighborhoods of
$u<x_1<x_2<x_3<x_4<v$
. As in Step 1, we can use small arc neighborhoods of
![]() $x_2,x_3,x_4$
to find a periodic point c with
$x_2,x_3,x_4$
to find a periodic point c with
![]() $u<x_1<c<v$
, and because
$u<x_1<c<v$
, and because
![]() $x_1$
is in the orbit of x, we may redefine
$x_1$
is in the orbit of x, we may redefine
![]() $x=x_1$
without changing
$x=x_1$
without changing
![]() $\omega _f(x)$
. Let r denote the period of c and put
$\omega _f(x)$
. Let r denote the period of c and put
![]() $g=f^r\kern-3pt.$
Because x is recurrent also for g, we have
$g=f^r\kern-3pt.$
Because x is recurrent also for g, we have
![]() $\mathrm {Orb}_g(x)\cap [u,c]$
infinite, so we can find two points
$\mathrm {Orb}_g(x)\cap [u,c]$
infinite, so we can find two points
![]() $x_5,x_6\in \mathrm {Orb}_g(x)$
with
$x_5,x_6\in \mathrm {Orb}_g(x)$
with
![]() $u<x_5<x_6<c$
and passing forward along the orbit, we can redefine
$u<x_5<x_6<c$
and passing forward along the orbit, we can redefine
![]() $x=x_6$
without changing
$x=x_6$
without changing
![]() $\omega _g(x)$
. In particular,
$\omega _g(x)$
. In particular,
![]() $x_5\in \omega _g(x)=\overline {\mathrm {Orb}_g(x)}$
, so we can choose
$x_5\in \omega _g(x)=\overline {\mathrm {Orb}_g(x)}$
, so we can choose
![]() $p\geq 1$
with
$p\geq 1$
with
![]() $g^p(x)$
close to
$g^p(x)$
close to
![]() $x_5$
so that
$x_5$
so that
![]() $u<g^p(x)<x<c$
.
$u<g^p(x)<x<c$
.
Let
![]() $l=\omega _{g^p}(x)$
. We have
$l=\omega _{g^p}(x)$
. We have
![]() $x\in l$
because x is recurrent and
$x\in l$
because x is recurrent and
![]() $a\in l$
because a is a fixed point in
$a\in l$
because a is a fixed point in
![]() $\omega _f(x)$
. Moreover,
$\omega _f(x)$
. Moreover,
![]() $c\not \in l$
as a result of Step 1. So let
$c\not \in l$
as a result of Step 1. So let
![]() $X_0, X_1$
denote the connected components of
$X_0, X_1$
denote the connected components of
![]() $X\setminus \{c\}$
containing x and a, respectively, and put
$X\setminus \{c\}$
containing x and a, respectively, and put
![]() $l_i=l\cap X_i$
. Then
$l_i=l\cap X_i$
. Then
![]() $l=l_0\cup~l_1$
expresses l as the disjoint union of two non-empty open subsets (in the topology induced from X to l). Recall that every
$l=l_0\cup~l_1$
expresses l as the disjoint union of two non-empty open subsets (in the topology induced from X to l). Recall that every
![]() $\omega $
-limit set
$\omega $
-limit set
![]() $\omega _f(x)$
is weakly incompressible, that is,
$\omega _f(x)$
is weakly incompressible, that is,
![]() $f(\overline {U})\not \subset U$
for any set
$f(\overline {U})\not \subset U$
for any set
![]() $U\subsetneq \omega _f(x)$
open in
$U\subsetneq \omega _f(x)$
open in
![]() $\omega _f(x)$
(see, e.g. [Reference Sarnak25]). Thus we have
$\omega _f(x)$
(see, e.g. [Reference Sarnak25]). Thus we have
![]() $g^p(l_0)\cap l_1 \neq \emptyset $
. Therefore, we may choose
$g^p(l_0)\cap l_1 \neq \emptyset $
. Therefore, we may choose
![]() $y\in l_0$
with
$y\in l_0$
with
![]() $g^p(y)\in l_1$
, and because
$g^p(y)\in l_1$
, and because
![]() $\mathrm {Orb}_{g^p}(x)$
is dense in
$\mathrm {Orb}_{g^p}(x)$
is dense in
![]() $l_0$
, we may choose y from the orbit of x. We finish the proof in two cases, depending on the location of y.
$l_0$
, we may choose y from the orbit of x. We finish the proof in two cases, depending on the location of y.
Suppose first that y is between x and c. In the ordering of the arc
![]() $[g^p(x),g^p(y)]$
, we have
$[g^p(x),g^p(y)]$
, we have
![]() $g^p(x) < x < y < c < g^p(y)$
. Put
$g^p(x) < x < y < c < g^p(y)$
. Put
![]() $I=[x,y]$
and
$I=[x,y]$
and
![]() $J=[y,c]$
. Clearly
$J=[y,c]$
. Clearly
![]() $g^p(I)\supseteq I\cup~J$
. Because
$g^p(I)\supseteq I\cup~J$
. Because
![]() $y\in \mathrm {Orb}_g(x)$
, we have
$y\in \mathrm {Orb}_g(x)$
, we have
![]() $\omega _{g}(y)=\omega _{g}(x)\supset \mathrm {Orb}_{g}(x)\ni g^p(x)$
. In particular, we may choose
$\omega _{g}(y)=\omega _{g}(x)\supset \mathrm {Orb}_{g}(x)\ni g^p(x)$
. In particular, we may choose
![]() $n>p$
to make
$n>p$
to make
![]() $g^{n}(y)$
as close to
$g^{n}(y)$
as close to
![]() $g^p(x)$
as we like, so that
$g^p(x)$
as we like, so that
![]() $x,y \in [g^{n}(y),c]$
. However, then
$x,y \in [g^{n}(y),c]$
. However, then
![]() $g^{n}(J) \supseteq I\cup J$
. We conclude that g possesses an arc horseshoe and thus g has positive topological entropy, which is a contradiction with
$g^{n}(J) \supseteq I\cup J$
. We conclude that g possesses an arc horseshoe and thus g has positive topological entropy, which is a contradiction with
![]() $h_{\mathrm {top}}(f)=0$
.
$h_{\mathrm {top}}(f)=0$
.
Suppose instead that x is between y and c. Then
![]() $c\in [g^p(x),g^p(y)]$
, so there is
$c\in [g^p(x),g^p(y)]$
, so there is
![]() $c_{-1}\in (x,y)$
with
$c_{-1}\in (x,y)$
with
![]() $g^p(c_{-1})=c$
. In the ordering of the arc
$g^p(c_{-1})=c$
. In the ordering of the arc
![]() $[y,g^p(y)]$
, we have
$[y,g^p(y)]$
, we have
![]() $y<c_{-1}<x<c$
and we also have
$y<c_{-1}<x<c$
and we also have
![]() $x\in (g^p(x),c)$
. Put
$x\in (g^p(x),c)$
. Put
![]() $I=[c_{-1},x]$
and
$I=[c_{-1},x]$
and
![]() $J=[x,c]$
. Because
$J=[x,c]$
. Because
![]() $y\in \mathrm {Orb}_g(x)\subset \omega _g(x)$
, we can find
$y\in \mathrm {Orb}_g(x)\subset \omega _g(x)$
, we can find
![]() $n>p$
with
$n>p$
with
![]() $g^n(x)$
as close to y as we like. In particular, we can get
$g^n(x)$
as close to y as we like. In particular, we can get
![]() $x,c_{-1}\in [g^n(x),c]$
. However then
$x,c_{-1}\in [g^n(x),c]$
. However then
![]() $g^n(I) \cap g^n(J) \supseteq I\cup J$
. Again we conclude that g has positive topological entropy, which is a contradiction. This ends the proof.
$g^n(I) \cap g^n(J) \supseteq I\cup J$
. Again we conclude that g has positive topological entropy, which is a contradiction. This ends the proof.
Theorem 3.6. If X is a dendrite in which
![]() $\overline {E(X)}$
is countable and if
$\overline {E(X)}$
is countable and if
![]() $f\colon X\to X$
has zero topological entropy, then every recurrent point for f is minimal.
$f\colon X\to X$
has zero topological entropy, then every recurrent point for f is minimal.
Proof. Let
![]() $x\in \mathrm {Rec}(f)$
. If x is periodic, then it is minimal, so assume x is not periodic. Let
$x\in \mathrm {Rec}(f)$
. If x is periodic, then it is minimal, so assume x is not periodic. Let
![]() $L=\omega (x)$
. Let
$L=\omega (x)$
. Let
![]() $M\subset L$
be a minimal set. By Lemma 3.5, L contains no periodic orbits, so M is an infinite minimal set. Then Proposition 3.1 applies and we get a sequence of f-periodic subdendrites
$M\subset L$
be a minimal set. By Lemma 3.5, L contains no periodic orbits, so M is an infinite minimal set. Then Proposition 3.1 applies and we get a sequence of f-periodic subdendrites
![]() $(D_k)_{k\geq 1}$
and periods
$(D_k)_{k\geq 1}$
and periods
![]() $(\alpha _k)$
satisfying properties (1)–(5) of that proposition. By Lemma 3.4 for all sufficiently large k, we have that
$(\alpha _k)$
satisfying properties (1)–(5) of that proposition. By Lemma 3.4 for all sufficiently large k, we have that
![]() $f^i(D_k)$
is a free arc for suitable i. Because M is infinite and
$f^i(D_k)$
is a free arc for suitable i. Because M is infinite and
![]() $D_k$
is periodic, we have
$D_k$
is periodic, we have
![]() $M\cap \operatorname {\mathrm {int}} f^i(D_k)\neq \emptyset $
and as a consequence,
$M\cap \operatorname {\mathrm {int}} f^i(D_k)\neq \emptyset $
and as a consequence,
![]() $Orb_f(x)\cap D_k\neq \emptyset $
, for every sufficiently large k. Hence,
$Orb_f(x)\cap D_k\neq \emptyset $
, for every sufficiently large k. Hence,
![]() $\bigcap _{k\geq 1}Orb_f(D_k)$
contains L, that is, property (4) still holds with L in the place of M.
$\bigcap _{k\geq 1}Orb_f(D_k)$
contains L, that is, property (4) still holds with L in the place of M.
We claim that property (5) also holds with L in the place of M. Fix k and denote
![]() $L_i=f^i(D_k)\cap L$
for
$L_i=f^i(D_k)\cap L$
for
![]() $0\leq i<\alpha _k-1$
. Observe that L does not contain periodic points, and the set
$0\leq i<\alpha _k-1$
. Observe that L does not contain periodic points, and the set
![]() $\mathrm {Orb}(f^i(D_k)\cap f^j(D_k))$
is always finite and invariant for any
$\mathrm {Orb}(f^i(D_k)\cap f^j(D_k))$
is always finite and invariant for any
![]() $i\neq j$
(can be empty) and hence
$i\neq j$
(can be empty) and hence
![]() $L_i \cap f^j(D_k)=\emptyset $
for
$L_i \cap f^j(D_k)=\emptyset $
for
![]() $i\neq j$
. This shows that the sets
$i\neq j$
. This shows that the sets
![]() $L_i \cap L_j=\emptyset $
for
$L_i \cap L_j=\emptyset $
for
![]() $i\neq j$
. Clearly
$i\neq j$
. Clearly
![]() $f(L_i) \subseteq L_{i+1 (\text {mod }\alpha _k)}$
, and
$f(L_i) \subseteq L_{i+1 (\text {mod }\alpha _k)}$
, and
![]() $f(L)=L$
because
$f(L)=L$
because
![]() $\omega $
-limit sets are always mapped onto themselves. This shows that
$\omega $
-limit sets are always mapped onto themselves. This shows that
![]() $f(L_i)=L_{i+1 (\text {mod } \alpha _k)}$
. In particular, we conclude that
$f(L_i)=L_{i+1 (\text {mod } \alpha _k)}$
. In particular, we conclude that
![]() $L_i$
is uncountable for each i.
$L_i$
is uncountable for each i.
Again using Lemma 3.4, choose k large enough that
![]() $f^i(D_k)$
is a free arc for some
$f^i(D_k)$
is a free arc for some
![]() $0\leq i<\alpha _k-1$
and let
$0\leq i<\alpha _k-1$
and let
![]() $A=f^i(D_k)$
denote that free arc. We have just shown that
$A=f^i(D_k)$
denote that free arc. We have just shown that
![]() $L_i=A\cap L$
is uncountable, so because A is a free arc, there are points from
$L_i=A\cap L$
is uncountable, so because A is a free arc, there are points from
![]() $\omega (x)$
in its interior. Thus we can find a point
$\omega (x)$
in its interior. Thus we can find a point
![]() $y=f^l(x)$
from the forward orbit of x in A. Then
$y=f^l(x)$
from the forward orbit of x in A. Then
![]() $\omega _f(x)=\omega _f(y)$
and y is also recurrent for f. Because
$\omega _f(x)=\omega _f(y)$
and y is also recurrent for f. Because
![]() $\mathrm {Rec}(f^{\alpha _k})=\mathrm {Rec}(f)$
, y is also recurrent for
$\mathrm {Rec}(f^{\alpha _k})=\mathrm {Rec}(f)$
, y is also recurrent for
![]() $f^{\alpha _k}$
. However, the restriction of
$f^{\alpha _k}$
. However, the restriction of
![]() $f^{\alpha _k}$
to A is an interval map with zero topological entropy. For such a map, all recurrent points are minimal points, see e.g. [Reference Bartoš, Bobok, Pyrih, Roth and Vejnar6, Ch. VI. Proposition 7]. Thus, y is a minimal point for
$f^{\alpha _k}$
to A is an interval map with zero topological entropy. For such a map, all recurrent points are minimal points, see e.g. [Reference Bartoš, Bobok, Pyrih, Roth and Vejnar6, Ch. VI. Proposition 7]. Thus, y is a minimal point for
![]() $f^{\alpha _k}$
, and hence also for f. This shows that
$f^{\alpha _k}$
, and hence also for f. This shows that
![]() $\omega _f(y)=\omega _f(x)$
is a minimal set, and hence x itself is minimal.
$\omega _f(y)=\omega _f(x)$
is a minimal set, and hence x itself is minimal.
4 Discrete spectrum in dendrites with
 $\overline {E(X)}$
countable
$\overline {E(X)}$
countable
By [Reference Li, Tu and Ye17, Theorem 1.5], each one-sided subshift with zero entropy can be extended to a dynamical system on the Gehman dendrite with zero topological entropy. This provides a plethora of examples of dynamical systems on a dendrite with a closed set of endpoints having zero topological entropy and invariant measures which do not have discrete spectrum. However, in the Gehman dendrite,
![]() $E(X)$
is uncountable, because
$E(X)$
is uncountable, because
![]() $E(X)$
is a Cantor set. Alternatively, each dendrite with
$E(X)$
is a Cantor set. Alternatively, each dendrite with
![]() $E(X)$
uncountable contains a copy of the Gehman dendrite (see e.g. [Reference Adler, Konheim and McAndrew2], cf. [Reference Li, Tu and Ye17]). So on all these dendrites, there exist dynamical systems with zero topological entropy and invariant measures not having discrete spectrum.
$E(X)$
uncountable contains a copy of the Gehman dendrite (see e.g. [Reference Adler, Konheim and McAndrew2], cf. [Reference Li, Tu and Ye17]). So on all these dendrites, there exist dynamical systems with zero topological entropy and invariant measures not having discrete spectrum.
Our work below shows that the opposite holds in the case of a dendrite X, where
![]() $\overline {E(X)}$
is countable: all invariant measures of zero-entropy mappings have discrete spectrum. So in the case of dendrites, the remaining case in Question 1.1 is when
$\overline {E(X)}$
is countable: all invariant measures of zero-entropy mappings have discrete spectrum. So in the case of dendrites, the remaining case in Question 1.1 is when
![]() $E(X)$
is countable but
$E(X)$
is countable but
![]() $\overline {E(X)}$
is uncountable. This case is left as a problem for further research.
$\overline {E(X)}$
is uncountable. This case is left as a problem for further research.
Lemma 4.1. Let
![]() $(X,f)$
be a topological dynamical system and suppose that all measures
$(X,f)$
be a topological dynamical system and suppose that all measures
![]() $\mu \in M_f(X)$
which are concentrated on
$\mu \in M_f(X)$
which are concentrated on
![]() $A_i$
have discrete spectrum, for each member
$A_i$
have discrete spectrum, for each member
![]() $A_i$
of some finite or countable collection of invariant Borel sets. Then any
$A_i$
of some finite or countable collection of invariant Borel sets. Then any
![]() $\mu \in M_f(X)$
which is concentrated on
$\mu \in M_f(X)$
which is concentrated on
![]() $\bigcup _i A_i$
also has discrete spectrum. In particular, if
$\bigcup _i A_i$
also has discrete spectrum. In particular, if
![]() $\mathrm {Rec}(f)\subseteq \bigcup _i A_i$
, then every
$\mathrm {Rec}(f)\subseteq \bigcup _i A_i$
, then every
![]() $\mu \in M_f(X)$
has discrete spectrum.
$\mu \in M_f(X)$
has discrete spectrum.
Proof. Let
![]() $\mu $
be any finite invariant measure concentrated on
$\mu $
be any finite invariant measure concentrated on
![]() $\bigcup _i A_i$
. Because each
$\bigcup _i A_i$
. Because each
![]() $A_i$
is invariant, that is,
$A_i$
is invariant, that is,
![]() $f(A_i)\subset A_i$
, and f preserves
$f(A_i)\subset A_i$
, and f preserves
![]() $\mu $
, we may assume by throwing away a set in X of
$\mu $
, we may assume by throwing away a set in X of
![]() $\mu $
-measure zero that
$\mu $
-measure zero that
![]() $f^{-1}(A_i)=A_i$
for each i.
$f^{-1}(A_i)=A_i$
for each i.
We may take the index set for the variable i to be
![]() $\{1,\ldots ,n\}$
in the finite case or
$\{1,\ldots ,n\}$
in the finite case or
![]() $\mathbb {N}$
in the countable case. Then putting
$\mathbb {N}$
in the countable case. Then putting
![]() $B_i = A_i \setminus \bigcup _{j<i} A_j$
for each i, we get a collection
$B_i = A_i \setminus \bigcup _{j<i} A_j$
for each i, we get a collection
![]() $\{B_i\}$
of pairwise disjoint invariant Borel sets. Now let
$\{B_i\}$
of pairwise disjoint invariant Borel sets. Now let
![]() $I=\{i~:~\mu (B_i)>0\}$
and write
$I=\{i~:~\mu (B_i)>0\}$
and write
![]() $\mu _i=\mu |_{B_i}$
for the (unnormalized) restriction of
$\mu _i=\mu |_{B_i}$
for the (unnormalized) restriction of
![]() $\mu $
to
$\mu $
to
![]() $B_i$
. Then we get a direct sum decomposition of Hilbert spaces
$B_i$
. Then we get a direct sum decomposition of Hilbert spaces
![]() $L^2_{\mu }(X) = \bigoplus _{i\in I} L^2_{\mu _i}(B_i).$
(Here in a direct sum
$L^2_{\mu }(X) = \bigoplus _{i\in I} L^2_{\mu _i}(B_i).$
(Here in a direct sum
![]() $\bigoplus H_i$
of Hilbert spaces, we include all
$\bigoplus H_i$
of Hilbert spaces, we include all
![]() $(v_i), v_i\in H_i$
such that
$(v_i), v_i\in H_i$
such that
![]() $\sum ||v_i||^2<\infty $
. We do not require that all but finitely many
$\sum ||v_i||^2<\infty $
. We do not require that all but finitely many
![]() $v_i$
vanish.) We may extend each function
$v_i$
vanish.) We may extend each function
![]() $\phi \in L^2_{\mu _i}(B_i)$
to an element of
$\phi \in L^2_{\mu _i}(B_i)$
to an element of
![]() $L^2_{\mu _i}(X)$
by letting
$L^2_{\mu _i}(X)$
by letting
![]() $\phi $
vanish outside of
$\phi $
vanish outside of
![]() $B_i$
. Because
$B_i$
. Because
![]() $f^{-1}(B_i)=B_i$
, we see that if
$f^{-1}(B_i)=B_i$
, we see that if
![]() $\phi \circ f = \lambda \phi $
holds
$\phi \circ f = \lambda \phi $
holds
![]() $\mu _i$
-almost everywhere (a.e) in
$\mu _i$
-almost everywhere (a.e) in
![]() $B_i$
, then by letting
$B_i$
, then by letting
![]() $\phi $
vanish outside
$\phi $
vanish outside
![]() $B_i$
, it continues to hold
$B_i$
, it continues to hold
![]() $\mu $
-a.e in X. Thus we have the equivalent direct sum decomposition
$\mu $
-a.e in X. Thus we have the equivalent direct sum decomposition
and an eigenfunction in a coordinate space is still an eigenfunction in the whole space. For each
![]() $i\in I$
, the normalized measure
$i\in I$
, the normalized measure
![]() $\mu _i/\mu (B_i)$
is an invariant probability measure for f concentrated on
$\mu _i/\mu (B_i)$
is an invariant probability measure for f concentrated on
![]() $B_i \subset A_i$
, so by hypothesis, the eigenfunctions of the Koopman operator on the space
$B_i \subset A_i$
, so by hypothesis, the eigenfunctions of the Koopman operator on the space
![]() $L^2_{\mu _i/\mu (B_i)}(X)$
have dense linear span. Dropping the normalizing constant, the same holds for
$L^2_{\mu _i/\mu (B_i)}(X)$
have dense linear span. Dropping the normalizing constant, the same holds for
![]() $L^2_{\mu _i}(X)$
. Passing through the direct sum decomposition, it follows that the eigenfunctions of the Koopman operator on the space
$L^2_{\mu _i}(X)$
. Passing through the direct sum decomposition, it follows that the eigenfunctions of the Koopman operator on the space
![]() $L^2_{\mu }(X)$
have dense linear span, that is,
$L^2_{\mu }(X)$
have dense linear span, that is,
![]() $\mu $
has discrete spectrum.
$\mu $
has discrete spectrum.
The last statement of the lemma follows by the Poincaré recurrence theorem, whereby if
![]() $\mathrm {Rec}(f) \subseteq \bigcup A_i$
, then every measure
$\mathrm {Rec}(f) \subseteq \bigcup A_i$
, then every measure
![]() $\mu \in M_f(X)$
is concentrated on
$\mu \in M_f(X)$
is concentrated on
![]() $\bigcup A_i$
.
$\bigcup A_i$
.
Lemma 4.2. Let X be a dendrite and suppose that
![]() $f\colon X\to X$
is a continuous map with zero topological entropy. If
$f\colon X\to X$
is a continuous map with zero topological entropy. If
![]() $D\subset X$
is a tree and
$D\subset X$
is a tree and
![]() $R\colon X\to D$
is a natural retraction, then the map
$R\colon X\to D$
is a natural retraction, then the map
![]() $F\colon D\to D$
given by
$F\colon D\to D$
given by
![]() $F=R\circ f$
has zero topological entropy.
$F=R\circ f$
has zero topological entropy.
Proof. Suppose that F has positive entropy. Then by [Reference Li, Oprocha and Zhang15], there exists an arc horseshoe
![]() $I_1,I_2$
with
$I_1,I_2$
with
![]() $F^{n_1}(I_1)\cap F^{n_2} (I_2) \supset I_1 \cup I_2$
for some
$F^{n_1}(I_1)\cap F^{n_2} (I_2) \supset I_1 \cup I_2$
for some
![]() $n_1,n_2\in \mathbb N$
. Then
$n_1,n_2\in \mathbb N$
. Then
![]() $F^{i}(I_j)$
is not a single point for any
$F^{i}(I_j)$
is not a single point for any
![]() $i=1,\ldots ,n_j$
and
$i=1,\ldots ,n_j$
and
![]() $j=1,2$
. However, if
$j=1,2$
. However, if
![]() $F(J)$
is non-degenerate for an arc J, then
$F(J)$
is non-degenerate for an arc J, then
![]() $f(J)\supset F(J)$
which implies that
$f(J)\supset F(J)$
which implies that
![]() $f^{n_1}(I_1)\cap f^{n_2}(I_2)\supset I_1\cup I_2$
which implies that f has positive topological entropy. A contradiction.
$f^{n_1}(I_1)\cap f^{n_2}(I_2)\supset I_1\cup I_2$
which implies that f has positive topological entropy. A contradiction.
Theorem 4.3. Let X be a dendrite such that
![]() $\overline {E(X)}$
is countable and let
$\overline {E(X)}$
is countable and let
![]() $f:X\to X$
be a continuous map with zero topological entropy. Then every measure
$f:X\to X$
be a continuous map with zero topological entropy. Then every measure
![]() $\mu \in M_f(X)$
has discrete spectrum.
$\mu \in M_f(X)$
has discrete spectrum.
Proof. Let
![]() $Z=\{z\in \overline {E(X)}~:~\omega _f(z)\text { is an infinite minimal set}\}.$
Following arguments in [Reference Naghmouchi21, Theorem 10.27], let
$Z=\{z\in \overline {E(X)}~:~\omega _f(z)\text { is an infinite minimal set}\}.$
Following arguments in [Reference Naghmouchi21, Theorem 10.27], let
![]() $(T_n)_{n \in \mathbb {N}} \subset X$
be an increasing sequence of topological trees with endpoints in
$(T_n)_{n \in \mathbb {N}} \subset X$
be an increasing sequence of topological trees with endpoints in
![]() $E(X)$
defined as follows. We inductively construct the sequence
$E(X)$
defined as follows. We inductively construct the sequence
![]() $(T_n)_{n\in \mathbb {N}}$
starting with
$(T_n)_{n\in \mathbb {N}}$
starting with
![]() $T_1 = \{e_1\}$
for some
$T_1 = \{e_1\}$
for some
![]() $e_1 \in E(X)$
. Then for
$e_1 \in E(X)$
. Then for
![]() $n\geq 1$
, we attach to
$n\geq 1$
, we attach to
![]() $T_n$
an arc
$T_n$
an arc
![]() $[e,e_{n+1}]$
whose one endpoint
$[e,e_{n+1}]$
whose one endpoint
![]() $e_{n+1}$
belongs to
$e_{n+1}$
belongs to
![]() $E(X)\setminus T_n$
and
$E(X)\setminus T_n$
and
![]() $e\in T_n$
. Because
$e\in T_n$
. Because
![]() $E(X)$
is countable, we can put every endpoint into one of the trees, that is, we let the sequence
$E(X)$
is countable, we can put every endpoint into one of the trees, that is, we let the sequence
![]() $(e_n)_{n \in \mathbb {N}}$
be an enumeration of
$(e_n)_{n \in \mathbb {N}}$
be an enumeration of
![]() $E(X)$
, and then
$E(X)$
, and then
![]() $\bigcup _{n\geq 1} T_n$
being a connected set must coincide with the whole dendrite X.
$\bigcup _{n\geq 1} T_n$
being a connected set must coincide with the whole dendrite X.
Let
![]() $\hat {T}_n=\bigcap _{i=0}^{\infty } f^{-i}(T_n)$
be the maximal invariant set completely contained in
$\hat {T}_n=\bigcap _{i=0}^{\infty } f^{-i}(T_n)$
be the maximal invariant set completely contained in
![]() $T_n$
. Let
$T_n$
. Let
![]() $\mathrm {Per}(f)$
be the set of periodic points of f. We claim that
$\mathrm {Per}(f)$
be the set of periodic points of f. We claim that
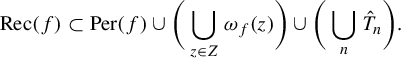 $$ \begin{align} \mathrm{Rec}(f) \subset \mathrm{Per}(f) \cup \bigg(\bigcup_{z\in Z}\omega_f(z)\bigg) \cup \bigg(\bigcup_{n} \hat{T}_n\bigg). \end{align} $$
$$ \begin{align} \mathrm{Rec}(f) \subset \mathrm{Per}(f) \cup \bigg(\bigcup_{z\in Z}\omega_f(z)\bigg) \cup \bigg(\bigcup_{n} \hat{T}_n\bigg). \end{align} $$
To see this, let x be a non-periodic recurrent point whose orbit is not contained in any of the trees
![]() $T_n$
. This means that there are points
$T_n$
. This means that there are points
![]() $f^{n_i}(x)$
which belong to
$f^{n_i}(x)$
which belong to
![]() $T_{m_i}\setminus T_{m_i-1}$
for some strictly increasing sequences
$T_{m_i}\setminus T_{m_i-1}$
for some strictly increasing sequences
![]() $m_i$
,
$m_i$
,
![]() $n_i \to \infty $
. Then the arcs
$n_i \to \infty $
. Then the arcs
![]() $[f^{n_i}(x), e_{m_i}]$
in X are pairwise disjoint, so by [Reference Misiurewicz and Marchioro19, Lemma 2.3], their diameters tend to zero. This shows that
$[f^{n_i}(x), e_{m_i}]$
in X are pairwise disjoint, so by [Reference Misiurewicz and Marchioro19, Lemma 2.3], their diameters tend to zero. This shows that
![]() $\liminf _{n\to \infty } d(f^n(x),E(X))=0$
. Therefore,
$\liminf _{n\to \infty } d(f^n(x),E(X))=0$
. Therefore,
![]() $\omega _f(x)\cap \overline {E(X)}\neq \emptyset $
. By Theorem 3.6,
$\omega _f(x)\cap \overline {E(X)}\neq \emptyset $
. By Theorem 3.6,
![]() $\omega _f(x)$
is a minimal set, so choosing
$\omega _f(x)$
is a minimal set, so choosing
![]() $z\in \omega _f(x)\cap \overline {E(X)}$
, we have
$z\in \omega _f(x)\cap \overline {E(X)}$
, we have
![]() $\omega _f(x)=\omega _f(z)$
. This establishes equation (4.2).
$\omega _f(x)=\omega _f(z)$
. This establishes equation (4.2).
Now observe that any finite invariant measure concentrated on
![]() $\mathrm {Per}(f)$
has discrete spectrum, see e.g. [Reference Li, Tu and Ye17, Theorem 2.3]. As for the sets
$\mathrm {Per}(f)$
has discrete spectrum, see e.g. [Reference Li, Tu and Ye17, Theorem 2.3]. As for the sets
![]() $\hat {T}_n$
, note that for each
$\hat {T}_n$
, note that for each
![]() $n\in \mathbb {N}$
, the map
$n\in \mathbb {N}$
, the map
![]() $F=R\circ f$
, where
$F=R\circ f$
, where
![]() $R\colon X\to T_n$
is a retraction, satisfies
$R\colon X\to T_n$
is a retraction, satisfies
![]() $F|_{\hat {T}_n}=f|_{\hat {T}_n}$
by the definition and therefore each f-invariant measure concentrated on
$F|_{\hat {T}_n}=f|_{\hat {T}_n}$
by the definition and therefore each f-invariant measure concentrated on
![]() $\hat {T}_n$
(a subset of a tree) has discrete spectrum, as, by [Reference Li, Tu and Ye17], all invariant measures of F have discrete spectrum.
$\hat {T}_n$
(a subset of a tree) has discrete spectrum, as, by [Reference Li, Tu and Ye17], all invariant measures of F have discrete spectrum.
Finally, we claim that any invariant measure concentrated on
![]() $\omega _f(z)$
,
$\omega _f(z)$
,
![]() $z\in Z$
, has discrete spectrum. Let
$z\in Z$
, has discrete spectrum. Let
![]() $(D_k)$
be the periodic subdendrites with periods
$(D_k)$
be the periodic subdendrites with periods
![]() $(\alpha _k)$
described in Proposition 3.1 and let
$(\alpha _k)$
described in Proposition 3.1 and let
![]() $\pi :(\omega _f(z),f)\to (\Omega ,\tau )$
be the factor map onto the odometer described in Lemma 3.2. Let
$\pi :(\omega _f(z),f)\to (\Omega ,\tau )$
be the factor map onto the odometer described in Lemma 3.2. Let
![]() $\mu \in M_f(X)$
be any invariant measure concentrated on
$\mu \in M_f(X)$
be any invariant measure concentrated on
![]() $\omega _f(z)$
. Then the pushforward measure
$\omega _f(z)$
. Then the pushforward measure
![]() $\pi _*(\mu )$
is invariant for the odometer, so by unique ergodicity, it is the Haar measure on
$\pi _*(\mu )$
is invariant for the odometer, so by unique ergodicity, it is the Haar measure on
![]() $\Omega $
and it has discrete spectrum as a consequence of [Reference Walters26, Theorem 3.5]. Now because
$\Omega $
and it has discrete spectrum as a consequence of [Reference Walters26, Theorem 3.5]. Now because
![]() $\omega _f(z)$
contains no periodic points, we know that
$\omega _f(z)$
contains no periodic points, we know that
![]() $\mu $
is non-atomic and therefore countable sets have measure zero. Then in the category of measure preserving transformations, the factor map
$\mu $
is non-atomic and therefore countable sets have measure zero. Then in the category of measure preserving transformations, the factor map
![]() $\pi :(\omega _f(z),\mu ,f)\to (\Omega ,\pi _*(\mu ),\tau )$
is in fact an isomorphism, because by Lemma 3.2, it is invertible except on a set of
$\pi :(\omega _f(z),\mu ,f)\to (\Omega ,\pi _*(\mu ),\tau )$
is in fact an isomorphism, because by Lemma 3.2, it is invertible except on a set of
![]() $\mu $
-measure zero. This implies that
$\mu $
-measure zero. This implies that
![]() $\mu $
has discrete spectrum.
$\mu $
has discrete spectrum.
We have shown that an invariant measure concentrated on any of the countably many invariant sets in equation (4.2) has discrete spectrum. By Lemma 4.1, this completes the proof.
Acknowledgements
We would like to thank M. Gröger and F. García-Ramos for pointing out the fact mentioned in Remark 3.3. M. Foryś-Krawiec was supported in part by the National Science Centre, Poland (NCN), grant SONATA BIS no. 2019/34/E/ST1/00237: ‘Topological and Dynamical Properties in Parameterized Families of Non-Hyperbolic Attractors: the inverse limit approach’. S. Roth was supported by Czech Republic RVO funding for IČ47813059.
 This research is part of a project that has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 883748.
This research is part of a project that has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 883748.




