Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-25T20:46:32.869Z Has data issue: false hasContentIssue false
  • English
  • Français

The expressiveness of quasiperiodic and minimal shifts of finite type

Part of: Topological dynamics Discrete mathematics in relation to computer science Computability and recursion theory

Published online by Cambridge University Press:  22 January 2020

BRUNO DURAND  and
ANDREI ROMASHCHENKO Open the ORCID record for ANDREI ROMASHCHENKO [Opens in a new window]
BRUNO DURAND
Affiliation:
LIRMM, Université Montpellier, Computer Science, Montpellier, France email bruno.durand@lirmm.fr, andrei.romashchenko@lirmm.fr
ANDREI ROMASHCHENKO
Affiliation:
LIRMM, Université Montpellier, Computer Science, Montpellier, France email bruno.durand@lirmm.fr, andrei.romashchenko@lirmm.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We study multidimensional minimal and quasiperiodic shifts of finite type. We prove for these classes several results that were previously known for the shifts of finite type in general, without restriction. We show that some quasiperiodic shifts of finite type admit only non-computable configurations; we characterize the classes of Turing degrees that can be represented by quasiperiodic shifts of finite type. We also transpose to the classes of minimal/quasiperiodic shifts of finite type some results on subdynamics previously known for effective shifts without restrictions: every effective minimal (quasiperiodic) shift of dimension 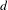$d$ can be represented as a projection of a subdynamics of a minimal (respectively, quasiperiodic) shift of finite type of dimension 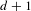$d+1$.

Keywords

minimal SFTquasiperiodicitytilings

MSC classification

Primary: 37B50: Multi-dimensional shifts of finite type, tiling dynamics
Secondary: 03D80: Applications of computability and recursion theory 68R05: Combinatorics
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 4 , April 2021 , pp. 1086 - 1138
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allauzen, C. and Durand, B.. Tiling problems. The Classical Decision Problem. Eds. Borger, E., Gradel, E. and Gurevich, Y.. Springer, Berlin, 1997.Google Scholar
Aubrun, N. and Sablik, M.. Simulation of effective subshifts by two-dimensional subshifts of finite type. Acta Appl. Math. 128(1) (2013), 35–63.10.1007/s10440-013-9808-5CrossRefGoogle Scholar
Avgustinovich, S. V., Fon-Der-Flaass, D. G. and Frid, A. E.. Arithmetical complexity of infinite words. Proc. Int. Colloquium on Words, Languages and Combinatorics III (Kyoto, Japan, 14–18 March 2000). World Scientific, River Edge, NJ, 2003, pp. 51–62.Google Scholar
Ballier, A.. Propriétés structurelles, combinatoires et logiques des pavages. PhD Thesis, Marseille, November 2009.Google Scholar
Ballier, A. and Jeandel, E.. Tilings and model theory. Proc. 1st Symp. on Cellular Automata Journées Automates Cellulaires (Uzès, France, 21–25 April, 2008). MCCME, Moscow, 2009, pp. 29–39.Google Scholar
Berger, R.. The undecidability of the domino problem. Mem. Amer. Math. Soc. 66 (1966).Google Scholar
Durand, B.. Tilings and quasiperiodicity. Theoret. Comput. Sci. 221(1) (1999), 61–75.CrossRefGoogle Scholar
Durand, B., Levin, L. and Shen, A.. Complex tilings. J. Symbol. Log. 73(2) (2008), 593–613.10.2178/jsl/1208359062CrossRefGoogle Scholar
Durand, B. and Romashchenko, A.. Quasiperiodicity and non-computability in tilings. Proc. 40th Int. Symp. on Mathematical Foundations of Computer Science (MFCS), 2015 (Lecture Notes in Computer Science, 9234) . Springer, Berlin, 2015, pp. 218–230.CrossRefGoogle Scholar
Durand, B. and Romashchenko, A.. On the expressive power of quasiperiodic SFT. Proc. 42nd Int. Symp. on Mathematical Foundations of Computer Science (Aalborg, Denmark, 21–25 August, 2017) (Leibniz International Proceedings in Informatics, 83) . Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik, pp. 5:1–5:14.Google Scholar
Durand, B., Romashchenko, A. and Shen, A.. Fixed-point tile sets and their applications. J. Comput. System Sci. 78(3) (2012), 731–764.10.1016/j.jcss.2011.11.001CrossRefGoogle Scholar
Gács, P.. Reliable computation with cellular automata. J. Comput. System Sci. 32(1) (1986), 15–78.10.1016/0022-0000(86)90002-4CrossRefGoogle Scholar
Gangloff, S. and Sablik, M.. Quantified block gluing, aperiodicity and entropy of multidimensional SFT. Preprint, 2017 arXiv:1706.01627.Google Scholar
Goodman-Strauss, C.. Lots of aperiodic sets of tiles. J. Combin. Theory Ser. A 160 (2018), 409–445.10.1016/j.jcta.2018.07.002CrossRefGoogle Scholar
Hanf, W.. Nonrecursive tilings of the plane. I. J. Symbolic Logic 39 (1974), 283–285.10.2307/2272640CrossRefGoogle Scholar
Hochman, M.. On the dynamics and recursive properties of multidimensional symbolic systems. Invent. Math. 176(1) (2009), 131–167.10.1007/s00222-008-0161-7CrossRefGoogle Scholar
Hochman, M. and Meyerovitch, T.. A characterization of the entropies of multidimensional shifts of finite type. Ann. of Math. (2) 171 (2010), 2011–2038.10.4007/annals.2010.171.2011CrossRefGoogle Scholar
Hochman, M. and Vanier, P.. Turing degree spectra of minimal subshifts. Proc. 12th Int. Computer Science Symposium (Russia, 2017) (Lecture Notes in Computer Science, 10304) . Springer, Berlin, 2017, pp. 154–161.Google Scholar
Jeandel, E.. Personal communication, 2015.Google Scholar
Jeandel, E. and Vanier, P.. Turing degrees of multidimensional SFTs. Theoret. Comput. Sci. 505 (2013), 81–92.CrossRefGoogle Scholar
Labbé, S.. A self-similar aperiodic set of 19 Wang tiles. Geom. Dedicata 201(1) (2019), 81–109.10.1007/s10711-018-0384-8CrossRefGoogle Scholar
Myers, D.. Nonrecursive tilings of the plane. II. J. Symbolic Logic 39 (1974), 286–294.CrossRefGoogle Scholar
Odifreddi, P.. Classical Recursion Theory: The Theory of Functions and Sets of Natural Numbers. Elsevier Science, Amsterdam, 1992.Google Scholar
Ollinger, N.. Two-by-two substitution systems and the undecidability of the domino problem. Logic and Theory of Algorithms: Proc. 4th Conf. on Computability in Europe, CiE 2008 (Athens, Greece, 15–20 June, 2008). Springer Science & Business Media, Berlin, 2008.Google Scholar
Robinson, R. M.. Undecidability and nonperiodicity for tilings of the plane. Invent. Math. 12 (1971), 177–209.10.1007/BF01418780CrossRefGoogle Scholar
Rumyantsev, A. and Ushakov, M.. Forbidden substrings, Kolmogorov complexity and almost periodic sequences. Proc. 23rd Ann. Symp. on Theoretical Aspects of Computer Science. Springer, Berlin, 2006, pp. 396–407.Google Scholar
Salimov, P.. On uniform recurrence of a direct product. Discrete Math. Theor. Comput. Sci. 12(4) (2010), 1–8.Google Scholar
Shen, A. and Vereshchagin, N.. Computable Functions. American Mathematical Society, Providence, RI, 2003.Google Scholar
Westrick, L. B.. Seas of squares with sizes from a 𝛱1 0 . Israel J. Math. 222(1) (2017), 431–462.CrossRefGoogle Scholar
Zinoviadis, C.. Hierarchy and expansiveness in two-dimensional subshifts of finite type. Proc. 9th Int. Conf. on Language and Automata Theory and Applications (LATA) 2015 (Nice, France, 2–6 March, 2015) (Lecture Notes in Computer Science, 8977) . Springer International, Cham, 2015, pp. 365–377.Google Scholar