Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-05-12T20:55:47.575Z Has data issue: false hasContentIssue false
  • English
  • Français

Kakutani equivalence for products of some special flows over rotations

Part of: Ergodic theory

Published online by Cambridge University Press:  28 January 2021

DAREN WEI Open the ORCID record for DAREN WEI [Opens in a new window]
DAREN WEI*
Affiliation:
Einstein Institute of Mathematics, The Hebrew University of Jerusalem, Givat Ram, Jerusalem9190401, Israel
*
e-mail: Daren.Wei@mail.huji.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

We study Kakutani equivalence for products of some special flows over rotations with roof function smooth except a singularity at 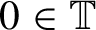$0\in \mathbb {T}$ . We estimate the Kakutani invariant for products of these flows with different powers of singularities and rotations from a full measure set. As a corollary, we obtain a countable family of pairwise non-Kakutani equivalent products of special flows over rotations.

Keywords

Kakutani equivalenceKakutani invariantsspecial flow

MSC classification

Primary: 37A35: Entropy and other invariants, isomorphism, classification
Secondary: 37A05: Measure-preserving transformations 37A20: Orbit equivalence, cocycles, ergodic equivalence relations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 4 , April 2022 , pp. 1548 - 1575
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

To the memory of my dearest teacher Prof. Anatole Katok whose careful guidance and warm advice will always stay in my heart.

References

Benhenda, M.. An uncountable family of pairwise non-Kakutani equivalent smooth diffeomorphisms. J. Anal. Math. 127 (2015), 129–178.10.1007/s11854-015-0027-zCrossRefGoogle Scholar
Beleznay, F. and Foreman, M.. The complexity of the collection of measure-distal transformations. Ergod. Th. & Dynam. Sys. 16(5) (1996), 929–962.10.1017/S0143385700010129CrossRefGoogle Scholar
Bronšteǐn, I. U.. Extensions of Minimal Transformation Groups. Martinus Nijhoff Publishers, The Hague, 1979 (translated from Russian).10.1007/978-94-009-9559-8CrossRefGoogle Scholar
Dye, H. A.. On groups of measure preserving transformation. I. Amer. J. Math. 81 (1959), 119–159.10.2307/2372852CrossRefGoogle Scholar
Dye, H. A.. On groups of measure preserving transformations. II. Amer. J. Math. 85 (1963), 551–576.10.2307/2373108CrossRefGoogle Scholar
Feldman, J.. New $K$ -automorphisms and a problem of Kakutani. Israel J. Math. 24(1) (1976), 16–38.10.1007/BF02761426CrossRefGoogle Scholar
Ferenczi, S.. Measure-theoretic complexity of ergodic systems. Israel J. Math. 100 (1997), 189–207.10.1007/BF02773640CrossRefGoogle Scholar
Fayad, B., Forni, G. and Kanigowski, A.. Lebesgue spectrum for area preserving flows on the two torus. J. Amer. Math. Soc. to appear, arXiv:1609.03757.Google Scholar
Fayad, B. and Kanigowski, A.. Multiple mixing for a class of conservative surface flows. Invent. Math. 203(2) (2016), 555–614.CrossRefGoogle Scholar
Foreman, M., Rudolph, D. and Weiss, B.. The conjugacy problem in ergodic theory. Ann. of Math. (2) 173 (3) (2011), 1529–1586.CrossRefGoogle Scholar
Foreman, M. and Weiss, B.. An anti-classification theorem for ergodic measure preserving transformations (English summary). J. Eur. Math. Soc. (JEMS) 6(3) (2004), 277–292.10.4171/JEMS/10CrossRefGoogle Scholar
Gerber, M. and Kunde, P.. A smooth zero-entropy diffeomorphism whose product with itself is loosely Bernoulli. J. Anal. Math. 141(2) (2020), 521–583 (English summary).10.1007/s11854-020-0108-5CrossRefGoogle Scholar
Katok, A.. Time change, monotone equivalence, and standard dynamical systems. Soviet Math. Dokl. 16(4) (1975), 986–990 (English translation).Google Scholar
Katok, A. B.. Monotone equivalence in ergodic theory. Math. USSR Izv. 11(1) (1977), 99.CrossRefGoogle Scholar
Kakutani, S.. Induced measure preserving transformations. Proc. Imp. Acad. Tokyo 19 (1943), 635–641.Google Scholar
Kanigowski, A.. Slow entropy for some smooth flows on surfaces. Israel J. Math. 226(2) (2018), 535–577 (English summary).CrossRefGoogle Scholar
Kanigowski, A. and De La Rue, T.. Product of two staircase rank one transformations that is not loosely Bernoulli. J. Anal. Math., to appear, arXiv:1812.08027.Google Scholar
Khinchin, A. Y.. Continued Fractions. University of Chicago Press, Chicago, 1964.Google Scholar
Kochergin, A. V.. Mixing in special flows over a shifting of segments and in smooth flows on surfaces. Mat. Sb. 96(138) (1975), 471–502.Google Scholar
Kanigowski, A., Vinhage, K. and Wei, D.. Kakutani equivalence of unipotent flows. Duke Math. J., to appear, arXiv:1805.01501.Google Scholar
Kanigowski, A. and Wei, D.. Product of two Kochergin flows with different exponents is not standard. Studia Math. 244(3) (2019), 265–283 (English summary).CrossRefGoogle Scholar
Ornstein, D. S., Rudolph, D. and Weiss, B.. Equivalence of Measure Preserving Transformations (Memoirs of the American Mathematical Society, 262). American Mathematical Society, Providence, RI, 1982.CrossRefGoogle Scholar
Ratner, M.. Horocycle flows are loosely Bernoulli. Israel J. Math. 31 (1978), 122–132.CrossRefGoogle Scholar
Ratner, M.. The Cartesian square of the horocycle flow is not loosely Bernoulli. Israel J. Math. 34(1) (1979), 72–96.CrossRefGoogle Scholar
Ratner, M.. Some invariants of Kakutani equivalence. Israel J. Math. 38(3) (1981), 231–240.CrossRefGoogle Scholar
Ratner, M.. Time change invariants for measure preserving flows. Modern Theory of Dynamical Systems (Contemporary Mathematics, 692). American Mathematical Society, Providence, RI, 2017, pp. 263–273 (English summary).CrossRefGoogle Scholar