No CrossRef data available.
Article contents
Non-realizability of the pure braid group as area-preserving homeomorphisms
Published online by Cambridge University Press: 11 June 2020
Abstract
Let 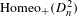 $\operatorname{Homeo}_{+}(D_{n}^{2})$ be the group of orientation-preserving homeomorphisms of
$\operatorname{Homeo}_{+}(D_{n}^{2})$ be the group of orientation-preserving homeomorphisms of 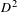 $D^{2}$ fixing the boundary pointwise and
$D^{2}$ fixing the boundary pointwise and  $n$ marked points as a set. The Nielsen realization problem for the braid group asks whether the natural projection
$n$ marked points as a set. The Nielsen realization problem for the braid group asks whether the natural projection 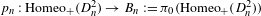 $p_{n}:\operatorname{Homeo}_{+}(D_{n}^{2})\rightarrow B_{n}:=\unicode[STIX]{x1D70B}_{0}(\operatorname{Homeo}_{+}(D_{n}^{2}))$ has a section over subgroups of
$p_{n}:\operatorname{Homeo}_{+}(D_{n}^{2})\rightarrow B_{n}:=\unicode[STIX]{x1D70B}_{0}(\operatorname{Homeo}_{+}(D_{n}^{2}))$ has a section over subgroups of 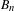 $B_{n}$ . All of the previous methods use either torsion or Thurston stability, which do not apply to the pure braid group
$B_{n}$ . All of the previous methods use either torsion or Thurston stability, which do not apply to the pure braid group 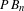 $PB_{n}$ , the subgroup of
$PB_{n}$ , the subgroup of 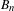 $B_{n}$ that fixes
$B_{n}$ that fixes  $n$ marked points pointwise. In this paper, we show that the pure braid group has no realization inside the area-preserving homeomorphisms using rotation numbers.
$n$ marked points pointwise. In this paper, we show that the pure braid group has no realization inside the area-preserving homeomorphisms using rotation numbers.
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s) 2020. Published by Cambridge University Press


