Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-27T16:23:18.524Z Has data issue: false hasContentIssue false
  • English
  • Français

Sharp constants in inequalities admitting the Calderón transference principle

Part of: Ergodic theory Harmonic analysis in several variables

Published online by Cambridge University Press:  04 August 2023

DARIUSZ KOSZ Open the ORCID record for DARIUSZ KOSZ [Opens in a new window]
DARIUSZ KOSZ*
Affiliation:
Basque Center for Applied Mathematics, 48009 Bilbao, Spain and Wrocław University of Science and Technology, 50-370 Wrocław, Poland
*
e-mail: dkosz@bcamath.org
Get access Rights & Permissions [Opens in a new window]

Abstract

The aim of this note is twofold. First, we prove an abstract version of the Calderón transference principle for inequalities of admissible type in the general commutative multilinear and multiparameter setting. Such an operation does not increase the constants in the transferred inequalities. Second, we use the last information to study a certain dichotomy arising in problems of finding the best constants in the weak type 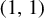$(1,1)$ and strong type $(p,p)$ inequalities for one-parameter ergodic maximal operators.

Keywords

Calderón transferencemaximal operatorsharp constant

MSC classification

Primary: 37A30: Ergodic theorems, spectral theory, Markov operators
Secondary: 42B25: Maximal functions, Littlewood-Paley theory
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , First View , pp. 1 - 12
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bergelson, V. and Leibman, A.. A nilpotent Roth theorem. Invent. Math. 147 (2002), 427–470.CrossRefGoogle Scholar
Birkhoff, G.. Proof of the ergodic theorem. Proc. Natl. Acad. Sci. USA 17 (1931), 656–660.CrossRefGoogle ScholarPubMed
Bourgain, J.. On the maximal ergodic theorem for certain subsets of the integers. Israel J. Math. 61 (1988), 39–72.CrossRefGoogle Scholar
Bourgain, J.. On the pointwise ergodic theorem on ${L}^p$ for arithmetic sets. Israel J. Math. 61 (1988), 73–84.CrossRefGoogle Scholar
Bourgain, J.. Pointwise ergodic theorems for arithmetic sets. Publ. Math. Inst. Hautes Études Sci. 69 (1989), 5–45, with an appendix by the author, H. Furstenberg, Y. Katznelson and D. S. Ornstein.CrossRefGoogle Scholar
Buczolich, Z. and Mauldin, R.. Divergent square averages. Ann. of Math. (2) 171 (2010), 1479–1530.CrossRefGoogle Scholar
Calderón, A.. Ergodic theory and translation invariant operators. Proc. Natl. Acad. Sci. USA 59 (1968), 349–353.CrossRefGoogle ScholarPubMed
Conze, J.-P.. Convergence des moyennes ergodiques pour des sous-suites. Mém. Soc. Math. Fr. (N.S.) 35 (1973), 7–15.Google Scholar
Grafakos, L. and Montgomery-Smith, S.. Best constants for uncentered maximal functions. Bull. Lond. Math. Soc. 29 (1997), 60–64.CrossRefGoogle Scholar
Halmos, P. R.. Lectures on Ergodic Theory. Mathematical Society of Japan, Tokyo, 1956.Google Scholar
Ionescu, A., Magyar, Á., Mirek, M. and Szarek, T. Z.. Polynomial averages and pointwise ergodic theorems on nilpotent groups. Invent. Math. 231 (2023), 1023–1140.CrossRefGoogle Scholar
Jones, R. L., Seeger, A. and Wright, J.. Strong variational and jump inequalities in harmonic analysis. Trans. Amer. Math. Soc. 360 (2008), pp. 6711–6742.CrossRefGoogle Scholar
Kosz, D., Mirek, M., Plewa, P. and Wróbel, B.. Some remarks on dimension-free estimates for the discrete Hardy–Littlewood maximal functions. Israel J. Math. 254 (2023), 1–38.CrossRefGoogle Scholar
Krause, B., Mirek, M. and Tao, T.. Pointwise ergodic theorems for non-conventional bilinear polynomial averages. Ann. of Math. (2) 195 (2022), 997–1109.CrossRefGoogle Scholar
Lépingle, D.. La variation d’ordre $p$ des semi-martingales. Z. Wahrscheinlichkeitstheorie und verw. Gebiete 36 (1976), 295–316.CrossRefGoogle Scholar
Melas, A. D.. The best constant for the centered Hardy–Littlewood maximal inequality. Ann. of Math. (2) 157 (2003), 647–688.CrossRefGoogle Scholar
Mirek, M., Słomian, W. and Szarek, T. Z.. Some remarks on oscillation inequalities. Ergod. Th. & Dynam. Sys. doi:10.1017/etds.2022.77. Published online 29 November 2022.CrossRefGoogle Scholar
Pisier, G. and Xu, Q. H.. The strong $p$ -variation of martingales and orthogonal series. Probab. Theory Related Fields 77 (1988), 497–514.CrossRefGoogle Scholar
Słomian, W.. Bootstrap methods in bounding discrete Radon operators. J. Funct. Anal. 283 (2022), 109650.CrossRefGoogle Scholar
Stein, E. M.. On limits of sequences of operators. Ann. of Math. (2) 74 (1961), 140–170.CrossRefGoogle Scholar
von Neumann, J.. Proof of the quasi-ergodic hypothesis. Proc. Natl. Acad. Sci. USA 18 (1932), 70–82.CrossRefGoogle Scholar