Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-06-08T02:28:38.453Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics and asymptotic profiles of endemic equilibrium for two frequency-dependent SIS epidemic models with cross-diffusion

Part of: Equations of mathematical physics and other areas of application Parabolic equations and systems Partial differential equations

Published online by Cambridge University Press:  18 September 2018

HUICONG LI ,
RUI PENG  and
TIAN XIANG
HUICONG LI
Affiliation:
School of Mathematics, Sun Yat-sen University, Guangzhou 510275, Guangdong Province, China email: lihuicong@mail.sysu.edu.cn
RUI PENG
Affiliation:
School of Mathematics and Statistics, Jiangsu Normal University, Xuzhou 221116, Jiangsu Province, China email: pengrui_seu@163.com
TIAN XIANG*
Affiliation:
Institute for Mathematical Sciences, Renmin University of China, Beijing 100872, China email: txiang@ruc.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is concerned with two frequency-dependent susceptible–infected–susceptible epidemic reaction–diffusion models in heterogeneous environment, with a cross-diffusion term modelling the effect that susceptible individuals tend to move away from higher concentration of infected individuals. It is first shown that the corresponding Neumann initial-boundary value problem in an n-dimensional bounded smooth domain possesses a unique global classical solution which is uniformly in-time bounded regardless of the strength of the cross-diffusion and the spatial dimension n. 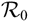It is further shown that, even in the presence of cross-diffusion, the models still admit threshold-type dynamics in terms of the basic reproduction number $\mathcal {R}_0$ – i.e. the unique disease-free equilibrium is globally stable if 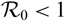$\mathcal {R}_0\lt1$, while if 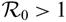$\mathcal {R}_0\gt1$, the disease is uniformly persistent and there is an endemic equilibrium (EE), which is globally stable in some special cases with weak chemotactic sensitivity. Our results on the asymptotic profiles of EE illustrate that restricting the motility of susceptible population may eliminate the infectious disease entirely for the first model with constant total population but fails for the second model with varying total population. In particular, this implies that such cross-diffusion does not contribute to the elimination of the infectious disease modelled by the second one.

Keywords

SIS epidemic reaction-advection-diffusionglobal existence and boundednessendemic equilibriumpersistence/extinctionasymptotic profile

MSC classification

Primary: 35K57: Reaction-diffusion equations
Secondary: 35A01: Existence problems 35B40: Asymptotic behavior of solutions 35Q92: PDEs in connection with biology and other natural sciences 92D25: Population dynamics (general)
Type
Papers
Information
European Journal of Applied Mathematics , Volume 31 , Issue 1 , February 2020 , pp. 26 - 56
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alikakos, N. (1979) An application of the invariance principle to reaction-diffusion equations. J. Differ. Equations 33, 201–225.CrossRefGoogle Scholar
Allen, L. J. S., Bolker, B. M., Lou, Y. & Nevai, A. L. (2007) Asymptotic profiles of the steady states for an SIS epidemic disease patch model. SIAM J. Appl. Math. 67, 1283–1309.CrossRefGoogle Scholar
Allen, L. J. S., Bolker, B. M., Lou, Y. & Nevai, A. L. (2008) Asymptotic profiles of the steady states for an SIS epidemic reaction-diffusion model. Discrete Contin. Dyn. Syst. 21, 1–20.Google Scholar
Bellomo, N., Bellouquid, A., Tao, Y. & Winkler, M. (2015) Toward a mathematical theory of Keller-Segel models of pattern formation in biological tissues. Math. Models Methods Appl. Sci. 25, 1663–1763.CrossRefGoogle Scholar
Brown, K. J., Dunne, P. C. & Gardner, R. A. (1981) A semilinear parabolic system arising in the theory of superconductivity. J. Differ. Equations 40, 232–252.CrossRefGoogle Scholar
Cao, X. (2015) Global bounded solutions of the higher-dimensional Keller-Segel system under smallness conditions in optimal spaces. Discrete Contin. Dyn. Syst. 35, 1891–1904.CrossRefGoogle Scholar
Cieślak, T., Laurencot, Ph. & Morales-Rodrigo, C. (2008) Global existence and convergence to steady states in a chemorepulsion system, equations, in parabolic and Navier–Stokes equations. Banach Center Publ. Polish Acad. Sci. Inst. Math. 81, 105–117.CrossRefGoogle Scholar
Cui, J., Tao, X. & Zhu, H. (2008) An SIS infection model incorporating media coverage. Rocky Mount. J. Math. 38, 1323–1334.CrossRefGoogle Scholar
Cui, R., Lam, K.-Y. & Lou, Y. (2017) Dynamics and asymptotic profiles of steady states of an epidemic model in advective environments. J. Differ. Equations 263, 2343–2373.CrossRefGoogle Scholar
Cui, R. & Lou, Y. (2016) A spatial SIS model in advective heterogeneous environments. J. Diff. Equations 261, 3305–3343.CrossRefGoogle Scholar
Deng, K. & Wu, Y. (2016) Dynamics of a susceptible-infected-susceptible epidemic reaction-diffusion model. Proc. Roy. Soc. Edinb. Sect. A 146, 929–946.CrossRefGoogle Scholar
Ding, W., Huang, W. & Kansakar, S. (2013) Traveling wave solutions for a diffusive SIS epidemic model. Discrete Contin. Dyn. Syst. Ser. B 18, 1291–1304.Google Scholar
Du, Y., Peng, R. & Wang, M. (2009) Effect of a protection zone in the diffusive Leslie predator-prey model. J. Differ. Equations 246, 3932–3956.CrossRefGoogle Scholar
Friedman, A. (1964) Partial Differential Equations of Parabolic Type, Prentice-Hall, Inc., Englewood Cliffs, NJ, xiv+347 pp.Google Scholar
Gao, D. & Ruan, S. (2011) An SIS patch model with variable transmission coefficients. Math. Biosci. 232, 110–115.CrossRefGoogle ScholarPubMed
Ge, J., Kim, K. I., Lin, Z. & Zhu, H. (2015) A SIS reaction-diffusion-advection model in a low-risk and high-risk domain. J. Differ. Equations 259, 5486–5509.CrossRefGoogle Scholar
Horstmann, D. & Winkler, M. (2005) Boundedness vs. blow-up in a chemotaxis system. J. Differ. Equations 215, 52–107.CrossRefGoogle Scholar
Huang, W., Han, M. & Liu, K. (2010) Dynamics of an SIS reaction-diffusion epidemic model for disease transmission. Math. Biosci. Eng. 7, 51–66.Google ScholarPubMed
Hutson, V., Lou, Y. & Mischaikow, K. (2005) Convergence in competition models with small diffusion coefficients. J. Differ. Equations 211, 135–161.CrossRefGoogle Scholar
Jäger, W. & Luckhaus, S. (1992) On explosions of solutions to a system of partial differential equations modelling chemotaxis. Trans. Amer. Math. Soc. 329, 819–824.CrossRefGoogle Scholar
Jin, H.-Y. & Xiang, T. (2016) Boundedness and exponential convergence in a chemotaxis model for tumor invasion. Nonlinearity 29, 3579–3596.CrossRefGoogle Scholar
Kuto, K., Matsuzawa, H. & Peng, R. (2017) Concentration profile of endemic equilibrium of a reaction-diffusion-advection SIS epidemic model. Calc. Var. Partial Differ. Equations 56(4), Art. 112, 1–28.CrossRefGoogle Scholar
Ladyzhenskaya, O., Solonnikov, V. & Uralceva, N. (1968) Linear and Quasilinear Equations of Parabolic Type, AMS, Providence, RI.CrossRefGoogle Scholar
Li, H., Peng, R. & Wang, F.-B. (2017) Varying total population enhances disease persistence: qualitative analysis on a diffusive SIS epidemic model. J. Differ. Equations 262, 885–913.CrossRefGoogle Scholar
Li, T., Pan, R. & Zhao, K. (2012) Global dynamics of a hyperbolic-parabolic model arising from chemotaxis. SIAM J. Appl. Math. 72, 417–443.CrossRefGoogle Scholar
Lou, Y. & Ni, W.-M. (1996) Diffusion, self-diffusion and cross-diffusion. J. Differ. Equations 131, 79–131.CrossRefGoogle Scholar
Magal, P. & Zhao, X.-Q. (2005) Global attractors and steady states for uniformly persistent dynamical systems. SIAM. J. Math. Anal. 37, 251–275.CrossRefGoogle Scholar
Peng, R. (2009) Asymptotic profiles of the positive steady state for an SIS epidemic reaction-diffusion model. I. J. Differ. Equations 247, 1096–1119.CrossRefGoogle Scholar
Peng, R. & Liu, S. (2009) Global stability of the steady states of an SIS epidemic reaction-diffusion model. Nonlinear Anal. 71, 239–247.CrossRefGoogle Scholar
Peng, R. & Yi, F. (2013) Asymptotic profile of the positive steady state for an SIS epidemic reaction-diffusion model: effects of epidemic risk and population movement. Phys. D 259, 8–25.CrossRefGoogle Scholar
Peng, R. & Zhao, X.-Q. (2012) A reaction-diffusion SIS epidemic model in a time-periodic environment. Nonlinearity 25, 1451–1471.CrossRefGoogle Scholar
Porzio, M. M. & Vespri, V. (1993) Hölder estimates for local solutions of some doubly nonlinear degenerate parabolic equations. J. Differ. Equations 103, 146–178.CrossRefGoogle Scholar
Tao, Y. (2013) Global dynamics in a higher-dimensional repulsion chemotaxis model with nonlinear sensitivity. Discrete Contin. Dyn. Syst. Ser. B 18, 2705–2722.CrossRefGoogle Scholar
Tao, Y. & Wang, Z.-A. (2013) Competing effects of attraction vs. repulsion in chemotaxis. Math. Models Methods Appl. Sci. 23, 1–36.CrossRefGoogle Scholar
Tao, Y. & Winkler, M. (2012) Eventual smoothness and stabilization of large-data solutions in a three-dimensional chemotaxis system with consumption of chemoattractant. J. Differ. Equations 252, 2520–2543.CrossRefGoogle Scholar
Winkler, M. (2010) Aggregation vs. global diffusive behavior in the higher-dimensional Keller-Segel model. J. Differ. Equations 248, 2889–2905.CrossRefGoogle Scholar
Winkler, M. (2010) Boundedness in the higher-dimensional parabolic-parabolic chemotaxis system with logistic source. Comm. Partial Differ. Equations 35, 1516–1537.CrossRefGoogle Scholar
Winkler, M. (2011) Blow-up in a higher-dimensional chemotaxis system despite logistic growth restriction. J. Math. Anal. Appl. 384, 261–272.CrossRefGoogle Scholar
Winkler, M. (2013) Finite-time blow-up in the higher-dimensional parabolic-parabolic Keller-Segel system. J. Math. Pures Appl. 100, 748–767.CrossRefGoogle Scholar
Winkler, M. (2014) Stabilization in a two-dimensional chemotaxis-Navier-Stokes system. Arch. Ration. Mech. Anal. 211, 455–487.CrossRefGoogle Scholar
Wu, Y. & Zou, X. (2016) Asymptotic profiles of steady states for a diffusive SIS epidemic model with mass action infection mechanism. J. Differ. Equations 261, 4424–4447.CrossRefGoogle Scholar
Zhao, X. (2017) Dynamical Systems in Population Biology, second edition, Springer-Verlag, New York.CrossRefGoogle Scholar