Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-20T00:13:01.284Z Has data issue: false hasContentIssue false
  • English
  • Français

Homogenisation of a two-phase problem with nonlinear dynamic Wentzell-interface condition for connected–disconnected porous media

Part of: Parabolic equations and systems Partial differential equations

Published online by Cambridge University Press:  21 June 2022

M. GAHN Open the ORCID record for M. GAHN [Opens in a new window]
M. GAHN*
Affiliation:
Interdisciplinary Center for Scientific Computing, University of Heidelberg, Im Neuenheimer Feld 205, Heidelberg 69120, Germany email: markus.gahn@iwr.uni-heidelberg.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate a reaction–diffusion problem in a two-component porous medium with a nonlinear interface condition between the different components. One component is connected and the other one is disconnected. The ratio between the microscopic pore scale and the size of the whole domain is described by the small parameter $\epsilon$. On the interface between the components, we consider a dynamic Wentzell-boundary condition, where the normal fluxes from the bulk domains are given by a reaction–diffusion equation for the traces of the bulk solutions, including nonlinear reaction kinetics depending on the solutions on both sides of the interface. Using two-scale techniques, we pass to the limit 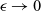$\epsilon \to 0$ and derive macroscopic models, where we need homogenisation results for surface diffusion. To cope with the nonlinear terms, we derive strong two-scale convergence results.

Keywords

Homogenisationtwo-scale convergencereaction–diffusion equationsnonlinear interface conditionssurface diffusion

MSC classification

Primary: 35B27: Homogenization; equations in media with periodic structure
Secondary: 35K57: Reaction-diffusion equations
Type
Papers
Information
European Journal of Applied Mathematics , Volume 34 , Issue 4 , August 2023 , pp. 617 - 641
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acerbi, E., Chiadò, V., Maso, G. D. & Percivale, D. (1992) An extension theorem from connected sets, and homogenization in general periodic domains. Nonlinear Anal. Theory Methods Appl. 18(5), 481–496.CrossRefGoogle Scholar
Allaire, G. (1992) Homogenization and two-scale convergence. SIAM J. Math. Anal. 23, 1482–1518.CrossRefGoogle Scholar
Allaire, G., Damlamian, A. & Hornung, U. (1996) Two-scale convergence on periodic surfaces and applications. In: Bourgeat, A. and Carasso, C. (editors), Proceedings of the International Conference on Mathematical Modelling of Flow Through Porous Media, World Scientific, Singapore, pp. 15–25.Google Scholar
Allaire, G. & Hutridurga, H. (2012) Homogenization of reactive flows in porous media and competition between bulk and surface diffusion. IMA J. Appl. Math. 77, 788–215.CrossRefGoogle Scholar
Alt, H. W. (2016) Linear Functional Analysis, Springer, Berlin Heidelberg.CrossRefGoogle Scholar
Amar, M. & Gianni, R. (2018) Laplace-Beltrami operator for the heat conduction in polymer coating of electronic devices. Discrete Cont. Dyn. Syst. B 23(4), 1739–1756.Google Scholar
Anguiano, M. (2020) Existence, uniqueness and homogenization of nonlinear parabolic problems with dynamical boundary conditions in perforated media. Mediterr. J. Math. 17, 1–22Google Scholar
Arbogast, T., Douglas, J. & Hornung, U. (1990) Derivation of the double porosity model of single phase flow via homogenization theory. SIAM J. Math. Anal. 27, 823–836.CrossRefGoogle Scholar
Bourgeat, A., Luckhaus, S. & Mikelić, A. (1996) Convergence of the homogenization process for a double-porosity model of immiscible two-phase flow. SIAM J. Math. Anal. 27, 1520–1543.CrossRefGoogle Scholar
Cioranescu, D., Damlamian, A., Donato, P., Griso, G. & Zaki, R. (2012) The periodic unfolding method in domains with holes. SIAM J. Math. Anal. 44(2), 718–760.CrossRefGoogle Scholar
Cioranescu, D., Damlamian, A. & Griso, G. (2008) The periodic unfolding method in homogenization. SIAM J. Math. Anal. 40, 1585–1620.CrossRefGoogle Scholar
Cioranescu, D., Griso, G. & Damlamian, A. (2018) The Periodic Unfolding Method, Springer, Singapore.CrossRefGoogle Scholar
Cioranescu, D. & Paulin, J. S. J. (1979) Homogenization in open sets with holes. J. Math. Pures Appl. 71, 590–607.Google Scholar
Donato, P. & Nguyen, K. H. L. (2015) Homogenization of diffusion problems with a nonlinear interfacial resistance. NoDEA Nonlinear Differ. Equations Appl. 22(5), 1345–1380.CrossRefGoogle Scholar
Friesecke, G., James, R. D. & Müller, S. (2002) A theorem on geometric rigidity and the derivation of nonlinear plate theory from three-dimensional elasticity. Commun. Pure Appl. Math. J. Issued Courant Inst. Math. Sci. 55(11), 1461–1506.10.1002/cpa.10048CrossRefGoogle Scholar
Gahn, M. (2017) Derivation of Effective Models for Reaction-Diffusion Processes in Multi-component Media. PhD thesis, Friedrich-Alexander-Universität Erlangen-Nürnberg, Shaker Verlag.Google Scholar
Gahn, M. (2019) Multi-scale modeling of processes in porous media - coupling reaction-diffusion processes in the solid and the fluid phase and on the separating interfaces. Discrete Contin. Dyn. Syst. Ser. B 24(12), 6511–6531.Google Scholar
Gahn, M. & Neuss-Radu, M. (2016) A characterization of relatively compact sets in $L^p(\Omega,B)$ . Stud. Univ. Babeş-Bolyai Math. 61(3), 279–290.Google Scholar
Gahn, M., Neuss-Radu, M. & Knabner, P. (2016) Homogenization of reaction–diffusion processes in a two-component porous medium with nonlinear flux conditions at the interface. SIAM J. Appl. Math. 76(5), 1819–1843.CrossRefGoogle Scholar
Gahn, M., Neuss-Radu, M. & Knabner, P. (2017) Derivation of an effective model for metabolic processes in living cells including substrate channeling. Vietnam J. Math. 45(1–2), 265–293.CrossRefGoogle Scholar
Galdi, G. P. (2011) An Introduction to the Mathematical Theory of the Navier–Stokes Equations . Springer Monographs in Mathematics, Springer-Verlag, New York, New York.Google Scholar
Graf, I. & Peter, M. A. (2014) A convergence result for the periodic unfolding method related to fast diffusion on manifolds. C. R. Acad. Sci. Paris Ser. I 352(6), 485–490.CrossRefGoogle Scholar
Graf, I. & Peter, M. A. (2014) Diffusion on surfaces and the boundary periodic unfolding operator with an application to carcinogenesis in human cells. SIAM J. Math. Anal. 46(4), 3025–3049.CrossRefGoogle Scholar
Hewitt, E. & Stromberg, K. (1975) Real and Abstract Analysis, Springer-Verlag, New York.Google Scholar
Hornung, U., Jäger, W. & Mikelić, A. (1994) Reactive transport through an array of cells with semi-permeable membranes. ESAIM Math. Model. Numer. Anal. 28, 59–94.CrossRefGoogle Scholar
Neuss-Radu, M. (1996) Some extensions of two-scale convergence. C. R. Acad. Sci. Paris Sér. I Math. 322, 899–904.Google Scholar
Neuss-Radu, M. & Jäger, W. (2007) Effective transmission conditions for reaction-diffusion processes in domains separated by an interface. SIAM J. Math. Anal. 39, 687–720.CrossRefGoogle Scholar
Nguetseng, G. (1989) A general convergence result for a functional related to the theory of homogenization. SIAM J. Math. Anal. 20, 608–623.CrossRefGoogle Scholar
Ptashnyk, M. & Roose, T. (2010) Derivation of a macroscopic model for transport of strongly sorbed solutes in the soil using homogenization theory. SIAM J. Appl. Math. 70, 2097–2118.CrossRefGoogle Scholar
Simon, J. (1987) Compact sets in the space ${L}^p(0,{T};{B})$ . Ann. Mat. Pura Appl. 146, 65–96.CrossRefGoogle Scholar
Vogt, C. (1982) A Homogenization Theorem Leading to a Volterra Integro-Differential Equation for Permeation Chromatography. SFB 123, University of Heidelberg, Preprint 155 and Diploma-thesis.Google Scholar
Winkel, B. S. (2004) Metabolic channeling in plants. Annu. Rev. Plant Biol. 55, 85–107.CrossRefGoogle ScholarPubMed