Hostname: page-component-784d4fb959-g549k Total loading time: 0 Render date: 2025-07-15T03:09:38.623Z Has data issue: false hasContentIssue false
  • English
  • Français

BRANCH GROUPS, ORBIT GROWTH, AND SUBGROUP GROWTH TYPES FOR PRO-$p$ GROUPS

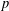Part of: Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  26 May 2020

YIFTACH BARNEA  and
JAN-CHRISTOPH SCHLAGE-PUCHTA
YIFTACH BARNEA
Affiliation:
Department of Mathematics, Royal Holloway, University of London, Egham, Surrey TW20 0EX, UK; y.barnea@rhul.ac.uk
JAN-CHRISTOPH SCHLAGE-PUCHTA
Affiliation:
Institut für Mathematik, Ulmenstr. 69, 18051Rostock, Germany; jan-christoph.schlage-puchta@uni-rostock.de

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In their book Subgroup Growth, Lubotzky and Segal asked: What are the possible types of subgroup growth of the pro-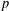$p$ group? In this paper, we construct certain extensions of the Grigorchuk group and the Gupta–Sidki groups, which have all possible types of subgroup growth between 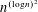$n^{(\log n)^{2}}$ and 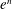$e^{n}$. Thus, we give an almost complete answer to Lubotzky and Segal’s question. In addition, we show that a class of pro-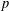$p$ branch groups, including the Grigorchuk group and the Gupta–Sidki groups, all have subgroup growth type 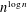$n^{\log n}$.

MSC classification

Primary: 20E07: Subgroup theorems; subgroup growth
Secondary: 20E08: Groups acting on trees 20E18: Limits, profinite groups

Information

Type
Algebra
Information
Forum of Mathematics, Pi , Volume 8 , 2020 , e10
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2020

References

Alexoudas, T., Klopsch, B. and Thillaisundaram, A., ‘Maximal subgroups of multi-edge spinal groups’, Groups Geom. Dyn. 10 (2016), 619–648.CrossRefGoogle Scholar
Ershov, M. and Jaikin-Zapirain, A., ‘Groups of positive weighted deficiency and their applications’, J. Reine Angew. Math. 677 (2013), 71–134.Google Scholar
Fernandez-Alcober, G. and Zugadi-Reizabal, A., ‘GGS-groups: order of congruence quotients and Hausdorff dimension’, Trans. Amer. Math. Soc. 366 (2014), 1993–2017.CrossRefGoogle Scholar
Garrido, A., ‘Abstract commensurability and the Gupta-Sidki group’, Groups Geom. Dyn. 10 (2016), 523–543.CrossRefGoogle Scholar
Grigorchuk, R. I., ‘Just infinite branch groups’, inNew Horizons in pro-p Groups (eds. du Sautoy, M., Segal, D. and Shalev, A.) Birkhäuser Progress in Mathematics, 184 (Birkhäuser Verlag, Basel, 2000), 121–179.CrossRefGoogle Scholar
Grigorchuk, R. I. and Wilson, J. S., ‘A structural property concerning abstract commensurability of subgroups’, J. Lond. Math. Soc. (2) 68 (2003), 671–682.CrossRefGoogle Scholar
Klopsch, B., 1999 ‘Substitution Groups, Subgroup Growth and Other Topics’, D.Phil. Thesis, University of Oxford.Google Scholar
Lubotzky, A. and Segal, D., Subgroup Growth, Birkhäuser Progress in Mathematics, 212 (Birkhäuser Verlag, Basel, 2003).CrossRefGoogle Scholar
Pervova, E. L., ‘Maximal subgroups of some non locally finite p-groups’, Internat. J. Algebra Comput. 15 (2005), 1129–1150.CrossRefGoogle Scholar
Pyber, L., ‘Groups of intermediate subgroup growth and a problem of Grothendieck’, Duke Math. J. 121 (2004), 169–188.CrossRefGoogle Scholar
Segal, D., ‘The finite images of finitely generated groups’, Proc. Lond. Math. Soc. (3) 82 (2001), 597–613.CrossRefGoogle Scholar
Segal, D. and Shalev, A., ‘Groups with fractionally exponential subgroup growth’, J. Pure Appl. Algebra 88 (1993), 205–223.CrossRefGoogle Scholar
Sidki, S., ‘On a 2-generated infinite 3-group: subgroups and automorphisms’, J. Algebra 110 (1987), 24–55.CrossRefGoogle Scholar
Shalev, A., ‘Growth functions p-adic analytic groups and groups of finite coclass’, J. Lond. Math. Soc. (2) 46 (1992), 111–122.CrossRefGoogle Scholar
Zugadi-Reizabal, A., 2011 ‘Hausdorff dimension in groups acting on the $p$-adic tree’, PhD Thesis, University of the Basque country Bilbao.Google Scholar