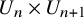1 Introduction
1.1 Arthur parameters and weak base change
1.1.1
In some sense, this paper is a sequel of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22], where we proved the global Gan-Gross-Prasad (see [Reference Gan, Gross and PrasadGGP12, section 24]) and the Ichino-Ikeda conjectures for a product of unitary groups
![]() $U(n)\times U(n+1)$
(see [Reference Ichino and IkedaII10] and [Reference HarrisHar14]). The goal of the present paper is two-fold: first, we state and prove an extension of these two conjectures to the case of some Eisenstein series. Second, we show that this extension, when applied to some specific Eisenstein series, implies the global Gan-Gross-Prasad conjecture and its refinement à la Ichino-Ikeda for general Bessel periods of unitary groups. To state our results, we first review the notion of Arthur parameter.
$U(n)\times U(n+1)$
(see [Reference Ichino and IkedaII10] and [Reference HarrisHar14]). The goal of the present paper is two-fold: first, we state and prove an extension of these two conjectures to the case of some Eisenstein series. Second, we show that this extension, when applied to some specific Eisenstein series, implies the global Gan-Gross-Prasad conjecture and its refinement à la Ichino-Ikeda for general Bessel periods of unitary groups. To state our results, we first review the notion of Arthur parameter.
1.1.2 Hermitian Arthur parameter.
Let
![]() $E/F$
be a quadratic extension of number fields and c be the nontrivial element of the Galois group
$E/F$
be a quadratic extension of number fields and c be the nontrivial element of the Galois group
![]() $\operatorname {\mathrm {Gal}}(E/F)$
. Let
$\operatorname {\mathrm {Gal}}(E/F)$
. Let
![]() $\mathbb {A}$
be the ring of adèles of F. Let
$\mathbb {A}$
be the ring of adèles of F. Let
![]() $n\geqslant 1$
be an integer. Let
$n\geqslant 1$
be an integer. Let
![]() $G_n$
be the group of automorphims of the E-vector space
$G_n$
be the group of automorphims of the E-vector space
![]() $E^n$
. We view
$E^n$
. We view
![]() $G_n$
as an F-group by Weil restriction. For an automorphic representation
$G_n$
as an F-group by Weil restriction. For an automorphic representation
![]() $\Pi $
of
$\Pi $
of
![]() $G_n(\mathbb {A})$
, we denote by
$G_n(\mathbb {A})$
, we denote by
![]() $\Pi ^*$
its conjugate-dual. Let us introduce some definitions. A discrete Hermitian Arthur parameter of
$\Pi ^*$
its conjugate-dual. Let us introduce some definitions. A discrete Hermitian Arthur parameter of
![]() $G_n$
is an irreducible automorphic representation
$G_n$
is an irreducible automorphic representation
![]() $\Pi $
of
$\Pi $
of
![]() $G_n(\mathbb {A})$
such that
$G_n(\mathbb {A})$
such that
-
•
 $\Pi $
is isomorphic to the full induced representation
$\Pi $
is isomorphic to the full induced representation
 $\operatorname {\mathrm {Ind}}_Q^{G_n}(\Pi _1\boxtimes \ldots \boxtimes \Pi _r)$
, where Q is a parabolic subgroup of
$\operatorname {\mathrm {Ind}}_Q^{G_n}(\Pi _1\boxtimes \ldots \boxtimes \Pi _r)$
, where Q is a parabolic subgroup of
 $G_n$
with Levi factor
$G_n$
with Levi factor
 $G_{n_1}\times \ldots \times G_{n_r}$
where
$G_{n_1}\times \ldots \times G_{n_r}$
where
 $n_1+\ldots +n_r=n$
;
$n_1+\ldots +n_r=n$
; -
•
 $\Pi _i$
is a conjugate self-dual cuspidal automorphic representation of
$\Pi _i$
is a conjugate self-dual cuspidal automorphic representation of
 $G_{n_i}(\mathbb {A})$
, and the Asai L-function
$G_{n_i}(\mathbb {A})$
, and the Asai L-function
 $L(s,\Pi _i,\mathrm {As}^{(-1)^{n+1}})$
has a pole at
$L(s,\Pi _i,\mathrm {As}^{(-1)^{n+1}})$
has a pole at
 $s=1$
for
$s=1$
for
 $1\leqslant i\leqslant r$
.
$1\leqslant i\leqslant r$
. -
• the representations
 $\Pi _i$
are mutually non-isomorphic for
$\Pi _i$
are mutually non-isomorphic for
 $1\leqslant i\leqslant r$
;
$1\leqslant i\leqslant r$
;
The integer r and the representations
![]() $(\Pi _i)_{1\leqslant i \leqslant r}$
are unique (up to a permutation). We set
$(\Pi _i)_{1\leqslant i \leqslant r}$
are unique (up to a permutation). We set
![]() $S_\Pi =(\mathbb {Z}/2\mathbb {Z})^{r}$
.
$S_\Pi =(\mathbb {Z}/2\mathbb {Z})^{r}$
.
For our purpose, we need more general Arthur parameters of
![]() $G_n$
, which we call regular Hermitian Arthur parameters and which are by definition the automorphic representations
$G_n$
, which we call regular Hermitian Arthur parameters and which are by definition the automorphic representations
![]() $\Pi $
of
$\Pi $
of
![]() $G_n$
such that
$G_n$
such that
-
•
 $\Pi $
is isomorphic to the full induced representation
$\Pi $
is isomorphic to the full induced representation
 $\operatorname {\mathrm {Ind}}_Q^{G_n}(\Pi _1\boxtimes \ldots \boxtimes \Pi _r \boxtimes \Pi _0\boxtimes \Pi _r^* \boxtimes \ldots \boxtimes \Pi _1^*)$
, where Q is a parabolic subgroup of
$\operatorname {\mathrm {Ind}}_Q^{G_n}(\Pi _1\boxtimes \ldots \boxtimes \Pi _r \boxtimes \Pi _0\boxtimes \Pi _r^* \boxtimes \ldots \boxtimes \Pi _1^*)$
, where Q is a parabolic subgroup of
 $G_n$
with Levi factor
$G_n$
with Levi factor
 $M_Q=G_{n_1}\times \ldots \times G_{n_r}\times G_{n_0}\times G_{n_r}\times \ldots \times G_{n_1},$
where
$M_Q=G_{n_1}\times \ldots \times G_{n_r}\times G_{n_0}\times G_{n_r}\times \ldots \times G_{n_1},$
where
 $n_0+2(n_1+\ldots +n_r)=n$
;
$n_0+2(n_1+\ldots +n_r)=n$
; -
•
 $\Pi _0$
is a discrete Hermitian Arthur parameter of
$\Pi _0$
is a discrete Hermitian Arthur parameter of
 $G_{n_0}$
;
$G_{n_0}$
; -
•
 $\Pi _i$
is a cuspidal automorphic representation of
$\Pi _i$
is a cuspidal automorphic representation of
 $G_{n_i}(\mathbb {A})$
(with character central trivial on
$G_{n_i}(\mathbb {A})$
(with character central trivial on
 $A_{G_{n_i}}^\infty $
) for
$A_{G_{n_i}}^\infty $
) for
 $1\leqslant i\leqslant r$
;
$1\leqslant i\leqslant r$
; -
• the representations
 $\Pi _1,\ldots ,\Pi _r,\Pi _1^*,\ldots ,\Pi _r^*$
are mutually non-isomorphic .
$\Pi _1,\ldots ,\Pi _r,\Pi _1^*,\ldots ,\Pi _r^*$
are mutually non-isomorphic .
The representation
![]() $\Pi _0$
is uniquely determined by
$\Pi _0$
is uniquely determined by
![]() $\Pi $
and is called the discrete component of
$\Pi $
and is called the discrete component of
![]() $\Pi $
. We set
$\Pi $
. We set
The parabolic subgroup Q depends on the ordering on the representations
![]() $\Pi _1,\ldots ,\Pi _r,\Pi _1^*,\ldots ,\Pi _r^*$
: we fix one.
$\Pi _1,\ldots ,\Pi _r,\Pi _1^*,\ldots ,\Pi _r^*$
: we fix one.
Let
![]() $\mathfrak {a}_{Q,\mathbb {C}}^*$
be the complex vector space of unramified characters of
$\mathfrak {a}_{Q,\mathbb {C}}^*$
be the complex vector space of unramified characters of
![]() $Q(\mathbb {A})$
. We have the real subspaces
$Q(\mathbb {A})$
. We have the real subspaces
![]() $\mathfrak {a}_Q^*$
and
$\mathfrak {a}_Q^*$
and
![]() $i\mathfrak {a}_Q^*$
, respectively, of real and unitary characters. Let w be the permutation that exchanges the two blocks
$i\mathfrak {a}_Q^*$
, respectively, of real and unitary characters. Let w be the permutation that exchanges the two blocks
![]() $G_{n_i}$
corresponding to
$G_{n_i}$
corresponding to
![]() $\Pi _i$
and
$\Pi _i$
and
![]() $\Pi _i^*$
for all
$\Pi _i^*$
for all
![]() $1\leqslant i\leqslant r$
. We set
$1\leqslant i\leqslant r$
. We set
For any
![]() $\lambda \in \mathfrak {a}_{\Pi ,\mathbb {C}}^*$
, we define
$\lambda \in \mathfrak {a}_{\Pi ,\mathbb {C}}^*$
, we define
![]() $\Pi _\lambda $
as the full induced representation
$\Pi _\lambda $
as the full induced representation
If
![]() $\lambda \in i\mathfrak {a}_\Pi ^*=\mathfrak {a}_{\Pi ,\mathbb {C}}^*\cap i \mathfrak {a}_Q^*$
, then
$\lambda \in i\mathfrak {a}_\Pi ^*=\mathfrak {a}_{\Pi ,\mathbb {C}}^*\cap i \mathfrak {a}_Q^*$
, then
![]() $\Pi _\lambda $
is irreducible.
$\Pi _\lambda $
is irreducible.
1.1.3 Unitary groups and (weak) base change
For any integer
![]() $n\geqslant 1$
, let
$n\geqslant 1$
, let
![]() $\mathcal {H}_n$
be the set of isomorphism classes of nondegenerate c-Hermitian spaces h over E of rank n. We identify any
$\mathcal {H}_n$
be the set of isomorphism classes of nondegenerate c-Hermitian spaces h over E of rank n. We identify any
![]() $h \in \mathcal {H}_n$
with a representative, and we denote by
$h \in \mathcal {H}_n$
with a representative, and we denote by
![]() $U(h)$
its automorphism group. Let
$U(h)$
its automorphism group. Let
![]() $h\in \mathcal {H}$
and
$h\in \mathcal {H}$
and
![]() $P\subset U(h)$
be a parabolic subgroup with Levi factor
$P\subset U(h)$
be a parabolic subgroup with Levi factor
![]() $M_P$
. There exist a decomposition
$M_P$
. There exist a decomposition
![]() $n_0+2(n_1+\ldots +n_r)=n$
and
$n_0+2(n_1+\ldots +n_r)=n$
and
![]() $h_{n_0} \in \mathcal {H}_{n_0}$
such that
$h_{n_0} \in \mathcal {H}_{n_0}$
such that
![]() $M_P$
is identified with
$M_P$
is identified with
![]() $G_{n_1}\times \ldots \times G_{n_r} \times U(h_{n_0})$
. Let
$G_{n_1}\times \ldots \times G_{n_r} \times U(h_{n_0})$
. Let
![]() $\sigma $
be a cuspidal automorphic subrepresentation of
$\sigma $
be a cuspidal automorphic subrepresentation of
![]() $M_P(\mathbb {A})$
(with central character trivial on the central subgroup
$M_P(\mathbb {A})$
(with central character trivial on the central subgroup
![]() $A_P^\infty $
defined in §2.1.6). Accordingly, we have
$A_P^\infty $
defined in §2.1.6). Accordingly, we have
![]() $\sigma =\Pi _1\boxtimes \ldots \boxtimes \Pi _r\boxtimes \sigma _0$
with
$\sigma =\Pi _1\boxtimes \ldots \boxtimes \Pi _r\boxtimes \sigma _0$
with
![]() $\Pi _i$
a cuspidal automorphic representation of
$\Pi _i$
a cuspidal automorphic representation of
![]() $G_{n_i}$
(with central character trivial on
$G_{n_i}$
(with central character trivial on
![]() $A_{G_{n_i}}^\infty $
).
$A_{G_{n_i}}^\infty $
).
We shall say that a regular Hermitian Arthur parameter
![]() $\Pi $
of
$\Pi $
of
![]() $G_n$
is a weak base-change of
$G_n$
is a weak base-change of
![]() $(P,\sigma )$
if there exist a parabolic subgroup Q of
$(P,\sigma )$
if there exist a parabolic subgroup Q of
![]() $G_n$
with Levi factor
$G_n$
with Levi factor
![]() $M_Q=G_{n_1}\times \ldots \times G_{n_r}\times G_{n_0}\times G_{n_r}\times \ldots \times G_{n_1}$
and a discrete Hermitian Arthur parameter
$M_Q=G_{n_1}\times \ldots \times G_{n_r}\times G_{n_0}\times G_{n_r}\times \ldots \times G_{n_1}$
and a discrete Hermitian Arthur parameter
![]() $\Pi _0$
of
$\Pi _0$
of
![]() $G_{n_0}$
such that
$G_{n_0}$
such that
-
1.
 $\Pi $
is isomorphic to the full induced representation
$\Pi $
is isomorphic to the full induced representation
 $\operatorname {\mathrm {Ind}}_Q^{G_n}(\Pi _1\boxtimes \ldots \boxtimes \Pi _r \boxtimes \Pi _0\boxtimes \Pi _r^* \boxtimes \ldots \boxtimes \Pi _1^*)$
;
$\operatorname {\mathrm {Ind}}_Q^{G_n}(\Pi _1\boxtimes \ldots \boxtimes \Pi _r \boxtimes \Pi _0\boxtimes \Pi _r^* \boxtimes \ldots \boxtimes \Pi _1^*)$
; -
2. for almost all places of F that split in E, the local component
 $\Pi _{0,v}$
is the split local base change of
$\Pi _{0,v}$
is the split local base change of
 $\sigma _{0,v}$
.
$\sigma _{0,v}$
.
Note that this implies that the representations
![]() $\Pi _1,\ldots ,\Pi _r,\Pi _1^*,\ldots ,\Pi _r^*$
are mutually non-isomorphic and that
$\Pi _1,\ldots ,\Pi _r,\Pi _1^*,\ldots ,\Pi _r^*$
are mutually non-isomorphic and that
![]() $\Pi _0$
is in fact the discrete component of
$\Pi _0$
is in fact the discrete component of
![]() $\Pi $
. If condition 2 above is satisfied, we shall also say that
$\Pi $
. If condition 2 above is satisfied, we shall also say that
![]() $\Pi _0$
is the weak base change of
$\Pi _0$
is the weak base change of
![]() $\sigma _0$
.
$\sigma _0$
.
If
![]() $\Pi $
is a weak base-change of
$\Pi $
is a weak base-change of
![]() $(P,\sigma )$
, we can naturally identify the space
$(P,\sigma )$
, we can naturally identify the space
![]() $\mathfrak {a}_{P,\mathbb {C}}^*$
of unramified characters of
$\mathfrak {a}_{P,\mathbb {C}}^*$
of unramified characters of
![]() $P(\mathbb {A})$
with
$P(\mathbb {A})$
with
![]() $\mathfrak {a}_{\Pi ,\mathbb {C}}^*$
, and so we will not distinguish between the two spaces. Thus, for
$\mathfrak {a}_{\Pi ,\mathbb {C}}^*$
, and so we will not distinguish between the two spaces. Thus, for
![]() $\lambda \in \mathfrak {a}_{\Pi ,\mathbb {C}}^*$
, we can consider the full induced representation
$\lambda \in \mathfrak {a}_{\Pi ,\mathbb {C}}^*$
, we can consider the full induced representation
![]() $\Sigma _\lambda =\operatorname {\mathrm {Ind}}_P^{U_h}(\sigma \otimes \lambda )$
.
$\Sigma _\lambda =\operatorname {\mathrm {Ind}}_P^{U_h}(\sigma \otimes \lambda )$
.
1.1.4
We can extend the notions above to the case of a product. Let
![]() $n,n'\geqslant 1$
be integers. A regular Hermitian Arthur parameter of
$n,n'\geqslant 1$
be integers. A regular Hermitian Arthur parameter of
![]() $G_{n}\times G_{n'}$
is then an automorphic representation of the form
$G_{n}\times G_{n'}$
is then an automorphic representation of the form
![]() $\Pi =\Pi _n\boxtimes \Pi _{n'}$
, where
$\Pi =\Pi _n\boxtimes \Pi _{n'}$
, where
![]() $\Pi _k$
is a regular Hermitian Arthur parameter of
$\Pi _k$
is a regular Hermitian Arthur parameter of
![]() $G_k$
for
$G_k$
for
![]() $k=n,n'$
. Then we set
$k=n,n'$
. Then we set
![]() $S_\Pi =S_{\Pi _n}\times S_{\Pi _{n'}}$
and
$S_\Pi =S_{\Pi _n}\times S_{\Pi _{n'}}$
and
![]() $\mathfrak {a}_{\Pi ,\mathbb {C}}^*=\mathfrak {a}_{\Pi _n,\mathbb {C}}^*\times \mathfrak {a}_{\Pi _{n'},\mathbb {C}}^* $
etc. For
$\mathfrak {a}_{\Pi ,\mathbb {C}}^*=\mathfrak {a}_{\Pi _n,\mathbb {C}}^*\times \mathfrak {a}_{\Pi _{n'},\mathbb {C}}^* $
etc. For
![]() $\lambda =(\lambda _n,\lambda _{n'})\in \mathfrak {a}_{\Pi ,\mathbb {C}}^*$
, we set
$\lambda =(\lambda _n,\lambda _{n'})\in \mathfrak {a}_{\Pi ,\mathbb {C}}^*$
, we set
![]() $\Pi _\lambda =\Pi _{n,\lambda _n}\boxtimes \Pi _{n',\lambda _{n'}}$
. A parameter
$\Pi _\lambda =\Pi _{n,\lambda _n}\boxtimes \Pi _{n',\lambda _{n'}}$
. A parameter
![]() $\Pi $
is discrete if both
$\Pi $
is discrete if both
![]() $\Pi _n$
and
$\Pi _n$
and
![]() $\Pi _{n'}$
are discrete.
$\Pi _{n'}$
are discrete.
Let
![]() $h\in \mathcal {H}_n$
and
$h\in \mathcal {H}_n$
and
![]() $h'\in \mathcal {H}_{n'}$
. Let
$h'\in \mathcal {H}_{n'}$
. Let
![]() $P=P_n\times P_{n'}$
be a parabolic subgroup of
$P=P_n\times P_{n'}$
be a parabolic subgroup of
![]() $U(h)\times U(h')$
. We say that a regular Hermitian Arthur parameter
$U(h)\times U(h')$
. We say that a regular Hermitian Arthur parameter
![]() $\Pi =\Pi _n\boxtimes \Pi _{n'}$
of
$\Pi =\Pi _n\boxtimes \Pi _{n'}$
of
![]() $G_n\times G_{n'}$
is a weak base-change of
$G_n\times G_{n'}$
is a weak base-change of
![]() $(P,\sigma )$
if
$(P,\sigma )$
if
![]() $\Pi _n$
and
$\Pi _n$
and
![]() $\Pi _{n'}$
are, respectively, weak base-changes of
$\Pi _{n'}$
are, respectively, weak base-changes of
![]() $(P_n,\sigma _n)$
and
$(P_n,\sigma _n)$
and
![]() $(P_{n'},\sigma _{n'})$
, where
$(P_{n'},\sigma _{n'})$
, where
![]() $\sigma =\sigma _n\boxtimes \sigma _{n'}$
.
$\sigma =\sigma _n\boxtimes \sigma _{n'}$
.
1.2 An extension of the Gan-Gross-Prasad conjecture to some Eisenstein series
1.2.1 Corank
 $1$
and regular Hermitian Arthur parameter
$1$
and regular Hermitian Arthur parameter
Let
![]() $n\geqslant 1$
. Consider the ‘corank
$n\geqslant 1$
. Consider the ‘corank
![]() $1$
’ case
$1$
’ case
![]() $G=G_n\times G_{n+1}$
. Let
$G=G_n\times G_{n+1}$
. Let
![]() $\Pi =\Pi _n\boxtimes \Pi _{n+1}$
be a regular Hermitian Arthur parameter of G. We can write
$\Pi =\Pi _n\boxtimes \Pi _{n+1}$
be a regular Hermitian Arthur parameter of G. We can write
![]() $\Pi _k=\operatorname {\mathrm {Ind}}_{Q_k}^{G_k}(\Pi _{1,k}\boxtimes \ldots \boxtimes \Pi _{r_k,k})$
for some parabolic subgroup
$\Pi _k=\operatorname {\mathrm {Ind}}_{Q_k}^{G_k}(\Pi _{1,k}\boxtimes \ldots \boxtimes \Pi _{r_k,k})$
for some parabolic subgroup
![]() $Q_k\subset G_k$
for
$Q_k\subset G_k$
for
![]() $k=n,n+1$
and some cuspidal automorphic representations of
$k=n,n+1$
and some cuspidal automorphic representations of
![]() $G_{n_{i,k}}(\mathbb {A})$
with
$G_{n_{i,k}}(\mathbb {A})$
with
![]() $n_{1,k}+\ldots +n_{r_k,k}=k$
. We shall say that the parameter
$n_{1,k}+\ldots +n_{r_k,k}=k$
. We shall say that the parameter
![]() $\Pi $
is H-regular if for all
$\Pi $
is H-regular if for all
![]() $1\leqslant i\leqslant r_n$
and
$1\leqslant i\leqslant r_n$
and
![]() $1\leqslant j\leqslant r_{n+1}$
, the representation
$1\leqslant j\leqslant r_{n+1}$
, the representation
![]() $\Pi _{i,n}$
is not isomorphic to the contragredient of
$\Pi _{i,n}$
is not isomorphic to the contragredient of
![]() $\Pi _{j,n+1}$
.
$\Pi _{j,n+1}$
.
Remark 1.2.1.1. In the core of the paper, H will stand for the diagonal subgroup
![]() $G_n$
of G, and the term H-regular refers to the fact that H-regular Hermitian Arthur parameter features some particularly nice properties with respect to the (regularized) Rankin-Selberg period over that subgroup (roughly stemming from the fact that the Rankin-Selberg L-function of
$G_n$
of G, and the term H-regular refers to the fact that H-regular Hermitian Arthur parameter features some particularly nice properties with respect to the (regularized) Rankin-Selberg period over that subgroup (roughly stemming from the fact that the Rankin-Selberg L-function of
![]() $\Pi $
has no poles). A discrete Hermitian Arthur parameter is necessarily H-regular. Otherwise, we would get a self-conjugate cuspidal representation
$\Pi $
has no poles). A discrete Hermitian Arthur parameter is necessarily H-regular. Otherwise, we would get a self-conjugate cuspidal representation
![]() $\Pi _i$
of
$\Pi _i$
of
![]() $G_{n_i}$
for some
$G_{n_i}$
for some
![]() $n_i\geqslant 1$
such that both Asai L-functions
$n_i\geqslant 1$
such that both Asai L-functions
![]() $L(s,\Pi _i,\mathrm {As}^{+})$
and
$L(s,\Pi _i,\mathrm {As}^{+})$
and
![]() $L(s,\Pi _i,\mathrm {As}^{-})$
have a pole at
$L(s,\Pi _i,\mathrm {As}^{-})$
have a pole at
![]() $s=1$
: this is not possible.
$s=1$
: this is not possible.
On the unitary side, let
![]() $h_0\in \mathcal {H}_1$
be the element of rank
$h_0\in \mathcal {H}_1$
be the element of rank
![]() $1$
given by the norm
$1$
given by the norm
![]() $N_{E/F}$
. Then we attach to any
$N_{E/F}$
. Then we attach to any
![]() $h\in \mathcal {H}_n$
the following algebraic groups over F:
$h\in \mathcal {H}_n$
the following algebraic groups over F:
-
• the product of unitary groups
 $U_h=U(h)\times U(h\oplus h_0)$
, where
$U_h=U(h)\times U(h\oplus h_0)$
, where
 $h\oplus h_0$
denotes the orthogonal sum;
$h\oplus h_0$
denotes the orthogonal sum; -
• the unitary group
 $U^{\prime }_h$
of automorphisms of h viewed as a subgroup of
$U^{\prime }_h$
of automorphisms of h viewed as a subgroup of
 $U_h$
by the obvious diagonal embedding.
$U_h$
by the obvious diagonal embedding.
1.2.2
Let
![]() $P=M_PN_P\subset U_h$
be a parabolic subgroup with Levi factor
$P=M_PN_P\subset U_h$
be a parabolic subgroup with Levi factor
![]() $M_P$
and unipotent radical
$M_P$
and unipotent radical
![]() $N_P$
. Let
$N_P$
. Let
![]() $\sigma $
be a cuspidal automorphic subrepresentation of
$\sigma $
be a cuspidal automorphic subrepresentation of
![]() $M_P(\mathbb {A})$
with central character trivial on
$M_P(\mathbb {A})$
with central character trivial on
![]() $A_P^\infty $
. Let
$A_P^\infty $
. Let
![]() $\mathcal {A}_{P,\sigma }(U_h)$
be the space of automorphic forms on the quotient
$\mathcal {A}_{P,\sigma }(U_h)$
be the space of automorphic forms on the quotient
![]() $A_P^\infty M_P(F) N_P(\mathbb {A})\backslash U_h(\mathbb {A})$
such that for all
$A_P^\infty M_P(F) N_P(\mathbb {A})\backslash U_h(\mathbb {A})$
such that for all
![]() $g\in U_h(\mathbb {A})$
,
$g\in U_h(\mathbb {A})$
,
belongs to the space of
![]() $\sigma $
. Here,
$\sigma $
. Here,
![]() $N_P$
is the unipotent radical of P and
$N_P$
is the unipotent radical of P and
![]() $\delta _P$
is the modular character of
$\delta _P$
is the modular character of
![]() $P(\mathbb {A})$
. The representation of
$P(\mathbb {A})$
. The representation of
![]() $U_h(\mathbb {A})$
on
$U_h(\mathbb {A})$
on
![]() $\mathcal {A}_{P,\sigma }(U_h)$
is isomorphic to the induced representation
$\mathcal {A}_{P,\sigma }(U_h)$
is isomorphic to the induced representation
![]() $\Sigma =\operatorname {\mathrm {Ind}}_P^{U_h}(\sigma )$
. Let
$\Sigma =\operatorname {\mathrm {Ind}}_P^{U_h}(\sigma )$
. Let
![]() $\varphi \in \mathcal {A}_{P,\sigma }(U_h)$
. For
$\varphi \in \mathcal {A}_{P,\sigma }(U_h)$
. For
![]() $\lambda \in \mathfrak {a}_{\Pi ,\mathbb {C}}^*$
, we introduce the Eisenstein series
$\lambda \in \mathfrak {a}_{\Pi ,\mathbb {C}}^*$
, we introduce the Eisenstein series
![]() $E(\varphi ,\lambda )$
and the Ichino-Yamana regularized period
$E(\varphi ,\lambda )$
and the Ichino-Yamana regularized period
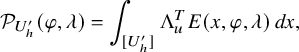 $$ \begin{align} \mathcal{P}_{U^{\prime}_h}(\varphi,\lambda)=\int_{[U_h^{\prime}]} \Lambda_u^TE(x,\varphi,\lambda)\,dx, \end{align} $$
$$ \begin{align} \mathcal{P}_{U^{\prime}_h}(\varphi,\lambda)=\int_{[U_h^{\prime}]} \Lambda_u^TE(x,\varphi,\lambda)\,dx, \end{align} $$
where
![]() $[U_h^{\prime }]=U_h^{\prime }(F)\backslash U_h^{\prime }(\mathbb {A})$
is equipped with the Tamagawa measure,
$[U_h^{\prime }]=U_h^{\prime }(F)\backslash U_h^{\prime }(\mathbb {A})$
is equipped with the Tamagawa measure,
![]() $\Lambda _u^T$
is the truncation operator introduced by Ichino-Yamana in [Reference Ichino and YamanaIY19] depending on an auxiliary parameter T whose definition is recalled in §3.3.2. The integral is absolutely convergent. Moreover, if the base change of
$\Lambda _u^T$
is the truncation operator introduced by Ichino-Yamana in [Reference Ichino and YamanaIY19] depending on an auxiliary parameter T whose definition is recalled in §3.3.2. The integral is absolutely convergent. Moreover, if the base change of
![]() $\Sigma $
is a H-regular Arthur parameter (which will be our assumption), then the integral does not depend on T (see proposition 3.5.3.1 below). In this case,
$\Sigma $
is a H-regular Arthur parameter (which will be our assumption), then the integral does not depend on T (see proposition 3.5.3.1 below). In this case,
![]() $\mathcal {P}_{U^{\prime }_h}(\varphi ,\lambda )$
is a meromorphic function, which is regular outside the singularities of the Eisenstein series. In particular, it is holomorphic on
$\mathcal {P}_{U^{\prime }_h}(\varphi ,\lambda )$
is a meromorphic function, which is regular outside the singularities of the Eisenstein series. In particular, it is holomorphic on
![]() $i\mathfrak {a}_{\Pi }^*$
.
$i\mathfrak {a}_{\Pi }^*$
.
1.2.3 The Gan-Gross-Prasad conjecture for some Eisenstein series
Theorem 1.2.3.1. Let
![]() $\Pi $
be a H-regular Hermitian Arthur parameter of G and let
$\Pi $
be a H-regular Hermitian Arthur parameter of G and let
![]() $\lambda \in i\mathfrak {a}_{\Pi }^*$
. The following two statements are equivalent:
$\lambda \in i\mathfrak {a}_{\Pi }^*$
. The following two statements are equivalent:
-
1. The complete Rankin-Selberg L-function of
 $\Pi _\lambda $
(including Archimedean places) satisfies
$\Pi _\lambda $
(including Archimedean places) satisfies  $$ \begin{align*}L\left(\frac12,\Pi_\lambda\right)\not=0;\end{align*} $$
$$ \begin{align*}L\left(\frac12,\Pi_\lambda\right)\not=0;\end{align*} $$
-
2. There exist
 $h\in \mathcal {H}_n$
, a parabolic subgroup
$h\in \mathcal {H}_n$
, a parabolic subgroup
 $P\subset U_h$
with Levi factor
$P\subset U_h$
with Levi factor
 $M_P$
and
$M_P$
and
 $\sigma $
an irreducible cuspidal automorphic subrepresentation of
$\sigma $
an irreducible cuspidal automorphic subrepresentation of
 $M_P(\mathbb {A})$
such that
$M_P(\mathbb {A})$
such that
 $\Pi $
is a weak base change of
$\Pi $
is a weak base change of
 $(P,\sigma )$
and the period integral
$(P,\sigma )$
and the period integral
 $\varphi \mapsto \mathcal {P}_{U^{\prime }_h}(\varphi ,\lambda )$
induces a nonzero linear form on
$\varphi \mapsto \mathcal {P}_{U^{\prime }_h}(\varphi ,\lambda )$
induces a nonzero linear form on
 $\mathcal {A}_{P,\sigma }(U_h)$
.
$\mathcal {A}_{P,\sigma }(U_h)$
.
Remark 1.2.3.2. The Levi subgroup
![]() $M_P$
is determined up to conjugation by the parameter
$M_P$
is determined up to conjugation by the parameter
![]() $\Pi $
. Moreover, we have
$\Pi $
. Moreover, we have
![]() $P=U_h$
if
$P=U_h$
if
![]() $\Pi $
is discrete. In this case, the theorem is proved in [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21, Theorem 1.8] if
$\Pi $
is discrete. In this case, the theorem is proved in [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21, Theorem 1.8] if
![]() $\Pi $
is cuspidal and in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Theorem 1.1.5.1] for a general discrete Hermitian parameter. The novelty of the theorem is to consider non-discrete Arthur parameters and thus periods of proper Eisenstein series on unitary groups.
$\Pi $
is cuspidal and in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Theorem 1.1.5.1] for a general discrete Hermitian parameter. The novelty of the theorem is to consider non-discrete Arthur parameters and thus periods of proper Eisenstein series on unitary groups.
1.2.4 Factorization of periods of some Eisenstein series à la Ichino-Ikeda
Let
![]() $h\in \mathcal {H}_n$
. Let P be a parabolic subgroup of
$h\in \mathcal {H}_n$
. Let P be a parabolic subgroup of
![]() $ U_h$
with Levi factor
$ U_h$
with Levi factor
![]() $M_P$
and let
$M_P$
and let
![]() $\sigma $
be an irreducible cuspidal automorphic subrepresentation of
$\sigma $
be an irreducible cuspidal automorphic subrepresentation of
![]() $M_P(\mathbb {A})$
such that the weak base change of
$M_P(\mathbb {A})$
such that the weak base change of
![]() $(P,\sigma )$
is a regular Hermitian Arthur parameter
$(P,\sigma )$
is a regular Hermitian Arthur parameter
![]() $\Pi $
. We have a restricted tensor product decomposition
$\Pi $
. We have a restricted tensor product decomposition
![]() $\sigma =\bigotimes _{v\in V_F}'\sigma _v$
over the set
$\sigma =\bigotimes _{v\in V_F}'\sigma _v$
over the set
![]() $V_F$
of places of F. We assume that
$V_F$
of places of F. We assume that
![]() $\sigma $
is tempered – that is, for every place v, the local representation
$\sigma $
is tempered – that is, for every place v, the local representation
![]() $\sigma _v$
is tempered. Let
$\sigma _v$
is tempered. Let
![]() $\lambda \in i\mathfrak {a}_\Pi ^*$
. We define
$\lambda \in i\mathfrak {a}_\Pi ^*$
. We define
![]() $\Pi _\lambda $
and
$\Pi _\lambda $
and
![]() $\Sigma _\lambda $
as above. Let
$\Sigma _\lambda $
as above. Let
![]() $\Sigma _{\lambda ,v}=\operatorname {\mathrm {Ind}}_P^{U_h}(\sigma _v\otimes \lambda )$
and
$\Sigma _{\lambda ,v}=\operatorname {\mathrm {Ind}}_P^{U_h}(\sigma _v\otimes \lambda )$
and
![]() $\Pi _{\lambda ,v}$
be their local components.
$\Pi _{\lambda ,v}$
be their local components.
We set
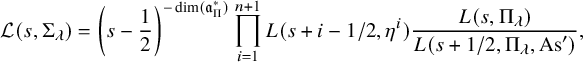 $$ \begin{align*} \mathcal{L}(s,\Sigma_\lambda)= \left(s-\frac12\right)^{-\dim(\mathfrak{a}_{\Pi}^*)} \prod_{i=1}^{n+1}L(s+i-1/2,\eta^i)\frac{L(s,\Pi_\lambda)}{L(s+1/2,\Pi_\lambda,\mathrm{As}')}, \end{align*} $$
$$ \begin{align*} \mathcal{L}(s,\Sigma_\lambda)= \left(s-\frac12\right)^{-\dim(\mathfrak{a}_{\Pi}^*)} \prod_{i=1}^{n+1}L(s+i-1/2,\eta^i)\frac{L(s,\Pi_\lambda)}{L(s+1/2,\Pi_\lambda,\mathrm{As}')}, \end{align*} $$
where
![]() $\eta $
denotes the quadratic idele class character associated to the extension
$\eta $
denotes the quadratic idele class character associated to the extension
![]() $E/F$
,
$E/F$
,
![]() $L(s,\eta ^i)$
is the completed Hecke L-function associated to
$L(s,\eta ^i)$
is the completed Hecke L-function associated to
![]() $\eta ^i$
and
$\eta ^i$
and
![]() $L(s,\Pi _\lambda ,\mathrm {As}')$
is the L-function associated to
$L(s,\Pi _\lambda ,\mathrm {As}')$
is the L-function associated to
![]() $\mathrm {As}^{(-1)^n}\boxtimes \mathrm {As}^{(-1)^{n+1}}$
. Note that with our hypothesis, the function
$\mathrm {As}^{(-1)^n}\boxtimes \mathrm {As}^{(-1)^{n+1}}$
. Note that with our hypothesis, the function
![]() $L(s,\Pi _\lambda ,\mathrm {As}')$
has a pole of order
$L(s,\Pi _\lambda ,\mathrm {As}')$
has a pole of order
![]() $\dim (\mathfrak {a}_{\Pi }^*)$
at
$\dim (\mathfrak {a}_{\Pi }^*)$
at
![]() $s=1$
. Thus, the function
$s=1$
. Thus, the function
![]() $(s-1)^{-\dim (\mathfrak {a}_{\Pi }^*)} L(s,\Pi _\lambda ,\mathrm {As}')$
is holomorphic and nonvanishing at
$(s-1)^{-\dim (\mathfrak {a}_{\Pi }^*)} L(s,\Pi _\lambda ,\mathrm {As}')$
is holomorphic and nonvanishing at
![]() $s=1$
. In particular, the function
$s=1$
. In particular, the function
![]() $\mathcal {L}(s,\Sigma _\lambda )$
is holomorphic at
$\mathcal {L}(s,\Sigma _\lambda )$
is holomorphic at
![]() $s=\frac 12$
.
$s=\frac 12$
.
We denote by
![]() $\mathcal {L}(s,\Sigma _{\lambda ,v})$
the corresponding quotient of local L-factors; namely, for s in some half-space, we have
$\mathcal {L}(s,\Sigma _{\lambda ,v})$
the corresponding quotient of local L-factors; namely, for s in some half-space, we have
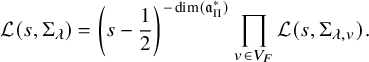 $$ \begin{align*} \mathcal{L}(s,\Sigma_\lambda)= \left(s-\frac12\right)^{-\dim(\mathfrak{a}_{\Pi}^*)} \prod_{v\in V_F} \mathcal{L}(s,\Sigma_{\lambda,v}). \end{align*} $$
$$ \begin{align*} \mathcal{L}(s,\Sigma_\lambda)= \left(s-\frac12\right)^{-\dim(\mathfrak{a}_{\Pi}^*)} \prod_{v\in V_F} \mathcal{L}(s,\Sigma_{\lambda,v}). \end{align*} $$
For each place v of F, we define a local normalized period
![]() $\mathcal {P}^\natural _{h,\sigma _v}: \Sigma _v\times \Sigma _v\to \mathbb {C}$
as follows:
$\mathcal {P}^\natural _{h,\sigma _v}: \Sigma _v\times \Sigma _v\to \mathbb {C}$
as follows:
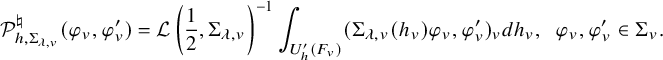 $$ \begin{align*}\mathcal{P}^\natural_{h,\Sigma_{\lambda,v}}(\varphi_v,\varphi^{\prime}_v)=\mathcal{L}\left(\frac12,\Sigma_{\lambda,v}\right)^{-1}\int_{U^{\prime}_h(F_v)} (\Sigma_{\lambda,v}(h_v)\varphi_v,\varphi^{\prime}_v)_v dh_v,\;\; \varphi_v,\varphi^{\prime}_v\in \Sigma_v.\end{align*} $$
$$ \begin{align*}\mathcal{P}^\natural_{h,\Sigma_{\lambda,v}}(\varphi_v,\varphi^{\prime}_v)=\mathcal{L}\left(\frac12,\Sigma_{\lambda,v}\right)^{-1}\int_{U^{\prime}_h(F_v)} (\Sigma_{\lambda,v}(h_v)\varphi_v,\varphi^{\prime}_v)_v dh_v,\;\; \varphi_v,\varphi^{\prime}_v\in \Sigma_v.\end{align*} $$
It depends on the choice of a Haar measure
![]() $dh_v$
on
$dh_v$
on
![]() $U^{\prime }_h(F_v)$
as well as an invariant inner product on
$U^{\prime }_h(F_v)$
as well as an invariant inner product on
![]() $\sigma _v$
which gives in the usual way an invariant product on
$\sigma _v$
which gives in the usual way an invariant product on
![]() $\Sigma _v$
denoted by
$\Sigma _v$
denoted by
![]() $(\cdot ,\cdot )_v$
. By the temperedness assumption, the integral is absolutely convergent [Reference HarrisHar14, Proposition 2.1] and the local factor
$(\cdot ,\cdot )_v$
. By the temperedness assumption, the integral is absolutely convergent [Reference HarrisHar14, Proposition 2.1] and the local factor
![]() $\mathcal {L}(s,\Sigma _{\lambda ,v})$
has neither zero nor pole at
$\mathcal {L}(s,\Sigma _{\lambda ,v})$
has neither zero nor pole at
![]() $s=\frac 12$
.
$s=\frac 12$
.
We introduce on
![]() $\mathcal {A}_{P,\sigma }(U_h)$
the Petersson inner product given by
$\mathcal {A}_{P,\sigma }(U_h)$
the Petersson inner product given by
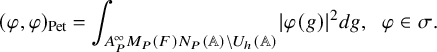 $$ \begin{align*}(\varphi,\varphi)_{\operatorname{\mathrm{Pet}}}=\int_{A_P^{\infty}M_P(F)N_P(\mathbb{A})\backslash U_h(\mathbb{A})} \lvert \varphi(g)\rvert^2 dg,\;\; \varphi\in \sigma.\end{align*} $$
$$ \begin{align*}(\varphi,\varphi)_{\operatorname{\mathrm{Pet}}}=\int_{A_P^{\infty}M_P(F)N_P(\mathbb{A})\backslash U_h(\mathbb{A})} \lvert \varphi(g)\rvert^2 dg,\;\; \varphi\in \sigma.\end{align*} $$
Recall that we have normalized the period integral
![]() $\mathcal {P}_{U_h^{\prime }}(\lambda )$
by choosing the invariant Tamagawa measures on
$\mathcal {P}_{U_h^{\prime }}(\lambda )$
by choosing the invariant Tamagawa measures on
![]() $[U_h^{\prime }]$
. We also normalize the Petersson product by using the quotient of Tamagawa measures. We assume that the local Haar measures
$[U_h^{\prime }]$
. We also normalize the Petersson product by using the quotient of Tamagawa measures. We assume that the local Haar measures
![]() $dh_v$
on
$dh_v$
on
![]() $U^{\prime }_h(F_v)$
are such that the product
$U^{\prime }_h(F_v)$
are such that the product
![]() $\prod _v dh_v$
gives the Tamagawa measure on
$\prod _v dh_v$
gives the Tamagawa measure on
![]() $U_h^{\prime }(\mathbb {A})$
.
$U_h^{\prime }(\mathbb {A})$
.
Theorem 1.2.4.1. Let
![]() $\Pi $
and
$\Pi $
and
![]() $(P,\sigma )$
as above. For
$(P,\sigma )$
as above. For
![]() $\lambda \in i\mathfrak {a}_\Pi ^*$
and every nonzero factorizable vector
$\lambda \in i\mathfrak {a}_\Pi ^*$
and every nonzero factorizable vector
![]() $\varphi =\otimes _v^{\prime } \varphi _v\in \mathcal {A}_{P,\sigma }(U_h)\simeq \otimes ^{\prime }_{v\in V_F} \Sigma _v$
, we have
$\varphi =\otimes _v^{\prime } \varphi _v\in \mathcal {A}_{P,\sigma }(U_h)\simeq \otimes ^{\prime }_{v\in V_F} \Sigma _v$
, we have
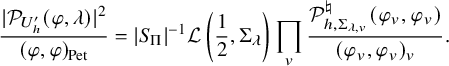 $$ \begin{align} \frac{\lvert \mathcal{P}_{U_h^{\prime}}(\varphi,\lambda)\rvert^2}{(\varphi, \varphi)_{\operatorname{\mathrm{Pet}}}}=\lvert S_\Pi\rvert^{-1} \mathcal{L}\left(\frac12,\Sigma_\lambda\right)\prod_v \frac{\mathcal{P}^\natural_{h,\Sigma_{\lambda,v}}(\varphi_v,\varphi_v)}{(\varphi_v,\varphi_v)_v}. \end{align} $$
$$ \begin{align} \frac{\lvert \mathcal{P}_{U_h^{\prime}}(\varphi,\lambda)\rvert^2}{(\varphi, \varphi)_{\operatorname{\mathrm{Pet}}}}=\lvert S_\Pi\rvert^{-1} \mathcal{L}\left(\frac12,\Sigma_\lambda\right)\prod_v \frac{\mathcal{P}^\natural_{h,\Sigma_{\lambda,v}}(\varphi_v,\varphi_v)}{(\varphi_v,\varphi_v)_v}. \end{align} $$
Remark 1.2.4.2. By [Reference HarrisHar14, Theorem 2.12] and our choice of measures, almost all factors in the right-hand side are equal to
![]() $1$
. As in remark 1.2.3.2, the statement reduces to [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Theorem 1.1.6.1] for a discrete Hermitian Arthur parameter
$1$
. As in remark 1.2.3.2, the statement reduces to [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Theorem 1.1.6.1] for a discrete Hermitian Arthur parameter
![]() $\Pi $
and even to [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21, Theorem 1.10] if
$\Pi $
and even to [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21, Theorem 1.10] if
![]() $\Pi $
is moreover simple.
$\Pi $
is moreover simple.
1.3 The case of Bessel periods
1.3.1
Let
![]() $n\geqslant m\geqslant 0$
be two integers of the same parity. We have
$n\geqslant m\geqslant 0$
be two integers of the same parity. We have
![]() $n=m+2r$
for some
$n=m+2r$
for some
![]() $r\geqslant 0$
. Recall that we denote by
$r\geqslant 0$
. Recall that we denote by
![]() $h_0$
the
$h_0$
the
![]() $1$
-dimensional Hermitian space given by the norm
$1$
-dimensional Hermitian space given by the norm
![]() $N_{E/F}$
. Let
$N_{E/F}$
. Let
![]() $h_s\in \mathcal {H}_2$
be the orthogonal sum of
$h_s\in \mathcal {H}_2$
be the orthogonal sum of
![]() $h_0$
and
$h_0$
and
![]() $-h_0$
. For any
$-h_0$
. For any
![]() $h\in \mathcal {H}_m$
, we define
$h\in \mathcal {H}_m$
, we define
![]() $\tilde h\in \mathcal {H}_n$
to be the orthogonal sum of h and r copies of
$\tilde h\in \mathcal {H}_n$
to be the orthogonal sum of h and r copies of
![]() $h_s$
denoted by
$h_s$
denoted by
![]() $h_s^1,\ldots , h_s^r$
. For each
$h_s^1,\ldots , h_s^r$
. For each
![]() $1\leqslant i\leqslant r$
, let
$1\leqslant i\leqslant r$
, let
![]() $(x_i,y_i) $
be a hyperbolic basis of
$(x_i,y_i) $
be a hyperbolic basis of
![]() $h_s^i$
; that is, we have
$h_s^i$
; that is, we have
![]() $h_s^i(x_i,x_i)=h_s^i(y_i,y_i)=0$
and
$h_s^i(x_i,x_i)=h_s^i(y_i,y_i)=0$
and
![]() $h_s^i(x_i,y_i)=1$
. We consider also the orthogonal sum
$h_s^i(x_i,y_i)=1$
. We consider also the orthogonal sum
![]() $h_{n+1}= \tilde h \oplus h_0 \in \mathcal {H}_{n+1}$
. We denote by
$h_{n+1}= \tilde h \oplus h_0 \in \mathcal {H}_{n+1}$
. We denote by
![]() $v_0$
the vector of
$v_0$
the vector of
![]() $h_{0}$
corresponding to
$h_{0}$
corresponding to
![]() $1\in E$
. We have a diagonal embedding
$1\in E$
. We have a diagonal embedding
for which the image of
![]() $U(h)$
in
$U(h)$
in
![]() $U(h_{n+1})$
is the subgroup which acts by the identity on
$U(h_{n+1})$
is the subgroup which acts by the identity on
![]() $h_0\oplus h_s^1\oplus \ldots \oplus h_s^r$
.
$h_0\oplus h_s^1\oplus \ldots \oplus h_s^r$
.
Let
![]() $B\subset U(h_{n+1})$
be the stabilizer of the isotropic flag
$B\subset U(h_{n+1})$
be the stabilizer of the isotropic flag
Let N be the unipotent radical of B. Then the group
![]() $U(h)$
normalizes N. Let
$U(h)$
normalizes N. Let
![]() $\mathcal {B}_h=U(h)\ltimes (\{1\}\times N)$
: this is the so-called Bessel subgroup of
$\mathcal {B}_h=U(h)\ltimes (\{1\}\times N)$
: this is the so-called Bessel subgroup of
![]() $\mathcal {G}_h$
.
$\mathcal {G}_h$
.
1.3.2 Bessel periods
Let
![]() $\psi :\mathbb {A}/F\to \mathbb {C}^\times $
be a nontrivial continuous character. We define a character
$\psi :\mathbb {A}/F\to \mathbb {C}^\times $
be a nontrivial continuous character. We define a character
![]() $\psi _N:[N]\to \mathbb {C}^\times $
by
$\psi _N:[N]\to \mathbb {C}^\times $
by
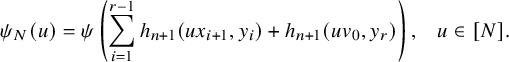 $$ \begin{align*} \psi_N(u)=\psi\left(\sum_{i=1}^{r-1} h_{n+1}(ux_{i+1},y_i)+h_{n+1}(uv_0,y_r) \right),\;\;\; u\in [N]. \end{align*} $$
$$ \begin{align*} \psi_N(u)=\psi\left(\sum_{i=1}^{r-1} h_{n+1}(ux_{i+1},y_i)+h_{n+1}(uv_0,y_r) \right),\;\;\; u\in [N]. \end{align*} $$
This character extends uniquely to a character
![]() $\psi _{\mathcal {B}_h}: [\mathcal {B}_h]\to \mathbb {C}^\times $
that coincides with
$\psi _{\mathcal {B}_h}: [\mathcal {B}_h]\to \mathbb {C}^\times $
that coincides with
![]() $\psi _N$
on
$\psi _N$
on
![]() $[N]$
and is trivial on
$[N]$
and is trivial on
![]() $[U(h)]$
. Let
$[U(h)]$
. Let
![]() $\sigma $
be a cuspidal automorphic subrepresentation of
$\sigma $
be a cuspidal automorphic subrepresentation of
![]() $\mathcal {G}_h(\mathbb {A})$
. We define the global Bessel period for
$\mathcal {G}_h(\mathbb {A})$
. We define the global Bessel period for
![]() $\varphi \in \sigma $
by the absolute convergent integral
$\varphi \in \sigma $
by the absolute convergent integral
1.3.3 The Gan-Gross-Prasad conjecture for Bessel periods
Let
![]() $G^\flat =G_{m}\times G_{2n+1}$
. We can now state our first theorem about Bessel periods.
$G^\flat =G_{m}\times G_{2n+1}$
. We can now state our first theorem about Bessel periods.
Theorem 1.3.3.1. Let
![]() $\Pi $
be a discrete Hermitian Arthur parameter of
$\Pi $
be a discrete Hermitian Arthur parameter of
![]() $G^\flat $
. The following assertions are equivalent:
$G^\flat $
. The following assertions are equivalent:
-
1. The complete Rankin-Selberg L-function of
 $\Pi $
satisfies
$\Pi $
satisfies  $$ \begin{align*} L\left(\frac12,\Pi\right)\not=0; \end{align*} $$
$$ \begin{align*} L\left(\frac12,\Pi\right)\not=0; \end{align*} $$
-
2. There exist a Hermitian form
 $h\in \mathcal {H}_m$
and an automorphic cuspidal subrepresentation
$h\in \mathcal {H}_m$
and an automorphic cuspidal subrepresentation
 $\sigma $
of
$\sigma $
of
 $\mathcal {G}_h(\mathbb {A})$
such that its weak base to
$\mathcal {G}_h(\mathbb {A})$
such that its weak base to
 $G^\flat $
is
$G^\flat $
is
 $\Pi $
and the Bessel period does not vanish identically on
$\Pi $
and the Bessel period does not vanish identically on $$ \begin{align*} \varphi \mapsto \mathcal{P}_{\mathcal{B}_h,\psi}(\varphi) \end{align*} $$
$$ \begin{align*} \varphi \mapsto \mathcal{P}_{\mathcal{B}_h,\psi}(\varphi) \end{align*} $$
 $\sigma $
.
$\sigma $
.
Remarks 1.3.3.2.
-
• The case
 $r=0$
is just a particular case of Theorem 1.3.3.1.
$r=0$
is just a particular case of Theorem 1.3.3.1. -
• Assume
 $m=0$
. Then the L-function is the constant function of value
$m=0$
. Then the L-function is the constant function of value
 $1$
. So the assertion
$1$
. So the assertion
 $1$
is automatically satisfied. However, the group
$1$
is automatically satisfied. However, the group
 $\mathcal {G}_h$
is the quasi-split unitary group
$\mathcal {G}_h$
is the quasi-split unitary group
 $U_{2r+1}$
of rank
$U_{2r+1}$
of rank
 $2r+1$
. Moreover, the Bessel subgroup is a maximal unipotent subgroup of
$2r+1$
. Moreover, the Bessel subgroup is a maximal unipotent subgroup of
 $U_{2r+1}$
. Then the Bessel period is the so-called Fourier-Whittaker coefficient. The theorem is proved in the work of Ginzburg-Rallis-Soudry; see [Reference Ginzburg, Rallis and SoudryGRS11].
$U_{2r+1}$
. Then the Bessel period is the so-called Fourier-Whittaker coefficient. The theorem is proved in the work of Ginzburg-Rallis-Soudry; see [Reference Ginzburg, Rallis and SoudryGRS11]. -
• The direction
 $2\Rightarrow 1$
is also proved by D. Jiang-L. Zhang; see [Reference Jiang and ZhangJZ20, Theorem 5.7].
$2\Rightarrow 1$
is also proved by D. Jiang-L. Zhang; see [Reference Jiang and ZhangJZ20, Theorem 5.7].
1.3.4
In our approach, Theorem 1.3.3.1 is a consequence of Theorem 1.2.3.1. To explain this, we may and shall assume
![]() $r>0$
. We start with a discrete Hermitian Arthur parameter
$r>0$
. We start with a discrete Hermitian Arthur parameter
![]() $\Pi $
of
$\Pi $
of
![]() $G^\flat $
. It can be written
$G^\flat $
. It can be written
![]() $\Pi =\Pi _m\boxtimes \Pi _{n+1}$
, where
$\Pi =\Pi _m\boxtimes \Pi _{n+1}$
, where
![]() $\Pi _m$
and
$\Pi _m$
and
![]() $\Pi _{n+1}$
are respective discrete parameters of
$\Pi _{n+1}$
are respective discrete parameters of
![]() $G_m$
and
$G_m$
and
![]() $G_{n+1}$
. Let
$G_{n+1}$
. Let
![]() $\alpha _1,\ldots ,\alpha _r$
be r characters of
$\alpha _1,\ldots ,\alpha _r$
be r characters of
![]() $E^\times \backslash \mathbb {A}_E^1$
such that the characters
$E^\times \backslash \mathbb {A}_E^1$
such that the characters
![]() $\alpha _1,\ldots ,\alpha _r,\alpha _1^*,\ldots ,\alpha _r^*$
are two by two distinct (we recall that
$\alpha _1,\ldots ,\alpha _r,\alpha _1^*,\ldots ,\alpha _r^*$
are two by two distinct (we recall that
![]() $\alpha _i^*$
denotes the conjugate-dual of
$\alpha _i^*$
denotes the conjugate-dual of
![]() $\alpha _i$
). Let
$\alpha _i$
). Let
![]() $Q_n\subset G_n$
be a parabolic subgroup of Levi factor
$Q_n\subset G_n$
be a parabolic subgroup of Levi factor
![]() $G_1^{r}\times G_{m}\times G_1^r$
. Then
$G_1^{r}\times G_{m}\times G_1^r$
. Then
is a regular Hermitian Arthur parameter of
![]() $G=G_n\times G_{n+1}$
. Even if
$G=G_n\times G_{n+1}$
. Even if
![]() $\tilde \Pi $
is not discrete, it is at least H-regular in the sense of §1.2.1: this is an obvious consequence of remark 1.2.1.1 and the assumption on the characters
$\tilde \Pi $
is not discrete, it is at least H-regular in the sense of §1.2.1: this is an obvious consequence of remark 1.2.1.1 and the assumption on the characters
![]() $\alpha _i$
. We have an identification
$\alpha _i$
. We have an identification
![]() $\mathbb {C}^r \simeq \mathfrak {a}_{\tilde \Pi ,\mathbb {C}}^*$
such that if
$\mathbb {C}^r \simeq \mathfrak {a}_{\tilde \Pi ,\mathbb {C}}^*$
such that if
![]() $\lambda _s\in \mathfrak {a}_{\tilde \Pi ,\mathbb {C}}^*$
is the image of
$\lambda _s\in \mathfrak {a}_{\tilde \Pi ,\mathbb {C}}^*$
is the image of
![]() $(s,\ldots ,s)$
with
$(s,\ldots ,s)$
with
![]() $s\in \mathbb {C}$
, we have
$s\in \mathbb {C}$
, we have
For simplicity, we set
![]() $\tilde \Pi _{s}=\tilde \Pi _{\lambda _s}$
. By elementary properties of Rankin-Selberg L-function, it is clear that assertion 1 of 1.3.3.1 is equivalent to
$\tilde \Pi _{s}=\tilde \Pi _{\lambda _s}$
. By elementary properties of Rankin-Selberg L-function, it is clear that assertion 1 of 1.3.3.1 is equivalent to
![]() $1'$
:
$1'$
:
-
1′. There exists
 $s\in i\mathbb {R}$
such that
$s\in i\mathbb {R}$
such that
 $L(\frac 12,\tilde \Pi _{s})\not =0$
.
$L(\frac 12,\tilde \Pi _{s})\not =0$
.
Let
![]() $h\in \mathcal {H}_m$
and
$h\in \mathcal {H}_m$
and
![]() $\sigma $
be an automorphic cuspidal subrepresentation of
$\sigma $
be an automorphic cuspidal subrepresentation of
![]() $\mathcal {G}_h$
whose weak base to
$\mathcal {G}_h$
whose weak base to
![]() $G^\flat $
is
$G^\flat $
is
![]() $\Pi $
. Let
$\Pi $
. Let
![]() $P_n\subset U(\tilde h)$
be the parabolic subgroup stabilizing the isotropic flag
$P_n\subset U(\tilde h)$
be the parabolic subgroup stabilizing the isotropic flag
(Note that this flag is opposite position to (1.3.1.1).) and set
![]() $P=P_n\times U(h_{n+1})$
; a parabolic subgroup of
$P=P_n\times U(h_{n+1})$
; a parabolic subgroup of
![]() $U_{\tilde h}=U(\tilde h)\times U(h_{n+1})$
. Then
$U_{\tilde h}=U(\tilde h)\times U(h_{n+1})$
. Then
![]() $G_1^r \times \mathcal {G}_h$
is a Levi factor
$G_1^r \times \mathcal {G}_h$
is a Levi factor
![]() $M_P$
of P. Set
$M_P$
of P. Set
![]() $\tilde \sigma = \alpha _1\boxtimes \ldots \boxtimes \alpha _r \boxtimes \sigma $
. This is an automorphic cuspidal representation of
$\tilde \sigma = \alpha _1\boxtimes \ldots \boxtimes \alpha _r \boxtimes \sigma $
. This is an automorphic cuspidal representation of
![]() $M_P(\mathbb {A})$
, and
$M_P(\mathbb {A})$
, and
![]() $\tilde \Pi $
is the weak base change of
$\tilde \Pi $
is the weak base change of
![]() $(P,\sigma )$
. Let
$(P,\sigma )$
. Let
![]() $\varphi \in \mathcal {A}_{P,\tilde \sigma }(U_{\tilde h})$
. As in subsection 1.2, we denote by
$\varphi \in \mathcal {A}_{P,\tilde \sigma }(U_{\tilde h})$
. As in subsection 1.2, we denote by
![]() $U^{\prime }_{\tilde h}$
the ‘diagonal’ subgroup of
$U^{\prime }_{\tilde h}$
the ‘diagonal’ subgroup of
![]() $U_{\tilde h}$
. In the case at hand, the restriction of the Eisenstein series
$U_{\tilde h}$
. In the case at hand, the restriction of the Eisenstein series
![]() $E(\varphi ,\lambda )$
to
$E(\varphi ,\lambda )$
to
![]() $[U^{\prime }_{\tilde h}]$
is rapidly decreasing for any
$[U^{\prime }_{\tilde h}]$
is rapidly decreasing for any
![]() $\lambda \in \mathfrak {a}_{\tilde \Pi ,\mathbb {C}}$
, where the Eisenstein series is regular, and for any such
$\lambda \in \mathfrak {a}_{\tilde \Pi ,\mathbb {C}}$
, where the Eisenstein series is regular, and for any such
![]() $\lambda $
, we have
$\lambda $
, we have
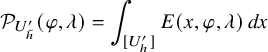 $$ \begin{align*} \mathcal{P}_{U^{\prime}_{\tilde h}}(\varphi,\lambda)=\int_{[U_h^{\prime}]} E(x,\varphi,\lambda)\,dx \end{align*} $$
$$ \begin{align*} \mathcal{P}_{U^{\prime}_{\tilde h}}(\varphi,\lambda)=\int_{[U_h^{\prime}]} E(x,\varphi,\lambda)\,dx \end{align*} $$
where the left-hand side is defined according to (1.2.2.1) and the right-hand side is absolutely convergent (see Proposition 3.5.3.1 assertion 3). Moreover, the map
![]() $s\mapsto \mathcal {P}_{U^{\prime }_{\tilde h}}(\varphi ,\lambda _s)$
is meromorphic and holomorphic on
$s\mapsto \mathcal {P}_{U^{\prime }_{\tilde h}}(\varphi ,\lambda _s)$
is meromorphic and holomorphic on
![]() $i\mathbb {R}$
. We prove in Proposition 8.8.2.1 that the map
$i\mathbb {R}$
. We prove in Proposition 8.8.2.1 that the map
![]() $\varphi \in \mathcal {A}_{\sigma }(\mathcal {G}_h)\mapsto \mathcal {P}_{\mathcal {B}_h,\psi }(\varphi )$
does not vanish identically if and only if there is
$\varphi \in \mathcal {A}_{\sigma }(\mathcal {G}_h)\mapsto \mathcal {P}_{\mathcal {B}_h,\psi }(\varphi )$
does not vanish identically if and only if there is
![]() $s\in \mathbb {C}$
such that the map
$s\in \mathbb {C}$
such that the map
![]() $\varphi \mapsto \mathcal {P}_{U^{\prime }_{\tilde h}}(\varphi ,\lambda _s)$
does not vanish identically on
$\varphi \mapsto \mathcal {P}_{U^{\prime }_{\tilde h}}(\varphi ,\lambda _s)$
does not vanish identically on
![]() $\mathcal {A}_{P,\tilde \sigma }(U_{\tilde h})$
. This last fact is eventually a consequence of some unfolding identity that roughly takes the following form:
$\mathcal {A}_{P,\tilde \sigma }(U_{\tilde h})$
. This last fact is eventually a consequence of some unfolding identity that roughly takes the following form:
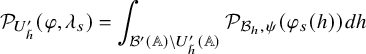 $$ \begin{align*}\mathcal{P}_{U^{\prime}_{\tilde h}}(\varphi,\lambda_s)=\int_{\mathcal{B}'(\mathbb{A})\backslash U^{\prime}_{\tilde h}(\mathbb{A})} \mathcal{P}_{\mathcal{B}_h,\psi}(\varphi_s(h))dh\end{align*} $$
$$ \begin{align*}\mathcal{P}_{U^{\prime}_{\tilde h}}(\varphi,\lambda_s)=\int_{\mathcal{B}'(\mathbb{A})\backslash U^{\prime}_{\tilde h}(\mathbb{A})} \mathcal{P}_{\mathcal{B}_h,\psi}(\varphi_s(h))dh\end{align*} $$
for
![]() $\varphi \in \mathcal {A}_{P,\tilde \sigma }(U_{\tilde h})$
, where
$\varphi \in \mathcal {A}_{P,\tilde \sigma }(U_{\tilde h})$
, where
![]() $\varphi _s$
stands for the corresponding element of
$\varphi _s$
stands for the corresponding element of
![]() $\operatorname {\mathrm {Ind}}_P^{U_{\tilde h}}(\tilde \sigma \otimes \lambda _s)$
(given through the choice of a suitable Iwasawa decomposition
$\operatorname {\mathrm {Ind}}_P^{U_{\tilde h}}(\tilde \sigma \otimes \lambda _s)$
(given through the choice of a suitable Iwasawa decomposition
![]() $U_{\tilde h}(\mathbb {A})=P(\mathbb {A})K$
that is implicit in the definition of the Eisenstein series
$U_{\tilde h}(\mathbb {A})=P(\mathbb {A})K$
that is implicit in the definition of the Eisenstein series
![]() $E(\varphi ,\lambda _s)$
) and
$E(\varphi ,\lambda _s)$
) and
![]() $\mathcal {B}'=U(h)\rtimes V$
with V the unipotent radical of the parabolic subgroup of
$\mathcal {B}'=U(h)\rtimes V$
with V the unipotent radical of the parabolic subgroup of
![]() $U(\tilde h)$
stabilizing the isotropic subspace
$U(\tilde h)$
stabilizing the isotropic subspace
![]() $\operatorname {\mathrm {vect}}(x_1,\ldots ,x_r)$
. It should be emphasized however that this identity does not make sense per se, as the Eulerian integral on the right-hand side is not absolutely convergent in general. More precisely, it has to be ‘interpreted in the sense of L-functions’, which requires some nontrivial unramified computations of local integrals involving Bessel functions. We refer the reader to Section 8 and, more specifically, 8.7 and 8.8 for details.
$\operatorname {\mathrm {vect}}(x_1,\ldots ,x_r)$
. It should be emphasized however that this identity does not make sense per se, as the Eulerian integral on the right-hand side is not absolutely convergent in general. More precisely, it has to be ‘interpreted in the sense of L-functions’, which requires some nontrivial unramified computations of local integrals involving Bessel functions. We refer the reader to Section 8 and, more specifically, 8.7 and 8.8 for details.
It follows that condition 2 of Theorem 1.3.3.1 holds for
![]() $h\in \mathcal {H}_m$
and
$h\in \mathcal {H}_m$
and
![]() $\sigma $
if and only if the following assertion holds:
$\sigma $
if and only if the following assertion holds:
-
2’. There exists
 $s\in i\mathbb {R}$
such that
$s\in i\mathbb {R}$
such that
 $\varphi \mapsto \mathcal {P}_{U^{\prime }_{\tilde h}}(\varphi ,\lambda _s)$
does not vanish identically on
$\varphi \mapsto \mathcal {P}_{U^{\prime }_{\tilde h}}(\varphi ,\lambda _s)$
does not vanish identically on
 $\mathcal {A}_{P,\sigma }(U_{\tilde h})$
.
$\mathcal {A}_{P,\sigma }(U_{\tilde h})$
.
It is then straightforward to deduce Theorem 1.3.3.1 from Theorem 1.2.3.1.
1.3.5 Local Bessel periods
From now on, we fix
![]() $h\in \mathcal {H}_m$
and a decomposition of the character
$h\in \mathcal {H}_m$
and a decomposition of the character
![]() $\psi =\otimes _{v\in V_F} \psi _v$
from which we get a decomposition
$\psi =\otimes _{v\in V_F} \psi _v$
from which we get a decomposition
![]() $\psi _{\mathcal {B}_h}= \otimes _{v\in V_F}\psi _{\mathcal {B}_h,v}$
, where
$\psi _{\mathcal {B}_h}= \otimes _{v\in V_F}\psi _{\mathcal {B}_h,v}$
, where
![]() $\psi _{\mathcal {B}_h,v}$
is a character of
$\psi _{\mathcal {B}_h,v}$
is a character of
![]() $\mathcal {B}_h(F_v)$
. Let v be a place of F. The integral
$\mathcal {B}_h(F_v)$
. Let v be a place of F. The integral
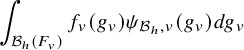 $$ \begin{align*} \int_{\mathcal{B}_h(F_v)} f_v(g_v) \psi_{\mathcal{B}_h,v}(g_v) dg_v \end{align*} $$
$$ \begin{align*} \int_{\mathcal{B}_h(F_v)} f_v(g_v) \psi_{\mathcal{B}_h,v}(g_v) dg_v \end{align*} $$
is well defined for a smooth and compactly supported function
![]() $f_v$
on
$f_v$
on
![]() $\mathcal {G}_h(F_v)$
and extends to a continuous linear form
$\mathcal {G}_h(F_v)$
and extends to a continuous linear form
![]() $ f_v\mapsto \mathcal {P}_{\mathcal {B}_h,\psi _v}(f_v)$
on the space of tempered functions; see subsection 8.4. It depends on the choice of a Haar measure on
$ f_v\mapsto \mathcal {P}_{\mathcal {B}_h,\psi _v}(f_v)$
on the space of tempered functions; see subsection 8.4. It depends on the choice of a Haar measure on
![]() $\mathcal {B}_h(F_v)$
.
$\mathcal {B}_h(F_v)$
.
Let
![]() $\sigma _v$
be a tempered irreducible representation of
$\sigma _v$
be a tempered irreducible representation of
![]() $\mathcal {G}_h(F_v)$
equipped with an invariant inner product
$\mathcal {G}_h(F_v)$
equipped with an invariant inner product
![]() $(\cdot ,\cdot )_v$
. Let
$(\cdot ,\cdot )_v$
. Let
![]() $\varphi _v$
and
$\varphi _v$
and
![]() $\varphi _v^{\prime }$
be vectors of
$\varphi _v^{\prime }$
be vectors of
![]() $\sigma _v$
. The associated matrix coefficient defined by
$\sigma _v$
. The associated matrix coefficient defined by
![]() $f_{ \varphi _v,\varphi _v^{\prime } }(g)= (\sigma _v(g) \varphi _v,\varphi ^{\prime }_v)_v$
for all
$f_{ \varphi _v,\varphi _v^{\prime } }(g)= (\sigma _v(g) \varphi _v,\varphi ^{\prime }_v)_v$
for all
![]() $g \in \mathcal {G}_h(F_v) $
belongs to this space and we set
$g \in \mathcal {G}_h(F_v) $
belongs to this space and we set
1.3.6 The Ichino-Ikeda conjecture for Bessel periods
Let
![]() $\sigma $
be a tempered automorphic cuspidal subrepresentation
$\sigma $
be a tempered automorphic cuspidal subrepresentation
![]() $\sigma $
of
$\sigma $
of
![]() $\mathcal {G}_h(\mathbb {A})$
. Tempered means that we have a decomposition
$\mathcal {G}_h(\mathbb {A})$
. Tempered means that we have a decomposition
![]() $\sigma =\otimes _{v\in V_F}' \sigma _v$
with
$\sigma =\otimes _{v\in V_F}' \sigma _v$
with
![]() $\sigma _v$
tempered for all v. We also assume that the weak base change of
$\sigma _v$
tempered for all v. We also assume that the weak base change of
![]() $\sigma $
to
$\sigma $
to
![]() $G^\flat $
is a discrete Hermitian parameter
$G^\flat $
is a discrete Hermitian parameter
![]() $\Pi $
. As in §1.2.4, we define the ratio of L-functions
$\Pi $
. As in §1.2.4, we define the ratio of L-functions
![]() $\mathcal {L}(s,\sigma )$
and its local counterparts
$\mathcal {L}(s,\sigma )$
and its local counterparts
![]() $\mathcal {L}(s,\sigma _v)$
for
$\mathcal {L}(s,\sigma _v)$
for
![]() $s\in \mathbb {C}$
. Explicitly, we have
$s\in \mathbb {C}$
. Explicitly, we have
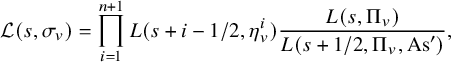 $$ \begin{align*} \mathcal{L}(s,\sigma_v)=\prod_{i=1}^{n+1}L(s+i-1/2,\eta^i_v)\frac{L(s,\Pi_v)}{L(s+1/2,\Pi_v,\mathrm{As}')}, \end{align*} $$
$$ \begin{align*} \mathcal{L}(s,\sigma_v)=\prod_{i=1}^{n+1}L(s+i-1/2,\eta^i_v)\frac{L(s,\Pi_v)}{L(s+1/2,\Pi_v,\mathrm{As}')}, \end{align*} $$
where
![]() $\mathrm {As}'=\mathrm {As}^{(-1)^m}\otimes \mathrm {As}^{(-1)^{n+1}}$
and
$\mathrm {As}'=\mathrm {As}^{(-1)^m}\otimes \mathrm {As}^{(-1)^{n+1}}$
and
![]() $\mathcal {L}(s,\sigma )$
is the product of the local factors in some half-plane. We use the local factor to define the normalized local Bessel period
$\mathcal {L}(s,\sigma )$
is the product of the local factors in some half-plane. We use the local factor to define the normalized local Bessel period
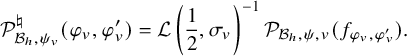 $$ \begin{align*} \mathcal{P}_{\mathcal{B}_h,\psi_v}^\natural( \varphi_v,\varphi^{\prime}_v)= \mathcal{L}\left(\frac12 ,\sigma_v\right)^{-1}\mathcal{P}_{\mathcal{B}_h,\psi,v}( f_{ \varphi_v,\varphi_v^{\prime} }). \end{align*} $$
$$ \begin{align*} \mathcal{P}_{\mathcal{B}_h,\psi_v}^\natural( \varphi_v,\varphi^{\prime}_v)= \mathcal{L}\left(\frac12 ,\sigma_v\right)^{-1}\mathcal{P}_{\mathcal{B}_h,\psi,v}( f_{ \varphi_v,\varphi_v^{\prime} }). \end{align*} $$
We assume that the product of local measures on
![]() $\mathcal {B}_h(F_v)$
gives the Tamagawa measure on
$\mathcal {B}_h(F_v)$
gives the Tamagawa measure on
![]() $\mathcal {B}_h(\mathbb {A})$
. On
$\mathcal {B}_h(\mathbb {A})$
. On
![]() $\sigma $
, we use the Petersson inner product
$\sigma $
, we use the Petersson inner product
![]() $(\cdot , \cdot )_{\operatorname {\mathrm {Pet}}}$
normalized by the Tamagawa measure on
$(\cdot , \cdot )_{\operatorname {\mathrm {Pet}}}$
normalized by the Tamagawa measure on
![]() $\mathcal {G}_h(\mathbb {A})$
.
$\mathcal {G}_h(\mathbb {A})$
.
Theorem 1.3.6.1. Let
![]() $\sigma $
and
$\sigma $
and
![]() $\Pi $
as above. For every nonzero factorizable vector
$\Pi $
as above. For every nonzero factorizable vector
![]() $\varphi =\otimes _v^{\prime } \varphi _v\in \sigma $
, we have
$\varphi =\otimes _v^{\prime } \varphi _v\in \sigma $
, we have
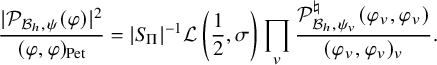 $$ \begin{align} \frac{\lvert \mathcal{P}_{\mathcal{B}_h,\psi}(\varphi)\rvert^2}{(\varphi, \varphi)_{\operatorname{\mathrm{Pet}}}}=\lvert S_\Pi\rvert^{-1} \mathcal{L}\left(\frac12,\sigma\right)\prod_v \frac{\mathcal{P}_{\mathcal{B}_h,\psi_v}^\natural(\varphi_v,\varphi_v)}{(\varphi_v,\varphi_v)_v}. \end{align} $$
$$ \begin{align} \frac{\lvert \mathcal{P}_{\mathcal{B}_h,\psi}(\varphi)\rvert^2}{(\varphi, \varphi)_{\operatorname{\mathrm{Pet}}}}=\lvert S_\Pi\rvert^{-1} \mathcal{L}\left(\frac12,\sigma\right)\prod_v \frac{\mathcal{P}_{\mathcal{B}_h,\psi_v}^\natural(\varphi_v,\varphi_v)}{(\varphi_v,\varphi_v)_v}. \end{align} $$
Remarks 1.3.6.2.
-
1. In the right-hand side, almost all factors are equal to
 $1$
; see [Reference LiuLiu16, Theorem 2.2].
$1$
; see [Reference LiuLiu16, Theorem 2.2]. -
2. The statement has been conjectured by Y. Liu in a more general context; see [Reference LiuLiu16, conjecture 2.5].
-
3. For
 $m=0$
, the group
$m=0$
, the group
 $\mathcal {G}_h$
is the quasi-split unitary group
$\mathcal {G}_h$
is the quasi-split unitary group
 $U_{2r+1}$
of rank
$U_{2r+1}$
of rank
 $2r+1$
. The theorem has been conjectured by Lapid and Mao, [Reference Lapid and MaoLM15, conjecture 1.1].
$2r+1$
. The theorem has been conjectured by Lapid and Mao, [Reference Lapid and MaoLM15, conjecture 1.1]. -
4. The proof we give is along the same lines as for Theorem 1.3.3.1; namely, it is eventually deduce it from Theorem 1.2.4.1 in a similar fashion.
1.4 On some spectral contributions of the Jacquet-Rallis trace formulas
1.4.1
In this subsection, we explain some new ingredients that play a role in the proof of Theorems 1.2.3.1 and 1.2.4.1. As many other contributions on the subject (among them, see [Reference ZhangZha14b], [Reference ZhangZha14a], [Reference XueXue19], [Reference Beuzart-PlessisBeu21], [Reference Beuzart-PlessisBP21], [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21], [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22]), we follow the strategy of the seminal paper [Reference Jacquet and RallisJR11] of Jacquet and Rallis. More precisely, besides the local harmonic analysis performed in the mentioned papers, our work is based on the geometric comparison, fully established in [Reference Chaudouard and ZydorCZ21], of the relative trace formulas constructed in [Reference ZydorZyd20] of the unitary groups
![]() $U_h$
for
$U_h$
for
![]() $h\in \mathcal {H}_n$
and the corresponding group G. However, to be able to exploit this comparison, we need to obtain more tractable expressions for the spectral contributions we are interested in.
$h\in \mathcal {H}_n$
and the corresponding group G. However, to be able to exploit this comparison, we need to obtain more tractable expressions for the spectral contributions we are interested in.
1.4.2
Let us first explain our result in the unitary case namely for the group
![]() $U=U_h$
and its subgroup
$U=U_h$
and its subgroup
![]() $U'=U_h^{\prime }$
. Let
$U'=U_h^{\prime }$
. Let
![]() $\mathfrak {X}(U)$
be the set of cuspidal data of U. According to the work of Zydor (see [Reference ZydorZyd20, section 4]), the contribution of
$\mathfrak {X}(U)$
be the set of cuspidal data of U. According to the work of Zydor (see [Reference ZydorZyd20, section 4]), the contribution of
![]() $\chi \in \mathfrak {X}(U)$
to the relative trace formula for the group U is built upon the absolutely convergent integral
$\chi \in \mathfrak {X}(U)$
to the relative trace formula for the group U is built upon the absolutely convergent integral
Here,
![]() $K^T_{f,\chi }$
is a suitably modified version à la Arthur of the
$K^T_{f,\chi }$
is a suitably modified version à la Arthur of the
![]() $\chi $
-part
$\chi $
-part
![]() $K_{f,\chi }$
of the automorphic kernel
$K_{f,\chi }$
of the automorphic kernel
![]() $K_f(x,y)=\sum _{\gamma \in U(F)}f(x^{-1}\gamma y)$
associated to a Schwartz function f on
$K_f(x,y)=\sum _{\gamma \in U(F)}f(x^{-1}\gamma y)$
associated to a Schwartz function f on
![]() $U(\mathbb {A})$
; see (3.2.2.1) below for the precise definition. It depends on a truncation paramerer T. It turns out that the integral above is an exponential-polynomial function in T whose purely polynomial part is constant and gives by definition the
$U(\mathbb {A})$
; see (3.2.2.1) below for the precise definition. It depends on a truncation paramerer T. It turns out that the integral above is an exponential-polynomial function in T whose purely polynomial part is constant and gives by definition the
![]() $\chi $
-contribution denoted by
$\chi $
-contribution denoted by
![]() $J^U_\chi (f)$
of the relative trace formula; see Theorem 3.2.3.1 for this slight extension of Zydor’s work to Schwartz test functions. The problem, however, is to get an expression for
$J^U_\chi (f)$
of the relative trace formula; see Theorem 3.2.3.1 for this slight extension of Zydor’s work to Schwartz test functions. The problem, however, is to get an expression for
![]() $J_\chi (f)$
that reflects the Langlands spectral decomposition of
$J_\chi (f)$
that reflects the Langlands spectral decomposition of
![]() $K_{f,\chi }$
and that is related to the periods (1.2.2.1) we are interested in. The starting point is the following new independent characterization of
$K_{f,\chi }$
and that is related to the periods (1.2.2.1) we are interested in. The starting point is the following new independent characterization of
![]() $J^U_\chi (f)$
: the integral
$J^U_\chi (f)$
: the integral
is absolutely convergent and is asymptotic to an polynomial exponential in the variable T whose purely polynomial term is constant and equal to
![]() $J_\chi ^U(f)$
; see Corollary 3.3.5.2. Here,
$J_\chi ^U(f)$
; see Corollary 3.3.5.2. Here,
![]() $K_{f,\chi } \Lambda ^T_u$
means that we have applied the Ichino-Yamana truncation operator
$K_{f,\chi } \Lambda ^T_u$
means that we have applied the Ichino-Yamana truncation operator
![]() $\Lambda ^T_u$
already mentioned in §1.2.2 to the right variable of the kernel
$\Lambda ^T_u$
already mentioned in §1.2.2 to the right variable of the kernel
![]() $K_{f,\chi }$
. Let us now assume that the cuspidal datum
$K_{f,\chi }$
. Let us now assume that the cuspidal datum
![]() $\chi $
is
$\chi $
is
![]() $(U,U')$
-regular in the sense of §3.5.2. Then the expression (1.4.2.1) does not depend on T and thus is equal to
$(U,U')$
-regular in the sense of §3.5.2. Then the expression (1.4.2.1) does not depend on T and thus is equal to
![]() $J_\chi ^U(f)$
. To state our result, we fix a representative
$J_\chi ^U(f)$
. To state our result, we fix a representative
![]() $(M_P,\sigma )$
where
$(M_P,\sigma )$
where
![]() $M_P$
is a Levi factor of a parabolic subgroup
$M_P$
is a Levi factor of a parabolic subgroup
![]() $P=M_PN_P$
of U and
$P=M_PN_P$
of U and
![]() $\sigma $
is a cuspidal automorphic representation of
$\sigma $
is a cuspidal automorphic representation of
![]() $M_P(\mathbb {A})$
. Let
$M_P(\mathbb {A})$
. Let
![]() $\mathcal {A}_{P,\sigma ,\operatorname {\mathrm {cusp}}}(U_h)$
be the space of automorphic forms on the quotient
$\mathcal {A}_{P,\sigma ,\operatorname {\mathrm {cusp}}}(U_h)$
be the space of automorphic forms on the quotient
![]() $A_P^\infty M_P(F) N_P(\mathbb {A})\backslash U(\mathbb {A})$
such that for all
$A_P^\infty M_P(F) N_P(\mathbb {A})\backslash U(\mathbb {A})$
such that for all
![]() $g\in U(\mathbb {A}),$
$g\in U(\mathbb {A}),$
belongs to the
![]() $\sigma $
-isotypic component of the space of cuspidal automorphic forms on the quotient
$\sigma $
-isotypic component of the space of cuspidal automorphic forms on the quotient
![]() $A_P^\infty M_P(F) \backslash M_P(\mathbb {A})$
. Working throughout Langlands spectral decomposition of
$A_P^\infty M_P(F) \backslash M_P(\mathbb {A})$
. Working throughout Langlands spectral decomposition of
![]() $K_{f,\chi }$
, we get (see Theorem 3.5.7.1):
$K_{f,\chi }$
, we get (see Theorem 3.5.7.1):
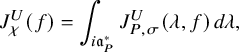 $$ \begin{align} J^U_\chi(f)= \int_{i\mathfrak{a}_P^*} J_{P,\sigma}^{U}(\lambda, f)\,d\lambda, \end{align} $$
$$ \begin{align} J^U_\chi(f)= \int_{i\mathfrak{a}_P^*} J_{P,\sigma}^{U}(\lambda, f)\,d\lambda, \end{align} $$
where the right-hand side is the absolutely convergent integral of the relative character defined by
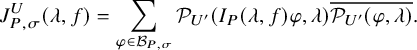 $$ \begin{align*} J_{P,\sigma}^{U}(\lambda, f)=\sum_{\varphi\in \mathcal{B}_{P,\sigma}} \mathcal{P}_{U'}(I_P(\lambda,f)\varphi,\lambda)\overline{ \mathcal{P}_{U'}(\varphi,\lambda) }. \end{align*} $$
$$ \begin{align*} J_{P,\sigma}^{U}(\lambda, f)=\sum_{\varphi\in \mathcal{B}_{P,\sigma}} \mathcal{P}_{U'}(I_P(\lambda,f)\varphi,\lambda)\overline{ \mathcal{P}_{U'}(\varphi,\lambda) }. \end{align*} $$
Here, the periods
![]() $\mathcal {P}_{U'}(\cdot ,\lambda )$
are those defined in (1.2.2.1), and
$\mathcal {P}_{U'}(\cdot ,\lambda )$
are those defined in (1.2.2.1), and
![]() $I_P(\lambda ,f)$
denotes the induced action of f twisted by
$I_P(\lambda ,f)$
denotes the induced action of f twisted by
![]() $\lambda $
. The sum is over some orthonormal basis
$\lambda $
. The sum is over some orthonormal basis
![]() $\mathcal {B}_{P,\sigma }$
of
$\mathcal {B}_{P,\sigma }$
of
![]() $\mathcal {A}_{P,\sigma ,\operatorname {\mathrm {cusp}}}(U)$
; see §3.5.5 for the Petersson inner product.
$\mathcal {A}_{P,\sigma ,\operatorname {\mathrm {cusp}}}(U)$
; see §3.5.5 for the Petersson inner product.
1.4.3
Let us turn to the linear case – namely,
![]() $G=G_n\times G_{n+1}$
. In this case, we have to consider two subgroups – namely,
$G=G_n\times G_{n+1}$
. In this case, we have to consider two subgroups – namely,
![]() $H=G_n$
diagonally embedded in G and
$H=G_n$
diagonally embedded in G and
![]() $G'=G_n^{\prime }\times G_{n+1}'$
, where
$G'=G_n^{\prime }\times G_{n+1}'$
, where
![]() $G^{\prime }_n=\mathrm {GL}(n,F)$
is naturally embedded in
$G^{\prime }_n=\mathrm {GL}(n,F)$
is naturally embedded in
![]() $G_n=\mathrm {GL}(n,E)$
. Let
$G_n=\mathrm {GL}(n,E)$
. Let
![]() $\chi $
be a cuspidal datum of G and let f be a Schwartz function on
$\chi $
be a cuspidal datum of G and let f be a Schwartz function on
![]() $G(\mathbb {A})$
. As before, we denote by
$G(\mathbb {A})$
. As before, we denote by
![]() $K_{f,\chi }$
the
$K_{f,\chi }$
the
![]() $\chi $
-part of the automorphic kernel. According to [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Theorem 1.2.4.1], the contribution
$\chi $
-part of the automorphic kernel. According to [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Theorem 1.2.4.1], the contribution
![]() $I_\chi (f)$
, as defined by Zydor in [Reference ZydorZyd20], is also the constant term of the polynomial exponential (in the variable T) which is asymptotic to the absolutely convergent integral
$I_\chi (f)$
, as defined by Zydor in [Reference ZydorZyd20], is also the constant term of the polynomial exponential (in the variable T) which is asymptotic to the absolutely convergent integral
Here,
![]() $ \eta _{G'}$
is the quadratic character defined in §4.1.1 and
$ \eta _{G'}$
is the quadratic character defined in §4.1.1 and
![]() $\Lambda _r^T$
is a truncation operator (in the parameter T) introduced by Ichino-Yamana and well-suited for the study of Rankin-Selberg period. Assume that
$\Lambda _r^T$
is a truncation operator (in the parameter T) introduced by Ichino-Yamana and well-suited for the study of Rankin-Selberg period. Assume that
![]() $\chi $
is represented by a pair
$\chi $
is represented by a pair
![]() $(M,\pi )$
, where M is the Levi factor of a parabolic subgroup P of G. We assume also that
$(M,\pi )$
, where M is the Levi factor of a parabolic subgroup P of G. We assume also that
![]() $\chi $
is
$\chi $
is
![]() $(G,H)$
-regular and Hermitian in the sense of §4.1.3. Then we have (see Theorem 4.1.8.1)
$(G,H)$
-regular and Hermitian in the sense of §4.1.3. Then we have (see Theorem 4.1.8.1)
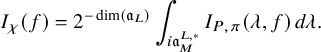 $$ \begin{align*} I_\chi(f)=2^{-\dim(\mathfrak{a}_L)}\int_{i\mathfrak{a}_M^{L,*}}I_{P,\pi}(\lambda,f)\,d\lambda. \end{align*} $$
$$ \begin{align*} I_\chi(f)=2^{-\dim(\mathfrak{a}_L)}\int_{i\mathfrak{a}_M^{L,*}}I_{P,\pi}(\lambda,f)\,d\lambda. \end{align*} $$
Here, L is a Levi subgroup of G containing M and determined by
![]() $\pi $
(see §4.1.4). For
$\pi $
(see §4.1.4). For
![]() $\lambda \in i\mathfrak {a}_M^{L,*}$
, the relative character
$\lambda \in i\mathfrak {a}_M^{L,*}$
, the relative character
![]() $I_{P,\pi }(\lambda ,f)$
is given by one of the two expressions
$I_{P,\pi }(\lambda ,f)$
is given by one of the two expressions
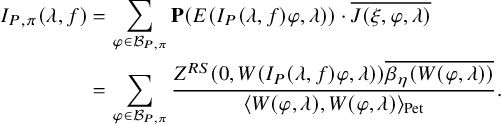 $$ \begin{align*} I_{P,\pi}(\lambda,f)&=\sum_{\varphi\in \mathcal{B}_{P,\pi}} \mathbf{P}(E(I_P(\lambda,f)\varphi,\lambda))\cdot \overline{J(\xi, \varphi,\lambda)}\\ &=\sum_{\varphi\in \mathcal{B}_{P,\pi}} \frac{Z^{RS}(0, W(I_P(\lambda,f)\varphi,\lambda)) \overline{\beta_\eta(W(\varphi,\lambda))} }{ \langle W(\varphi,\lambda),W(\varphi,\lambda)\rangle_{\operatorname{\mathrm{Pet}}}}. \end{align*} $$
$$ \begin{align*} I_{P,\pi}(\lambda,f)&=\sum_{\varphi\in \mathcal{B}_{P,\pi}} \mathbf{P}(E(I_P(\lambda,f)\varphi,\lambda))\cdot \overline{J(\xi, \varphi,\lambda)}\\ &=\sum_{\varphi\in \mathcal{B}_{P,\pi}} \frac{Z^{RS}(0, W(I_P(\lambda,f)\varphi,\lambda)) \overline{\beta_\eta(W(\varphi,\lambda))} }{ \langle W(\varphi,\lambda),W(\varphi,\lambda)\rangle_{\operatorname{\mathrm{Pet}}}}. \end{align*} $$
The sums are over some orthonormal bases
![]() $\mathcal {B}_{P,\pi }$
for the Petersson inner product of the space
$\mathcal {B}_{P,\pi }$
for the Petersson inner product of the space
![]() $\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(G)$
(defined as above). The first expression is built upon
$\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(G)$
(defined as above). The first expression is built upon
![]() $\mathbf {P}(E(\varphi ,\lambda ))$
and
$\mathbf {P}(E(\varphi ,\lambda ))$
and
![]() $J(\xi , \varphi ,\lambda )$
. The former is the regularized Rankin-Selberg period à la Ichino-Yamana (see [Reference Ichino and YamanaIY15]) of the Eisenstein series associated to the pair
$J(\xi , \varphi ,\lambda )$
. The former is the regularized Rankin-Selberg period à la Ichino-Yamana (see [Reference Ichino and YamanaIY15]) of the Eisenstein series associated to the pair
![]() $(P,\pi )$
. The latter is the intertwining (Flicker-Rallis) period of Jacquet-Lapid-Rogawski [Reference Jacquet, Lapid and RogawskiJLR99]. The second expression uses Whittaker functionals
$(P,\pi )$
. The latter is the intertwining (Flicker-Rallis) period of Jacquet-Lapid-Rogawski [Reference Jacquet, Lapid and RogawskiJLR99]. The second expression uses Whittaker functionals
![]() $W(\varphi ,\lambda )$
associated to Eisenstein series and linear forms on the Whittaker models of
$W(\varphi ,\lambda )$
associated to Eisenstein series and linear forms on the Whittaker models of
![]() $\operatorname {\mathrm {Ind}}_{P(\mathbb {A})}^{G(\mathbb {A})}(\pi \otimes \lambda )$
equipped with the Petersson product
$\operatorname {\mathrm {Ind}}_{P(\mathbb {A})}^{G(\mathbb {A})}(\pi \otimes \lambda )$
equipped with the Petersson product
![]() $\langle \cdot , \cdot \rangle _{\operatorname {\mathrm {Pet}}}$
. The linear forms
$\langle \cdot , \cdot \rangle _{\operatorname {\mathrm {Pet}}}$
. The linear forms
![]() $Z^{RS}$
and
$Z^{RS}$
and
![]() $\beta _\eta $
are counterparts of the period and the intertwining period. In the Rankin-Selberg case, the link is recalled in Proposition 4.2.5.1: it is based on [Reference Ichino and YamanaIY15] which generalizes the classical Rankin-Selberg theory. In the Flicker-Rallis case, the precise relation is given in Proposition 4.2.7.1, which generalizes the work of Flicker [Reference FlickerFli88]. Besides some reductions based on [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, section 9], the bulk of the proof of proposition is the object of Section 5. Note also that we prove in Section 5 a result that is of independent interest: we express a basic intertwining period of Jacquet-Lapid-Rogawski in terms of an integral of a Whittaker functional; see Theorem 5.5.1.1. The second expression of the relative character is better suited for the proof of Theorem 1.2.4.1. In Section 6, we give an alternative proof of this spectral expansion of
$\beta _\eta $
are counterparts of the period and the intertwining period. In the Rankin-Selberg case, the link is recalled in Proposition 4.2.5.1: it is based on [Reference Ichino and YamanaIY15] which generalizes the classical Rankin-Selberg theory. In the Flicker-Rallis case, the precise relation is given in Proposition 4.2.7.1, which generalizes the work of Flicker [Reference FlickerFli88]. Besides some reductions based on [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, section 9], the bulk of the proof of proposition is the object of Section 5. Note also that we prove in Section 5 a result that is of independent interest: we express a basic intertwining period of Jacquet-Lapid-Rogawski in terms of an integral of a Whittaker functional; see Theorem 5.5.1.1. The second expression of the relative character is better suited for the proof of Theorem 1.2.4.1. In Section 6, we give an alternative proof of this spectral expansion of
![]() $I_\chi (f)$
, for
$I_\chi (f)$
, for
![]() $(G,H)$
-regular
$(G,H)$
-regular
![]() $\chi $
, that is based on the theory of Zeta integrals.
$\chi $
, that is based on the theory of Zeta integrals.
Finally, let us remark that if
![]() $\chi $
is a
$\chi $
is a
![]() $(U,U')$
-regular cuspidal datum of U attached to a cuspidal representation of
$(U,U')$
-regular cuspidal datum of U attached to a cuspidal representation of
![]() $M_{P_n}(\mathbb {A})\times U(h\oplus h_0)(\mathbb {A})$
for some parabolic subgroup
$M_{P_n}(\mathbb {A})\times U(h\oplus h_0)(\mathbb {A})$
for some parabolic subgroup
![]() $P_n$
of
$P_n$
of
![]() $U(h)$
, then the modified kernel
$U(h)$
, then the modified kernel
![]() $K^T_{f,\chi }(x,y) $
coincides with the usual
$K^T_{f,\chi }(x,y) $
coincides with the usual
![]() $\chi $
-part of the kernel. Then one can directly get the expression (1.4.2.2) in which the
$\chi $
-part of the kernel. Then one can directly get the expression (1.4.2.2) in which the
![]() $U'$
-periods are absolutely convergent. This includes, in particular, the Eisenstein series needed for the deduction of the Gan-Gross-Prasad and Ichino-Ikeda conjectures for general Bessel periods, as outlined in subsection 1.3.
$U'$
-periods are absolutely convergent. This includes, in particular, the Eisenstein series needed for the deduction of the Gan-Gross-Prasad and Ichino-Ikeda conjectures for general Bessel periods, as outlined in subsection 1.3.
1.5 Organization of the paper
1.5.1
The reader will find the main notations and some prelimary results in Section 2. The Section 3 is devoted to the study of some spectral contributions of the Jacquet-Rallis trace formula for unitary groups. The main general result is Theorem 3.2.3.1, which gives a more tractable expression to compute spectral contributions. The proof of Theorem 3.2.3.1 is the bulk of subsections 3.3 and 3.4. Then in subsection 3.5, the spectral contribution for some cuspidal data are explicitly given in terms of relative characters (see Theorem 3.5.7.1). In Section 4, we turn to the Jacquet-Rallis trace formula for general linear groups. The main result is Theorem 4.1.8.1, which expresses the spectral contribution for some cuspidal data in terms of relative characters. In subsection 4.2, we show that these relative characters can expressed in terms of Whittaker functionals; see Theorem 4.2.8.1. The main result of Section 5 is Theorem 5.5.1.1, which relates some basic intertwining period of Jacquet-Lapid-Rogawski to some integral of a Whittaker functional: it is used in the proof of Theorem 4.2.8.1, but it is also of independent interest. Its proof occupies the whole part of Section 5. As explained above, we provide in Section 6 an alternative proof for the description of the spectral contributions to the Jacquet-Rallis trace formula for general linear groups that can be obtained by combining Theorem 4.1.8.1 with Theorem 4.2.8.1. In Section 7, we explain the proof of Theorems 1.2.3.1 and 1.2.4.1 based on the comparison of the Jacquet-Rallis trace formulas and the results obtained before. The aim of the final Section 8 is to establish the reduction of Theorems 1.3.3.1 and 1.3.6.1 to special cases of Theorems 1.2.3.1 and 1.2.4.1, respectively. Its most technical part is in subsection 8.7, where necessary unramified computation is performed. Finally, Appendix A presents a probably well-known extension of Weyl’s character formula to non-connected groups that is necessary for the unramified computation.
2 Preliminaries
2.1 Algebraic and adelic groups
2.1.1
We shall try to follow the usual notations of Arthur and the main notations of the previous article [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22]. For the reader’s convenience, we briefly recall our choices.
2.1.2
We denote by F a number field,
![]() $V_F$
(resp.
$V_F$
(resp.
![]() $V_{F,\infty }$
) the set of its places (resp. Archimedean places) and
$V_{F,\infty }$
) the set of its places (resp. Archimedean places) and
![]() $\mathbb {A}$
its ring of adèles. For
$\mathbb {A}$
its ring of adèles. For
![]() $v\in V_F$
, let
$v\in V_F$
, let
![]() $F_v$
be its completion at v. For any finite subset
$F_v$
be its completion at v. For any finite subset
![]() $S\subset V_F$
, we set
$S\subset V_F$
, we set
![]() $F_S=\otimes _{v\in S}F_v$
and
$F_S=\otimes _{v\in S}F_v$
and
![]() $F_\infty =F_{V_{F,\infty }}$
. We denote by
$F_\infty =F_{V_{F,\infty }}$
. We denote by
![]() $ | \cdot | $
the morphism
$ | \cdot | $
the morphism
![]() $ \mathbb {A}^\times \to \mathbb {R}_+^\times $
given by the product of normalized absolute values
$ \mathbb {A}^\times \to \mathbb {R}_+^\times $
given by the product of normalized absolute values
![]() $|\cdot |_v$
on each
$|\cdot |_v$
on each
![]() $ F_v $
.
$ F_v $
.
2.1.3
Let G be a reductive group defined over F. All the subgroups of G we consider are assumed to be defined over F. We fix
![]() $P_0\subset G$
a minimal parabolic subgroup and
$P_0\subset G$
a minimal parabolic subgroup and
![]() $M_0$
a Levi factor of
$M_0$
a Levi factor of
![]() $P_0$
. A parabolic subgroup of G which contains
$P_0$
. A parabolic subgroup of G which contains
![]() $P_0$
, resp.
$P_0$
, resp.
![]() $M_0$
, is said to be standard, resp. semi-standard. Let P be a semi-standard parabolic subgroup of G. It has a Levi decomposition
$M_0$
, is said to be standard, resp. semi-standard. Let P be a semi-standard parabolic subgroup of G. It has a Levi decomposition
![]() $P=M_PN_P$
such that
$P=M_PN_P$
such that
![]() $M_P$
is a semi-standard Levi factor (that is,
$M_P$
is a semi-standard Levi factor (that is,
![]() $M_0\subset M_P$
) and
$M_0\subset M_P$
) and
![]() $N_P$
is the unipotent radical of P. Such a group
$N_P$
is the unipotent radical of P. Such a group
![]() $M_P$
is called a semi-standard Levi subgroup of G. It is said to be standard if, moreover, P is standard. Let
$M_P$
is called a semi-standard Levi subgroup of G. It is said to be standard if, moreover, P is standard. Let
![]() $X^*(P)$
be the group of rational characters of P defined over F. Attached to P are real vector spaces
$X^*(P)$
be the group of rational characters of P defined over F. Attached to P are real vector spaces
![]() $\mathfrak {a}_P^*=X^*(P)\otimes _{\mathbb {Z}}\mathbb {R}$
and
$\mathfrak {a}_P^*=X^*(P)\otimes _{\mathbb {Z}}\mathbb {R}$
and
![]() $\mathfrak {a}_P=\operatorname {\mathrm {Hom}}_{\mathbb {Z}}(X^*(P),\mathbb {R})$
in canonical duality:
$\mathfrak {a}_P=\operatorname {\mathrm {Hom}}_{\mathbb {Z}}(X^*(P),\mathbb {R})$
in canonical duality:
If
![]() $P\subset Q\subset G$
, we have natural maps
$P\subset Q\subset G$
, we have natural maps
![]() $\mathfrak {a}_Q^*\to \mathfrak {a}_P^*$
and
$\mathfrak {a}_Q^*\to \mathfrak {a}_P^*$
and
![]() $\mathfrak {a}_P\to \mathfrak {a}_Q$
. The kernel of the second one is denoted by
$\mathfrak {a}_P\to \mathfrak {a}_Q$
. The kernel of the second one is denoted by
![]() $\mathfrak {a}_P^Q$
. We have natural decomposition
$\mathfrak {a}_P^Q$
. We have natural decomposition
![]() $\mathfrak {a}_P=\mathfrak {a}_P^Q\oplus \mathfrak {a}_Q$
and dually
$\mathfrak {a}_P=\mathfrak {a}_P^Q\oplus \mathfrak {a}_Q$
and dually
![]() $\mathfrak {a}_P^*=\mathfrak {a}_P^{Q,*}\oplus \mathfrak {a}_Q^*$
. We put a subscript
$\mathfrak {a}_P^*=\mathfrak {a}_P^{Q,*}\oplus \mathfrak {a}_Q^*$
. We put a subscript
![]() $\mathbb {C}$
to denote the extension of scalars to
$\mathbb {C}$
to denote the extension of scalars to
![]() $\mathbb {C}$
. Then one has a decomposition
$\mathbb {C}$
. Then one has a decomposition
where
![]() $i^2=-1$
. We shall denote by
$i^2=-1$
. We shall denote by
![]() $\Re $
and
$\Re $
and
![]() $\Im $
the associated projections. The complex conjugate is then defined by
$\Im $
the associated projections. The complex conjugate is then defined by
![]() $\bar \lambda =\Re (\lambda )-i\Im (\lambda )$
. Note that the spaces
$\bar \lambda =\Re (\lambda )-i\Im (\lambda )$
. Note that the spaces
![]() $\mathfrak {a}_P^Q$
,
$\mathfrak {a}_P^Q$
,
![]() $\mathfrak {a}_P^{Q,*}$
depend only on the Levi factors
$\mathfrak {a}_P^{Q,*}$
depend only on the Levi factors
![]() $M_Q$
and
$M_Q$
and
![]() $M_P$
and thus are also denoted by
$M_P$
and thus are also denoted by
![]() $\mathfrak {a}_{M_P}^{M_Q}$
,
$\mathfrak {a}_{M_P}^{M_Q}$
,
![]() $\mathfrak {a}_{M_P}^{M_Q,*}$
etc.
$\mathfrak {a}_{M_P}^{M_Q,*}$
etc.
Let
![]() $\operatorname {\mathrm {Ad}}_{P}^Q$
be the adjoint action of
$\operatorname {\mathrm {Ad}}_{P}^Q$
be the adjoint action of
![]() $M_P$
on the Lie algebra of
$M_P$
on the Lie algebra of
![]() $M_Q\cap N_P$
. Let
$M_Q\cap N_P$
. Let
![]() $\rho _P^Q$
be the unique element of
$\rho _P^Q$
be the unique element of
![]() $\mathfrak {a}_{P}^{Q,*}$
such that for every
$\mathfrak {a}_{P}^{Q,*}$
such that for every
![]() $m\in M_P(\mathbb {A})$
, we have
$m\in M_P(\mathbb {A})$
, we have
For every
![]() $g\in G(\mathbb {A})$
, we set
$g\in G(\mathbb {A})$
, we set
If the context is clear, we set
![]() $\rho _P=\rho _P^G$
and
$\rho _P=\rho _P^G$
and
![]() $\delta _P=\delta _P^G$
. Usually, we replace the subscript
$\delta _P=\delta _P^G$
. Usually, we replace the subscript
![]() $P_0$
simply by
$P_0$
simply by
![]() $0$
(for example,
$0$
(for example,
![]() $\mathfrak {a}_0=\mathfrak {a}_{P_0}$
,
$\mathfrak {a}_0=\mathfrak {a}_{P_0}$
,
![]() $\rho _0=\rho _{P_0}$
, etc.).
$\rho _0=\rho _{P_0}$
, etc.).
2.1.4
Let
![]() $P $
be a standard parabolic subgroups of G. Let
$P $
be a standard parabolic subgroups of G. Let
![]() $A_P=A_{M_P}$
be the maximal central F-split torus of
$A_P=A_{M_P}$
be the maximal central F-split torus of
![]() $M_P$
. Let
$M_P$
. Let
![]() $\Delta _{0}^P$
be the set of simple roots of
$\Delta _{0}^P$
be the set of simple roots of
![]() $A_{0}$
in
$A_{0}$
in
![]() $M_P\cap P_0$
. Let
$M_P\cap P_0$
. Let
![]() $\Delta _P^Q$
be the image of
$\Delta _P^Q$
be the image of
![]() $\Delta _{0}^Q\setminus \Delta _{0}^P$
by the projection
$\Delta _{0}^Q\setminus \Delta _{0}^P$
by the projection
![]() $\mathfrak {a}_{0}^*\to \mathfrak {a}_P^*$
. It is a basis of
$\mathfrak {a}_{0}^*\to \mathfrak {a}_P^*$
. It is a basis of
![]() $\mathfrak {a}_P^{Q,*}$
whose dual basis is the subset of coweights
$\mathfrak {a}_P^{Q,*}$
whose dual basis is the subset of coweights
![]() $\hat \Delta _P^{Q,\vee }\subset \mathfrak {a}_P^Q$
. We have also the set of coroots
$\hat \Delta _P^{Q,\vee }\subset \mathfrak {a}_P^Q$
. We have also the set of coroots
![]() $\Delta _P^{Q,\vee }$
which is a basis of
$\Delta _P^{Q,\vee }$
which is a basis of
![]() $\mathfrak {a}_P^{Q}$
. We have the dual basis given by the set of simple weights
$\mathfrak {a}_P^{Q}$
. We have the dual basis given by the set of simple weights
![]() $\hat {\Delta }_P^Q \subset \mathfrak {a}_P^{Q,*}$
. The sets
$\hat {\Delta }_P^Q \subset \mathfrak {a}_P^{Q,*}$
. The sets
![]() $\Delta _P^Q$
and
$\Delta _P^Q$
and
![]() $\hat {\Delta }_P^Q$
determine open cones in
$\hat {\Delta }_P^Q$
determine open cones in
![]() $\mathfrak {a}_{0}$
whose characteristic functions are denoted respectively by
$\mathfrak {a}_{0}$
whose characteristic functions are denoted respectively by
![]() $\tau _P^Q$
and
$\tau _P^Q$
and
![]() $\hat {\tau }_P^Q$
. We set
$\hat {\tau }_P^Q$
. We set
We define similarly
![]() $\mathfrak {a}_P^{Q+}$
using roots instead of coroots. If
$\mathfrak {a}_P^{Q+}$
using roots instead of coroots. If
![]() $Q=G$
, the exponent G is omitted.
$Q=G$
, the exponent G is omitted.
2.1.5
Let W be the Weyl group of
![]() $(G,A_{0})$
– namely, the quotient of the normalizer of
$(G,A_{0})$
– namely, the quotient of the normalizer of
![]() $A_0$
in
$A_0$
in
![]() $G(F)$
by
$G(F)$
by
![]() $M_0$
. For
$M_0$
. For
![]() $P=M_P N_P$
and
$P=M_P N_P$
and
![]() $Q=M_QN_Q$
two standard parabolic subgroups of
$Q=M_QN_Q$
two standard parabolic subgroups of
![]() $ G $
, we denote by
$ G $
, we denote by
![]() $W(P,Q)$
or
$W(P,Q)$
or
![]() $W(M_P,M_Q)$
the set of
$W(M_P,M_Q)$
the set of
![]() $w\in W$
such that
$w\in W$
such that
![]() $w\Delta ^P_0=\Delta _0^Q$
. For
$w\Delta ^P_0=\Delta _0^Q$
. For
![]() $w\in W(P,Q)$
, we have
$w\in W(P,Q)$
, we have
![]() $wM_Pw^{-1}=M_Q$
. When
$wM_Pw^{-1}=M_Q$
. When
![]() $P=Q$
, the group
$P=Q$
, the group
![]() $W(P,P)$
is simply denoted by
$W(P,P)$
is simply denoted by
![]() $W(P)$
or
$W(P)$
or
![]() $W(M_P)$
. We will also write
$W(M_P)$
. We will also write
![]() $W^{M_P}$
for the Weyl group of
$W^{M_P}$
for the Weyl group of
![]() $(M_P,A_0)$
.
$(M_P,A_0)$
.
2.1.6
Let
![]() $ K=\prod _{v\in V_F} K_v\subset G (\mathbb {A}) $
be a ‘good’ maximal compact subgroup in good position relative to
$ K=\prod _{v\in V_F} K_v\subset G (\mathbb {A}) $
be a ‘good’ maximal compact subgroup in good position relative to
![]() $M_0$
(called ‘admissible’ in [Reference ArthurArt81, p. 9]). We write
$M_0$
(called ‘admissible’ in [Reference ArthurArt81, p. 9]). We write
where
![]() $K_\infty =\prod _{v\in V_{F,\infty }} K_v$
and
$K_\infty =\prod _{v\in V_{F,\infty }} K_v$
and
![]() $K^\infty =\prod _{v\in V_F\setminus V_{F,\infty }} K_v$
. We have a homomorphism
$K^\infty =\prod _{v\in V_F\setminus V_{F,\infty }} K_v$
. We have a homomorphism
![]() $H_P:P(\mathbb {A})\to \mathfrak {a}_P$
such that
$H_P:P(\mathbb {A})\to \mathfrak {a}_P$
such that
![]() $\langle \chi , H_P(p) \rangle = \log | \chi (p) | $
for any
$\langle \chi , H_P(p) \rangle = \log | \chi (p) | $
for any
![]() $p\in P(\mathbb {A})$
and
$p\in P(\mathbb {A})$
and
![]() $\chi \in X^*(P)$
. By Iwasawa decomposition
$\chi \in X^*(P)$
. By Iwasawa decomposition
![]() $G(\mathbb {A})=P(\mathbb {A})K$
, it extends to a map
$G(\mathbb {A})=P(\mathbb {A})K$
, it extends to a map
![]() $H_P:G(\mathbb {A})\to \mathfrak {a}_P$
which is left-invariant by
$H_P:G(\mathbb {A})\to \mathfrak {a}_P$
which is left-invariant by
![]() $M_P(F)N_P(\mathbb {A})$
and right-invariant by K. We denote
$M_P(F)N_P(\mathbb {A})$
and right-invariant by K. We denote
![]() $A_P^\infty =A_{M_P}^\infty $
the neutral component of the group of real points of the maximal
$A_P^\infty =A_{M_P}^\infty $
the neutral component of the group of real points of the maximal
![]() $\mathbb {Q}$
-split torus of the Weil restriction
$\mathbb {Q}$
-split torus of the Weil restriction
![]() $\operatorname {\mathrm {Res}}_{F/\mathbb {Q}}(A_P)$
. Then the restriction of
$\operatorname {\mathrm {Res}}_{F/\mathbb {Q}}(A_P)$
. Then the restriction of
![]() $H_P$
to
$H_P$
to
![]() $A_P^\infty $
is an isomorphism.
$A_P^\infty $
is an isomorphism.
We set
![]() $[G]_P=M_P(F)N_P(\mathbb {A})\backslash G(\mathbb {A})$
and
$[G]_P=M_P(F)N_P(\mathbb {A})\backslash G(\mathbb {A})$
and
![]() $[G]_{P,0}=A_P^\infty M_P(F) N_P(\mathbb {A})\backslash G(\mathbb {A})$
. Let
$[G]_{P,0}=A_P^\infty M_P(F) N_P(\mathbb {A})\backslash G(\mathbb {A})$
. Let
![]() $[G]^1_P$
be the subset of
$[G]^1_P$
be the subset of
![]() $[G]_P$
where the map
$[G]_P$
where the map
![]() $H_P$
vanishes. If
$H_P$
vanishes. If
![]() $P=G$
, we shall omit the subscript P.
$P=G$
, we shall omit the subscript P.
2.1.7
We fix a height
![]() $\|\cdot \|$
on
$\|\cdot \|$
on
![]() $G(\mathbb {A})$
as in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, section 2.4]. Let
$G(\mathbb {A})$
as in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, section 2.4]. Let
![]() $P\subset G$
be a standard parabolic subgroup. We set for
$P\subset G$
be a standard parabolic subgroup. We set for
![]() $x\in [G]_P$
$x\in [G]_P$
2.1.8 Haar measures
Let us explain briefly our choice and notations of measures; see [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, section 2.3] for more details. We fix a nontrivial continuous additive character
![]() $\psi ':\mathbb {A}/F\to \mathbb {C}^\times $
. For each place
$\psi ':\mathbb {A}/F\to \mathbb {C}^\times $
. For each place
![]() $v\in V_F$
, the local component
$v\in V_F$
, the local component
![]() $\psi ^{\prime }_v$
of
$\psi ^{\prime }_v$
of
![]() $\psi '$
determines an autodual Haar measure on
$\psi '$
determines an autodual Haar measure on
![]() $F_v$
. The choice of an invariant rational volume form on G then determines a Haar measure
$F_v$
. The choice of an invariant rational volume form on G then determines a Haar measure
![]() $dg_v$
on
$dg_v$
on
![]() $G(F_v)$
. We have an Artin-Tate L-function
$G(F_v)$
. We have an Artin-Tate L-function
![]() $L_G(s)= \prod _{v\in V_F} L_{G,v}(s)$
; see [Reference GrossGro97] and more generally
$L_G(s)= \prod _{v\in V_F} L_{G,v}(s)$
; see [Reference GrossGro97] and more generally
![]() $L_G^S(s)= \prod _{v\in V_F\setminus S} L_{G,v}(s)$
for
$L_G^S(s)= \prod _{v\in V_F\setminus S} L_{G,v}(s)$
for
![]() $S\subset V_F$
finite. Then
$S\subset V_F$
finite. Then
![]() $\Delta ^{S,*}_G$
(simply
$\Delta ^{S,*}_G$
(simply
![]() $\Delta ^*_G$
if S is empty) is defined to be the leading coefficient in the Laurent expansion of
$\Delta ^*_G$
if S is empty) is defined to be the leading coefficient in the Laurent expansion of
![]() $L_G(s)$
at
$L_G(s)$
at
![]() $s=0$
. We also set
$s=0$
. We also set
![]() $\Delta _{G,v}=L_{G,v}(0)$
. The Tamagawa measure
$\Delta _{G,v}=L_{G,v}(0)$
. The Tamagawa measure
![]() $dg$
on
$dg$
on
![]() $G(\mathbb {A})$
is defined by
$G(\mathbb {A})$
is defined by
![]() $dg=dg_S\times dg^S$
, where
$dg=dg_S\times dg^S$
, where
![]() $dg_S=\prod _{v\in S} dg_v$
and
$dg_S=\prod _{v\in S} dg_v$
and
![]() $dg^S=(\Delta _G^{S,*})^{-1}\prod _{v\notin S} \Delta _{G,v}dg_v$
for
$dg^S=(\Delta _G^{S,*})^{-1}\prod _{v\notin S} \Delta _{G,v}dg_v$
for
![]() $S\subset V_F$
finite.
$S\subset V_F$
finite.
We equip
![]() $\mathfrak {a}_P$
with the Haar measure that gives a covolume
$\mathfrak {a}_P$
with the Haar measure that gives a covolume
![]() $1$
to the lattice
$1$
to the lattice
![]() $\operatorname {\mathrm {Hom}}(X^*(P),\mathbb {Z})$
and
$\operatorname {\mathrm {Hom}}(X^*(P),\mathbb {Z})$
and
![]() $i\mathfrak {a}_{P}^{*}$
with the dual Haar measure. The group
$i\mathfrak {a}_{P}^{*}$
with the dual Haar measure. The group
![]() $ A_P ^ \infty $
is equipped with the Haar measure compatible with the isomorphism
$ A_P ^ \infty $
is equipped with the Haar measure compatible with the isomorphism
![]() $ A_P ^ \infty \simeq \mathfrak {a}_ {P} $
induced by the map
$ A_P ^ \infty \simeq \mathfrak {a}_ {P} $
induced by the map
![]() $H_P$
. The groups
$H_P$
. The groups
![]() $\mathfrak {a}_P^G\simeq \mathfrak {a}_P/\mathfrak {a}_G$
and
$\mathfrak {a}_P^G\simeq \mathfrak {a}_P/\mathfrak {a}_G$
and
![]() $i\mathfrak {a}_P^{G,*}\simeq i\mathfrak {a}_P^*/i\mathfrak {a}_G^*$
are provided with the quotient Haar measures.
$i\mathfrak {a}_P^{G,*}\simeq i\mathfrak {a}_P^*/i\mathfrak {a}_G^*$
are provided with the quotient Haar measures.
The homogeneous space
![]() $[G]$
(resp.
$[G]$
(resp.
![]() $[G]^1\simeq [G]_0$
) is equipped with the quotient of the Tamagawa measure on
$[G]^1\simeq [G]_0$
) is equipped with the quotient of the Tamagawa measure on
![]() $G(\mathbb {A})$
by the counting measure on
$G(\mathbb {A})$
by the counting measure on
![]() $G(F)$
(resp. by the product of the counting measure on
$G(F)$
(resp. by the product of the counting measure on
![]() $G(F)$
with the Haar measure we fixed on
$G(F)$
with the Haar measure we fixed on
![]() $A_G^\infty $
). For P a standard parabolic subgroup, we equip similarly
$A_G^\infty $
). For P a standard parabolic subgroup, we equip similarly
![]() $[G]_{P}$
with the quotient of the Tamagawa measure on
$[G]_{P}$
with the quotient of the Tamagawa measure on
![]() $G(\mathbb {A})$
by the product of the counting measure on
$G(\mathbb {A})$
by the product of the counting measure on
![]() $M_P(F)$
with the Tamagawa measure on
$M_P(F)$
with the Tamagawa measure on
![]() $N_P(\mathbb {A})$
. Since the action by left translation of
$N_P(\mathbb {A})$
. Since the action by left translation of
![]() $a\in A_P^\infty $
on
$a\in A_P^\infty $
on
![]() $[G]_P$
multiplies the measure by
$[G]_P$
multiplies the measure by
![]() $\delta _P(a)^{-1}$
, taking the quotient by the Haar measure on
$\delta _P(a)^{-1}$
, taking the quotient by the Haar measure on
![]() $A_P^\infty $
induces a ‘semi-invariant’ measure on
$A_P^\infty $
induces a ‘semi-invariant’ measure on
![]() $[G]_{P,0}=A_P^\infty \backslash [G]_P$
.
$[G]_{P,0}=A_P^\infty \backslash [G]_P$
.
2.2 Space of functions
2.2.1
For two positive functions f and g on a set X, we write
![]() $ f(x)\ll g(x), \; x\in X$
if there exists a constant
$ f(x)\ll g(x), \; x\in X$
if there exists a constant
![]() $C>0$
such that
$C>0$
such that
![]() $f(x)\leqslant Cg(x)$
for every
$f(x)\leqslant Cg(x)$
for every
![]() $x\in X$
. We write
$x\in X$
. We write
![]() $ f(x)\sim g(x), \; x\in X$
if
$ f(x)\sim g(x), \; x\in X$
if
![]() $f(x)\ll g(x)$
and
$f(x)\ll g(x)$
and
![]() $g(x)\ll f(x)$
.
$g(x)\ll f(x)$
.
2.2.2
For every
![]() $C\in \mathbb {R}\cup \{-\infty \}$
with
$C\in \mathbb {R}\cup \{-\infty \}$
with
![]() $D>C$
, we set
$D>C$
, we set
![]() $\mathcal {H}_{>C}=\{z\in \mathbb {C}\mid \Re (z)>C \}$
.
$\mathcal {H}_{>C}=\{z\in \mathbb {C}\mid \Re (z)>C \}$
.
2.2.3 Schwartz spaces
As before, G is a reductive group defined over F. We let
![]() $\mathfrak {g}_\infty $
be the Lie algebra of
$\mathfrak {g}_\infty $
be the Lie algebra of
![]() $G(F_\infty )$
and
$G(F_\infty )$
and
![]() $\mathcal {U}(\mathfrak {g}_\infty )$
be the enveloping algebra of its complexification and
$\mathcal {U}(\mathfrak {g}_\infty )$
be the enveloping algebra of its complexification and
![]() $\mathcal {Z}(\mathfrak {g}_\infty )\subset \mathcal {U}(\mathfrak {g}_\infty )$
be its center.
$\mathcal {Z}(\mathfrak {g}_\infty )\subset \mathcal {U}(\mathfrak {g}_\infty )$
be its center.
We shall briefly review several useful locally convex topological spaces of functions; see [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, section 2.5] for more details. Let
![]() $\mathcal {S}(G(\mathbb {A}))$
be the Schwartz space of
$\mathcal {S}(G(\mathbb {A}))$
be the Schwartz space of
![]() $G(\mathbb {A})$
: it contains the dense subspace
$G(\mathbb {A})$
: it contains the dense subspace
![]() $C_c^\infty (G(\mathbb {A}))$
of smooth and compactly supported functions. Let
$C_c^\infty (G(\mathbb {A}))$
of smooth and compactly supported functions. Let
![]() $P\subset G$
be a standard parabolic subgroup. Let
$P\subset G$
be a standard parabolic subgroup. Let
![]() $\mathcal {S}^0([G]_P)$
be the space of measurable functions
$\mathcal {S}^0([G]_P)$
be the space of measurable functions
![]() $\varphi :[G]_P\to \mathbb {C}$
such that
$\varphi :[G]_P\to \mathbb {C}$
such that
for every
![]() $N>0$
. Let
$N>0$
. Let
![]() $\mathcal {S}([G]_P)$
be the Schwartz space of
$\mathcal {S}([G]_P)$
be the Schwartz space of
![]() $[G]_P$
that is the space of smooth functions
$[G]_P$
that is the space of smooth functions
![]() $\varphi :[G]_P\to \mathbb {C}$
such that for every
$\varphi :[G]_P\to \mathbb {C}$
such that for every
![]() $N>0$
and
$N>0$
and
![]() $X\in \mathcal {U}(\mathfrak {g}_\infty )$
, we have
$X\in \mathcal {U}(\mathfrak {g}_\infty )$
, we have
The space of functions of uniform moderate growth on
![]() $[G]_P$
is defined as
$[G]_P$
is defined as
where
![]() $\mathcal {T}_N([G]_P)$
is the space of smooth functions
$\mathcal {T}_N([G]_P)$
is the space of smooth functions
![]() $\varphi : [G]_P\to \mathbb {C}$
such that for every
$\varphi : [G]_P\to \mathbb {C}$
such that for every
![]() $X\in \mathcal {U}(\mathfrak {g}_\infty )$
, we have
$X\in \mathcal {U}(\mathfrak {g}_\infty )$
, we have
All these spaces are equipped with locally convex topologies. The space
![]() $\mathcal {S}^0([G]_P)$
is equipped with the family of semi-norms
$\mathcal {S}^0([G]_P)$
is equipped with the family of semi-norms
![]() $\lVert \cdot \rVert _{\infty ,N}$
; it is a Fréchet space. The spaces
$\lVert \cdot \rVert _{\infty ,N}$
; it is a Fréchet space. The spaces
![]() $\mathcal {S}(G(\mathbb {A}))$
,
$\mathcal {S}(G(\mathbb {A}))$
,
![]() $\mathcal {S}([G]_P)$
,
$\mathcal {S}([G]_P)$
,
![]() $\mathcal {T}_N([G]_P)$
and
$\mathcal {T}_N([G]_P)$
and
![]() $\mathcal {T}([G]_P)$
are LF-spaces: we refer the reader to [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, section 2.5] for a precise description of the topology.
$\mathcal {T}([G]_P)$
are LF-spaces: we refer the reader to [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, section 2.5] for a precise description of the topology.
2.2.4 Automorphic forms
Here, we refer the reader to [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, section 2.7] for more details. The space
![]() $\mathcal {A}_P(G)$
of automorphic forms on
$\mathcal {A}_P(G)$
of automorphic forms on
![]() $[G]_P$
is the subspace of
$[G]_P$
is the subspace of
![]() $\mathcal {Z}(\mathfrak {g}_\infty )$
-finite functions in
$\mathcal {Z}(\mathfrak {g}_\infty )$
-finite functions in
![]() $\mathcal {T}([G]_P)$
. Let
$\mathcal {T}([G]_P)$
. Let
![]() $\mathcal {A}_{P,\operatorname {\mathrm {cusp}}}(G)\subset \mathcal {A}_P(G)$
be the subspace of cuspidal automorphic forms: these are the functions
$\mathcal {A}_{P,\operatorname {\mathrm {cusp}}}(G)\subset \mathcal {A}_P(G)$
be the subspace of cuspidal automorphic forms: these are the functions
![]() $\varphi \in \mathcal {A}_P(G)$
such that
$\varphi \in \mathcal {A}_P(G)$
such that
![]() $\varphi _Q=0$
for every proper parabolic subgroup
$\varphi _Q=0$
for every proper parabolic subgroup
![]() $Q\subsetneq P$
. The constant term
$Q\subsetneq P$
. The constant term
![]() $\varphi _Q$
is defined by
$\varphi _Q$
is defined by
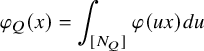 $$ \begin{align*} \varphi_Q(x)=\int_{[N_Q]} \varphi(ux) du \end{align*} $$
$$ \begin{align*} \varphi_Q(x)=\int_{[N_Q]} \varphi(ux) du \end{align*} $$
for all
![]() $x\in G(\mathbb {A})$
. A cuspidal automorphic representation
$x\in G(\mathbb {A})$
. A cuspidal automorphic representation
![]() $\pi $
of
$\pi $
of
![]() $M_P(\mathbb {A})$
is a topologically irreducible subrepresentation of
$M_P(\mathbb {A})$
is a topologically irreducible subrepresentation of
![]() $\mathcal {A}_{\operatorname {\mathrm {cusp}}}(M_P)$
. For every
$\mathcal {A}_{\operatorname {\mathrm {cusp}}}(M_P)$
. For every
![]() $\lambda \in \mathfrak {a}_{P,\mathbb {C}}^*$
, we define
$\lambda \in \mathfrak {a}_{P,\mathbb {C}}^*$
, we define
![]() $\pi _\lambda =\pi \otimes \lambda $
as the space of functions of the form
$\pi _\lambda =\pi \otimes \lambda $
as the space of functions of the form
for
![]() $ \varphi \in \pi $
.
$ \varphi \in \pi $
.
We denote by
![]() $\mathcal {A}_{\pi ,\operatorname {\mathrm {cusp}}}(M_P)$
the
$\mathcal {A}_{\pi ,\operatorname {\mathrm {cusp}}}(M_P)$
the
![]() $\pi $
-isotypic component of
$\pi $
-isotypic component of
![]() $\mathcal {A}_{\operatorname {\mathrm {cusp}}}(M_P)$
. The normalized smooth induction
$\mathcal {A}_{\operatorname {\mathrm {cusp}}}(M_P)$
. The normalized smooth induction
![]() $\operatorname {\mathrm {Ind}}_{P(\mathbb {A})}^{G(\mathbb {A})}(\mathcal {A}_{\pi ,\operatorname {\mathrm {cusp}}}(M_P))$
is denoted by
$\operatorname {\mathrm {Ind}}_{P(\mathbb {A})}^{G(\mathbb {A})}(\mathcal {A}_{\pi ,\operatorname {\mathrm {cusp}}}(M_P))$
is denoted by
![]() $\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(G) $
and is identified with the space of automorphic forms
$\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(G) $
and is identified with the space of automorphic forms
![]() $\varphi \in \mathcal {A}_{P}(G)$
such that
$\varphi \in \mathcal {A}_{P}(G)$
such that
belongs to
![]() $\mathcal {A}_{\pi ,\operatorname {\mathrm {cusp}}}(M_P)$
for every
$\mathcal {A}_{\pi ,\operatorname {\mathrm {cusp}}}(M_P)$
for every
![]() $g\in G(\mathbb {A})$
. The algebra
$g\in G(\mathbb {A})$
. The algebra
![]() $\mathcal {S}(G(\mathbb {A}))$
acts on
$\mathcal {S}(G(\mathbb {A}))$
acts on
![]() $\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(G)$
by right convolution. For every
$\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(G)$
by right convolution. For every
![]() $\lambda \in \mathfrak {a}_{P,\mathbb {C}}^*$
, we denote by
$\lambda \in \mathfrak {a}_{P,\mathbb {C}}^*$
, we denote by
![]() $I(\lambda )$
the action on
$I(\lambda )$
the action on
![]() $\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(G)$
we get by transport from the action of
$\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(G)$
we get by transport from the action of
![]() $\mathcal {S}(G(\mathbb {A}))$
on
$\mathcal {S}(G(\mathbb {A}))$
on
![]() $\mathcal {A}_{P,\pi _\lambda , \operatorname {\mathrm {cusp}}}$
and the identification
$\mathcal {A}_{P,\pi _\lambda , \operatorname {\mathrm {cusp}}}$
and the identification
![]() $\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}\to \mathcal {A}_{P,\pi _\lambda ,\operatorname {\mathrm {cusp}}}$
given by
$\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}\to \mathcal {A}_{P,\pi _\lambda ,\operatorname {\mathrm {cusp}}}$
given by
![]() $\varphi \mapsto \exp (\langle \lambda , H_P(.)\rangle )\varphi $
. Assume that the central character of
$\varphi \mapsto \exp (\langle \lambda , H_P(.)\rangle )\varphi $
. Assume that the central character of
![]() $\pi $
is unitary. Then we equip
$\pi $
is unitary. Then we equip
![]() $\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(G)$
with the Petersson inner product given by
$\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(G)$
with the Petersson inner product given by
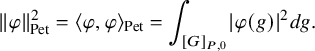 $$ \begin{align*} \| \varphi\|^2_{\operatorname{\mathrm{Pet}}}= \langle \varphi,\varphi\rangle_{\operatorname{\mathrm{Pet}}}=\int_{[G]_{P,0}} \lvert \varphi(g)\rvert^2 dg. \end{align*} $$
$$ \begin{align*} \| \varphi\|^2_{\operatorname{\mathrm{Pet}}}= \langle \varphi,\varphi\rangle_{\operatorname{\mathrm{Pet}}}=\int_{[G]_{P,0}} \lvert \varphi(g)\rvert^2 dg. \end{align*} $$
Note that for every cuspidal automorphic representation
![]() $\pi $
of
$\pi $
of
![]() $M_P(\mathbb {A})$
, there exists a unique
$M_P(\mathbb {A})$
, there exists a unique
![]() $\lambda \in \mathfrak {a}_{P,\mathbb {C}}^*$
such that the central character of
$\lambda \in \mathfrak {a}_{P,\mathbb {C}}^*$
such that the central character of
![]() $\pi _\lambda $
is trivial on
$\pi _\lambda $
is trivial on
![]() $A_M^\infty $
. Unless otherwise stated, the cuspidal automorphic representations we consider are always normalized in the sense that they are assumed to have a central character which is trivial on
$A_M^\infty $
. Unless otherwise stated, the cuspidal automorphic representations we consider are always normalized in the sense that they are assumed to have a central character which is trivial on
![]() $A_M^\infty $
.
$A_M^\infty $
.
Let
![]() $\hat K$
be the set of isomorphism classes of irreducible unitary representations of K. A K-basis
$\hat K$
be the set of isomorphism classes of irreducible unitary representations of K. A K-basis
![]() $\mathcal {B}_{P,\pi }$
of
$\mathcal {B}_{P,\pi }$
of
![]() $\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(G)$
is by definition the union over of
$\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(G)$
is by definition the union over of
![]() $\tau \in \hat K$
of orthonormal bases
$\tau \in \hat K$
of orthonormal bases
![]() $\mathcal {B}_{P,\pi ,\tau }$
for the Petersson inner product of the finite dimensional subspaces
$\mathcal {B}_{P,\pi ,\tau }$
for the Petersson inner product of the finite dimensional subspaces
![]() $\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(G,\tau )$
of functions in
$\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(G,\tau )$
of functions in
![]() $\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(G)$
which transform under K according to
$\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(G)$
which transform under K according to
![]() $\tau $
.
$\tau $
.
For any
![]() $\varphi \in \mathcal {A}_{P,\operatorname {\mathrm {cusp}}}(G)$
,
$\varphi \in \mathcal {A}_{P,\operatorname {\mathrm {cusp}}}(G)$
,
![]() $g\in G(\mathbb {A})$
and
$g\in G(\mathbb {A})$
and
![]() $\lambda \in \mathfrak {a}_{P,\mathbb {C}}^{*}$
and any parabolic subgroup
$\lambda \in \mathfrak {a}_{P,\mathbb {C}}^{*}$
and any parabolic subgroup
![]() $Q\supset P$
, we introduce the Eisenstein series
$Q\supset P$
, we introduce the Eisenstein series
The right-hand side is convergent for
![]() $\Re (\lambda )$
in a suitable cone, and for more general
$\Re (\lambda )$
in a suitable cone, and for more general
![]() $\lambda $
, the left-hand side is given by meromorphic continuation. Let P and Q be standard parabolic subgroups of G. For any
$\lambda $
, the left-hand side is given by meromorphic continuation. Let P and Q be standard parabolic subgroups of G. For any
![]() $w\in W(P,Q)$
and
$w\in W(P,Q)$
and
![]() $\lambda \in \mathfrak {a}_{P,\mathbb {C}}^{*}$
, we have the intertwining operator
$\lambda \in \mathfrak {a}_{P,\mathbb {C}}^{*}$
, we have the intertwining operator
For more details and continuity properties of these constructions, we refer the reader to [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, §§ 2.7.3, 2.7.4].
2.2.5 Cuspidal datum
Let
![]() $P\subset G$
be a standard parabolic subgroup of G. Let
$P\subset G$
be a standard parabolic subgroup of G. Let
![]() $L^2([G]_P)$
be the space of square integrable functions on
$L^2([G]_P)$
be the space of square integrable functions on
![]() $[G]_P$
. Let
$[G]_P$
. Let
![]() $\mathfrak {X}(G)$
be the set of cuspidal data of G. Recall that
$\mathfrak {X}(G)$
be the set of cuspidal data of G. Recall that
![]() $\mathfrak {X}(G)$
is the quotient of the set of pairs
$\mathfrak {X}(G)$
is the quotient of the set of pairs
![]() $(M_P,\pi )$
such that
$(M_P,\pi )$
such that
-
• P is a standard parabolic subgroup of G;
-
•
 $\pi $
is the isomorphism class of a cuspidal automorphic representation of
$\pi $
is the isomorphism class of a cuspidal automorphic representation of
 $M_P(\mathbb {A})$
with central character trivial on
$M_P(\mathbb {A})$
with central character trivial on
 $A_P^\infty $
$A_P^\infty $
by the following equivalence relation:
![]() $(M_P,\pi )\sim (M_Q,\tau )$
if there exists
$(M_P,\pi )\sim (M_Q,\tau )$
if there exists
![]() $w\in W(P,Q)$
such that
$w\in W(P,Q)$
such that
![]() $w\pi w^{-1}\simeq \tau $
. Then for any standard parabolic subgroup P of G, we have the Langlands decomposition (see [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, section 2.9] for more details):
$w\pi w^{-1}\simeq \tau $
. Then for any standard parabolic subgroup P of G, we have the Langlands decomposition (see [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, section 2.9] for more details):
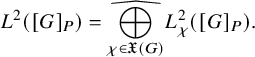 $$ \begin{align*} L^2([G]_P)=\widehat{\bigoplus_{\chi\in \mathfrak{X}(G)}} L^2_{\chi}([G]_P). \end{align*} $$
$$ \begin{align*} L^2([G]_P)=\widehat{\bigoplus_{\chi\in \mathfrak{X}(G)}} L^2_{\chi}([G]_P). \end{align*} $$
The Schwartz algebra acts on
![]() $L^2([G]_P)$
and for each
$L^2([G]_P)$
and for each
![]() $\chi \in \mathfrak {X}(G)$
on
$\chi \in \mathfrak {X}(G)$
on
![]() $L^2_{\chi }([G]_P)$
by right convolution. For each
$L^2_{\chi }([G]_P)$
by right convolution. For each
![]() $f\in \mathcal {S}(G(\mathbb {A}))$
, we get integral operators whose kernels are denoted respectively by
$f\in \mathcal {S}(G(\mathbb {A}))$
, we get integral operators whose kernels are denoted respectively by
![]() $K_{f,P}$
and
$K_{f,P}$
and
![]() $K_{f,P,\chi }$
. We shall use also the decomposition
$K_{f,P,\chi }$
. We shall use also the decomposition
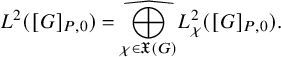 $$ \begin{align*} L^2([G]_{P,0})=\widehat{\bigoplus_{\chi\in \mathfrak{X}(G)}} L^2_{\chi}([G]_{P,0}). \end{align*} $$
$$ \begin{align*} L^2([G]_{P,0})=\widehat{\bigoplus_{\chi\in \mathfrak{X}(G)}} L^2_{\chi}([G]_{P,0}). \end{align*} $$
2.3 Around Arthur’s partition
2.3.1
Let
![]() $T_1,T\in \mathfrak {a}_0$
and P be a standard parabolic subgroup of G. We define
$T_1,T\in \mathfrak {a}_0$
and P be a standard parabolic subgroup of G. We define
and
2.3.2 Siegel domains
Let
![]() $T_-\in \mathfrak {a}_0^{G}$
and
$T_-\in \mathfrak {a}_0^{G}$
and
![]() $\omega _0\subset P_0(\mathbb {A})^1$
be a compact subset such that
$\omega _0\subset P_0(\mathbb {A})^1$
be a compact subset such that
![]() $P_0(\mathbb {A})^1=P_0(F)\omega _0$
. Let P be a standard parabolic subgroup of G. We define
$P_0(\mathbb {A})^1=P_0(F)\omega _0$
. Let P be a standard parabolic subgroup of G. We define
There exists
![]() $T_-\in -\mathfrak {a}_0^{G,+}$
such that for all standard parabolic subgroup of G, we have
$T_-\in -\mathfrak {a}_0^{G,+}$
such that for all standard parabolic subgroup of G, we have
![]() $G(\mathbb {A})=P(F)\mathfrak {s}_P(\omega _0,T_-,K)$
.We will fix
$G(\mathbb {A})=P(F)\mathfrak {s}_P(\omega _0,T_-,K)$
.We will fix
![]() $T_-$
and
$T_-$
and
![]() $\omega _0$
and we set
$\omega _0$
and we set
![]() $\mathfrak {s}_P= \mathfrak {s}_P(\omega _0,T,K)$
: this is a Siegel domain of
$\mathfrak {s}_P= \mathfrak {s}_P(\omega _0,T,K)$
: this is a Siegel domain of
![]() $[G]_P$
.
$[G]_P$
.
Note that for any standard parabolic subgroup P of G, we have
![]() $\|x\|\sim \|x\|_P$
for
$\|x\|\sim \|x\|_P$
for
![]() $x\in \mathfrak {s}_P$
; see [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, (2.4.1.3)].
$x\in \mathfrak {s}_P$
; see [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, (2.4.1.3)].
2.3.3
For any standard parabolic subgroup P of G and
![]() $T\in \mathfrak {a}_0^+$
, we consider the characteristic function
$T\in \mathfrak {a}_0^+$
, we consider the characteristic function
![]() $F^P(\cdot ,T)$
of
$F^P(\cdot ,T)$
of
![]() $\omega _0 A_0^{P,\infty }(T_-,T)K\subset \mathfrak {s}_P$
. This function descends on
$\omega _0 A_0^{P,\infty }(T_-,T)K\subset \mathfrak {s}_P$
. This function descends on
![]() $[G]_P $
. There is a point
$[G]_P $
. There is a point
![]() $T_0\in \mathfrak {a}_0^{G,+}$
such that for all
$T_0\in \mathfrak {a}_0^{G,+}$
such that for all
![]() $T\in T_0+\mathfrak {a}_0^{G,+}$
and all standard parabolic subgroup Q of G, we have the following formula which gives a partition of
$T\in T_0+\mathfrak {a}_0^{G,+}$
and all standard parabolic subgroup Q of G, we have the following formula which gives a partition of
![]() $[G]_Q$
(see [Reference ArthurArt78, Lemma 6.4] and also [Reference Labesse and WaldspurgerLW13, Proposition 3.6.3]):
$[G]_Q$
(see [Reference ArthurArt78, Lemma 6.4] and also [Reference Labesse and WaldspurgerLW13, Proposition 3.6.3]):
Note that the relation implies a simpler definition of
![]() $F^P(\cdot ,T)$
for
$F^P(\cdot ,T)$
for
![]() $T\in T_0+\mathfrak {a}_0^{G,+}$
; the function
$T\in T_0+\mathfrak {a}_0^{G,+}$
; the function
![]() $F^P(\cdot ,T)$
is the characteristic function of the following set:
$F^P(\cdot ,T)$
is the characteristic function of the following set:
Indeed, this is a straightforward consequence of [Reference ArthurArt85, Lemma 2.1] and the definition of the operator
![]() $\Lambda ^T$
there.
$\Lambda ^T$
there.
We shall use several times the following simple lemma.
Lemma 2.3.3.1. Let
![]() $P\subset Q$
be parabolic subgroup of G. Let
$P\subset Q$
be parabolic subgroup of G. Let
![]() $g\in G(\mathbb {A})$
be such that
$g\in G(\mathbb {A})$
be such that
![]() $F^P( g,T) \tau _P^Q(H_P( g)-T)=1$
. Then we have
$F^P( g,T) \tau _P^Q(H_P( g)-T)=1$
. Then we have
In particular, if
![]() $g\in \mathfrak {s}_P$
, then
$g\in \mathfrak {s}_P$
, then
![]() $g\in \mathfrak {s}_Q$
.
$g\in \mathfrak {s}_Q$
.
Proof. Let
![]() $\alpha \in \Delta _0^Q\setminus \Delta _0^P$
. We write
$\alpha \in \Delta _0^Q\setminus \Delta _0^P$
. We write
![]() $\alpha =\alpha _P+\alpha ^P$
according to the decomposition
$\alpha =\alpha _P+\alpha ^P$
according to the decomposition
![]() $\mathfrak {a}_0^*= \mathfrak {a}_P^*\oplus \mathfrak {a}_0^{P,*}$
. Since we have
$\mathfrak {a}_0^*= \mathfrak {a}_P^*\oplus \mathfrak {a}_0^{P,*}$
. Since we have
![]() $\langle \alpha ^P,\beta ^\vee \rangle =\langle \alpha ,\beta ^\vee \rangle \leqslant 0$
for all
$\langle \alpha ^P,\beta ^\vee \rangle =\langle \alpha ,\beta ^\vee \rangle \leqslant 0$
for all
![]() $\beta \in \Delta _0^P$
, we know that
$\beta \in \Delta _0^P$
, we know that
![]() $\alpha ^P$
is a non-positive linear combination of elements of
$\alpha ^P$
is a non-positive linear combination of elements of
![]() $\hat \Delta _0^P$
. Thus, the condition
$\hat \Delta _0^P$
. Thus, the condition
![]() $F^{P}(g,T) =1$
implies that
$F^{P}(g,T) =1$
implies that
The condition
![]() $\tau _P^{Q}(H_P(g)-T)=1$
implies that we have
$\tau _P^{Q}(H_P(g)-T)=1$
implies that we have
![]() $\langle \alpha _P, H_0(g)\rangle> \langle \alpha _P, T\rangle $
. We conclude that
$\langle \alpha _P, H_0(g)\rangle> \langle \alpha _P, T\rangle $
. We conclude that
![]() $\langle \alpha , H_0(g)\rangle> \langle \alpha , T\rangle $
for all
$\langle \alpha , H_0(g)\rangle> \langle \alpha , T\rangle $
for all
![]() $\alpha \in \Delta _0^Q\setminus \Delta _0^P$
. The last assertion is then obvious since T is positive.
$\alpha \in \Delta _0^Q\setminus \Delta _0^P$
. The last assertion is then obvious since T is positive.
2.3.4
Let
![]() $\phi :\mathfrak {a}_0\to \mathbb {C}$
be a function and let
$\phi :\mathfrak {a}_0\to \mathbb {C}$
be a function and let
![]() $T\in T_0+\mathfrak {a}_0^{G,+}$
. For any standard parabolic subgroup Q of G, we define for all
$T\in T_0+\mathfrak {a}_0^{G,+}$
. For any standard parabolic subgroup Q of G, we define for all
![]() $g\in [G]_Q$
,
$g\in [G]_Q$
,
We will mainly use
![]() $d_Q(\lambda ,g,T)$
for
$d_Q(\lambda ,g,T)$
for
![]() $\lambda \in \mathfrak {a}_0^*$
. The next proposition shows that the function
$\lambda \in \mathfrak {a}_0^*$
. The next proposition shows that the function
![]() $d_Q(\lambda ,\cdot ,T)$
is an example of a function that satisfies [Reference FrankeFra98, Proposition 2.1] (such a kind of function is also used in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, § 2.4.3]).
$d_Q(\lambda ,\cdot ,T)$
is an example of a function that satisfies [Reference FrankeFra98, Proposition 2.1] (such a kind of function is also used in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, § 2.4.3]).
Proposition 2.3.4.1. Let
![]() $\lambda \in \mathfrak {a}_0^*$
and
$\lambda \in \mathfrak {a}_0^*$
and
![]() $Q\subset G$
a parabolic subgroup.
$Q\subset G$
a parabolic subgroup.
-
1. Let
 $\mathcal {T} \subset T_0+\mathfrak {a}_0^{G,+}$
be a compact subset. We have for all
$\mathcal {T} \subset T_0+\mathfrak {a}_0^{G,+}$
be a compact subset. We have for all $$ \begin{align*}\exp(\langle \lambda, H_0(g)\rangle) \sim d_Q(\lambda,g,T)\end{align*} $$
$$ \begin{align*}\exp(\langle \lambda, H_0(g)\rangle) \sim d_Q(\lambda,g,T)\end{align*} $$
 $g \in \mathfrak {s}_Q$
and
$g \in \mathfrak {s}_Q$
and
 $T\in \mathcal {T}$
. In particular, all functions
$T\in \mathcal {T}$
. In particular, all functions
 $d_Q(\lambda ,T)$
are equivalent for
$d_Q(\lambda ,T)$
are equivalent for
 $T\in \mathcal {T}$
.
$T\in \mathcal {T}$
.
-
2. Let
 $\mathcal {K}$
be a compact subset of
$\mathcal {K}$
be a compact subset of
 $G(\mathbb {A})$
and let
$G(\mathbb {A})$
and let
 $T\in T_0+\mathfrak {a}_0^{G,+}$
. We have for all
$T\in T_0+\mathfrak {a}_0^{G,+}$
. We have for all $$ \begin{align*}d_Q(\lambda,g,T)\sim d_Q(\lambda ,gc,T)\end{align*} $$
$$ \begin{align*}d_Q(\lambda,g,T)\sim d_Q(\lambda ,gc,T)\end{align*} $$
 $g \in [G]_Q$
,
$g \in [G]_Q$
,
 $c\in \mathcal {K}$
.
$c\in \mathcal {K}$
.
Proof. 1. If we write
![]() $\lambda =\lambda _Q+\lambda ^Q$
according to the decomposition
$\lambda =\lambda _Q+\lambda ^Q$
according to the decomposition
![]() $\mathfrak {a}_0^*=\mathfrak {a}_Q^{*}+\mathfrak {a}_0^{Q,*}$
, we see that
$\mathfrak {a}_0^*=\mathfrak {a}_Q^{*}+\mathfrak {a}_0^{Q,*}$
, we see that
![]() $d_Q(\lambda ,g,T)=\exp (\langle \lambda _Q,H_Q(g)\rangle ) d_Q(\lambda ^Q,g,T)$
for all
$d_Q(\lambda ,g,T)=\exp (\langle \lambda _Q,H_Q(g)\rangle ) d_Q(\lambda ^Q,g,T)$
for all
![]() $T\in T_0+\mathfrak {a}_0^+$
and all
$T\in T_0+\mathfrak {a}_0^+$
and all
![]() $g\in [G]_Q$
. Since we also have
$g\in [G]_Q$
. Since we also have
![]() $\exp (\langle \lambda , H_0(g)\rangle )= \exp (\langle \lambda _Q,H_Q(g)\rangle ) \exp (\langle \lambda ^Q,H_0(g)\rangle )$
, we may and shall assume that
$\exp (\langle \lambda , H_0(g)\rangle )= \exp (\langle \lambda _Q,H_Q(g)\rangle ) \exp (\langle \lambda ^Q,H_0(g)\rangle )$
, we may and shall assume that
![]() $\lambda \in \mathfrak {a}_0^{Q,*}$
. Let
$\lambda \in \mathfrak {a}_0^{Q,*}$
. Let
![]() $g\in \mathfrak {s}_Q$
and
$g\in \mathfrak {s}_Q$
and
![]() $T\in \mathcal {T}$
. There exists
$T\in \mathcal {T}$
. There exists
![]() $P \subset Q$
such that
$P \subset Q$
such that
![]() $F^P(g,T)\tau _P^Q(H_P(g)-T)=1$
. Then, by definition, we get
$F^P(g,T)\tau _P^Q(H_P(g)-T)=1$
. Then, by definition, we get
![]() $d_Q(\lambda ,g,T)=\exp (\langle \lambda , H_P(g)\rangle ) $
. It suffices to prove that
$d_Q(\lambda ,g,T)=\exp (\langle \lambda , H_P(g)\rangle ) $
. It suffices to prove that
![]() $H_0(g)-H_P(g)$
stays in a compact subset which depends only on
$H_0(g)-H_P(g)$
stays in a compact subset which depends only on
![]() $\mathcal {T}$
for any
$\mathcal {T}$
for any
![]() $g\in \mathfrak {s}_P$
such that
$g\in \mathfrak {s}_P$
such that
![]() $F^P(g,T)=1$
. In fact, the latter condition implies
$F^P(g,T)=1$
. In fact, the latter condition implies
![]() $\langle \varpi , H_0(g)\rangle \leqslant \langle \varpi , T\rangle $
for all
$\langle \varpi , H_0(g)\rangle \leqslant \langle \varpi , T\rangle $
for all
![]() $\varpi \in \hat \Delta ^P_0$
, and
$\varpi \in \hat \Delta ^P_0$
, and
![]() $g\in \mathfrak {s}_P$
implies that
$g\in \mathfrak {s}_P$
implies that
![]() $\langle \alpha , H_0(g)\rangle \geqslant \langle \alpha , T_-\rangle $
for all
$\langle \alpha , H_0(g)\rangle \geqslant \langle \alpha , T_-\rangle $
for all
![]() $\alpha \in \hat \Delta ^P_0$
. Hence, the projection of
$\alpha \in \hat \Delta ^P_0$
. Hence, the projection of
![]() $H_0(g)$
on
$H_0(g)$
on
![]() $\mathfrak {a}_0^{P}$
stays in a fixed compact subset, but this projection is nothing else but
$\mathfrak {a}_0^{P}$
stays in a fixed compact subset, but this projection is nothing else but
![]() $H_0(g)-H_P(g)$
.
$H_0(g)-H_P(g)$
.
2. First, we observe that
![]() $H_0(kc)$
stays in a fixed compact for
$H_0(kc)$
stays in a fixed compact for
![]() $k\in K$
and
$k\in K$
and
![]() $c\in \mathcal {K}$
. By assertion 1, we may replace T by any element in
$c\in \mathcal {K}$
. By assertion 1, we may replace T by any element in
![]() $T_0+\mathfrak {a}_0^{G,+}$
. In particular, we may and shall assume that T is such that
$T_0+\mathfrak {a}_0^{G,+}$
. In particular, we may and shall assume that T is such that
![]() $T-H_0(kc)\in T_0+\mathfrak {a}_0^{G,+}$
for all
$T-H_0(kc)\in T_0+\mathfrak {a}_0^{G,+}$
for all
![]() $k\in K$
and
$k\in K$
and
![]() $c\in \mathcal {K}$
. For any
$c\in \mathcal {K}$
. For any
![]() $g\in G(\mathbb {A})$
, we shall denote
$g\in G(\mathbb {A})$
, we shall denote
![]() $k(g)$
an element of K such that
$k(g)$
an element of K such that
![]() $gk(g)^{-1}\in P_0(\mathbb {A})$
.
$gk(g)^{-1}\in P_0(\mathbb {A})$
.
Let
![]() $g\in G(\mathbb {A})$
and
$g\in G(\mathbb {A})$
and
![]() $c\in \mathcal {K}$
. Then there exist a unique parabolic sugroup
$c\in \mathcal {K}$
. Then there exist a unique parabolic sugroup
![]() $P \subset Q$
and
$P \subset Q$
and
![]() $\delta \in Q(F)$
such that
$\delta \in Q(F)$
such that
![]() $F^P(\delta gc,T)\tau _P^Q(H_P(\delta gc)-T)=1$
. Observe that
$F^P(\delta gc,T)\tau _P^Q(H_P(\delta gc)-T)=1$
. Observe that
![]() $H_0(\delta gc)=H_0(\delta g)+H_0(k(\delta g) c)$
. We deduce on the one hand that
$H_0(\delta gc)=H_0(\delta g)+H_0(k(\delta g) c)$
. We deduce on the one hand that
![]() $\tau _P^Q(H_P(\delta g)-(T-H_0(k(\delta g)c))=1$
is equivalent to
$\tau _P^Q(H_P(\delta g)-(T-H_0(k(\delta g)c))=1$
is equivalent to
![]() $\tau _P^Q(H_P(\delta gc)-T)=1$
, and on the other hand, we also have
$\tau _P^Q(H_P(\delta gc)-T)=1$
, and on the other hand, we also have
![]() $F^P(\delta g,T-H_0(k(\delta g)c))=1$
; indeed, for all
$F^P(\delta g,T-H_0(k(\delta g)c))=1$
; indeed, for all
![]() $\varpi \in \hat \Delta ^P$
, we have
$\varpi \in \hat \Delta ^P$
, we have
 $$ \begin{align*} \langle \varpi,H_0(\delta g)\rangle&= \langle \varpi,H_0(\delta gc)\rangle - \langle \varpi,H_0(k(\delta g) c)\rangle \\ &\leqslant \langle \varpi,T - H_0(k(\delta g) c)\rangle \end{align*} $$
$$ \begin{align*} \langle \varpi,H_0(\delta g)\rangle&= \langle \varpi,H_0(\delta gc)\rangle - \langle \varpi,H_0(k(\delta g) c)\rangle \\ &\leqslant \langle \varpi,T - H_0(k(\delta g) c)\rangle \end{align*} $$
since
![]() $F^{P}(\delta gc,T)=1$
. From this, we get
$F^{P}(\delta gc,T)=1$
. From this, we get
Using assertion 1 and the fact that
![]() $H_0(k(\delta g) c)$
stays in a fixed compact set, we can easily conclude.
$H_0(k(\delta g) c)$
stays in a fixed compact set, we can easily conclude.
Lemma 2.3.4.2. Let
![]() $Q\subset R$
be standard parabolic subgroups of G. There exists
$Q\subset R$
be standard parabolic subgroups of G. There exists
![]() $T_1\in T_0+\mathfrak {a}_0^{G,+}$
such that for all
$T_1\in T_0+\mathfrak {a}_0^{G,+}$
such that for all
![]() $T\in T_1+\mathfrak {a}_0^{G,+}$
, all
$T\in T_1+\mathfrak {a}_0^{G,+}$
, all
![]() $\lambda \in \mathfrak {a}_0^*$
and all
$\lambda \in \mathfrak {a}_0^*$
and all
![]() $g\in G(\mathbb {A})$
such that
$g\in G(\mathbb {A})$
such that
![]() $F^{Q}(g,T)\tau _Q^{R}(H_Q(g)-T)=1$
, we have
$F^{Q}(g,T)\tau _Q^{R}(H_Q(g)-T)=1$
, we have
Proof. Both the hypothesis and the conclusion are invariant under left translation by
![]() $Q(F)$
. It suffices to prove the result for
$Q(F)$
. It suffices to prove the result for
![]() $g\in \mathfrak {s}_Q$
such that
$g\in \mathfrak {s}_Q$
such that
![]() $F^{Q}(g,T)\tau _Q^{R}(H_Q(g)-T)=1$
. First, there exists a unique standard parabolic subgroup
$F^{Q}(g,T)\tau _Q^{R}(H_Q(g)-T)=1$
. First, there exists a unique standard parabolic subgroup
![]() $P\subset Q$
such that
$P\subset Q$
such that
![]() $F^{P}(g,T_0)\tau _P^{Q}(H_Q(g)-T_0)=1$
. In the proof of Proposition 2.3.4.1, we have shown that
$F^{P}(g,T_0)\tau _P^{Q}(H_Q(g)-T_0)=1$
. In the proof of Proposition 2.3.4.1, we have shown that
![]() $H_0(g)-H_P(g)$
stays in a fixed compact subset for
$H_0(g)-H_P(g)$
stays in a fixed compact subset for
![]() $g\in \mathfrak {s}_Q$
such that
$g\in \mathfrak {s}_Q$
such that
![]() $F^{P}(g,T_0)=1$
. In particular, we can assume that for such elements g, we have
$F^{P}(g,T_0)=1$
. In particular, we can assume that for such elements g, we have
By Lemma 2.3.3.1, we have
![]() $\langle \alpha , H_0(g)\rangle> \langle \alpha , T\rangle $
for all
$\langle \alpha , H_0(g)\rangle> \langle \alpha , T\rangle $
for all
![]() $\alpha \in \Delta _0^R\setminus \Delta _0^Q$
. So we have for all
$\alpha \in \Delta _0^R\setminus \Delta _0^Q$
. So we have for all
![]() $\alpha \in \Delta _0^R\setminus \Delta _0^Q$
,
$\alpha \in \Delta _0^R\setminus \Delta _0^Q$
,
 $$ \begin{align*} \langle \alpha_P, H_0(g)\rangle = \langle \alpha, H_P(g)\rangle&= \langle \alpha, H_0(g)\rangle+ \langle \alpha, H_P(g)-H_0(g)\rangle\\ &> \langle \alpha, T\rangle+ \langle \alpha, H_P(g)-H_0(g)\rangle\\ &\geqslant \langle \alpha, T_1 \rangle + \langle \alpha, H_P(g)-H_0(g)\rangle\\ &>\langle \alpha_P,T_0\rangle \end{align*} $$
$$ \begin{align*} \langle \alpha_P, H_0(g)\rangle = \langle \alpha, H_P(g)\rangle&= \langle \alpha, H_0(g)\rangle+ \langle \alpha, H_P(g)-H_0(g)\rangle\\ &> \langle \alpha, T\rangle+ \langle \alpha, H_P(g)-H_0(g)\rangle\\ &\geqslant \langle \alpha, T_1 \rangle + \langle \alpha, H_P(g)-H_0(g)\rangle\\ &>\langle \alpha_P,T_0\rangle \end{align*} $$
by (2.3.4.1). In particular, we see that we have
![]() $\tau _P^{R}(H_Q(g)-T_0)=1$
. Thus, by definition,
$\tau _P^{R}(H_Q(g)-T_0)=1$
. Thus, by definition,
![]() $d_R(\lambda ,g,T_0)=\exp (\langle \lambda ,H_P(g)\rangle )=d_Q(\lambda ,g,T_0)$
.
$d_R(\lambda ,g,T_0)=\exp (\langle \lambda ,H_P(g)\rangle )=d_Q(\lambda ,g,T_0)$
.
Proposition 2.3.4.3. Let
![]() $Q\subset R$
be standard parabolic subgroups of G such that
$Q\subset R$
be standard parabolic subgroups of G such that
![]() $\Delta _0^R\setminus \Delta _0^Q =\{\alpha \}$
for some simple root
$\Delta _0^R\setminus \Delta _0^Q =\{\alpha \}$
for some simple root
![]() $\alpha $
. Let c such that
$\alpha $
. Let c such that
![]() $c> \langle \alpha , T_{0,P}\rangle $
for all parabolic subgroups
$c> \langle \alpha , T_{0,P}\rangle $
for all parabolic subgroups
![]() $P\subset Q$
.
$P\subset Q$
.
For any
![]() $g\in G(\mathbb {A})$
, there is at most one element
$g\in G(\mathbb {A})$
, there is at most one element
![]() $\delta \in Q(F)\backslash R(F)$
such that
$\delta \in Q(F)\backslash R(F)$
such that
![]() $d_Q(\alpha ,\delta g,T_0)>\exp (c)$
.
$d_Q(\alpha ,\delta g,T_0)>\exp (c)$
.
Proof. Let
![]() $g\in G(\mathbb {A})$
such that
$g\in G(\mathbb {A})$
such that
![]() $d_Q(\alpha , g,T_0)>\exp (c)$
. Using left translations by
$d_Q(\alpha , g,T_0)>\exp (c)$
. Using left translations by
![]() $Q(F)$
, we may and shall assume that there exists a standard parabolic subgroup
$Q(F)$
, we may and shall assume that there exists a standard parabolic subgroup
![]() $P\subset Q$
such that
$P\subset Q$
such that
![]() $F^P(g,T_0) \tau _P^Q(H_P( g)-T_0)=1$
. Then the condition
$F^P(g,T_0) \tau _P^Q(H_P( g)-T_0)=1$
. Then the condition
![]() $d_Q(\alpha , g,T_0)>\exp (c)$
is equivalent to
$d_Q(\alpha , g,T_0)>\exp (c)$
is equivalent to
![]() $\langle \alpha , H_P(g)\rangle>c$
, and so
$\langle \alpha , H_P(g)\rangle>c$
, and so
![]() $\langle \alpha , H_P(g)\rangle>\langle \alpha , T_{0,P}\rangle $
. So we have also
$\langle \alpha , H_P(g)\rangle>\langle \alpha , T_{0,P}\rangle $
. So we have also
![]() $F^P(g,T_0) \tau _P^R(H_P( g)-T_0)=1$
. Now the uniqueness follows from the partition (2.3.3.1) applies to
$F^P(g,T_0) \tau _P^R(H_P( g)-T_0)=1$
. Now the uniqueness follows from the partition (2.3.3.1) applies to
![]() $[G]_R$
.
$[G]_R$
.
3 On the spectral expansion of the Jacquet-Rallis trace formula for unitary groups
3.1 Notations
3.1.1
Let
![]() $E/F$
be a quadratic extension of number fields and c be the nontrivial element of the Galois group
$E/F$
be a quadratic extension of number fields and c be the nontrivial element of the Galois group
![]() $\operatorname {\mathrm {Gal}}(E/F)$
. Let
$\operatorname {\mathrm {Gal}}(E/F)$
. Let
![]() $\mathbb {A}$
be the ring of adèles of F. Let
$\mathbb {A}$
be the ring of adèles of F. Let
![]() $n\geqslant 0$
be an integer. Let
$n\geqslant 0$
be an integer. Let
![]() $\mathcal {H}_n$
be the set of isomorphism classes of pairs
$\mathcal {H}_n$
be the set of isomorphism classes of pairs
![]() $(V,h)$
, where V is a E-vector space of dimension n and h a nondegenerate c-Hermitian form on V. For any
$(V,h)$
, where V is a E-vector space of dimension n and h a nondegenerate c-Hermitian form on V. For any
![]() $(V,h)\in \mathcal {H}_n$
, we identify
$(V,h)\in \mathcal {H}_n$
, we identify
![]() $(V,h)$
with a representative, and we shall denote by
$(V,h)$
with a representative, and we shall denote by
![]() $U(V,h)$
or simply
$U(V,h)$
or simply
![]() $U(h)$
its automorphisms group. We will fix
$U(h)$
its automorphisms group. We will fix
![]() $(V_0,h_0)\in \mathcal {H}_1$
.
$(V_0,h_0)\in \mathcal {H}_1$
.
3.1.2
We attach to any
![]() $h\in \mathcal {H}_n$
the following algebraic groups over F:
$h\in \mathcal {H}_n$
the following algebraic groups over F:
-
• the unitary group
 $U^{\prime }_h=U(h)$
of automorphisms of h;
$U^{\prime }_h=U(h)$
of automorphisms of h; -
• the unitary group
 $U^{\prime \prime }_h= U(h\oplus h_0) $
where
$U^{\prime \prime }_h= U(h\oplus h_0) $
where
 $h\oplus h_0$
denoted the orthogonal sum;
$h\oplus h_0$
denoted the orthogonal sum; -
• the product of unitary groups
 $U_h=U_h^{\prime }\times U_h^{\prime \prime }$
.
$U_h=U_h^{\prime }\times U_h^{\prime \prime }$
.
We have an embedding
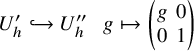 $$ \begin{align} U_h^{\prime}\hookrightarrow U_h^{\prime\prime} \ \ \ g\mapsto \begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix} \end{align} $$
$$ \begin{align} U_h^{\prime}\hookrightarrow U_h^{\prime\prime} \ \ \ g\mapsto \begin{pmatrix} g & 0 \\ 0 & 1 \end{pmatrix} \end{align} $$
and a diagonal embedding
![]() $U^{\prime }_h\hookrightarrow U_h$
.
$U^{\prime }_h\hookrightarrow U_h$
.
3.1.3
Let
![]() $n\geqslant 1$
be an integer and
$n\geqslant 1$
be an integer and
![]() $(V,h)\in \mathcal {H}_n$
. We fix a parabolic subgroup
$(V,h)\in \mathcal {H}_n$
. We fix a parabolic subgroup
![]() $P_0^{\prime }$
of
$P_0^{\prime }$
of
![]() $U_h^{\prime }$
and a Levi factor
$U_h^{\prime }$
and a Levi factor
![]() $M_0^{\prime }$
of
$M_0^{\prime }$
of
![]() $P_0^{\prime }$
both defined over F and minimal for these properties. As a parabolic subgroup,
$P_0^{\prime }$
both defined over F and minimal for these properties. As a parabolic subgroup,
![]() $P_0^{\prime }$
is the stabilizer of a flag of totally isotropic subspaces of V. Let
$P_0^{\prime }$
is the stabilizer of a flag of totally isotropic subspaces of V. Let
![]() $P_0^{\prime \prime }$
be the parabolic subgroup of
$P_0^{\prime \prime }$
be the parabolic subgroup of
![]() $U^{\prime \prime }_h$
stabilizing the same flag. Let
$U^{\prime \prime }_h$
stabilizing the same flag. Let
![]() $M_0^{\prime \prime }$
be the unique Levi factor of
$M_0^{\prime \prime }$
be the unique Levi factor of
![]() $P_0^{\prime \prime }$
that contains
$P_0^{\prime \prime }$
that contains
![]() $M_0^{\prime }$
. Then
$M_0^{\prime }$
. Then
![]() $P_0=P_0^{\prime }\times P_0^{\prime \prime }$
is a parabolic subgroup of
$P_0=P_0^{\prime }\times P_0^{\prime \prime }$
is a parabolic subgroup of
![]() $U_h$
with Levi factor
$U_h$
with Levi factor
![]() $M_0=M_0^{\prime }\times M_0^{\prime \prime }$
. We fix also a pair
$M_0=M_0^{\prime }\times M_0^{\prime \prime }$
. We fix also a pair
![]() $(B_0^{\prime \prime },T_0^{\prime \prime })$
consisting of a minimal parabolic F-subgroup of
$(B_0^{\prime \prime },T_0^{\prime \prime })$
consisting of a minimal parabolic F-subgroup of
![]() $U_h^{\prime \prime }$
and a Levi factor defined over F. We may and shall assume
$U_h^{\prime \prime }$
and a Levi factor defined over F. We may and shall assume
![]() $B_0^{\prime \prime }\subset P_0^{\prime \prime }$
and
$B_0^{\prime \prime }\subset P_0^{\prime \prime }$
and
![]() $T_0^{\prime \prime }\subset M_0^{\prime \prime }$
. We fix maximal good compact subgroups
$T_0^{\prime \prime }\subset M_0^{\prime \prime }$
. We fix maximal good compact subgroups
![]() $K_h^{\prime }\subset U_h^{\prime }(\mathbb {A})$
and
$K_h^{\prime }\subset U_h^{\prime }(\mathbb {A})$
and
![]() $K_h^{\prime \prime }\subset U_h^{\prime \prime }(\mathbb {A})$
, respectively, in good position relative to
$K_h^{\prime \prime }\subset U_h^{\prime \prime }(\mathbb {A})$
, respectively, in good position relative to
![]() $M_0^{\prime }$
and
$M_0^{\prime }$
and
![]() $T_0^{\prime \prime }$
in the sense of §2.1.6. We set
$T_0^{\prime \prime }$
in the sense of §2.1.6. We set
![]() $K_h=K_h^{\prime }\times K_h^{\prime \prime }\subset U_h(\mathbb {A})$
. Any
$K_h=K_h^{\prime }\times K_h^{\prime \prime }\subset U_h(\mathbb {A})$
. Any
![]() $g\in U_h=U_h^{\prime }\times U_h^{\prime \prime }$
will be written
$g\in U_h=U_h^{\prime }\times U_h^{\prime \prime }$
will be written
![]() $(g',g")$
without any further comment.
$(g',g")$
without any further comment.
From now on,
![]() $(V,h)$
is fixed, and we shall omit it in the notations; thus, we have
$(V,h)$
is fixed, and we shall omit it in the notations; thus, we have
![]() $U=U_h$
,
$U=U_h$
,
![]() $U'=U^{\prime }_h $
and so on.
$U'=U^{\prime }_h $
and so on.
3.1.4
Let
![]() $\mathcal {F}_0^{\prime }$
be the set of parabolic subgroups of
$\mathcal {F}_0^{\prime }$
be the set of parabolic subgroups of
![]() $U'$
that contain
$U'$
that contain
![]() $P_0^{\prime }$
. For any
$P_0^{\prime }$
. For any
![]() $P'\in \mathcal {F}_0^{\prime }$
, let
$P'\in \mathcal {F}_0^{\prime }$
, let
![]() $P"$
be the parabolic subgroup of
$P"$
be the parabolic subgroup of
![]() $U'$
which stabilizes the flag of totally isotropic subspaces of V that defines
$U'$
which stabilizes the flag of totally isotropic subspaces of V that defines
![]() $P'$
. Note that
$P'$
. Note that
![]() $P"\cap U'=P'$
. We get a one-to-one map
$P"\cap U'=P'$
. We get a one-to-one map
from
![]() $\mathcal {F}_0^{\prime }$
onto a subset, denoted by
$\mathcal {F}_0^{\prime }$
onto a subset, denoted by
![]() $\mathcal {F}_0$
of parabolic subgroups of U. For any standard parabolic subgroup
$\mathcal {F}_0$
of parabolic subgroups of U. For any standard parabolic subgroup
![]() $P'$
of
$P'$
of
![]() $U'$
, resp.
$U'$
, resp.
![]() $P"$
of
$P"$
of
![]() $U"$
, resp. P of U, we will denote by
$U"$
, resp. P of U, we will denote by
![]() $\Delta _0^{P'}$
, resp.
$\Delta _0^{P'}$
, resp.
![]() $\Delta _0^{P"}$
, resp.
$\Delta _0^{P"}$
, resp.
![]() $\Delta _0^{P}$
, the set of simple roots of
$\Delta _0^{P}$
, the set of simple roots of
![]() $A_{M_0^{\prime }}$
, resp.
$A_{M_0^{\prime }}$
, resp.
![]() $A_{T_0^{\prime \prime }}$
, resp.
$A_{T_0^{\prime \prime }}$
, resp.
![]() $A_{M_0^{\prime }\times T_0^{\prime \prime }}$
in
$A_{M_0^{\prime }\times T_0^{\prime \prime }}$
in
![]() $P_0^{\prime }\cap M_{P'}$
, resp.
$P_0^{\prime }\cap M_{P'}$
, resp.
![]() $B_0^{\prime \prime }\cap M_{P"}$
, resp.
$B_0^{\prime \prime }\cap M_{P"}$
, resp.
![]() $(P_0^{\prime }\times B_0^{\prime \prime })\cap M_P$
. We set
$(P_0^{\prime }\times B_0^{\prime \prime })\cap M_P$
. We set
![]() $\mathfrak {a}_0^{\prime }=\mathfrak {a}_{M_0^{\prime }}=\mathfrak {a}_{P_0^{\prime }}$
. The inclusion
$\mathfrak {a}_0^{\prime }=\mathfrak {a}_{M_0^{\prime }}=\mathfrak {a}_{P_0^{\prime }}$
. The inclusion
![]() $P_0^{\prime }\subset P_0^{\prime \prime }$
gives an identification
$P_0^{\prime }\subset P_0^{\prime \prime }$
gives an identification
![]() $\mathfrak {a}_{P_0^{\prime \prime }}=\mathfrak {a}_{P_0^{\prime }}=\mathfrak {a}_0^{\prime }$
. Using the map
$\mathfrak {a}_{P_0^{\prime \prime }}=\mathfrak {a}_{P_0^{\prime }}=\mathfrak {a}_0^{\prime }$
. Using the map
![]() $a_{B_0^{\prime \prime }}^*\to \mathfrak {a}_{P_0^{\prime \prime }}^*=\mathfrak {a}_{P_0^{\prime }}^*$
dual to the inclusion
$a_{B_0^{\prime \prime }}^*\to \mathfrak {a}_{P_0^{\prime \prime }}^*=\mathfrak {a}_{P_0^{\prime }}^*$
dual to the inclusion
![]() $A_{P_0^{\prime \prime }}\subset A_{T_0^{\prime \prime }}$
, we see that any
$A_{P_0^{\prime \prime }}\subset A_{T_0^{\prime \prime }}$
, we see that any
![]() $\lambda \in \mathfrak {a}_{B_0^{\prime \prime }}^*$
defined a linear map
$\lambda \in \mathfrak {a}_{B_0^{\prime \prime }}^*$
defined a linear map
![]() $\mathfrak {a}_0^{\prime }\to \mathbb {R}$
still denoted by
$\mathfrak {a}_0^{\prime }\to \mathbb {R}$
still denoted by
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $P'\in \mathcal {F}_0^{\prime }$
and
$P'\in \mathcal {F}_0^{\prime }$
and
![]() $P"\subset U"$
be the associated parabolic subgroup. Observe that if
$P"\subset U"$
be the associated parabolic subgroup. Observe that if
![]() $\lambda $
is a simple root
$\lambda $
is a simple root
![]() $\tilde \alpha \in \Delta _0^{U"}\setminus \Delta _0^{P"}$
, the linear map
$\tilde \alpha \in \Delta _0^{U"}\setminus \Delta _0^{P"}$
, the linear map
![]() $\mathfrak {a}_0^{\prime }\to \mathbb {R}$
we get is equal, up to a positive constant, to a unique root
$\mathfrak {a}_0^{\prime }\to \mathbb {R}$
we get is equal, up to a positive constant, to a unique root
![]() $\alpha \in \Delta _0^{U'}\setminus \Delta _0^{P'}$
.
$\alpha \in \Delta _0^{U'}\setminus \Delta _0^{P'}$
.
Following §2.3.2, we have the notion of Siegel domains. They depend on auxiliary choices
![]() $\omega _0^{\prime },T_-'$
for
$\omega _0^{\prime },T_-'$
for
![]() $U'$
and
$U'$
and
![]() $\omega _0^{\prime \prime },T_-"$
for
$\omega _0^{\prime \prime },T_-"$
for
![]() $U"$
. The Siegel domains for
$U"$
. The Siegel domains for
![]() $U=U'\times U"$
will be the product of Siegel domains for
$U=U'\times U"$
will be the product of Siegel domains for
![]() $U'$
and
$U'$
and
![]() $U"$
. We may and shall assume that
$U"$
. We may and shall assume that
![]() $T_-'$
and
$T_-'$
and
![]() $T_-"$
are chosen so that
$T_-"$
are chosen so that
We fix a height
![]() $\|\cdot \|$
on
$\|\cdot \|$
on
![]() $U(\mathbb {A})$
; see §2.1.7. By (diagonal) restriction, this gives a height on
$U(\mathbb {A})$
; see §2.1.7. By (diagonal) restriction, this gives a height on
![]() $U'(\mathbb {A})$
. Note that for P and
$U'(\mathbb {A})$
. Note that for P and
![]() $P'$
as above, we have
$P'$
as above, we have
![]() $\|x\|_{P'}\sim \|x\|_P$
for
$\|x\|_{P'}\sim \|x\|_P$
for
![]() $x\in U'(\mathbb {A})$
, as it follows from [Reference Beuzart-PlessisBeu21, proposition A.1.1 (ix)].
$x\in U'(\mathbb {A})$
, as it follows from [Reference Beuzart-PlessisBeu21, proposition A.1.1 (ix)].
3.1.5
We fix a point
![]() $T_0\in \mathfrak {a}_{0}'$
as in §2.3.3, and we set
$T_0\in \mathfrak {a}_{0}'$
as in §2.3.3, and we set
for any
![]() $P'\in \mathcal {F}^{\prime }_0$
and
$P'\in \mathcal {F}^{\prime }_0$
and
![]() $\lambda \in \mathfrak {a}_0^*$
. The precise choice of
$\lambda \in \mathfrak {a}_0^*$
. The precise choice of
![]() $T_0$
is irrelevant in the sequel, and we will not use this notation anymore. We proceed in the same way to define
$T_0$
is irrelevant in the sequel, and we will not use this notation anymore. We proceed in the same way to define
![]() $d_{P"}(\lambda )$
.
$d_{P"}(\lambda )$
.
Proposition 3.1.5.1.
-
1. Let
 $\lambda \in \mathfrak {a}_{B_0^{\prime \prime }}^*$
. We have (3.1.5.1)
$\lambda \in \mathfrak {a}_{B_0^{\prime \prime }}^*$
. We have (3.1.5.1) $$ \begin{align} d_{P"}(\lambda,x)\sim d_{P'}(\lambda,x) \ \ x\in [U']_{P'}. \end{align} $$
$$ \begin{align} d_{P"}(\lambda,x)\sim d_{P'}(\lambda,x) \ \ x\in [U']_{P'}. \end{align} $$
-
2. For
 $\tilde \alpha \in \Delta _0^{U"}\setminus \Delta _0^{P"}$
, there exists
$\tilde \alpha \in \Delta _0^{U"}\setminus \Delta _0^{P"}$
, there exists
 $r>0$
such that where
$r>0$
such that where $$ \begin{align*} d_{P"}(\tilde\alpha,x)\sim d_{P'}(\alpha,x)^r \ \ x\in [U']_{P'}, \end{align*} $$
$$ \begin{align*} d_{P"}(\tilde\alpha,x)\sim d_{P'}(\alpha,x)^r \ \ x\in [U']_{P'}, \end{align*} $$
 $\alpha \in \Delta _0^{U'}\setminus \Delta _0^{P'}$
is deduced from
$\alpha \in \Delta _0^{U'}\setminus \Delta _0^{P'}$
is deduced from
 $\tilde \alpha $
as above.
$\tilde \alpha $
as above.
Proof. 1. Both sides of (3.1.5.1) are invariant by left
![]() $P'(F)$
-translation. Thus, it suffices to prove the equivalence on
$P'(F)$
-translation. Thus, it suffices to prove the equivalence on
![]() $\mathfrak {s}_{P'}= \omega _0^{\prime } A_{P_0^{\prime }}^{P',\infty }(T_-') K'$
. Note that if
$\mathfrak {s}_{P'}= \omega _0^{\prime } A_{P_0^{\prime }}^{P',\infty }(T_-') K'$
. Note that if
![]() $a\in A_{P_0^{\prime }}^{P',\infty }(T_-')$
, then
$a\in A_{P_0^{\prime }}^{P',\infty }(T_-')$
, then
![]() $a^{-1}\omega _0^{\prime }a $
is included in a fixed compact subset
$a^{-1}\omega _0^{\prime }a $
is included in a fixed compact subset
![]() $\mathcal {K}\subset U'(\mathbb {A})$
that does not depend on a. Thus, by Proposition 2.3.4.1 assertion 2, we have
$\mathcal {K}\subset U'(\mathbb {A})$
that does not depend on a. Thus, by Proposition 2.3.4.1 assertion 2, we have
![]() $d_{P"}(xa k)\sim d_{P"}(a)$
for
$d_{P"}(xa k)\sim d_{P"}(a)$
for
![]() $x\in \omega _0^{\prime }$
,
$x\in \omega _0^{\prime }$
,
![]() $a\in A_{P_0^{\prime }}^{P',\infty }(T_-')$
and
$a\in A_{P_0^{\prime }}^{P',\infty }(T_-')$
and
![]() $k\in K'$
. By the inclusion (3.1.4.2) and Proposition 2.3.4.1 assertion 1, we have
$k\in K'$
. By the inclusion (3.1.4.2) and Proposition 2.3.4.1 assertion 1, we have
![]() $d_{P"}(a)\sim \exp (\langle \lambda , H_{B_0^{\prime \prime }}(a)\rangle )$
for
$d_{P"}(a)\sim \exp (\langle \lambda , H_{B_0^{\prime \prime }}(a)\rangle )$
for
![]() $a\in A_{P_0^{\prime }}^{P',\infty }(T_-')$
. Then we have
$a\in A_{P_0^{\prime }}^{P',\infty }(T_-')$
. Then we have
![]() $H_{B_0^{\prime \prime }}(a)=H_{P_0^{\prime }}(a)=H_{P_0^{\prime }}(xak)$
and
$H_{B_0^{\prime \prime }}(a)=H_{P_0^{\prime }}(a)=H_{P_0^{\prime }}(xak)$
and
![]() $\exp (\langle \lambda , H_{B_0^{\prime \prime }}(a)\rangle ) \sim d_{P'}(\lambda ,xak)$
by Proposition 2.3.4.1 assertion 1 applied to
$\exp (\langle \lambda , H_{B_0^{\prime \prime }}(a)\rangle ) \sim d_{P'}(\lambda ,xak)$
by Proposition 2.3.4.1 assertion 1 applied to
![]() $P'$
. 2. is a consequence of 1 and the fact that the restriction of
$P'$
. 2. is a consequence of 1 and the fact that the restriction of
![]() $\tilde \alpha $
to
$\tilde \alpha $
to
![]() $\mathfrak {a}_0^{\prime }$
is
$\mathfrak {a}_0^{\prime }$
is
![]() $r\alpha $
for some
$r\alpha $
for some
![]() $r>0$
.
$r>0$
.
3.1.6 Sufficiently positive T
We will fix an euclidean norm
![]() $\lVert .\rVert $
on
$\lVert .\rVert $
on
![]() $\mathfrak {a}_0^{\prime }$
, invariant by the Weyl group. For
$\mathfrak {a}_0^{\prime }$
, invariant by the Weyl group. For
![]() $T\in \mathfrak {a}_{0}'$
, let
$T\in \mathfrak {a}_{0}'$
, let
We will fix
![]() $C>0$
and
$C>0$
and
![]() $\varepsilon>0$
, respectively, large and small enough constants. We shall throughout assume that T is ‘sufficiently positive’; that is, we assume T satisfies the inequality
$\varepsilon>0$
, respectively, large and small enough constants. We shall throughout assume that T is ‘sufficiently positive’; that is, we assume T satisfies the inequality
![]() $d(T)\geqslant \max (\varepsilon \lVert T\rVert ,C)$
. In particular, we shall assume that Lemma 2.3.4.2 holds for any sufficiently positive T and our functions
$d(T)\geqslant \max (\varepsilon \lVert T\rVert ,C)$
. In particular, we shall assume that Lemma 2.3.4.2 holds for any sufficiently positive T and our functions
![]() $d_{P'}(\lambda )$
and
$d_{P'}(\lambda )$
and
![]() $d_{P"}(\lambda )$
.
$d_{P"}(\lambda )$
.
3.2 Truncated kernel
3.2.1
Let
![]() $f\in \mathcal {S}(U(\mathbb {A}))$
. For any cuspidal datum
$f\in \mathcal {S}(U(\mathbb {A}))$
. For any cuspidal datum
![]() $\chi \in \mathfrak {X}(U)$
and any standard parabolic subgroup P of U, we get kernels
$\chi \in \mathfrak {X}(U)$
and any standard parabolic subgroup P of U, we get kernels
![]() $K_{f,P}$
, resp.
$K_{f,P}$
, resp.
![]() $K_{f,P,\chi }$
; see §2.2.5. If
$K_{f,P,\chi }$
; see §2.2.5. If
![]() $P=U$
, we shall omit the subscript U.
$P=U$
, we shall omit the subscript U.
3.2.2
For any
![]() $T\in \mathfrak {a}_0^{\prime }$
,
$T\in \mathfrak {a}_0^{\prime }$
,
![]() $x,y\in U'(\mathbb {A})$
and
$x,y\in U'(\mathbb {A})$
and
![]() $\chi \in \mathfrak {X}(U)$
, we set
$\chi \in \mathfrak {X}(U)$
, we set
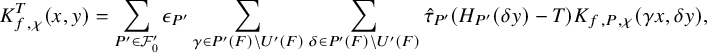 $$ \begin{align} K_{f,\chi}^{T}(x,y) = \sum_{ P'\in \mathcal{F}_0^{\prime}} \epsilon_{P'} \sum_{\gamma \in P'(F)\backslash U'(F)} \sum_{\delta \in P' (F) \backslash U'(F)} \hat \tau_{P'}(H_{P'}(\delta y ) - T)K_{f,P, \chi}(\gamma x, \delta y), \end{align} $$
$$ \begin{align} K_{f,\chi}^{T}(x,y) = \sum_{ P'\in \mathcal{F}_0^{\prime}} \epsilon_{P'} \sum_{\gamma \in P'(F)\backslash U'(F)} \sum_{\delta \in P' (F) \backslash U'(F)} \hat \tau_{P'}(H_{P'}(\delta y ) - T)K_{f,P, \chi}(\gamma x, \delta y), \end{align} $$
where we set
and
![]() $K_{f,P, \chi }$
is the kernel attached to the parabolic subgroup P of U image of
$K_{f,P, \chi }$
is the kernel attached to the parabolic subgroup P of U image of
![]() $P'$
by (3.1.4.1). Recall that we set
$P'$
by (3.1.4.1). Recall that we set
![]() $\hat \tau _{P'}=\hat \tau _{P'}^{U'}$
.
$\hat \tau _{P'}=\hat \tau _{P'}^{U'}$
.
Remark 3.2.2.1. This is the kernel used in [Reference ZydorZyd20] for compactly supported functions. Since we consider more general test functions, we need a comment here. Let P and
![]() $P'$
be as above. First, the sum over
$P'$
be as above. First, the sum over
![]() $\delta \in P' (F) \backslash U'(F)$
may be taken in a finite set which depends on y (see [Reference ArthurArt78] Lemma 5.1). Second, by [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Lemma 2.10.1.1], there exists
$\delta \in P' (F) \backslash U'(F)$
may be taken in a finite set which depends on y (see [Reference ArthurArt78] Lemma 5.1). Second, by [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Lemma 2.10.1.1], there exists
![]() $N_0>0$
such that for any
$N_0>0$
such that for any
![]() $N>0$
and any continuous semi-norm
$N>0$
and any continuous semi-norm
![]() $\|\cdot \|_{N'}$
on
$\|\cdot \|_{N'}$
on
![]() $\mathcal {T}_{N'}([U]_P)$
with
$\mathcal {T}_{N'}([U]_P)$
with
![]() $N'=N+N_0$
, there exists a continuous semi-norm
$N'=N+N_0$
, there exists a continuous semi-norm
![]() $\|\cdot \|_{\mathcal {S}}$
on
$\|\cdot \|_{\mathcal {S}}$
on
![]() $\mathcal {S}(U(\mathbb {A}))$
such that we have
$\mathcal {S}(U(\mathbb {A}))$
such that we have
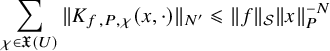 $$ \begin{align} \sum_{\chi\in \mathfrak{X}(U)} \|K_{f,P,\chi}(x,\cdot)\|_{N'} \leqslant \|f\|_{\mathcal{S}} \|x\|_P^{-N} \end{align} $$
$$ \begin{align} \sum_{\chi\in \mathfrak{X}(U)} \|K_{f,P,\chi}(x,\cdot)\|_{N'} \leqslant \|f\|_{\mathcal{S}} \|x\|_P^{-N} \end{align} $$
for all
![]() $x\in [U]_P$
and
$x\in [U]_P$
and
![]() $f\in \mathcal {S}(U(\mathbb {A}))$
. It follows that the sum over
$f\in \mathcal {S}(U(\mathbb {A}))$
. It follows that the sum over
![]() $\gamma \in P'(F)\backslash U'(F)$
is absolutely convergent.
$\gamma \in P'(F)\backslash U'(F)$
is absolutely convergent.
3.2.3
The next theorem is an extension to Schwartz test functions of the work of Zydor in [Reference ZydorZyd20, section 4]. The proof will be given in subsection 3.4 below.
Theorem 3.2.3.1. Let
![]() $T \in \mathfrak {a}_{0}'$
be sufficiently positive.
$T \in \mathfrak {a}_{0}'$
be sufficiently positive.
-
1. We have
 $$\begin{align*}\sum_{\chi \in \mathfrak{X}(U)} \int_{[U']\times [U']}| K^T_{f,\chi}(x,y) | \, dxdy < \infty. \end{align*}$$
$$\begin{align*}\sum_{\chi \in \mathfrak{X}(U)} \int_{[U']\times [U']}| K^T_{f,\chi}(x,y) | \, dxdy < \infty. \end{align*}$$
-
2. Let
 $\chi \in \mathfrak {X}(U)$
. As a function of T, the integral (3.2.3.1)coincides with an exponential-polynomial function in T whose purely polynomial part is constant and denoted by
$\chi \in \mathfrak {X}(U)$
. As a function of T, the integral (3.2.3.1)coincides with an exponential-polynomial function in T whose purely polynomial part is constant and denoted by $$ \begin{align} J_\chi^{U,T}(f)=\int_{[U']\times [U']} K^T_{f,\chi}(x,y) \, dxdy \end{align} $$
$$ \begin{align} J_\chi^{U,T}(f)=\int_{[U']\times [U']} K^T_{f,\chi}(x,y) \, dxdy \end{align} $$
 $J^U_\chi (f)$
.
$J^U_\chi (f)$
.
-
3. For any
 $\chi \in \mathfrak {X}(U)$
, the distribution
$\chi \in \mathfrak {X}(U)$
, the distribution
 $J_\chi ^U$
is continuous, left and right
$J_\chi ^U$
is continuous, left and right
 $U'(\mathbb {A})$
-invariant.
$U'(\mathbb {A})$
-invariant. -
4. The sum
(3.2.3.2)is absolutely convergent and defines a continuous distribution $$ \begin{align} J^U(f)= \sum_{\chi\in \mathfrak{X}(U)} J^U_{\chi}(f) \end{align} $$
$$ \begin{align} J^U(f)= \sum_{\chi\in \mathfrak{X}(U)} J^U_{\chi}(f) \end{align} $$
 $J^U$
.
$J^U$
.
3.3 Truncation operator and distributions
 $J_\chi ^U$
$J_\chi ^U$
3.3.1
The goal of this section is to state Theorem 3.3.5.1, which gives the asymptotics of the distributions
![]() $J_\chi ^{U,T}(f)$
defined in Theorem 3.2.3.1 when the parameter goes to infinity. The theorem will be useful for subsequent computations in Section 3.5.
$J_\chi ^{U,T}(f)$
defined in Theorem 3.2.3.1 when the parameter goes to infinity. The theorem will be useful for subsequent computations in Section 3.5.
3.3.2 The Ichino-Yamana truncation operator
Let
![]() $T\in \mathfrak {a}_{0}'$
sufficiently positive. In [Reference Ichino and YamanaIY19], Ichino-Yamana defined a truncation operator which transforms functions of uniform moderate growth on
$T\in \mathfrak {a}_{0}'$
sufficiently positive. In [Reference Ichino and YamanaIY19], Ichino-Yamana defined a truncation operator which transforms functions of uniform moderate growth on
![]() $[U"]$
into rapidly decreasing functions on
$[U"]$
into rapidly decreasing functions on
![]() $[U']$
; see [Reference Ichino and YamanaIY19, lemma 2.2]. By applying it to the right component of
$[U']$
; see [Reference Ichino and YamanaIY19, lemma 2.2]. By applying it to the right component of
![]() $[U]=[U']\times [U"]$
, we get a truncation operator which we denote by
$[U]=[U']\times [U"]$
, we get a truncation operator which we denote by
![]() $\Lambda ^T_u$
. It associates to any function
$\Lambda ^T_u$
. It associates to any function
![]() $\varphi $
on
$\varphi $
on
![]() $[U]$
the function on
$[U]$
the function on
![]() $[U']$
defined by the following formula: for any
$[U']$
defined by the following formula: for any
![]() $x\in [U']$
,
$x\in [U']$
,
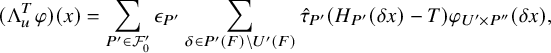 $$ \begin{align} (\Lambda^T_u\varphi)(x)= \sum_{ P' \in \mathcal{F}_0^{\prime} } \epsilon_{P'} \sum_{\delta \in P'(F)\backslash U'(F) } \hat\tau_{P'}(H_{P'}(\delta x)-T) \varphi_{U'\times P"}( \delta x), \end{align} $$
$$ \begin{align} (\Lambda^T_u\varphi)(x)= \sum_{ P' \in \mathcal{F}_0^{\prime} } \epsilon_{P'} \sum_{\delta \in P'(F)\backslash U'(F) } \hat\tau_{P'}(H_{P'}(\delta x)-T) \varphi_{U'\times P"}( \delta x), \end{align} $$
where we follow notations involved in (3.2.2.1) and in §3.1.4. Moreover,
![]() $\varphi _{U'\times P"}$
is the constant term of
$\varphi _{U'\times P"}$
is the constant term of
![]() $\varphi $
along the parabolic subgroup
$\varphi $
along the parabolic subgroup
![]() $U'\times P"$
of U, where
$U'\times P"$
of U, where
![]() $P'\times P"$
is the image of
$P'\times P"$
is the image of
![]() $P'$
by (3.1.4.1). We shall recall and precise the main properties of
$P'$
by (3.1.4.1). We shall recall and precise the main properties of
![]() $\Lambda _u^T$
.
$\Lambda _u^T$
.
Remark 3.3.2.1. To avoid confusions, we emphasize that in (3.3.2.1), the map
![]() $\varphi _{U'\times P"}$
is evaluated at
$\varphi _{U'\times P"}$
is evaluated at
![]() $ \delta x\in U'(\mathbb {A})$
where
$ \delta x\in U'(\mathbb {A})$
where
![]() $U'$
is viewed as a diagonal subgroup of U.
$U'$
is viewed as a diagonal subgroup of U.
3.3.3 Properties of
 $\Lambda _u^T$
$\Lambda _u^T$
Proposition 3.3.3.1.
-
1. The map
 $\varphi \mapsto \Lambda ^T_u\varphi $
induces a linear continuous map from
$\varphi \mapsto \Lambda ^T_u\varphi $
induces a linear continuous map from
 $\mathcal {T}([U])$
to
$\mathcal {T}([U])$
to
 $\mathcal {S}^0([U'])$
.
$\mathcal {S}^0([U'])$
. -
2. For every
 $N_1,N_2>0$
and
$N_1,N_2>0$
and
 $r>0$
, there exists a continuous semi-norm
$r>0$
, there exists a continuous semi-norm
 $\|.\|$
on
$\|.\|$
on
 $\mathcal {T}_{N_1}([U])$
such that for all
$\mathcal {T}_{N_1}([U])$
such that for all $$ \begin{align*} | (\Lambda^T_u\varphi )(x)- F^{U'}(x,T)\varphi(x) | \leqslant e^{-r \|T\|} \|x\|_{U'}^{-N_2} \|\varphi\| \end{align*} $$
$$ \begin{align*} | (\Lambda^T_u\varphi )(x)- F^{U'}(x,T)\varphi(x) | \leqslant e^{-r \|T\|} \|x\|_{U'}^{-N_2} \|\varphi\| \end{align*} $$
 $x\in [U']$
,
$x\in [U']$
,
 $\varphi \in \mathcal {T}_{N_1}([U])$
and
$\varphi \in \mathcal {T}_{N_1}([U])$
and
 $T\in \mathfrak {a}_0^{\prime }$
sufficiently positive.
$T\in \mathfrak {a}_0^{\prime }$
sufficiently positive.
Proof. The assertion 1 can be easily extracted from [Reference Ichino and YamanaIY19, (proof of) lemma 2.2]. For the convenience of the reader, we give some details. First, it suffices to show that for any
![]() $N>0$
, there exists a continuous semi-norm
$N>0$
, there exists a continuous semi-norm
![]() $\|.\|$
on
$\|.\|$
on
![]() $\mathcal {T}([U])$
such that for all
$\mathcal {T}([U])$
such that for all
![]() $\varphi \in \mathcal {T}([U])$
, we have
$\varphi \in \mathcal {T}([U])$
, we have
We recall that
![]() $\|\psi \|_{\infty ,N}=\sup _{x\in [U']} \|x\|_{U'}^{N} |\psi (x)|$
for any function
$\|\psi \|_{\infty ,N}=\sup _{x\in [U']} \|x\|_{U'}^{N} |\psi (x)|$
for any function
![]() $\psi $
on
$\psi $
on
![]() $[U']$
. We can write for
$[U']$
. We can write for
![]() $x\in [U']$
,
$x\in [U']$
,
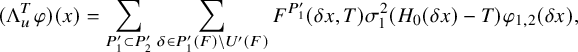 $$ \begin{align} (\Lambda^T_u\varphi)(x)=\sum_{P_1^{\prime}\subset P_2^{\prime} } \sum_{\delta \in P_1^{\prime}(F)\backslash U'(F)} F^{P_1^{\prime}}(\delta x,T) \sigma_1^2(H_0(\delta x)-T) \varphi_{1,2}(\delta x), \end{align} $$
$$ \begin{align} (\Lambda^T_u\varphi)(x)=\sum_{P_1^{\prime}\subset P_2^{\prime} } \sum_{\delta \in P_1^{\prime}(F)\backslash U'(F)} F^{P_1^{\prime}}(\delta x,T) \sigma_1^2(H_0(\delta x)-T) \varphi_{1,2}(\delta x), \end{align} $$
where
![]() $H_0=H_{P_0^{\prime }}$
and
$H_0=H_{P_0^{\prime }}$
and
![]() $\sigma _1^2=\sigma _{P_1^{\prime }}^{P_2^{\prime }}$
is the eponymous function with values in
$\sigma _1^2=\sigma _{P_1^{\prime }}^{P_2^{\prime }}$
is the eponymous function with values in
![]() $\{0,1\}$
introduced by Arthur in [Reference ArthurArt78, section 6] for the group
$\{0,1\}$
introduced by Arthur in [Reference ArthurArt78, section 6] for the group
![]() $U'$
and
$U'$
and
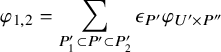 $$ \begin{align} \varphi_{1,2}=\sum_{P_1^{\prime}\subset P'\subset P_2^{\prime}} \epsilon_{P'} \varphi_{U'\times P"} \end{align} $$
$$ \begin{align} \varphi_{1,2}=\sum_{P_1^{\prime}\subset P'\subset P_2^{\prime}} \epsilon_{P'} \varphi_{U'\times P"} \end{align} $$
with
![]() $\varphi _{U'\times P"} $
as above. Note that if
$\varphi _{U'\times P"} $
as above. Note that if
![]() $P_1^{\prime }=P_2^{\prime }$
, then
$P_1^{\prime }=P_2^{\prime }$
, then
![]() $\sigma _1^2=0$
unless
$\sigma _1^2=0$
unless
![]() $P_1^{\prime }=P_2^{\prime }=U'$
. In this case, the corresponding term is
$P_1^{\prime }=P_2^{\prime }=U'$
. In this case, the corresponding term is
![]() $F^{U'}(x,T) \varphi (x)$
for which the result is obvious. The other cases are deduced from the next lemma, which also gives assertion 2.
$F^{U'}(x,T) \varphi (x)$
for which the result is obvious. The other cases are deduced from the next lemma, which also gives assertion 2.
Lemma 3.3.3.2. Assume
![]() $P_1^{\prime }\subsetneq P_2^{\prime }$
. For every
$P_1^{\prime }\subsetneq P_2^{\prime }$
. For every
![]() $N_1,N_2>0$
and
$N_1,N_2>0$
and
![]() $r>0$
, there exists a continuous semi-norm
$r>0$
, there exists a continuous semi-norm
![]() $\|.\|$
on
$\|.\|$
on
![]() $\mathcal {T}_{N_1}([U])$
such that
$\mathcal {T}_{N_1}([U])$
such that
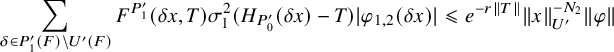 $$ \begin{align*} \sum_{\delta \in P_1^{\prime}(F)\backslash U'(F)} F^{P_1^{\prime}}(\delta x,T) \sigma_1^2(H_{P_0^{\prime}}(\delta x)-T) |\varphi_{1,2}(\delta x)| \leqslant e^{-r \|T\|} \|x\|_{U'}^{-N_2} \|\varphi\| \end{align*} $$
$$ \begin{align*} \sum_{\delta \in P_1^{\prime}(F)\backslash U'(F)} F^{P_1^{\prime}}(\delta x,T) \sigma_1^2(H_{P_0^{\prime}}(\delta x)-T) |\varphi_{1,2}(\delta x)| \leqslant e^{-r \|T\|} \|x\|_{U'}^{-N_2} \|\varphi\| \end{align*} $$
for all
![]() $x\in [U']$
,
$x\in [U']$
,
![]() $\varphi \in \mathcal {T}_{N_1}([U])$
and
$\varphi \in \mathcal {T}_{N_1}([U])$
and
![]() $T\in \mathfrak {a}_0^{\prime }$
sufficiently positive.
$T\in \mathfrak {a}_0^{\prime }$
sufficiently positive.
3.3.4 Proof of Lemma 3.3.3.2
Let g be an element in
![]() $U(\mathbb {A})$
which we write
$U(\mathbb {A})$
which we write
![]() $g=(g',g")$
with
$g=(g',g")$
with
![]() $g'\in U'(\mathbb {A})$
and
$g'\in U'(\mathbb {A})$
and
![]() $g"\in U"(\mathbb {A})$
. Let
$g"\in U"(\mathbb {A})$
. Let
![]() $N>0$
. By [Reference Mœglin and WaldspurgerMW94, preuves du lemme I.2.10 et du corollaire I.2.11], for any
$N>0$
. By [Reference Mœglin and WaldspurgerMW94, preuves du lemme I.2.10 et du corollaire I.2.11], for any
![]() $\lambda $
which is a linear combination of elements of
$\lambda $
which is a linear combination of elements of
![]() $\Delta _0^{P^{\prime \prime }_{2}}\setminus \Delta _0^{P^{\prime \prime }_{1}}$
with positive coefficients, there exists a continuous semi-norm
$\Delta _0^{P^{\prime \prime }_{2}}\setminus \Delta _0^{P^{\prime \prime }_{1}}$
with positive coefficients, there exists a continuous semi-norm
![]() $\|\cdot \|$
on
$\|\cdot \|$
on
![]() $\mathcal {T}_N([U])$
such that
$\mathcal {T}_N([U])$
such that
for all
![]() $g\in U(\mathbb {A})$
such that
$g\in U(\mathbb {A})$
such that
![]() $g'\in U'(\mathbb {A})$
,
$g'\in U'(\mathbb {A})$
,
![]() $g"\in \mathfrak {s}_{P^{\prime \prime }_2}$
and all
$g"\in \mathfrak {s}_{P^{\prime \prime }_2}$
and all
![]() $\varphi \in \mathcal {T}_N([U])$
. We want to apply this majorization to an element
$\varphi \in \mathcal {T}_N([U])$
. We want to apply this majorization to an element
![]() $g=(x,x)$
where
$g=(x,x)$
where
![]() $x\in U'(\mathbb {A})$
satisfies
$x\in U'(\mathbb {A})$
satisfies
![]() $F^{P_1^{\prime }}( x,T)\sigma _1^2(H_{P_0^{\prime }}( x)-T)=1$
. Since this condition and the map
$F^{P_1^{\prime }}( x,T)\sigma _1^2(H_{P_0^{\prime }}( x)-T)=1$
. Since this condition and the map
![]() $x\in U'(\mathbb {A})\mapsto \varphi _{1,2}(x,x)$
are
$x\in U'(\mathbb {A})\mapsto \varphi _{1,2}(x,x)$
are
![]() $P_1^{\prime }(F)$
-left invariant, we may assume that
$P_1^{\prime }(F)$
-left invariant, we may assume that
![]() $x\in \mathfrak {s}_{P_1^{\prime }}$
. By [Reference ArthurArt78, lemma 6.1], x also satisfies
$x\in \mathfrak {s}_{P_1^{\prime }}$
. By [Reference ArthurArt78, lemma 6.1], x also satisfies
![]() $F^{P_1^{\prime }}(y,T)\tau _{P_1^{\prime }}^{P_2^{\prime }}(H_{P_1^{\prime }}(y)-T)=1$
, so by Lemma 2.3.3.1, we have
$F^{P_1^{\prime }}(y,T)\tau _{P_1^{\prime }}^{P_2^{\prime }}(H_{P_1^{\prime }}(y)-T)=1$
, so by Lemma 2.3.3.1, we have
![]() $x\in \mathfrak {s}_{P_2^{\prime }}$
. We can deduce from the proof of Proposition 3.1.5.1 and the majorization (3.3.4.1) that there exists a fixed compact subset
$x\in \mathfrak {s}_{P_2^{\prime }}$
. We can deduce from the proof of Proposition 3.1.5.1 and the majorization (3.3.4.1) that there exists a fixed compact subset
![]() $\mathcal {K}\subset U'(\mathbb {A})$
such that
$\mathcal {K}\subset U'(\mathbb {A})$
such that
![]() $\mathfrak {s}_{P_2^{\prime }}\subset \mathfrak {s}_{P^{\prime \prime }_2}\mathcal {K}$
and that there exists a continuous semi-norm
$\mathfrak {s}_{P_2^{\prime }}\subset \mathfrak {s}_{P^{\prime \prime }_2}\mathcal {K}$
and that there exists a continuous semi-norm
![]() $\|\cdot \|$
on
$\|\cdot \|$
on
![]() $\mathcal {T}_N([U])$
such that
$\mathcal {T}_N([U])$
such that
for all
![]() $x\in \mathfrak {s}_{P^{\prime }_2}$
and
$x\in \mathfrak {s}_{P^{\prime }_2}$
and
![]() $\varphi \in \mathcal {T}_N([U])$
. Here, we wrote x instead of
$\varphi \in \mathcal {T}_N([U])$
. Here, we wrote x instead of
![]() $(x,x)$
in the left-hand side. Since the restriction to
$(x,x)$
in the left-hand side. Since the restriction to
![]() $\mathfrak {a}_{P_0^{\prime }}$
of elements of
$\mathfrak {a}_{P_0^{\prime }}$
of elements of
![]() $\Delta _0^{P^{\prime \prime }_{2}}\setminus \Delta _0^{P^{\prime \prime }_{1}}$
are (up to some positive constants) the restriction of elements of
$\Delta _0^{P^{\prime \prime }_{2}}\setminus \Delta _0^{P^{\prime \prime }_{1}}$
are (up to some positive constants) the restriction of elements of
![]() $\Delta _0^{P^{\prime }_{2}}\setminus \Delta _0^{P^{\prime }_{1}}$
, we can conclude by the next Lemma 3.3.4.1 and the fact that, for all
$\Delta _0^{P^{\prime }_{2}}\setminus \Delta _0^{P^{\prime }_{1}}$
, we can conclude by the next Lemma 3.3.4.1 and the fact that, for all
![]() $N>0$
, there exists
$N>0$
, there exists
![]() $c,N'>0$
such that for all
$c,N'>0$
such that for all
![]() $x\in [U']$
,
$x\in [U']$
,
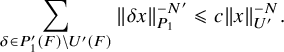 $$ \begin{align*} \sum_{\delta \in P_1^{\prime}(F)\backslash U'(F)} \|\delta x\|_{P_1}^{-N'}\leqslant c \|x\|_{U'}^{-N}. \end{align*} $$
$$ \begin{align*} \sum_{\delta \in P_1^{\prime}(F)\backslash U'(F)} \|\delta x\|_{P_1}^{-N'}\leqslant c \|x\|_{U'}^{-N}. \end{align*} $$
Lemma 3.3.4.1. For every
![]() $N\geqslant 0$
and
$N\geqslant 0$
and
![]() $r>0$
, there exists
$r>0$
, there exists
![]() $t>0$
and
$t>0$
and
![]() $C>0$
such that for any
$C>0$
such that for any
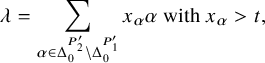 $$ \begin{align} \lambda=\sum_{\alpha\in \Delta_0^{P^{\prime}_{2}}\setminus \Delta_0^{P^{\prime}_{1}}}x_\alpha \alpha \text{ with } x_\alpha>t, \end{align} $$
$$ \begin{align} \lambda=\sum_{\alpha\in \Delta_0^{P^{\prime}_{2}}\setminus \Delta_0^{P^{\prime}_{1}}}x_\alpha \alpha \text{ with } x_\alpha>t, \end{align} $$
we have
for all
![]() $x\in \mathfrak {s}_{P_1^{\prime }}$
and
$x\in \mathfrak {s}_{P_1^{\prime }}$
and
![]() $T\in \mathfrak {a}_0^{\prime }$
sufficiently positive.
$T\in \mathfrak {a}_0^{\prime }$
sufficiently positive.
Proof. Any
![]() $H_1\in \mathfrak {a}_{P_1^{\prime }}$
can be written
$H_1\in \mathfrak {a}_{P_1^{\prime }}$
can be written
![]() $H_1=H_1^2+H_2$
according to the decomposition
$H_1=H_1^2+H_2$
according to the decomposition
![]() $\mathfrak {a}_{P_1^{\prime }}= \mathfrak {a}_{P_1^{\prime }}^{P_2^{\prime }}\oplus \mathfrak {a}_{P_2^{\prime }}$
. By [Reference ArthurArt80, Corollary 6.2], there is
$\mathfrak {a}_{P_1^{\prime }}= \mathfrak {a}_{P_1^{\prime }}^{P_2^{\prime }}\oplus \mathfrak {a}_{P_2^{\prime }}$
. By [Reference ArthurArt80, Corollary 6.2], there is
![]() $c_1>0$
such that
$c_1>0$
such that
for all
![]() $H_1\in \mathfrak {a}_{P_1^{\prime }}$
such that
$H_1\in \mathfrak {a}_{P_1^{\prime }}$
such that
![]() $\sigma _1^2(H_1)\not =1$
. There exist
$\sigma _1^2(H_1)\not =1$
. There exist
![]() $c_2,c_3,c_4>0$
such that for all
$c_2,c_3,c_4>0$
such that for all
![]() $x\in \mathfrak {s}_{P_1^{\prime }}$
, we have
$x\in \mathfrak {s}_{P_1^{\prime }}$
, we have
where we set
![]() $H_0=H_{P_0^{\prime }}$
. We assume from now on that we have
$H_0=H_{P_0^{\prime }}$
. We assume from now on that we have
In particular, we have
![]() $x\in \mathfrak {s}_{P_2^{\prime }}$
as we have already seen it in §3.3.4 – discussion below (3.3.4.1). According to (3.3.4.4), the norm of
$x\in \mathfrak {s}_{P_2^{\prime }}$
as we have already seen it in §3.3.4 – discussion below (3.3.4.1). According to (3.3.4.4), the norm of
![]() $H_{0}(x)$
is bounded in terms of the norm of the projection of
$H_{0}(x)$
is bounded in terms of the norm of the projection of
![]() $H_{0}(x)$
on
$H_{0}(x)$
on
![]() $\mathfrak {a}_{P_0^{\prime }}^{P_2^{\prime }}$
, so up to some positive constant, it is bounded by
$\mathfrak {a}_{P_0^{\prime }}^{P_2^{\prime }}$
, so up to some positive constant, it is bounded by
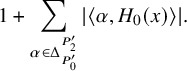 $$ \begin{align*} 1+\sum_{\alpha\in \Delta_{P_0^{\prime}}^{P_2^{\prime}} }|\langle \alpha ,H_{0}(x)\rangle|. \end{align*} $$
$$ \begin{align*} 1+\sum_{\alpha\in \Delta_{P_0^{\prime}}^{P_2^{\prime}} }|\langle \alpha ,H_{0}(x)\rangle|. \end{align*} $$
Since we assume
![]() $F^{P_1^{\prime }}( x,T)=1$
and
$F^{P_1^{\prime }}( x,T)=1$
and
![]() $x\in \mathfrak {s}_{P_1^{\prime }}$
, the norm of the projection of
$x\in \mathfrak {s}_{P_1^{\prime }}$
, the norm of the projection of
![]() $H_{0}(x)$
on
$H_{0}(x)$
on
![]() $\mathfrak {a}_{P_0^{\prime }}^{P_1^{\prime }}$
is bounded by some multiple of
$\mathfrak {a}_{P_0^{\prime }}^{P_1^{\prime }}$
is bounded by some multiple of
![]() $\|T\|$
. For all
$\|T\|$
. For all
![]() $\alpha \in \Delta _{P_0^{\prime }}^{P_2^{\prime }}\setminus \Delta _{P_0^{\prime }}^{P_1^{\prime }}$
, we have
$\alpha \in \Delta _{P_0^{\prime }}^{P_2^{\prime }}\setminus \Delta _{P_0^{\prime }}^{P_1^{\prime }}$
, we have
![]() $\langle \alpha ,H_{0}(x)\rangle>\langle \alpha ,T\rangle \geqslant 0$
since we assume
$\langle \alpha ,H_{0}(x)\rangle>\langle \alpha ,T\rangle \geqslant 0$
since we assume
![]() $\sigma _1^2(H_0( x)-T)\not =0$
; see [Reference ArthurArt78, lemma 6.1]. Hence, we deduce that there exist
$\sigma _1^2(H_0( x)-T)\not =0$
; see [Reference ArthurArt78, lemma 6.1]. Hence, we deduce that there exist
![]() $c_5,c_6$
such that for all
$c_5,c_6$
such that for all
![]() $x\in \mathfrak {s}_{P_1^{\prime }}$
that satisfy (3.3.4.5), we have
$x\in \mathfrak {s}_{P_1^{\prime }}$
that satisfy (3.3.4.5), we have
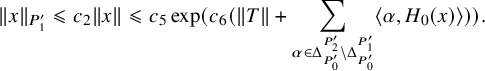 $$ \begin{align*} \|x\|_{P_1^{\prime}}\leqslant c_2\|x\| \leqslant c_5 \exp( c_6 (\|T\|+ \sum_{ \alpha\in \Delta_{P_0^{\prime}}^{P_2^{\prime}}\setminus \Delta_{P_0^{\prime}}^{P_1^{\prime}} }\langle \alpha ,H_{0}(x)\rangle)). \end{align*} $$
$$ \begin{align*} \|x\|_{P_1^{\prime}}\leqslant c_2\|x\| \leqslant c_5 \exp( c_6 (\|T\|+ \sum_{ \alpha\in \Delta_{P_0^{\prime}}^{P_2^{\prime}}\setminus \Delta_{P_0^{\prime}}^{P_1^{\prime}} }\langle \alpha ,H_{0}(x)\rangle)). \end{align*} $$
The lemma is then obvious since for such x, and all
![]() $\alpha \in \Delta _{P_0^{\prime }}^{P_2^{\prime }}\setminus \Delta _{P_0^{\prime }}^{P_1^{\prime }}$
and any sufficiently positive T (see §3.1.6), we have
$\alpha \in \Delta _{P_0^{\prime }}^{P_2^{\prime }}\setminus \Delta _{P_0^{\prime }}^{P_1^{\prime }}$
and any sufficiently positive T (see §3.1.6), we have
![]() $\langle \alpha ,H_{0}(x)\rangle>\langle \alpha ,T\rangle \geqslant \varepsilon \|T\|$
.
$\langle \alpha ,H_{0}(x)\rangle>\langle \alpha ,T\rangle \geqslant \varepsilon \|T\|$
.
3.3.5
We can apply the operator
![]() $\Lambda _u^T$
to the right variable of the kernel
$\Lambda _u^T$
to the right variable of the kernel
![]() $K_{f,\chi }(x,y)$
: we get a function on
$K_{f,\chi }(x,y)$
: we get a function on
![]() $[U]\times [U']$
denoted by
$[U]\times [U']$
denoted by
![]() $K_{f,\chi }\Lambda ^T_u$
.
$K_{f,\chi }\Lambda ^T_u$
.
Theorem 3.3.5.1.
-
1. For all
 $T\in \mathfrak {a}_0^{\prime }$
sufficiently positive, there exists a continuous semi-norm
$T\in \mathfrak {a}_0^{\prime }$
sufficiently positive, there exists a continuous semi-norm
 $\|.\|$
on
$\|.\|$
on
 $\mathcal {S}(U(\mathbb {A}))$
such that for all
$\mathcal {S}(U(\mathbb {A}))$
such that for all
 $f\in \mathcal {S}(U(\mathbb {A}))$
, we have (3.3.5.1)
$f\in \mathcal {S}(U(\mathbb {A}))$
, we have (3.3.5.1) $$ \begin{align} \sum_{\chi\in \mathfrak{X}(U) }\int_{[U']\times [U']} \left| (K_{f,\chi}\Lambda^T_u)(x,y) \right|\, dxdy \leqslant \|f\|. \end{align} $$
$$ \begin{align} \sum_{\chi\in \mathfrak{X}(U) }\int_{[U']\times [U']} \left| (K_{f,\chi}\Lambda^T_u)(x,y) \right|\, dxdy \leqslant \|f\|. \end{align} $$
-
2. For all
 $r>0$
, there exists a continuous semi-norm
$r>0$
, there exists a continuous semi-norm
 $\|.\|$
on
$\|.\|$
on
 $\mathcal {S}(U(\mathbb {A}))$
such that for any
$\mathcal {S}(U(\mathbb {A}))$
such that for any
 $T\in \mathfrak {a}_0^{\prime }$
sufficiently positive and
$T\in \mathfrak {a}_0^{\prime }$
sufficiently positive and
 $f\in \mathcal {S}(U(\mathbb {A}))$
, we have (3.3.5.2)
$f\in \mathcal {S}(U(\mathbb {A}))$
, we have (3.3.5.2) $$ \begin{align} \sum_{\chi\in \mathfrak{X}(U) } \left| J_\chi^{U,T}(f) - \int_{[U']\times [U']} (K_{f,\chi}\Lambda^T_u )(x,y) \, dxdy \right| \leqslant e^{-r\|T\|}\|f\|. \end{align} $$
$$ \begin{align} \sum_{\chi\in \mathfrak{X}(U) } \left| J_\chi^{U,T}(f) - \int_{[U']\times [U']} (K_{f,\chi}\Lambda^T_u )(x,y) \, dxdy \right| \leqslant e^{-r\|T\|}\|f\|. \end{align} $$
From Theorem 3.2.3.1 assertion 2 and from Theorem 3.3.5.1, we get the following:
Corollary 3.3.5.2. The absolutely convergent integral
is asymptotic to an exponential-polynomial in the variable T whose purely polynomial term is constant and equal to
![]() $J_\chi ^U(f)$
.
$J_\chi ^U(f)$
.
3.4 Proof of main theorems
3.4.1 Proof of Theorem 3.3.5.1 assertion 1
Let
![]() $N_1,N_2>0$
. Let
$N_1,N_2>0$
. Let
![]() $N_0>0$
be as in Remark 3.2.2.1 (for
$N_0>0$
be as in Remark 3.2.2.1 (for
![]() $P=U$
). We set
$P=U$
). We set
![]() $N_1^{\prime }=N_1+N_0$
. Let
$N_1^{\prime }=N_1+N_0$
. Let
![]() $T\in \mathfrak {a}_0^{\prime }$
be sufficiently positive. By Proposition 3.3.3.1, there exists a continuous semi-norm
$T\in \mathfrak {a}_0^{\prime }$
be sufficiently positive. By Proposition 3.3.3.1, there exists a continuous semi-norm
![]() $\|\cdot \|_{N^{\prime }_1}$
on
$\|\cdot \|_{N^{\prime }_1}$
on
![]() $\mathcal {T}_{N^{\prime }_1}([U])$
such that for all
$\mathcal {T}_{N^{\prime }_1}([U])$
such that for all
![]() $\chi \in \mathfrak {X}(U)$
, all
$\chi \in \mathfrak {X}(U)$
, all
![]() $x\in [U]$
and
$x\in [U]$
and
![]() $y\in [U']$
, we have
$y\in [U']$
, we have
Then, by Remark 3.2.2.1, more particularly the majorization (3.2.2.3) for
![]() $P=U$
, there exists a continuous semi-norm
$P=U$
, there exists a continuous semi-norm
![]() $\|\cdot \|_{\mathcal {S}}$
on
$\|\cdot \|_{\mathcal {S}}$
on
![]() $\mathcal {S}(U(\mathbb {A}))$
such that for all
$\mathcal {S}(U(\mathbb {A}))$
such that for all
![]() $x\in [U]$
and
$x\in [U]$
and
![]() $y\in [U']$
,
$y\in [U']$
,
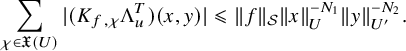 $$ \begin{align*} \sum_{\chi\in \mathfrak{X}(U) } |( K_{f,\chi} \Lambda^T_u)(x,y)|\leqslant \|f\|_{\mathcal{S}} \|x\|_{U}^{-N_1}\|y\|_{U'}^{-N_2}. \end{align*} $$
$$ \begin{align*} \sum_{\chi\in \mathfrak{X}(U) } |( K_{f,\chi} \Lambda^T_u)(x,y)|\leqslant \|f\|_{\mathcal{S}} \|x\|_{U}^{-N_1}\|y\|_{U'}^{-N_2}. \end{align*} $$
Now the map
![]() $(x,y)\mapsto \|x\|_{U}^{-N_1}\|y\|_{U'}^{-N_2}$
is integrable on
$(x,y)\mapsto \|x\|_{U}^{-N_1}\|y\|_{U'}^{-N_2}$
is integrable on
![]() $[U']\times [U']$
for large
$[U']\times [U']$
for large
![]() $N_1,N_2$
; see [Reference Beuzart-PlessisBeu21, Proposition A.1.1 (ix)].
$N_1,N_2$
; see [Reference Beuzart-PlessisBeu21, Proposition A.1.1 (ix)].
3.4.2 Asymptotics of several truncated kernels
We shall use the two following results.
Theorem 3.4.2.1. For every
![]() $N_1,N_2, r>0$
, there exists a continuous semi-norm
$N_1,N_2, r>0$
, there exists a continuous semi-norm
![]() $\|.\|$
on
$\|.\|$
on
![]() $\mathcal {S}(U(\mathbb {A}))$
such that
$\mathcal {S}(U(\mathbb {A}))$
such that
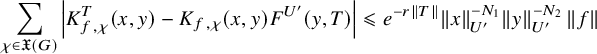 $$ \begin{align} \sum_{\chi\in \mathfrak{X}(G)} \left\lvert K^T_{f,\chi}(x,y)- K_{f,\chi}(x,y)F^{U'}(y,T)\right\rvert \leqslant e^{-r \| T\|} \| x\|^{-N_1}_{U'} \| y\|^{-N_2} _{U'} \, \lVert f\rVert \end{align} $$
$$ \begin{align} \sum_{\chi\in \mathfrak{X}(G)} \left\lvert K^T_{f,\chi}(x,y)- K_{f,\chi}(x,y)F^{U'}(y,T)\right\rvert \leqslant e^{-r \| T\|} \| x\|^{-N_1}_{U'} \| y\|^{-N_2} _{U'} \, \lVert f\rVert \end{align} $$
for
![]() $f\in \mathcal {S}(U(\mathbb {A}))$
,
$f\in \mathcal {S}(U(\mathbb {A}))$
,
![]() $(x,y)\in [U']\times [U']$
and
$(x,y)\in [U']\times [U']$
and
![]() $T\in \mathfrak {a}_{0}'$
sufficiently positive.
$T\in \mathfrak {a}_{0}'$
sufficiently positive.
The proof of Theorem 3.4.2.1 will be given in §3.4.5 below.
Corollary 3.4.2.2. For every
![]() $N_1,N_2, r>0$
, there exists a continuous semi-norm
$N_1,N_2, r>0$
, there exists a continuous semi-norm
![]() $\|.\|$
on
$\|.\|$
on
![]() $\mathcal {S}(U(\mathbb {A}))$
such that
$\mathcal {S}(U(\mathbb {A}))$
such that
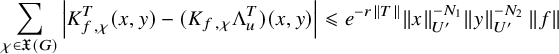 $$ \begin{align} \sum_{\chi\in \mathfrak{X}(G)} \left\lvert K^T_{f,\chi}(x,y)- (K_{f,\chi}\Lambda^T_u)(x,y)\right\rvert \leqslant e^{-r \| T\|} \| x\|^{-N_1}_{U'} \| y\|^{-N_2} _{U'} \, \lVert f\rVert \end{align} $$
$$ \begin{align} \sum_{\chi\in \mathfrak{X}(G)} \left\lvert K^T_{f,\chi}(x,y)- (K_{f,\chi}\Lambda^T_u)(x,y)\right\rvert \leqslant e^{-r \| T\|} \| x\|^{-N_1}_{U'} \| y\|^{-N_2} _{U'} \, \lVert f\rVert \end{align} $$
for
![]() $f\in \mathcal {S}(U(\mathbb {A}))$
,
$f\in \mathcal {S}(U(\mathbb {A}))$
,
![]() $(x,y)\in [U']\times [U']$
and
$(x,y)\in [U']\times [U']$
and
![]() $T\in \mathfrak {a}_{0}'$
sufficiently positive.
$T\in \mathfrak {a}_{0}'$
sufficiently positive.
Proof. Let
![]() $N_1,N_1^{\prime },N_2>0$
be as in §3.4.1. By assertion 2 of Proposition 3.3.3.1, for every
$N_1,N_1^{\prime },N_2>0$
be as in §3.4.1. By assertion 2 of Proposition 3.3.3.1, for every
![]() $r>0$
, there exists a continuous semi-norm
$r>0$
, there exists a continuous semi-norm
![]() $\|\cdot \|_{N^{\prime }_1}$
on
$\|\cdot \|_{N^{\prime }_1}$
on
![]() $\mathcal {T}_{N^{\prime }_1}([U])$
such that for all
$\mathcal {T}_{N^{\prime }_1}([U])$
such that for all
![]() $f\in \mathcal {S}(U(\mathbb {A}))$
,
$f\in \mathcal {S}(U(\mathbb {A}))$
,
![]() $\chi \in \mathfrak {X}(U)$
,
$\chi \in \mathfrak {X}(U)$
,
![]() $x\in [U]$
,
$x\in [U]$
,
![]() $y\in [U']$
and
$y\in [U']$
and
![]() $T\in \mathfrak {a}_{0}'$
sufficiently positive, we have
$T\in \mathfrak {a}_{0}'$
sufficiently positive, we have
From this and the majorization (3.2.2.3) (for
![]() $P=G$
), we deduce that there exists a continuous semi-norm
$P=G$
), we deduce that there exists a continuous semi-norm
![]() $\|\cdot \|_{\mathcal {S}}$
on
$\|\cdot \|_{\mathcal {S}}$
on
![]() $\mathcal {S}(U(\mathbb {A}))$
such that for all
$\mathcal {S}(U(\mathbb {A}))$
such that for all
![]() $f\in \mathcal {S}(U(\mathbb {A}))$
,
$f\in \mathcal {S}(U(\mathbb {A}))$
,
![]() $x\in [U]$
,
$x\in [U]$
,
![]() $y\in [U']$
and
$y\in [U']$
and
![]() $T\in \mathfrak {a}_{0}'$
sufficiently positive, we have
$T\in \mathfrak {a}_{0}'$
sufficiently positive, we have
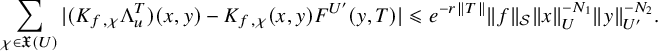 $$ \begin{align*} \sum_{\chi\in \mathfrak{X}(U) } |( K_{f,\chi} \Lambda^T_u)(x,y)-K_{f,\chi}(x,y) F^{U'}(y,T)|\leqslant e^{-r\|T\|} \|f\|_{\mathcal{S}} \|x\|_{U}^{-N_1}\|y\|_{U'}^{-N_2}. \end{align*} $$
$$ \begin{align*} \sum_{\chi\in \mathfrak{X}(U) } |( K_{f,\chi} \Lambda^T_u)(x,y)-K_{f,\chi}(x,y) F^{U'}(y,T)|\leqslant e^{-r\|T\|} \|f\|_{\mathcal{S}} \|x\|_{U}^{-N_1}\|y\|_{U'}^{-N_2}. \end{align*} $$
By [Reference Beuzart-PlessisBeu21, Proposition A.1.1 (ix)], we have
![]() $\|x\|_U\sim \|x\|_{U'}$
for
$\|x\|_U\sim \|x\|_{U'}$
for
![]() $x\in [U']$
. The corollary is then a straightforward consequence of the inequality above and Theorem 3.4.2.1.
$x\in [U']$
. The corollary is then a straightforward consequence of the inequality above and Theorem 3.4.2.1.
3.4.3 Proof of Theorem 3.2.3.1
First, we mention that all the statements but the continuity are stated and proved for compactly supported functions; see [Reference ZydorZyd20, theorems 4.1, 4.5 and 4.7]. We just need the extension to Schwartz functions. The assertion 1 of Theorem 3.2.3.1 is a direct consequence of Corollary 3.4.2.2 and assertion 1 of Theorem 3.3.5.1. This gives also the continuity of the distributions
![]() $J_\chi ^{U,T}$
and their sum over
$J_\chi ^{U,T}$
and their sum over
![]() $\chi \in \mathfrak {X}(U)$
.
$\chi \in \mathfrak {X}(U)$
.
The assertion 2 of Theorem 3.2.3.1 can be proved as in [Reference ZydorZyd20, proof of theorems 4.5]. We take for granted the obvious extension of Corollary 3.4.2.2 and Theorem 3.3.5.1 assertion 1 to the auxiliary kernels of [Reference ZydorZyd20, section 4.1] relative to some parabolic subgroups of U. Indeed, it can be proved with the same technics and is left to the reader. In particular, the formula of [Reference ZydorZyd20, proposition 4.4] holds for Schwartz functions, and each term in right-hand side of the formula (among them
![]() $J_\chi ^U(f)$
) is a continuous distribution. From this, we deduce assertion 3 of Theorem 3.2.3.1 as in [Reference ZydorZyd20, theorem 4.7]. Finally, assertion 4 follows from assertion 1.
$J_\chi ^U(f)$
) is a continuous distribution. From this, we deduce assertion 3 of Theorem 3.2.3.1 as in [Reference ZydorZyd20, theorem 4.7]. Finally, assertion 4 follows from assertion 1.
3.4.4 Proof of Theorem 3.3.5.1 assertion 2
It is an obvious application of Corollary 3.4.2.2.
3.4.5 Proof of Theorem 3.4.2.1
We shall use the notation of the proof of Proposition 3.3.3.1. We start from the expression for all
![]() $x,y\in [U']$
$x,y\in [U']$
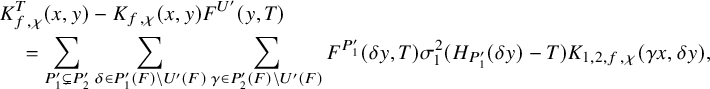 $$ \begin{align*} & K_{f,\chi}^{T}(x,y) -K_{f,\chi}(x,y)F^{U'}(y,T)\\ & \quad = \sum_{ P_1^{\prime}\subsetneq P_2^{\prime}} \sum_{\delta \in P^{\prime}_1 (F) \backslash U'(F)} \sum_{\gamma\in P_2^{\prime}(F)\backslash U'(F)}F^{P_1^{\prime}}(\delta y,T) \sigma_{1}^{2}(H_{P_1^{\prime}}(\delta y)-T) K_{1,2, f, \chi}(\gamma x,\delta y), \end{align*} $$
$$ \begin{align*} & K_{f,\chi}^{T}(x,y) -K_{f,\chi}(x,y)F^{U'}(y,T)\\ & \quad = \sum_{ P_1^{\prime}\subsetneq P_2^{\prime}} \sum_{\delta \in P^{\prime}_1 (F) \backslash U'(F)} \sum_{\gamma\in P_2^{\prime}(F)\backslash U'(F)}F^{P_1^{\prime}}(\delta y,T) \sigma_{1}^{2}(H_{P_1^{\prime}}(\delta y)-T) K_{1,2, f, \chi}(\gamma x,\delta y), \end{align*} $$
where
![]() $\sigma _{1}^{2}=\sigma _{P_1^{\prime }}^{P_2^{\prime }}$
is as in (3.3.3.1), the sum is over
$\sigma _{1}^{2}=\sigma _{P_1^{\prime }}^{P_2^{\prime }}$
is as in (3.3.3.1), the sum is over
![]() $P_1^{\prime },P_2^{\prime }\in \mathcal {F}_0^{\prime }$
and we set for
$P_1^{\prime },P_2^{\prime }\in \mathcal {F}_0^{\prime }$
and we set for
![]() $x\in P_2^{\prime }(F)\backslash U'(\mathbb {A})$
and
$x\in P_2^{\prime }(F)\backslash U'(\mathbb {A})$
and
![]() $y\in P_1^{\prime }(F)\backslash U'(\mathbb {A})$
,
$y\in P_1^{\prime }(F)\backslash U'(\mathbb {A})$
,
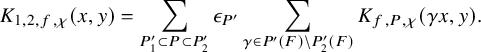 $$ \begin{align*} K_{1,2, f,\chi}(x,y)=\sum_{P_1^{\prime}\subset P\subset P_2^{\prime}} \epsilon_{P'} \sum_{\gamma \in P'(F)\backslash P_2^{\prime}(F)} K_{f,P, \chi}(\gamma x,y). \end{align*} $$
$$ \begin{align*} K_{1,2, f,\chi}(x,y)=\sum_{P_1^{\prime}\subset P\subset P_2^{\prime}} \epsilon_{P'} \sum_{\gamma \in P'(F)\backslash P_2^{\prime}(F)} K_{f,P, \chi}(\gamma x,y). \end{align*} $$
From now on, we fix
![]() $P_1^{\prime }\subsetneq P_2^{\prime }$
. Let
$P_1^{\prime }\subsetneq P_2^{\prime }$
. Let
![]() $\alpha \in \Delta ^{P_2^{\prime }}_0\setminus \Delta ^{P_1^{\prime }}_0$
and let
$\alpha \in \Delta ^{P_2^{\prime }}_0\setminus \Delta ^{P_1^{\prime }}_0$
and let
![]() $P_1^{\prime }\subsetneq \, ^\alpha P_1^{\prime }\subset P_2^{\prime }$
be defined by
$P_1^{\prime }\subsetneq \, ^\alpha P_1^{\prime }\subset P_2^{\prime }$
be defined by
![]() $ \Delta ^{^\alpha P_1^{\prime }}_0= \Delta ^{P_1^{\prime }}_0\cup \{\alpha \}$
. For any
$ \Delta ^{^\alpha P_1^{\prime }}_0= \Delta ^{P_1^{\prime }}_0\cup \{\alpha \}$
. For any
![]() $\, ^\alpha P_1^{\prime }\subset P'\subset P_2^{\prime }$
, we denote by
$\, ^\alpha P_1^{\prime }\subset P'\subset P_2^{\prime }$
, we denote by
![]() $P_\alpha ^{\prime }$
the parabolic subgroup
$P_\alpha ^{\prime }$
the parabolic subgroup
![]() $P_1^{\prime }\subset P_\alpha ^{\prime }\subsetneq P'$
defined by
$P_1^{\prime }\subset P_\alpha ^{\prime }\subsetneq P'$
defined by
![]() $\Delta _0^{P_\alpha ^{\prime }}=\Delta ^{P'}_0\setminus \{\alpha \}$
.
$\Delta _0^{P_\alpha ^{\prime }}=\Delta ^{P'}_0\setminus \{\alpha \}$
.
We denote by P and
![]() $P_\alpha $
the parabolic subgroups associated to
$P_\alpha $
the parabolic subgroups associated to
![]() $P'$
and
$P'$
and
![]() $P^{\prime }_\alpha $
(see the map (3.1.4.1)). For any
$P^{\prime }_\alpha $
(see the map (3.1.4.1)). For any
![]() $\, ^\alpha P_1^{\prime }\subset P'\subset P_2^{\prime }$
, we set for
$\, ^\alpha P_1^{\prime }\subset P'\subset P_2^{\prime }$
, we set for
![]() $x\in P'(F)\backslash U'(\mathbb {A})$
and
$x\in P'(F)\backslash U'(\mathbb {A})$
and
![]() $y\in P_1^{\prime }(F)\backslash U'(\mathbb {A})$
,
$y\in P_1^{\prime }(F)\backslash U'(\mathbb {A})$
,
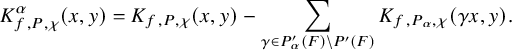 $$ \begin{align*} K^\alpha_{f,P,\chi}(x,y)= K_{f,P,\chi}(x,y)- \sum_{\gamma \in P_\alpha^{\prime}(F)\backslash P'(F)} K_{f,P_\alpha,\chi}(\gamma x,y). \end{align*} $$
$$ \begin{align*} K^\alpha_{f,P,\chi}(x,y)= K_{f,P,\chi}(x,y)- \sum_{\gamma \in P_\alpha^{\prime}(F)\backslash P'(F)} K_{f,P_\alpha,\chi}(\gamma x,y). \end{align*} $$
Note that we have for all
![]() $x\in P_2^{\prime }(F)\backslash U'(\mathbb {A})$
and
$x\in P_2^{\prime }(F)\backslash U'(\mathbb {A})$
and
![]() $y\in P_1^{\prime }(F)\backslash U'(\mathbb {A})$
,
$y\in P_1^{\prime }(F)\backslash U'(\mathbb {A})$
,
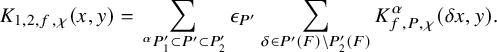 $$ \begin{align} K_{1,2, f,\chi}(x,y)=\sum_{\,^\alpha P_1^{\prime}\subset P'\subset P_2^{\prime}} \epsilon_{P'} \sum_{\delta \in P'(F)\backslash P_2^{\prime}(F)} K^\alpha_{f,P,\chi}(\delta x,y). \end{align} $$
$$ \begin{align} K_{1,2, f,\chi}(x,y)=\sum_{\,^\alpha P_1^{\prime}\subset P'\subset P_2^{\prime}} \epsilon_{P'} \sum_{\delta \in P'(F)\backslash P_2^{\prime}(F)} K^\alpha_{f,P,\chi}(\delta x,y). \end{align} $$
We fix
![]() $P'$
as in the sum above, and we start by majorizing each
$P'$
as in the sum above, and we start by majorizing each
![]() $K^\alpha _{P,\chi ,f}( x,y)$
.
$K^\alpha _{P,\chi ,f}( x,y)$
.
Lemma 3.4.5.1. There exists
![]() $n_0>0$
such that for any
$n_0>0$
such that for any
![]() $n_1,n_2>0$
, there is a continuous semi-norm
$n_1,n_2>0$
, there is a continuous semi-norm
![]() $\|\cdot \|$
on
$\|\cdot \|$
on
![]() $\mathcal {S}(U(\mathbb {A}))$
such that
$\mathcal {S}(U(\mathbb {A}))$
such that
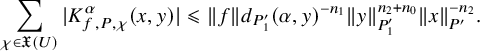 $$ \begin{align*} \sum_{\chi\in \mathfrak{X}(U)} |K^{\alpha}_{f,P,\chi}(x,y)| \leqslant \|f\| d_{P_1^{\prime}}(\alpha,y)^{-n_1}\|y\|^{n_2+n_0}_{P^{\prime}_1} \|x\|_{P'}^{-n_2}. \end{align*} $$
$$ \begin{align*} \sum_{\chi\in \mathfrak{X}(U)} |K^{\alpha}_{f,P,\chi}(x,y)| \leqslant \|f\| d_{P_1^{\prime}}(\alpha,y)^{-n_1}\|y\|^{n_2+n_0}_{P^{\prime}_1} \|x\|_{P'}^{-n_2}. \end{align*} $$
for all
![]() $x\in P'(F)\backslash U'(\mathbb {A})$
,
$x\in P'(F)\backslash U'(\mathbb {A})$
,
![]() $y \in P_1^{\prime }(F)\backslash U'(\mathbb {A})$
and
$y \in P_1^{\prime }(F)\backslash U'(\mathbb {A})$
and
![]() $T\in \mathfrak {a}_0^+$
sufficiently positive such that
$T\in \mathfrak {a}_0^+$
sufficiently positive such that
Proof. Let
![]() $y \in U'(\mathbb {A})$
. By using left translation by
$y \in U'(\mathbb {A})$
. By using left translation by
![]() $P_1^{\prime }(F)$
, we may and shall assume that
$P_1^{\prime }(F)$
, we may and shall assume that
![]() $y\in \mathfrak {s}_{P^{\prime }_1}$
. Assume that y satisfies also the Condition (3.4.5.2): by [Reference ArthurArt78, lemma 6.1], y thus satisfies
$y\in \mathfrak {s}_{P^{\prime }_1}$
. Assume that y satisfies also the Condition (3.4.5.2): by [Reference ArthurArt78, lemma 6.1], y thus satisfies
![]() $F^{P_1^{\prime }}(y,T)\tau _{P_1^{\prime }}^{P_2^{\prime }}(H_{P_1^{\prime }}(y)-T)=1$
. By Lemma 2.3.3.1 and then Lemma 2.3.4.2, we have
$F^{P_1^{\prime }}(y,T)\tau _{P_1^{\prime }}^{P_2^{\prime }}(H_{P_1^{\prime }}(y)-T)=1$
. By Lemma 2.3.3.1 and then Lemma 2.3.4.2, we have
![]() $y\in \mathfrak {s}_{P_2^{\prime }}$
and
$y\in \mathfrak {s}_{P_2^{\prime }}$
and
![]() $d_{P_\alpha ^{\prime }}(\alpha ,y)=d_{P_1^{\prime }}(\alpha ,y)$
. Since we have
$d_{P_\alpha ^{\prime }}(\alpha ,y)=d_{P_1^{\prime }}(\alpha ,y)$
. Since we have
![]() $\|y\|_{P^{\prime }_1} \sim \|y\|$
for
$\|y\|_{P^{\prime }_1} \sim \|y\|$
for
![]() $y\in \mathfrak {s}_{P^{\prime }_1}$
and
$y\in \mathfrak {s}_{P^{\prime }_1}$
and
![]() $d_{P_\alpha ^{\prime }}(\alpha ,y)\sim \exp (\langle \alpha , H_{P_0^{\prime }}(y)\rangle )$
for
$d_{P_\alpha ^{\prime }}(\alpha ,y)\sim \exp (\langle \alpha , H_{P_0^{\prime }}(y)\rangle )$
for
![]() $y\in \mathfrak {s}_{P^{\prime }_\alpha }$
, we may and shall freely replace
$y\in \mathfrak {s}_{P^{\prime }_\alpha }$
, we may and shall freely replace
![]() $ d_{P_1^{\prime }}(\alpha ,y)$
by either
$ d_{P_1^{\prime }}(\alpha ,y)$
by either
![]() $d_{P_\alpha ^{\prime }}(\alpha ,y)$
or
$d_{P_\alpha ^{\prime }}(\alpha ,y)$
or
![]() $\exp (\langle \alpha , H_{P_0^{\prime }}(y)\rangle )$
and
$\exp (\langle \alpha , H_{P_0^{\prime }}(y)\rangle )$
and
![]() $\|y\|_{P^{\prime }_1} $
by
$\|y\|_{P^{\prime }_1} $
by
![]() $\|y\|$
in the inequality we have to prove.
$\|y\|$
in the inequality we have to prove.
Let us observe that we have
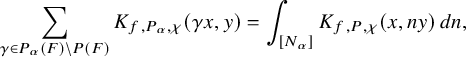 $$ \begin{align*} \sum_{\gamma\in P_\alpha(F)\backslash P(F)}K_{f,P_\alpha,\chi}(\gamma x,y)=\int_{[N_\alpha]} K_{f,P,\chi}(x,n y)\, dn, \end{align*} $$
$$ \begin{align*} \sum_{\gamma\in P_\alpha(F)\backslash P(F)}K_{f,P_\alpha,\chi}(\gamma x,y)=\int_{[N_\alpha]} K_{f,P,\chi}(x,n y)\, dn, \end{align*} $$
where
![]() $N_\alpha =N_{P_\alpha }$
. We have
$N_\alpha =N_{P_\alpha }$
. We have
![]() $P_\alpha =P_\alpha ^{\prime }\times P_\alpha ^{\prime \prime }$
, where
$P_\alpha =P_\alpha ^{\prime }\times P_\alpha ^{\prime \prime }$
, where
![]() $P_\alpha ^{\prime }\subset P'$
and
$P_\alpha ^{\prime }\subset P'$
and
![]() $P_\alpha ^{\prime \prime }\subset P"$
are maximal parabolic subgroups. We set
$P_\alpha ^{\prime \prime }\subset P"$
are maximal parabolic subgroups. We set
![]() $N_\alpha ^{\prime \prime }=N_{P_\alpha ^{\prime \prime }}$
. We denote by
$N_\alpha ^{\prime \prime }=N_{P_\alpha ^{\prime \prime }}$
. We denote by
![]() $\tilde \alpha $
the unique element of
$\tilde \alpha $
the unique element of
![]() $\Delta _0^{P"}\setminus \Delta _0^{P_\alpha ^{\prime \prime }}$
.
$\Delta _0^{P"}\setminus \Delta _0^{P_\alpha ^{\prime \prime }}$
.
Thus, we see that
![]() $K^\alpha _{P,\chi ,f}(x,y)$
is the sum of three terms:
$K^\alpha _{P,\chi ,f}(x,y)$
is the sum of three terms:
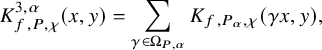 $$ \begin{align} K^{3,\alpha}_{f,P,\chi}(x,y)=\sum_{\gamma\in \Omega_{P,\alpha}} K_{f,P_\alpha, \chi}(\gamma x,y), \end{align} $$
$$ \begin{align} K^{3,\alpha}_{f,P,\chi}(x,y)=\sum_{\gamma\in \Omega_{P,\alpha}} K_{f,P_\alpha, \chi}(\gamma x,y), \end{align} $$
where
![]() $\Omega _{P,\alpha }$
is the complement in
$\Omega _{P,\alpha }$
is the complement in
![]() $P_\alpha (F)\backslash P(F)$
of the diagonal image of
$P_\alpha (F)\backslash P(F)$
of the diagonal image of
![]() $P'(F)$
.
$P'(F)$
.
By a variant of (3.3.4.2), for all
![]() $n_1,n_2>0$
, there exists a continuous semi-norm
$n_1,n_2>0$
, there exists a continuous semi-norm
![]() $\|\cdot \|$
on
$\|\cdot \|$
on
![]() $\mathcal {T}_{n_2}([U])$
such that for all
$\mathcal {T}_{n_2}([U])$
such that for all
![]() $f\in \mathcal {S}(U(\mathbb {A}))$
,
$f\in \mathcal {S}(U(\mathbb {A}))$
,
![]() $\chi \in \mathfrak {X}(U)$
,
$\chi \in \mathfrak {X}(U)$
,
![]() $x\in [U]_P$
and
$x\in [U]_P$
and
![]() $y\in \mathfrak {s}_{P'}$
, we have
$y\in \mathfrak {s}_{P'}$
, we have
By [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Lemma 2.10.1.1], there exists
![]() $n_0>0$
such that for any
$n_0>0$
such that for any
![]() $n_2>0$
and any continuous semi-norm
$n_2>0$
and any continuous semi-norm
![]() $\|\cdot \|$
on
$\|\cdot \|$
on
![]() $\mathcal {T}_{n_2}([U])$
, there is a continuous semi-norm
$\mathcal {T}_{n_2}([U])$
, there is a continuous semi-norm
![]() $\|\cdot \|_{\mathcal {S}}$
on
$\|\cdot \|_{\mathcal {S}}$
on
![]() $\mathcal {S}(U(\mathbb {A}))$
such that
$\mathcal {S}(U(\mathbb {A}))$
such that
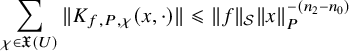 $$ \begin{align*} \sum_{\chi\in \mathfrak{X}(U)} \|K_{f,P,\chi}(x,\cdot)\| \leqslant \|f\|_{\mathcal{S}} \|x\|_P^{-(n_2-n_0)} \end{align*} $$
$$ \begin{align*} \sum_{\chi\in \mathfrak{X}(U)} \|K_{f,P,\chi}(x,\cdot)\| \leqslant \|f\|_{\mathcal{S}} \|x\|_P^{-(n_2-n_0)} \end{align*} $$
for all
![]() $f\in \mathcal {S}(U(\mathbb {A}))$
and
$f\in \mathcal {S}(U(\mathbb {A}))$
and
![]() $x\in [U]_P$
. We conclude that there exists
$x\in [U]_P$
. We conclude that there exists
![]() $n_0$
such for all
$n_0$
such for all
![]() $n_1,n_2>0$
, there is a semi-norm
$n_1,n_2>0$
, there is a semi-norm
![]() $\|\cdot \|_{\mathcal {S}}$
on
$\|\cdot \|_{\mathcal {S}}$
on
![]() $\mathcal {S}(U(\mathbb {A}))$
such that
$\mathcal {S}(U(\mathbb {A}))$
such that
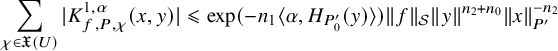 $$ \begin{align} \sum_{\chi\in \mathfrak{X}(U)}|K^{1,\alpha}_{f,P,\chi}(x,y)|\leqslant \exp(- n_1\langle \alpha, H_{P_0^{\prime}}(y)\rangle) \|f\|_{\mathcal{S}} \|y\|^{n_2+n_0} \|x\|_{P'}^{-n_2} \end{align} $$
$$ \begin{align} \sum_{\chi\in \mathfrak{X}(U)}|K^{1,\alpha}_{f,P,\chi}(x,y)|\leqslant \exp(- n_1\langle \alpha, H_{P_0^{\prime}}(y)\rangle) \|f\|_{\mathcal{S}} \|y\|^{n_2+n_0} \|x\|_{P'}^{-n_2} \end{align} $$
for all
![]() $f\in \mathcal {S}(U(\mathbb {A}))$
,
$f\in \mathcal {S}(U(\mathbb {A}))$
,
![]() $x\in [U']_{P'}$
and
$x\in [U']_{P'}$
and
![]() $y\in \mathfrak {s}_{P'}$
. In the same way, one proves that the bounds (3.4.5.6) holds for
$y\in \mathfrak {s}_{P'}$
. In the same way, one proves that the bounds (3.4.5.6) holds for
![]() $K^{2,\alpha }_{f,P,\chi }(x,y)$
.
$K^{2,\alpha }_{f,P,\chi }(x,y)$
.
We introduce the weight function
for
![]() $x=(x',x")\in [U]_{P_\alpha }=[U]_{P_\alpha ^{\prime }}\times [U]_{P_\alpha ^{\prime \prime }}$
. In the following, we shall view
$x=(x',x")\in [U]_{P_\alpha }=[U]_{P_\alpha ^{\prime }}\times [U]_{P_\alpha ^{\prime \prime }}$
. In the following, we shall view
![]() $\alpha +\tilde \alpha $
as an element of
$\alpha +\tilde \alpha $
as an element of
![]() $\mathfrak {a}_{P_0^{\prime }}^*\oplus \mathfrak {a}_{B_0^{\prime \prime }}^*$
. By [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Lemma 2.10.1.1], there exists
$\mathfrak {a}_{P_0^{\prime }}^*\oplus \mathfrak {a}_{B_0^{\prime \prime }}^*$
. By [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Lemma 2.10.1.1], there exists
![]() $n_0>0$
such that for any
$n_0>0$
such that for any
![]() $n_1,n_2>0$
, there is a continuous semi-norm
$n_1,n_2>0$
, there is a continuous semi-norm
![]() $\|\cdot \|_{\mathcal {S}}$
on
$\|\cdot \|_{\mathcal {S}}$
on
![]() $\mathcal {S}(U(\mathbb {A}))$
such that
$\mathcal {S}(U(\mathbb {A}))$
such that
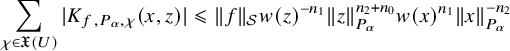 $$ \begin{align*} \sum_{\chi\in \mathfrak{X}(U)} |K_{f,P_\alpha,\chi}(x,z)| \leqslant \|f\|_{\mathcal{S}} w(z)^{-n_1}\|z\|^{n_2+n_0}_{P_\alpha} w(x)^{n_1}\|x\|_{P_\alpha}^{-n_2} \end{align*} $$
$$ \begin{align*} \sum_{\chi\in \mathfrak{X}(U)} |K_{f,P_\alpha,\chi}(x,z)| \leqslant \|f\|_{\mathcal{S}} w(z)^{-n_1}\|z\|^{n_2+n_0}_{P_\alpha} w(x)^{n_1}\|x\|_{P_\alpha}^{-n_2} \end{align*} $$
for all
![]() $f\in \mathcal {S}(U(\mathbb {A}))$
and
$f\in \mathcal {S}(U(\mathbb {A}))$
and
![]() $x,z\in [U]_{P_\alpha }$
. Thus, for all
$x,z\in [U]_{P_\alpha }$
. Thus, for all
![]() $x\in P'(F)\backslash U'(\mathbb {A})$
and
$x\in P'(F)\backslash U'(\mathbb {A})$
and
![]() $z\in [U']_{P_\alpha ^{\prime }}$
, we have
$z\in [U']_{P_\alpha ^{\prime }}$
, we have
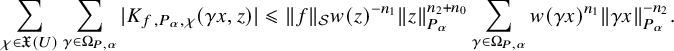 $$ \begin{align} \sum_{\chi\in \mathfrak{X}(U)} \sum_{\gamma \in \Omega_{P,\alpha}}|K_{f,P_\alpha,\chi}(\gamma x, z)| \leqslant \|f\|_{\mathcal{S}} w(z)^{-n_1} \|z\|^{n_2+n_0}_{P_\alpha} \sum_{\gamma \in \Omega_{P,\alpha}}w(\gamma x)^{n_1}\|\gamma x\|_{P_\alpha}^{-n_2}. \end{align} $$
$$ \begin{align} \sum_{\chi\in \mathfrak{X}(U)} \sum_{\gamma \in \Omega_{P,\alpha}}|K_{f,P_\alpha,\chi}(\gamma x, z)| \leqslant \|f\|_{\mathcal{S}} w(z)^{-n_1} \|z\|^{n_2+n_0}_{P_\alpha} \sum_{\gamma \in \Omega_{P,\alpha}}w(\gamma x)^{n_1}\|\gamma x\|_{P_\alpha}^{-n_2}. \end{align} $$
By Proposition 2.3.4.3, there is
![]() $c>0$
such that for all
$c>0$
such that for all
![]() $\gamma =(\gamma ',\gamma ")\in P(F)=P'(F)\times P"(F)$
and any
$\gamma =(\gamma ',\gamma ")\in P(F)=P'(F)\times P"(F)$
and any
![]() $x\in U'(\mathbb {A})$
(viewed as a diagonal element of
$x\in U'(\mathbb {A})$
(viewed as a diagonal element of
![]() $U(\mathbb {A})$
) such that
$U(\mathbb {A})$
) such that
![]() $w(\gamma x)>c$
, we have
$w(\gamma x)>c$
, we have
![]() $\gamma "\in P_\alpha ^{\prime \prime }(F)\gamma '$
. Thus, such a
$\gamma "\in P_\alpha ^{\prime \prime }(F)\gamma '$
. Thus, such a
![]() $\gamma $
cannot belong to the subset
$\gamma $
cannot belong to the subset
![]() $\Omega _{P,\alpha }$
. In this way, for
$\Omega _{P,\alpha }$
. In this way, for
![]() $x\in U'(\mathbb {A})$
, we have
$x\in U'(\mathbb {A})$
, we have
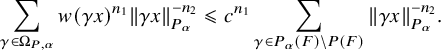 $$ \begin{align} \sum_{\gamma \in \Omega_{P,\alpha}}w(\gamma x)^{n_1}\|\gamma x\|_{P_\alpha}^{-n_2} \leqslant c^{n_1} \sum_{\gamma \in P_\alpha(F)\backslash P(F)} \|\gamma x\|_{P_\alpha}^{-n_2}. \end{align} $$
$$ \begin{align} \sum_{\gamma \in \Omega_{P,\alpha}}w(\gamma x)^{n_1}\|\gamma x\|_{P_\alpha}^{-n_2} \leqslant c^{n_1} \sum_{\gamma \in P_\alpha(F)\backslash P(F)} \|\gamma x\|_{P_\alpha}^{-n_2}. \end{align} $$
By Proposition 3.1.5.1, we have
![]() $w(z)\sim d_{P_\alpha ^{\prime }}(\alpha ,z)^r$
for some
$w(z)\sim d_{P_\alpha ^{\prime }}(\alpha ,z)^r$
for some
![]() $r>0$
and all
$r>0$
and all
![]() $z\in [U']_{P^{\prime }_\alpha }$
. We deduce from (3.4.5.7) and (3.4.5.8) that there exists
$z\in [U']_{P^{\prime }_\alpha }$
. We deduce from (3.4.5.7) and (3.4.5.8) that there exists
![]() $n_0>0$
such that for any
$n_0>0$
such that for any
![]() $n_1,n_2>0$
, there is a continuous semi-norm
$n_1,n_2>0$
, there is a continuous semi-norm
![]() $\|\cdot \|_{\mathcal {S}}$
on
$\|\cdot \|_{\mathcal {S}}$
on
![]() $\mathcal {S}(U(\mathbb {A}))$
such that
$\mathcal {S}(U(\mathbb {A}))$
such that
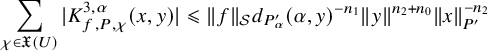 $$ \begin{align*} \sum_{\chi\in \mathfrak{X}(U)} |K^{3,\alpha}_{f,P,\chi}(x,y)| \leqslant \|f\|_{\mathcal{S}} d_{P_\alpha^{\prime}}(\alpha,y)^{-n_1}\|y\|^{n_2+n_0} \|x\|_{P'}^{-n_2} \end{align*} $$
$$ \begin{align*} \sum_{\chi\in \mathfrak{X}(U)} |K^{3,\alpha}_{f,P,\chi}(x,y)| \leqslant \|f\|_{\mathcal{S}} d_{P_\alpha^{\prime}}(\alpha,y)^{-n_1}\|y\|^{n_2+n_0} \|x\|_{P'}^{-n_2} \end{align*} $$
for
![]() $y\in \mathfrak {s}_{P_\alpha ^{\prime }}$
and
$y\in \mathfrak {s}_{P_\alpha ^{\prime }}$
and
![]() $x\in P'(F)\backslash U'(\mathbb {A})$
. The conclusion is clear.
$x\in P'(F)\backslash U'(\mathbb {A})$
. The conclusion is clear.
Lemma 3.4.5.2. There exists
![]() $n_0>0$
such that for any
$n_0>0$
such that for any
![]() $n_2>0$
and any
$n_2>0$
and any
![]() $\lambda $
in the open convex cone generated by
$\lambda $
in the open convex cone generated by
![]() $\Delta _0^{P_2^{\prime }}\setminus \Delta _0^{P_1^{\prime }}$
, there is a continuous semi-norm
$\Delta _0^{P_2^{\prime }}\setminus \Delta _0^{P_1^{\prime }}$
, there is a continuous semi-norm
![]() $\|\cdot \|$
on
$\|\cdot \|$
on
![]() $\mathcal {S}(U(\mathbb {A}))$
such that
$\mathcal {S}(U(\mathbb {A}))$
such that
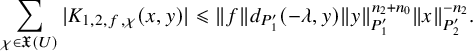 $$ \begin{align*} \sum_{\chi\in \mathfrak{X}(U)}|K_{1,2, f,\chi}(x,y)|\leqslant \|f\| d_{P_1^{\prime}}(-\lambda,y)\|y\|^{n_2+n_0}_{P^{\prime}_1} \|x\|_{P^{\prime}_2}^{-n_2}. \end{align*} $$
$$ \begin{align*} \sum_{\chi\in \mathfrak{X}(U)}|K_{1,2, f,\chi}(x,y)|\leqslant \|f\| d_{P_1^{\prime}}(-\lambda,y)\|y\|^{n_2+n_0}_{P^{\prime}_1} \|x\|_{P^{\prime}_2}^{-n_2}. \end{align*} $$
for all
![]() $f\in \mathcal {S}(U(\mathbb {A}))$
,
$f\in \mathcal {S}(U(\mathbb {A}))$
,
![]() $T\in \mathfrak {a}_0^{\prime }$
sufficiently positive,
$T\in \mathfrak {a}_0^{\prime }$
sufficiently positive,
![]() $x\in P_2^{\prime }(F)\backslash U'(\mathbb {A})$
and
$x\in P_2^{\prime }(F)\backslash U'(\mathbb {A})$
and
![]() $y\in P_1^{\prime }(F)\backslash U'(\mathbb {A})$
such that
$y\in P_1^{\prime }(F)\backslash U'(\mathbb {A})$
such that
![]() $F^{P_1^{\prime }}(y,T) \sigma _{1}^{2}(H_{P_1^{\prime }}(y)-T) =1$
.
$F^{P_1^{\prime }}(y,T) \sigma _{1}^{2}(H_{P_1^{\prime }}(y)-T) =1$
.
Proof. Let
![]() $P_1^{\prime }\subset P'\subset P_2^{\prime }$
and
$P_1^{\prime }\subset P'\subset P_2^{\prime }$
and
![]() $\alpha \in \Delta _0^{P_2^{\prime }}\setminus \Delta _0^{P_1^{\prime }}$
. By Lemma 3.4.5.1, there exists
$\alpha \in \Delta _0^{P_2^{\prime }}\setminus \Delta _0^{P_1^{\prime }}$
. By Lemma 3.4.5.1, there exists
![]() $n_0>0$
such that for all
$n_0>0$
such that for all
![]() $n_1,n_2>0$
, there is a continuous semi-norm
$n_1,n_2>0$
, there is a continuous semi-norm
![]() $\|\cdot \|$
on
$\|\cdot \|$
on
![]() $\mathcal {S}(U(\mathbb {A}))$
such that for all f, T and y as in the statement and all
$\mathcal {S}(U(\mathbb {A}))$
such that for all f, T and y as in the statement and all
![]() $x\in P'(F)\backslash U'(\mathbb {A})$
, we have
$x\in P'(F)\backslash U'(\mathbb {A})$
, we have
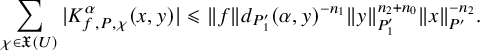 $$ \begin{align*} \sum_{\chi\in \mathfrak{X}(U)} |K^{\alpha}_{f,P,\chi}(x,y)| \leqslant \|f\| d_{P_1^{\prime}}(\alpha,y)^{-n_1}\|y\|^{n_2+n_0}_{P^{\prime}_1} \|x\|_{P'}^{-n_2}. \end{align*} $$
$$ \begin{align*} \sum_{\chi\in \mathfrak{X}(U)} |K^{\alpha}_{f,P,\chi}(x,y)| \leqslant \|f\| d_{P_1^{\prime}}(\alpha,y)^{-n_1}\|y\|^{n_2+n_0}_{P^{\prime}_1} \|x\|_{P'}^{-n_2}. \end{align*} $$
Using the decomposition (3.4.5.1), we see that there exists
![]() $n_0>0$
such that for any
$n_0>0$
such that for any
![]() $n_1,n_2>0$
, there is a continuous semi-norm
$n_1,n_2>0$
, there is a continuous semi-norm
![]() $\|\cdot \|$
on
$\|\cdot \|$
on
![]() $\mathcal {S}(U(\mathbb {A}))$
such that
$\mathcal {S}(U(\mathbb {A}))$
such that
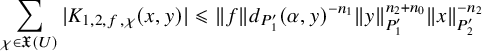 $$ \begin{align*} \sum_{\chi\in \mathfrak{X}(U)}|K_{1,2, f,\chi}(x,y)|\leqslant \|f\| d_{P_1^{\prime}}(\alpha,y)^{-n_1}\|y\|^{n_2+n_0}_{P^{\prime}_1} \|x\|_{P_2^{\prime}}^{-n_2} \end{align*} $$
$$ \begin{align*} \sum_{\chi\in \mathfrak{X}(U)}|K_{1,2, f,\chi}(x,y)|\leqslant \|f\| d_{P_1^{\prime}}(\alpha,y)^{-n_1}\|y\|^{n_2+n_0}_{P^{\prime}_1} \|x\|_{P_2^{\prime}}^{-n_2} \end{align*} $$
for all f, T, x and y as in the statement. The result follows easily.
Let
![]() $n_0$
be as in Lemma 3.4.5.2. For any
$n_0$
be as in Lemma 3.4.5.2. For any
![]() $n_1,n_2,r>0$
, there are
$n_1,n_2,r>0$
, there are
![]() $\lambda $
and
$\lambda $
and
![]() $C>0$
as in Lemma 3.3.4.1 such that for all
$C>0$
as in Lemma 3.3.4.1 such that for all
![]() $y\in P_1^{\prime }(F)\backslash U'(\mathbb {A})$
and
$y\in P_1^{\prime }(F)\backslash U'(\mathbb {A})$
and
![]() $T\in \mathfrak {a}_0^{\prime }$
sufficiently positive, we have
$T\in \mathfrak {a}_0^{\prime }$
sufficiently positive, we have
This indeed follows from Lemma 3.3.4.1: we may take
![]() $y\in \mathfrak {s}_{P_1^{\prime }}$
and use the fact that
$y\in \mathfrak {s}_{P_1^{\prime }}$
and use the fact that
![]() $d_{P_1^{\prime }}(-\lambda ,y)$
is equivalent to
$d_{P_1^{\prime }}(-\lambda ,y)$
is equivalent to
![]() $\exp (\langle -\lambda , H_{P_0^{\prime }}(y)\rangle )$
for
$\exp (\langle -\lambda , H_{P_0^{\prime }}(y)\rangle )$
for
![]() $y\in \mathfrak {s}_{P_1^{\prime }}$
(see Proposition 2.3.4.1).
$y\in \mathfrak {s}_{P_1^{\prime }}$
(see Proposition 2.3.4.1).
As a consequence, we get by Lemma 3.4.5.2 that for any
![]() $n_1,n_2>0$
, there exists a continuous semi-norm
$n_1,n_2>0$
, there exists a continuous semi-norm
![]() $\|\cdot \|$
on
$\|\cdot \|$
on
![]() $\mathcal {S}(U(\mathbb {A}))$
such that
$\mathcal {S}(U(\mathbb {A}))$
such that
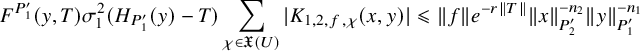 $$ \begin{align*} F^{P_1^{\prime}}(y,T) \sigma_{1}^{2}(H_{P_1^{\prime}}(y)-T) \sum_{\chi\in \mathfrak{X}(U)}|K_{1,2, f,\chi}(x,y)|\leqslant \|f\| e^{-r\|T\|} \|x\|_{P^{\prime}_2}^{-n_2} \|y\|^{-n_1 }_{P^{\prime}_1} \end{align*} $$
$$ \begin{align*} F^{P_1^{\prime}}(y,T) \sigma_{1}^{2}(H_{P_1^{\prime}}(y)-T) \sum_{\chi\in \mathfrak{X}(U)}|K_{1,2, f,\chi}(x,y)|\leqslant \|f\| e^{-r\|T\|} \|x\|_{P^{\prime}_2}^{-n_2} \|y\|^{-n_1 }_{P^{\prime}_1} \end{align*} $$
for all T sufficiently positive, all
![]() $x\in P_2^{\prime }(F)\backslash U^{\prime }(\mathbb {A})$
and
$x\in P_2^{\prime }(F)\backslash U^{\prime }(\mathbb {A})$
and
![]() $ y\in P_1^{\prime }(F)\backslash U^{\prime }(\mathbb {A})$
and all
$ y\in P_1^{\prime }(F)\backslash U^{\prime }(\mathbb {A})$
and all
![]() $f\in \mathcal {S}(U(\mathbb {A}))$
. It is then straightforward to get Theorem 3.4.2.1.
$f\in \mathcal {S}(U(\mathbb {A}))$
. It is then straightforward to get Theorem 3.4.2.1.
3.5 The
 $(U,U')$
-regular contribution in the Jacquet-Rallis trace formula
$(U,U')$
-regular contribution in the Jacquet-Rallis trace formula
3.5.1
The goal of the section is to get Theorem 3.5.7.1 below which gives a computation of the distributions
![]() $J_\chi ^{U}$
of Theorem 3.2.3.1 in terms of relative characters for some specific cuspidal data which we are going to define.
$J_\chi ^{U}$
of Theorem 3.2.3.1 in terms of relative characters for some specific cuspidal data which we are going to define.
3.5.2
Recall that we have
![]() $U=U'\times U"$
. Let
$U=U'\times U"$
. Let
![]() $\chi =(\chi ',\chi ")\in \mathfrak {X}(U)=\mathfrak {X}(U')\times \mathfrak {X}(U")$
be a cuspidal datum. Let
$\chi =(\chi ',\chi ")\in \mathfrak {X}(U)=\mathfrak {X}(U')\times \mathfrak {X}(U")$
be a cuspidal datum. Let
![]() $(M=M'\times M",\pi =\pi '\boxtimes \pi ")$
be a representative where
$(M=M'\times M",\pi =\pi '\boxtimes \pi ")$
be a representative where
![]() $M=M_P$
is standard Levi subgroup of a standard parabolic subgroup P of U. For any integer r, we set
$M=M_P$
is standard Levi subgroup of a standard parabolic subgroup P of U. For any integer r, we set
![]() $G_r=\operatorname {\mathrm {Res}}_{E/F} \mathrm {GL}(r,E)$
. We can find hermitian forms
$G_r=\operatorname {\mathrm {Res}}_{E/F} \mathrm {GL}(r,E)$
. We can find hermitian forms
![]() $h'$
and
$h'$
and
![]() $h"$
respectively of rank
$h"$
respectively of rank
![]() $n'$
and
$n'$
and
![]() $n"$
, integers
$n"$
, integers
![]() $n_1^{\prime },\ldots , n_{r'}^{\prime }$
and
$n_1^{\prime },\ldots , n_{r'}^{\prime }$
and
![]() $n_1^{\prime \prime },\ldots , n_{r"}^{\prime \prime }$
and for
$n_1^{\prime \prime },\ldots , n_{r"}^{\prime \prime }$
and for
![]() $1\leqslant i\leqslant r'$
cuspidal representations
$1\leqslant i\leqslant r'$
cuspidal representations
![]() $\pi _i^{\prime }$
of
$\pi _i^{\prime }$
of
![]() $G_{n_i^{\prime }}(\mathbb {A})$
(with central character trivial on
$G_{n_i^{\prime }}(\mathbb {A})$
(with central character trivial on
![]() $A_{G_{n_i^{\prime }}}^\infty $
) and for
$A_{G_{n_i^{\prime }}}^\infty $
) and for
![]() $1\leqslant i\leqslant r"$
cuspidal representations
$1\leqslant i\leqslant r"$
cuspidal representations
![]() $\pi _i^{\prime \prime }$
of
$\pi _i^{\prime \prime }$
of
![]() $G_{n_i^{\prime \prime }}(\mathbb {A})$
(with central character trivial on
$G_{n_i^{\prime \prime }}(\mathbb {A})$
(with central character trivial on
![]() $A_{G_{n_i^{\prime \prime }}}^\infty $
), cuspidal representations
$A_{G_{n_i^{\prime \prime }}}^\infty $
), cuspidal representations
![]() $\sigma '$
and
$\sigma '$
and
![]() $\sigma "$
respectively of
$\sigma "$
respectively of
![]() $U(h')(\mathbb {A})$
and
$U(h')(\mathbb {A})$
and
![]() $U(h")(\mathbb {A})$
such that such that
$U(h")(\mathbb {A})$
such that such that
-
•
 $n'+2(n_1^{\prime }+\ldots +n_{r'}^{\prime })=n$
and
$n'+2(n_1^{\prime }+\ldots +n_{r'}^{\prime })=n$
and
 $n"+2(n_1^{\prime \prime }+\ldots +n_{r"}^{\prime \prime })=n+1$
;
$n"+2(n_1^{\prime \prime }+\ldots +n_{r"}^{\prime \prime })=n+1$
; -
•
 $M'\simeq G_{n_1^{\prime }}\times \ldots \times G_{n_{r'}^{\prime }} \times U(h')$
and
$M'\simeq G_{n_1^{\prime }}\times \ldots \times G_{n_{r'}^{\prime }} \times U(h')$
and
 $M"\simeq G_{n_1^{\prime \prime }}\times \ldots \times G_{n^{\prime \prime }_{r"}} \times U(h")$
;
$M"\simeq G_{n_1^{\prime \prime }}\times \ldots \times G_{n^{\prime \prime }_{r"}} \times U(h")$
; -
•
 $\pi '=\pi _1^{\prime }\boxtimes \ldots \boxtimes \pi _{r'}^{\prime }\boxtimes \sigma '$
and
$\pi '=\pi _1^{\prime }\boxtimes \ldots \boxtimes \pi _{r'}^{\prime }\boxtimes \sigma '$
and
 $\pi "=\pi _1^{\prime \prime }\boxtimes \ldots \boxtimes \pi _{r"}^{\prime \prime }\boxtimes \sigma "$
accordingly.
$\pi "=\pi _1^{\prime \prime }\boxtimes \ldots \boxtimes \pi _{r"}^{\prime \prime }\boxtimes \sigma "$
accordingly.
We shall say that
![]() $\chi $
is
$\chi $
is
-
• U-regular (or simply regular) if both
 $\chi '$
and
$\chi '$
and
 $\chi "$
are regular. We say that
$\chi "$
are regular. We say that
 $\chi '$
is regular if the representations
$\chi '$
is regular if the representations
 $\pi _1^{\prime },\ldots ,\pi _{r'}^{\prime }, (\pi _1^{\prime })^{*},\ldots , (\pi _{r^{\prime }}^{\prime })^{*}$
are two by two distinct (the same definition applies to
$\pi _1^{\prime },\ldots ,\pi _{r'}^{\prime }, (\pi _1^{\prime })^{*},\ldots , (\pi _{r^{\prime }}^{\prime })^{*}$
are two by two distinct (the same definition applies to
 $\chi "$
). Here,
$\chi "$
). Here,
 $\pi ^*$
means the conjugate dual of the representation
$\pi ^*$
means the conjugate dual of the representation
 $\pi $
.
$\pi $
. -
•
 $U'$
-regular if for each
$U'$
-regular if for each
 $1\leqslant i\leqslant r'$
and
$1\leqslant i\leqslant r'$
and
 $1\leqslant j\leqslant r"$
such that
$1\leqslant j\leqslant r"$
such that
 $n_i^{\prime }=n_j^{\prime \prime }$
, the representations
$n_i^{\prime }=n_j^{\prime \prime }$
, the representations
 $(\pi _i^{\prime })^\vee $
(the contragredient of
$(\pi _i^{\prime })^\vee $
(the contragredient of
 $\pi _i^{\prime }$
) and
$\pi _i^{\prime }$
) and
 $\pi _j^{\prime \prime }$
are neither isomorphic nor conjugate dual;
$\pi _j^{\prime \prime }$
are neither isomorphic nor conjugate dual; -
•
 $(U,U')$
-regular if it is both U-regular and
$(U,U')$
-regular if it is both U-regular and
 $U'$
-regular.
$U'$
-regular.
3.5.3
Let
![]() $\varphi \in \mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(U)$
. Let
$\varphi \in \mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(U)$
. Let
![]() $\lambda \in \mathfrak {a}_{P,\mathbb {C}}^*$
such that the Eisenstein series
$\lambda \in \mathfrak {a}_{P,\mathbb {C}}^*$
such that the Eisenstein series
![]() $E(\varphi ,\lambda )$
on
$E(\varphi ,\lambda )$
on
![]() $[U]$
is regular at
$[U]$
is regular at
![]() $\lambda $
. For
$\lambda $
. For
![]() $T\in \mathfrak {a}_0^{\prime }$
, we denote by
$T\in \mathfrak {a}_0^{\prime }$
, we denote by
![]() $\Lambda ^T_u E(\varphi ,\lambda )$
the function on
$\Lambda ^T_u E(\varphi ,\lambda )$
the function on
![]() $[U']$
obtained from
$[U']$
obtained from
![]() $E(\varphi ,\lambda )$
by truncation by the operator defined in (3.3.2.1). The following proposition is basic to our calculation.
$E(\varphi ,\lambda )$
by truncation by the operator defined in (3.3.2.1). The following proposition is basic to our calculation.
Proposition 3.5.3.1. Let
![]() $T\in \mathfrak {a}_0^{\prime }$
sufficiently positive.
$T\in \mathfrak {a}_0^{\prime }$
sufficiently positive.
-
1. The integral
(3.5.3.1)is absolutely convergent. $$ \begin{align} \int_{[U']} \Lambda^T_u E(x,\varphi,\lambda)\, dx \end{align} $$
$$ \begin{align} \int_{[U']} \Lambda^T_u E(x,\varphi,\lambda)\, dx \end{align} $$
-
2. If the spectral datum
 $\chi $
defined by
$\chi $
defined by
 $(M,\pi )$
is
$(M,\pi )$
is
 $U'$
-regular, then the integral (3.5.3.1) does not depend on T.
$U'$
-regular, then the integral (3.5.3.1) does not depend on T. -
3. Write
 $P=P'\times P"$
. If
$P=P'\times P"$
. If
 $P'=U'$
or
$P'=U'$
or
 $P"=U"$
, then we have (3.5.3.2)where the left-hand side is absolutely convergent.
$P"=U"$
, then we have (3.5.3.2)where the left-hand side is absolutely convergent. $$ \begin{align} \int_{[U']} \Lambda^T_u E(x,\varphi,\lambda)\, dx=\int_{[U']} E(x,\varphi,\lambda)\, dx, \end{align} $$
$$ \begin{align} \int_{[U']} \Lambda^T_u E(x,\varphi,\lambda)\, dx=\int_{[U']} E(x,\varphi,\lambda)\, dx, \end{align} $$
Proof. 1. The absolute convergence follows from the uniform moderate growth of Eisenstein series and the basic properties of the truncation operator
![]() $\Lambda ^T_u$
recalled in Proposition 3.3.3.1.
$\Lambda ^T_u$
recalled in Proposition 3.3.3.1.
2. To analyse the dependence on T, we shall use the following formula (adapted from [Reference Ichino and YamanaIY19, eq. (2.2)]): for any
![]() $T'\in \mathfrak {a}_0^{\prime }$
and any smooth function
$T'\in \mathfrak {a}_0^{\prime }$
and any smooth function
![]() $\varphi $
on
$\varphi $
on
![]() $[U]$
, we have for any
$[U]$
, we have for any
![]() $x\in U'(\mathbb {A})$
,
$x\in U'(\mathbb {A})$
,
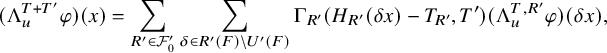 $$ \begin{align} (\Lambda^{T+T'}_u\varphi)(x)=\sum_{R'\in \mathcal{F}_0^{\prime}} \sum_{\delta \in R'(F)\backslash U'(F)} \Gamma_{R'}(H_{R'}(\delta x)-T_{R'},T') (\Lambda^{T,R'}_u\varphi)(\delta x), \end{align} $$
$$ \begin{align} (\Lambda^{T+T'}_u\varphi)(x)=\sum_{R'\in \mathcal{F}_0^{\prime}} \sum_{\delta \in R'(F)\backslash U'(F)} \Gamma_{R'}(H_{R'}(\delta x)-T_{R'},T') (\Lambda^{T,R'}_u\varphi)(\delta x), \end{align} $$
where the function
![]() $\Gamma _{R'}(\cdot ,T')$
is compactly supported on
$\Gamma _{R'}(\cdot ,T')$
is compactly supported on
![]() $\mathfrak {a}_{R'}$
(for the precise definition, see p.9 of [Reference Ichino and YamanaIY19]); moreover, we set for any
$\mathfrak {a}_{R'}$
(for the precise definition, see p.9 of [Reference Ichino and YamanaIY19]); moreover, we set for any
![]() $x\in U'(\mathbb {A})$
,
$x\in U'(\mathbb {A})$
,
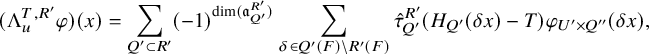 $$ \begin{align*} (\Lambda^{T,R'}_u\varphi)(x)=\sum_{Q'\subset R'} (-1)^{\dim(\mathfrak{a}_{Q'}^{R'})}\sum_{\delta \in Q'(F)\backslash R'(F)}\hat\tau_{Q'}^{R'}(H_{Q'}(\delta x)-T) \varphi_{U'\times Q"}(\delta x), \end{align*} $$
$$ \begin{align*} (\Lambda^{T,R'}_u\varphi)(x)=\sum_{Q'\subset R'} (-1)^{\dim(\mathfrak{a}_{Q'}^{R'})}\sum_{\delta \in Q'(F)\backslash R'(F)}\hat\tau_{Q'}^{R'}(H_{Q'}(\delta x)-T) \varphi_{U'\times Q"}(\delta x), \end{align*} $$
where the sum is over the set of standard parabolic subgroups
![]() $Q'$
of
$Q'$
of
![]() $R'$
and
$R'$
and
![]() $\varphi _{U'\times Q"}$
is the constant term along
$\varphi _{U'\times Q"}$
is the constant term along
![]() $U'\times Q"$
, where
$U'\times Q"$
, where
![]() $Q'\times Q"$
is the image of
$Q'\times Q"$
is the image of
![]() $Q'$
by the map (3.1.4.1). For
$Q'$
by the map (3.1.4.1). For
![]() $R'=U'$
, we recover the operator
$R'=U'$
, we recover the operator
![]() $\Lambda ^{T}_u$
.
$\Lambda ^{T}_u$
.
Using (3.5.3.3) and some Iwasawa decomposition, we see that assertion 2 follows from the following vanishing statement: for any proper standard parabolic subgroups
![]() $R'$
of
$R'$
of
![]() $U'$
, we have for some Haar measure on K,
$U'$
, we have for some Haar measure on K,
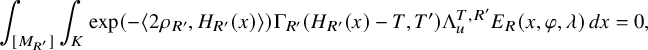 $$ \begin{align*} \int_{[M_{R'}]} \int_K \exp(-\langle 2\rho_{R'},H_{R'}(x)\rangle) \Gamma_{R'}(H_{R'}(x)-T,T') \Lambda^{T,R'}_uE_{R}( x,\varphi,\lambda)\, dx=0, \end{align*} $$
$$ \begin{align*} \int_{[M_{R'}]} \int_K \exp(-\langle 2\rho_{R'},H_{R'}(x)\rangle) \Gamma_{R'}(H_{R'}(x)-T,T') \Lambda^{T,R'}_uE_{R}( x,\varphi,\lambda)\, dx=0, \end{align*} $$
where
![]() $E_{R}( \varphi ,\lambda )$
is the constant term of
$E_{R}( \varphi ,\lambda )$
is the constant term of
![]() $E(\varphi ,\lambda )$
along the parabolic subgroup R, the image of
$E(\varphi ,\lambda )$
along the parabolic subgroup R, the image of
![]() $R'$
by the map (3.1.4.1).
$R'$
by the map (3.1.4.1).
Using the usual computation of the constant term of (cuspidal) Eisenstein series, we are reduced to prove that
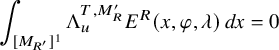 $$ \begin{align} \int_{[M_{R'}]^1} \Lambda^{T,M_R'}_u E^{R}( x,\varphi,\lambda)\, dx=0 \end{align} $$
$$ \begin{align} \int_{[M_{R'}]^1} \Lambda^{T,M_R'}_u E^{R}( x,\varphi,\lambda)\, dx=0 \end{align} $$
for all parabolic subgroup
![]() $P\subset R$
, all
$P\subset R$
, all
![]() $\varphi \in \mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(U)$
such that the class of
$\varphi \in \mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(U)$
such that the class of
![]() $(M_P,\pi )$
is
$(M_P,\pi )$
is
![]() $U'$
-regular. Here,
$U'$
-regular. Here,
![]() $E^{R}(\varphi ,\lambda )$
denotes the Eisenstein series relative to R.
$E^{R}(\varphi ,\lambda )$
denotes the Eisenstein series relative to R.
Let us prove this last claim. The reasoning here is very similar to that of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, proof of proposition 5.1.4.1], so we will be quite brief. There exist a hermitian form
![]() $h'$
of rank m and integers
$h'$
of rank m and integers
![]() $n_1,\ldots ,n_r$
such that
$n_1,\ldots ,n_r$
such that
![]() $m+2(n_1+\ldots +n_r)=n$
$m+2(n_1+\ldots +n_r)=n$
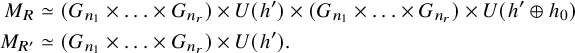 $$ \begin{align*} M_{R} & \simeq (G_{n_1}\times\ldots\times G_{n_r})\times U(h') \times (G_{n_1}\times\ldots\times G_{n_r})\times U(h'\oplus h_0)\\ M_{R'} &\simeq (G_{n_1}\times\ldots\times G_{n_r})\times U(h'). \end{align*} $$
$$ \begin{align*} M_{R} & \simeq (G_{n_1}\times\ldots\times G_{n_r})\times U(h') \times (G_{n_1}\times\ldots\times G_{n_r})\times U(h'\oplus h_0)\\ M_{R'} &\simeq (G_{n_1}\times\ldots\times G_{n_r})\times U(h'). \end{align*} $$
The embedding
![]() $M_{R'}\subset M_{R}$
is given by the product of the diagonal embeddings
$M_{R'}\subset M_{R}$
is given by the product of the diagonal embeddings
![]() $G_{n_1}\times \ldots \times G_{n_r}\subset (G_{n_1}\times \ldots \times G_{n_r})^2$
and
$G_{n_1}\times \ldots \times G_{n_r}\subset (G_{n_1}\times \ldots \times G_{n_r})^2$
and
![]() $ U(h')\subset U(h')\times U(h'\oplus h_0)$
. Then the operator
$ U(h')\subset U(h')\times U(h'\oplus h_0)$
. Then the operator
![]() $ \Lambda ^{T,M_R'}_u$
is the product of
$ \Lambda ^{T,M_R'}_u$
is the product of
-
• the usual Arthur operator attached to
 $G_{n_1}\times \ldots \times G_{n_r}$
viewed as an operator on functions on
$G_{n_1}\times \ldots \times G_{n_r}$
viewed as an operator on functions on
 $[G_{n_1}\times \ldots \times G_{n_r}]\times [G_{n_1}\times \ldots \times G_{n_r}]$
acting on the second factor;
$[G_{n_1}\times \ldots \times G_{n_r}]\times [G_{n_1}\times \ldots \times G_{n_r}]$
acting on the second factor; -
• the operator
 $ \Lambda ^{T,U(h')}_u$
defined relatively to the embedding
$ \Lambda ^{T,U(h')}_u$
defined relatively to the embedding
 $ U(h')\subset U(h')\times U(h'\oplus h_0)$
.
$ U(h')\subset U(h')\times U(h'\oplus h_0)$
.
We see that in (3.5.3.4), each integral over
![]() $G_{n_i}$
can be interpreted as a scalar product of an Eisenstein series and a truncated Eisenstein series. By Langlands’ computation of this scalar product and our
$G_{n_i}$
can be interpreted as a scalar product of an Eisenstein series and a truncated Eisenstein series. By Langlands’ computation of this scalar product and our
![]() $U'$
-regularity assumption, we get the expected vanishing.
$U'$
-regularity assumption, we get the expected vanishing.
3. If
![]() $P'=U'$
or
$P'=U'$
or
![]() $P"=U"$
, then on the one hand, the cuspidal datum defined by
$P"=U"$
, then on the one hand, the cuspidal datum defined by
![]() $(M,\pi )$
is automatically
$(M,\pi )$
is automatically
![]() $U'$
-regular. Thus, the left-hand side of (3.5.3.2) does not depend on T. On the other hand, the restriction of
$U'$
-regular. Thus, the left-hand side of (3.5.3.2) does not depend on T. On the other hand, the restriction of
![]() $E(\varphi ,\lambda )$
to
$E(\varphi ,\lambda )$
to
![]() $[U']$
is rapidly decreasing. So the right-hand side of (3.5.3.2) is absolutely convergent. Now the equality (3.5.3.2) is a straightforward consequence of assertion 2 of Proposition 3.3.3.1 and the dominated convergence theorem.
$[U']$
is rapidly decreasing. So the right-hand side of (3.5.3.2) is absolutely convergent. Now the equality (3.5.3.2) is a straightforward consequence of assertion 2 of Proposition 3.3.3.1 and the dominated convergence theorem.
3.5.4 Ichino-Yamana regularized period
Assume that the cuspidal datum defined by
![]() $(M,\pi )$
is
$(M,\pi )$
is
![]() $U'$
-regular. Following [Reference Ichino and YamanaIY19], we define the regularized period of
$U'$
-regular. Following [Reference Ichino and YamanaIY19], we define the regularized period of
![]() $E(\varphi ,\lambda )$
for
$E(\varphi ,\lambda )$
for
![]() $\varphi \in \mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(U)$
and
$\varphi \in \mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(U)$
and
![]() $\lambda \in \mathfrak {a}_{P,\mathbb {C}}^*$
by
$\lambda \in \mathfrak {a}_{P,\mathbb {C}}^*$
by
where the right-hand side is the absolutely convergent integral (3.5.3.1) attached to the Eisenstein series
![]() $E(\varphi ,\lambda )$
for any
$E(\varphi ,\lambda )$
for any
![]() $T\in \mathfrak {a}_0^{\prime }$
sufficiently positive. It does not depend on T by Proposition 3.5.3.1 assertion 2. It is meromorphic in
$T\in \mathfrak {a}_0^{\prime }$
sufficiently positive. It does not depend on T by Proposition 3.5.3.1 assertion 2. It is meromorphic in
![]() $\lambda $
and holomorphic when
$\lambda $
and holomorphic when
![]() $E(\varphi ,\lambda )$
is regular, in particular on
$E(\varphi ,\lambda )$
is regular, in particular on
![]() $i\mathfrak {a}_P^*$
. The map
$i\mathfrak {a}_P^*$
. The map
![]() $\varphi \mapsto \mathcal {P}_{U'}(\varphi ,\lambda )$
is continuous.
$\varphi \mapsto \mathcal {P}_{U'}(\varphi ,\lambda )$
is continuous.
3.5.5 Relative character
We keep our assumption on
![]() $(M,\pi )$
. Let
$(M,\pi )$
. Let
![]() $\lambda \in \mathfrak {a}_{P,\mathbb {C}}^*$
. We define the relative character
$\lambda \in \mathfrak {a}_{P,\mathbb {C}}^*$
. We define the relative character
![]() $J_{P,\pi }^U(\lambda , f)$
by
$J_{P,\pi }^U(\lambda , f)$
by
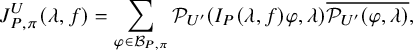 $$ \begin{align} J_{P,\pi}^{U}(\lambda, f)=\sum_{\varphi\in \mathcal{B}_{P,\pi}} \mathcal{P}_{U'}(I_P(\lambda,f)\varphi,\lambda)\overline{ \mathcal{P}_{U'}(\varphi,\lambda) }, \end{align} $$
$$ \begin{align} J_{P,\pi}^{U}(\lambda, f)=\sum_{\varphi\in \mathcal{B}_{P,\pi}} \mathcal{P}_{U'}(I_P(\lambda,f)\varphi,\lambda)\overline{ \mathcal{P}_{U'}(\varphi,\lambda) }, \end{align} $$
where
![]() $f\in \mathcal {S}(U(\mathbb {A}))$
and
$f\in \mathcal {S}(U(\mathbb {A}))$
and
![]() $ \mathcal {B}_{P,\pi }$
is a K-basis of
$ \mathcal {B}_{P,\pi }$
is a K-basis of
![]() $\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(U)$
in the sense of §2.2.4. Outside the singularities of the involved Eisenstein series, the sum is absolutely convergent. It is holomorphic on
$\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(U)$
in the sense of §2.2.4. Outside the singularities of the involved Eisenstein series, the sum is absolutely convergent. It is holomorphic on
![]() $i\mathfrak {a}_{P}^*$
. It does not depend on the choice of
$i\mathfrak {a}_{P}^*$
. It does not depend on the choice of
![]() $\mathcal {B}_{P,\pi }$
and it defines a continuous linear form on
$\mathcal {B}_{P,\pi }$
and it defines a continuous linear form on
![]() $\mathcal {S}(U(\mathbb {A}))$
(see [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, proposition 2.8.4.1])). For further use, we observe the following simple functional equation.
$\mathcal {S}(U(\mathbb {A}))$
(see [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, proposition 2.8.4.1])). For further use, we observe the following simple functional equation.
Proposition 3.5.5.1. Let P and
![]() $P_1$
be standard parabolic subgroup of U of respective standard Levi factors M and
$P_1$
be standard parabolic subgroup of U of respective standard Levi factors M and
![]() $M_1$
. Assume that the pairs
$M_1$
. Assume that the pairs
![]() $(M,\pi )$
and
$(M,\pi )$
and
![]() $(M_1,\pi _1)$
define the same
$(M_1,\pi _1)$
define the same
![]() $U'$
-regular cuspidal datum. Then for
$U'$
-regular cuspidal datum. Then for
![]() $w\in W(M,M_1)$
such that
$w\in W(M,M_1)$
such that
![]() $\pi _1=w\pi $
and
$\pi _1=w\pi $
and
![]() $\lambda \in i\mathfrak {a}_{P}^*$
, we have
$\lambda \in i\mathfrak {a}_{P}^*$
, we have
Proof. This is an immediate consequence of the functional equation
![]() $E(\varphi ,\lambda )=E(M(w,\lambda )\varphi ,w\lambda )$
of Eisenstein series and the fact that for
$E(\varphi ,\lambda )=E(M(w,\lambda )\varphi ,w\lambda )$
of Eisenstein series and the fact that for
![]() $\lambda \in i\mathfrak {a}_{P}^*$
, the intertwining operator sends a K-basis of
$\lambda \in i\mathfrak {a}_{P}^*$
, the intertwining operator sends a K-basis of
![]() $\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(U)$
to a K-basis of
$\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(U)$
to a K-basis of
![]() $\mathcal {A}_{P,\pi _1,\operatorname {\mathrm {cusp}}}(U)$
.
$\mathcal {A}_{P,\pi _1,\operatorname {\mathrm {cusp}}}(U)$
.
3.5.6 Some auxiliary results
For further use, we state and prove some useful results.
Lemma 3.5.6.1. Let
![]() $\chi \in \mathfrak {X}(U)$
be a U-regular cuspidal datum. For any standard parabolic subgroup P of U and any representative
$\chi \in \mathfrak {X}(U)$
be a U-regular cuspidal datum. For any standard parabolic subgroup P of U and any representative
![]() $(M_P,\pi )$
of
$(M_P,\pi )$
of
![]() $\chi $
, we have for all
$\chi $
, we have for all
![]() $f\in \mathcal {S}(U(\mathbb {A}))$
and
$f\in \mathcal {S}(U(\mathbb {A}))$
and
![]() $x,y\in [U]$
,
$x,y\in [U]$
,
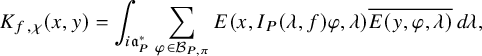 $$ \begin{align} K_{f,\chi}(x,y)=\int_{i\mathfrak{a}_P^{*}} \sum_{\varphi \in \mathcal{B}_{P,\pi}} E(x,I_P(\lambda,f)\varphi,\lambda)\overline{E(y,\varphi,\lambda)}\, d\lambda, \end{align} $$
$$ \begin{align} K_{f,\chi}(x,y)=\int_{i\mathfrak{a}_P^{*}} \sum_{\varphi \in \mathcal{B}_{P,\pi}} E(x,I_P(\lambda,f)\varphi,\lambda)\overline{E(y,\varphi,\lambda)}\, d\lambda, \end{align} $$
where
![]() $\mathcal {B}_{P,\pi }$
is a K-basis as above.
$\mathcal {B}_{P,\pi }$
is a K-basis as above.
Proof. Let
![]() $\chi \in \mathfrak {X}(U)$
and
$\chi \in \mathfrak {X}(U)$
and
![]() $x,y\in [U]$
. We start from the general spectral expansion (see [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, lemma 2.10.2.1])
$x,y\in [U]$
. We start from the general spectral expansion (see [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, lemma 2.10.2.1])
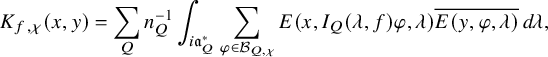 $$ \begin{align} K_{f,\chi}(x,y)=\sum_{Q} n_Q^{-1}\int_{i\mathfrak{a}_Q^{*}} \sum_{\varphi \in \mathcal{B}_{Q,\chi}} E(x,I_Q(\lambda,f)\varphi,\lambda)\overline{E(y,\varphi,\lambda)}\, d\lambda, \end{align} $$
$$ \begin{align} K_{f,\chi}(x,y)=\sum_{Q} n_Q^{-1}\int_{i\mathfrak{a}_Q^{*}} \sum_{\varphi \in \mathcal{B}_{Q,\chi}} E(x,I_Q(\lambda,f)\varphi,\lambda)\overline{E(y,\varphi,\lambda)}\, d\lambda, \end{align} $$
where the sum is over the set of standard parabolic subgroups Q of U; the integer
![]() $n_Q$
is the number of semi-standard parabolic subgroups of U which admits the same semi-standard Levi component as Q. The set
$n_Q$
is the number of semi-standard parabolic subgroups of U which admits the same semi-standard Levi component as Q. The set
![]() $\mathcal {B}_{Q,\chi }$
is a K-basis of the space
$\mathcal {B}_{Q,\chi }$
is a K-basis of the space
![]() $\mathcal {A}_{Q,\chi ,\operatorname {\mathrm {disc}}}^0(U)$
(we refer the reader to [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, § 2.10.2] for the notation). From now on, we assume moreover that
$\mathcal {A}_{Q,\chi ,\operatorname {\mathrm {disc}}}^0(U)$
(we refer the reader to [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, § 2.10.2] for the notation). From now on, we assume moreover that
![]() $\chi $
is U-regular. Let
$\chi $
is U-regular. Let
![]() $(M_P,\pi )$
be a representative of
$(M_P,\pi )$
be a representative of
![]() $\chi $
with P a standard parabolic subgroup of G. Let Q be a standard parabolic subgroup of G. Then the space
$\chi $
with P a standard parabolic subgroup of G. Let Q be a standard parabolic subgroup of G. Then the space
![]() $\mathcal {A}_{Q,\chi ,\operatorname {\mathrm {disc}}}^0(U)$
has the following simple description:
$\mathcal {A}_{Q,\chi ,\operatorname {\mathrm {disc}}}^0(U)$
has the following simple description:
In particular, this space is zero unless Q and P are associated, which we assume from now on. As a consequence, we may and shall assume that
![]() $\mathcal {B}_{Q,\chi }$
is a union over
$\mathcal {B}_{Q,\chi }$
is a union over
![]() $w\in W(P,Q)$
of K-bases
$w\in W(P,Q)$
of K-bases
![]() $\mathcal {B}_{Q,w\pi }$
of
$\mathcal {B}_{Q,w\pi }$
of
![]() $\mathcal {A}_{Q,w\pi ,\operatorname {\mathrm {cusp}}}(U)$
. In this way, by the same argument as in the proof of Proposition 3.5.5.1, we see that we have for all
$\mathcal {A}_{Q,w\pi ,\operatorname {\mathrm {cusp}}}(U)$
. In this way, by the same argument as in the proof of Proposition 3.5.5.1, we see that we have for all
![]() $w\in W(P,Q)$
and
$w\in W(P,Q)$
and
![]() $\lambda \in i\mathfrak {a}_Q^*$
,
$\lambda \in i\mathfrak {a}_Q^*$
,
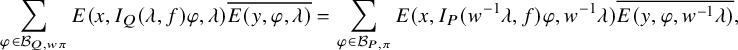 $$ \begin{align*} \sum_{\varphi \in \mathcal{B}_{Q,w\pi}} E(x,I_Q(\lambda,f)\varphi,\lambda)\overline{E(y,\varphi,\lambda)}= \sum_{\varphi \in \mathcal{B}_{P,\pi}} E(x,I_P(w^{-1}\lambda,f)\varphi,w^{-1}\lambda)\overline{E(y,\varphi,w^{-1}\lambda)}, \end{align*} $$
$$ \begin{align*} \sum_{\varphi \in \mathcal{B}_{Q,w\pi}} E(x,I_Q(\lambda,f)\varphi,\lambda)\overline{E(y,\varphi,\lambda)}= \sum_{\varphi \in \mathcal{B}_{P,\pi}} E(x,I_P(w^{-1}\lambda,f)\varphi,w^{-1}\lambda)\overline{E(y,\varphi,w^{-1}\lambda)}, \end{align*} $$
where
![]() $\mathcal {B}_{P,\pi }$
is a K-basis of
$\mathcal {B}_{P,\pi }$
is a K-basis of
![]() $\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(U)$
. So we get by the change of variables
$\mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(U)$
. So we get by the change of variables
![]() $\lambda \mapsto w^{-1}\lambda $
,
$\lambda \mapsto w^{-1}\lambda $
,
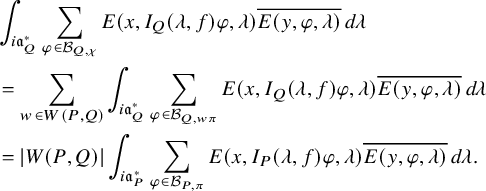 $$ \begin{align*} & \int_{i\mathfrak{a}_Q^{*}} \sum_{\varphi \in \mathcal{B}_{Q,\chi}} E(x,I_Q(\lambda,f)\varphi,\lambda)\overline{E(y,\varphi,\lambda)}\, d\lambda\\ & = \sum_{ w\in W(P,Q) }\int_{i\mathfrak{a}_Q^{*}} \sum_{\varphi \in \mathcal{B}_{Q,w\pi}} E(x,I_Q(\lambda,f)\varphi,\lambda)\overline{E(y,\varphi,\lambda)}\, d\lambda\\ & = |W(P,Q)| \int_{i\mathfrak{a}_P^{*}} \sum_{\varphi \in \mathcal{B}_{P,\pi}} E(x,I_P(\lambda,f)\varphi,\lambda)\overline{E(y,\varphi,\lambda)} \, d\lambda. \end{align*} $$
$$ \begin{align*} & \int_{i\mathfrak{a}_Q^{*}} \sum_{\varphi \in \mathcal{B}_{Q,\chi}} E(x,I_Q(\lambda,f)\varphi,\lambda)\overline{E(y,\varphi,\lambda)}\, d\lambda\\ & = \sum_{ w\in W(P,Q) }\int_{i\mathfrak{a}_Q^{*}} \sum_{\varphi \in \mathcal{B}_{Q,w\pi}} E(x,I_Q(\lambda,f)\varphi,\lambda)\overline{E(y,\varphi,\lambda)}\, d\lambda\\ & = |W(P,Q)| \int_{i\mathfrak{a}_P^{*}} \sum_{\varphi \in \mathcal{B}_{P,\pi}} E(x,I_P(\lambda,f)\varphi,\lambda)\overline{E(y,\varphi,\lambda)} \, d\lambda. \end{align*} $$
This gives the result since we have
![]() $\sum _Q |W(P,Q)| n_Q^{-1}=1$
where the sum is taken over standard parabolic subgroups Q. Note that in the second line above the integral over
$\sum _Q |W(P,Q)| n_Q^{-1}=1$
where the sum is taken over standard parabolic subgroups Q. Note that in the second line above the integral over
![]() $i\mathfrak {a}_Q^{*}$
is absolutely convergent. Let us check this. By Dixmier-Malliavin theorem, we may and shall assume that we have
$i\mathfrak {a}_Q^{*}$
is absolutely convergent. Let us check this. By Dixmier-Malliavin theorem, we may and shall assume that we have
![]() $f=f_1\ast f^*_2$
for some
$f=f_1\ast f^*_2$
for some
![]() $f_1,f_2\in \mathcal {S}(U(\mathbb {A}))$
, where
$f_1,f_2\in \mathcal {S}(U(\mathbb {A}))$
, where
![]() $*$
denotes the convolution product and we have set
$*$
denotes the convolution product and we have set
![]() $f_2^*(g)=\overline {f_2(g^{-1})}$
. By a standard change of basis argument, we have for all
$f_2^*(g)=\overline {f_2(g^{-1})}$
. By a standard change of basis argument, we have for all
![]() $x_1,x_2\in U(\mathbb {A})$
,
$x_1,x_2\in U(\mathbb {A})$
,
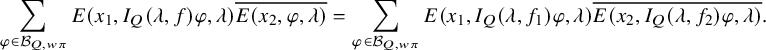 $$ \begin{align*} \sum_{\varphi \in \mathcal{B}_{Q,w\pi}} E(x_1,I_Q(\lambda,f)\varphi,\lambda)\overline{E(x_2,\varphi,\lambda)}= \sum_{\varphi \in \mathcal{B}_{Q,w\pi}} E(x_1,I_Q(\lambda,f_1)\varphi,\lambda)\overline{E(x_2,I_Q(\lambda,f_2)\varphi,\lambda)}. \end{align*} $$
$$ \begin{align*} \sum_{\varphi \in \mathcal{B}_{Q,w\pi}} E(x_1,I_Q(\lambda,f)\varphi,\lambda)\overline{E(x_2,\varphi,\lambda)}= \sum_{\varphi \in \mathcal{B}_{Q,w\pi}} E(x_1,I_Q(\lambda,f_1)\varphi,\lambda)\overline{E(x_2,I_Q(\lambda,f_2)\varphi,\lambda)}. \end{align*} $$
By Cauchy-Schwarz inequality, the expression
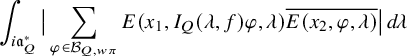 $$ \begin{align*} \int_{i\mathfrak{a}_Q^{*}} \big| \sum_{\varphi \in \mathcal{B}_{Q,w\pi}} E(x_1,I_Q(\lambda,f)\varphi,\lambda)\overline{E(x_2,\varphi,\lambda)}\big| \, d\lambda \end{align*} $$
$$ \begin{align*} \int_{i\mathfrak{a}_Q^{*}} \big| \sum_{\varphi \in \mathcal{B}_{Q,w\pi}} E(x_1,I_Q(\lambda,f)\varphi,\lambda)\overline{E(x_2,\varphi,\lambda)}\big| \, d\lambda \end{align*} $$
is bounded above by the square-root of the product over
![]() $i=1,2$
of
$i=1,2$
of
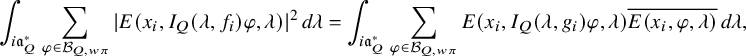 $$ \begin{align*} \int_{i\mathfrak{a}_Q^{*}} \sum_{\varphi \in \mathcal{B}_{Q,w\pi}} |E(x_i,I_Q(\lambda,f_i)\varphi,\lambda)|^2\, d\lambda = \int_{i\mathfrak{a}_Q^{*}} \sum_{\varphi \in \mathcal{B}_{Q,w\pi}} E(x_i,I_Q(\lambda,g_i)\varphi,\lambda)\overline{E(x_i,\varphi,\lambda)}\, d\lambda, \end{align*} $$
$$ \begin{align*} \int_{i\mathfrak{a}_Q^{*}} \sum_{\varphi \in \mathcal{B}_{Q,w\pi}} |E(x_i,I_Q(\lambda,f_i)\varphi,\lambda)|^2\, d\lambda = \int_{i\mathfrak{a}_Q^{*}} \sum_{\varphi \in \mathcal{B}_{Q,w\pi}} E(x_i,I_Q(\lambda,g_i)\varphi,\lambda)\overline{E(x_i,\varphi,\lambda)}\, d\lambda, \end{align*} $$
where we have set
![]() $g_i=f_i\ast f_i^*$
. By the same argument, we see that the spectral expansion of
$g_i=f_i\ast f_i^*$
. By the same argument, we see that the spectral expansion of
![]() $K_{g_i}(x,x)$
deduced from (3.5.6.2) is a sum of non-negative terms, and thus, the last expression above is bounded above by
$K_{g_i}(x,x)$
deduced from (3.5.6.2) is a sum of non-negative terms, and thus, the last expression above is bounded above by
![]() $K_{g_i}(x_i,x_i)$
times
$K_{g_i}(x_i,x_i)$
times
![]() $n_Q$
.
$n_Q$
.
Let
![]() $T_1,T_2$
be two sufficiently positive points in
$T_1,T_2$
be two sufficiently positive points in
![]() $\mathfrak {a}_0^{\prime }$
. Let
$\mathfrak {a}_0^{\prime }$
. Let
![]() $\Lambda ^{T_1}_uK_{f,\chi }\Lambda ^{T_2}_u$
be the function of two variables we get when we apply on
$\Lambda ^{T_1}_uK_{f,\chi }\Lambda ^{T_2}_u$
be the function of two variables we get when we apply on
![]() $K_{f,\chi }$
the truncation operators
$K_{f,\chi }$
the truncation operators
![]() $\Lambda ^{T_1}_u$
and
$\Lambda ^{T_1}_u$
and
![]() $\Lambda ^{T_2}_u$
, respectively, on the left and right variables.
$\Lambda ^{T_2}_u$
, respectively, on the left and right variables.
Lemma 3.5.6.2. Let
![]() $\chi \in \mathfrak {X}(U)$
be a U-regular cuspidal datum. For any standard parabolic subgroup P of U and any representative
$\chi \in \mathfrak {X}(U)$
be a U-regular cuspidal datum. For any standard parabolic subgroup P of U and any representative
![]() $(M_P,\pi )$
of
$(M_P,\pi )$
of
![]() $\chi $
, we have for all
$\chi $
, we have for all
![]() $f\in \mathcal {S}(U(\mathbb {A}))$
and
$f\in \mathcal {S}(U(\mathbb {A}))$
and
![]() $x,y\in [U']$
,
$x,y\in [U']$
,
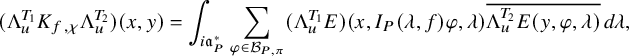 $$ \begin{align} (\Lambda^{T_1}_uK_{f,\chi}\Lambda^{T_2}_u) (x,y)=\int_{i\mathfrak{a}_P^{*}} \sum_{\varphi \in \mathcal{B}_{P,\pi}} (\Lambda^{T_1}_uE)(x,I_P(\lambda,f)\varphi,\lambda)\overline{\Lambda^{T_2}_uE(y,\varphi,\lambda)}\, d\lambda, \end{align} $$
$$ \begin{align} (\Lambda^{T_1}_uK_{f,\chi}\Lambda^{T_2}_u) (x,y)=\int_{i\mathfrak{a}_P^{*}} \sum_{\varphi \in \mathcal{B}_{P,\pi}} (\Lambda^{T_1}_uE)(x,I_P(\lambda,f)\varphi,\lambda)\overline{\Lambda^{T_2}_uE(y,\varphi,\lambda)}\, d\lambda, \end{align} $$
where
![]() $\mathcal {B}_{P,\pi }$
is a K-basis as above.
$\mathcal {B}_{P,\pi }$
is a K-basis as above.
Proof. This is a variant of the proof of Lemma 3.5.6.1. Simply instead of (3.5.6.2), we start from the spectral expansion for any
![]() $\chi \in \mathfrak {X}(U)$
:
$\chi \in \mathfrak {X}(U)$
:
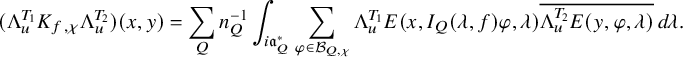 $$ \begin{align} (\Lambda^{T_1}_uK_{f,\chi}\Lambda^{T_2}_u) (x,y)=\sum_{Q} n_Q^{-1}\int_{i\mathfrak{a}_Q^{*}} \sum_{\varphi \in \mathcal{B}_{Q,\chi}} \Lambda^{T_1}_uE(x,I_Q(\lambda,f)\varphi,\lambda)\overline{\Lambda^{T_2}_uE(y,\varphi,\lambda)}\, d\lambda. \end{align} $$
$$ \begin{align} (\Lambda^{T_1}_uK_{f,\chi}\Lambda^{T_2}_u) (x,y)=\sum_{Q} n_Q^{-1}\int_{i\mathfrak{a}_Q^{*}} \sum_{\varphi \in \mathcal{B}_{Q,\chi}} \Lambda^{T_1}_uE(x,I_Q(\lambda,f)\varphi,\lambda)\overline{\Lambda^{T_2}_uE(y,\varphi,\lambda)}\, d\lambda. \end{align} $$
The proof of this expansion is similar to that of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, proof of lemma 4.2.3.1] and thus is left to the reader.
Remark 3.5.6.3. Assume we have
![]() $f=f_1*f_2^*$
as in the proof of Lemma 3.5.6.1; one has the following bound (proved by the same method as in the proof of Lemma 3.5.6.1): there exists
$f=f_1*f_2^*$
as in the proof of Lemma 3.5.6.1; one has the following bound (proved by the same method as in the proof of Lemma 3.5.6.1): there exists
![]() $c>0$
(independent of
$c>0$
(independent of
![]() $f_1$
and
$f_1$
and
![]() $f_2$
) such that for all
$f_2$
) such that for all
![]() $x_1,x_2\in [U']$
,
$x_1,x_2\in [U']$
,
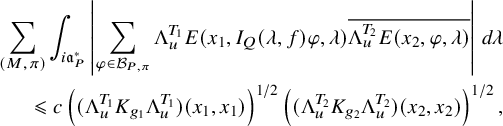 $$ \begin{align} \sum_{(M,\pi) } \int_{i\mathfrak{a}_P^{*}} \left| \sum_{\varphi \in \mathcal{B}_{P,\pi}} \Lambda^{T_1}_uE(x_1,I_Q(\lambda,f)\varphi,\lambda)\overline{\Lambda^{T_2}_uE(x_2,\varphi,\lambda)}\right|\, d\lambda\\ \nonumber \leqslant c \left((\Lambda^{T_1}_uK_{g_1} \Lambda^{T_1}_u)(x_1,x_1) \right)^{1/2} \left((\Lambda^{T_2}_uK_{g_2} \Lambda^{T_2}_u)(x_2,x_2) \right)^{1/2}, \end{align} $$
$$ \begin{align} \sum_{(M,\pi) } \int_{i\mathfrak{a}_P^{*}} \left| \sum_{\varphi \in \mathcal{B}_{P,\pi}} \Lambda^{T_1}_uE(x_1,I_Q(\lambda,f)\varphi,\lambda)\overline{\Lambda^{T_2}_uE(x_2,\varphi,\lambda)}\right|\, d\lambda\\ \nonumber \leqslant c \left((\Lambda^{T_1}_uK_{g_1} \Lambda^{T_1}_u)(x_1,x_1) \right)^{1/2} \left((\Lambda^{T_2}_uK_{g_2} \Lambda^{T_2}_u)(x_2,x_2) \right)^{1/2}, \end{align} $$
where the first sum is over a set of representatives
![]() $(M,\pi )$
of U-regular cuspidal data of U and we have set
$(M,\pi )$
of U-regular cuspidal data of U and we have set
![]() $g_i=f_i\ast f_i^*$
.
$g_i=f_i\ast f_i^*$
.
Proposition 3.5.6.4. There exists a semi-norm on
![]() $\mathcal {S}(U(\mathbb {A}))$
such that for all
$\mathcal {S}(U(\mathbb {A}))$
such that for all
![]() $f\in \mathcal {S}(U(\mathbb {A}))$
,
$f\in \mathcal {S}(U(\mathbb {A}))$
,
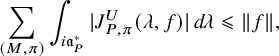 $$ \begin{align} \sum_{(M,\pi) } \int_{i\mathfrak{a}_{P}^*} |J^U_{P,\pi}(\lambda,f)|\, d\lambda \leqslant \|f\|, \end{align} $$
$$ \begin{align} \sum_{(M,\pi) } \int_{i\mathfrak{a}_{P}^*} |J^U_{P,\pi}(\lambda,f)|\, d\lambda \leqslant \|f\|, \end{align} $$
where the sum is over a set of representatives
![]() $(M,\pi )$
of
$(M,\pi )$
of
![]() $(U,U')$
-regular cuspidal data of U and P is the standard parabolic subgroup of which M is the standard Levi factor.
$(U,U')$
-regular cuspidal data of U and P is the standard parabolic subgroup of which M is the standard Levi factor.
Proof. By uniform boundedness principle, it suffices to prove that the expression (3.5.6.7) is finite for each f. Let T be a sufficiently positive point in
![]() $\mathfrak {a}_0^{\prime }$
such that for all representatives
$\mathfrak {a}_0^{\prime }$
such that for all representatives
![]() $(M_P,\pi )$
of
$(M_P,\pi )$
of
![]() $(U,U')$
-regular cuspidal data of U with P a standard parabolic subgroup of U and for all
$(U,U')$
-regular cuspidal data of U with P a standard parabolic subgroup of U and for all
![]() $\varphi \in \mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(U)$
, we have
$\varphi \in \mathcal {A}_{P,\pi ,\operatorname {\mathrm {cusp}}}(U)$
, we have
Recall that the map
![]() $\varphi \mapsto \mathcal {P}_{U'}(\varphi ,\lambda )$
is continuous. It follows from [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Proposition 2.8.41] that we have for
$\varphi \mapsto \mathcal {P}_{U'}(\varphi ,\lambda )$
is continuous. It follows from [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Proposition 2.8.41] that we have for
![]() $\lambda \in i\mathfrak {a}_P^*$
,
$\lambda \in i\mathfrak {a}_P^*$
,
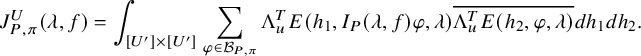 $$ \begin{align*} J_{P,\pi}^U(\lambda,f)=\int_{[U']\times [U']} \sum_{\varphi\in \mathcal{B}_{P,\pi}} \Lambda^T_uE(h_1,I_P(\lambda,f)\varphi,\lambda) \overline{\Lambda^T_uE(h_2,\varphi,\lambda)} dh_1dh_2. \end{align*} $$
$$ \begin{align*} J_{P,\pi}^U(\lambda,f)=\int_{[U']\times [U']} \sum_{\varphi\in \mathcal{B}_{P,\pi}} \Lambda^T_uE(h_1,I_P(\lambda,f)\varphi,\lambda) \overline{\Lambda^T_uE(h_2,\varphi,\lambda)} dh_1dh_2. \end{align*} $$
Now it suffices to show that we have
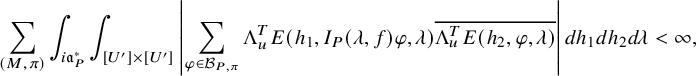 $$ \begin{align} \sum_{(M,\pi)} \int_{i\mathfrak{a}_P^*} \int_{[U']\times [U']} \left\lvert \sum_{\varphi\in \mathcal{B}_{P,\pi}} \Lambda^T_uE(h_1,I_P(\lambda,f)\varphi,\lambda) \overline{\Lambda^T_uE(h_2,\varphi,\lambda)} \right\rvert dh_1dh_2 d\lambda <\infty, \end{align} $$
$$ \begin{align} \sum_{(M,\pi)} \int_{i\mathfrak{a}_P^*} \int_{[U']\times [U']} \left\lvert \sum_{\varphi\in \mathcal{B}_{P,\pi}} \Lambda^T_uE(h_1,I_P(\lambda,f)\varphi,\lambda) \overline{\Lambda^T_uE(h_2,\varphi,\lambda)} \right\rvert dh_1dh_2 d\lambda <\infty, \end{align} $$
where the outer sum is as in (3.5.6.7). To show the convergence of (3.5.6.9) for a fixed function
![]() $f\in \mathcal {S}(U(\mathbb {A}))$
, we may and shall assume, by Dixmier-Malliavin theorem, that
$f\in \mathcal {S}(U(\mathbb {A}))$
, we may and shall assume, by Dixmier-Malliavin theorem, that
![]() $f=f_1\ast f^*_2$
(the notations are those used in the proof of lemma 3.5.6.1). But then we can apply the bound (3.5.6.6). In this way, we see that the left-hand side of (3.5.6.9) is bounded above by (up to some irrelevant constant) by
$f=f_1\ast f^*_2$
(the notations are those used in the proof of lemma 3.5.6.1). But then we can apply the bound (3.5.6.6). In this way, we see that the left-hand side of (3.5.6.9) is bounded above by (up to some irrelevant constant) by
 $$ \begin{align*} \operatorname{\mathrm{vol}}([U']) \left( \prod_{i=1}^2 \int_{[U']} (\Lambda^{T}_uK_{g_i}\Lambda^T_u )(x,x)\,dx \right)^{1/2}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{vol}}([U']) \left( \prod_{i=1}^2 \int_{[U']} (\Lambda^{T}_uK_{g_i}\Lambda^T_u )(x,x)\,dx \right)^{1/2}. \end{align*} $$
The volume of
![]() $[U']$
is finite, and the integral
$[U']$
is finite, and the integral
is absolutely convergent by properties of truncation operator (see Proposition 3.3.3.1) and the fact that the kernel is slowly increasing; see [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Lemma 2.10.1.1]. Note that the derivatives of the kernel
![]() $K_{g_i}$
are related to the kernel associated to derivatives of
$K_{g_i}$
are related to the kernel associated to derivatives of
![]() $g_i$
; see also the proof of Theorem 3.5.7.1 where this fact is used. So we can conclude.
$g_i$
; see also the proof of Theorem 3.5.7.1 where this fact is used. So we can conclude.
3.5.7
We can now state and prove the main result of this section.
Theorem 3.5.7.1. Let
![]() $\chi \in \mathfrak {X}(U)$
be a
$\chi \in \mathfrak {X}(U)$
be a
![]() $(U,U')$
-regular cuspidal datum. For any standard parabolic subgroup P of U and any representative
$(U,U')$
-regular cuspidal datum. For any standard parabolic subgroup P of U and any representative
![]() $(M_P,\pi )$
of
$(M_P,\pi )$
of
![]() $\chi $
, we have
$\chi $
, we have
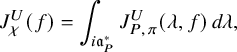 $$ \begin{align*} J^U_\chi(f)= \int_{i\mathfrak{a}_P^*} J_{P,\pi}^{U}(\lambda, f)\,d\lambda, \end{align*} $$
$$ \begin{align*} J^U_\chi(f)= \int_{i\mathfrak{a}_P^*} J_{P,\pi}^{U}(\lambda, f)\,d\lambda, \end{align*} $$
where the integral in the right-hand side is absolutely convergent.
Proof. Let
![]() $(M_P,\pi )$
be a representative of a
$(M_P,\pi )$
be a representative of a
![]() $(U,U')$
-regular cuspidal datum
$(U,U')$
-regular cuspidal datum
![]() $\chi $
with P a standard parabolic subgroup of U. Let
$\chi $
with P a standard parabolic subgroup of U. Let
![]() $T_1,T_2$
be two sufficiently positive points in
$T_1,T_2$
be two sufficiently positive points in
![]() $\mathfrak {a}_0^{\prime }$
such that (3.5.6.8) holds for
$\mathfrak {a}_0^{\prime }$
such that (3.5.6.8) holds for
![]() $T=T_1,T_2$
. We shall use the spectral expansion given by Lemma 3.5.6.2. Using (3.5.6.6), we get (as in the proof of Proposition 3.5.6.4)
$T=T_1,T_2$
. We shall use the spectral expansion given by Lemma 3.5.6.2. Using (3.5.6.6), we get (as in the proof of Proposition 3.5.6.4)
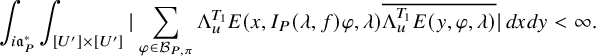 $$ \begin{align*} \int_{i\mathfrak{a}_{P}^*} \int_{[U']\times [U']} |\sum_{\varphi \in \mathcal{B}_{P,\pi}}\Lambda^{T_1}_u E(x,I_P(\lambda,f) \varphi,\lambda) \overline{ \Lambda^{T_1}_u E(y,\varphi,\lambda)}|\, dxdy<\infty. \end{align*} $$
$$ \begin{align*} \int_{i\mathfrak{a}_{P}^*} \int_{[U']\times [U']} |\sum_{\varphi \in \mathcal{B}_{P,\pi}}\Lambda^{T_1}_u E(x,I_P(\lambda,f) \varphi,\lambda) \overline{ \Lambda^{T_1}_u E(y,\varphi,\lambda)}|\, dxdy<\infty. \end{align*} $$
Using this and Fubini theorem, we see that we can integrate the spectral expansion (3.5.6.4) over
![]() $[U']\times [U'] $
and permute the adelic and the complex integrals. Using the definition of the relative character (3.5.5.1) built upon the periods (3.5.4.1), we have by [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Proposition 2.8.41],
$[U']\times [U'] $
and permute the adelic and the complex integrals. Using the definition of the relative character (3.5.5.1) built upon the periods (3.5.4.1), we have by [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Proposition 2.8.41],
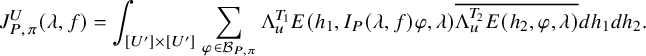 $$ \begin{align*} J_{P,\pi}^U(\lambda,f)=\int_{[U']\times [U']} \sum_{\varphi\in \mathcal{B}_{P,\pi}} \Lambda^{T_1}_uE(h_1,I_P(\lambda,f)\varphi,\lambda) \overline{\Lambda^{T_2}_uE(h_2,\varphi,\lambda)} dh_1dh_2. \end{align*} $$
$$ \begin{align*} J_{P,\pi}^U(\lambda,f)=\int_{[U']\times [U']} \sum_{\varphi\in \mathcal{B}_{P,\pi}} \Lambda^{T_1}_uE(h_1,I_P(\lambda,f)\varphi,\lambda) \overline{\Lambda^{T_2}_uE(h_2,\varphi,\lambda)} dh_1dh_2. \end{align*} $$
So we can conclude that we have
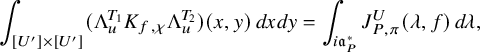 $$ \begin{align} \int_{[U']\times [U'] } (\Lambda^{T_1}_uK_{f,\chi}\Lambda^{T_2}_u) (x,y)\, dxdy=\int_{i\mathfrak{a}_P^{*}} J^U_{P,\pi}(\lambda, f)\,d\lambda, \end{align} $$
$$ \begin{align} \int_{[U']\times [U'] } (\Lambda^{T_1}_uK_{f,\chi}\Lambda^{T_2}_u) (x,y)\, dxdy=\int_{i\mathfrak{a}_P^{*}} J^U_{P,\pi}(\lambda, f)\,d\lambda, \end{align} $$
where both sides are absolutely convergent. Note that the right-hand side of (3.5.7.1), and hence the left-hand side, depend neither on
![]() $T_1$
nor on
$T_1$
nor on
![]() $T_2$
.
$T_2$
.
We fix
![]() $T_2\in \mathfrak {a}_0^{\prime }$
sufficiently positive. By Proposition 3.3.3.1 assertion 2,
$T_2\in \mathfrak {a}_0^{\prime }$
sufficiently positive. By Proposition 3.3.3.1 assertion 2,
![]() $\Lambda ^{T_1}_uK_{f,\chi }\Lambda ^{T_2}_u$
converges to
$\Lambda ^{T_1}_uK_{f,\chi }\Lambda ^{T_2}_u$
converges to
![]() $K_{f,\chi }\Lambda ^{T_2}_u$
pointwise when
$K_{f,\chi }\Lambda ^{T_2}_u$
pointwise when
![]() $d(T_1)\to +\infty $
(see §3.1.6). We want to apply the dominated convergence theorem. Let
$d(T_1)\to +\infty $
(see §3.1.6). We want to apply the dominated convergence theorem. Let
![]() $N,N'>0$
. By Proposition 3.3.3.1 assertion 2, there exists a continuous semi-norm
$N,N'>0$
. By Proposition 3.3.3.1 assertion 2, there exists a continuous semi-norm
![]() $\|\cdot \|_{N'}$
on
$\|\cdot \|_{N'}$
on
![]() $\mathcal {T}_{N'}([U])$
(which does not depend on
$\mathcal {T}_{N'}([U])$
(which does not depend on
![]() $T_1$
) such that we have for all
$T_1$
) such that we have for all
![]() $x,y\in [U']$
and all
$x,y\in [U']$
and all
![]() $f\in \mathcal {S}(U)$
,
$f\in \mathcal {S}(U)$
,
Let
![]() $J\subset U(\mathbb {A}_f)$
be a compact open subgroup and
$J\subset U(\mathbb {A}_f)$
be a compact open subgroup and
![]() $S(U(\mathbb {A}))^J\subset S(U(\mathbb {A}))$
be the subspace of right-J-invariant functions. There are finite families
$S(U(\mathbb {A}))^J\subset S(U(\mathbb {A}))$
be the subspace of right-J-invariant functions. There are finite families
![]() $(N_i)_{i\in I}$
of integers and
$(N_i)_{i\in I}$
of integers and
![]() $(X_i)_{i\in I}$
of elements of
$(X_i)_{i\in I}$
of elements of
![]() $\mathcal {U}(\mathfrak {u}_\infty )$
such that we have for all
$\mathcal {U}(\mathfrak {u}_\infty )$
such that we have for all
![]() $x,y\in [U']$
and
$x,y\in [U']$
and
![]() $f\in S(U(\mathbb {A}))^J$
, we have
$f\in S(U(\mathbb {A}))^J$
, we have
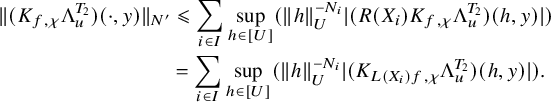 $$ \begin{align*} \| (K_{f,\chi}\Lambda^{T_2}_u)(\cdot ,y)\|_{N'}&\leqslant \sum_{i\in I} \sup_{h\in [U]} (\|h\|^{-N_i}_U| (R(X_i) K_{f,\chi}\Lambda^{T_2}_u)(h,y)|)\\ &=\sum_{i\in I} \sup_{h\in [U]} (\|h\|^{-N_i}_U | (K_{L(X_i)f,\chi}\Lambda^{T_2}_u)(h,y)|). \end{align*} $$
$$ \begin{align*} \| (K_{f,\chi}\Lambda^{T_2}_u)(\cdot ,y)\|_{N'}&\leqslant \sum_{i\in I} \sup_{h\in [U]} (\|h\|^{-N_i}_U| (R(X_i) K_{f,\chi}\Lambda^{T_2}_u)(h,y)|)\\ &=\sum_{i\in I} \sup_{h\in [U]} (\|h\|^{-N_i}_U | (K_{L(X_i)f,\chi}\Lambda^{T_2}_u)(h,y)|). \end{align*} $$
Here,
![]() $R(X_i) K_{f,\chi }$
means that we apply the differential operator
$R(X_i) K_{f,\chi }$
means that we apply the differential operator
![]() $R(X_i)$
on the left variable of
$R(X_i)$
on the left variable of
![]() $K_{f,\chi }$
. We also use the fact that we have
$K_{f,\chi }$
. We also use the fact that we have
![]() $R(X_i) K_{f,\chi }=K_{L(X_i)f,\chi }$
for some right-invariant differential operator
$R(X_i) K_{f,\chi }=K_{L(X_i)f,\chi }$
for some right-invariant differential operator
![]() $L(X_i)$
. Now we can use (3.2.2.3) and Proposition 3.3.3.1 assertion 1 applied to the operator
$L(X_i)$
. Now we can use (3.2.2.3) and Proposition 3.3.3.1 assertion 1 applied to the operator
![]() $\Lambda ^{T_2}_u$
to see that for all
$\Lambda ^{T_2}_u$
to see that for all
![]() $n_1>0$
, there exists a continuous semi-norm
$n_1>0$
, there exists a continuous semi-norm
![]() $\|\cdot \|_{\mathcal {S}}$
on
$\|\cdot \|_{\mathcal {S}}$
on
![]() $\mathcal {S}(U(\mathbb {A}))$
such that for all
$\mathcal {S}(U(\mathbb {A}))$
such that for all
![]() $x\in [U]$
,
$x\in [U]$
,
![]() $y\in [U']$
and all
$y\in [U']$
and all
![]() $f\in \mathcal {S}(U(\mathbb {A}))$
, we have
$f\in \mathcal {S}(U(\mathbb {A}))$
, we have
We deduce that for any
![]() $n_2>0$
, there exists
$n_2>0$
, there exists
![]() $c>0$
(which depends on
$c>0$
(which depends on
![]() $T_2$
,
$T_2$
,
![]() $n_2$
and
$n_2$
and
![]() $f\in \mathcal {S}(U(\mathbb {A}))$
but not on
$f\in \mathcal {S}(U(\mathbb {A}))$
but not on
![]() $T_1$
) such that for all
$T_1$
) such that for all
![]() $x,y\in [U']$
,
$x,y\in [U']$
,
By choosing
![]() $n_2$
large enough so that
$n_2$
large enough so that
![]() $(x,y)\mapsto \| x\|_{U'}^{-n_2} \| y\|_{U'}^{-n_2} $
is integrable over
$(x,y)\mapsto \| x\|_{U'}^{-n_2} \| y\|_{U'}^{-n_2} $
is integrable over
![]() $[U']\times [U'] $
, we can apply the dominated convergence theorem to get
$[U']\times [U'] $
, we can apply the dominated convergence theorem to get
We have seen that the left-hand side depends neither on
![]() $T_1$
nor on
$T_1$
nor on
![]() $T_2$
. So the right-hand side is also independent of
$T_2$
. So the right-hand side is also independent of
![]() $T_2$
. We can conclude from Corollary 3.3.5.2 that the right-hand side is in fact equal to
$T_2$
. We can conclude from Corollary 3.3.5.2 that the right-hand side is in fact equal to
![]() $J_\chi ^U(f)$
.
$J_\chi ^U(f)$
.
4 The
 $(G,H)$
-regular contribution in the Jacquet-Rallis trace formula
$(G,H)$
-regular contribution in the Jacquet-Rallis trace formula
4.1 Statement and proof
4.1.1
Let
![]() $E/F$
be a quadratic extension of number fields. Let
$E/F$
be a quadratic extension of number fields. Let
![]() $\mathbb {A}$
be the ring of adèles of F and
$\mathbb {A}$
be the ring of adèles of F and
![]() $\eta =\eta _{E/F}$
be the quadratic character of the group
$\eta =\eta _{E/F}$
be the quadratic character of the group
![]() $\mathbb {A}^\times $
attached to
$\mathbb {A}^\times $
attached to
![]() $E/F$
. Let
$E/F$
. Let
![]() $n\geqslant 1$
and
$n\geqslant 1$
and
![]() $G^{\prime }_n=\mathrm {GL}_{n,F}$
be the algebraic group of F-linear automorphisms of
$G^{\prime }_n=\mathrm {GL}_{n,F}$
be the algebraic group of F-linear automorphisms of
![]() $F^n$
. We view as an F-subgroup of
$F^n$
. We view as an F-subgroup of
![]() $G_n=\operatorname {\mathrm {Res}}_{E/F} (G_n^{\prime } \times _FE)$
. We denote by c the Galois involution of
$G_n=\operatorname {\mathrm {Res}}_{E/F} (G_n^{\prime } \times _FE)$
. We denote by c the Galois involution of
![]() $G_n$
. Let
$G_n$
. Let
![]() $\eta _{G^{\prime }_n}$
be the character of
$\eta _{G^{\prime }_n}$
be the character of
![]() $G^{\prime }_n(\mathbb {A})$
given by
$G^{\prime }_n(\mathbb {A})$
given by
for all
![]() $h\in G^{\prime }_n(\mathbb {A})$
. Let
$h\in G^{\prime }_n(\mathbb {A})$
. Let
![]() $(B_n^{\prime },T_n^{\prime })$
be a pair where
$(B_n^{\prime },T_n^{\prime })$
be a pair where
![]() $B_n^{\prime }$
is the Borel subgroup
$B_n^{\prime }$
is the Borel subgroup
![]() $G_n^{\prime }$
of upper triangular matrices and
$G_n^{\prime }$
of upper triangular matrices and
![]() $T_n^{\prime }$
is the maximal torus of
$T_n^{\prime }$
is the maximal torus of
![]() $ G' _n$
of diagonal matrices. Let
$ G' _n$
of diagonal matrices. Let
![]() $(B_n,T_n)$
be the pair deduced from
$(B_n,T_n)$
be the pair deduced from
![]() $(B_n^{\prime },T_n^{\prime })$
by extension of scalars to E and restriction to F: it is a pair of a minimal parabolic subgroup of
$(B_n^{\prime },T_n^{\prime })$
by extension of scalars to E and restriction to F: it is a pair of a minimal parabolic subgroup of
![]() $ G_n $
and its Levi factor. Let
$ G_n $
and its Levi factor. Let
![]() $ K_n \subset G_n (\mathbb {A}) $
and
$ K_n \subset G_n (\mathbb {A}) $
and
![]() $ K ^{\prime }_n= K_n \cap G^{\prime }_n (\mathbb {A}) \subset G ^{\prime }_n(\mathbb {A}) $
be the ‘standard’ maximal compact subgroups. We set
$ K ^{\prime }_n= K_n \cap G^{\prime }_n (\mathbb {A}) \subset G ^{\prime }_n(\mathbb {A}) $
be the ‘standard’ maximal compact subgroups. We set
where the right-hand side is defined in §2.1.4.
We set
![]() $G=G_n\times G_{n+1}$
and
$G=G_n\times G_{n+1}$
and
![]() $G'=G_n^{\prime }\times G_{n+1}'$
(see §4.1.1). Let c be the Galois involution of G whose fixed points set if
$G'=G_n^{\prime }\times G_{n+1}'$
(see §4.1.1). Let c be the Galois involution of G whose fixed points set if
![]() $G'$
. The reductive groups G and
$G'$
. The reductive groups G and
![]() $G'$
are equipped with the pairs
$G'$
are equipped with the pairs
![]() $(B_n\times B_{n+1},T_n\times T_{n+1})$
and
$(B_n\times B_{n+1},T_n\times T_{n+1})$
and
![]() $(B_n^{\prime }\times B_{n+1}',T_n^{\prime }\times T_{n+1}')$
. Let
$(B_n^{\prime }\times B_{n+1}',T_n^{\prime }\times T_{n+1}')$
. Let
![]() $K=K_n\times K_{n+1}\subset G(\mathbb {A})$
and
$K=K_n\times K_{n+1}\subset G(\mathbb {A})$
and
![]() $K'= K \cap G' (\mathbb {A})$
. We denote by
$K'= K \cap G' (\mathbb {A})$
. We denote by
![]() $\eta _{G'}$
the character
$\eta _{G'}$
the character
![]() $\eta _{G^{\prime }_n}\boxtimes \eta _{G^{\prime }_{n+1}}$
of
$\eta _{G^{\prime }_n}\boxtimes \eta _{G^{\prime }_{n+1}}$
of
![]() $G'(\mathbb {A})$
. Let H be the image of the diagonal embedding
$G'(\mathbb {A})$
. Let H be the image of the diagonal embedding
Let
![]() $\pi $
be a cuspidal automorphic representation of
$\pi $
be a cuspidal automorphic representation of
![]() $G(\mathbb {A})$
with central character trivial on
$G(\mathbb {A})$
with central character trivial on
![]() $A_G^\infty $
. As in §3.5.2, we denote by
$A_G^\infty $
. As in §3.5.2, we denote by
![]() $\pi ^*$
the conjugate-dual representation of
$\pi ^*$
the conjugate-dual representation of
![]() $G(\mathbb {A})$
. We shall say that
$G(\mathbb {A})$
. We shall say that
![]() $\pi $
is self conjugate-dual if
$\pi $
is self conjugate-dual if
![]() $\pi \simeq \pi ^*$
and that
$\pi \simeq \pi ^*$
and that
![]() $\pi $
is
$\pi $
is
![]() $G'$
-distinguished, resp.
$G'$
-distinguished, resp.
![]() $(G',\eta )$
-distinguished, if the linear form (called the Flicker-Rallis period)
$(G',\eta )$
-distinguished, if the linear form (called the Flicker-Rallis period)
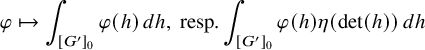 $$ \begin{align} \varphi \mapsto \int_{[G']_0} \varphi(h)\,dh, \text{ resp.} \int_{[G']_0} \varphi(h)\eta(\det(h))\,dh \end{align} $$
$$ \begin{align} \varphi \mapsto \int_{[G']_0} \varphi(h)\,dh, \text{ resp.} \int_{[G']_0} \varphi(h)\eta(\det(h))\,dh \end{align} $$
does not vanish identically on
![]() $\mathcal {A}_{\pi ,\operatorname {\mathrm {cusp}}}(G)$
. Then
$\mathcal {A}_{\pi ,\operatorname {\mathrm {cusp}}}(G)$
. Then
![]() $\pi $
is self conjugate-dual if and only if
$\pi $
is self conjugate-dual if and only if
![]() $\pi $
is either
$\pi $
is either
![]() $G'$
-distinguished or
$G'$
-distinguished or
![]() $(G',\eta )$
-distinguished and it cannot be both (see [Reference FlickerFli88]). Note that since we are working with general linear groups, we shall omit the subscript
$(G',\eta )$
-distinguished and it cannot be both (see [Reference FlickerFli88]). Note that since we are working with general linear groups, we shall omit the subscript
![]() $\operatorname {\mathrm {cusp}}$
and we shall write simply
$\operatorname {\mathrm {cusp}}$
and we shall write simply
![]() $\mathcal {A}_{\pi }(G)$
for the space
$\mathcal {A}_{\pi }(G)$
for the space
![]() $\mathcal {A}_{\pi ,\operatorname {\mathrm {cusp}}}(G)$
. The same rule is applied to the space
$\mathcal {A}_{\pi ,\operatorname {\mathrm {cusp}}}(G)$
. The same rule is applied to the space
![]() $\mathcal {A}_{P,\pi }(G)$
if
$\mathcal {A}_{P,\pi }(G)$
if
![]() $\pi $
is a cuspidal automorphic representation of
$\pi $
is a cuspidal automorphic representation of
![]() $M_P(\mathbb {A})$
.
$M_P(\mathbb {A})$
.
4.1.2 Caution
Since it is easy to get confused, we want to emphasize some consequences of our choices of measures. Let P be a standard parabolic subgroup of G and let
![]() $P'=P\cap G'$
. The restriction map
$P'=P\cap G'$
. The restriction map
![]() $X^*(P)\to X^*(P')$
identifies
$X^*(P)\to X^*(P')$
identifies
![]() $X^*(P)$
with a subgroup of
$X^*(P)$
with a subgroup of
![]() $X^*(P')$
of index
$X^*(P')$
of index
![]() $2^{\dim (\mathfrak {a}_P)}$
. It induces an isomorphism
$2^{\dim (\mathfrak {a}_P)}$
. It induces an isomorphism
![]() $ \mathfrak {a}_{P'} \to \mathfrak {a}_ {P }$
which does not preserve the Haar measures: the pullback to
$ \mathfrak {a}_{P'} \to \mathfrak {a}_ {P }$
which does not preserve the Haar measures: the pullback to
![]() $\mathfrak {a}_{P'}$
of the Haar measure on
$\mathfrak {a}_{P'}$
of the Haar measure on
![]() $\mathfrak {a}_P$
is
$\mathfrak {a}_P$
is
![]() $2^{\dim (\mathfrak {a}_P)}$
times the Haar measure on
$2^{\dim (\mathfrak {a}_P)}$
times the Haar measure on
![]() $\mathfrak {a}_{P'}$
. In the same way, the groups
$\mathfrak {a}_{P'}$
. In the same way, the groups
![]() $A_P^\infty $
and
$A_P^\infty $
and
![]() $A_{P'}^\infty $
are canonically identified, but the Haar measure on
$A_{P'}^\infty $
are canonically identified, but the Haar measure on
![]() $A_P^\infty $
is
$A_P^\infty $
is
![]() $2^{\dim (\mathfrak {a}_P)}$
times the Haar measure on
$2^{\dim (\mathfrak {a}_P)}$
times the Haar measure on
![]() $A_{P'}^\infty $
.
$A_{P'}^\infty $
.
Note also that for all
![]() $x\in G'(\mathbb {A})$
, we have
$x\in G'(\mathbb {A})$
, we have
4.1.3 The
 $(G,H)$
-regular and Hermitian cuspidal data
$(G,H)$
-regular and Hermitian cuspidal data
Let
![]() $\chi =(\chi _n,\chi _{n+1})\in \mathfrak {X}(G)=\mathfrak {X}(G_n) \times \mathfrak {X}(G_{n+1})$
be a cuspidal datum. Let
$\chi =(\chi _n,\chi _{n+1})\in \mathfrak {X}(G)=\mathfrak {X}(G_n) \times \mathfrak {X}(G_{n+1})$
be a cuspidal datum. Let
![]() $(M,\pi )$
be a representative in the class of
$(M,\pi )$
be a representative in the class of
![]() $\chi $
with
$\chi $
with
![]() $M=M_P$
for a standard parabolic subgroup P of G. We write
$M=M_P$
for a standard parabolic subgroup P of G. We write
![]() $M=M_n\times M_{n+1}$
and
$M=M_n\times M_{n+1}$
and
![]() $\pi =\pi _n\boxtimes \pi _{n+1}$
accordingly. Let
$\pi =\pi _n\boxtimes \pi _{n+1}$
accordingly. Let
![]() $j\in \{n,n+1\}$
. We write
$j\in \{n,n+1\}$
. We write
![]() $M_j=G_{n_{1,j}}\times \ldots \times G_{n_{r_j,j}}$
for some integer
$M_j=G_{n_{1,j}}\times \ldots \times G_{n_{r_j,j}}$
for some integer
![]() $r_j\geqslant 1$
and
$r_j\geqslant 1$
and
![]() $\pi _j=\sigma _{1,j} \boxtimes \ldots \boxtimes \sigma _{r_j,j}$
accordingly.
$\pi _j=\sigma _{1,j} \boxtimes \ldots \boxtimes \sigma _{r_j,j}$
accordingly.
We shall say that
![]() $\chi $
is
$\chi $
is
-
• G-regular (or simply regular) if for all
 $j\in \{n,n+1\}$
and
$j\in \{n,n+1\}$
and
 $1\leqslant i,i'\leqslant r_j$
such that
$1\leqslant i,i'\leqslant r_j$
such that
 $n_{i,j}=n_{i',j}$
and
$n_{i,j}=n_{i',j}$
and
 $\sigma _{i,j}=\sigma _{i',j}$
, we have
$\sigma _{i,j}=\sigma _{i',j}$
, we have
 $i'=i$
.
$i'=i$
. -
• H-regular if for
 $1\leqslant i \leqslant r_n$
and all
$1\leqslant i \leqslant r_n$
and all
 $1\leqslant j \leqslant r_{n+1}$
, if
$1\leqslant j \leqslant r_{n+1}$
, if
 $n_{i,n}=n_{j,n+1}$
, the representation
$n_{i,n}=n_{j,n+1}$
, the representation
 $\sigma _{i,n}$
is not isomorphic to the contragredient of
$\sigma _{i,n}$
is not isomorphic to the contragredient of
 $\sigma _{j,n+1}$
;
$\sigma _{j,n+1}$
; -
•
 $(G,H)$
-regular if it is both G-regular and H-regular;
$(G,H)$
-regular if it is both G-regular and H-regular; -
• Hermitian if
 $\pi =\pi ^*$
and if the representation
$\pi =\pi ^*$
and if the representation
 $\sigma _{i,j}$
is
$\sigma _{i,j}$
is
 $\eta _{G^{\prime }_{j}}$
-distinguished for all
$\eta _{G^{\prime }_{j}}$
-distinguished for all
 $1\leqslant i\leqslant r_j$
and
$1\leqslant i\leqslant r_j$
and
 $j\in \{n,n+1\}$
such that
$j\in \{n,n+1\}$
such that
 $\sigma _{i,j}=\sigma _{i,j}^*$
.
$\sigma _{i,j}=\sigma _{i,j}^*$
.
4.1.4
We fix a
![]() $(G,H)$
-regular and Hermitian cuspidal datum
$(G,H)$
-regular and Hermitian cuspidal datum
![]() $\chi $
. With the notations as above, we may and shall choose the representative
$\chi $
. With the notations as above, we may and shall choose the representative
![]() $(M,\pi )$
such that for all
$(M,\pi )$
such that for all
![]() $j\in \{n,n+1\}$
, there exists an integer
$j\in \{n,n+1\}$
, there exists an integer
![]() $s_j\geqslant 0$
such that the following conditions are satisfied:
$s_j\geqslant 0$
such that the following conditions are satisfied:
-
1.
 $2 s_j\leqslant r_j$
and for all odd i such that
$2 s_j\leqslant r_j$
and for all odd i such that
 $1\leqslant i <2s_j$
, we have
$1\leqslant i <2s_j$
, we have
 $\sigma _{i+1,j}=\sigma _{i,j}^*$
(in particular,
$\sigma _{i+1,j}=\sigma _{i,j}^*$
(in particular,
 $\sigma _{i,j}\not =\sigma _{i,j}^*$
);
$\sigma _{i,j}\not =\sigma _{i,j}^*$
); -
2. for all
 $i>2s_j$
, we have
$i>2s_j$
, we have
 $\sigma _{i,j}=\sigma _{i,j}^*$
.
$\sigma _{i,j}=\sigma _{i,j}^*$
.
Let
![]() $L=L_n\times L_{n+1}$
be the standard Levi subgroup of G such that for all
$L=L_n\times L_{n+1}$
be the standard Levi subgroup of G such that for all
![]() $j\in \{n,n+1\}$
, we have
$j\in \{n,n+1\}$
, we have
Let
![]() $\xi \in W(M)$
such that
$\xi \in W(M)$
such that
![]() $\xi ^2=1$
and
$\xi ^2=1$
and
![]() $\mathfrak {a}_M^{L}$
is the kernel of
$\mathfrak {a}_M^{L}$
is the kernel of
![]() $\xi +\operatorname {\mathrm {Id}}$
for the natural action of
$\xi +\operatorname {\mathrm {Id}}$
for the natural action of
![]() $W(M)$
on
$W(M)$
on
![]() $\mathfrak {a}_M$
. We denote by Q the standard parabolic subgroup of Levi L.
$\mathfrak {a}_M$
. We denote by Q the standard parabolic subgroup of Levi L.
4.1.5 Intertwining period
We identify the Weyl group of G with the group of permutation matrix. In this way, we identify
![]() $\xi $
with an element of
$\xi $
with an element of
![]() $L(F)$
. Let
$L(F)$
. Let
![]() $\tilde {\xi }\in L(F)$
such that
$\tilde {\xi }\in L(F)$
such that
![]() $\tilde \xi c(\tilde \xi )^{-1}=\xi $
, where c is the Galois involution of G. We define the F-subgroups
$\tilde \xi c(\tilde \xi )^{-1}=\xi $
, where c is the Galois involution of G. We define the F-subgroups
![]() $P_{\tilde \xi }$
,
$P_{\tilde \xi }$
,
![]() $M_{\tilde \xi }$
and
$M_{\tilde \xi }$
and
![]() $N_{\tilde \xi }$
of
$N_{\tilde \xi }$
of
![]() $G'$
, respectively, by
$G'$
, respectively, by
We have the Levi decomposition
![]() $P_{\tilde \xi }=M_{\tilde \xi } N_{\tilde \xi }$
, where
$P_{\tilde \xi }=M_{\tilde \xi } N_{\tilde \xi }$
, where
![]() $M_{\tilde \xi }$
is reductive and
$M_{\tilde \xi }$
is reductive and
![]() $N_{\tilde \xi }$
is unipotent. Let
$N_{\tilde \xi }$
is unipotent. Let
![]() $Q'=Q\cap G'$
: this is a standard parabolic subgroup of
$Q'=Q\cap G'$
: this is a standard parabolic subgroup of
![]() $G'$
of Levi factor
$G'$
of Levi factor
![]() $L'=L\cap G$
. Observe that we have
$L'=L\cap G$
. Observe that we have
![]() $ A_{M_{\tilde \xi }}^\infty =A_L^\infty $
,
$ A_{M_{\tilde \xi }}^\infty =A_L^\infty $
,
![]() $M_{\tilde \xi }\subset L'$
and
$M_{\tilde \xi }\subset L'$
and
![]() $ N_{\tilde \xi }= N_{Q'}$
.
$ N_{\tilde \xi }= N_{Q'}$
.
The map
![]() $a\mapsto H_P({\tilde \xi } a {\tilde \xi }^{-1})$
identifies
$a\mapsto H_P({\tilde \xi } a {\tilde \xi }^{-1})$
identifies
![]() $A_{M_{\tilde \xi }}^\infty $
with the subspace
$A_{M_{\tilde \xi }}^\infty $
with the subspace
![]() $\mathfrak {a}_{L}$
. In particular, we have
$\mathfrak {a}_{L}$
. In particular, we have
![]() $\langle \lambda , H_P({\tilde \xi } a {\tilde \xi }^{-1})\rangle =0$
for any
$\langle \lambda , H_P({\tilde \xi } a {\tilde \xi }^{-1})\rangle =0$
for any
![]() $a\in A_{M_{\tilde \xi }}^\infty $
and
$a\in A_{M_{\tilde \xi }}^\infty $
and
![]() $\lambda \in \mathfrak {a}_{M,\mathbb {C}}^{L,*}$
. We define the intertwining period for all
$\lambda \in \mathfrak {a}_{M,\mathbb {C}}^{L,*}$
. We define the intertwining period for all
![]() $\varphi \in \mathcal {A}_{P,\pi }(G)$
and
$\varphi \in \mathcal {A}_{P,\pi }(G)$
and
![]() $\lambda \in \mathfrak {a}_{M,\mathbb {C}}^{L,*}$
by
$\lambda \in \mathfrak {a}_{M,\mathbb {C}}^{L,*}$
by
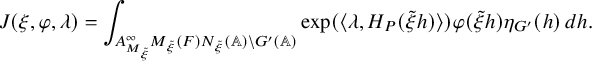 $$ \begin{align} J(\xi,\varphi,\lambda)=\int_{ A_{M_{\tilde \xi}}^\infty M_{\tilde\xi}(F) N_{\tilde\xi} (\mathbb{A})\backslash G'(\mathbb{A})} \exp(\langle \lambda,H_P(\tilde\xi h)\rangle) \varphi(\tilde\xi h)\eta_{G'}(h) \,dh. \end{align} $$
$$ \begin{align} J(\xi,\varphi,\lambda)=\int_{ A_{M_{\tilde \xi}}^\infty M_{\tilde\xi}(F) N_{\tilde\xi} (\mathbb{A})\backslash G'(\mathbb{A})} \exp(\langle \lambda,H_P(\tilde\xi h)\rangle) \varphi(\tilde\xi h)\eta_{G'}(h) \,dh. \end{align} $$
Here, the group
![]() $N_{\tilde \xi } (\mathbb {A}) A_{M_{\tilde \xi }}^\infty M_{\tilde \xi }(F)$
is equipped with a right-invariant Haar measure. However, this measure is not left-invariant: the modular character is given by
$N_{\tilde \xi } (\mathbb {A}) A_{M_{\tilde \xi }}^\infty M_{\tilde \xi }(F)$
is equipped with a right-invariant Haar measure. However, this measure is not left-invariant: the modular character is given by
see [Reference Jacquet, Lapid and RogawskiJLR99, VII p.221]. The integral in (4.1.5.4) is understood as a right-
![]() $G'(\mathbb {A})$
-invariant linear form on the space of
$G'(\mathbb {A})$
-invariant linear form on the space of
![]() $(N_{\tilde \xi } (\mathbb {A}) A_{M_{\tilde \xi }}^\infty M_{\tilde \xi }(F),\delta _{P,\tilde \xi })$
-equivariant functions. This space contains
$(N_{\tilde \xi } (\mathbb {A}) A_{M_{\tilde \xi }}^\infty M_{\tilde \xi }(F),\delta _{P,\tilde \xi })$
-equivariant functions. This space contains
for
![]() $\lambda \in \mathfrak {a}_{M,\mathbb {C}}^{L,*}$
. The integral (4.1.5.4) makes sense at least formally. It is, in fact, absolutely convergent for
$\lambda \in \mathfrak {a}_{M,\mathbb {C}}^{L,*}$
. The integral (4.1.5.4) makes sense at least formally. It is, in fact, absolutely convergent for
![]() $\lambda $
such that
$\lambda $
such that
![]() $\langle \lambda ,\alpha ^\vee \rangle $
is large enough for any
$\langle \lambda ,\alpha ^\vee \rangle $
is large enough for any
![]() $\alpha ^\vee \in \Delta _P^{Q,\vee }$
and it admits a meromorphic continuation to
$\alpha ^\vee \in \Delta _P^{Q,\vee }$
and it admits a meromorphic continuation to
![]() $\mathfrak {a}_{M,\mathbb {C}}^{L,*}$
. It does not depend on a specific choice of
$\mathfrak {a}_{M,\mathbb {C}}^{L,*}$
. It does not depend on a specific choice of
![]() $\tilde \xi $
. For all these properties, we refer the reader to [Reference Jacquet, Lapid and RogawskiJLR99, theorem 23 and (proof of) lemma 32]. In the same way, for any
$\tilde \xi $
. For all these properties, we refer the reader to [Reference Jacquet, Lapid and RogawskiJLR99, theorem 23 and (proof of) lemma 32]. In the same way, for any
![]() $\phi \in \mathcal {A}_{L\cap P,\pi }(L)$
, one defines the intertwining period
$\phi \in \mathcal {A}_{L\cap P,\pi }(L)$
, one defines the intertwining period
![]() $J^L(\xi ,\phi ,\lambda )$
by analytic continuation of the integral
$J^L(\xi ,\phi ,\lambda )$
by analytic continuation of the integral
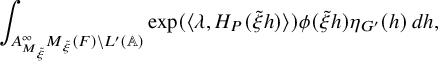 $$ \begin{align*} \int_{ A_{M_{\tilde \xi}}^\infty M_{\tilde\xi}(F) \backslash L'(\mathbb{A})}\exp(\langle \lambda,H_P(\tilde\xi h)\rangle) \phi(\tilde\xi h )\eta_{G'}(h) \,dh, \end{align*} $$
$$ \begin{align*} \int_{ A_{M_{\tilde \xi}}^\infty M_{\tilde\xi}(F) \backslash L'(\mathbb{A})}\exp(\langle \lambda,H_P(\tilde\xi h)\rangle) \phi(\tilde\xi h )\eta_{G'}(h) \,dh, \end{align*} $$
which is convergent for
![]() $\lambda $
in some cone in
$\lambda $
in some cone in
![]() $\mathfrak {a}_{M,\mathbb {C}}^{L,*}$
. Let
$\mathfrak {a}_{M,\mathbb {C}}^{L,*}$
. Let
![]() $dk'$
be the Haar measure on
$dk'$
be the Haar measure on
![]() $K'$
such that the Iwasawa decomposition
$K'$
such that the Iwasawa decomposition
![]() $G'(\mathbb {A})=L'(\mathbb {A})N_{Q'}(\mathbb {A})K'$
is compatible with the various choices of measures. The following ‘parabolic descent’ will be useful:
$G'(\mathbb {A})=L'(\mathbb {A})N_{Q'}(\mathbb {A})K'$
is compatible with the various choices of measures. The following ‘parabolic descent’ will be useful:
Lemma 4.1.5.1. For all
![]() $\varphi \in \mathcal {A}_{P,\pi }(G)$
and
$\varphi \in \mathcal {A}_{P,\pi }(G)$
and
![]() $\lambda \in \mathfrak {a}_{M,\mathbb {C}}^{L,*}$
, we have
$\lambda \in \mathfrak {a}_{M,\mathbb {C}}^{L,*}$
, we have
where we set
Proof. We refer the reader to [Reference Jacquet, Lapid and RogawskiJLR99, (proof of) lemma 32].
However, by [Reference LapidLap06, lemma 8.1 case 2], we have in our situation
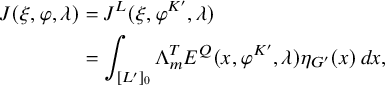 $$ \begin{align} \nonumber J(\xi,\varphi,\lambda)&= J^L(\xi,\varphi^{K'},\lambda)\\ &=\int_{[L']_0} \Lambda^T_m E^Q(x,\varphi^{K'},\lambda)\eta_{G'}(x)\, dx, \end{align} $$
$$ \begin{align} \nonumber J(\xi,\varphi,\lambda)&= J^L(\xi,\varphi^{K'},\lambda)\\ &=\int_{[L']_0} \Lambda^T_m E^Q(x,\varphi^{K'},\lambda)\eta_{G'}(x)\, dx, \end{align} $$
where the truncation operator
![]() $\Lambda ^T_m$
is essentially that introduced in [Reference Jacquet, Lapid and RogawskiJLR99]. More precisely, we decompose
$\Lambda ^T_m$
is essentially that introduced in [Reference Jacquet, Lapid and RogawskiJLR99]. More precisely, we decompose
![]() $L=L_n\times L_{n+1}$
as in (4.1.4.1): on a factor
$L=L_n\times L_{n+1}$
as in (4.1.4.1): on a factor
![]() $G_{n_r+n_{r+1},j}$
with
$G_{n_r+n_{r+1},j}$
with
![]() $j=n,n+1$
and r an odd integer such that
$j=n,n+1$
and r an odd integer such that
![]() $1\leqslant r< 2s_j$
, the truncation operator is exactly that of [Reference Jacquet, Lapid and RogawskiJLR99, IV] and it is trivial on a factor
$1\leqslant r< 2s_j$
, the truncation operator is exactly that of [Reference Jacquet, Lapid and RogawskiJLR99, IV] and it is trivial on a factor
![]() $G_{n_r,j}$
with
$G_{n_r,j}$
with
![]() $r_j\geqslant r>2s_j$
. The Eisenstein series
$r_j\geqslant r>2s_j$
. The Eisenstein series
![]() $E^Q(x,\varphi ^{K'},\lambda )$
is holomorphic on
$E^Q(x,\varphi ^{K'},\lambda )$
is holomorphic on
![]() $i\mathfrak {a}_M^{L,*}$
. The basic properties of the truncation operator
$i\mathfrak {a}_M^{L,*}$
. The basic properties of the truncation operator
![]() $\Lambda ^T_m$
(see [Reference Jacquet, Lapid and RogawskiJLR99, IV]) implies that the integral of the truncated Eisenstein series (4.1.5.6) is meromorphic on
$\Lambda ^T_m$
(see [Reference Jacquet, Lapid and RogawskiJLR99, IV]) implies that the integral of the truncated Eisenstein series (4.1.5.6) is meromorphic on
![]() $\mathfrak {a}_{M,\mathbb {C}}^{L,*}$
and even holomorphic on
$\mathfrak {a}_{M,\mathbb {C}}^{L,*}$
and even holomorphic on
![]() $i\mathfrak {a}_M^{L,*}$
. We deduce that the meromorphic continuation of
$i\mathfrak {a}_M^{L,*}$
. We deduce that the meromorphic continuation of
![]() $J(\xi ,\varphi ,\lambda )$
is holomorphic on
$J(\xi ,\varphi ,\lambda )$
is holomorphic on
![]() $i\mathfrak {a}_M^{L,*}$
and that, for
$i\mathfrak {a}_M^{L,*}$
and that, for
![]() $\lambda \in i\mathfrak {a}_M^{L,*}$
, the map
$\lambda \in i\mathfrak {a}_M^{L,*}$
, the map
![]() $\varphi \mapsto J(\xi ,\varphi ,\lambda )$
is continuous on
$\varphi \mapsto J(\xi ,\varphi ,\lambda )$
is continuous on
![]() $\mathcal {A}_{P,\pi }(G)$
.
$\mathcal {A}_{P,\pi }(G)$
.
4.1.6 Rankin-Selberg period
Let
![]() $T\in \mathfrak {a}_{n+1}^+$
be a sufficiently positive parameter. Let
$T\in \mathfrak {a}_{n+1}^+$
be a sufficiently positive parameter. Let
![]() $\varphi \in \mathcal {A}_{P,\pi }(G)$
and
$\varphi \in \mathcal {A}_{P,\pi }(G)$
and
![]() $\lambda \in \mathfrak {a}_M^*$
. Let
$\lambda \in \mathfrak {a}_M^*$
. Let
![]() $\mathbf {P}(E(\varphi ,\lambda ))$
be the regularized Rankin-Selberg period of the Eisenstein series
$\mathbf {P}(E(\varphi ,\lambda ))$
be the regularized Rankin-Selberg period of the Eisenstein series
![]() $E(\varphi ,\lambda )$
defined by Ichino-Yamana in [Reference Ichino and YamanaIY15]. Because we assume that
$E(\varphi ,\lambda )$
defined by Ichino-Yamana in [Reference Ichino and YamanaIY15]. Because we assume that
![]() $(M,\pi )$
is H-regular, the period is given by the truncated integral
$(M,\pi )$
is H-regular, the period is given by the truncated integral
where
![]() $\Lambda _r^T $
is the Ichino-Yamana truncation operator (whose definition is recalled in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, eq. (3.3.2.1)]). In fact, as the notation suggests, the right-hand side of (4.1.6.1) does not depend on T (the proof of this property is the same as the proof of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, proposition 5.1.4.1]). In particular,
$\Lambda _r^T $
is the Ichino-Yamana truncation operator (whose definition is recalled in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, eq. (3.3.2.1)]). In fact, as the notation suggests, the right-hand side of (4.1.6.1) does not depend on T (the proof of this property is the same as the proof of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, proposition 5.1.4.1]). In particular,
![]() $ \mathbf {P}(E(\varphi ,\lambda ))$
inherits analytic properties of the Eisenstein series
$ \mathbf {P}(E(\varphi ,\lambda ))$
inherits analytic properties of the Eisenstein series
![]() $E(\varphi ,\lambda )$
. Thus, it is holomorphic on
$E(\varphi ,\lambda )$
. Thus, it is holomorphic on
![]() $i\mathfrak {a}_M^{*}$
and the map
$i\mathfrak {a}_M^{*}$
and the map
![]() $\varphi \mapsto \mathbf {P}(E(\varphi ,\lambda ))$
is continuous.
$\varphi \mapsto \mathbf {P}(E(\varphi ,\lambda ))$
is continuous.
4.1.7 The relative character
For any
![]() $\psi $
and
$\psi $
and
![]() $\varphi \in \mathcal {A}_{P,\pi }(G)$
, the expression
$\varphi \in \mathcal {A}_{P,\pi }(G)$
, the expression
is holomorphic on
![]() $i\mathfrak {a}_M^{L,*}$
and gives a continuous pairing on
$i\mathfrak {a}_M^{L,*}$
and gives a continuous pairing on
![]() $\mathcal {A}_{P,\pi }(G)$
. By [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, proposition 2.8.4.1], for any
$\mathcal {A}_{P,\pi }(G)$
. By [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, proposition 2.8.4.1], for any
![]() $f\in \mathcal {S}(G(\mathbb {A}))$
and any
$f\in \mathcal {S}(G(\mathbb {A}))$
and any
![]() $\lambda \in i\mathfrak {a}_M^{L,*}$
, we can define the relative character
$\lambda \in i\mathfrak {a}_M^{L,*}$
, we can define the relative character
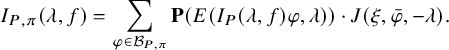 $$ \begin{align*} I_{P,\pi}(\lambda,f)=\sum_{\varphi\in \mathcal{B}_{P,\pi}} \mathbf{P}(E(I_P(\lambda,f)\varphi,\lambda))\cdot J(\xi, \bar\varphi,-\lambda). \end{align*} $$
$$ \begin{align*} I_{P,\pi}(\lambda,f)=\sum_{\varphi\in \mathcal{B}_{P,\pi}} \mathbf{P}(E(I_P(\lambda,f)\varphi,\lambda))\cdot J(\xi, \bar\varphi,-\lambda). \end{align*} $$
where the sum is over a K-basis
![]() $\mathcal {B}_{P,\pi }$
. We get a continuous map
$\mathcal {B}_{P,\pi }$
. We get a continuous map
![]() $f \mapsto (\lambda \mapsto I_{P,\pi }(\lambda ,f))$
from
$f \mapsto (\lambda \mapsto I_{P,\pi }(\lambda ,f))$
from
![]() $\mathcal {S}(G(\mathbb {A}))$
to the space of Schwartz functions on
$\mathcal {S}(G(\mathbb {A}))$
to the space of Schwartz functions on
![]() $i\mathfrak {a}_M^{L,*}$
: this is a slight extension of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, proposition 4.1.10.1] which basically relies on bounds of Eisenstein series due to Lapid in [Reference LapidLap06, proposition 6.1]. Note also that this is also an easy consequence of the inequality given in [Reference ChaudouardCha22, proof of proposition 7.2.3.2].
$i\mathfrak {a}_M^{L,*}$
: this is a slight extension of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, proposition 4.1.10.1] which basically relies on bounds of Eisenstein series due to Lapid in [Reference LapidLap06, proposition 6.1]. Note also that this is also an easy consequence of the inequality given in [Reference ChaudouardCha22, proof of proposition 7.2.3.2].
4.1.8 The
 $(G,H)$
-regular contribution to the Jacquet-Rallis trace formula
$(G,H)$
-regular contribution to the Jacquet-Rallis trace formula
The contribution to the Jacquet-Rallis trace formula of a cuspidal datum
![]() $\chi $
is a distribution denoted by
$\chi $
is a distribution denoted by
![]() $I_\chi $
and defined in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, theorem 3.2.4.1]. In the case of a Hermitian
$I_\chi $
and defined in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, theorem 3.2.4.1]. In the case of a Hermitian
![]() $(G,H)$
-regular cuspidal datum, the next theorem relates this contribution to the relative character defined above.
$(G,H)$
-regular cuspidal datum, the next theorem relates this contribution to the relative character defined above.
Theorem 4.1.8.1. Let
![]() $\chi \in \mathfrak {X}(G)$
be a
$\chi \in \mathfrak {X}(G)$
be a
![]() $(G,H)$
-regular cuspidal datum.
$(G,H)$
-regular cuspidal datum.
-
1. If
 $\chi $
is not Hermitian, we have
$\chi $
is not Hermitian, we have
 $I_\chi =0$
.
$I_\chi =0$
. -
2. Assume that
 $\chi $
is, moreover, Hermitian and let
$\chi $
is, moreover, Hermitian and let
 $(M_P,\pi )$
and L be as in §4.1.4. For all
$(M_P,\pi )$
and L be as in §4.1.4. For all
 $f\in \mathcal {S}(G(\mathbb {A}))$
, we have (4.1.8.1)where the integral in the right-hand side is absolutely convergent.
$f\in \mathcal {S}(G(\mathbb {A}))$
, we have (4.1.8.1)where the integral in the right-hand side is absolutely convergent. $$ \begin{align} I_\chi(f)=2^{-\dim(\mathfrak{a}_L)} \int_{i\mathfrak{a}_M^{L,*}}I_{P,\pi}(\lambda,f)\,d\lambda, \end{align} $$
$$ \begin{align} I_\chi(f)=2^{-\dim(\mathfrak{a}_L)} \int_{i\mathfrak{a}_M^{L,*}}I_{P,\pi}(\lambda,f)\,d\lambda, \end{align} $$
4.1.9 Proof of Theorem 4.1.8.1
Let
![]() $\chi \in \mathfrak {X}(G)$
be a
$\chi \in \mathfrak {X}(G)$
be a
![]() $(G,H)$
-regular cuspidal datum. Let
$(G,H)$
-regular cuspidal datum. Let
![]() $f\in \mathcal {S}(G(\mathbb {A}))$
and let
$f\in \mathcal {S}(G(\mathbb {A}))$
and let
![]() $K_{\chi }$
be the kernel of the right convolution by f on
$K_{\chi }$
be the kernel of the right convolution by f on
![]() $L^2_\chi ([G])$
. By [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, proposition 3.3.8.1 and theorem 3.3.9.1], the contribution
$L^2_\chi ([G])$
. By [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, proposition 3.3.8.1 and theorem 3.3.9.1], the contribution
![]() $I_\chi (f)$
is the constant term in the asymptotic expansion in
$I_\chi (f)$
is the constant term in the asymptotic expansion in
![]() $T\in \mathfrak {a}_{n+1}^+$
of the absolutely convergent integral
$T\in \mathfrak {a}_{n+1}^+$
of the absolutely convergent integral
By [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, lemma 5.2.2.1], we have for all
![]() $h\in [H]$
,
$h\in [H]$
,
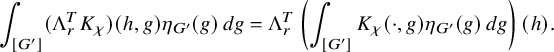 $$ \begin{align} \int_{[G'] } (\Lambda_r^TK_\chi) (h,g)\eta_{G'}(g)\,dg= \Lambda_r^T\left(\int_{[G'] } K_\chi (\cdot,g)\eta_{G'}(g)\,dg\right)(h). \end{align} $$
$$ \begin{align} \int_{[G'] } (\Lambda_r^TK_\chi) (h,g)\eta_{G'}(g)\,dg= \Lambda_r^T\left(\int_{[G'] } K_\chi (\cdot,g)\eta_{G'}(g)\,dg\right)(h). \end{align} $$
Then we have the following lemma:
Lemma 4.1.9.1. Let
![]() $\chi \in \mathfrak {X}(G)$
be a
$\chi \in \mathfrak {X}(G)$
be a
![]() $(G,H)$
-regular cuspidal datum. For all
$(G,H)$
-regular cuspidal datum. For all
![]() $x\in G(\mathbb {A})$
, the absolutely convergent integral
$x\in G(\mathbb {A})$
, the absolutely convergent integral
vanishes unless
![]() $\chi $
is Hermitian. If
$\chi $
is Hermitian. If
![]() $\chi $
is Hermitian and represented by
$\chi $
is Hermitian and represented by
![]() $(M_P,\pi )$
, we have
$(M_P,\pi )$
, we have
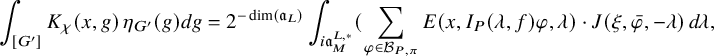 $$ \begin{align} \int_{[G']} K_\chi(x,g)\,\eta_{G'}(g)dg=2^{-\dim(\mathfrak{a}_{L})} \int_{i\mathfrak{a}_{M}^{L,*}} (\sum_{\varphi\in \mathcal{B}_{P,\pi}} E(x,I_P(\lambda,f)\varphi,\lambda)\cdot J(\xi, \bar\varphi,-\lambda) \, d\lambda, \end{align} $$
$$ \begin{align} \int_{[G']} K_\chi(x,g)\,\eta_{G'}(g)dg=2^{-\dim(\mathfrak{a}_{L})} \int_{i\mathfrak{a}_{M}^{L,*}} (\sum_{\varphi\in \mathcal{B}_{P,\pi}} E(x,I_P(\lambda,f)\varphi,\lambda)\cdot J(\xi, \bar\varphi,-\lambda) \, d\lambda, \end{align} $$
where the Levi subgroup L is that defined in §4.1.4 and
![]() $\mathcal {B}_{P,\pi }$
is a K-basis.
$\mathcal {B}_{P,\pi }$
is a K-basis.
Proof. For brevity reasons, we shall get the lemma as a simple application of a much more difficult result – namely, [Reference ChaudouardCha22, Theorem 7.2.4.1]. Our situation is essentially that of [Reference ChaudouardCha22, Theorem 7.2.4.1] except that we are working here with a product of two general linear groups and our Flicker-Rallis periods are twisted by the caracter
![]() $\eta _{G'}$
. Note that the absolute convergence of (4.1.9.3) results from [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Lemma 2.10.1.1]. Let
$\eta _{G'}$
. Note that the absolute convergence of (4.1.9.3) results from [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Lemma 2.10.1.1]. Let
![]() $(M,\pi )$
be a representative of the
$(M,\pi )$
be a representative of the
![]() $(G,H)$
-regular cuspidal datum
$(G,H)$
-regular cuspidal datum
![]() $\chi $
with P a standard parabolic subgroup of G and
$\chi $
with P a standard parabolic subgroup of G and
![]() $M=M_P$
. Let
$M=M_P$
. Let
![]() $P_1$
be standard parabolic subgroup of G and set
$P_1$
be standard parabolic subgroup of G and set
![]() $M_1=M_{P_1}$
. There is a finite set
$M_1=M_{P_1}$
. There is a finite set
![]() $\Pi _{\chi }(M_1)$
used in the statement of [Reference ChaudouardCha22, theorem 7.2.4.1]. There is no need to recall the general definition given in [Reference ChaudouardCha22, § 7.1.1]: indeed, because
$\Pi _{\chi }(M_1)$
used in the statement of [Reference ChaudouardCha22, theorem 7.2.4.1]. There is no need to recall the general definition given in [Reference ChaudouardCha22, § 7.1.1]: indeed, because
![]() $\chi $
is G-regular, either
$\chi $
is G-regular, either
![]() $P_1$
and P are not associated in which case
$P_1$
and P are not associated in which case
![]() $\Pi _{\chi }(M_1)$
is empty or
$\Pi _{\chi }(M_1)$
is empty or
![]() $\Pi _{\chi }(M_1)$
is the set of
$\Pi _{\chi }(M_1)$
is the set of
![]() $w\pi $
with
$w\pi $
with
![]() $w\in W(P,P_1)$
.
$w\in W(P,P_1)$
.
We can extract from [Reference ChaudouardCha22, theorem 7.2.4.1] that (4.1.9.3) is equal to the absolutely convergent expression
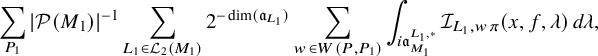 $$ \begin{align} \sum_{P_1} |\mathcal{P}(M_1)|^{-1}\sum_{L_1\in \mathcal{L}_2(M_1)} 2^{-\dim(\mathfrak{a}_{L_1})} \sum_{w\in W(P,P_1)} \int_{i\mathfrak{a}_{M_1}^{L_1,*}} \mathcal{I}_{L_1,w\pi}(x,f,\lambda)\, d\lambda, \end{align} $$
$$ \begin{align} \sum_{P_1} |\mathcal{P}(M_1)|^{-1}\sum_{L_1\in \mathcal{L}_2(M_1)} 2^{-\dim(\mathfrak{a}_{L_1})} \sum_{w\in W(P,P_1)} \int_{i\mathfrak{a}_{M_1}^{L_1,*}} \mathcal{I}_{L_1,w\pi}(x,f,\lambda)\, d\lambda, \end{align} $$
where the sum is over the set of standard parabolic sugroups
![]() $P_1$
of G and
$P_1$
of G and
![]() $M_1=M_{P_1}$
, the number of parabolic subgroups of Levi M is denoted by
$M_1=M_{P_1}$
, the number of parabolic subgroups of Levi M is denoted by
![]() $|\mathcal {P}(M)|$
, the set
$|\mathcal {P}(M)|$
, the set
![]() $\mathcal {L}_2(M_1)$
is a subset of the set of Levi subgroups of G containing
$\mathcal {L}_2(M_1)$
is a subset of the set of Levi subgroups of G containing
![]() $M_1$
(see [Reference ChaudouardCha22, § 2.2.3]) and
$M_1$
(see [Reference ChaudouardCha22, § 2.2.3]) and
![]() $\mathcal {I}_{L_1,w\pi }(x,f,\lambda )$
is mutatis mutandis the relative character that essentially appears in the statement of [Reference ChaudouardCha22, theorem 7.2.4.1]. The main difference is that we are working here on a product of two linear groups and that the relative character is built upon Eisenstein series and the intertwining periods defined in [Reference ChaudouardCha22, § 5.1.4] but twisted by the character
$\mathcal {I}_{L_1,w\pi }(x,f,\lambda )$
is mutatis mutandis the relative character that essentially appears in the statement of [Reference ChaudouardCha22, theorem 7.2.4.1]. The main difference is that we are working here on a product of two linear groups and that the relative character is built upon Eisenstein series and the intertwining periods defined in [Reference ChaudouardCha22, § 5.1.4] but twisted by the character
![]() $\eta _{G'}$
. Let
$\eta _{G'}$
. Let
![]() $M_1,L_1$
and
$M_1,L_1$
and
![]() $w\in W(P,P_1)$
be as in (4.1.9.5) and let
$w\in W(P,P_1)$
be as in (4.1.9.5) and let
![]() $x\in G(\mathbb {A})$
and
$x\in G(\mathbb {A})$
and
![]() $\lambda \in i\mathfrak {a}_{M_1}^{L_1,*}$
. Rather than spell out the exact definition of
$\lambda \in i\mathfrak {a}_{M_1}^{L_1,*}$
. Rather than spell out the exact definition of
![]() $\mathcal {I}_{L_1,w\pi }(x,f,\lambda )$
, we will explain it in the particular case that concerns us. Before doing that, we owe a detailed explanation to the careful reader who will certainly have noticed the apparent discrepancy of a factor
$\mathcal {I}_{L_1,w\pi }(x,f,\lambda )$
, we will explain it in the particular case that concerns us. Before doing that, we owe a detailed explanation to the careful reader who will certainly have noticed the apparent discrepancy of a factor
![]() $2^{\dim (\mathfrak {a}_G)}$
. The reason is the following: [Reference ChaudouardCha22, theorem 7.2.4.1] gives in fact the spectral expansion of
$2^{\dim (\mathfrak {a}_G)}$
. The reason is the following: [Reference ChaudouardCha22, theorem 7.2.4.1] gives in fact the spectral expansion of
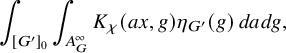 $$ \begin{align*} \int_{[G']_0 } \int_{A_G^\infty} K_\chi (ax,g)\eta_{G'}(g)\,dadg, \end{align*} $$
$$ \begin{align*} \int_{[G']_0 } \int_{A_G^\infty} K_\chi (ax,g)\eta_{G'}(g)\,dadg, \end{align*} $$
whereas we are working with
 $$ \begin{align*} \int_{[G'] } K_\chi (x,g)\eta_{G'}(g)\,dg=2^{-\dim(\mathfrak{a}_G)}\int_{[G']_0 } \int_{A_G^\infty} K_\chi (ax,g)\eta_{G'}(g)\,dadg. \end{align*} $$
$$ \begin{align*} \int_{[G'] } K_\chi (x,g)\eta_{G'}(g)\,dg=2^{-\dim(\mathfrak{a}_G)}\int_{[G']_0 } \int_{A_G^\infty} K_\chi (ax,g)\eta_{G'}(g)\,dadg. \end{align*} $$
The equality above comes from the difference between the respective measures on
![]() $A_G^\infty $
and
$A_G^\infty $
and
![]() $A_{G'}^\infty $
; see §4.1.2.
$A_{G'}^\infty $
; see §4.1.2.
By the fact that
![]() $\chi $
is G-regular and by the basic properties of the cuspidal intertwining periods (see [Reference Jacquet, Lapid and RogawskiJLR99, theorem 23]), we see that the relative character
$\chi $
is G-regular and by the basic properties of the cuspidal intertwining periods (see [Reference Jacquet, Lapid and RogawskiJLR99, theorem 23]), we see that the relative character
![]() $\mathcal {I}_{L_1,w\pi }(x,f,\lambda )$
vanishes unless
$\mathcal {I}_{L_1,w\pi }(x,f,\lambda )$
vanishes unless
![]() $\chi $
is Hermitian. So we get the first assertion, and we assume from now on that
$\chi $
is Hermitian. So we get the first assertion, and we assume from now on that
![]() $\chi $
is moreover Hermitian. Note that, by definition, we have for all
$\chi $
is moreover Hermitian. Note that, by definition, we have for all
![]() $\mu \in i\mathfrak {a}_M^{L,*}$
,
$\mu \in i\mathfrak {a}_M^{L,*}$
,
 $$ \begin{align} \mathcal{I}_{L,\pi}(x,f,\mu)=\sum_{\varphi\in \mathcal{B}_{P,\pi}} E(x,I_P(\mu,f)\varphi,\mu)\cdot J(\xi, \bar\varphi,-\mu). \end{align} $$
$$ \begin{align} \mathcal{I}_{L,\pi}(x,f,\mu)=\sum_{\varphi\in \mathcal{B}_{P,\pi}} E(x,I_P(\mu,f)\varphi,\mu)\cdot J(\xi, \bar\varphi,-\mu). \end{align} $$
We claim that we have
Moreover, it follows from the fact that
![]() $\chi $
is G-regular and Hermitian that for all Levi subgroup
$\chi $
is G-regular and Hermitian that for all Levi subgroup
![]() $L_1\in \mathcal {L}_2(M)$
and all
$L_1\in \mathcal {L}_2(M)$
and all
![]() $\mu \in \mathfrak {a}_M^{L_1,*}$
, we have
$\mu \in \mathfrak {a}_M^{L_1,*}$
, we have
Let us assume (4.1.9.7) for the moment, and let us finish the proof of (4.1.9.4). By (4.1.9.7) and (4.1.9.8) and the change of variables
![]() $\lambda \mapsto w^{-1}\lambda $
, we see that (4.1.9.5) is equal to
$\lambda \mapsto w^{-1}\lambda $
, we see that (4.1.9.5) is equal to
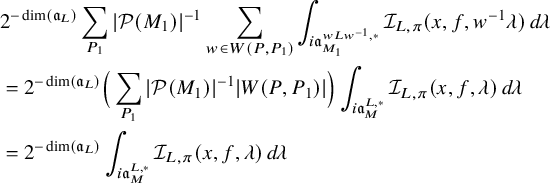 $$ \begin{align*} &2^{-\dim(\mathfrak{a}_{L})} \sum_{P_1} |\mathcal{P}(M_1)|^{-1} \sum_{w\in W(P,P_1)} \int_{i\mathfrak{a}_{M_1}^{wLw^{-1},*}} \mathcal{I}_{L,\pi}(x,f,w^{-1}\lambda)\, d\lambda\\ &=2^{-\dim(\mathfrak{a}_{L})}\Big(\sum_{P_1} |\mathcal{P}(M_1)|^{-1} |W(P,P_1)| \Big)\int_{i\mathfrak{a}_{M}^{L,*}} \mathcal{I}_{L,\pi}(x,f,\lambda)\, d\lambda\\ &=2^{-\dim(\mathfrak{a}_{L})}\int_{i\mathfrak{a}_{M}^{L,*}} \mathcal{I}_{L,\pi}(x,f,\lambda)\, d\lambda \end{align*} $$
$$ \begin{align*} &2^{-\dim(\mathfrak{a}_{L})} \sum_{P_1} |\mathcal{P}(M_1)|^{-1} \sum_{w\in W(P,P_1)} \int_{i\mathfrak{a}_{M_1}^{wLw^{-1},*}} \mathcal{I}_{L,\pi}(x,f,w^{-1}\lambda)\, d\lambda\\ &=2^{-\dim(\mathfrak{a}_{L})}\Big(\sum_{P_1} |\mathcal{P}(M_1)|^{-1} |W(P,P_1)| \Big)\int_{i\mathfrak{a}_{M}^{L,*}} \mathcal{I}_{L,\pi}(x,f,\lambda)\, d\lambda\\ &=2^{-\dim(\mathfrak{a}_{L})}\int_{i\mathfrak{a}_{M}^{L,*}} \mathcal{I}_{L,\pi}(x,f,\lambda)\, d\lambda \end{align*} $$
since
![]() $\sum _{P_1} |\mathcal {P}(M_1)|^{-1} |W(P,P_1)| =1$
where the various sums are over standard parabolic subgroups
$\sum _{P_1} |\mathcal {P}(M_1)|^{-1} |W(P,P_1)| =1$
where the various sums are over standard parabolic subgroups
![]() $P_1$
.
$P_1$
.
Let us prove the claim (4.1.9.7). We start from
![]() $M_1,L_1,\lambda ,w$
as in (4.1.9.5). By (4.1.9.8), we may and shall assume that we have
$M_1,L_1,\lambda ,w$
as in (4.1.9.5). By (4.1.9.8), we may and shall assume that we have
![]() $L_1=wLw^{-1}$
. Let
$L_1=wLw^{-1}$
. Let
![]() $Q_1$
be a parabolic subgroup of Levi
$Q_1$
be a parabolic subgroup of Levi
![]() $L_1$
. Let
$L_1$
. Let
![]() $P_2$
be a standard parabolic subgroup of G and let
$P_2$
be a standard parabolic subgroup of G and let
![]() $w_1\in W(P_1,P_2)$
such that
$w_1\in W(P_1,P_2)$
such that
![]() $P_2\subset w_1 Q_1w_1^{-1}$
. Using the definition of intertwining periods given in [Reference ChaudouardCha22, § 5.1.4], the functional equation of Eisenstein series and a standard basis change relying on the fact that the intertwining operator
$P_2\subset w_1 Q_1w_1^{-1}$
. Using the definition of intertwining periods given in [Reference ChaudouardCha22, § 5.1.4], the functional equation of Eisenstein series and a standard basis change relying on the fact that the intertwining operator
![]() $M(w_1,\lambda )$
induces a unitary isomorphism from
$M(w_1,\lambda )$
induces a unitary isomorphism from
![]() $\mathcal {A}_{P_1,w\pi }(G)$
onto
$\mathcal {A}_{P_1,w\pi }(G)$
onto
![]() $\mathcal {A}_{P_1,w_1w\pi }(G)$
, we see that we have
$\mathcal {A}_{P_1,w_1w\pi }(G)$
, we see that we have
with
![]() $L_2=w_1L_1w_1^{-1}$
. Thus, we are reduced to prove (4.1.9.7) in the special case where the Levi subgroup
$L_2=w_1L_1w_1^{-1}$
. Thus, we are reduced to prove (4.1.9.7) in the special case where the Levi subgroup
![]() $L_1=wLw^{-1}$
is standard. But then (4.1.9.7) follows from the same arguments as before, namely the functional equation of Eisenstein series and a standard basis change and the functional equation of intertwining periods, namely [Reference Jacquet, Lapid and RogawskiJLR99, theorem 31] completed with [Reference LapidLap06, lemma 8.1]. For a similar statement, see [Reference LapidLap06, proposition 8.2]. This finishes the proof.
$L_1=wLw^{-1}$
is standard. But then (4.1.9.7) follows from the same arguments as before, namely the functional equation of Eisenstein series and a standard basis change and the functional equation of intertwining periods, namely [Reference Jacquet, Lapid and RogawskiJLR99, theorem 31] completed with [Reference LapidLap06, lemma 8.1]. For a similar statement, see [Reference LapidLap06, proposition 8.2]. This finishes the proof.
It follows from Lemma 4.1.9.1 that, for
![]() $h\in [H]$
, we have
$h\in [H]$
, we have
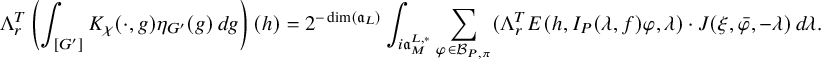 $$ \begin{align} \Lambda_r^T\left(\int_{[G'] } K_\chi (\cdot,g)\eta_{G'}(g)\,dg\right)(h)= 2^{-\dim(\mathfrak{a}_{L})} \int_{i\mathfrak{a}_{M}^{L,*}} \sum_{\varphi\in \mathcal{B}_{P,\pi}} (\Lambda_r^TE(h,I_P(\lambda,f)\varphi,\lambda)\cdot J(\xi, \bar\varphi,-\lambda) \, d\lambda. \end{align} $$
$$ \begin{align} \Lambda_r^T\left(\int_{[G'] } K_\chi (\cdot,g)\eta_{G'}(g)\,dg\right)(h)= 2^{-\dim(\mathfrak{a}_{L})} \int_{i\mathfrak{a}_{M}^{L,*}} \sum_{\varphi\in \mathcal{B}_{P,\pi}} (\Lambda_r^TE(h,I_P(\lambda,f)\varphi,\lambda)\cdot J(\xi, \bar\varphi,-\lambda) \, d\lambda. \end{align} $$
To get this, we have to permute the truncation operator with the sum and the integral. However, one observes that for a fixed
![]() $h\in [H]$
, the truncation operator is a finite sum of constant terms. So to get (4.1.9.9), one has basically to permute the integral over
$h\in [H]$
, the truncation operator is a finite sum of constant terms. So to get (4.1.9.9), one has basically to permute the integral over
![]() $i\mathfrak {a}_{M}^{L,*}$
and the integral that gives a constant term. So, by Fubini theorem, it suffices to show that for any parabolic subgroup Q of G, the sum
$i\mathfrak {a}_{M}^{L,*}$
and the integral that gives a constant term. So, by Fubini theorem, it suffices to show that for any parabolic subgroup Q of G, the sum
 $$ \begin{align*} \sum_{\varphi\in \mathcal{B}_{P,\pi}} \int_{N_Q}| E(nh,I_P(\lambda,f)\varphi,\lambda)| \, dn \cdot |J(\xi, \bar\varphi,-\lambda) | \end{align*} $$
$$ \begin{align*} \sum_{\varphi\in \mathcal{B}_{P,\pi}} \int_{N_Q}| E(nh,I_P(\lambda,f)\varphi,\lambda)| \, dn \cdot |J(\xi, \bar\varphi,-\lambda) | \end{align*} $$
is a Schwartz function in the variable
![]() $\lambda \in i\mathfrak {a}_M^{L,*}$
. But this is a variant of [Reference LapidLap06, Lemma 7.4]; it is also an easy consequence of [Reference ChaudouardCha22, proposition 7.2.3.2]. The last step is to observe that
$\lambda \in i\mathfrak {a}_M^{L,*}$
. But this is a variant of [Reference LapidLap06, Lemma 7.4]; it is also an easy consequence of [Reference ChaudouardCha22, proposition 7.2.3.2]. The last step is to observe that
 $$ \begin{align} \int_{[H]} \int_{i\mathfrak{a}_{M}^{L,*}} \sum_{\varphi\in \mathcal{B}_{P,\pi}} \Lambda_r^TE(h,I_P(\lambda,f)\varphi,\lambda)\cdot J(\xi, \bar\varphi,-\lambda) \, d\lambda dh\\ \nonumber = \int_{i\mathfrak{a}_{M}^{L,*}} \sum_{\varphi\in \mathcal{B}_{P,\pi}} \int_{[H]} \Lambda_r^TE(h,I_P(\lambda,f)\varphi,\lambda)\, dh\cdot J(\xi, \bar\varphi,-\lambda) \, d\lambda \end{align} $$
$$ \begin{align} \int_{[H]} \int_{i\mathfrak{a}_{M}^{L,*}} \sum_{\varphi\in \mathcal{B}_{P,\pi}} \Lambda_r^TE(h,I_P(\lambda,f)\varphi,\lambda)\cdot J(\xi, \bar\varphi,-\lambda) \, d\lambda dh\\ \nonumber = \int_{i\mathfrak{a}_{M}^{L,*}} \sum_{\varphi\in \mathcal{B}_{P,\pi}} \int_{[H]} \Lambda_r^TE(h,I_P(\lambda,f)\varphi,\lambda)\, dh\cdot J(\xi, \bar\varphi,-\lambda) \, d\lambda \end{align} $$
and to use (4.1.6.1) to recognize the relative character
![]() $I_{P,\pi }(\lambda , f)$
in the inner sum. Once again by a variant of [Reference LapidLap06, Lemma 7.4] (or by [Reference ChaudouardCha22, proposition 7.2.3.2]) and the basic properties of truncation operator (see [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, proposition 3.3.2.1]), we have
$I_{P,\pi }(\lambda , f)$
in the inner sum. Once again by a variant of [Reference LapidLap06, Lemma 7.4] (or by [Reference ChaudouardCha22, proposition 7.2.3.2]) and the basic properties of truncation operator (see [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, proposition 3.3.2.1]), we have
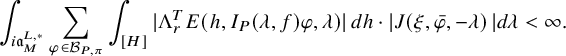 $$ \begin{align*} \int_{i\mathfrak{a}_{M}^{L,*}} \sum_{\varphi\in \mathcal{B}_{P,\pi}} \int_{[H]}| \Lambda_r^TE(h,I_P(\lambda,f)\varphi,\lambda)|\, dh\cdot |J(\xi, \bar\varphi,-\lambda) \, |d\lambda <\infty. \end{align*} $$
$$ \begin{align*} \int_{i\mathfrak{a}_{M}^{L,*}} \sum_{\varphi\in \mathcal{B}_{P,\pi}} \int_{[H]}| \Lambda_r^TE(h,I_P(\lambda,f)\varphi,\lambda)|\, dh\cdot |J(\xi, \bar\varphi,-\lambda) \, |d\lambda <\infty. \end{align*} $$
We can again conclude with Fubini’s theorem.
4.2 The relative character in terms of Whittaker functions
4.2.1
We keep the notations of the previous subsection. Let
![]() $N=N_n\times N_{n+1}$
and
$N=N_n\times N_{n+1}$
and
![]() $N_H=N_n$
be viewed as a diagonal subgroup of N. Let
$N_H=N_n$
be viewed as a diagonal subgroup of N. Let
![]() $N'=N\cap G'$
.
$N'=N\cap G'$
.
4.2.2
We fix a nontrivial additive character
![]() $\psi ':\mathbb {A}/F\to \mathbb {C}^\times $
. We deduce a character
$\psi ':\mathbb {A}/F\to \mathbb {C}^\times $
. We deduce a character
![]() $\psi :\mathbb {A}_E/E\to \mathbb {C}^\times $
trivial on
$\psi :\mathbb {A}_E/E\to \mathbb {C}^\times $
trivial on
![]() $\mathbb {A}$
by
$\mathbb {A}$
by
![]() $\psi (z)=\psi '( \mathrm {Tr}_{E/F}(\tau z))$
, where
$\psi (z)=\psi '( \mathrm {Tr}_{E/F}(\tau z))$
, where
![]() $\tau \in E^\times $
is such that
$\tau \in E^\times $
is such that
![]() $c(\tau )=-\tau $
. We define a regular character
$c(\tau )=-\tau $
. We define a regular character
![]() $\psi _n:[N_n]\to \mathbb {C}^\times $
by
$\psi _n:[N_n]\to \mathbb {C}^\times $
by
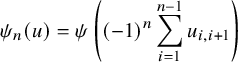 $$ \begin{align*} \psi_n(u)=\psi \left((-1)^n \sum_{i=1}^{n-1}u_{i,i+1}\right) \end{align*} $$
$$ \begin{align*} \psi_n(u)=\psi \left((-1)^n \sum_{i=1}^{n-1}u_{i,i+1}\right) \end{align*} $$
for any
![]() $u\in [N_n]$
. In the same way, we get a character
$u\in [N_n]$
. In the same way, we get a character
![]() $\psi _{n+1}$
of
$\psi _{n+1}$
of
![]() $[N_{n+1}]$
. Thus, we have a character
$[N_{n+1}]$
. Thus, we have a character
![]() $\psi _{N}=\psi _n\boxtimes \psi _{n+1}$
of
$\psi _{N}=\psi _n\boxtimes \psi _{n+1}$
of
![]() $[N]$
. By construction,
$[N]$
. By construction,
![]() $\psi _N$
is trivial on the subgroups
$\psi _N$
is trivial on the subgroups
![]() $N'$
and
$N'$
and
![]() $N_H$
.
$N_H$
.
4.2.3
Recall that we have fixed a pair
![]() $(M,\pi )$
with
$(M,\pi )$
with
![]() $M=M_P$
(see §§4.1.3 and 4.1.4). Let
$M=M_P$
(see §§4.1.3 and 4.1.4). Let
![]() $\lambda \in i\mathfrak {a}_{P}^{G,*}$
. Let
$\lambda \in i\mathfrak {a}_{P}^{G,*}$
. Let
![]() $\pi _\lambda $
be the representation
$\pi _\lambda $
be the representation
![]() $\pi $
twisted by the character
$\pi $
twisted by the character
![]() $m\mapsto \exp (\langle \lambda ,H_M(m\rangle )$
and let
$m\mapsto \exp (\langle \lambda ,H_M(m\rangle )$
and let
![]() $\Pi _\lambda =\operatorname {\mathrm {Ind}}_{P(\mathbb {A})}^{G(\mathbb {A})}(\pi _\lambda )$
be the induced representation. The representation
$\Pi _\lambda =\operatorname {\mathrm {Ind}}_{P(\mathbb {A})}^{G(\mathbb {A})}(\pi _\lambda )$
be the induced representation. The representation
![]() $\Pi _\lambda $
is irreducible, unitary and generic. Let
$\Pi _\lambda $
is irreducible, unitary and generic. Let
![]() $\mathcal {W}(\Pi _\lambda ,\psi _N)$
be its Whittaker model with respect to the character
$\mathcal {W}(\Pi _\lambda ,\psi _N)$
be its Whittaker model with respect to the character
![]() $\psi _N$
.
$\psi _N$
.
For any
![]() $\varphi \in \mathcal {A}_{P,\pi }(G)$
and
$\varphi \in \mathcal {A}_{P,\pi }(G)$
and
![]() $g\in G(\mathbb {A})$
, let
$g\in G(\mathbb {A})$
, let
We may and shall identify
![]() $g\mapsto W(g,\varphi ,\lambda )$
with an element of
$g\mapsto W(g,\varphi ,\lambda )$
with an element of
![]() $\mathcal {W}(\Pi _\lambda ,\psi _N)$
.
$\mathcal {W}(\Pi _\lambda ,\psi _N)$
.
4.2.4
Let
![]() $W\in \mathcal {W}(\Pi _\lambda ,\psi _N)$
. By [Reference Jacquet, Piatetskii-Shapiro and ShalikaJPSS83] and [Reference JacquetJac09], the integral
$W\in \mathcal {W}(\Pi _\lambda ,\psi _N)$
. By [Reference Jacquet, Piatetskii-Shapiro and ShalikaJPSS83] and [Reference JacquetJac09], the integral
converges for
![]() $\Re (s)\gg 0$
and extends to a meromorphic function on
$\Re (s)\gg 0$
and extends to a meromorphic function on
![]() $\mathbb {C}$
which is holomorphic at
$\mathbb {C}$
which is holomorphic at
![]() $s=0$
. Let
$s=0$
. Let
![]() $\mathcal {P}=\mathcal {P}_n\times \mathcal {P}_{n+1}$
be the product of the respective mirabolic subgroups
$\mathcal {P}=\mathcal {P}_n\times \mathcal {P}_{n+1}$
be the product of the respective mirabolic subgroups
![]() $\mathcal {P}_n$
and
$\mathcal {P}_n$
and
![]() $\mathcal {P}_{n+1}$
of
$\mathcal {P}_{n+1}$
of
![]() $G_n$
and
$G_n$
and
![]() $G_{n+1}$
. Let
$G_{n+1}$
. Let
![]() $\mathcal {P}'=\mathcal {P}\cap G'$
. We put
$\mathcal {P}'=\mathcal {P}\cap G'$
. We put
![]() $\mathrm {As}_G=\mathrm {As}^{(-1)^{n+1}}\boxtimes \mathrm {As}^{(-1)^n}$
. For any finite set
$\mathrm {As}_G=\mathrm {As}^{(-1)^{n+1}}\boxtimes \mathrm {As}^{(-1)^n}$
. For any finite set
![]() $S\subset V_F$
, we set
$S\subset V_F$
, we set
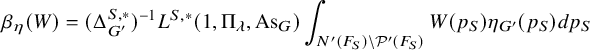 $$ \begin{align*}\beta_\eta(W)=(\Delta^{S,*}_{G'})^{-1}L^{S,*}(1,\Pi_\lambda,\mathrm{As}_G)\int_{N'(F_S)\backslash \mathcal{P}'(F_S)} W(p_S) \eta_{G'}(p_S) dp_S\end{align*} $$
$$ \begin{align*}\beta_\eta(W)=(\Delta^{S,*}_{G'})^{-1}L^{S,*}(1,\Pi_\lambda,\mathrm{As}_G)\int_{N'(F_S)\backslash \mathcal{P}'(F_S)} W(p_S) \eta_{G'}(p_S) dp_S\end{align*} $$
and
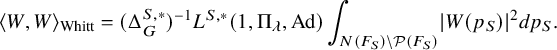 $$ \begin{align*}\langle W,W\rangle_{\mathrm{Whitt}}=(\Delta^{S,*}_{G})^{-1}L^{S,*}(1,\Pi_\lambda,\operatorname{\mathrm{Ad}})\int_{N(F_S)\backslash \mathcal{P}(F_S)} \lvert W(p_S)\rvert^2 dp_S.\end{align*} $$
$$ \begin{align*}\langle W,W\rangle_{\mathrm{Whitt}}=(\Delta^{S,*}_{G})^{-1}L^{S,*}(1,\Pi_\lambda,\operatorname{\mathrm{Ad}})\int_{N(F_S)\backslash \mathcal{P}(F_S)} \lvert W(p_S)\rvert^2 dp_S.\end{align*} $$
Here and hereafter,
![]() $L^*(1)$
means the leading coefficient in the Laurent expansion of the meromorphic function
$L^*(1)$
means the leading coefficient in the Laurent expansion of the meromorphic function
![]() $L(s)$
at
$L(s)$
at
![]() $s=1$
. The above expressions converge and are independent of S as soon as it is chosen sufficiently large according to the level of W (see [Reference FlickerFli88] and [Reference Jacquet and ShalikaJS81b]).
$s=1$
. The above expressions converge and are independent of S as soon as it is chosen sufficiently large according to the level of W (see [Reference FlickerFli88] and [Reference Jacquet and ShalikaJS81b]).
4.2.5
Proposition 4.2.5.1. For any
![]() $\varphi \in \mathcal {A}_{P,\pi }(G)$
, we have
$\varphi \in \mathcal {A}_{P,\pi }(G)$
, we have
Proof. This is a straightforward application of results of Ichino-Yamana and the fact that
![]() $(M,\pi )$
is H-regular. First, for any
$(M,\pi )$
is H-regular. First, for any
![]() $T\in \mathfrak {a}_{n+1}^+ $
and any
$T\in \mathfrak {a}_{n+1}^+ $
and any
![]() $s\in \mathbb {C}$
, the integral
$s\in \mathbb {C}$
, the integral
converges and defines a holomorphic function in the variable s. Moreover, since
![]() $(M,\pi )$
is H-regular, it does not depend on T (see [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, proof of proposition 5.1.4.1]). Because of this, (4.2.5.1) is the regularized Rankin-Selberg period of
$(M,\pi )$
is H-regular, it does not depend on T (see [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, proof of proposition 5.1.4.1]). Because of this, (4.2.5.1) is the regularized Rankin-Selberg period of
![]() $h\mapsto E(h,\varphi ,\lambda ) |\det (h)|^s$
defined in [Reference Ichino and YamanaIY15]. By [Reference Ichino and YamanaIY15, theorem 1.1], we deduce that (4.2.5.1) is equal to
$h\mapsto E(h,\varphi ,\lambda ) |\det (h)|^s$
defined in [Reference Ichino and YamanaIY15]. By [Reference Ichino and YamanaIY15, theorem 1.1], we deduce that (4.2.5.1) is equal to
![]() $Z^{\mathrm {RS}}(s, W(\varphi ,\lambda ))$
. It suffices to take
$Z^{\mathrm {RS}}(s, W(\varphi ,\lambda ))$
. It suffices to take
![]() $s=0$
to get the result.
$s=0$
to get the result.
4.2.6
Proposition 4.2.6.1. For any
![]() $\varphi \in \mathcal {A}_{P,\pi }(G)$
, we have
$\varphi \in \mathcal {A}_{P,\pi }(G)$
, we have
Proof. This is the proof of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, proposition 8.1.2.1]), the main assumption there being that
![]() $(M,\pi )$
is regular.
$(M,\pi )$
is regular.
4.2.7
Proposition 4.2.7.1. For any
![]() $\varphi \in \mathcal {A}_{P,\pi }(G)$
, we have
$\varphi \in \mathcal {A}_{P,\pi }(G)$
, we have
Proof. We shall follow the notations of §§4.1.4 and 4.1.5. Let
![]() $\lambda \in \mathfrak {a}_{M,\mathbb {C}}^{L,*}$
. For all
$\lambda \in \mathfrak {a}_{M,\mathbb {C}}^{L,*}$
. For all
![]() $\varphi \in \mathcal {A}_{P,\operatorname {\mathrm {cusp}}}(G)$
, we have the Eisenstein series
$\varphi \in \mathcal {A}_{P,\operatorname {\mathrm {cusp}}}(G)$
, we have the Eisenstein series
![]() $E^Q(\varphi ,\lambda )$
defined in (2.2.4.1), and we set for all
$E^Q(\varphi ,\lambda )$
defined in (2.2.4.1), and we set for all
![]() $g\in G(\mathbb {A})$
,
$g\in G(\mathbb {A})$
,
Let
![]() $\mathcal {P}_L$
the mirabolic subgroup of L (defined as the product of the mirabolic subgroups of its factors in the decomposition into a product of general linear groups). We set
$\mathcal {P}_L$
the mirabolic subgroup of L (defined as the product of the mirabolic subgroups of its factors in the decomposition into a product of general linear groups). We set
![]() $\mathcal {P}_{L'}=\mathcal {P}_L\cap L'$
. Let
$\mathcal {P}_{L'}=\mathcal {P}_L\cap L'$
. Let
![]() $\mathrm {As}_{L_n}$
(resp.
$\mathrm {As}_{L_n}$
(resp.
![]() $\mathrm {As}_{L_{n+1}}$
) be the tensor product of
$\mathrm {As}_{L_{n+1}}$
) be the tensor product of
![]() $\mathrm {As}^{(-1)^{n+1}}$
(resp.
$\mathrm {As}^{(-1)^{n+1}}$
(resp.
![]() $\mathrm {As}^{(-1)^{n}}$
) for each factor in the decomposition of
$\mathrm {As}^{(-1)^{n}}$
) for each factor in the decomposition of
![]() $L_n$
, resp.
$L_n$
, resp.
![]() $L_{n+1}$
, into a product of general linear groups. Let
$L_{n+1}$
, into a product of general linear groups. Let
![]() $\mathrm {As}_L=\mathrm {As}_{L_n}\boxtimes \mathrm {As}_{L_{n+1}}$
. Let
$\mathrm {As}_L=\mathrm {As}_{L_n}\boxtimes \mathrm {As}_{L_{n+1}}$
. Let
![]() $\Pi ^Q_\lambda =\operatorname {\mathrm {Ind}}_{P(\mathbb {A})}^{Q(\mathbb {A})}(\pi _\lambda )$
be the induced representation. It follows from our hypothesis on
$\Pi ^Q_\lambda =\operatorname {\mathrm {Ind}}_{P(\mathbb {A})}^{Q(\mathbb {A})}(\pi _\lambda )$
be the induced representation. It follows from our hypothesis on
![]() $\pi $
and from [Reference FlickerFli92, proposition 2.6] that
$\pi $
and from [Reference FlickerFli92, proposition 2.6] that
![]() $\Pi ^Q_\lambda $
is
$\Pi ^Q_\lambda $
is
![]() $(L',\eta _{G'})$
-distinguished.
$(L',\eta _{G'})$
-distinguished.
Let
![]() $\varphi \in \mathcal {A}_{P,\pi }(G)$
. First, by Lemma 4.1.5.1, we have
$\varphi \in \mathcal {A}_{P,\pi }(G)$
. First, by Lemma 4.1.5.1, we have
where
![]() $\varphi ^{K'}$
is defined in (4.1.5.5). Then using [Reference ZhangZha14a, proposition 3.2], [Reference FlickerFli88] and Theorem 5.5.1.1 in section 5 below, we can compute the intertwining period
$\varphi ^{K'}$
is defined in (4.1.5.5). Then using [Reference ZhangZha14a, proposition 3.2], [Reference FlickerFli88] and Theorem 5.5.1.1 in section 5 below, we can compute the intertwining period
![]() $J^L(\xi ,\varphi ^{K'},\lambda )$
in terms of
$J^L(\xi ,\varphi ^{K'},\lambda )$
in terms of
![]() $W_L$
: we deduce that, for S a large enough set of places,
$W_L$
: we deduce that, for S a large enough set of places,
![]() $J(\xi ,\varphi ,\lambda )$
is equal to
$J(\xi ,\varphi ,\lambda )$
is equal to
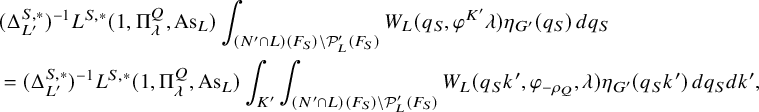 $$ \begin{align*} &(\Delta_{L'}^{S,*})^{-1} L^{S,*}(1,\Pi^Q_\lambda,\mathrm{As}_{L}) \int_{(N'\cap L)(F_S)\backslash \mathcal{P}^{\prime}_L(F_S)} {W}_L(q_S ,\varphi^{K'}\lambda) \eta_{G'}(q_S ) \, dq_S\\ &=(\Delta_{L'}^{S,*})^{-1} L^{S,*}(1,\Pi^Q_\lambda,\mathrm{As}_{L}) \int_{K'} \int_{(N'\cap L)(F_S)\backslash \mathcal{P}^{\prime}_L(F_S)} {W}_L(q_S k',\varphi_{-\rho_Q},\lambda) \eta_{G'}(q_S k') \, dq_Sdk', \end{align*} $$
$$ \begin{align*} &(\Delta_{L'}^{S,*})^{-1} L^{S,*}(1,\Pi^Q_\lambda,\mathrm{As}_{L}) \int_{(N'\cap L)(F_S)\backslash \mathcal{P}^{\prime}_L(F_S)} {W}_L(q_S ,\varphi^{K'}\lambda) \eta_{G'}(q_S ) \, dq_S\\ &=(\Delta_{L'}^{S,*})^{-1} L^{S,*}(1,\Pi^Q_\lambda,\mathrm{As}_{L}) \int_{K'} \int_{(N'\cap L)(F_S)\backslash \mathcal{P}^{\prime}_L(F_S)} {W}_L(q_S k',\varphi_{-\rho_Q},\lambda) \eta_{G'}(q_S k') \, dq_Sdk', \end{align*} $$
where
![]() $\varphi (g)=\exp (-\rho _Q,H_Q(g)\rangle )\varphi (g)$
. For
$\varphi (g)=\exp (-\rho _Q,H_Q(g)\rangle )\varphi (g)$
. For
![]() $g\in G(F_S)$
, set
$g\in G(F_S)$
, set
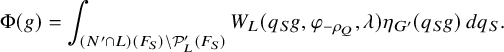 $$ \begin{align*} \Phi(g)= \int_{(N'\cap L)(F_S)\backslash \mathcal{P}^{\prime}_L(F_S)} {W}_L(q_S g,\varphi_{-\rho_Q},\lambda) \eta_{G'}(q_S g) \, dq_S. \end{align*} $$
$$ \begin{align*} \Phi(g)= \int_{(N'\cap L)(F_S)\backslash \mathcal{P}^{\prime}_L(F_S)} {W}_L(q_S g,\varphi_{-\rho_Q},\lambda) \eta_{G'}(q_S g) \, dq_S. \end{align*} $$
The map
![]() $\Phi $
is left-invariant by
$\Phi $
is left-invariant by
![]() $L'(F_S)$
as follows from the first assertion of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, theorem 9.1.7.1]. We deduce that it is also left-invariant by
$L'(F_S)$
as follows from the first assertion of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, theorem 9.1.7.1]. We deduce that it is also left-invariant by
![]() $Q'(F_S)$
. Using the equality (4.1.2.1), we get that
$Q'(F_S)$
. Using the equality (4.1.2.1), we get that
![]() $J(\xi ,\varphi ,\lambda )$
is equal to
$J(\xi ,\varphi ,\lambda )$
is equal to
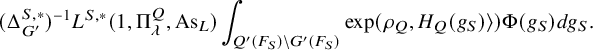 $$ \begin{align*} (\Delta_{G'}^{S,*})^{-1}L^{S,*}(1,\Pi^Q_\lambda,\mathrm{As}_{L}) \int_{Q'(F_S)\backslash G'(F_S)} \exp(\rho_Q,H_Q(g_S)\rangle) \Phi(g_S)dg_S. \end{align*} $$
$$ \begin{align*} (\Delta_{G'}^{S,*})^{-1}L^{S,*}(1,\Pi^Q_\lambda,\mathrm{As}_{L}) \int_{Q'(F_S)\backslash G'(F_S)} \exp(\rho_Q,H_Q(g_S)\rangle) \Phi(g_S)dg_S. \end{align*} $$
Now we can appeal to the equality of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, theorem 9.1.7.1] to get that the last line is equal to
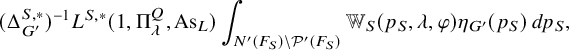 $$ \begin{align*} (\Delta_{G'}^{S,*})^{-1}L^{S,*}(1,\Pi^Q_\lambda,\mathrm{As}_{L}) \int_{N'(F_S)\backslash\mathcal{P}'(F_S)}\mathbb{W}_S(p_S,\lambda,\varphi)\eta_{G'}(p_S ) \, dp_S, \end{align*} $$
$$ \begin{align*} (\Delta_{G'}^{S,*})^{-1}L^{S,*}(1,\Pi^Q_\lambda,\mathrm{As}_{L}) \int_{N'(F_S)\backslash\mathcal{P}'(F_S)}\mathbb{W}_S(p_S,\lambda,\varphi)\eta_{G'}(p_S ) \, dp_S, \end{align*} $$
where
![]() $\mathbb {W}_S(g_S,\lambda ,\varphi )$
stands for the Jacquet integral given by the value at
$\mathbb {W}_S(g_S,\lambda ,\varphi )$
stands for the Jacquet integral given by the value at
![]() $s=0$
of the holomorphic continuation of the integral:
$s=0$
of the holomorphic continuation of the integral:
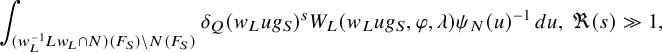 $$ \begin{align*} \int_{ (w_L^{-1}L w_L\cap N)(F_S) \backslash N(F_S) } \delta_Q(w_L u g_S)^{s} {W}_L(w_Lu g_S ,\varphi,\lambda) \psi_N(u)^{-1}\,du , \ \Re(s)\gg 1, \end{align*} $$
$$ \begin{align*} \int_{ (w_L^{-1}L w_L\cap N)(F_S) \backslash N(F_S) } \delta_Q(w_L u g_S)^{s} {W}_L(w_Lu g_S ,\varphi,\lambda) \psi_N(u)^{-1}\,du , \ \Re(s)\gg 1, \end{align*} $$
where
![]() $w_L$
is the permutation matrix that represents the product of the longest elements respectively of the Weyl groups of L and of G. To conclude, it suffices to observe that for any
$w_L$
is the permutation matrix that represents the product of the longest elements respectively of the Weyl groups of L and of G. To conclude, it suffices to observe that for any
![]() $g_S\in G(\mathbb {A}_S)$
,
$g_S\in G(\mathbb {A}_S)$
,
Indeed, this follows from computations of [Reference ShahidiSha81, section 4] and the fact that the functions
![]() $L^{S}(s,\Pi ^Q_\lambda ,\mathrm {As}_{L})$
and
$L^{S}(s,\Pi ^Q_\lambda ,\mathrm {As}_{L})$
and
![]() $L^{S}(s,\Pi _\lambda ,\mathrm {As}) $
have a pole of same order at
$L^{S}(s,\Pi _\lambda ,\mathrm {As}) $
have a pole of same order at
![]() $s=1$
since the cuspidal datum associated to
$s=1$
since the cuspidal datum associated to
![]() $(M,\pi )$
is G-regular and Hermitian.
$(M,\pi )$
is G-regular and Hermitian.
4.2.8
Let
![]() $\mathcal {B}_{P,\pi }$
be a K-basis of
$\mathcal {B}_{P,\pi }$
be a K-basis of
![]() $\mathcal {A}_{P,\pi }(G)$
. For any
$\mathcal {A}_{P,\pi }(G)$
. For any
![]() $f\in \mathcal {S}(G(\mathbb {A}))$
, we define
$f\in \mathcal {S}(G(\mathbb {A}))$
, we define
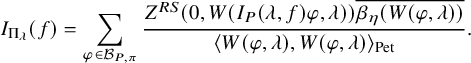 $$ \begin{align} I_{\Pi_\lambda}(f)=\sum_{\varphi\in \mathcal{B}_{P,\pi}} \frac{Z^{RS}(0, W(I_P(\lambda,f)\varphi,\lambda)) \overline{\beta_\eta(W(\varphi,\lambda))} }{ \langle W(\varphi,\lambda),W(\varphi,\lambda)\rangle_{\operatorname{\mathrm{Pet}}}}. \end{align} $$
$$ \begin{align} I_{\Pi_\lambda}(f)=\sum_{\varphi\in \mathcal{B}_{P,\pi}} \frac{Z^{RS}(0, W(I_P(\lambda,f)\varphi,\lambda)) \overline{\beta_\eta(W(\varphi,\lambda))} }{ \langle W(\varphi,\lambda),W(\varphi,\lambda)\rangle_{\operatorname{\mathrm{Pet}}}}. \end{align} $$
Theorem 4.2.8.1.
-
1. The series (4.2.8.1) converges, does not depend on the choice of
 $\mathcal {B}_{P,\pi }$
and defines a continuous distribution on
$\mathcal {B}_{P,\pi }$
and defines a continuous distribution on
 $\mathcal {S}(G(\mathbb {A}))$
.
$\mathcal {S}(G(\mathbb {A}))$
. -
2. We have
 $I_{\Pi _\lambda }(f)=I_{P,\pi }(\lambda ,f)$
.
$I_{\Pi _\lambda }(f)=I_{P,\pi }(\lambda ,f)$
.
5 Intertwining periods and Whittaker functions
5.1 Notations
5.1.1
We follow the notations of §4.1.1. However, in this section, we set
![]() $G=G_{2n}$
and
$G=G_{2n}$
and
![]() $G'=G^{\prime }_{2n}$
. Let
$G'=G^{\prime }_{2n}$
. Let
![]() $P=MN$
be the maximal standard parabolic subgroup of G where its standard Levi factor M is
$P=MN$
be the maximal standard parabolic subgroup of G where its standard Levi factor M is
![]() $G_n\times G_n$
. Let
$G_n\times G_n$
. Let
![]() $\sigma $
be an irreducible cuspidal automorphic representation of
$\sigma $
be an irreducible cuspidal automorphic representation of
![]() $G_n$
with central character trivial on
$G_n$
with central character trivial on
![]() $A_{G_n}^\infty $
. Let
$A_{G_n}^\infty $
. Let
![]() $\pi =\sigma \boxtimes \sigma ^*$
: this a cuspidal representation of M.
$\pi =\sigma \boxtimes \sigma ^*$
: this a cuspidal representation of M.
5.1.2
We set
and the subset of involutions
We have the following lemma:
Lemma 5.1.2.1. (Jacquet-Lapid-Rogawski, see [Reference Jacquet, Lapid and RogawskiJLR99, proposition 20]). Any double coset in
![]() $P(F)\backslash G(F)/ G'(F)$
has a representative
$P(F)\backslash G(F)/ G'(F)$
has a representative
![]() $\tilde \xi $
such that
$\tilde \xi $
such that
![]() $\xi =\tilde \xi c(\tilde \xi )^{-1}$
belongs to
$\xi =\tilde \xi c(\tilde \xi )^{-1}$
belongs to
![]() $\, _PW_{P,2}$
. The map
$\, _PW_{P,2}$
. The map
![]() $P(F)\tilde \xi G'(F) \mapsto \xi $
is well defined and induces a bijection from
$P(F)\tilde \xi G'(F) \mapsto \xi $
is well defined and induces a bijection from
![]() $P(F)\backslash G(F)/ G'(F)$
onto
$P(F)\backslash G(F)/ G'(F)$
onto
![]() $ _PW_{P,2}$
.
$ _PW_{P,2}$
.
For any
![]() $\tilde \xi \in G(F)$
such that
$\tilde \xi \in G(F)$
such that
![]() $\tilde \xi c(\tilde \xi )^{-1}$
belongs to
$\tilde \xi c(\tilde \xi )^{-1}$
belongs to
![]() $\, _PW_{P,2}$
, we set
$\, _PW_{P,2}$
, we set
![]() $ P_{\tilde \xi }=G'\cap \tilde \xi ^{-1}P \tilde \xi $
and
$ P_{\tilde \xi }=G'\cap \tilde \xi ^{-1}P \tilde \xi $
and
![]() $M_{\tilde \xi }=G'\cap \tilde \xi ^{-1}M \tilde \xi $
. Note that
$M_{\tilde \xi }=G'\cap \tilde \xi ^{-1}M \tilde \xi $
. Note that
![]() $M_{\tilde \xi }$
is a Levi factor of
$M_{\tilde \xi }$
is a Levi factor of
![]() $P_{\tilde \xi }$
.
$P_{\tilde \xi }$
.
5.1.3
We fix
![]() $\tau \in E$
such that
$\tau \in E$
such that
![]() $c(\tau )=-\tau $
. Let
$c(\tau )=-\tau $
. Let
 $$ \begin{align*} \tilde\xi_0= \begin{pmatrix} I_n & \tau I_n\\ I_n & -\tau I_n \end{pmatrix} \text{ and } \xi_0=\tilde\xi_0 c(\tilde\xi_0)^{-1}. \end{align*} $$
$$ \begin{align*} \tilde\xi_0= \begin{pmatrix} I_n & \tau I_n\\ I_n & -\tau I_n \end{pmatrix} \text{ and } \xi_0=\tilde\xi_0 c(\tilde\xi_0)^{-1}. \end{align*} $$
We have
![]() $\xi _0\in \, _PW_{P,2}$
and
$\xi _0\in \, _PW_{P,2}$
and
![]() $ P_{\tilde \xi _0}=M_{\tilde \xi _0}$
.
$ P_{\tilde \xi _0}=M_{\tilde \xi _0}$
.
Let
![]() $\varphi \in \mathcal {A}_{P,\pi }(G)$
. For any
$\varphi \in \mathcal {A}_{P,\pi }(G)$
. For any
![]() $\lambda \in \mathfrak {a}_{P,\mathbb {C}}^{G,*}$
, we consider the intertwining period (due to Jacquet-Lapid-Rogawski; see [Reference Jacquet, Lapid and RogawskiJLR99])
$\lambda \in \mathfrak {a}_{P,\mathbb {C}}^{G,*}$
, we consider the intertwining period (due to Jacquet-Lapid-Rogawski; see [Reference Jacquet, Lapid and RogawskiJLR99])
 $$ \begin{align} J(\xi_0,\varphi,\lambda)=\int_{ A_{M_{\tilde \xi_0}}^\infty M_{\tilde\xi_0}(F) \backslash G'(\mathbb{A})} \exp(\langle \lambda,H_P(\tilde\xi h)\rangle) \varphi(\tilde\xi h)\,dh. \end{align} $$
$$ \begin{align} J(\xi_0,\varphi,\lambda)=\int_{ A_{M_{\tilde \xi_0}}^\infty M_{\tilde\xi_0}(F) \backslash G'(\mathbb{A})} \exp(\langle \lambda,H_P(\tilde\xi h)\rangle) \varphi(\tilde\xi h)\,dh. \end{align} $$
Note that we have
![]() $A_{M_{\tilde \xi _0}}^\infty =A_{G'}^\infty $
. Let
$A_{M_{\tilde \xi _0}}^\infty =A_{G'}^\infty $
. Let
![]() $\alpha $
be the unique root in
$\alpha $
be the unique root in
![]() $\Delta _P$
. The integral above is absolutely convergent if
$\Delta _P$
. The integral above is absolutely convergent if
![]() $\Re (\langle \alpha ,\lambda \rangle )\gg 0$
. Moreover, it admits a meromorphic continuation to
$\Re (\langle \alpha ,\lambda \rangle )\gg 0$
. Moreover, it admits a meromorphic continuation to
![]() $\mathfrak {a}_{P,\mathbb {C}}^{G,*}$
; see [Reference Jacquet, Lapid and RogawskiJLR99, theorem 23].
$\mathfrak {a}_{P,\mathbb {C}}^{G,*}$
; see [Reference Jacquet, Lapid and RogawskiJLR99, theorem 23].
5.2 Epstein series and intertwining periods
5.2.1
The group G acts on the right on the space of rows of size
![]() $2n$
(identified to
$2n$
(identified to
![]() $E^{2n}$
). Let
$E^{2n}$
). Let
![]() $\mathcal {P}$
be the stabilizer of
$\mathcal {P}$
be the stabilizer of
![]() $e_{2n}=(0,\ldots ,0,1)$
. Let
$e_{2n}=(0,\ldots ,0,1)$
. Let
![]() $\mathcal {P}'=\mathcal {P}\cap G'$
.
$\mathcal {P}'=\mathcal {P}\cap G'$
.
Let
![]() $\Phi \in \mathcal {S}(\mathbb {A}^{2n})$
. For any
$\Phi \in \mathcal {S}(\mathbb {A}^{2n})$
. For any
![]() $s\in \mathbb {C}$
such that
$s\in \mathbb {C}$
such that
![]() $\Re (s)>1$
and any
$\Re (s)>1$
and any
![]() $h\in [G']$
, the Epstein series is defined by the following absolutely convergent integral:
$h\in [G']$
, the Epstein series is defined by the following absolutely convergent integral:
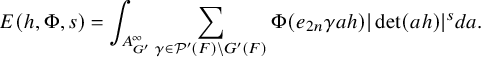 $$ \begin{align*} E(h,\Phi,s)=\int_{A_{G'}^\infty} \sum_{\gamma\in \mathcal{P}'(F)\backslash G'(F)} \Phi(e_{2n}\gamma ah) |\det(ah)|^s da. \end{align*} $$
$$ \begin{align*} E(h,\Phi,s)=\int_{A_{G'}^\infty} \sum_{\gamma\in \mathcal{P}'(F)\backslash G'(F)} \Phi(e_{2n}\gamma ah) |\det(ah)|^s da. \end{align*} $$
Here,
![]() $|\cdot |$
is the product over all places v of F of normalized absolute values of the completions
$|\cdot |$
is the product over all places v of F of normalized absolute values of the completions
![]() $F_v$
. The map
$F_v$
. The map
![]() $s\mapsto E(\Phi ,s)$
extends to a meromorphic function valued in
$s\mapsto E(\Phi ,s)$
extends to a meromorphic function valued in
![]() $\mathcal {T}([G'])$
with simple poles at
$\mathcal {T}([G'])$
with simple poles at
![]() $s=0$
,
$s=0$
,
![]() $1$
of respective residues
$1$
of respective residues
![]() $\Phi (0)$
and
$\Phi (0)$
and
![]() $\widehat {\Phi }(0)$
(cf. [Reference Jacquet and ShalikaJS81b, Lemma 4.2]).
$\widehat {\Phi }(0)$
(cf. [Reference Jacquet and ShalikaJS81b, Lemma 4.2]).
5.2.2
Let
![]() $\tilde \xi \in G(F)$
such that
$\tilde \xi \in G(F)$
such that
![]() $\xi =\tilde \xi c(\tilde \xi )^{-1}$
belongs to
$\xi =\tilde \xi c(\tilde \xi )^{-1}$
belongs to
![]() $\, _PW_{P,2}$
. We assume also
$\, _PW_{P,2}$
. We assume also
![]() $\xi \not =1$
. Let
$\xi \not =1$
. Let
![]() $\varphi \in \mathcal {A}_{P,\pi }(G)$
. We define
$\varphi \in \mathcal {A}_{P,\pi }(G)$
. We define
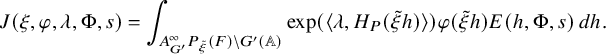 $$ \begin{align} J(\xi,\varphi,\lambda,\Phi,s)=\int_{ A_{G'}^\infty P_{\tilde\xi}(F) \backslash G'(\mathbb{A})} \exp(\langle \lambda,H_P(\tilde\xi h)\rangle) \varphi(\tilde\xi h) E(h,\Phi,s)\,dh. \end{align} $$
$$ \begin{align} J(\xi,\varphi,\lambda,\Phi,s)=\int_{ A_{G'}^\infty P_{\tilde\xi}(F) \backslash G'(\mathbb{A})} \exp(\langle \lambda,H_P(\tilde\xi h)\rangle) \varphi(\tilde\xi h) E(h,\Phi,s)\,dh. \end{align} $$
If it is well defined, this integral does not depend on
![]() $\tilde \xi $
provided that we have
$\tilde \xi $
provided that we have
![]() $\xi =\tilde \xi c(\tilde \xi )^{-1}$
, hence the notation.
$\xi =\tilde \xi c(\tilde \xi )^{-1}$
, hence the notation.
Proposition 5.2.2.1. Assume
![]() $\xi \not =1$
.
$\xi \not =1$
.
-
1. There exists
 $r>0$
such that for each for any
$r>0$
such that for each for any
 $\lambda $
in the domain, and any
$\lambda $
in the domain, and any $$ \begin{align*}\mathcal{D}_r=\{\lambda\in \mathfrak{a}_{P,\mathbb{C}}^{G,*} \mid \Re(\langle \lambda,\alpha^\vee\rangle)>r\},\end{align*} $$
$$ \begin{align*}\mathcal{D}_r=\{\lambda\in \mathfrak{a}_{P,\mathbb{C}}^{G,*} \mid \Re(\langle \lambda,\alpha^\vee\rangle)>r\},\end{align*} $$
 $s\in \mathbb {C}\setminus \{0,1\}$
the integral (5.2.2.1) converges absolutely. It also converges uniformly for
$s\in \mathbb {C}\setminus \{0,1\}$
the integral (5.2.2.1) converges absolutely. It also converges uniformly for
 $\Re (\lambda )$
in a compact subset of
$\Re (\lambda )$
in a compact subset of
 $\mathcal {D}_r$
and s in a compact subset of
$\mathcal {D}_r$
and s in a compact subset of
 $\mathbb {C}\setminus \{0,1\}$
.
$\mathbb {C}\setminus \{0,1\}$
.
-
2. The map
 $(\lambda ,s)\mapsto J(\xi ,\varphi ,\lambda ,\Phi ,s)$
is holomorphic on
$(\lambda ,s)\mapsto J(\xi ,\varphi ,\lambda ,\Phi ,s)$
is holomorphic on
 $ \mathcal {D}_r \times \mathbb {C}\setminus \{0,1\}$
.
$ \mathcal {D}_r \times \mathbb {C}\setminus \{0,1\}$
. -
3. If
 $\xi \not =\xi _0$
, the map has a holomorphic extension to
$\xi \not =\xi _0$
, the map has a holomorphic extension to
 $\mathcal {D}_r \times \mathbb {C}$
.
$\mathcal {D}_r \times \mathbb {C}$
. -
4. If
 $\xi =\xi _0$
, the map has simple poles at
$\xi =\xi _0$
, the map has simple poles at
 $s=0,1$
with respective residues:
$s=0,1$
with respective residues:  $$ \begin{align*} \Phi(0) J(\xi_0,\varphi,\lambda) \text{ and } \hat\Phi(0) J(\xi_0,\varphi,\lambda). \end{align*} $$
$$ \begin{align*} \Phi(0) J(\xi_0,\varphi,\lambda) \text{ and } \hat\Phi(0) J(\xi_0,\varphi,\lambda). \end{align*} $$
Proof. We fix a compact subset
![]() $\Omega $
of
$\Omega $
of
![]() $\mathbb {C}$
. We can write
$\mathbb {C}$
. We can write
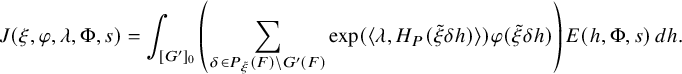 $$ \begin{align*} J(\xi,\varphi,\lambda,\Phi,s)=\int_{ [G']_0} \left(\sum_{ \delta \in P_{\tilde\xi}(F) \backslash G'(F) } \exp(\langle \lambda,H_P(\tilde\xi \delta h)\rangle) \varphi(\tilde\xi \delta h) \right) E(h,\Phi,s)\,dh. \end{align*} $$
$$ \begin{align*} J(\xi,\varphi,\lambda,\Phi,s)=\int_{ [G']_0} \left(\sum_{ \delta \in P_{\tilde\xi}(F) \backslash G'(F) } \exp(\langle \lambda,H_P(\tilde\xi \delta h)\rangle) \varphi(\tilde\xi \delta h) \right) E(h,\Phi,s)\,dh. \end{align*} $$
We shall use the following two facts:
-
• there exist
 $C,t>0$
such that for all
$C,t>0$
such that for all
 $h\in G'(\mathbb {A})^1$
and
$h\in G'(\mathbb {A})^1$
and
 $s\in \Omega $
, (5.2.2.2)
$s\in \Omega $
, (5.2.2.2) $$ \begin{align} |s(s-1)E(h,\Phi,s)| \leqslant C \|h\|_{G'}^t. \end{align} $$
$$ \begin{align} |s(s-1)E(h,\Phi,s)| \leqslant C \|h\|_{G'}^t. \end{align} $$
-
• there exists
 $r>0$
such that for any
$r>0$
such that for any
 $t>0$
and any
$t>0$
and any
 $\lambda \in \mathcal {D}_r$
, there exists
$\lambda \in \mathcal {D}_r$
, there exists
 $C>0$
such that for all
$C>0$
such that for all
 $h\in G'(\mathbb {A})^1$
, (5.2.2.3)
$h\in G'(\mathbb {A})^1$
, (5.2.2.3) $$ \begin{align} \sum_{ \delta \in P_{\tilde\xi}(F) \backslash G'(F) } |\exp(\langle \lambda,H_P(\tilde\xi \delta h)\rangle) \varphi(\tilde\xi \delta h)| \leqslant C \|h\|_{G'}^{-t}. \end{align} $$
$$ \begin{align} \sum_{ \delta \in P_{\tilde\xi}(F) \backslash G'(F) } |\exp(\langle \lambda,H_P(\tilde\xi \delta h)\rangle) \varphi(\tilde\xi \delta h)| \leqslant C \|h\|_{G'}^{-t}. \end{align} $$
Moreover, in (5.2.2.3), the constant C may be chosen uniformly for
![]() $\lambda $
such that
$\lambda $
such that
![]() $\Re (\lambda )$
belongs to a compact subset of
$\Re (\lambda )$
belongs to a compact subset of
![]() $\mathcal {D}_r$
. This can be extracted from the proof of [Reference Jacquet, Lapid and RogawskiJLR99, theorem 23], more precisely from the combination of proposition 24 and the lines following (58) of [Reference Jacquet, Lapid and RogawskiJLR99].
$\mathcal {D}_r$
. This can be extracted from the proof of [Reference Jacquet, Lapid and RogawskiJLR99, theorem 23], more precisely from the combination of proposition 24 and the lines following (58) of [Reference Jacquet, Lapid and RogawskiJLR99].
We get the holomorphic continuation with at most simple poles at
![]() $s=0,1$
. Up to a factor
$s=0,1$
. Up to a factor
![]() $\Phi (0) $
or
$\Phi (0) $
or
![]() $\hat \Phi (0) $
, the residue is given by
$\hat \Phi (0) $
, the residue is given by
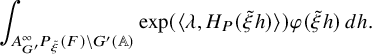 $$ \begin{align*} \int_{ A_{G'}^\infty P_{\tilde\xi}(F) \backslash G'(\mathbb{A})} \exp(\langle \lambda,H_P(\tilde\xi h)\rangle) \varphi(\tilde\xi h) \,dh. \end{align*} $$
$$ \begin{align*} \int_{ A_{G'}^\infty P_{\tilde\xi}(F) \backslash G'(\mathbb{A})} \exp(\langle \lambda,H_P(\tilde\xi h)\rangle) \varphi(\tilde\xi h) \,dh. \end{align*} $$
This integral converges absolutely thanks to the majorization (5.2.2.3). According to the proof of [Reference Jacquet, Lapid and RogawskiJLR99, theorem 23], the integral vanishes unless
![]() $\xi =\xi _0$
. In this case, the integral is nothing else but
$\xi =\xi _0$
. In this case, the integral is nothing else but
![]() $J(\xi _0,\varphi ,\lambda )$
.
$J(\xi _0,\varphi ,\lambda )$
.
5.3 Period of a pseudo-Eisenstein series: first computation
5.3.1
Let
![]() $\omega $
be the central character of
$\omega $
be the central character of
![]() $\pi $
. By restriction, it induces a unitary character of
$\pi $
. By restriction, it induces a unitary character of
![]() $Z_G'(\mathbb {A})$
. Let
$Z_G'(\mathbb {A})$
. Let
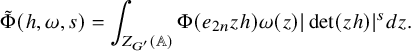 $$ \begin{align*} \tilde\Phi(h,\omega, s)=\int_{Z_{G'}(\mathbb{A})} \Phi(e_{2n} zh) \omega(z) |\det(zh)|^s dz. \end{align*} $$
$$ \begin{align*} \tilde\Phi(h,\omega, s)=\int_{Z_{G'}(\mathbb{A})} \Phi(e_{2n} zh) \omega(z) |\det(zh)|^s dz. \end{align*} $$
The integral is convergent for
![]() $\Re (s)>\frac 1n$
. Let
$\Re (s)>\frac 1n$
. Let
![]() $P^{\prime }_1=\mathcal {P}' Z_{G'}$
. This is a parabolic subgroup of
$P^{\prime }_1=\mathcal {P}' Z_{G'}$
. This is a parabolic subgroup of
![]() $G'$
of type
$G'$
of type
![]() $(2n-1,1)$
. Then we have
$(2n-1,1)$
. Then we have
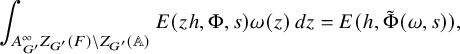 $$ \begin{align*} \int_{A_{G'}^\infty Z_{G'}(F) \backslash Z_{G'}(\mathbb{A})} E(zh,\Phi,s)\omega(z)\, dz=E(h,\tilde\Phi(\omega, s)), \end{align*} $$
$$ \begin{align*} \int_{A_{G'}^\infty Z_{G'}(F) \backslash Z_{G'}(\mathbb{A})} E(zh,\Phi,s)\omega(z)\, dz=E(h,\tilde\Phi(\omega, s)), \end{align*} $$
where
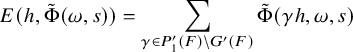 $$ \begin{align*} E(h,\tilde\Phi(\omega, s))= \sum_{\gamma\in P_1^{\prime}(F)\backslash G'(F)} \tilde\Phi(\gamma h,\omega, s) \end{align*} $$
$$ \begin{align*} E(h,\tilde\Phi(\omega, s))= \sum_{\gamma\in P_1^{\prime}(F)\backslash G'(F)} \tilde\Phi(\gamma h,\omega, s) \end{align*} $$
is a usual Eisenstein series, which is convergent for
![]() $\Re (s)>1$
. By the classical computation of the constant term of an Eisenstein series, there exist a finite set I and families
$\Re (s)>1$
. By the classical computation of the constant term of an Eisenstein series, there exist a finite set I and families
![]() $(\varphi _{i,s})_{i\in I}\in \mathcal {A}_{P'}(G')^I$
and
$(\varphi _{i,s})_{i\in I}\in \mathcal {A}_{P'}(G')^I$
and
![]() $(\mu _{i,s})_{i\in I} \in \mathfrak {a}_{P,\mathbb {C}}^{G,*}$
for any
$(\mu _{i,s})_{i\in I} \in \mathfrak {a}_{P,\mathbb {C}}^{G,*}$
for any
![]() $s\in \mathbb {C}$
such that the following conditions are satisfied for any
$s\in \mathbb {C}$
such that the following conditions are satisfied for any
![]() $i\in I$
:
$i\in I$
:
-
• the map
 $s\mapsto \mu _{i,s}$
is affine;
$s\mapsto \mu _{i,s}$
is affine; -
• the map
 $s\mapsto \varphi _{i,s}$
is a meromorphic function;
$s\mapsto \varphi _{i,s}$
is a meromorphic function; -
• we have
 $\varphi _{i,s}(ah)=\varphi _{i,s}(h)$
for any
$\varphi _{i,s}(ah)=\varphi _{i,s}(h)$
for any
 $h\in G'(\mathbb {A})$
and
$h\in G'(\mathbb {A})$
and
 $a\in A_{M'}^{\infty }$
;
$a\in A_{M'}^{\infty }$
; -
• we have for any
 $a\in A_{M'}^{\infty }$
,
$a\in A_{M'}^{\infty }$
,
 $m\in M'(\mathbb {A})^1$
and
$m\in M'(\mathbb {A})^1$
and
 $k\in K'$
, (5.3.1.1)
$k\in K'$
, (5.3.1.1) $$ \begin{align} \int_{[N_{P'}]} E(namk ,\tilde\Phi(\omega, s))dn= \sum_{i\in I} \varphi_{i,s}(mk) \exp(\langle \mu_{i,s},H_{P}(a)\rangle). \end{align} $$
$$ \begin{align} \int_{[N_{P'}]} E(namk ,\tilde\Phi(\omega, s))dn= \sum_{i\in I} \varphi_{i,s}(mk) \exp(\langle \mu_{i,s},H_{P}(a)\rangle). \end{align} $$
5.3.2
We shall simply say that a map
![]() $\beta :\mathfrak {a}_{P,\mathbb {C}}^{G,*}\to \mathbb {C}$
is a Paley-Wiener function if it is given by the Fourier-Laplace transform of a compactly supported smooth function on
$\beta :\mathfrak {a}_{P,\mathbb {C}}^{G,*}\to \mathbb {C}$
is a Paley-Wiener function if it is given by the Fourier-Laplace transform of a compactly supported smooth function on
![]() $\mathfrak {a}_P^{G,*}$
.
$\mathfrak {a}_P^{G,*}$
.
5.3.3
In the following, we consider the following objects:
-
•
 $\beta $
a Paley-Wiener function;
$\beta $
a Paley-Wiener function; -
•
 $f\in C_c^\infty (G(F_\infty ))$
a decomposable function;
$f\in C_c^\infty (G(F_\infty ))$
a decomposable function; -
•
 $\kappa \in \mathfrak {a}_P^*$
;
$\kappa \in \mathfrak {a}_P^*$
; -
•
 $\varphi \in \mathcal {A}_{P,\pi }(G)$
.
$\varphi \in \mathcal {A}_{P,\pi }(G)$
.
From these, one defines the pseudo-Eisenstein series
where B is the function on
![]() $A_G^\infty N(\mathbb {A})M(F)\backslash G(\mathbb {A})$
given by
$A_G^\infty N(\mathbb {A})M(F)\backslash G(\mathbb {A})$
given by
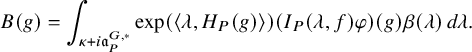 $$ \begin{align*} B(g)= \int_{ \kappa+i\mathfrak{a}_P^{G,*}} \exp(\langle \lambda,H_P(g)\rangle) (I_P(\lambda,f)\varphi)(g) \beta(\lambda) \,d\lambda. \end{align*} $$
$$ \begin{align*} B(g)= \int_{ \kappa+i\mathfrak{a}_P^{G,*}} \exp(\langle \lambda,H_P(g)\rangle) (I_P(\lambda,f)\varphi)(g) \beta(\lambda) \,d\lambda. \end{align*} $$
In the following, we shall assume that
![]() $\kappa $
is in the region of convergence of the Eisenstein series
$\kappa $
is in the region of convergence of the Eisenstein series
![]() $E(\varphi ,\lambda )$
. Then we have
$E(\varphi ,\lambda )$
. Then we have
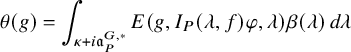 $$ \begin{align*} \theta(g)= \int_{\kappa+i\mathfrak{a}_P^{G,*}}E(g, I_P(\lambda,f)\varphi,\lambda) \beta(\lambda)\, d\lambda \end{align*} $$
$$ \begin{align*} \theta(g)= \int_{\kappa+i\mathfrak{a}_P^{G,*}}E(g, I_P(\lambda,f)\varphi,\lambda) \beta(\lambda)\, d\lambda \end{align*} $$
for any
![]() $g\in G(\mathbb {A})$
.
$g\in G(\mathbb {A})$
.
We fix
![]() $r>2$
that satisfies the conditions of Proposition 5.2.2.1. In the following, we assume moreover that
$r>2$
that satisfies the conditions of Proposition 5.2.2.1. In the following, we assume moreover that
![]() $\kappa $
is such that
$\kappa $
is such that
![]() $\langle \kappa , \alpha ^\vee \rangle>r$
.
$\langle \kappa , \alpha ^\vee \rangle>r$
.
5.3.4
Proposition 5.3.4.1. Let
![]() $s\in \mathbb {C} \setminus \{0,1\}$
. Assume that
$s\in \mathbb {C} \setminus \{0,1\}$
. Assume that
![]() $\beta $
vanishes at the points
$\beta $
vanishes at the points
![]() $-\mu _{i,s}$
for
$-\mu _{i,s}$
for
![]() $i\in I$
. Then we have
$i\in I$
. Then we have
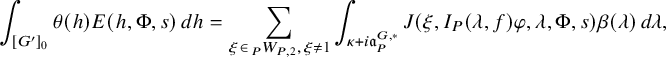 $$ \begin{align} \int_{[G']_0} \theta(h) E(h,\Phi,s)\,dh= \sum_{\xi\in \,_PW_{P,2}, \xi\not=1 }\int_{\kappa+i\mathfrak{a}_P^{G,*}} J(\xi,I_P(\lambda,f)\varphi,\lambda,\Phi,s) \beta(\lambda)\, d\lambda, \end{align} $$
$$ \begin{align} \int_{[G']_0} \theta(h) E(h,\Phi,s)\,dh= \sum_{\xi\in \,_PW_{P,2}, \xi\not=1 }\int_{\kappa+i\mathfrak{a}_P^{G,*}} J(\xi,I_P(\lambda,f)\varphi,\lambda,\Phi,s) \beta(\lambda)\, d\lambda, \end{align} $$
where both sides are absolutely convergent.
Proof. Because
![]() $\theta (h)$
is rapidly decreasing, the left-hand side is absolutely convergent. Using the majorizations (5.2.2.2) and (5.2.2.3) given in the proof of Proposition 5.2.2.1, we see that the right-hand side of (5.3.4.1) is also absolutely convergent.
$\theta (h)$
is rapidly decreasing, the left-hand side is absolutely convergent. Using the majorizations (5.2.2.2) and (5.2.2.3) given in the proof of Proposition 5.2.2.1, we see that the right-hand side of (5.3.4.1) is also absolutely convergent.
By the Lemma 5.1.2.1, the left-hand side of (5.3.4.1) is given by
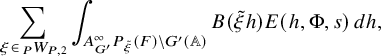 $$ \begin{align} \sum_{\xi\in \,_PW_{P,2}} \int_{ A_{G'}^{\infty} P_{\tilde\xi}(F)\backslash G'(\mathbb{A}) } B(\tilde\xi h) E(h,\Phi,s)\,dh, \end{align} $$
$$ \begin{align} \sum_{\xi\in \,_PW_{P,2}} \int_{ A_{G'}^{\infty} P_{\tilde\xi}(F)\backslash G'(\mathbb{A}) } B(\tilde\xi h) E(h,\Phi,s)\,dh, \end{align} $$
where
![]() $\tilde \xi \in G(F)$
is any element such that
$\tilde \xi \in G(F)$
is any element such that
![]() $\xi =\tilde \xi c(\tilde \xi )^{-1}$
.
$\xi =\tilde \xi c(\tilde \xi )^{-1}$
.
Assume
![]() $\xi \not =1$
. Using the definition of B and permuting the adelic and the complex integrals, we get that
$\xi \not =1$
. Using the definition of B and permuting the adelic and the complex integrals, we get that
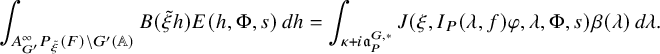 $$ \begin{align*} \int_{ A_{G'}^{\infty} P_{\tilde\xi}(F)\backslash G'(\mathbb{A}) } B(\tilde\xi h) E(h,\Phi,s)\,dh=\int_{\kappa+i\mathfrak{a}_P^{G,*}} J(\xi,I_P(\lambda,f)\varphi,\lambda,\Phi,s) \beta(\lambda)\, d\lambda. \end{align*} $$
$$ \begin{align*} \int_{ A_{G'}^{\infty} P_{\tilde\xi}(F)\backslash G'(\mathbb{A}) } B(\tilde\xi h) E(h,\Phi,s)\,dh=\int_{\kappa+i\mathfrak{a}_P^{G,*}} J(\xi,I_P(\lambda,f)\varphi,\lambda,\Phi,s) \beta(\lambda)\, d\lambda. \end{align*} $$
This permutation is easily justified by the majorization (5.2.2.3) and the fact that
![]() $\beta $
is a Paley-Wiener function. We have to compute the term corresponding to
$\beta $
is a Paley-Wiener function. We have to compute the term corresponding to
![]() $\xi =1$
(for which we take
$\xi =1$
(for which we take
![]() $\tilde \xi =1$
), namely
$\tilde \xi =1$
), namely
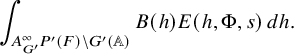 $$ \begin{align*} \int_{ A_{G'}^{\infty} P'(F)\backslash G'(\mathbb{A}) } B( h) E(h,\Phi,s)\,dh. \end{align*} $$
$$ \begin{align*} \int_{ A_{G'}^{\infty} P'(F)\backslash G'(\mathbb{A}) } B( h) E(h,\Phi,s)\,dh. \end{align*} $$
We will show that this integral vanishes. Using Iwasawa decomposition, we can write it as follows:
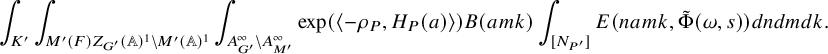 $$ \begin{align} \int_{K'} \int_{ M'(F)Z_{G'}(\mathbb{A})^1\backslash M'(\mathbb{A})^1}\int_{ A_{G'}^{\infty}\backslash A_{M'}^\infty} \exp( \langle -\rho_P,H_P(a)\rangle) B(a m k) \int_{[N_{P'}]}E( n amk ,\tilde\Phi(\omega,s)) dn dm dk. \end{align} $$
$$ \begin{align} \int_{K'} \int_{ M'(F)Z_{G'}(\mathbb{A})^1\backslash M'(\mathbb{A})^1}\int_{ A_{G'}^{\infty}\backslash A_{M'}^\infty} \exp( \langle -\rho_P,H_P(a)\rangle) B(a m k) \int_{[N_{P'}]}E( n amk ,\tilde\Phi(\omega,s)) dn dm dk. \end{align} $$
According to the shape of the constant term in (5.3.1.1), we are reduced to fix
![]() $i\in I$
,
$i\in I$
,
![]() $m\in M'(\mathbb {A})^1$
,
$m\in M'(\mathbb {A})^1$
,
![]() $k\in K'$
and to show the vanishing of
$k\in K'$
and to show the vanishing of
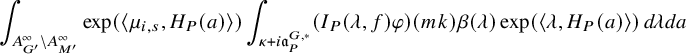 $$ \begin{align*} \int_{ A_{G'}^{\infty}\backslash A_{M'}^\infty} \exp(\langle \mu_{i,s} ,H_P(a)\rangle)\int_{ \kappa+i\mathfrak{a}_P^{G,*}} (I_P(\lambda,f)\varphi)(mk) \beta(\lambda)\exp(\langle \lambda,H_P(a)\rangle) \,d\lambda da \end{align*} $$
$$ \begin{align*} \int_{ A_{G'}^{\infty}\backslash A_{M'}^\infty} \exp(\langle \mu_{i,s} ,H_P(a)\rangle)\int_{ \kappa+i\mathfrak{a}_P^{G,*}} (I_P(\lambda,f)\varphi)(mk) \beta(\lambda)\exp(\langle \lambda,H_P(a)\rangle) \,d\lambda da \end{align*} $$
for any
![]() $m\in M'(\mathbb {A})^1$
and
$m\in M'(\mathbb {A})^1$
and
![]() $k\in K'$
. By Fourier inversion, this is, up to a constant,
$k\in K'$
. By Fourier inversion, this is, up to a constant,
and we are done.
5.4 Period of a pseudo-Eisenstein series: computation in terms of the Whittaker functional
5.4.1
We fix a nontrivial character
![]() $\psi ':\mathbb {A}/F\to \mathbb {C}^\times $
. We define
$\psi ':\mathbb {A}/F\to \mathbb {C}^\times $
. We define
![]() $\psi :[N_{2n}]\to \mathbb {C}^\times $
by
$\psi :[N_{2n}]\to \mathbb {C}^\times $
by
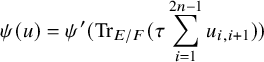 $$ \begin{align*} \psi(u)=\psi'( \mathrm{Tr}_{E/F}(\tau\sum_{i=1}^{2n-1}u_{i,i+1})) \end{align*} $$
$$ \begin{align*} \psi(u)=\psi'( \mathrm{Tr}_{E/F}(\tau\sum_{i=1}^{2n-1}u_{i,i+1})) \end{align*} $$
for
![]() $u=(u_{i,j})\in N_{2n}(\mathbb {A})$
. Note that
$u=(u_{i,j})\in N_{2n}(\mathbb {A})$
. Note that
![]() $\psi $
is trivial on
$\psi $
is trivial on
![]() $N_{2n}'(\mathbb {A})$
, where
$N_{2n}'(\mathbb {A})$
, where
![]() $N_{2n}'=N_{2n}\cap G'$
.
$N_{2n}'=N_{2n}\cap G'$
.
5.4.2 A variant of mirabolic subgroups
For all
![]() $1\leqslant i \leqslant 2n$
, we define the following subgroup of
$1\leqslant i \leqslant 2n$
, we define the following subgroup of
![]() $G_{2n}$
:
$G_{2n}$
:
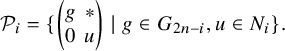 $$ \begin{align*} \mathcal{P}_i=\{ \begin{pmatrix} g & * \\ 0 & u \end{pmatrix}\mid g\in G_{2n-i}, u\in N_{i} \}. \end{align*} $$
$$ \begin{align*} \mathcal{P}_i=\{ \begin{pmatrix} g & * \\ 0 & u \end{pmatrix}\mid g\in G_{2n-i}, u\in N_{i} \}. \end{align*} $$
Note that
![]() $\mathcal {P}_1$
is the mirabolic subgroup
$\mathcal {P}_1$
is the mirabolic subgroup
![]() $\mathcal {P}$
defined in §5.2.1 and
$\mathcal {P}$
defined in §5.2.1 and
![]() $\mathcal {P}_{2n}=B_{2n}$
. We denote by
$\mathcal {P}_{2n}=B_{2n}$
. We denote by
![]() $N_{\mathcal {P}_i}$
the unipotent radical of
$N_{\mathcal {P}_i}$
the unipotent radical of
![]() $\mathcal {P}_i$
. Let
$\mathcal {P}_i$
. Let
![]() $P_i$
be the standard parabolic subgroup of G of type
$P_i$
be the standard parabolic subgroup of G of type
![]() $(2n-i,i)$
. We have
$(2n-i,i)$
. We have
![]() $\mathcal {P}_i\subset P_i$
and
$\mathcal {P}_i\subset P_i$
and
![]() $P_n$
is the parabolic subgroup P defined in §5.1.1. We denote by an upper script
$P_n$
is the parabolic subgroup P defined in §5.1.1. We denote by an upper script
![]() $'$
the subgroups obtained by intersection with
$'$
the subgroups obtained by intersection with
![]() $G'$
that is
$G'$
that is
![]() $\mathcal {P}_i^{\prime }=\mathcal {P}_i\cap G'$
.
$\mathcal {P}_i^{\prime }=\mathcal {P}_i\cap G'$
.
For any smooth function
![]() $\phi $
on
$\phi $
on
![]() $\mathcal {P}_i(F)\backslash G(\mathbb {A})$
, we put for
$\mathcal {P}_i(F)\backslash G(\mathbb {A})$
, we put for
![]() $g\in G(\mathbb {A})$
,
$g\in G(\mathbb {A})$
,
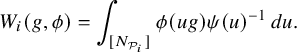 $$ \begin{align*} W_i(g,\phi)=\int_{[N_{\mathcal{P}_i}]} \phi(ug)\psi(u)^{-1}\,du. \end{align*} $$
$$ \begin{align*} W_i(g,\phi)=\int_{[N_{\mathcal{P}_i}]} \phi(ug)\psi(u)^{-1}\,du. \end{align*} $$
When
![]() $i=2n$
, we have
$i=2n$
, we have
![]() $N_{\mathcal {P}_i}=N_{2n}$
and we omit the subscript: we set
$N_{\mathcal {P}_i}=N_{2n}$
and we omit the subscript: we set
![]() $W=W_{2n}$
.
$W=W_{2n}$
.
5.4.3
For any
![]() $\varphi \in \mathcal {A}_{P,\pi }(G)$
and
$\varphi \in \mathcal {A}_{P,\pi }(G)$
and
![]() $\lambda \in \mathfrak {a}_{P,\mathbb {C}}^{G,*}$
such that
$\lambda \in \mathfrak {a}_{P,\mathbb {C}}^{G,*}$
such that
![]() $\Re (\langle \lambda ,\alpha ^\vee \rangle )$
is large enough, we define
$\Re (\langle \lambda ,\alpha ^\vee \rangle )$
is large enough, we define
One has in the convergence region
and so the integral has a meromorphic continuation to
![]() $\mathfrak {a}_{P,\mathbb {C}}^{G,*}$
. It factors through the Fourier coefficient
$\mathfrak {a}_{P,\mathbb {C}}^{G,*}$
. It factors through the Fourier coefficient
5.4.4
We view
![]() $W_M^\psi (1,\cdot )$
as a Whittaker functional on
$W_M^\psi (1,\cdot )$
as a Whittaker functional on
![]() $\pi $
. Let
$\pi $
. Let
![]() $\pi =\otimes _{v\in V_F}'\pi _v$
be a decomposition of
$\pi =\otimes _{v\in V_F}'\pi _v$
be a decomposition of
![]() $\pi $
as a restricted tensor product of representations
$\pi $
as a restricted tensor product of representations
![]() $\pi _v$
of
$\pi _v$
of
![]() $M(F_v)$
. According to this decomposition, we fix a Whittaker functionnal
$M(F_v)$
. According to this decomposition, we fix a Whittaker functionnal
![]() $W_{M,v}^\psi $
on
$W_{M,v}^\psi $
on
![]() $\pi _v$
such that
$\pi _v$
such that
![]() $W_M^\psi (1,\cdot )=\otimes _{v\in V_F} W_{M,v}^\psi $
. Let
$W_M^\psi (1,\cdot )=\otimes _{v\in V_F} W_{M,v}^\psi $
. Let
![]() $V_{F,\infty }\subset S\subset V_F$
be a finite set such that all objects
$V_{F,\infty }\subset S\subset V_F$
be a finite set such that all objects
![]() $\pi $
,
$\pi $
,
![]() $\Phi $
,
$\Phi $
,
![]() $\psi $
,
$\psi $
,
![]() $E/F$
are unramified outside S. We put
$E/F$
are unramified outside S. We put
![]() $W_{M,S}^{\psi }=\otimes _{v\in S} W_{M,v}^\psi $
. For any
$W_{M,S}^{\psi }=\otimes _{v\in S} W_{M,v}^\psi $
. For any
![]() $\lambda \in i\mathfrak {a}_{P,\mathbb {C}}^{G,*}$
, let
$\lambda \in i\mathfrak {a}_{P,\mathbb {C}}^{G,*}$
, let
![]() $\pi _{v,\lambda }$
be the representation of
$\pi _{v,\lambda }$
be the representation of
![]() $M(F_v)$
given by
$M(F_v)$
given by
![]() $\pi _{v,\lambda }(m)=\exp (\langle \lambda , H_M(m)\rangle ) \pi _{v}(m)$
for
$\pi _{v,\lambda }(m)=\exp (\langle \lambda , H_M(m)\rangle ) \pi _{v}(m)$
for
![]() $m\in M(F_v)$
. Let
$m\in M(F_v)$
. Let
![]() $\Pi _{v,\lambda }=\operatorname {\mathrm {Ind}}_{P(F_v)}^{G(F_v)} (\pi _{v,\lambda })$
and
$\Pi _{v,\lambda }=\operatorname {\mathrm {Ind}}_{P(F_v)}^{G(F_v)} (\pi _{v,\lambda })$
and
![]() $\Pi _v=\Pi _{v,\lambda =0}$
. We put
$\Pi _v=\Pi _{v,\lambda =0}$
. We put
![]() $\Pi _S=\otimes _{v\in S}\Pi _v$
.
$\Pi _S=\otimes _{v\in S}\Pi _v$
.
For any
![]() $g_S\in G(F_S)$
and
$g_S\in G(F_S)$
and
![]() $\phi \in \Pi _S$
, we define the Jacquet integral by the analytic continuation of
$\phi \in \Pi _S$
, we define the Jacquet integral by the analytic continuation of
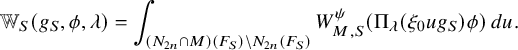 $$ \begin{align} \mathbb{W}_S(g_S,\phi,\lambda)=\int_{(N_{2n}\cap M)(F_S) \backslash N_{2n}(F_S)} W_{M,S}^{\psi}(\Pi_\lambda(\xi_0 ug_S)\phi) \, du. \end{align} $$
$$ \begin{align} \mathbb{W}_S(g_S,\phi,\lambda)=\int_{(N_{2n}\cap M)(F_S) \backslash N_{2n}(F_S)} W_{M,S}^{\psi}(\Pi_\lambda(\xi_0 ug_S)\phi) \, du. \end{align} $$
For any
![]() $v\notin S$
, let
$v\notin S$
, let
![]() $W_v^\psi (\cdot , \pi _\lambda )$
be the
$W_v^\psi (\cdot , \pi _\lambda )$
be the
![]() $K_v$
-invariant Whittaker function such that
$K_v$
-invariant Whittaker function such that
![]() $W_v^\psi (1,\pi _\lambda )=1$
. We shall identify
$W_v^\psi (1,\pi _\lambda )=1$
. We shall identify
![]() $\varphi $
with
$\varphi $
with
![]() $\varphi _S \otimes \varphi ^S$
, where
$\varphi _S \otimes \varphi ^S$
, where
![]() $\varphi _S\in \Pi _S $
and
$\varphi _S\in \Pi _S $
and
![]() $\varphi ^S\in \otimes _{v\notin S}'\Pi _v$
is
$\varphi ^S\in \otimes _{v\notin S}'\Pi _v$
is
![]() $K^S$
-invariant. Then we have
$K^S$
-invariant. Then we have
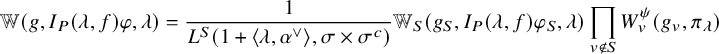 $$ \begin{align} \mathbb{W}(g, I_P(\lambda,f)\varphi,\lambda)= \frac1{L^S(1+\langle\lambda,\alpha^\vee\rangle, \sigma\times \sigma^c)}\mathbb{W}_S(g_S,I_P(\lambda,f)\varphi_S,\lambda) \prod_{v\notin S} W_v^\psi(g_v,\pi_\lambda) \end{align} $$
$$ \begin{align} \mathbb{W}(g, I_P(\lambda,f)\varphi,\lambda)= \frac1{L^S(1+\langle\lambda,\alpha^\vee\rangle, \sigma\times \sigma^c)}\mathbb{W}_S(g_S,I_P(\lambda,f)\varphi_S,\lambda) \prod_{v\notin S} W_v^\psi(g_v,\pi_\lambda) \end{align} $$
for all
![]() $g=(g_S, (g_v)_{v\notin S})\in G(\mathbb {A})$
.
$g=(g_S, (g_v)_{v\notin S})\in G(\mathbb {A})$
.
Proposition 5.4.4.1. There is
![]() $s_0\in \mathbb {R}$
such that for any
$s_0\in \mathbb {R}$
such that for any
![]() $\lambda \in \kappa +i\mathfrak {a}_P^{G,*}$
and any
$\lambda \in \kappa +i\mathfrak {a}_P^{G,*}$
and any
![]() $s\in \mathcal {H}_{>s_0}$
, the integral
$s\in \mathcal {H}_{>s_0}$
, the integral
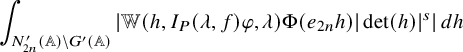 $$ \begin{align*} \int_{N_{2n}'(\mathbb{A})\backslash G'(\mathbb{A})}| \mathbb{W}(h, I_P(\lambda,f)\varphi,\lambda) \Phi(e_{2n}h) |\det(h)|^s |\,dh \end{align*} $$
$$ \begin{align*} \int_{N_{2n}'(\mathbb{A})\backslash G'(\mathbb{A})}| \mathbb{W}(h, I_P(\lambda,f)\varphi,\lambda) \Phi(e_{2n}h) |\det(h)|^s |\,dh \end{align*} $$
is absolutely convergent and uniformly bounded on compact subsets of
![]() $\mathcal {H}_{>s_0}$
.
$\mathcal {H}_{>s_0}$
.
Proof. We shall use (5.4.4.2). First, the factor
![]() ${L^S(1+\langle \lambda ,\alpha ^\vee \rangle , \sigma \times \sigma ^c)}^{-1}$
is bounded uniformy for
${L^S(1+\langle \lambda ,\alpha ^\vee \rangle , \sigma \times \sigma ^c)}^{-1}$
is bounded uniformy for
![]() $\lambda $
such
$\lambda $
such
![]() $\langle \Re (\lambda ),\alpha ^\vee \rangle \geqslant 2$
. We have
$\langle \Re (\lambda ),\alpha ^\vee \rangle \geqslant 2$
. We have
![]() $\Phi =\Phi _S\otimes \Phi ^S$
, where
$\Phi =\Phi _S\otimes \Phi ^S$
, where
![]() $\Phi ^S$
is the characteristic function of
$\Phi ^S$
is the characteristic function of
![]() $(\mathcal {O}^S)^{2n}$
. By (the proof of) [Reference Beuzart-PlessisBP18, proposition 2.6.1 and lemma 3.3.1], there exists
$(\mathcal {O}^S)^{2n}$
. By (the proof of) [Reference Beuzart-PlessisBP18, proposition 2.6.1 and lemma 3.3.1], there exists
![]() $s_0\in \mathbb {R}$
such that for any
$s_0\in \mathbb {R}$
such that for any
![]() $\lambda \in \kappa +i\mathfrak {a}_P^{G,*}$
and any
$\lambda \in \kappa +i\mathfrak {a}_P^{G,*}$
and any
![]() $s\in \mathcal {H}_{>s_0}$
, the integral
$s\in \mathcal {H}_{>s_0}$
, the integral
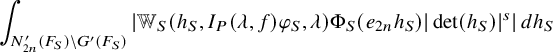 $$ \begin{align*} \int_{N_{2n}'(F_S)\backslash G'(F_S)}| \mathbb{W}_S(h_S, I_P(\lambda,f)\varphi_S,\lambda) \Phi_S(e_{2n}h_S) |\det(h_S)|^s |\,dh_S \end{align*} $$
$$ \begin{align*} \int_{N_{2n}'(F_S)\backslash G'(F_S)}| \mathbb{W}_S(h_S, I_P(\lambda,f)\varphi_S,\lambda) \Phi_S(e_{2n}h_S) |\det(h_S)|^s |\,dh_S \end{align*} $$
is convergent and uniformly bounded on compact subsets of
![]() $\mathcal {H}_{>s_0}$
. So we are left with
$\mathcal {H}_{>s_0}$
. So we are left with
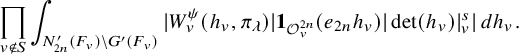 $$ \begin{align*} \prod_{v\notin S} \int_{N_{2n}'(F_v)\backslash G'(F_v)} |W_v^\psi(h_v,\pi_\lambda)| \mathbf{1}_{\mathcal{O}_v^{2n}}(e_{2n}h_v) |\det(h_v)|_v^s |\,dh_v. \end{align*} $$
$$ \begin{align*} \prod_{v\notin S} \int_{N_{2n}'(F_v)\backslash G'(F_v)} |W_v^\psi(h_v,\pi_\lambda)| \mathbf{1}_{\mathcal{O}_v^{2n}}(e_{2n}h_v) |\det(h_v)|_v^s |\,dh_v. \end{align*} $$
Then we can use the Iwasawa decomposition and the bound of [Reference Jacquet, Piatetski-Shapiro and ShalikaJPSS79, proposition 2.4.1] since we may assume that S is large enough so that for
![]() $v\notin S$
the cardinality of the residue field of
$v\notin S$
the cardinality of the residue field of
![]() $F_v$
is bigger than n. The details are left to the reader (see also [Reference Ichino and YamanaIY15, proof of lemma 4.5]).
$F_v$
is bigger than n. The details are left to the reader (see also [Reference Ichino and YamanaIY15, proof of lemma 4.5]).
5.4.5
We consider the situation of §5.3.3.
Proposition 5.4.5.1. There is
![]() $s_0\in \mathbb {R}$
such that for any
$s_0\in \mathbb {R}$
such that for any
![]() $s\in \mathcal {H}_{>s_0}$
and any Paley-Wiener function
$s\in \mathcal {H}_{>s_0}$
and any Paley-Wiener function
![]() $\beta $
that vanishes at the points
$\beta $
that vanishes at the points
![]() $\pm s\alpha /2$
, we have
$\pm s\alpha /2$
, we have
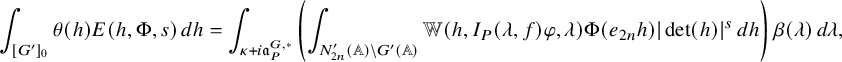 $$ \begin{align} \int_{[G']_0} \theta(h) E(h,\Phi,s)\,dh= \int_{\kappa+i\mathfrak{a}_P^{G,*}} \left(\int_{N_{2n}'(\mathbb{A})\backslash G'(\mathbb{A})}\mathbb{W}(h, I_P(\lambda,f)\varphi,\lambda) \Phi(e_{2n}h)|\det(h)|^s \,dh \right) \beta(\lambda)\, d\lambda, \end{align} $$
$$ \begin{align} \int_{[G']_0} \theta(h) E(h,\Phi,s)\,dh= \int_{\kappa+i\mathfrak{a}_P^{G,*}} \left(\int_{N_{2n}'(\mathbb{A})\backslash G'(\mathbb{A})}\mathbb{W}(h, I_P(\lambda,f)\varphi,\lambda) \Phi(e_{2n}h)|\det(h)|^s \,dh \right) \beta(\lambda)\, d\lambda, \end{align} $$
where the two sides are given by absolutely convergent integrals.
Before giving the proof (which is to find in §§5.4.6-5.4.8 below), we shall give a corollary.
Corollary 5.4.5.2. There is
![]() $s_0\in \mathbb {R}$
such that for any
$s_0\in \mathbb {R}$
such that for any
![]() $\lambda \in \kappa +i\mathfrak {a}_P^{G,*}$
and
$\lambda \in \kappa +i\mathfrak {a}_P^{G,*}$
and
![]() $s\in \mathcal {H}_{>s_0}$
, we have
$s\in \mathcal {H}_{>s_0}$
, we have
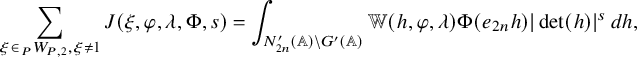 $$ \begin{align*} \sum_{\xi\in \,_PW_{P,2}, \xi\not=1 }J(\xi,\varphi,\lambda,\Phi,s)= \int_{N_{2n}'(\mathbb{A})\backslash G'(\mathbb{A})}\mathbb{W}(h, \varphi,\lambda) \Phi(e_{2n}h)|\det(h)|^s \,dh, \end{align*} $$
$$ \begin{align*} \sum_{\xi\in \,_PW_{P,2}, \xi\not=1 }J(\xi,\varphi,\lambda,\Phi,s)= \int_{N_{2n}'(\mathbb{A})\backslash G'(\mathbb{A})}\mathbb{W}(h, \varphi,\lambda) \Phi(e_{2n}h)|\det(h)|^s \,dh, \end{align*} $$
where the right-hand side is given by an absolutely and uniformly convergent integral on compact subsets of
![]() $\mathcal {H}_{>s_0}$
.
$\mathcal {H}_{>s_0}$
.
Proof. The combination of Propositions 5.3.4.1 and 5.4.5.1 implies (see [Reference Lapid and RogawskiLR03, lemma 9.1.2] for a simple argument)
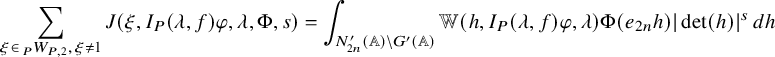 $$ \begin{align*} \sum_{\xi\in \,_PW_{P,2}, \xi\not=1 }J(\xi,I_P(\lambda,f)\varphi,\lambda,\Phi,s)= \int_{N_{2n}'(\mathbb{A})\backslash G'(\mathbb{A})}\mathbb{W}(h, I_P(\lambda,f)\varphi,\lambda) \Phi(e_{2n}h)|\det(h)|^s \,dh \end{align*} $$
$$ \begin{align*} \sum_{\xi\in \,_PW_{P,2}, \xi\not=1 }J(\xi,I_P(\lambda,f)\varphi,\lambda,\Phi,s)= \int_{N_{2n}'(\mathbb{A})\backslash G'(\mathbb{A})}\mathbb{W}(h, I_P(\lambda,f)\varphi,\lambda) \Phi(e_{2n}h)|\det(h)|^s \,dh \end{align*} $$
for any
![]() $\lambda \in \kappa +i\mathfrak {a}_P^{G,*}$
. Since we can find f such that
$\lambda \in \kappa +i\mathfrak {a}_P^{G,*}$
. Since we can find f such that
![]() $I_P(\lambda ,f)\varphi =\varphi $
, we get the result.
$I_P(\lambda ,f)\varphi =\varphi $
, we get the result.
5.4.6 Proof of Proposition 5.4.5.1
We first recall the well-known computation of the constant term of a pseudo Eisenstein series.
Lemma 5.4.6.1. For
![]() $1\leqslant i \leqslant 2n$
, the constant term of
$1\leqslant i \leqslant 2n$
, the constant term of
![]() $\theta $
along
$\theta $
along
![]() $P_i$
, defined by
$P_i$
, defined by
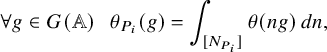 $$ \begin{align*} \forall g\in G(\mathbb{A})\ \ \ \theta_{P_i}(g)=\int_{[N_{P_i}]} \theta(ng)\, dn, \end{align*} $$
$$ \begin{align*} \forall g\in G(\mathbb{A})\ \ \ \theta_{P_i}(g)=\int_{[N_{P_i}]} \theta(ng)\, dn, \end{align*} $$
vanishes unless
![]() $i\in \{n,2n\}$
. Moreover, we have
$i\in \{n,2n\}$
. Moreover, we have
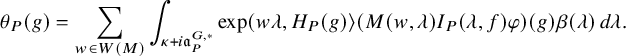 $$ \begin{align*} \theta_{P}(g)=\sum_{w\in W(M)} \int_{\kappa+i\mathfrak{a}_P^{G,*}} \exp(w\lambda, H_P(g)\rangle (M(w,\lambda)I_P(\lambda,f)\varphi)(g) \beta(\lambda)\, d\lambda. \end{align*} $$
$$ \begin{align*} \theta_{P}(g)=\sum_{w\in W(M)} \int_{\kappa+i\mathfrak{a}_P^{G,*}} \exp(w\lambda, H_P(g)\rangle (M(w,\lambda)I_P(\lambda,f)\varphi)(g) \beta(\lambda)\, d\lambda. \end{align*} $$
Unfolding the Epstein series, we get
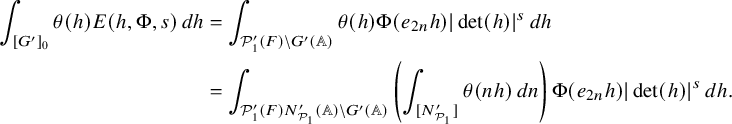 $$ \begin{align*} \int_{[G']_0} \theta(h) E(h,\Phi,s)\, dh&=\int_{\mathcal{P}^{\prime}_1(F)\backslash G'(\mathbb{A})} \theta(h) \Phi(e_{2n}h)|\det(h)|^s \,dh\\ &= \int_{\mathcal{P}^{\prime}_1(F)N^{\prime}_{\mathcal{P}_1}(\mathbb{A})\backslash G'(\mathbb{A})} \left(\int_{[N^{\prime}_{\mathcal{P}_1}]} \theta(nh) \, dn\right)\Phi(e_{2n}h)|\det(h)|^s \,dh. \end{align*} $$
$$ \begin{align*} \int_{[G']_0} \theta(h) E(h,\Phi,s)\, dh&=\int_{\mathcal{P}^{\prime}_1(F)\backslash G'(\mathbb{A})} \theta(h) \Phi(e_{2n}h)|\det(h)|^s \,dh\\ &= \int_{\mathcal{P}^{\prime}_1(F)N^{\prime}_{\mathcal{P}_1}(\mathbb{A})\backslash G'(\mathbb{A})} \left(\int_{[N^{\prime}_{\mathcal{P}_1}]} \theta(nh) \, dn\right)\Phi(e_{2n}h)|\det(h)|^s \,dh. \end{align*} $$
The Fourier expansion of the map
![]() $n\in [N_{\mathcal {P}_1}]\mapsto \theta (nh)$
gives
$n\in [N_{\mathcal {P}_1}]\mapsto \theta (nh)$
gives
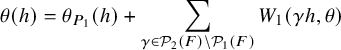 $$ \begin{align*} \theta(h)=\theta_{P_1}(h)+ \sum_{\gamma\in \mathcal{P}_{2}(F)\backslash \mathcal{P}_{1}(F)} W_1(\gamma h, \theta) \end{align*} $$
$$ \begin{align*} \theta(h)=\theta_{P_1}(h)+ \sum_{\gamma\in \mathcal{P}_{2}(F)\backslash \mathcal{P}_{1}(F)} W_1(\gamma h, \theta) \end{align*} $$
from which we deduce
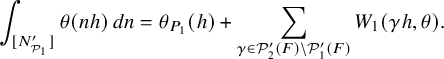 $$ \begin{align*} \int_{[N^{\prime}_{\mathcal{P}_1}]} \theta(nh) \, dn=\theta_{P_1}(h)+ \sum_{\gamma\in \mathcal{P}_{2}'(F)\backslash \mathcal{P}_{1}'(F)} W_1(\gamma h, \theta). \end{align*} $$
$$ \begin{align*} \int_{[N^{\prime}_{\mathcal{P}_1}]} \theta(nh) \, dn=\theta_{P_1}(h)+ \sum_{\gamma\in \mathcal{P}_{2}'(F)\backslash \mathcal{P}_{1}'(F)} W_1(\gamma h, \theta). \end{align*} $$
If
![]() $n>1$
, then
$n>1$
, then
![]() $\theta _{P_1}=0$
(see Lemma 5.4.6.1). In particular, we get
$\theta _{P_1}=0$
(see Lemma 5.4.6.1). In particular, we get
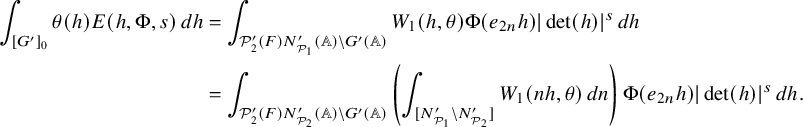 $$ \begin{align*} \int_{[G']_0} \theta(h) E(h,\Phi,s)\, dh &=\int_{\mathcal{P}^{\prime}_2(F) N^{\prime}_{\mathcal{P}_1}(\mathbb{A}) \backslash G'(\mathbb{A})} W_1(h, \theta)\Phi(e_{2n}h)|\det(h)|^s \,dh\\ &=\int_{\mathcal{P}^{\prime}_2(F)N^{\prime}_{\mathcal{P}_2}(\mathbb{A})\backslash G'(\mathbb{A})} \left(\int_{[ N^{\prime}_{\mathcal{P}_1}\backslash N^{\prime}_{\mathcal{P}_2}]} W_1(nh,\theta) \, dn\right)\Phi(e_{2n}h)|\det(h)|^s \,dh. \end{align*} $$
$$ \begin{align*} \int_{[G']_0} \theta(h) E(h,\Phi,s)\, dh &=\int_{\mathcal{P}^{\prime}_2(F) N^{\prime}_{\mathcal{P}_1}(\mathbb{A}) \backslash G'(\mathbb{A})} W_1(h, \theta)\Phi(e_{2n}h)|\det(h)|^s \,dh\\ &=\int_{\mathcal{P}^{\prime}_2(F)N^{\prime}_{\mathcal{P}_2}(\mathbb{A})\backslash G'(\mathbb{A})} \left(\int_{[ N^{\prime}_{\mathcal{P}_1}\backslash N^{\prime}_{\mathcal{P}_2}]} W_1(nh,\theta) \, dn\right)\Phi(e_{2n}h)|\det(h)|^s \,dh. \end{align*} $$
Next, using the Fourier expansion of
![]() $n\in [N_{\mathcal {P}_2}\cap M_{P_1}]\mapsto W_1(nh,\theta ) $
, we get
$n\in [N_{\mathcal {P}_2}\cap M_{P_1}]\mapsto W_1(nh,\theta ) $
, we get
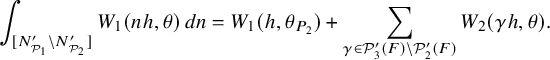 $$ \begin{align*} \int_{[ N^{\prime}_{\mathcal{P}_1}\backslash N^{\prime}_{\mathcal{P}_2}]} W_1(nh,\theta) \, dn=W_1(h,\theta_{P_2}) + \sum_{\gamma\in \mathcal{P}_{3}'(F)\backslash \mathcal{P}_{2}'(F)} W_2(\gamma h, \theta). \end{align*} $$
$$ \begin{align*} \int_{[ N^{\prime}_{\mathcal{P}_1}\backslash N^{\prime}_{\mathcal{P}_2}]} W_1(nh,\theta) \, dn=W_1(h,\theta_{P_2}) + \sum_{\gamma\in \mathcal{P}_{3}'(F)\backslash \mathcal{P}_{2}'(F)} W_2(\gamma h, \theta). \end{align*} $$
If
![]() $n>2$
, we have
$n>2$
, we have
![]() $\theta _{P_2}=0$
(see Lemma 5.4.6.1). By recursion, we get that the left-hand side of (5.4.5.1) is the sum of
$\theta _{P_2}=0$
(see Lemma 5.4.6.1). By recursion, we get that the left-hand side of (5.4.5.1) is the sum of
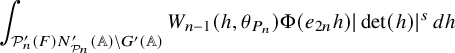 $$ \begin{align} \int_{\mathcal{P}^{\prime}_n(F) N^{\prime}_{\mathcal{P}_n}(\mathbb{A}) \backslash G'(\mathbb{A})} W_{n-1}(h, \theta_{P_n})\Phi(e_{2n}h)|\det(h)|^s \,dh \end{align} $$
$$ \begin{align} \int_{\mathcal{P}^{\prime}_n(F) N^{\prime}_{\mathcal{P}_n}(\mathbb{A}) \backslash G'(\mathbb{A})} W_{n-1}(h, \theta_{P_n})\Phi(e_{2n}h)|\det(h)|^s \,dh \end{align} $$
and
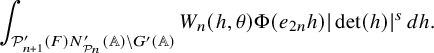 $$ \begin{align} \int_{\mathcal{P}^{\prime}_{n+1}(F) N^{\prime}_{\mathcal{P}_n}(\mathbb{A}) \backslash G'(\mathbb{A})} W_n(h,\theta) \Phi(e_{2n}h)|\det(h)|^s \,dh. \end{align} $$
$$ \begin{align} \int_{\mathcal{P}^{\prime}_{n+1}(F) N^{\prime}_{\mathcal{P}_n}(\mathbb{A}) \backslash G'(\mathbb{A})} W_n(h,\theta) \Phi(e_{2n}h)|\det(h)|^s \,dh. \end{align} $$
The manipulation is justified as in [Reference Ichino and YamanaIY15, corollary 4.3 and bottom of p. 697]. The next step is to compute both expressions. Let us start with the second.
5.4.7 Computation of (5.4.6.2)
We can continue the process. Since
![]() $\theta _{P_k}=0$
for
$\theta _{P_k}=0$
for
![]() $k>n$
,
$k>n$
,
![]() $W=W_{2n}$
and
$W=W_{2n}$
and
![]() $\mathcal {P}^{\prime }_{2n}(F) N^{\prime }_{\mathcal {P}_{2n}}(\mathbb {A})=N^{\prime }_{2n}(\mathbb {A})$
, we get that (5.4.6.2) is equal to
$\mathcal {P}^{\prime }_{2n}(F) N^{\prime }_{\mathcal {P}_{2n}}(\mathbb {A})=N^{\prime }_{2n}(\mathbb {A})$
, we get that (5.4.6.2) is equal to
Using (5.4.3.1), we also have
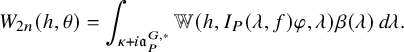 $$ \begin{align*} W_{2n}(h,\theta)= \int_{\kappa+i\mathfrak{a}_P^{G,*}} \mathbb{W}(h, I_P(\lambda,f)\varphi,\lambda) \beta(\lambda)\, d\lambda. \end{align*} $$
$$ \begin{align*} W_{2n}(h,\theta)= \int_{\kappa+i\mathfrak{a}_P^{G,*}} \mathbb{W}(h, I_P(\lambda,f)\varphi,\lambda) \beta(\lambda)\, d\lambda. \end{align*} $$
To get the right-hand side of (5.4.5.1),we just need to permute the adelic integral and the integral over
![]() $\lambda $
. This is justified by Proposition 5.4.4.1. To conclude, it suffices to show that (5.4.6.1) vanishes: this is done in the next §.
$\lambda $
. This is justified by Proposition 5.4.4.1. To conclude, it suffices to show that (5.4.6.1) vanishes: this is done in the next §.
5.4.8 Vanishing of (5.4.6.1)
Recall that
![]() $P_n=P$
. Using the Iwasawa decomposition, we get that the expression (5.4.6.1) is equal to
$P_n=P$
. Using the Iwasawa decomposition, we get that the expression (5.4.6.1) is equal to
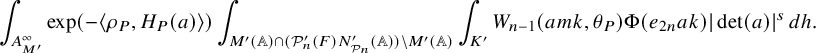 $$ \begin{align} \int_{A_{M'}^{\infty}} \exp(-\langle \rho_P,H_P(a)\rangle) \int_{ M'(\mathbb{A})\cap (\mathcal{P}^{\prime}_n(F) N^{\prime}_{\mathcal{P}_n}(\mathbb{A}) )\backslash M'(\mathbb{A})} \int_{K'}W_{n-1}(amk, \theta_{P})\Phi(e_{2n}ak)|\det(a)|^s \,dh. \end{align} $$
$$ \begin{align} \int_{A_{M'}^{\infty}} \exp(-\langle \rho_P,H_P(a)\rangle) \int_{ M'(\mathbb{A})\cap (\mathcal{P}^{\prime}_n(F) N^{\prime}_{\mathcal{P}_n}(\mathbb{A}) )\backslash M'(\mathbb{A})} \int_{K'}W_{n-1}(amk, \theta_{P})\Phi(e_{2n}ak)|\det(a)|^s \,dh. \end{align} $$
By Lemma 5.4.6.1, we see that the expression
![]() $W_{n-1}(amk, \theta _{P})$
is the sum over
$W_{n-1}(amk, \theta _{P})$
is the sum over
![]() $w\in W(M)$
of
$w\in W(M)$
of
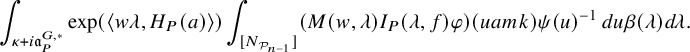 $$ \begin{align*} \int_{\kappa+i\mathfrak{a}_P^{G,*}} \exp(\langle w\lambda,H_P(a)\rangle) \int_{[N_{\mathcal{P}_{n-1}}]}(M(w,\lambda)I_P(\lambda,f)\varphi )(uamk)\psi(u)^{-1}\, du \beta(\lambda) d\lambda. \end{align*} $$
$$ \begin{align*} \int_{\kappa+i\mathfrak{a}_P^{G,*}} \exp(\langle w\lambda,H_P(a)\rangle) \int_{[N_{\mathcal{P}_{n-1}}]}(M(w,\lambda)I_P(\lambda,f)\varphi )(uamk)\psi(u)^{-1}\, du \beta(\lambda) d\lambda. \end{align*} $$
Writing
![]() $u=u_P u_M$
with
$u=u_P u_M$
with
![]() $u_M\in (N_{\mathcal {P}_{n-1}}\cap M)$
and
$u_M\in (N_{\mathcal {P}_{n-1}}\cap M)$
and
![]() $u_P\in (N_{\mathcal {P}_{n-1}}\cap N_P)$
, we see that
$u_P\in (N_{\mathcal {P}_{n-1}}\cap N_P)$
, we see that
Let
![]() $A^{\infty }_{\mathcal {P}_n^{\prime }}$
be the stabilizer of
$A^{\infty }_{\mathcal {P}_n^{\prime }}$
be the stabilizer of
![]() $e_{2n}$
in
$e_{2n}$
in
![]() $A^{\infty }_{M'}$
. We have
$A^{\infty }_{M'}$
. We have
![]() $|\det (a)|^s=\exp (s\langle \alpha , H_P(a)\rangle /2)$
. The contribution in (5.4.8.1) corresponding to
$|\det (a)|^s=\exp (s\langle \alpha , H_P(a)\rangle /2)$
. The contribution in (5.4.8.1) corresponding to
![]() $w\in W(M)$
factors through the integral:
$w\in W(M)$
factors through the integral:
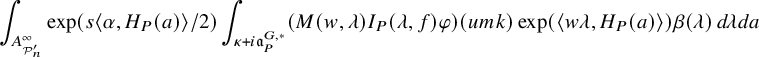 $$ \begin{align} \int_{A_{\mathcal{P}^{\prime}_n}^{\infty}} \exp(s\langle \alpha, H_P(a)\rangle/2) \int_{\kappa+i\mathfrak{a}_P^{G,*}} (M(w,\lambda)I_P(\lambda,f)\varphi )(umk) \exp(\langle w\lambda,H_P(a)\rangle)\beta(\lambda) \, d\lambda da \end{align} $$
$$ \begin{align} \int_{A_{\mathcal{P}^{\prime}_n}^{\infty}} \exp(s\langle \alpha, H_P(a)\rangle/2) \int_{\kappa+i\mathfrak{a}_P^{G,*}} (M(w,\lambda)I_P(\lambda,f)\varphi )(umk) \exp(\langle w\lambda,H_P(a)\rangle)\beta(\lambda) \, d\lambda da \end{align} $$
for some Haar measure on
![]() $A_{\mathcal {P}'}^{\infty }$
. If
$A_{\mathcal {P}'}^{\infty }$
. If
![]() $w=1$
, the expression (5.4.8.2) is simply
$w=1$
, the expression (5.4.8.2) is simply
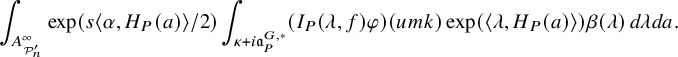 $$ \begin{align*} \int_{A_{\mathcal{P}^{\prime}_n}^{\infty}} \exp(s\langle \alpha, H_P(a)\rangle/2) \int_{\kappa+i\mathfrak{a}_P^{G,*}} (I_P(\lambda,f)\varphi )(umk) \exp(\langle \lambda,H_P(a)\rangle)\beta(\lambda) \, d\lambda da. \end{align*} $$
$$ \begin{align*} \int_{A_{\mathcal{P}^{\prime}_n}^{\infty}} \exp(s\langle \alpha, H_P(a)\rangle/2) \int_{\kappa+i\mathfrak{a}_P^{G,*}} (I_P(\lambda,f)\varphi )(umk) \exp(\langle \lambda,H_P(a)\rangle)\beta(\lambda) \, d\lambda da. \end{align*} $$
By Fourier inversion, it is, up to a constant,
![]() $(I_P(-s\alpha /2,f)\varphi )(umk)\beta (-s\alpha /2)$
and thus vanishes.
$(I_P(-s\alpha /2,f)\varphi )(umk)\beta (-s\alpha /2)$
and thus vanishes.
If
![]() $w\not =1$
, then
$w\not =1$
, then
![]() $w\lambda =-\lambda $
and the expression (5.4.8.2) can be written as
$w\lambda =-\lambda $
and the expression (5.4.8.2) can be written as
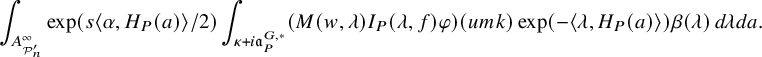 $$ \begin{align*} \int_{A_{\mathcal{P}^{\prime}_n}^{\infty}} \exp(s\langle \alpha, H_P(a)\rangle/2) \int_{\kappa+i\mathfrak{a}_P^{G,*}} (M(w,\lambda)I_P(\lambda, f)\varphi )(umk) \exp(- \langle \lambda,H_P(a)\rangle)\beta(\lambda) \, d\lambda da. \end{align*} $$
$$ \begin{align*} \int_{A_{\mathcal{P}^{\prime}_n}^{\infty}} \exp(s\langle \alpha, H_P(a)\rangle/2) \int_{\kappa+i\mathfrak{a}_P^{G,*}} (M(w,\lambda)I_P(\lambda, f)\varphi )(umk) \exp(- \langle \lambda,H_P(a)\rangle)\beta(\lambda) \, d\lambda da. \end{align*} $$
Assume that
![]() $\Re (s)$
is large enough so that
$\Re (s)$
is large enough so that
![]() $\Re (s) \langle \alpha ,\alpha ^\vee \rangle> 2 \langle \kappa ,\alpha ^\vee \rangle $
. One can check that there exists c such that the inner integral vanishes unless
$\Re (s) \langle \alpha ,\alpha ^\vee \rangle> 2 \langle \kappa ,\alpha ^\vee \rangle $
. One can check that there exists c such that the inner integral vanishes unless
![]() $\langle \alpha , H_P(a)\rangle \leqslant c$
. Thus, one can restrict the outer integral to this ‘half-line’. Then we can permute the two integrals. By Cauchy formula, we get that it is, up to a constant,
$\langle \alpha , H_P(a)\rangle \leqslant c$
. Thus, one can restrict the outer integral to this ‘half-line’. Then we can permute the two integrals. By Cauchy formula, we get that it is, up to a constant,
![]() $(M(w,s \alpha /2) I_P(s\alpha /2, f) \varphi )(umk)\beta ( s\alpha /2)$
, and thus, it also vanishes. This concludes the proof of Proposition 5.4.5.1.
$(M(w,s \alpha /2) I_P(s\alpha /2, f) \varphi )(umk)\beta ( s\alpha /2)$
, and thus, it also vanishes. This concludes the proof of Proposition 5.4.5.1.
5.5 Final result
5.5.1
We keep the notations of previous sections. Let
![]() $\lambda \in \mathfrak {a}_{P,\mathbb {C}}^{G,*}$
. For
$\lambda \in \mathfrak {a}_{P,\mathbb {C}}^{G,*}$
. For
![]() $s\in \mathbb {C}$
, let
$s\in \mathbb {C}$
, let
![]() $L^S(s,\Pi _\lambda ,\mathrm {As})$
be the Asai L-function ‘outside S’. We have
$L^S(s,\Pi _\lambda ,\mathrm {As})$
be the Asai L-function ‘outside S’. We have
The factor
![]() $L^S(s, \sigma \times \sigma ^\vee ) $
has a simple pole at
$L^S(s, \sigma \times \sigma ^\vee ) $
has a simple pole at
![]() $s=1$
and we set
$s=1$
and we set
Then we get an analytic function in
![]() $\lambda $
by setting
$\lambda $
by setting
Theorem 5.5.1.1. We have the following equality of meromorphic functions on
![]() $i\mathfrak {a}_{P,\mathbb {C}}^{G,*}$
:
$i\mathfrak {a}_{P,\mathbb {C}}^{G,*}$
:
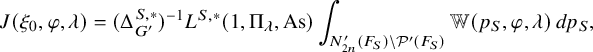 $$ \begin{align*} J(\xi_0,\varphi,\lambda) &= (\Delta_{G'}^{S,*})^{-1} L^{S,*}(1,\Pi_\lambda,\mathrm{As}) \int_{N_{2n}'(F_S)\backslash \mathcal{P}'(F_S)}\mathbb{W}(p_S,\varphi,\lambda)\, dp_S, \end{align*} $$
$$ \begin{align*} J(\xi_0,\varphi,\lambda) &= (\Delta_{G'}^{S,*})^{-1} L^{S,*}(1,\Pi_\lambda,\mathrm{As}) \int_{N_{2n}'(F_S)\backslash \mathcal{P}'(F_S)}\mathbb{W}(p_S,\varphi,\lambda)\, dp_S, \end{align*} $$
where the integral is absolutely convergent, and the left-hand side and the integrand in the right-hand side are respectively defined in (5.1.3.1) and (5.4.3.1). Moreover, both sides of the equality are holomorphic at
![]() $\lambda \in i\mathfrak {a}_{P}^{G,*}$
in the following cases:
$\lambda \in i\mathfrak {a}_{P}^{G,*}$
in the following cases:
-
•
 $\sigma $
is not
$\sigma $
is not
 $G_n^{\prime }$
-distinguished;
$G_n^{\prime }$
-distinguished; -
•
 $\sigma $
is
$\sigma $
is
 $G_n^{\prime }$
-distinguished and
$G_n^{\prime }$
-distinguished and
 $\lambda \not =0$
.
$\lambda \not =0$
.
5.5.2 Proof of Theorem 5.5.1.1
By (5.4.4.2), we have for all
![]() $g_S\in G(F_S)$
,
$g_S\in G(F_S)$
,
Let
![]() $\Phi _S$
a test function in the Schwartz space
$\Phi _S$
a test function in the Schwartz space
![]() $\mathcal {S}(F_S^{2n})$
. Let us consider the following integrals:
$\mathcal {S}(F_S^{2n})$
. Let us consider the following integrals:
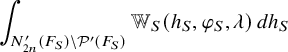 $$ \begin{align} \int_{N_{2n}'(F_S)\backslash \mathcal{P}'(F_S)} \mathbb{W}_S(h_S, \varphi_S,\lambda) \,dh_S \end{align} $$
$$ \begin{align} \int_{N_{2n}'(F_S)\backslash \mathcal{P}'(F_S)} \mathbb{W}_S(h_S, \varphi_S,\lambda) \,dh_S \end{align} $$
and
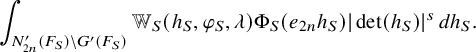 $$ \begin{align} \int_{N_{2n}'(F_S)\backslash G'(F_S)} \mathbb{W}_S(h_S, \varphi_S,\lambda) \Phi_S(e_{2n}h_S) |\det(h_S)|^s \,dh_S. \end{align} $$
$$ \begin{align} \int_{N_{2n}'(F_S)\backslash G'(F_S)} \mathbb{W}_S(h_S, \varphi_S,\lambda) \Phi_S(e_{2n}h_S) |\det(h_S)|^s \,dh_S. \end{align} $$
Lemma 5.5.2.1.
-
1. There exists
 $\eta>0$
(resp. and
$\eta>0$
(resp. and
 $\varepsilon>0$
) such that the integral (5.5.2.1), resp. (5.5.2.2), is absolutely convergent and holomorphic on the subset of
$\varepsilon>0$
) such that the integral (5.5.2.1), resp. (5.5.2.2), is absolutely convergent and holomorphic on the subset of
 $\lambda \in \mathfrak {a}_{P}^{G,*}$
such that
$\lambda \in \mathfrak {a}_{P}^{G,*}$
such that
 $|\langle \Re (\lambda ),\alpha ^\vee \rangle |<\eta $
, resp. and
$|\langle \Re (\lambda ),\alpha ^\vee \rangle |<\eta $
, resp. and
 $s\in \mathcal {H}_{1-\varepsilon }$
.
$s\in \mathcal {H}_{1-\varepsilon }$
. -
2. The integral (5.5.2.2) admits a meromorphic continuation to
 $\mathbb {C}\times \mathfrak {a}_{P,\mathbb {C}}^{G,*}$
denoted by
$\mathbb {C}\times \mathfrak {a}_{P,\mathbb {C}}^{G,*}$
denoted by
 $Z_S(s,\lambda ,\Phi _S)$
.
$Z_S(s,\lambda ,\Phi _S)$
. -
3. For any
 $c> 0$
, there exists
$c> 0$
, there exists
 $s_1\in \mathbb {R}$
such that for
$s_1\in \mathbb {R}$
such that for
 $s\in \mathcal {H}_{s_1}$
and
$s\in \mathcal {H}_{s_1}$
and
 $|\langle \Re (\lambda ),\alpha ^\vee \rangle |<c$
, the integral (5.5.2.2) is absolutely convergent and coincides with
$|\langle \Re (\lambda ),\alpha ^\vee \rangle |<c$
, the integral (5.5.2.2) is absolutely convergent and coincides with
 $Z_S(s,\lambda ,\Phi _S)$
.
$Z_S(s,\lambda ,\Phi _S)$
.
Proof. All the results are slight variations on [Reference Beuzart-PlessisBP18, lemma 3.3.1, lemma 3.3.2 and section 3.10]. To get the convergence of (5.5.2.1) or the precise lower bound
![]() $1-\varepsilon $
, we need to observe that
$1-\varepsilon $
, we need to observe that
![]() $\varphi _S$
belongs to the induced representation of the S-component of an irreducible automorphic cuspidal representation of
$\varphi _S$
belongs to the induced representation of the S-component of an irreducible automorphic cuspidal representation of
![]() $M(\mathbb {A})$
. As such, it is an irreducible, generic and unitary representation. We can now use the classification of local irreductible generic and unitary representations as fully induced from essentially discrete series with exponents in
$M(\mathbb {A})$
. As such, it is an irreducible, generic and unitary representation. We can now use the classification of local irreductible generic and unitary representations as fully induced from essentially discrete series with exponents in
![]() $]-1/2;1/2[$
(see, for example, [Reference TadićTad09], [Reference ZelevinskyZel80] and [Reference Badulescu and RenardBR10, Theorem 8.2.]).
$]-1/2;1/2[$
(see, for example, [Reference TadićTad09], [Reference ZelevinskyZel80] and [Reference Badulescu and RenardBR10, Theorem 8.2.]).
Let
![]() $\Phi =\Phi _S\otimes \Phi ^S$
, where
$\Phi =\Phi _S\otimes \Phi ^S$
, where
![]() $\Phi _S$
is the Schwartz space
$\Phi _S$
is the Schwartz space
![]() $\mathcal {S}(F_S^{2n})$
and
$\mathcal {S}(F_S^{2n})$
and
![]() $\Phi ^S$
is the characteristic function of
$\Phi ^S$
is the characteristic function of
![]() $(\mathcal {O}^{S})^{2n}$
. Let
$(\mathcal {O}^{S})^{2n}$
. Let
![]() $c> \langle \kappa ,\alpha ^\vee \rangle $
. By Lemma 5.5.2.1 assertion 3, there exists
$c> \langle \kappa ,\alpha ^\vee \rangle $
. By Lemma 5.5.2.1 assertion 3, there exists
![]() $s_1\in \mathbb {R}$
such that for
$s_1\in \mathbb {R}$
such that for
![]() $s\in \mathcal {H}_{s_1}$
and
$s\in \mathcal {H}_{s_1}$
and
![]() $|\langle \Re (\lambda ),\alpha ^\vee \rangle |<c$
, the integral (5.5.2.2) is absolutely convergent. We may and shall assume that
$|\langle \Re (\lambda ),\alpha ^\vee \rangle |<c$
, the integral (5.5.2.2) is absolutely convergent. We may and shall assume that
![]() $s_1$
is large enough so that Proposition 5.4.4.1 holds for
$s_1$
is large enough so that Proposition 5.4.4.1 holds for
![]() $s_1$
. Then by the factorization (5.4.4.2), some local computations [Reference FlickerFli88] and Lemma 5.5.2.1 assertion 2, we have
$s_1$
. Then by the factorization (5.4.4.2), some local computations [Reference FlickerFli88] and Lemma 5.5.2.1 assertion 2, we have
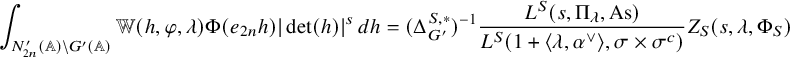 $$ \begin{align*} \int_{N_{2n}'(\mathbb{A})\backslash G'(\mathbb{A})}\mathbb{W}(h, \varphi,\lambda) \Phi(e_{2n}h)|\det(h)|^s \,dh= (\Delta_{G'}^{S,*})^{-1} \frac{L^S(s,\Pi_\lambda,\mathrm{As}) }{ L^S(1+\langle\lambda,\alpha^\vee\rangle, \sigma\times \sigma^c)}Z_S(s,\lambda,\Phi_S)\\ \end{align*} $$
$$ \begin{align*} \int_{N_{2n}'(\mathbb{A})\backslash G'(\mathbb{A})}\mathbb{W}(h, \varphi,\lambda) \Phi(e_{2n}h)|\det(h)|^s \,dh= (\Delta_{G'}^{S,*})^{-1} \frac{L^S(s,\Pi_\lambda,\mathrm{As}) }{ L^S(1+\langle\lambda,\alpha^\vee\rangle, \sigma\times \sigma^c)}Z_S(s,\lambda,\Phi_S)\\ \end{align*} $$
for any
![]() $\lambda \in \kappa +i\mathfrak {a}_P^{G,*}$
and
$\lambda \in \kappa +i\mathfrak {a}_P^{G,*}$
and
![]() $s\in \mathcal {H}_{>s_1}$
. By analytic continuation of the equality of Corollary 5.4.5.2, we have
$s\in \mathcal {H}_{>s_1}$
. By analytic continuation of the equality of Corollary 5.4.5.2, we have
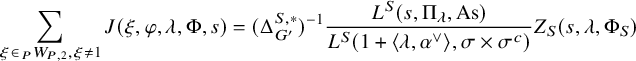 $$ \begin{align*} \sum_{\xi\in \,_PW_{P,2}, \xi\not=1 }J(\xi,\varphi,\lambda,\Phi,s)= (\Delta_{G'}^{S,*})^{-1} \frac{L^S(s,\Pi_\lambda,\mathrm{As}) }{ L^S(1+\langle\lambda,\alpha^\vee\rangle, \sigma\times \sigma^c)} Z_S(s,\lambda,\Phi_S) \end{align*} $$
$$ \begin{align*} \sum_{\xi\in \,_PW_{P,2}, \xi\not=1 }J(\xi,\varphi,\lambda,\Phi,s)= (\Delta_{G'}^{S,*})^{-1} \frac{L^S(s,\Pi_\lambda,\mathrm{As}) }{ L^S(1+\langle\lambda,\alpha^\vee\rangle, \sigma\times \sigma^c)} Z_S(s,\lambda,\Phi_S) \end{align*} $$
for all
![]() $s\in \mathbb {C}$
and
$s\in \mathbb {C}$
and
![]() $\lambda \in \mathcal {D}_r$
given by Proposition 5.2.2.1. We can compute the residue of the left-hand side at
$\lambda \in \mathcal {D}_r$
given by Proposition 5.2.2.1. We can compute the residue of the left-hand side at
![]() $s=1$
following Proposition 5.2.2.1. We get
$s=1$
following Proposition 5.2.2.1. We get
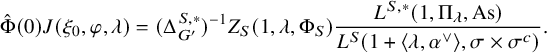 $$ \begin{align} \hat\Phi(0) J(\xi_0,\varphi,\lambda) = (\Delta_{G'}^{S,*})^{-1} Z_S(1,\lambda,\Phi_S) \frac{L^{S,*}(1,\Pi_\lambda,\mathrm{As}) }{ L^S(1+\langle\lambda,\alpha^\vee\rangle, \sigma\times \sigma^c)}. \end{align} $$
$$ \begin{align} \hat\Phi(0) J(\xi_0,\varphi,\lambda) = (\Delta_{G'}^{S,*})^{-1} Z_S(1,\lambda,\Phi_S) \frac{L^{S,*}(1,\Pi_\lambda,\mathrm{As}) }{ L^S(1+\langle\lambda,\alpha^\vee\rangle, \sigma\times \sigma^c)}. \end{align} $$
Both sides are analytic in
![]() $\lambda $
. Thus, the equality for
$\lambda $
. Thus, the equality for
![]() $\lambda \in i\mathfrak {a}_{P}^{G,*}$
. But by Lemma 5.5.2.1 assertion 1 and assertion 2, one has
$\lambda \in i\mathfrak {a}_{P}^{G,*}$
. But by Lemma 5.5.2.1 assertion 1 and assertion 2, one has
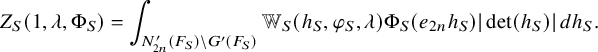 $$ \begin{align*} Z_S(1,\lambda,\Phi_S)= \int_{N_{2n}'(F_S)\backslash G'(F_S)} \mathbb{W}_S(h_S, \varphi_S,\lambda) \Phi_S(e_{2n}h_S) |\det(h_S)| \,dh_S. \end{align*} $$
$$ \begin{align*} Z_S(1,\lambda,\Phi_S)= \int_{N_{2n}'(F_S)\backslash G'(F_S)} \mathbb{W}_S(h_S, \varphi_S,\lambda) \Phi_S(e_{2n}h_S) |\det(h_S)| \,dh_S. \end{align*} $$
Let
![]() $\bar {N}_1$
be the unipotent radical of the opposite of the parabolic subgroup
$\bar {N}_1$
be the unipotent radical of the opposite of the parabolic subgroup
![]() $P_1$
defined in §5.4.2. The standard Levi factor of
$P_1$
defined in §5.4.2. The standard Levi factor of
![]() $P_1$
decomposes as
$P_1$
decomposes as
![]() $G_{2n-1}\times G_1$
. Thus, we have
$G_{2n-1}\times G_1$
. Thus, we have
![]() $N_{2n}' \backslash P_1^{\prime }\simeq N_{2n}' \backslash \mathcal {P}'\times G_1^{\prime }$
. By a usual decomposition of measures, we get
$N_{2n}' \backslash P_1^{\prime }\simeq N_{2n}' \backslash \mathcal {P}'\times G_1^{\prime }$
. By a usual decomposition of measures, we get
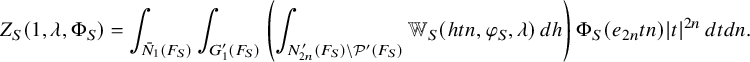 $$ \begin{align*} Z_S(1,\lambda,\Phi_S) &= \int_{ \bar{N}_1(F_S) } \int_{G_1^{\prime}(F_S)}\left(\int_{N_{2n}'(F_S)\backslash \mathcal{P}'(F_S)} \mathbb{W}_S(h t n , \varphi_S,\lambda) \,dh\right) \Phi_S(e_{2n}tn )|t|^{2n} \, dt dn. \end{align*} $$
$$ \begin{align*} Z_S(1,\lambda,\Phi_S) &= \int_{ \bar{N}_1(F_S) } \int_{G_1^{\prime}(F_S)}\left(\int_{N_{2n}'(F_S)\backslash \mathcal{P}'(F_S)} \mathbb{W}_S(h t n , \varphi_S,\lambda) \,dh\right) \Phi_S(e_{2n}tn )|t|^{2n} \, dt dn. \end{align*} $$
However, we have also
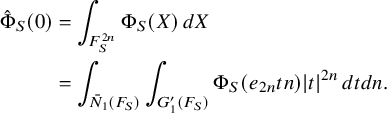 $$ \begin{align*} \hat\Phi_S(0) &=\int_{F_S^{2n}} \Phi_S(X) \,dX\\ &= \int_{ \bar{N}_1(F_S) } \int_{G_1^{\prime}(F_S)} \Phi_S(e_{2n}tn )|t|^{2n} \, dt dn. \end{align*} $$
$$ \begin{align*} \hat\Phi_S(0) &=\int_{F_S^{2n}} \Phi_S(X) \,dX\\ &= \int_{ \bar{N}_1(F_S) } \int_{G_1^{\prime}(F_S)} \Phi_S(e_{2n}tn )|t|^{2n} \, dt dn. \end{align*} $$
Since (5.5.2.3) holds for any Schwartz function
![]() $\Phi _S$
, we get that
$\Phi _S$
, we get that
![]() $J(\xi _0,\varphi ,\lambda ) $
is equal to
$J(\xi _0,\varphi ,\lambda ) $
is equal to
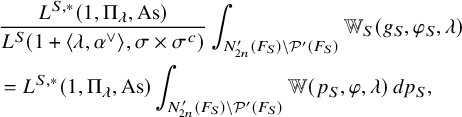 $$ \begin{align*} & \frac{L^{S,*}(1,\Pi_\lambda,\mathrm{As}) }{L^S(1+\langle\lambda,\alpha^\vee\rangle, \sigma\times \sigma^c)}\int_{N_{2n}'(F_S)\backslash \mathcal{P}'(F_S)}\mathbb{W}_S(g_S,\varphi_S,\lambda)\\ &= L^{S,*}(1,\Pi_\lambda,\mathrm{As}) \int_{N_{2n}'(F_S)\backslash \mathcal{P}'(F_S)}\mathbb{W}(p_S,\varphi,\lambda)\, dp_S, \end{align*} $$
$$ \begin{align*} & \frac{L^{S,*}(1,\Pi_\lambda,\mathrm{As}) }{L^S(1+\langle\lambda,\alpha^\vee\rangle, \sigma\times \sigma^c)}\int_{N_{2n}'(F_S)\backslash \mathcal{P}'(F_S)}\mathbb{W}_S(g_S,\varphi_S,\lambda)\\ &= L^{S,*}(1,\Pi_\lambda,\mathrm{As}) \int_{N_{2n}'(F_S)\backslash \mathcal{P}'(F_S)}\mathbb{W}(p_S,\varphi,\lambda)\, dp_S, \end{align*} $$
where we have used the factorization (5.4.4.2). In the first expression above, the integral is holomorphic on
![]() $i\mathfrak {a}_P^{G,*}$
; see Lemma 5.5.2.1. Using the factorization of
$i\mathfrak {a}_P^{G,*}$
; see Lemma 5.5.2.1. Using the factorization of
![]() $L^S(s, \sigma \times \sigma ^c)$
in terms of Asai L-functions
$L^S(s, \sigma \times \sigma ^c)$
in terms of Asai L-functions
![]() $L(s,\sigma ,As^{\pm })$
, we get
$L(s,\sigma ,As^{\pm })$
, we get
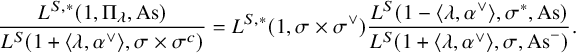 $$ \begin{align*} \frac{L^{S,*}(1,\Pi_\lambda,\mathrm{As}) }{L^S(1+\langle\lambda,\alpha^\vee\rangle, \sigma\times \sigma^c)}= L^{S,*}(1, \sigma\times \sigma^\vee) \frac{L^S(1-\langle\lambda,\alpha^\vee\rangle,\sigma^*,\mathrm{As})}{L^S(1+\langle\lambda,\alpha^\vee\rangle,\sigma,\mathrm{As}^-)}. \end{align*} $$
$$ \begin{align*} \frac{L^{S,*}(1,\Pi_\lambda,\mathrm{As}) }{L^S(1+\langle\lambda,\alpha^\vee\rangle, \sigma\times \sigma^c)}= L^{S,*}(1, \sigma\times \sigma^\vee) \frac{L^S(1-\langle\lambda,\alpha^\vee\rangle,\sigma^*,\mathrm{As})}{L^S(1+\langle\lambda,\alpha^\vee\rangle,\sigma,\mathrm{As}^-)}. \end{align*} $$
On
![]() $i\mathfrak {a}_P^{G,*}$
, the L-function
$i\mathfrak {a}_P^{G,*}$
, the L-function
![]() $L^S(1+\langle \lambda ,\alpha ^\vee \rangle ,\sigma ,\mathrm {As}^-)$
does not vanish by [Reference ShahidiSha81, theorem 5.1] and
$L^S(1+\langle \lambda ,\alpha ^\vee \rangle ,\sigma ,\mathrm {As}^-)$
does not vanish by [Reference ShahidiSha81, theorem 5.1] and
![]() $L^S(1-\langle \lambda ,\alpha ^\vee \rangle ,\sigma ^*,\mathrm {As})$
is holomorphic unless
$L^S(1-\langle \lambda ,\alpha ^\vee \rangle ,\sigma ^*,\mathrm {As})$
is holomorphic unless
![]() $\lambda =0$
and
$\lambda =0$
and
![]() $\sigma ^*$
(thus
$\sigma ^*$
(thus
![]() $\sigma $
) is
$\sigma $
) is
![]() $G_n^{\prime }$
-distinguished (see [Reference FlickerFli88]). On the other hand, if
$G_n^{\prime }$
-distinguished (see [Reference FlickerFli88]). On the other hand, if
![]() $\sigma $
is not
$\sigma $
is not
![]() $G_n^{\prime }$
-distinguished, then
$G_n^{\prime }$
-distinguished, then
![]() $J(\xi _0,\varphi ,\lambda ) $
is known to be holomorphic on
$J(\xi _0,\varphi ,\lambda ) $
is known to be holomorphic on
![]() $i\mathfrak {a}_{P}^{G,*}$
; see [Reference LapidLap06, lemma 8.1]. Otherwise,
$i\mathfrak {a}_{P}^{G,*}$
; see [Reference LapidLap06, lemma 8.1]. Otherwise,
![]() $J(\xi _0,\varphi ,\lambda ) $
is holomorphic on
$J(\xi _0,\varphi ,\lambda ) $
is holomorphic on
![]() $i\mathfrak {a}_{P}^{G,*}\setminus \{0\}$
, but it may have a simple pole at
$i\mathfrak {a}_{P}^{G,*}\setminus \{0\}$
, but it may have a simple pole at
![]() $\lambda =0$
.
$\lambda =0$
.
6 The
 $(G,H)$
-regular contribution to the Jacquet-Rallis trace formula: alternative proof
$(G,H)$
-regular contribution to the Jacquet-Rallis trace formula: alternative proof
6.1 Statement
6.1.1
The goal of this section is to provide an alternative proof of the following combination of Theorem 4.1.8.1 and Theorem 4.2.8.1.
Theorem 6.1.1.1. Let
![]() $\chi \in \mathfrak {X}(G)$
be a
$\chi \in \mathfrak {X}(G)$
be a
![]() $(G,H)$
-regular cuspidal datum and let
$(G,H)$
-regular cuspidal datum and let
![]() $f\in \mathcal {S}(G(\mathbb {A}))$
. Then,
$f\in \mathcal {S}(G(\mathbb {A}))$
. Then,
-
1. If
 $\chi $
is not Hermitian, we have
$\chi $
is not Hermitian, we have
 $I_\chi (f)=0$
.
$I_\chi (f)=0$
. -
2. If
 $\chi $
is Hermitian, we have (6.1.1.1)where we recall that
$\chi $
is Hermitian, we have (6.1.1.1)where we recall that $$ \begin{align} I_\chi(f)=2^{-\dim(\mathfrak{a}_L)}\int_{i\mathfrak{a}_M^{L,*}} I_{\Pi_\lambda}(f) d\lambda, \end{align} $$
$$ \begin{align} I_\chi(f)=2^{-\dim(\mathfrak{a}_L)}\int_{i\mathfrak{a}_M^{L,*}} I_{\Pi_\lambda}(f) d\lambda, \end{align} $$
 $(M,\pi )$
is a pair representing
$(M,\pi )$
is a pair representing
 $\chi $
,
$\chi $
,
 $L\supset M$
is the Levi subgroup defined by (4.1.4.1),
$L\supset M$
is the Levi subgroup defined by (4.1.4.1),
 $\Pi _\lambda $
stands for the induced representation
$\Pi _\lambda $
stands for the induced representation
 $\operatorname {\mathrm {Ind}}_{P(\mathbb {A})}^{G(\mathbb {A})}(\pi _\lambda )$
, for P a chosen parabolic subgroup with Levi factor M, and
$\operatorname {\mathrm {Ind}}_{P(\mathbb {A})}^{G(\mathbb {A})}(\pi _\lambda )$
, for P a chosen parabolic subgroup with Levi factor M, and
 $I_{\Pi _\lambda }$
is the relative character defined by (4.2.8.1).
$I_{\Pi _\lambda }$
is the relative character defined by (4.2.8.1).
More precisely, the proof will be very similar to that given in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Section 8] and is based on two ingredients of independent interests. The first one is that the Rankin-Selberg period (over H) admits a continuous extension to the space
![]() $\mathcal {T}_\chi ([G])$
of functions of uniform moderate growth supported on a H-regular cuspidal datum
$\mathcal {T}_\chi ([G])$
of functions of uniform moderate growth supported on a H-regular cuspidal datum
![]() $\chi $
and that this extension can moreover be described in terms of the analytic continuation of Zeta integrals of Rankin Selberg type. This was already established in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Section 7]. The second ingredient is an explicit spectral decomposition of the Flicker-Rallis period (over
$\chi $
and that this extension can moreover be described in terms of the analytic continuation of Zeta integrals of Rankin Selberg type. This was already established in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Section 7]. The second ingredient is an explicit spectral decomposition of the Flicker-Rallis period (over
![]() $G'$
) restricted to
$G'$
) restricted to
![]() $\mathcal {S}_\chi ([G'])$
when the cuspidal datum
$\mathcal {S}_\chi ([G'])$
when the cuspidal datum
![]() $\chi $
is (G-)regular. This was already done in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Section 6] under the stronger assumption that
$\chi $
is (G-)regular. This was already done in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Section 6] under the stronger assumption that
![]() $\chi $
is
$\chi $
is
![]() $*$
-regular. The aim of the subsection 6.2 is to state and prove the extension of this result to the regular case. Once established, we will be able to give a proof of Theorem 6.1.1.1 in subsection 6.3 in much the same lines as [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, §8.2].
$*$
-regular. The aim of the subsection 6.2 is to state and prove the extension of this result to the regular case. Once established, we will be able to give a proof of Theorem 6.1.1.1 in subsection 6.3 in much the same lines as [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, §8.2].
6.2 Spectral decomposition of the Flicker-Rallis period for regular cuspidal data
6.2.1 Zeta integrals
Let
![]() $n\geqslant 0$
be an integer. We will freely use the notation introduced in Section 4. For every
$n\geqslant 0$
be an integer. We will freely use the notation introduced in Section 4. For every
![]() $f\in \mathcal {T}([G_n])$
, we denote by
$f\in \mathcal {T}([G_n])$
, we denote by
its Whittaker function and, for
![]() $\phi \in \mathcal {S}(\mathbb {A}^n)$
, we set
$\phi \in \mathcal {S}(\mathbb {A}^n)$
, we set
This expression is absolutely convergent for
![]() $\Re (s)$
sufficiently large. More precisely, for every
$\Re (s)$
sufficiently large. More precisely, for every
![]() $N>0$
, there exists
$N>0$
, there exists
![]() $c>0$
such that
$c>0$
such that
![]() $Z_\psi ^{\mathrm {FR}}(s,f,\phi )$
converges for
$Z_\psi ^{\mathrm {FR}}(s,f,\phi )$
converges for
![]() $s\in \mathcal {H}_{>c}$
(see [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Theorem 6.2.5.1]).
$s\in \mathcal {H}_{>c}$
(see [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Theorem 6.2.5.1]).
6.2.2 Flicker-Rallis period
Recall that for every
![]() $f\in \mathcal {C}([G_n])$
, the period integral
$f\in \mathcal {C}([G_n])$
, the period integral
is convergent [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Theorem 6.2.6.1].
6.2.3 Hermitian cuspidal data
Let
![]() $\chi \in \mathfrak {X}(G_n)$
be a cuspidal datum. Then, we can find a pair
$\chi \in \mathfrak {X}(G_n)$
be a cuspidal datum. Then, we can find a pair
![]() $(M,\pi )$
representing
$(M,\pi )$
representing
![]() $\chi $
with
$\chi $
with
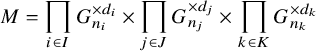 $$ \begin{align*}M=\prod_{i\in I} G_{n_i}^{\times d_i} \times \prod_{j\in J} G_{n_j}^{\times d_j} \times \prod_{k\in K} G_{n_k}^{\times d_k}\end{align*} $$
$$ \begin{align*}M=\prod_{i\in I} G_{n_i}^{\times d_i} \times \prod_{j\in J} G_{n_j}^{\times d_j} \times \prod_{k\in K} G_{n_k}^{\times d_k}\end{align*} $$
and
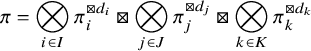 $$ \begin{align*}\pi=\bigotimes_{i\in I} \pi_i^{\boxtimes d_i} \boxtimes \bigotimes_{j\in J} \pi_j^{\boxtimes d_j} \boxtimes \bigotimes_{k\in K} \pi_k^{\boxtimes d_k}\end{align*} $$
$$ \begin{align*}\pi=\bigotimes_{i\in I} \pi_i^{\boxtimes d_i} \boxtimes \bigotimes_{j\in J} \pi_j^{\boxtimes d_j} \boxtimes \bigotimes_{k\in K} \pi_k^{\boxtimes d_k}\end{align*} $$
for some disjoint finite sets I, J, K, families of positive integers
![]() $(n_l)_{l\in I\cup J\cup K}$
,
$(n_l)_{l\in I\cup J\cup K}$
,
![]() $(d_l)_{l\in I\cup J\cup K}$
and a family of distinct cuspidal automorphic representations
$(d_l)_{l\in I\cup J\cup K}$
and a family of distinct cuspidal automorphic representations
![]() $(\pi _l)_{l\in I\cup J\cup K}$
satisfying
$(\pi _l)_{l\in I\cup J\cup K}$
satisfying
-
• For every
 $i\in I$
,
$i\in I$
,
 $\pi _i\not \simeq \pi _i^*$
;
$\pi _i\not \simeq \pi _i^*$
; -
• For every
 $j\in J$
,
$j\in J$
,
 $\pi _j\simeq \pi _j^*$
and
$\pi _j\simeq \pi _j^*$
and
 $L(s,\pi _j,\mathrm {As}^{(-1)^{n+1}})$
has no pole at
$L(s,\pi _j,\mathrm {As}^{(-1)^{n+1}})$
has no pole at
 $s=1$
;
$s=1$
; -
• For every
 $k\in K$
,
$k\in K$
,
 $\pi _k\simeq \pi _k^*$
and
$\pi _k\simeq \pi _k^*$
and
 $L(s,\pi _k,\mathrm {As}^{(-1)^{n+1}})$
has a pole at
$L(s,\pi _k,\mathrm {As}^{(-1)^{n+1}})$
has a pole at
 $s=1$
.
$s=1$
.
Fixing data as above (which are unique up to reordering), we recall that
![]() $\chi $
is said Hermitian (see §4.1.3) if the following condition is satisfied:
$\chi $
is said Hermitian (see §4.1.3) if the following condition is satisfied:
-
(6.2.3.1) For every
 $i\in I$
, there exists
$i\in I$
, there exists
 $i^*\in I$
such that
$i^*\in I$
such that
 $\pi _{i^*}\simeq \pi _i^*$
and for every
$\pi _{i^*}\simeq \pi _i^*$
and for every
 $j\in J$
,
$j\in J$
,
 $d_j$
is even.
$d_j$
is even.
6.2.4
Assume furthermore that
![]() $\chi $
is regular in the sense of §4.1.3 or [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, §2.9.7] and fix a pair
$\chi $
is regular in the sense of §4.1.3 or [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, §2.9.7] and fix a pair
![]() $(M,\pi )$
representing
$(M,\pi )$
representing
![]() $\chi $
together with data I, J, K,
$\chi $
together with data I, J, K,
![]() $(n_l)_{l\in I\cup J\cup K}$
,
$(n_l)_{l\in I\cup J\cup K}$
,
![]() $(d_l)_{l\in I\cup J\cup K}$
,
$(d_l)_{l\in I\cup J\cup K}$
,
![]() $(\pi _l)_{l\in I\cup J\cup K}$
as in the previous paragraph. By the regularity assumption, we have
$(\pi _l)_{l\in I\cup J\cup K}$
as in the previous paragraph. By the regularity assumption, we have
![]() $d_l=1$
for every
$d_l=1$
for every
![]() $l\in I\cup J\cup K$
. Moreover,
$l\in I\cup J\cup K$
. Moreover,
![]() $\chi $
is Hermitian if and only if
$\chi $
is Hermitian if and only if
![]() $J=\emptyset $
and there exists an involution
$J=\emptyset $
and there exists an involution
![]() $i\mapsto i^*$
of I without fixed point such that
$i\mapsto i^*$
of I without fixed point such that
![]() $\pi _{i^*}=\pi _i^*$
for every
$\pi _{i^*}=\pi _i^*$
for every
![]() $i\in I$
. If this is the case, we choose a subset
$i\in I$
. If this is the case, we choose a subset
![]() $I'\subset I$
such that I is the disjoint union of
$I'\subset I$
such that I is the disjoint union of
![]() $I'$
and
$I'$
and
![]() $(I')^*=\{i^*\mid i\in I' \}$
, and we define a Levi subgroup
$(I')^*=\{i^*\mid i\in I' \}$
, and we define a Levi subgroup
![]() $L\supset M$
by
$L\supset M$
by
6.2.5
Let P be a parabolic subgroup with Levi factor M. For every
![]() $\lambda \in \mathfrak {a}_{M,\mathbb {C}}^*$
and
$\lambda \in \mathfrak {a}_{M,\mathbb {C}}^*$
and
![]() $f\in \mathcal {C}([G_n])$
, we set
$f\in \mathcal {C}([G_n])$
, we set
and
where
![]() $f_{\Pi _\lambda }\in \mathcal {T}([G_n])$
is defined as in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Eq. (2.9.8.14)].
$f_{\Pi _\lambda }\in \mathcal {T}([G_n])$
is defined as in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Eq. (2.9.8.14)].
Assuming that
![]() $\chi $
is Hermitian, we define for every
$\chi $
is Hermitian, we define for every
![]() $\lambda \in i\mathfrak {a}_{M}^{L,*}$
a linear form
$\lambda \in i\mathfrak {a}_{M}^{L,*}$
a linear form
![]() $\beta _n$
on
$\beta _n$
on
![]() $\mathcal {W}(\Pi _\lambda ,\psi _n)$
by setting
$\mathcal {W}(\Pi _\lambda ,\psi _n)$
by setting
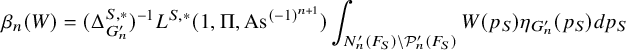 $$ \begin{align*}\beta_n(W)=(\Delta^{S,*}_{G_n^{\prime}})^{-1} L^{S,*}(1,\Pi,\mathrm{As}^{(-1)^{n+1}}) \int_{N_n^{\prime}(F_S)\backslash \mathcal{P}_n^{\prime}(F_S)} W(p_S) \eta_{G^{\prime}_n}(p_S)dp_S\end{align*} $$
$$ \begin{align*}\beta_n(W)=(\Delta^{S,*}_{G_n^{\prime}})^{-1} L^{S,*}(1,\Pi,\mathrm{As}^{(-1)^{n+1}}) \int_{N_n^{\prime}(F_S)\backslash \mathcal{P}_n^{\prime}(F_S)} W(p_S) \eta_{G^{\prime}_n}(p_S)dp_S\end{align*} $$
for every
![]() $W\in \mathcal {W}(\Pi _\lambda ,\psi _n)$
, where S is a sufficiently large finite set of places of F (depending on W). That the above integral is convergent follows from [Reference Beuzart-PlessisBP18, Proposition 2.6.1, Lemma 3.3.1], [Reference Jacquet and ShalikaJS81b], and moreover, the product stabilizes for S sufficiently large by the unramified computation of [Reference FlickerFli88, Proposition 3].
$W\in \mathcal {W}(\Pi _\lambda ,\psi _n)$
, where S is a sufficiently large finite set of places of F (depending on W). That the above integral is convergent follows from [Reference Beuzart-PlessisBP18, Proposition 2.6.1, Lemma 3.3.1], [Reference Jacquet and ShalikaJS81b], and moreover, the product stabilizes for S sufficiently large by the unramified computation of [Reference FlickerFli88, Proposition 3].
6.2.6
Theorem 6.2.6.1. Let
![]() $\chi \in \mathfrak {X}^{\operatorname {\mathrm {reg}}}(G_n)$
for which we adopt the notation introduced in the previous three paragraphs. Then, for every
$\chi \in \mathfrak {X}^{\operatorname {\mathrm {reg}}}(G_n)$
for which we adopt the notation introduced in the previous three paragraphs. Then, for every
![]() $f\in \mathcal {C}_\chi ([G_n])$
and
$f\in \mathcal {C}_\chi ([G_n])$
and
![]() $\phi \in \mathcal {S}(\mathbb {A}^n)$
, we have
$\phi \in \mathcal {S}(\mathbb {A}^n)$
, we have
-
1. If
 $\chi $
is Hermitian, the function
$\chi $
is Hermitian, the function
 $\lambda \in i\mathfrak {a}_M^{L,*}\mapsto \beta _n(W_{f,\Pi _\lambda })$
is Schwartz and the resulting map (6.2.6.1)is continuous.
$\lambda \in i\mathfrak {a}_M^{L,*}\mapsto \beta _n(W_{f,\Pi _\lambda })$
is Schwartz and the resulting map (6.2.6.1)is continuous. $$ \begin{align} \mathcal{C}_\chi([G_n])\to \mathcal{S}(i\mathfrak{a}_M^{L,*}),\;\; f\mapsto \left( \lambda\in i\mathfrak{a}_M^{L,*}\mapsto \beta_n(W_{f,\Pi_\lambda})\right) \end{align} $$
$$ \begin{align} \mathcal{C}_\chi([G_n])\to \mathcal{S}(i\mathfrak{a}_M^{L,*}),\;\; f\mapsto \left( \lambda\in i\mathfrak{a}_M^{L,*}\mapsto \beta_n(W_{f,\Pi_\lambda})\right) \end{align} $$
-
2. The function
 $s\mapsto (s-1)Z_\psi ^{\mathrm {FR}}(s,{}^0 f,\phi )$
admits an analytic continuation to
$s\mapsto (s-1)Z_\psi ^{\mathrm {FR}}(s,{}^0 f,\phi )$
admits an analytic continuation to
 $\mathcal {H}_{>1}$
with a limit at
$\mathcal {H}_{>1}$
with a limit at
 $s=1$
, and setting
$s=1$
, and setting
 $Z_\psi ^{\mathrm {FR},*}(1,{}^0f,\phi ):=\lim \limits _{s\to 1^+} (s-1)Z_\psi ^{\mathrm {FR}}(s,{}^0f,\phi )$
, we have (6.2.6.2)
$Z_\psi ^{\mathrm {FR},*}(1,{}^0f,\phi ):=\lim \limits _{s\to 1^+} (s-1)Z_\psi ^{\mathrm {FR}}(s,{}^0f,\phi )$
, we have (6.2.6.2) $$ \begin{align} Z_\psi^{\mathrm{FR},*}(1,{}^0f,\phi)=\left\{\begin{array}{ll} 2^{1-\dim(\mathfrak{a}_L)}\widehat{\phi}(0) \int_{i\mathfrak{a}_{M}^{L,*}}\beta_n(W_{f,\Pi_\lambda}) d\lambda \mbox{ if } \chi \mbox{ is Hermitian}, \\ \\ 0 \mbox{ otherwise.} \end{array}\right. \end{align} $$
$$ \begin{align} Z_\psi^{\mathrm{FR},*}(1,{}^0f,\phi)=\left\{\begin{array}{ll} 2^{1-\dim(\mathfrak{a}_L)}\widehat{\phi}(0) \int_{i\mathfrak{a}_{M}^{L,*}}\beta_n(W_{f,\Pi_\lambda}) d\lambda \mbox{ if } \chi \mbox{ is Hermitian}, \\ \\ 0 \mbox{ otherwise.} \end{array}\right. \end{align} $$
-
3. The equality
(6.2.6.3) $$ \begin{align} \widehat{\phi}(0)P_{G^{\prime}_n}(f)=\frac{1}{2}Z_\psi^{\mathrm{FR},*}(1,{}^0f,\phi). \end{align} $$
$$ \begin{align} \widehat{\phi}(0)P_{G^{\prime}_n}(f)=\frac{1}{2}Z_\psi^{\mathrm{FR},*}(1,{}^0f,\phi). \end{align} $$
6.2.7
We note the following immediate corollary of Theorem 6.2.6.1.
Corollary 6.2.7.1. Let
![]() $\chi \in \mathfrak {X}^{\operatorname {\mathrm {reg}}}(G_n)$
for which we adopt the notation introduced in the paragraphs 6.2.4 and 6.2.5. Then, for every
$\chi \in \mathfrak {X}^{\operatorname {\mathrm {reg}}}(G_n)$
for which we adopt the notation introduced in the paragraphs 6.2.4 and 6.2.5. Then, for every
![]() $f\in \mathcal {C}_\chi ([G_n])$
, we have
$f\in \mathcal {C}_\chi ([G_n])$
, we have
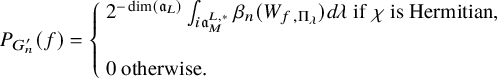 $$ \begin{align} P_{G^{\prime}_n}(f)=\left\{\begin{array}{ll} 2^{-\dim(\mathfrak{a}_L)} \int_{i\mathfrak{a}_{M}^{L,*}}\beta_n(W_{f,\Pi_\lambda}) d\lambda \mbox{ if } \chi \mbox{ is Hermitian}, \\ \\ 0 \mbox{ otherwise.} \end{array}\right. \end{align} $$
$$ \begin{align} P_{G^{\prime}_n}(f)=\left\{\begin{array}{ll} 2^{-\dim(\mathfrak{a}_L)} \int_{i\mathfrak{a}_{M}^{L,*}}\beta_n(W_{f,\Pi_\lambda}) d\lambda \mbox{ if } \chi \mbox{ is Hermitian}, \\ \\ 0 \mbox{ otherwise.} \end{array}\right. \end{align} $$
6.2.8 Proof of Theorem 6.2.6.1 1. and 2.
Here, we prove parts 1 and 2 of Theorem 6.2.6.1. We will explain how to deduce the last part in the next subsection. The proof is actually along the same lines as that of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Theorem 6.2.5.1]. Therefore, we will be brief on the parts that are similar.
Set
and let
![]() $\mathcal {A}_0$
be the subspace of vectors
$\mathcal {A}_0$
be the subspace of vectors
![]() $\underline {x}=(x_{\ell })_{\ell \in I\cup J\cup K}\in \mathcal {A}$
such that
$\underline {x}=(x_{\ell })_{\ell \in I\cup J\cup K}\in \mathcal {A}$
such that
![]() $\sum _{\ell \in I\cup J \cup K} x_\ell =0$
. We equip
$\sum _{\ell \in I\cup J \cup K} x_\ell =0$
. We equip
![]() $\mathcal {A}$
with the product of Lebesgue measures and
$\mathcal {A}$
with the product of Lebesgue measures and
![]() $\mathcal {A}_0$
with the unique measure inducing on
$\mathcal {A}_0$
with the unique measure inducing on
![]() $\mathcal {A}/\mathcal {A}_0\simeq i\mathbb {R}$
the Lebesgue measure via the map
$\mathcal {A}/\mathcal {A}_0\simeq i\mathbb {R}$
the Lebesgue measure via the map
![]() $\underline {x}\mapsto \sum _{\ell \in I\cup J \cup K} x_\ell $
. We identify
$\underline {x}\mapsto \sum _{\ell \in I\cup J \cup K} x_\ell $
. We identify
![]() $\mathcal {A}$
with
$\mathcal {A}$
with
![]() $i\mathfrak {a}_M^*$
by sending
$i\mathfrak {a}_M^*$
by sending
![]() $\underline {x}\in \mathcal {A}$
to the unramified character
$\underline {x}\in \mathcal {A}$
to the unramified character
We note that this isomorphism sends
![]() $\mathcal {A}_0$
onto
$\mathcal {A}_0$
onto
![]() $i\mathfrak {a}_M^{G_r,*}$
. Furthermore, by our choice of measure on
$i\mathfrak {a}_M^{G_r,*}$
. Furthermore, by our choice of measure on
![]() $i\mathfrak {a}_M^*$
(see §2.1.8 as well as [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Eq. (2.3.1.1)]), this isomorphism sends the Haar measure just described on
$i\mathfrak {a}_M^*$
(see §2.1.8 as well as [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Eq. (2.3.1.1)]), this isomorphism sends the Haar measure just described on
![]() $\mathcal {A}$
to
$\mathcal {A}$
to
![]() $(2\pi )^{r}P$
times the Haar measure on
$(2\pi )^{r}P$
times the Haar measure on
![]() $i\mathfrak {a}_M^*$
, where we have set
$i\mathfrak {a}_M^*$
, where we have set
Set
![]() $f_{\underline {x}}=f_{\Pi _{\underline {x}}}$
for every
$f_{\underline {x}}=f_{\Pi _{\underline {x}}}$
for every
![]() $\underline {x}\in \mathcal {A}$
. Then, by a computation completely similar to that leading to [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Eq. (6.3.0.3)] (using one of the main results of [Reference LapidLap13]), we have
$\underline {x}\in \mathcal {A}$
. Then, by a computation completely similar to that leading to [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Eq. (6.3.0.3)] (using one of the main results of [Reference LapidLap13]), we have
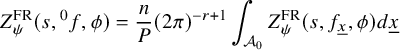 $$ \begin{align*} Z_\psi^{\mathrm{FR}}(s,{}^0f,\phi)=\frac{n}{P}(2\pi)^{-r+1}\int_{\mathcal{A}_0} Z_\psi^{\mathrm{FR}}(s,f_{\underline{x}},\phi) d\underline{x} \end{align*} $$
$$ \begin{align*} Z_\psi^{\mathrm{FR}}(s,{}^0f,\phi)=\frac{n}{P}(2\pi)^{-r+1}\int_{\mathcal{A}_0} Z_\psi^{\mathrm{FR}}(s,f_{\underline{x}},\phi) d\underline{x} \end{align*} $$
for
![]() $\Re (s)\gg 1$
.
$\Re (s)\gg 1$
.
Let
![]() $S_0$
be a finite set of places of F including the Archimedean ones and outside of which
$S_0$
be a finite set of places of F including the Archimedean ones and outside of which
![]() $\pi $
is unramified and let
$\pi $
is unramified and let
![]() $S_{0,f}\subset S_0$
be the subset of finite places. We fix, for every
$S_{0,f}\subset S_0$
be the subset of finite places. We fix, for every
![]() $l\in I\cup J\cup K$
and
$l\in I\cup J\cup K$
and
![]() $v\in S_{0,f}$
, polynomials
$v\in S_{0,f}$
, polynomials
![]() $Q_l(T), Q_{l,v}(T)\in \mathbb {C}[T]$
with all their roots in
$Q_l(T), Q_{l,v}(T)\in \mathbb {C}[T]$
with all their roots in
![]() $\mathcal {H}_{]0,1[}$
and
$\mathcal {H}_{]0,1[}$
and
![]() $\mathcal {H}_{]q_v^{-1},1[}$
, respectively, such that the products
$\mathcal {H}_{]q_v^{-1},1[}$
, respectively, such that the products
![]() $s\mapsto Q_l(s) L_\infty (s,\pi _l,\mathrm {As}^{(-1)^{n+1}})$
and
$s\mapsto Q_l(s) L_\infty (s,\pi _l,\mathrm {As}^{(-1)^{n+1}})$
and
![]() $s\mapsto Q_{l,v}(q_v^{-s})L_v(s,\pi _l,\mathrm {As}^{(-1)^{n+1}})$
have no pole in
$s\mapsto Q_{l,v}(q_v^{-s})L_v(s,\pi _l,\mathrm {As}^{(-1)^{n+1}})$
have no pole in
![]() $\mathcal {H}_{]0,1[}$
. Let
$\mathcal {H}_{]0,1[}$
. Let
![]() $I_0$
be the set of
$I_0$
be the set of
![]() $i\in I$
for which there exists
$i\in I$
for which there exists
![]() $i^*\in I$
(necessarily unique by regularity of
$i^*\in I$
(necessarily unique by regularity of
![]() $\chi $
) satisfying
$\chi $
) satisfying
![]() $\pi _{i^*}=\pi _i^*$
and fix a subset
$\pi _{i^*}=\pi _i^*$
and fix a subset
![]() $I'\subset I_0$
such that
$I'\subset I_0$
such that
![]() $I_0$
is the disjoint union of
$I_0$
is the disjoint union of
![]() $I'$
and
$I'$
and
![]() $(I')^*$
. Set
$(I')^*$
. Set
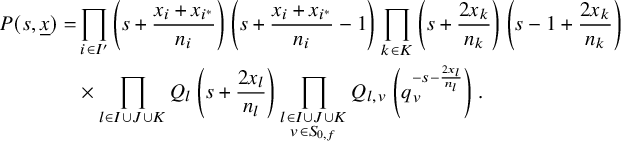 $$\begin{align*}\begin{aligned} P(s,\underline{x})= & \prod_{i\in I'} \left(s+\frac{x_i+x_{i^*}}{n_i}\right)\left(s+\frac{x_i+x_{i^*}}{n_i}-1\right)\prod_{k\in K} \left(s+\frac{2x_k}{n_k}\right)\left(s-1+\frac{2x_k}{n_k}\right)\\ & \times \prod_{l\in I\cup J\cup K} Q_l \left(s+\frac{2x_l}{n_l}\right) \prod_{\substack{l\in I\cup J \cup K\\ v\in S_{0,f}}} Q_{l,v}\left(q_v^{-s-\frac{2x_l}{n_l}}\right). \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} P(s,\underline{x})= & \prod_{i\in I'} \left(s+\frac{x_i+x_{i^*}}{n_i}\right)\left(s+\frac{x_i+x_{i^*}}{n_i}-1\right)\prod_{k\in K} \left(s+\frac{2x_k}{n_k}\right)\left(s-1+\frac{2x_k}{n_k}\right)\\ & \times \prod_{l\in I\cup J\cup K} Q_l \left(s+\frac{2x_l}{n_l}\right) \prod_{\substack{l\in I\cup J \cup K\\ v\in S_{0,f}}} Q_{l,v}\left(q_v^{-s-\frac{2x_l}{n_l}}\right). \end{aligned}\end{align*}$$
Then, we can prove exactly as in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, §6.3] that the two functions
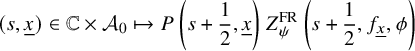 $$ \begin{align*} (s,\underline{x})\in \mathbb{C}\times \mathcal{A}_0\mapsto P\left(s+\frac{1}{2},\underline{x}\right)Z_\psi^{\mathrm{FR}} \left(s+\frac{1}{2},f_{\underline{x}},\phi \right) \end{align*} $$
$$ \begin{align*} (s,\underline{x})\in \mathbb{C}\times \mathcal{A}_0\mapsto P\left(s+\frac{1}{2},\underline{x}\right)Z_\psi^{\mathrm{FR}} \left(s+\frac{1}{2},f_{\underline{x}},\phi \right) \end{align*} $$
and
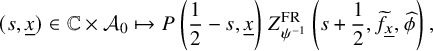 $$ \begin{align*} (s,\underline{x})\in \mathbb{C}\times \mathcal{A}_0\mapsto P\left(\frac{1}{2}-s,\underline{x}\right)Z_{\psi^{-1}}^{\mathrm{FR}} \left(s+\frac{1}{2},\widetilde{f}_{\underline{x}},\widehat{\phi} \right), \end{align*} $$
$$ \begin{align*} (s,\underline{x})\in \mathbb{C}\times \mathcal{A}_0\mapsto P\left(\frac{1}{2}-s,\underline{x}\right)Z_{\psi^{-1}}^{\mathrm{FR}} \left(s+\frac{1}{2},\widetilde{f}_{\underline{x}},\widehat{\phi} \right), \end{align*} $$
where
![]() $\widetilde {f}_{\underline {x}}(g)=f_{\underline {x}}({}^t g^{-1})$
, satisfy the conditions of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Corollary A.0.11.1]. Therefore, by the conclusion of this corollary, the map
$\widetilde {f}_{\underline {x}}(g)=f_{\underline {x}}({}^t g^{-1})$
, satisfy the conditions of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Corollary A.0.11.1]. Therefore, by the conclusion of this corollary, the map
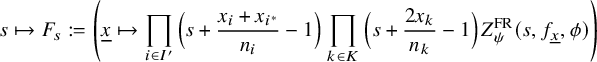 $$ \begin{align*}s\mapsto F_s:=\left(\underline{x}\mapsto \prod_{i\in I'} \Big(s+\frac{x_i+x_{i^*}}{n_i}-1 \Big)\prod_{k\in K} \Big(s+\frac{2x_k}{n_k}-1 \Big) Z_\psi^{\mathrm{FR}}(s,f_{\underline{x}},\phi) \right)\end{align*} $$
$$ \begin{align*}s\mapsto F_s:=\left(\underline{x}\mapsto \prod_{i\in I'} \Big(s+\frac{x_i+x_{i^*}}{n_i}-1 \Big)\prod_{k\in K} \Big(s+\frac{2x_k}{n_k}-1 \Big) Z_\psi^{\mathrm{FR}}(s,f_{\underline{x}},\phi) \right)\end{align*} $$
induces a holomorphic map
![]() $\mathcal {H}_{1-\epsilon }\to \mathcal {S}(\mathcal {A}_0)$
for some
$\mathcal {H}_{1-\epsilon }\to \mathcal {S}(\mathcal {A}_0)$
for some
![]() $\epsilon>0$
. This already implies that
$\epsilon>0$
. This already implies that
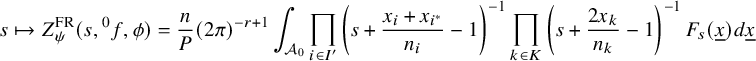 $$ \begin{align*}s\mapsto Z_\psi^{\mathrm{FR}}(s,{}^0f,\phi)=\frac{n}{P}(2\pi)^{-r+1}\int_{\mathcal{A}_0} \prod_{i\in I'} \left(s+\frac{x_i+x_{i^*}}{n_i}-1\right)^{-1}\prod_{k\in K} \left(s+\frac{2x_k}{n_k}-1 \right)^{-1} F_s(\underline{x}) d\underline{x}\end{align*} $$
$$ \begin{align*}s\mapsto Z_\psi^{\mathrm{FR}}(s,{}^0f,\phi)=\frac{n}{P}(2\pi)^{-r+1}\int_{\mathcal{A}_0} \prod_{i\in I'} \left(s+\frac{x_i+x_{i^*}}{n_i}-1\right)^{-1}\prod_{k\in K} \left(s+\frac{2x_k}{n_k}-1 \right)^{-1} F_s(\underline{x}) d\underline{x}\end{align*} $$
has an analytic continuation to
![]() $\mathcal {H}_{>1}$
. Moreover, if
$\mathcal {H}_{>1}$
. Moreover, if
![]() $\chi $
is not Hermitian, the linear forms
$\chi $
is not Hermitian, the linear forms
![]() $\underline {x}\in \mathcal {A}_0\mapsto x_i+x_{i^*}$
,
$\underline {x}\in \mathcal {A}_0\mapsto x_i+x_{i^*}$
,
![]() $i\in I'$
, and
$i\in I'$
, and
![]() $\underline {x}\in \mathcal {A}_0\mapsto x_k$
,
$\underline {x}\in \mathcal {A}_0\mapsto x_k$
,
![]() $k\in K$
, are linearly independent, and thus, by [Reference Beuzart-PlessisBP21, Lemma 3.11],
$k\in K$
, are linearly independent, and thus, by [Reference Beuzart-PlessisBP21, Lemma 3.11],
![]() $Z_\psi ^{\mathrm {FR}}(s,{}^0f,\phi )$
has a limit as
$Z_\psi ^{\mathrm {FR}}(s,{}^0f,\phi )$
has a limit as
![]() $s\to 1$
.
$s\to 1$
.
We assume from now on that
![]() $\chi $
is Hermitian so that
$\chi $
is Hermitian so that
![]() $I=I'\cup (I')^*$
and
$I=I'\cup (I')^*$
and
![]() $J=\emptyset $
. Set
$J=\emptyset $
. Set
![]() $\mathcal {A}^L=(i\mathbb {R})^{I'}$
,
$\mathcal {A}^L=(i\mathbb {R})^{I'}$
,
![]() $\mathcal {A}'=(i\mathbb {R})^{I'\cup K}$
and let
$\mathcal {A}'=(i\mathbb {R})^{I'\cup K}$
and let
![]() $\mathcal {A}^{\prime }_0$
be the subspace of
$\mathcal {A}^{\prime }_0$
be the subspace of
![]() $\underline {x}\in \mathcal {A}'$
such that
$\underline {x}\in \mathcal {A}'$
such that
![]() $\sum _{i\in I'} x_i+\sum _{k\in K} x_k=0$
. We have a short exact sequence
$\sum _{i\in I'} x_i+\sum _{k\in K} x_k=0$
. We have a short exact sequence
where the first map sends
![]() $\underline {x}\in \mathcal {A}^L$
to the vector
$\underline {x}\in \mathcal {A}^L$
to the vector
![]() $\underline {y}\in \mathcal {A}_0$
with coordinates
$\underline {y}\in \mathcal {A}_0$
with coordinates
![]() $y_i=x_i$
for
$y_i=x_i$
for
![]() $i\in I'$
,
$i\in I'$
,
![]() $y_i=-x_{i^*}$
for
$y_i=-x_{i^*}$
for
![]() $i\in (I')^*$
and
$i\in (I')^*$
and
![]() $y_k=0$
for
$y_k=0$
for
![]() $k\in K$
, whereas the second map is given by
$k\in K$
, whereas the second map is given by
We equip
![]() $\mathcal {A}^L$
and
$\mathcal {A}^L$
and
![]() $\mathcal {A}'$
with the products of Lebesgue measures and
$\mathcal {A}'$
with the products of Lebesgue measures and
![]() $\mathcal {A}^{\prime }_0$
as before with the unique measure inducing on
$\mathcal {A}^{\prime }_0$
as before with the unique measure inducing on
![]() $\mathcal {A}'/\mathcal {A}^{\prime }_0\simeq i\mathbb {R}$
the Lebesgue measure. Then, it is easy to see that the above exact sequence is compatible with the different Haar measures. In particular, we have
$\mathcal {A}'/\mathcal {A}^{\prime }_0\simeq i\mathbb {R}$
the Lebesgue measure. Then, it is easy to see that the above exact sequence is compatible with the different Haar measures. In particular, we have
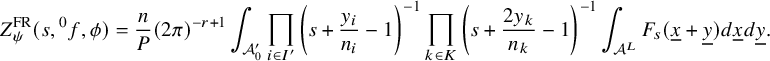 $$ \begin{align*}Z_\psi^{\mathrm{FR}}(s,{}^0f,\phi)=\frac{n}{P}(2\pi)^{-r+1}\int_{\mathcal{A}^{\prime}_0} \prod_{i\in I'} \left(s+\frac{y_i}{n_i}-1\right)^{-1}\prod_{k\in K} \left(s+\frac{2y_k}{n_k}-1 \right)^{-1} \int_{\mathcal{A}^L} F_s(\underline{x}+\underline{y}) d\underline{x} d\underline{y}.\end{align*} $$
$$ \begin{align*}Z_\psi^{\mathrm{FR}}(s,{}^0f,\phi)=\frac{n}{P}(2\pi)^{-r+1}\int_{\mathcal{A}^{\prime}_0} \prod_{i\in I'} \left(s+\frac{y_i}{n_i}-1\right)^{-1}\prod_{k\in K} \left(s+\frac{2y_k}{n_k}-1 \right)^{-1} \int_{\mathcal{A}^L} F_s(\underline{x}+\underline{y}) d\underline{x} d\underline{y}.\end{align*} $$
From this and [Reference Beuzart-PlessisBP21, Proposition 3.12], we obtain
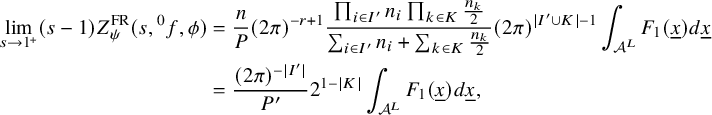 $$ \begin{align} \lim\limits_{s\to 1^+} (s-1)Z_\psi^{\mathrm{FR}}(s,{}^0f,\phi) & =\frac{n}{P}(2\pi)^{-r+1} \frac{\prod_{i\in I'} n_i \prod_{k\in K} \frac{n_k}{2}}{\sum_{i\in I'} n_i+\sum_{k\in K} \frac{n_k}{2}} (2\pi)^{\lvert I'\cup K\rvert-1}\int_{\mathcal{A}^L} F_1(\underline{x}) d\underline{x} \\ \nonumber & =\frac{(2\pi)^{-\lvert I'\rvert}}{P'} 2^{1-\lvert K\rvert}\int_{\mathcal{A}^L} F_1(\underline{x}) d\underline{x}, \end{align} $$
$$ \begin{align} \lim\limits_{s\to 1^+} (s-1)Z_\psi^{\mathrm{FR}}(s,{}^0f,\phi) & =\frac{n}{P}(2\pi)^{-r+1} \frac{\prod_{i\in I'} n_i \prod_{k\in K} \frac{n_k}{2}}{\sum_{i\in I'} n_i+\sum_{k\in K} \frac{n_k}{2}} (2\pi)^{\lvert I'\cup K\rvert-1}\int_{\mathcal{A}^L} F_1(\underline{x}) d\underline{x} \\ \nonumber & =\frac{(2\pi)^{-\lvert I'\rvert}}{P'} 2^{1-\lvert K\rvert}\int_{\mathcal{A}^L} F_1(\underline{x}) d\underline{x}, \end{align} $$
where we have set
![]() $P'=\prod _{i\in I'} n_i$
. Furthermore, from the unramified computation of [Reference FlickerFli88, Proposition 3] and [Reference Beuzart-PlessisBP21, Lemma 2.16.3], we have
$P'=\prod _{i\in I'} n_i$
. Furthermore, from the unramified computation of [Reference FlickerFli88, Proposition 3] and [Reference Beuzart-PlessisBP21, Lemma 2.16.3], we have
for
![]() $\underline {x}\in \mathcal {A}^L$
. However, the isomorphism
$\underline {x}\in \mathcal {A}^L$
. However, the isomorphism
![]() $\mathcal {A}\simeq i\mathfrak {a}_M^*$
sends
$\mathcal {A}\simeq i\mathfrak {a}_M^*$
sends
![]() $\mathcal {A}^L$
onto
$\mathcal {A}^L$
onto
![]() $i\mathfrak {a}_M^{L,*}$
and sends the measure on
$i\mathfrak {a}_M^{L,*}$
and sends the measure on
![]() $\mathcal {A}^L$
to
$\mathcal {A}^L$
to
![]() $\frac {(2\pi )^{\lvert I'\rvert } P'}{2^{\lvert I'\rvert }}$
times the measure on
$\frac {(2\pi )^{\lvert I'\rvert } P'}{2^{\lvert I'\rvert }}$
times the measure on
![]() $i\mathfrak {a}_M^{L,*}$
. As, by [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Corollary A.0.11.1], the function
$i\mathfrak {a}_M^{L,*}$
. As, by [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Corollary A.0.11.1], the function
![]() $F_1$
is Schwartz, so is the function
$F_1$
is Schwartz, so is the function
![]() $\lambda \in i\mathfrak {a}_M^{L,*}\mapsto \beta _n(W_{f,\Pi _\lambda })$
. Moreover, that the map (6.2.6.1) is continuous follows from (6.2.8.2) together with [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Theorem 6.2.5.1 1., Eq. (A.0.4.3)] and the closed graph theorem. Finally, combining (6.2.8.1) with (6.2.8.2) and the above comparison of measures readily gives the identity (6.2.6.2) and ends the proof of Theorem 6.2.6.1 2.
$\lambda \in i\mathfrak {a}_M^{L,*}\mapsto \beta _n(W_{f,\Pi _\lambda })$
. Moreover, that the map (6.2.6.1) is continuous follows from (6.2.8.2) together with [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Theorem 6.2.5.1 1., Eq. (A.0.4.3)] and the closed graph theorem. Finally, combining (6.2.8.1) with (6.2.8.2) and the above comparison of measures readily gives the identity (6.2.6.2) and ends the proof of Theorem 6.2.6.1 2.
6.2.9 Proof of Theorem 6.2.6.1 3.
The proof of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Theorem 6.2.6.1] applies verbatim noting that in loc. cit. the condition that
![]() $\chi $
is
$\chi $
is
![]() $*$
-regular is only used at the end of the proof to show that the family of bilinear forms denoted by
$*$
-regular is only used at the end of the proof to show that the family of bilinear forms denoted by
on
![]() $\mathcal {C}_\chi ([M_r])\times \mathcal {S}(\mathbb {A}^{n-r})$
extends holomorphically to
$\mathcal {C}_\chi ([M_r])\times \mathcal {S}(\mathbb {A}^{n-r})$
extends holomorphically to
![]() $\mathcal {H}_{s>1}$
. However, thanks to the proof of part 2 of Theorem 6.2.6.1 given in the previous subsection, we know that this property continues to hold for cuspidal data that are only assumed to be regular.
$\mathcal {H}_{s>1}$
. However, thanks to the proof of part 2 of Theorem 6.2.6.1 given in the previous subsection, we know that this property continues to hold for cuspidal data that are only assumed to be regular.
6.3 Proof of Theorem 6.1.1.1
Since
![]() $\chi $
is H-regular, by [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Theorem 7.1.3.1], the period integral
$\chi $
is H-regular, by [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Theorem 7.1.3.1], the period integral
extends continuously to a linear form on
![]() $\mathcal {T}_\chi ([G])$
that we shall denote by
$\mathcal {T}_\chi ([G])$
that we shall denote by
![]() $P_H^*$
. Then, by the very same argument as for [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Eq. (8.2.3.5)], we have
$P_H^*$
. Then, by the very same argument as for [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Eq. (8.2.3.5)], we have
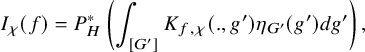 $$ \begin{align} I_\chi(f)=P_H^*\left(\int_{[G']} K_{f,\chi}(.,g') \eta_{G'}(g') dg' \right), \end{align} $$
$$ \begin{align} I_\chi(f)=P_H^*\left(\int_{[G']} K_{f,\chi}(.,g') \eta_{G'}(g') dg' \right), \end{align} $$
where the inner integral is taken in
![]() $\mathcal {T}_N([G])$
for N large enough. Furthermore, applying Corollary 6.2.7.1 instead of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Corollary 6.2.7.1], the discussion of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, §8.2.4] shows that this inner integral is identically zero if
$\mathcal {T}_N([G])$
for N large enough. Furthermore, applying Corollary 6.2.7.1 instead of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Corollary 6.2.7.1], the discussion of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, §8.2.4] shows that this inner integral is identically zero if
![]() $\chi $
is not Hermitian, whereas otherwise, it leads to the following expansion:
$\chi $
is not Hermitian, whereas otherwise, it leads to the following expansion:
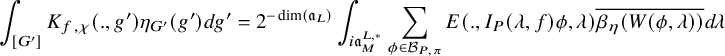 $$ \begin{align} \int_{[G']} K_{f,\chi}(.,g') \eta_{G'}(g') dg'=2^{-\dim(\mathfrak{a}_L)}\int_{i\mathfrak{a}_M^{L,*}} \sum_{\phi\in \mathcal{B}_{P,\pi}} E(.,I_P(\lambda,f)\phi,\lambda) \overline{\beta_\eta(W(\phi,\lambda))} d\lambda \end{align} $$
$$ \begin{align} \int_{[G']} K_{f,\chi}(.,g') \eta_{G'}(g') dg'=2^{-\dim(\mathfrak{a}_L)}\int_{i\mathfrak{a}_M^{L,*}} \sum_{\phi\in \mathcal{B}_{P,\pi}} E(.,I_P(\lambda,f)\phi,\lambda) \overline{\beta_\eta(W(\phi,\lambda))} d\lambda \end{align} $$
for
![]() $\mathcal {B}_{P,\pi }$
a K-basis of
$\mathcal {B}_{P,\pi }$
a K-basis of
![]() $I_{P(\mathbb {A})}^{G(\mathbb {A})}(\pi )$
. We assume from now on that
$I_{P(\mathbb {A})}^{G(\mathbb {A})}(\pi )$
. We assume from now on that
![]() $\chi $
is Hermitian. We claim the following:
$\chi $
is Hermitian. We claim the following:
-
(6.3.0.3) There exists
 $N>0$
such that for every
$N>0$
such that for every
 $\lambda \in i\mathfrak {a}_M^{L,*}$
, the series(6.3.0.4)converges absolutely in
$\lambda \in i\mathfrak {a}_M^{L,*}$
, the series(6.3.0.4)converges absolutely in $$ \begin{align} \sum_{\phi\in \mathcal{B}_{P,\pi}} E(.,I_P(\lambda,f)\phi,\lambda) \overline{\beta_\eta(W(\phi,\lambda))} \end{align} $$
$$ \begin{align} \sum_{\phi\in \mathcal{B}_{P,\pi}} E(.,I_P(\lambda,f)\phi,\lambda) \overline{\beta_\eta(W(\phi,\lambda))} \end{align} $$
 $\mathcal {T}_N([G])$
, and furthermore, the integral over
$\mathcal {T}_N([G])$
, and furthermore, the integral over
 $i\mathfrak {a}_M^{L,*}$
in the right-hand side of (6.3.0.2) converges absolutely in
$i\mathfrak {a}_M^{L,*}$
in the right-hand side of (6.3.0.2) converges absolutely in
 $\mathcal {T}_N([G])$
.
$\mathcal {T}_N([G])$
.
Indeed, that the series (6.3.0.4) converges absolutely in
![]() $\mathcal {T}_N([G])$
for large enough N (independent of
$\mathcal {T}_N([G])$
for large enough N (independent of
![]() $\lambda $
) follows from [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Theorem 2.9.8.1]. Note that for every
$\lambda $
) follows from [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Theorem 2.9.8.1]. Note that for every
![]() $\lambda \in i\mathfrak {a}_M^{L,*}$
and
$\lambda \in i\mathfrak {a}_M^{L,*}$
and
![]() $g\in [G]$
, we have
$g\in [G]$
, we have
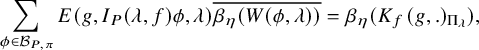 $$ \begin{align*}\sum_{\phi\in \mathcal{B}_{P,\pi}} E(g,I_P(\lambda,f)\phi,\lambda) \overline{\beta_\eta(W(\phi,\lambda))}=\beta_\eta(K_f(g,.)_{\Pi_\lambda}),\end{align*} $$
$$ \begin{align*}\sum_{\phi\in \mathcal{B}_{P,\pi}} E(g,I_P(\lambda,f)\phi,\lambda) \overline{\beta_\eta(W(\phi,\lambda))}=\beta_\eta(K_f(g,.)_{\Pi_\lambda}),\end{align*} $$
where
![]() $K_f(g,.)_{\Pi _\lambda }$
denotes the projection of the function
$K_f(g,.)_{\Pi _\lambda }$
denotes the projection of the function
![]() $K_{f}(g,.)\in \mathcal {S}([G])$
to
$K_{f}(g,.)\in \mathcal {S}([G])$
to
![]() $\Pi _\lambda $
as defined in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Eq. (2.9.8.14)]. Moreover, by [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Lemma 2.10.1.1], for every continuous semi-norm
$\Pi _\lambda $
as defined in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Eq. (2.9.8.14)]. Moreover, by [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Lemma 2.10.1.1], for every continuous semi-norm
![]() $\mu $
on
$\mu $
on
![]() $\mathcal {S}([G])$
, we can find
$\mathcal {S}([G])$
, we can find
![]() $N_\mu>0$
such that for every
$N_\mu>0$
such that for every
![]() $f'\in \mathcal {S}(G(\mathbb {A}))$
, we have
$f'\in \mathcal {S}(G(\mathbb {A}))$
, we have
In particular, combining this estimate with the first part of Theorem 6.2.6.1, we deduce that for each
![]() $d>0$
, we can find
$d>0$
, we can find
![]() $N_d>0$
such that, for
$N_d>0$
such that, for
![]() $f'\in \mathcal {S}(G(\mathbb {A}))$
, we have
$f'\in \mathcal {S}(G(\mathbb {A}))$
, we have
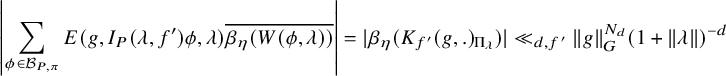 $$ \begin{align*}\left\lvert \sum_{\phi\in \mathcal{B}_{P,\pi}} E(g,I_P(\lambda,f')\phi,\lambda) \overline{\beta_\eta(W(\phi,\lambda))} \right\rvert=\lvert \beta_\eta(K_{f'}(g,.)_{\Pi_\lambda})\rvert \ll_{d,f'} \lVert g\rVert_G^{N_d} (1+\lVert \lambda\rVert)^{-d}\end{align*} $$
$$ \begin{align*}\left\lvert \sum_{\phi\in \mathcal{B}_{P,\pi}} E(g,I_P(\lambda,f')\phi,\lambda) \overline{\beta_\eta(W(\phi,\lambda))} \right\rvert=\lvert \beta_\eta(K_{f'}(g,.)_{\Pi_\lambda})\rvert \ll_{d,f'} \lVert g\rVert_G^{N_d} (1+\lVert \lambda\rVert)^{-d}\end{align*} $$
for
![]() $(\lambda ,g)\in i\mathfrak {a}_M^{L,*}\times [G]$
. Choosing d such that
$(\lambda ,g)\in i\mathfrak {a}_M^{L,*}\times [G]$
. Choosing d such that
![]() $\lambda \mapsto (1+\lVert \lambda \rVert )^{-d}$
is integrable on
$\lambda \mapsto (1+\lVert \lambda \rVert )^{-d}$
is integrable on
![]() $i\mathfrak {a}_M^{L,*}$
and applying the above inequality to
$i\mathfrak {a}_M^{L,*}$
and applying the above inequality to
![]() $f'=R(X)f$
for
$f'=R(X)f$
for
![]() $X\in \mathcal {U}(\mathfrak {g})$
gives the second part of (6.3.0.3).
$X\in \mathcal {U}(\mathfrak {g})$
gives the second part of (6.3.0.3).
We now need to recall how the extension
![]() $P_H^*$
is defined in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Theorem 7.1.3.1]: for
$P_H^*$
is defined in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Theorem 7.1.3.1]: for
![]() $\Phi \in \mathcal {T}_\chi ([G])$
, the integral
$\Phi \in \mathcal {T}_\chi ([G])$
, the integral
where
![]() $W_\Phi (h):=\int _{[N]}\Phi (uh) \psi _N(u)^{-1}du$
, a priori only defined when
$W_\Phi (h):=\int _{[N]}\Phi (uh) \psi _N(u)^{-1}du$
, a priori only defined when
![]() $\Re (s)$
is sufficiently large, admits an analytic continuation to
$\Re (s)$
is sufficiently large, admits an analytic continuation to
![]() $\mathbb {C}$
and we have
$\mathbb {C}$
and we have
Therefore, by continuity of
![]() $P_H^*$
, (6.3.0.2) and (6.3.0.3), we obtain
$P_H^*$
, (6.3.0.2) and (6.3.0.3), we obtain
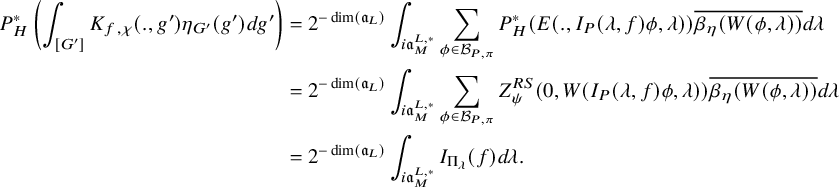 $$\begin{align*}\begin{aligned} P_H^*\left(\int_{[G']} K_{f,\chi}(.,g') \eta_{G'}(g') dg' \right) & =2^{-\dim(\mathfrak{a}_L)}\int_{i\mathfrak{a}_M^{L,*}} \sum_{\phi\in \mathcal{B}_{P,\pi}} P_H^*(E(.,I_P(\lambda,f)\phi,\lambda)) \overline{\beta_\eta(W(\phi,\lambda))} d\lambda \\ & =2^{-\dim(\mathfrak{a}_L)}\int_{i\mathfrak{a}_M^{L,*}} \sum_{\phi\in \mathcal{B}_{P,\pi}} Z^{RS}_\psi(0,W(I_P(\lambda,f)\phi,\lambda)) \overline{\beta_\eta(W(\phi,\lambda))} d\lambda \\ & =2^{-\dim(\mathfrak{a}_L)}\int_{i\mathfrak{a}_M^{L,*}} I_{\Pi_\lambda}(f) d\lambda. \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} P_H^*\left(\int_{[G']} K_{f,\chi}(.,g') \eta_{G'}(g') dg' \right) & =2^{-\dim(\mathfrak{a}_L)}\int_{i\mathfrak{a}_M^{L,*}} \sum_{\phi\in \mathcal{B}_{P,\pi}} P_H^*(E(.,I_P(\lambda,f)\phi,\lambda)) \overline{\beta_\eta(W(\phi,\lambda))} d\lambda \\ & =2^{-\dim(\mathfrak{a}_L)}\int_{i\mathfrak{a}_M^{L,*}} \sum_{\phi\in \mathcal{B}_{P,\pi}} Z^{RS}_\psi(0,W(I_P(\lambda,f)\phi,\lambda)) \overline{\beta_\eta(W(\phi,\lambda))} d\lambda \\ & =2^{-\dim(\mathfrak{a}_L)}\int_{i\mathfrak{a}_M^{L,*}} I_{\Pi_\lambda}(f) d\lambda. \end{aligned}\end{align*}$$
Together with (6.3.0.1), this ends the proof of the theorem.
7 Proof of Gan-Gross-Prasad conjecture: Eisenstein case
7.1 Global comparison of relative characters
7.1.1 Notations
We follow the notations of Sections 3 and 4. In particular, we fix an integer
![]() $n\geqslant 1$
. We consider the group
$n\geqslant 1$
. We consider the group
![]() $G=G_n\times G_{n+1}$
and, for
$G=G_n\times G_{n+1}$
and, for
![]() $h\in \mathcal {H}_n$
, the groups
$h\in \mathcal {H}_n$
, the groups
![]() $U_h^{\prime }\subset U_h$
. Since n is fixed, we drop it from the notation:
$U_h^{\prime }\subset U_h$
. Since n is fixed, we drop it from the notation:
![]() $\mathcal {H}=\mathcal {H}_n$
. The various Haar measures are those considered in §2.1.8.
$\mathcal {H}=\mathcal {H}_n$
. The various Haar measures are those considered in §2.1.8.
7.1.2
Let
![]() $V_{F,\infty }\subset S_0\subset V_F$
be a finite set of places containing all the places that are ramified in E. For every
$V_{F,\infty }\subset S_0\subset V_F$
be a finite set of places containing all the places that are ramified in E. For every
![]() $v\in V_F$
, we set
$v\in V_F$
, we set
![]() $E_v=E\otimes _F F_v$
, and when
$E_v=E\otimes _F F_v$
, and when
![]() $v\notin V_{F,\infty }$
, we denote by
$v\notin V_{F,\infty }$
, we denote by
![]() $\mathcal {O}_{E_v}\subset E_v$
its ring of integers. Let
$\mathcal {O}_{E_v}\subset E_v$
its ring of integers. Let
![]() $\mathcal {H}^\circ \subset \mathcal {H}$
be the (finite) subset of Hermitian spaces of rank n over E that admits a selfdual
$\mathcal {H}^\circ \subset \mathcal {H}$
be the (finite) subset of Hermitian spaces of rank n over E that admits a selfdual
![]() $\mathcal {O}_{E_v}$
-lattice for every
$\mathcal {O}_{E_v}$
-lattice for every
![]() $v\notin S_0$
. For each
$v\notin S_0$
. For each
![]() $h\in \mathcal {H}^\circ $
, the group
$h\in \mathcal {H}^\circ $
, the group
![]() $U_h$
is then defined over
$U_h$
is then defined over
![]() $\mathcal {O}_F^{S_0}$
, and we fix a choice of such a model. For
$\mathcal {O}_F^{S_0}$
, and we fix a choice of such a model. For
![]() $v\notin S_0$
, we define the open compact subgroups
$v\notin S_0$
, we define the open compact subgroups
![]() $K_{h,v}=U_h(\mathcal {O}_v)$
and
$K_{h,v}=U_h(\mathcal {O}_v)$
and
![]() $K_v=G(\mathcal {O}_v)$
, respectively, of
$K_v=G(\mathcal {O}_v)$
, respectively, of
![]() $U_h(F_v)$
and
$U_h(F_v)$
and
![]() $G(F_v)$
. We set
$G(F_v)$
. We set
We choose also for each
![]() $v\in S_0$
some maximal compact subgroup
$v\in S_0$
some maximal compact subgroup
![]() $K_{h,v}\subset U_h(F_v)$
and
$K_{h,v}\subset U_h(F_v)$
and
![]() $K_v\subset G(F_v)$
(see §3.1.3).
$K_v\subset G(F_v)$
(see §3.1.3).
Let
![]() $v\notin S_0$
. We denote by
$v\notin S_0$
. We denote by
![]() $\mathcal {S}^\circ (U_h(F_v))$
, resp.
$\mathcal {S}^\circ (U_h(F_v))$
, resp.
![]() $\mathcal {S}^{\circ }(G(F_v))$
, the corresponding spherical Hecke algebra. We have the base change homomorphism
$\mathcal {S}^{\circ }(G(F_v))$
, the corresponding spherical Hecke algebra. We have the base change homomorphism
We denote by
![]() $\mathcal {S}^{\circ }(U_h(\mathbb {A}^{S_0}))$
, resp.
$\mathcal {S}^{\circ }(U_h(\mathbb {A}^{S_0}))$
, resp.
![]() $\mathcal {S}^{\circ }(G(\mathbb {A}^{S_0}))$
, the restricted tensor product of
$\mathcal {S}^{\circ }(G(\mathbb {A}^{S_0}))$
, the restricted tensor product of
![]() $\mathcal {S}^\circ (U_h(F_v))$
, resp.
$\mathcal {S}^\circ (U_h(F_v))$
, resp.
![]() $\mathcal {S}^{\circ }(G(F_v))$
, for
$\mathcal {S}^{\circ }(G(F_v))$
, for
![]() $v\notin S_0$
. We set
$v\notin S_0$
. We set
![]() $BC_h^{S_0}=\otimes _{v\notin S_0} BC_{h,v}$
.
$BC_h^{S_0}=\otimes _{v\notin S_0} BC_{h,v}$
.
We also denote by
![]() $ \mathcal {S}^\circ (G(\mathbb {A}))\subset \mathcal {S} (G(\mathbb {A}))$
and
$ \mathcal {S}^\circ (G(\mathbb {A}))\subset \mathcal {S} (G(\mathbb {A}))$
and
![]() $\mathcal {S}^\circ (U_h(\mathbb {A}))\subset \mathcal {S}(U_h(\mathbb {A}))$
, for
$\mathcal {S}^\circ (U_h(\mathbb {A}))\subset \mathcal {S}(U_h(\mathbb {A}))$
, for
![]() $h\in \mathcal {H}^\circ $
, the subspaces of functions that are, respectively, bi-
$h\in \mathcal {H}^\circ $
, the subspaces of functions that are, respectively, bi-
![]() $K^\circ $
-invariant and bi-
$K^\circ $
-invariant and bi-
![]() $K_h^\circ $
-invariant.
$K_h^\circ $
-invariant.
7.1.3 Transfer
Let
![]() $h\in \mathcal {H}^\circ $
. We shall say that
$h\in \mathcal {H}^\circ $
. We shall say that
![]() $f_{S_0}\in \mathcal {S}(G(F_{S_0}))$
and
$f_{S_0}\in \mathcal {S}(G(F_{S_0}))$
and
![]() $f_{S_0}^h \in \mathcal {S}(U_h(F_{S_0}))$
are transfers if the functions
$f_{S_0}^h \in \mathcal {S}(U_h(F_{S_0}))$
are transfers if the functions
![]() $f_{S_0}$
and
$f_{S_0}$
and
![]() $f_{S_0}^h$
have matching regular orbital integrals in the sense of [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21, Definition 4.4].
$f_{S_0}^h$
have matching regular orbital integrals in the sense of [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21, Definition 4.4].
7.1.4 Cuspidal datum
 $\chi _0$
and H-regular Hermitian Arthur parameter
$\chi _0$
and H-regular Hermitian Arthur parameter
 $\Pi $
$\Pi $
Let P be a standard parabolic subgroup of G and
![]() $\pi $
be a cuspidal automorphic representation of
$\pi $
be a cuspidal automorphic representation of
![]() $M=M_P$
. Let
$M=M_P$
. Let
![]() $\chi _0\in \mathfrak {X}(G)$
be the class of the pair
$\chi _0\in \mathfrak {X}(G)$
be the class of the pair
![]() $(M_P,\pi )$
. We assume henceforth that
$(M_P,\pi )$
. We assume henceforth that
![]() $\chi _0$
is a Hermitian
$\chi _0$
is a Hermitian
![]() $(G,H)$
-regular cuspidal datum in the sense of §4.1.3. We assume also that
$(G,H)$
-regular cuspidal datum in the sense of §4.1.3. We assume also that
![]() $(M,\pi )$
satisfies the conditions of §4.1.4 and that L is the standard Levi subgroup containing M defined in this §. Set
$(M,\pi )$
satisfies the conditions of §4.1.4 and that L is the standard Levi subgroup containing M defined in this §. Set
![]() $\Pi =\operatorname {\mathrm {Ind}}_P^G(\pi )$
: this is a H-regular Hermitian Arthur parameter in the sense of §1.2.1. We assume that
$\Pi =\operatorname {\mathrm {Ind}}_P^G(\pi )$
: this is a H-regular Hermitian Arthur parameter in the sense of §1.2.1. We assume that
![]() $S_0$
is large enough so that
$S_0$
is large enough so that
![]() $\Pi $
admits
$\Pi $
admits
![]() $K^\circ $
-fixed vectors. Let
$K^\circ $
-fixed vectors. Let
![]() $\Pi _0$
be the discrete component of
$\Pi _0$
be the discrete component of
![]() $\Pi $
(see §1.1.2).
$\Pi $
(see §1.1.2).
The group
![]() $S_\Pi =S_{\Pi _0}$
is defined in §§1.1.2 and 1.1.4. Its order can be computed as follows:
$S_\Pi =S_{\Pi _0}$
is defined in §§1.1.2 and 1.1.4. Its order can be computed as follows:
For any
![]() $\lambda \in i\mathfrak {a}_M^{L,*}$
, we shall use the distribution
$\lambda \in i\mathfrak {a}_M^{L,*}$
, we shall use the distribution
![]() $I_{P,\pi }(\lambda ,\cdot )$
on
$I_{P,\pi }(\lambda ,\cdot )$
on
![]() $\mathcal {S}(G(\mathbb {A}))$
defined in §4.1.7.
$\mathcal {S}(G(\mathbb {A}))$
defined in §4.1.7.
7.1.5
Let
![]() $S^{\prime }_0$
be the union of
$S^{\prime }_0$
be the union of
![]() $S_0\setminus V_{F,\infty }$
and the set of all finite places of F that are inert in E. Let
$S_0\setminus V_{F,\infty }$
and the set of all finite places of F that are inert in E. Let
![]() $h\in \mathcal {H}^\circ $
and let
$h\in \mathcal {H}^\circ $
and let
![]() $\mathfrak {X}_\Pi ^h\subset \mathfrak {X}(U_h)$
be the set of cuspidal data represented by pairs
$\mathfrak {X}_\Pi ^h\subset \mathfrak {X}(U_h)$
be the set of cuspidal data represented by pairs
![]() $(M_h,\sigma )$
such that
$(M_h,\sigma )$
such that
![]() $M_h$
is the standard Levi factor of a standard parabolic sugroup
$M_h$
is the standard Levi factor of a standard parabolic sugroup
![]() $P_h$
of
$P_h$
of
![]() $U_h$
and
$U_h$
and
![]() $\sigma $
is a cuspidal automorphic representation of
$\sigma $
is a cuspidal automorphic representation of
![]() $M_h(\mathbb {A})$
such that
$M_h(\mathbb {A})$
such that
-
•
 $\Pi $
is a weak base change of
$\Pi $
is a weak base change of
 $(P_h,\sigma )$
(in the sense of §§1.1.3 and 1.1.4);
$(P_h,\sigma )$
(in the sense of §§1.1.3 and 1.1.4); -
•
 $\sigma $
is
$\sigma $
is
 $\prod _{v\notin S_0} (M_h(F_v)\cap K_{h,v})$
-unramified;
$\prod _{v\notin S_0} (M_h(F_v)\cap K_{h,v})$
-unramified; -
• with the identifications
 $M_h=G^\sharp \times U$
where
$M_h=G^\sharp \times U$
where
 $G^\sharp $
is a product of linear groups and
$G^\sharp $
is a product of linear groups and
 $U=U(h_{n_0})\times U(h_{n_0^{\prime }})$
for some
$U=U(h_{n_0})\times U(h_{n_0^{\prime }})$
for some
 $h_{n^{\prime }_0} \in \mathcal {H}_{n_0}$
and
$h_{n^{\prime }_0} \in \mathcal {H}_{n_0}$
and
 $h_{n_0} \in \mathcal {H}_{n_0^{\prime }}$
and
$h_{n_0} \in \mathcal {H}_{n_0^{\prime }}$
and
 $\sigma =\sigma ^\sharp \boxtimes \sigma _0$
accordingly (where
$\sigma =\sigma ^\sharp \boxtimes \sigma _0$
accordingly (where
 $\sigma _0$
is a cuspidal automorphic representation of
$\sigma _0$
is a cuspidal automorphic representation of
 $U(\mathbb {A})$
), for all
$U(\mathbb {A})$
), for all
 $v\notin S_0^{\prime }\cup V_{F,\infty }$
, the representation
$v\notin S_0^{\prime }\cup V_{F,\infty }$
, the representation
 $\Pi _{0,v}$
is the split base change of the representation
$\Pi _{0,v}$
is the split base change of the representation
 $\sigma _{0,v}$
.
$\sigma _{0,v}$
.
Since
![]() $\Pi $
is a H-regular Hermitian Arthur parameter, the class of
$\Pi $
is a H-regular Hermitian Arthur parameter, the class of
![]() $(M_h,\sigma )$
is
$(M_h,\sigma )$
is
![]() $(U,U')$
-regular in the sense of §3.5.2. Moreover, there is a natural isomorphism
$(U,U')$
-regular in the sense of §3.5.2. Moreover, there is a natural isomorphism
More precisely, we wrote
![]() $M_h=G^\sharp \times U$
, where
$M_h=G^\sharp \times U$
, where
![]() $G^\sharp $
is a product of linear groups
$G^\sharp $
is a product of linear groups
![]() $G_{m_i}$
for some integers
$G_{m_i}$
for some integers
![]() $m_i$
and
$m_i$
and
![]() $1\leqslant i \leqslant s$
so that
$1\leqslant i \leqslant s$
so that
![]() $\mathfrak {a}_{M_h}^*=\oplus _{i=1}^s \mathfrak {a}_{G_{m_i}}^*$
. But the product
$\mathfrak {a}_{M_h}^*=\oplus _{i=1}^s \mathfrak {a}_{G_{m_i}}^*$
. But the product
![]() $\prod _{i=1}^s (G_{m_i}\times G_{m_i})$
is also a factor in the decomposition of M into a product of linear groups. So the space
$\prod _{i=1}^s (G_{m_i}\times G_{m_i})$
is also a factor in the decomposition of M into a product of linear groups. So the space
![]() $\mathfrak {a}_{M_h}^*\oplus \mathfrak {a}_{M_h}^*=\oplus _{i=1}^s (\mathfrak {a}_{G_{m_i}}^*\oplus \mathfrak {a}_{G_{m_i}}^*)$
is a subspace of
$\mathfrak {a}_{M_h}^*\oplus \mathfrak {a}_{M_h}^*=\oplus _{i=1}^s (\mathfrak {a}_{G_{m_i}}^*\oplus \mathfrak {a}_{G_{m_i}}^*)$
is a subspace of
![]() $\mathfrak {a}_M^{*}$
. The antidiagonal map
$\mathfrak {a}_M^{*}$
. The antidiagonal map
![]() $x\mapsto (x,-x)$
then identifies
$x\mapsto (x,-x)$
then identifies
![]() $\mathfrak {a}_{M_h}^*$
with a subspace of
$\mathfrak {a}_{M_h}^*$
with a subspace of
![]() $\mathfrak {a}_{M_h}^*\oplus \mathfrak {a}_{M_h}^*$
and thus of
$\mathfrak {a}_{M_h}^*\oplus \mathfrak {a}_{M_h}^*$
and thus of
![]() $\mathfrak {a}_M^{*}$
, and this subspace is precisely
$\mathfrak {a}_M^{*}$
, and this subspace is precisely
![]() $\mathfrak {a}_M^{L,*}$
.
$\mathfrak {a}_M^{L,*}$
.
Remarks 7.1.5.1. The base change map
![]() $bc$
depends implicitly on the choice of the pair
$bc$
depends implicitly on the choice of the pair
![]() $(M_h,\sigma )$
. Indeed, if
$(M_h,\sigma )$
. Indeed, if
![]() $(M_{1,h},\sigma _1)$
is a pair equivalent to
$(M_{1,h},\sigma _1)$
is a pair equivalent to
![]() $(M_h,\sigma )$
and if
$(M_h,\sigma )$
and if
![]() $w\in W(M_h,M_{1,h})$
is such that
$w\in W(M_h,M_{1,h})$
is such that
![]() $\sigma _1=w\cdot \sigma $
, then
$\sigma _1=w\cdot \sigma $
, then
![]() $bc_{(M_{1,h},\sigma _1)}=w \circ bc_{(M_h,\sigma )}$
(where we view w as a map
$bc_{(M_{1,h},\sigma _1)}=w \circ bc_{(M_h,\sigma )}$
(where we view w as a map
![]() $\mathfrak {a}_{M_h}^*\to \mathfrak {a}_{M_{1,h}}^*$
). In order to not burden the notation, we shall omit the subscript
$\mathfrak {a}_{M_h}^*\to \mathfrak {a}_{M_{1,h}}^*$
). In order to not burden the notation, we shall omit the subscript
![]() $(M_h,\sigma )$
from the notation
$(M_h,\sigma )$
from the notation
![]() $bc$
in (7.1.5.1).
$bc$
in (7.1.5.1).
We warn also the reader that the map (7.1.5.1) does not preserve the various choices of Haar measures. In fact, the pullback of the measure on
![]() $\mathfrak {a}_{M_h}^*$
is
$\mathfrak {a}_{M_h}^*$
is
![]() $2^{\dim (\mathfrak {a}_{M}^L)}$
times the measure on
$2^{\dim (\mathfrak {a}_{M}^L)}$
times the measure on
![]() $\mathfrak {a}_M^{L,*}$
.
$\mathfrak {a}_M^{L,*}$
.
For any
![]() $\lambda \in i\mathfrak {a}_{M}^{L,*}$
, we set
$\lambda \in i\mathfrak {a}_{M}^{L,*}$
, we set
where the sum is over a set of representatives
![]() $(M_h,\sigma )$
of classes in
$(M_h,\sigma )$
of classes in
![]() $\mathfrak {X}_\Pi ^h$
and
$\mathfrak {X}_\Pi ^h$
and
![]() $J^{h}_{P_h,\sigma }(bc(\lambda ),f)=J^{U_h}_{P_h,\sigma }(bc(\lambda ),f)$
is the distribution introduced in §3.5.5. By Proposition 3.5.5.1 and remarks 7.1.5.1, the distribution does not depend on the choice of the representative.
$J^{h}_{P_h,\sigma }(bc(\lambda ),f)=J^{U_h}_{P_h,\sigma }(bc(\lambda ),f)$
is the distribution introduced in §3.5.5. By Proposition 3.5.5.1 and remarks 7.1.5.1, the distribution does not depend on the choice of the representative.
The sum above is a priori absolutely convergent and the convergence is uniform on compact subset of
![]() $i\mathfrak {a}_M^{L,*}$
(as follows from from a reinforcement of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, proposition 2.8.4.1] based on results of Müller; see [Reference MüllerMül98, corollary 0.3]). In particular, the expression
$i\mathfrak {a}_M^{L,*}$
(as follows from from a reinforcement of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, proposition 2.8.4.1] based on results of Müller; see [Reference MüllerMül98, corollary 0.3]). In particular, the expression
![]() $J^{h}_{\Pi }(\lambda ,f)$
is holomorphic for
$J^{h}_{\Pi }(\lambda ,f)$
is holomorphic for
![]() $\lambda \in i\mathfrak {a}_{M}^{L,*}$
.
$\lambda \in i\mathfrak {a}_{M}^{L,*}$
.
7.1.6 A global relative characters identity
Theorem 7.1.6.1. Let
![]() $f\in \mathcal {S}^\circ (G(\mathbb {A}))$
and
$f\in \mathcal {S}^\circ (G(\mathbb {A}))$
and
![]() $f^h\in \mathcal {S}^\circ (U_h(\mathbb {A}))$
for every
$f^h\in \mathcal {S}^\circ (U_h(\mathbb {A}))$
for every
![]() $h\in \mathcal {H}^\circ $
. Assume that the following properties are satisfied for every
$h\in \mathcal {H}^\circ $
. Assume that the following properties are satisfied for every
![]() $h\in \mathcal {H}^\circ $
:
$h\in \mathcal {H}^\circ $
:
-
1.
 $f=(\Delta _H^{S_0,*} \Delta _{G'}^{S_0,*} ) f_{S_0}\otimes f^{S_0}$
with
$f=(\Delta _H^{S_0,*} \Delta _{G'}^{S_0,*} ) f_{S_0}\otimes f^{S_0}$
with
 $f_{S_0}\in \mathcal {S}(G(F_{S_0}))$
and
$f_{S_0}\in \mathcal {S}(G(F_{S_0}))$
and
 $f^{S_0}\in \mathcal {S}^{\circ }(G(\mathbb {A}^{S_0}))$
.
$f^{S_0}\in \mathcal {S}^{\circ }(G(\mathbb {A}^{S_0}))$
. -
2.
 $f^h= (\Delta _{U_h^{\prime }}^{S_0})^2f^h_{S_0}\otimes f^{h,S_0}$
with
$f^h= (\Delta _{U_h^{\prime }}^{S_0})^2f^h_{S_0}\otimes f^{h,S_0}$
with
 $f_{S_0}^h \in \mathcal {S}(U_h(F_{S_0}))$
and
$f_{S_0}^h \in \mathcal {S}(U_h(F_{S_0}))$
and
 $f^{h,S_0} \in \mathcal {S}^{\circ }(U_h(\mathbb {A}^{S_0}))$
.
$f^{h,S_0} \in \mathcal {S}^{\circ }(U_h(\mathbb {A}^{S_0}))$
. -
3. The functions
 $f_{S_0}$
and
$f_{S_0}$
and
 $f_{S_0}^h$
are transfers.
$f_{S_0}^h$
are transfers. -
4.
 $f^{h,S_0}=BC^{S_0}_h(f^{S_0})$
$f^{h,S_0}=BC^{S_0}_h(f^{S_0})$
-
5. The function
 $f^{S_0}$
is a product of a smooth compactly supported function on the restricted product
$f^{S_0}$
is a product of a smooth compactly supported function on the restricted product
 $\prod _{v\notin S_0^{\prime }\cup V_{F,\infty }}' G(F_v)$
by the characteristic function of
$\prod _{v\notin S_0^{\prime }\cup V_{F,\infty }}' G(F_v)$
by the characteristic function of
 $\prod _{v\in S_0^{\prime }\setminus S_0} G(\mathcal {O}_v)$
.
$\prod _{v\in S_0^{\prime }\setminus S_0} G(\mathcal {O}_v)$
.
Then for any
![]() $\lambda \in i\mathfrak {a}_M^{L,*}$
, we have
$\lambda \in i\mathfrak {a}_M^{L,*}$
, we have
Remark 7.1.6.2. If
![]() $\Pi $
is a discrete Arthur parameter (that is,
$\Pi $
is a discrete Arthur parameter (that is,
![]() $L=M$
), the statement reduces to [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, proposition 10.1.6.1]. As we observed in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22], if the assumptions hold for the set
$L=M$
), the statement reduces to [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, proposition 10.1.6.1]. As we observed in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22], if the assumptions hold for the set
![]() $S_0$
, they also hold for any large enough finite set containing
$S_0$
, they also hold for any large enough finite set containing
![]() $S_0$
.
$S_0$
.
7.1.7 Proof of Theorem 7.1.6.1
As in [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21] and [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22], our proof is based on the global comparison of Jacquet-Rallis trace formulas and the use of multipliers to isolate some spectral contributions. However, the spectral contributions we consider here are continuous in nature, and we need further considerations.
In [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Theorem 3.2.4.1], we defined a distribution I on
![]() $\mathcal {S}(G(\mathbb {A}))$
: this is the ‘Jacquet-Rallis trace formula’ for G. For unitary groups, we have an analogous distribution
$\mathcal {S}(G(\mathbb {A}))$
: this is the ‘Jacquet-Rallis trace formula’ for G. For unitary groups, we have an analogous distribution
![]() $J^h=J^{U_h}$
on
$J^h=J^{U_h}$
on
![]() $\mathcal {S}(U_h(\mathbb {A}))$
for each
$\mathcal {S}(U_h(\mathbb {A}))$
for each
![]() $h\in \mathcal {H}$
(see Theorem 3.2.3.1). By [Reference Chaudouard and ZydorCZ21, théorème 1.6.1.1], we have for functions f and
$h\in \mathcal {H}$
(see Theorem 3.2.3.1). By [Reference Chaudouard and ZydorCZ21, théorème 1.6.1.1], we have for functions f and
![]() $f^h$
as in the statement
$f^h$
as in the statement
In the following, for each finite place outside
![]() $S_0$
, we fix open compact subgroups
$S_0$
, we fix open compact subgroups
![]() $K_v^{\prime }\subset K_v$
and
$K_v^{\prime }\subset K_v$
and
![]() $K_{h,v}'\subset K_{h,v}$
of finite index. We set
$K_{h,v}'\subset K_{h,v}$
of finite index. We set
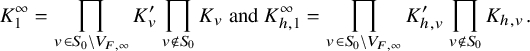 $$ \begin{align*} K^\infty_1=\prod_{v\in S_0\setminus V_{F,\infty} } K_v^{\prime} \prod_{v\notin S_0} K_v\text{ and } K^\infty_{h,1}=\prod_{v\in S_0\setminus V_{F,\infty} } K_{h,v}' \prod_{v\notin S_0}K_{h,v}. \end{align*} $$
$$ \begin{align*} K^\infty_1=\prod_{v\in S_0\setminus V_{F,\infty} } K_v^{\prime} \prod_{v\notin S_0} K_v\text{ and } K^\infty_{h,1}=\prod_{v\in S_0\setminus V_{F,\infty} } K_{h,v}' \prod_{v\notin S_0}K_{h,v}. \end{align*} $$
We denote by
![]() $\mathcal {S}(G(\mathbb {A}),K_1^\infty )\subset \mathcal {S}^\circ (G(\mathbb {A}))$
, resp.
$\mathcal {S}(G(\mathbb {A}),K_1^\infty )\subset \mathcal {S}^\circ (G(\mathbb {A}))$
, resp.
![]() $\mathcal {S}(U_h(\mathbb {A}),K_{h,1}^\infty )\subset \mathcal {S}^\circ (U_h(\mathbb {A}))$
, the subalgebras of bi-
$\mathcal {S}(U_h(\mathbb {A}),K_{h,1}^\infty )\subset \mathcal {S}^\circ (U_h(\mathbb {A}))$
, the subalgebras of bi-
![]() $K_1^\infty $
(resp. bi-
$K_1^\infty $
(resp. bi-
![]() $K_{h,1}^\infty $
) invariant functions. Since we can shrink
$K_{h,1}^\infty $
) invariant functions. Since we can shrink
![]() $ K^\infty _1$
and
$ K^\infty _1$
and
![]() $K^\infty _{h,1}$
if necessary, it suffices to prove the theorem for functions in these subalgebras.
$K^\infty _{h,1}$
if necessary, it suffices to prove the theorem for functions in these subalgebras.
We denote by
![]() $\mathcal {M}^{S_0^{\prime }}(G(\mathbb {A}))$
, resp.
$\mathcal {M}^{S_0^{\prime }}(G(\mathbb {A}))$
, resp.
![]() $\mathcal {M}^{S_0^{\prime }}(U_h(\mathbb {A}))$
, the algebra of
$\mathcal {M}^{S_0^{\prime }}(U_h(\mathbb {A}))$
, the algebra of
![]() $S_0^{\prime }$
-multipliers defined in [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21, definition 3.5] relatively to the subgroup
$S_0^{\prime }$
-multipliers defined in [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21, definition 3.5] relatively to the subgroup
![]() $\prod _{v\notin S_0^{\prime }} K_v$
, resp.
$\prod _{v\notin S_0^{\prime }} K_v$
, resp.
![]() $\prod _{v\notin S_0^{\prime }} K_{h,v}$
. Any multiplier
$\prod _{v\notin S_0^{\prime }} K_{h,v}$
. Any multiplier
![]() $\mu \in \mathcal {M}^{S_0^{\prime }}(G(\mathbb {A}))$
, resp.
$\mu \in \mathcal {M}^{S_0^{\prime }}(G(\mathbb {A}))$
, resp.
![]() $\mu \in \mathcal {M}^{S_0^{\prime }}(U_h(\mathbb {A}))$
, gives rise to a linear operator
$\mu \in \mathcal {M}^{S_0^{\prime }}(U_h(\mathbb {A}))$
, gives rise to a linear operator
![]() $\mu \ast $
of the algebra
$\mu \ast $
of the algebra
![]() $\mathcal {S}(G(\mathbb {A}),K_1^\infty )$
, resp.
$\mathcal {S}(G(\mathbb {A}),K_1^\infty )$
, resp.
![]() $\mathcal {S}(U_h(\mathbb {A}),K_{h,1}^\infty )$
. For every admissible irreducible representation
$\mathcal {S}(U_h(\mathbb {A}),K_{h,1}^\infty )$
. For every admissible irreducible representation
![]() $\rho $
of
$\rho $
of
![]() $G(\mathbb {A})$
, resp. of
$G(\mathbb {A})$
, resp. of
![]() $U_h(\mathbb {A})$
, there exists a complex number
$U_h(\mathbb {A})$
, there exists a complex number
![]() $\mu (\rho )$
such that
$\mu (\rho )$
such that
![]() $\rho (\mu \ast f)=\mu (\rho ) \rho (f)$
for all
$\rho (\mu \ast f)=\mu (\rho ) \rho (f)$
for all
![]() $f\in \mathcal {S}^\circ (G(\mathbb {A}),K_1^\infty )$
, resp.
$f\in \mathcal {S}^\circ (G(\mathbb {A}),K_1^\infty )$
, resp.
![]() $f\in \mathcal {S}^\circ (U_h(\mathbb {A}),K_{h,1}^\infty )$
. Note that
$f\in \mathcal {S}^\circ (U_h(\mathbb {A}),K_{h,1}^\infty )$
. Note that
![]() $\mu (\rho )$
depends only on the infinitesimal character of the archimedean component of
$\mu (\rho )$
depends only on the infinitesimal character of the archimedean component of
![]() $\rho $
and on the components outside
$\rho $
and on the components outside
![]() $S_0^{\prime }$
. Moreover, if Q is a standard parabolic subgroup of G, resp.
$S_0^{\prime }$
. Moreover, if Q is a standard parabolic subgroup of G, resp.
![]() $U_h$
, and if
$U_h$
, and if
![]() $\rho $
is an admissible irreducible representation of the Levi component
$\rho $
is an admissible irreducible representation of the Levi component
![]() $M_Q(\mathbb {A})$
, then we have for any
$M_Q(\mathbb {A})$
, then we have for any
![]() $\lambda \in \mathfrak {a}_{Q,\mathbb {C}}^*$
and
$\lambda \in \mathfrak {a}_{Q,\mathbb {C}}^*$
and
![]() $R_\lambda =\operatorname {\mathrm {Ind}}_{Q}^G(\rho _\lambda )$
, resp.
$R_\lambda =\operatorname {\mathrm {Ind}}_{Q}^G(\rho _\lambda )$
, resp.
![]() $\operatorname {\mathrm {Ind}}_{Q}^{U_h}(\rho _\lambda )$
,
$\operatorname {\mathrm {Ind}}_{Q}^{U_h}(\rho _\lambda )$
,
where
![]() $\mu ( R_\lambda ) \in \mathbb {C}$
and the map
$\mu ( R_\lambda ) \in \mathbb {C}$
and the map
![]() $\lambda \mapsto \mu ( R_\lambda ) $
is holomorphic.
$\lambda \mapsto \mu ( R_\lambda ) $
is holomorphic.
The following two lemmas are based on [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21, theorem 3.17] and a strong multiplicity one theorem of Ramakrishnan; see [Reference RamakrishnanRam18].
Lemma 7.1.7.1. Let
![]() $h\in \mathcal {H}^\circ $
and
$h\in \mathcal {H}^\circ $
and
![]() $\lambda \in i\mathfrak {a}_{M}^{L,*}$
in general position. Then there exists a multiplier
$\lambda \in i\mathfrak {a}_{M}^{L,*}$
in general position. Then there exists a multiplier
![]() $\mu _h\in \mathcal {M}^{S_0^{\prime }}(U_h(\mathbb {A}))$
such that
$\mu _h\in \mathcal {M}^{S_0^{\prime }}(U_h(\mathbb {A}))$
such that
-
1. For all
 $f^h\in \mathcal {S}(U_h(\mathbb {A}),K_{h,1}^\infty )$
, the right convolution by
$f^h\in \mathcal {S}(U_h(\mathbb {A}),K_{h,1}^\infty )$
, the right convolution by
 $\mu _h*f^h$
sends
$\mu _h*f^h$
sends
 $L^2([U_h])$
into
$L^2([U_h])$
into  $$ \begin{align*} \widehat{ \oplus}_{\chi\in \mathfrak{X}^h_\Pi} L^2_\chi([U_h]). \end{align*} $$
$$ \begin{align*} \widehat{ \oplus}_{\chi\in \mathfrak{X}^h_\Pi} L^2_\chi([U_h]). \end{align*} $$
-
2. For
 $(M_h,\sigma )\in \mathfrak {X}_{\Pi }^h$
, we have
$(M_h,\sigma )\in \mathfrak {X}_{\Pi }^h$
, we have
 $\mu _h(\operatorname {\mathrm {Ind}}_{P_h}^{U_h}(\sigma _{bc(\lambda )}))=1$
.
$\mu _h(\operatorname {\mathrm {Ind}}_{P_h}^{U_h}(\sigma _{bc(\lambda )}))=1$
.
Proof. By [Reference Ginzburg, Rallis and SoudryGRS11], there exists at least one
![]() $h^\flat \in \mathcal {H}^\circ $
such that the set
$h^\flat \in \mathcal {H}^\circ $
such that the set
![]() $\mathfrak {X}_\Pi ^{h^\flat }$
is nonempty. We fix such a form
$\mathfrak {X}_\Pi ^{h^\flat }$
is nonempty. We fix such a form
![]() $h^\flat $
and a pair
$h^\flat $
and a pair
![]() $(M_{h^\flat },\sigma ^\flat )$
. Let
$(M_{h^\flat },\sigma ^\flat )$
. Let
![]() $\lambda \in i\mathfrak {a}_{M}^{L,*}$
in general position. Let
$\lambda \in i\mathfrak {a}_{M}^{L,*}$
in general position. Let
![]() $h\in \mathcal {H}^\circ $
and let
$h\in \mathcal {H}^\circ $
and let
![]() $\mathfrak {X}^h_\lambda $
be the set of cuspidal data of
$\mathfrak {X}^h_\lambda $
be the set of cuspidal data of
![]() $U_h$
represented by pairs
$U_h$
represented by pairs
![]() $(M_Q,\rho )$
with
$(M_Q,\rho )$
with
![]() $Q\subset U_h$
a standard parabolic subgroup for which there exists
$Q\subset U_h$
a standard parabolic subgroup for which there exists
![]() $\lambda '\in \mathfrak {a}_{Q,\mathbb {C}}^*$
such that
$\lambda '\in \mathfrak {a}_{Q,\mathbb {C}}^*$
such that
-
(A) the Archimedean infinitesimal characters of
 $\operatorname {\mathrm {Ind}}_{P_{h^\flat }}^{U_{h^\flat }}(\sigma _{bc(\lambda )}^\flat )$
and
$\operatorname {\mathrm {Ind}}_{P_{h^\flat }}^{U_{h^\flat }}(\sigma _{bc(\lambda )}^\flat )$
and
 $\operatorname {\mathrm {Ind}}_{Q}^{U_h}(\rho _{\lambda '})$
are the same;
$\operatorname {\mathrm {Ind}}_{Q}^{U_h}(\rho _{\lambda '})$
are the same; -
(B) for all finite places v outside
 $S_0^{\prime }$
, the irreducible representation
$S_0^{\prime }$
, the irreducible representation
 $\operatorname {\mathrm {Ind}}_{P_{h^\flat }(F_v)}^{U_{h^\flat }(F_v)}(\sigma _{bc(\lambda ),v}^\flat )$
is a constituent of
$\operatorname {\mathrm {Ind}}_{P_{h^\flat }(F_v)}^{U_{h^\flat }(F_v)}(\sigma _{bc(\lambda ),v}^\flat )$
is a constituent of
 $\operatorname {\mathrm {Ind}}_{Q(F_v)}^{U_h(F_v)}(\rho _{\lambda ',v})$
.
$\operatorname {\mathrm {Ind}}_{Q(F_v)}^{U_h(F_v)}(\rho _{\lambda ',v})$
.
By [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21, theorem 3.19], there exists a
![]() $S_0^{\prime }$
-multiplier
$S_0^{\prime }$
-multiplier
![]() $\mu _h$
such that
$\mu _h$
such that
-
(C) For all
 $f^h\in \mathcal {S}(U_h(\mathbb {A}),K_{h,1}^\infty )$
, the right convolution by
$f^h\in \mathcal {S}(U_h(\mathbb {A}),K_{h,1}^\infty )$
, the right convolution by
 $\mu _h*f^h$
sends
$\mu _h*f^h$
sends
 $L^2([U_h])$
into
$L^2([U_h])$
into  $$ \begin{align*} \widehat{ \oplus}_{\chi\in \mathfrak{X}^h_\lambda} L^2_\chi([U_h]). \end{align*} $$
$$ \begin{align*} \widehat{ \oplus}_{\chi\in \mathfrak{X}^h_\lambda} L^2_\chi([U_h]). \end{align*} $$
-
(D)
 $\mu _h(\operatorname {\mathrm {Ind}}_{P_{h^\flat }}^{U_{h^\flat }}(\sigma _{bc(\lambda )}^\flat ))=1$
.
$\mu _h(\operatorname {\mathrm {Ind}}_{P_{h^\flat }}^{U_{h^\flat }}(\sigma _{bc(\lambda )}^\flat ))=1$
.
Let
![]() $\lambda '\in \mathfrak {a}_{Q,\mathbb {C}}^*$
and
$\lambda '\in \mathfrak {a}_{Q,\mathbb {C}}^*$
and
![]() $(M_Q,\rho )$
be a representative of an element
$(M_Q,\rho )$
be a representative of an element
![]() $\mathfrak {X}^h_\lambda $
such that conditions (A) and (B) hold. We can write the Levi factor
$\mathfrak {X}^h_\lambda $
such that conditions (A) and (B) hold. We can write the Levi factor
![]() $M_Q$
of Q as a product
$M_Q$
of Q as a product
![]() $G^\sharp \times U_0$
, where
$G^\sharp \times U_0$
, where
![]() $G^\sharp $
is a product of linear groups and
$G^\sharp $
is a product of linear groups and
![]() $U_0$
is a product of two unitary groups. Accordingly, we write
$U_0$
is a product of two unitary groups. Accordingly, we write
![]() $\rho =\rho ^\sharp \times \rho _0$
. Let
$\rho =\rho ^\sharp \times \rho _0$
. Let
![]() $Q_E=\operatorname {\mathrm {Res}}_{E/F}(Q\times _F E)$
and let
$Q_E=\operatorname {\mathrm {Res}}_{E/F}(Q\times _F E)$
and let
![]() $\lambda _E'\in \mathfrak {a}_{Q_E}^*$
be the base change of
$\lambda _E'\in \mathfrak {a}_{Q_E}^*$
be the base change of
![]() $\lambda '$
. Observe that
$\lambda '$
. Observe that
![]() $\Pi _v$
is generic for all places v and is the split base of the representation
$\Pi _v$
is generic for all places v and is the split base of the representation
![]() $\operatorname {\mathrm {Ind}}_{P_{h^\flat }(F_v)}^{U_{h^\flat }(F_v)}(\sigma _{bc(\lambda ),v}^\flat )$
for finite
$\operatorname {\mathrm {Ind}}_{P_{h^\flat }(F_v)}^{U_{h^\flat }(F_v)}(\sigma _{bc(\lambda ),v}^\flat )$
for finite
![]() $v\notin S_0^{\prime }$
. So the representation
$v\notin S_0^{\prime }$
. So the representation
![]() $\operatorname {\mathrm {Ind}}_{P_{h^\flat }(F_v)}^{U_{h^\flat }(F_v)}(\sigma _{bc(\lambda ),v}^\flat )$
is also generic, and thus,
$\operatorname {\mathrm {Ind}}_{P_{h^\flat }(F_v)}^{U_{h^\flat }(F_v)}(\sigma _{bc(\lambda ),v}^\flat )$
is also generic, and thus,
![]() $\operatorname {\mathrm {Ind}}_{Q(F_v)}^{U_h(F_v)}(\rho _{\lambda ',v})$
and
$\operatorname {\mathrm {Ind}}_{Q(F_v)}^{U_h(F_v)}(\rho _{\lambda ',v})$
and
![]() $\rho _{\lambda ',v}$
are also generic for finite
$\rho _{\lambda ',v}$
are also generic for finite
![]() $v\notin S_0^{\prime }$
. By [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21, Theorem 4.14 (1)], there exists an isobaric automorphic representation
$v\notin S_0^{\prime }$
. By [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21, Theorem 4.14 (1)], there exists an isobaric automorphic representation
![]() $\rho _E$
of
$\rho _E$
of
![]() $M_{Q_E}$
such that the split base change of
$M_{Q_E}$
such that the split base change of
![]() $\rho $
is
$\rho $
is
![]() $\rho _E$
at almost all split places. By the strong multiplicity one theorem of Ramakrishnan (see [Reference RamakrishnanRam18]), we deduce that the isobaric automorphic representations of
$\rho _E$
at almost all split places. By the strong multiplicity one theorem of Ramakrishnan (see [Reference RamakrishnanRam18]), we deduce that the isobaric automorphic representations of
![]() $G(\mathbb {A})$
associated to
$G(\mathbb {A})$
associated to
![]() $(P,\pi \otimes {\lambda })$
and
$(P,\pi \otimes {\lambda })$
and
![]() $(Q_E,\rho _{E}\otimes \lambda ^{\prime }_E)$
are isomorphic. Using [Reference Jacquet and ShalikaJS81a, theorem 4.4] and the fact that
$(Q_E,\rho _{E}\otimes \lambda ^{\prime }_E)$
are isomorphic. Using [Reference Jacquet and ShalikaJS81a, theorem 4.4] and the fact that
![]() $\lambda $
is in general position, we conclude that, up to a change of representative, we have
$\lambda $
is in general position, we conclude that, up to a change of representative, we have
![]() $P \subset Q_E$
, the inclusion given by base change
$P \subset Q_E$
, the inclusion given by base change
![]() $\mathfrak {a}_Q^*\subset \mathfrak {a}_{Q_E}^* $
induces an isomorphism of
$\mathfrak {a}_Q^*\subset \mathfrak {a}_{Q_E}^* $
induces an isomorphism of
![]() $\mathfrak {a}_Q^*$
onto
$\mathfrak {a}_Q^*$
onto
![]() $\mathfrak {a}_{M}^{L,*}$
which identifies
$\mathfrak {a}_{M}^{L,*}$
which identifies
![]() $\lambda '$
to
$\lambda '$
to
![]() $bc(\lambda )$
, the representation
$bc(\lambda )$
, the representation
![]() $\Pi _0$
is the weak base change of
$\Pi _0$
is the weak base change of
![]() $\rho _0$
and
$\rho _0$
and
![]() $\operatorname {\mathrm {Ind}}_{Q_E}^G(\rho ^\sharp \boxtimes \Pi _0 \boxtimes \rho ^{\sharp ,*})=\Pi $
. Using condition (B), we deduce that
$\operatorname {\mathrm {Ind}}_{Q_E}^G(\rho ^\sharp \boxtimes \Pi _0 \boxtimes \rho ^{\sharp ,*})=\Pi $
. Using condition (B), we deduce that
![]() $\Pi _{0,v}$
is also the split base change of
$\Pi _{0,v}$
is also the split base change of
![]() $\rho _{0,v}$
for all finite places v outside
$\rho _{0,v}$
for all finite places v outside
![]() $S_0^{\prime }$
. We get that
$S_0^{\prime }$
. We get that
![]() $\mathfrak {X}^h_\lambda \subset \mathfrak {X}^h_\Pi $
, and so (C) implies assertion 1.
$\mathfrak {X}^h_\lambda \subset \mathfrak {X}^h_\Pi $
, and so (C) implies assertion 1.
Still, we have to check assertion 2. Let
![]() $(M_{Q},\rho )$
be a representative of an element in
$(M_{Q},\rho )$
be a representative of an element in
![]() $ \mathfrak {X}^h_\Pi $
. We claim that
$ \mathfrak {X}^h_\Pi $
. We claim that
![]() $\operatorname {\mathrm {Ind}}_{Q}^{U_h}(\rho )$
and
$\operatorname {\mathrm {Ind}}_{Q}^{U_h}(\rho )$
and
![]() $\operatorname {\mathrm {Ind}}_{P_{h^\flat }}^{U_{h^\flat }}(\sigma _{bc(\lambda )}^\flat )$
have the same Archimedean infinitesimal character and have the same local component for all finite places v outside
$\operatorname {\mathrm {Ind}}_{P_{h^\flat }}^{U_{h^\flat }}(\sigma _{bc(\lambda )}^\flat )$
have the same Archimedean infinitesimal character and have the same local component for all finite places v outside
![]() $S_0^{\prime }$
. The latter condition follows directly from the definition of the set
$S_0^{\prime }$
. The latter condition follows directly from the definition of the set
![]() $ \mathfrak {X}^h_\Pi $
and the fact that the split base is injective. The former condition follows from [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21, Theorem 4.14 (4)] (applied to
$ \mathfrak {X}^h_\Pi $
and the fact that the split base is injective. The former condition follows from [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21, Theorem 4.14 (4)] (applied to
![]() $\rho $
) and the fact that the base change map is injective at the level of archimedean infinitesimal characters. Since condition 2 depends only on the components of
$\rho $
) and the fact that the base change map is injective at the level of archimedean infinitesimal characters. Since condition 2 depends only on the components of
![]() $\operatorname {\mathrm {Ind}}_{Q}^{U_h}(\rho )$
on
$\operatorname {\mathrm {Ind}}_{Q}^{U_h}(\rho )$
on
![]() $V_F\setminus S_0^{\prime }$
, we see that (D) implies assertion 2.
$V_F\setminus S_0^{\prime }$
, we see that (D) implies assertion 2.
Lemma 7.1.7.2. Let
![]() $\lambda \in i\mathfrak {a}_{M}^{L,*}$
. Then there exists a multiplier
$\lambda \in i\mathfrak {a}_{M}^{L,*}$
. Then there exists a multiplier
![]() $\mu \in \mathcal {M}^{S_0^{\prime }}(G(\mathbb {A}))$
such that
$\mu \in \mathcal {M}^{S_0^{\prime }}(G(\mathbb {A}))$
such that
-
1. For all
 $f\in \mathcal {S}(G(\mathbb {A}),K_{h,1}^\infty )$
, the right convolution by
$f\in \mathcal {S}(G(\mathbb {A}),K_{h,1}^\infty )$
, the right convolution by
 $\mu *f$
sends
$\mu *f$
sends
 $L^2(G(F)A_G(\mathbb {A})\backslash G(\mathbb {A}) )$
into
$L^2(G(F)A_G(\mathbb {A})\backslash G(\mathbb {A}) )$
into
 $L^2_{\chi _0}([G])$
.
$L^2_{\chi _0}([G])$
. -
2. We have
 $\mu (\Pi _\lambda )=1$
.
$\mu (\Pi _\lambda )=1$
.
Proof. The proof is similar to (but simpler than) that of Lemma 7.1.7.1 and is based on [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21, Theorem 1.3]).
Let
![]() $\lambda _0$
be an element of
$\lambda _0$
be an element of
![]() $i\mathfrak {a}_{M}^{L,*}$
in general position. Let
$i\mathfrak {a}_{M}^{L,*}$
in general position. Let
![]() $\mu \in \mathcal {M}^{S_0^{\prime }}(G(\mathbb {A}))$
and
$\mu \in \mathcal {M}^{S_0^{\prime }}(G(\mathbb {A}))$
and
![]() $\mu _h\in \mathcal {M}^{S_0^{\prime }}(U_h(\mathbb {A}))$
for
$\mu _h\in \mathcal {M}^{S_0^{\prime }}(U_h(\mathbb {A}))$
for
![]() $h\in \mathcal {H}^\circ $
satisfying assertions of Lemmas 7.1.7.1 and 7.1.7.2 for
$h\in \mathcal {H}^\circ $
satisfying assertions of Lemmas 7.1.7.1 and 7.1.7.2 for
![]() $\lambda =\lambda _0$
. We may and we shall also assume that
$\lambda =\lambda _0$
. We may and we shall also assume that
![]() $\mu ^h$
is the ‘base change’ of
$\mu ^h$
is the ‘base change’ of
![]() $\mu $
(see [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21, Lemma 4.12]). Let
$\mu $
(see [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21, Lemma 4.12]). Let
![]() $f\in \mathcal {S}(G(\mathbb {A}),K_1^\infty )$
, and for
$f\in \mathcal {S}(G(\mathbb {A}),K_1^\infty )$
, and for
![]() $h\in \mathcal {H}^\circ $
, let
$h\in \mathcal {H}^\circ $
, let
![]() $f^h\in \mathcal {S}(U_h(\mathbb {A}),K_{h,1}^\infty )$
that satisfy the hypotheses of Theorem 7.1.6.1. Then
$f^h\in \mathcal {S}(U_h(\mathbb {A}),K_{h,1}^\infty )$
that satisfy the hypotheses of Theorem 7.1.6.1. Then
![]() $\mu \ast f$
and
$\mu \ast f$
and
![]() $\mu ^h\ast f^h$
, for
$\mu ^h\ast f^h$
, for
![]() $h\in \mathcal {H}^\circ $
still satisfy the hypotheses (see [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21, Proposition 4.8]). Hence, by (7.1.7.1), we have
$h\in \mathcal {H}^\circ $
still satisfy the hypotheses (see [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21, Proposition 4.8]). Hence, by (7.1.7.1), we have
It follows from Lemma 7.1.7.2 and [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Proposition 3.3.3.1 and Theorem 3.3.9.1] that we have
![]() $I_{}(\mu \ast f)=I_{\chi _0}(\mu \ast f)$
. In the same way, Lemma 7.1.7.1 and Corollary 3.3.5.2 show that the right-hand side of (7.1.7.2) reduces to
$I_{}(\mu \ast f)=I_{\chi _0}(\mu \ast f)$
. In the same way, Lemma 7.1.7.1 and Corollary 3.3.5.2 show that the right-hand side of (7.1.7.2) reduces to
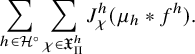 $$ \begin{align*} \sum_{h\in\mathcal{H}^\circ} \sum_{\chi\in \mathfrak{X}_\Pi^h } J_{\chi}^h(\mu_h*f^h). \end{align*} $$
$$ \begin{align*} \sum_{h\in\mathcal{H}^\circ} \sum_{\chi\in \mathfrak{X}_\Pi^h } J_{\chi}^h(\mu_h*f^h). \end{align*} $$
By Theorems 3.5.7.1 and 4.1.8.1 and by an elementary change of variables, we get
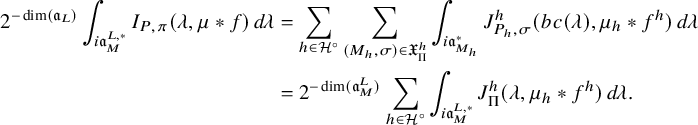 $$ \begin{align} \nonumber 2^{-\dim(\mathfrak{a}_L)}\int_{i\mathfrak{a}_M^{L,*}} I_{P,\pi}(\lambda,\mu*f)\, d\lambda&=\sum_{h\in\mathcal{H}^\circ} \sum_{(M_h,\sigma)\in \mathfrak{X}_\Pi^h} \int_{i\mathfrak{a}_{M_h}^*} J_{P_h,\sigma}^h(bc(\lambda),\mu_h*f^h)\, d\lambda\\ &=2^{-\dim(\mathfrak{a}_M^L)}\sum_{h\in\mathcal{H}^\circ } \int_{i\mathfrak{a}_{M}^{L,*}} J_{\Pi}^h(\lambda,\mu_h*f^h)\, d\lambda. \end{align} $$
$$ \begin{align} \nonumber 2^{-\dim(\mathfrak{a}_L)}\int_{i\mathfrak{a}_M^{L,*}} I_{P,\pi}(\lambda,\mu*f)\, d\lambda&=\sum_{h\in\mathcal{H}^\circ} \sum_{(M_h,\sigma)\in \mathfrak{X}_\Pi^h} \int_{i\mathfrak{a}_{M_h}^*} J_{P_h,\sigma}^h(bc(\lambda),\mu_h*f^h)\, d\lambda\\ &=2^{-\dim(\mathfrak{a}_M^L)}\sum_{h\in\mathcal{H}^\circ } \int_{i\mathfrak{a}_{M}^{L,*}} J_{\Pi}^h(\lambda,\mu_h*f^h)\, d\lambda. \end{align} $$
Let
![]() $v_1,v_2$
two finite places outside
$v_1,v_2$
two finite places outside
![]() $S_0^{\prime }$
with distinct residual characteristics. Let
$S_0^{\prime }$
with distinct residual characteristics. Let
![]() $S_1\subset V_F\setminus S_0^{\prime }$
be a finite set of finite places. We assume that
$S_1\subset V_F\setminus S_0^{\prime }$
be a finite set of finite places. We assume that
![]() $S_1$
contains
$S_1$
contains
![]() $v_1$
and
$v_1$
and
![]() $v_2$
. Let
$v_2$
. Let
![]() $\mathcal {A}_{S_1}$
be the spherical algebra
$\mathcal {A}_{S_1}$
be the spherical algebra
![]() $\otimes _{v\in S_1}\mathcal {S}^\circ (G(F_{v}))$
. Let
$\otimes _{v\in S_1}\mathcal {S}^\circ (G(F_{v}))$
. Let
![]() $g\in \mathcal {A}_{S_1}$
. For all
$g\in \mathcal {A}_{S_1}$
. For all
![]() $h\in \mathcal {H}^\circ $
, let
$h\in \mathcal {H}^\circ $
, let
![]() $g^h=(\otimes _{v\in S_1} BC_{h,v})(g)$
be its base change to
$g^h=(\otimes _{v\in S_1} BC_{h,v})(g)$
be its base change to
![]() $\otimes _{v\in S_1}\mathcal {S}^\circ (U_h(F_{v}))$
. The assumptions of Theorem 7.1.6.1 still hold for the convolutions
$\otimes _{v\in S_1}\mathcal {S}^\circ (U_h(F_{v}))$
. The assumptions of Theorem 7.1.6.1 still hold for the convolutions
![]() $f*g$
and
$f*g$
and
![]() $f^h*g^h$
. Note that we have for any
$f^h*g^h$
. Note that we have for any
![]() $\lambda \in i\mathfrak {a}_{M}^{L,*}$
,
$\lambda \in i\mathfrak {a}_{M}^{L,*}$
,
where
![]() $\hat g$
is the Satake transform and
$\hat g$
is the Satake transform and
![]() $\hat g(\Pi _{\lambda ,S_1})$
is the scalar by which g acts on
$\hat g(\Pi _{\lambda ,S_1})$
is the scalar by which g acts on
![]() $\Pi _{\lambda ,S_1}=\otimes _{v\in S_1} \Pi _{\lambda ,v} $
. For all
$\Pi _{\lambda ,S_1}=\otimes _{v\in S_1} \Pi _{\lambda ,v} $
. For all
![]() $\lambda \in i\mathfrak {a}_M^{L,*}$
, we set
$\lambda \in i\mathfrak {a}_M^{L,*}$
, we set
The equality (7.1.7.3) implies that for all
![]() $g\in \mathcal {A}_{S_1}$
, we have
$g\in \mathcal {A}_{S_1}$
, we have
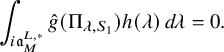 $$ \begin{align*} \int_{i\mathfrak{a}_M^{L,*}} \hat g(\Pi_{\lambda,S_1}) h(\lambda) \, d\lambda =0. \end{align*} $$
$$ \begin{align*} \int_{i\mathfrak{a}_M^{L,*}} \hat g(\Pi_{\lambda,S_1}) h(\lambda) \, d\lambda =0. \end{align*} $$
Let
![]() $\mathcal {T}_{S_1}:\lambda \in i\mathfrak {a}_M^{L,*} \mapsto \Pi _{\lambda ,S_1}$
. Because
$\mathcal {T}_{S_1}:\lambda \in i\mathfrak {a}_M^{L,*} \mapsto \Pi _{\lambda ,S_1}$
. Because
![]() $v_1$
and
$v_1$
and
![]() $v_2$
have distinct residual characteristics, the morphism from
$v_2$
have distinct residual characteristics, the morphism from
![]() $i\mathfrak {a}_M^{*}$
to the group of unramified characters of
$i\mathfrak {a}_M^{*}$
to the group of unramified characters of
![]() $M(F_{v_1}\times F_{v_2}) $
given by
$M(F_{v_1}\times F_{v_2}) $
given by
![]() $\lambda \in i\mathfrak {a}_M^{*} \mapsto (x\in M(F_{v_1}\times F_{v_2}) \mapsto \exp (\langle \lambda ,H_P(x)\rangle )$
is injective. We deduce that the map
$\lambda \in i\mathfrak {a}_M^{*} \mapsto (x\in M(F_{v_1}\times F_{v_2}) \mapsto \exp (\langle \lambda ,H_P(x)\rangle )$
is injective. We deduce that the map
![]() $\mathcal {T}_{\{v_1,v_2\}}$
has finite fibers of uniformly bounded cardinality. In particular, the map
$\mathcal {T}_{\{v_1,v_2\}}$
has finite fibers of uniformly bounded cardinality. In particular, the map
![]() $\mathcal {T}_{S_1}$
has the same property with the same bound. By Stone-Weierstrass theorem, the set
$\mathcal {T}_{S_1}$
has the same property with the same bound. By Stone-Weierstrass theorem, the set
![]() $\{\hat g \mid g\in \mathcal {A}_{S_1}\}$
is dense in the set of continuous fonctions on the unramified unitary dual of
$\{\hat g \mid g\in \mathcal {A}_{S_1}\}$
is dense in the set of continuous fonctions on the unramified unitary dual of
![]() $\prod _{v\in S_1} G(F_v)$
.The push-forward of the measure
$\prod _{v\in S_1} G(F_v)$
.The push-forward of the measure
![]() $h(\lambda )\, d\lambda $
by the map
$h(\lambda )\, d\lambda $
by the map
![]() $\mathcal {T}_{S_1}$
is thus zero. In this way, we get that for almost all
$\mathcal {T}_{S_1}$
is thus zero. In this way, we get that for almost all
![]() $\lambda \in i\mathfrak {a}_M^{L,*}$
,
$\lambda \in i\mathfrak {a}_M^{L,*}$
,
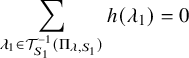 $$ \begin{align} \sum_{\lambda_1\in \mathcal{T}^{-1}_{S_1}(\Pi_{\lambda,S_1}) } h(\lambda_1) =0 \end{align} $$
$$ \begin{align} \sum_{\lambda_1\in \mathcal{T}^{-1}_{S_1}(\Pi_{\lambda,S_1}) } h(\lambda_1) =0 \end{align} $$
for all finite sets
![]() $S_1$
, as above. By continuity of h, this equality holds for all
$S_1$
, as above. By continuity of h, this equality holds for all
![]() $\lambda \in i\mathfrak {a}_M^{L,*}$
and in particular for
$\lambda \in i\mathfrak {a}_M^{L,*}$
and in particular for
![]() $\lambda =\lambda _0$
.
$\lambda =\lambda _0$
.
Let us write
![]() $\mathcal {T}^{-1}_{S_1}(\Pi _{\lambda _0,S_1})=\{\lambda _0, \lambda _1,\ldots ,\lambda _j\}$
, where
$\mathcal {T}^{-1}_{S_1}(\Pi _{\lambda _0,S_1})=\{\lambda _0, \lambda _1,\ldots ,\lambda _j\}$
, where
![]() $j+1$
is the cardinality of this set. Let
$j+1$
is the cardinality of this set. Let
![]() $1\leqslant i \leqslant j$
. If
$1\leqslant i \leqslant j$
. If
![]() $\Pi _{\lambda _i}\not =\Pi _{\lambda _0}$
, by the strong multiplicity one theorem of Ramakrishnan (see [Reference RamakrishnanRam18]), there exists a finite place
$\Pi _{\lambda _i}\not =\Pi _{\lambda _0}$
, by the strong multiplicity one theorem of Ramakrishnan (see [Reference RamakrishnanRam18]), there exists a finite place
![]() $v_i\notin S_0^{\prime }\cup S_1$
such that
$v_i\notin S_0^{\prime }\cup S_1$
such that
![]() $\Pi _{\lambda _i,v_i}\not =\Pi _{\lambda _0,v_i}$
. Since we may enlarge
$\Pi _{\lambda _i,v_i}\not =\Pi _{\lambda _0,v_i}$
. Since we may enlarge
![]() $S_1$
by adding such a place
$S_1$
by adding such a place
![]() $v_i$
, we will assume without loss of generality that for any
$v_i$
, we will assume without loss of generality that for any
![]() $\lambda \in \mathcal {T}^{-1}_{S_1}(\Pi _{\lambda _0,S_1})$
, we have
$\lambda \in \mathcal {T}^{-1}_{S_1}(\Pi _{\lambda _0,S_1})$
, we have
![]() $\Pi _\lambda =\Pi _{\lambda _0}$
. By [Reference Jacquet and ShalikaJS81a, theorem 4.4] and the fact that the cuspidal datum
$\Pi _\lambda =\Pi _{\lambda _0}$
. By [Reference Jacquet and ShalikaJS81a, theorem 4.4] and the fact that the cuspidal datum
![]() $(M,\pi )$
is G-regular, we have even
$(M,\pi )$
is G-regular, we have even
![]() $\pi _\lambda =\pi _{\lambda _0}$
, and thus,
$\pi _\lambda =\pi _{\lambda _0}$
, and thus,
![]() $\lambda =\lambda _0$
. So (7.1.7.4) reduces to
$\lambda =\lambda _0$
. So (7.1.7.4) reduces to
![]() $h(\lambda _0)=0$
. Because
$h(\lambda _0)=0$
. Because
![]() $\lambda _0$
is in general position, we may use Condition 2 of Lemmas 7.1.7.1 and 7.1.7.2: we get
$\lambda _0$
is in general position, we may use Condition 2 of Lemmas 7.1.7.1 and 7.1.7.2: we get
So we get (7.1.6.1) for
![]() $\lambda $
in general position, and so for all
$\lambda $
in general position, and so for all
![]() $\lambda \in i\mathfrak {a}_M^{L,*}$
, since both members of (7.1.6.1) are continuous (and even analytic).
$\lambda \in i\mathfrak {a}_M^{L,*}$
, since both members of (7.1.6.1) are continuous (and even analytic).
7.2 Proof of Theorem 1.2.3.1
7.2.1
Once we have Theorem 7.1.6.1, the proof of Theorem 1.2.3.1 is very similar to the proof of [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, theorem 1.1.5.1]. For the reader’s convenience, we recall some steps. We use notations of Section 7.1. Let
![]() $\Pi =\operatorname {\mathrm {Ind}}_P^G(\pi )$
be a H-regular Hermitian Arthur parameter of G and let
$\Pi =\operatorname {\mathrm {Ind}}_P^G(\pi )$
be a H-regular Hermitian Arthur parameter of G and let
![]() $\lambda \in i\mathfrak {a}_{M}^{L,*}$
. The relative character
$\lambda \in i\mathfrak {a}_{M}^{L,*}$
. The relative character
![]() $I_{\Pi _\lambda }$
defined in (4.2.8.1) is built upon two linear forms – namely,
$I_{\Pi _\lambda }$
defined in (4.2.8.1) is built upon two linear forms – namely,
![]() $Z^{RS}(0)$
and
$Z^{RS}(0)$
and
![]() $\beta _\eta $
. The linear form
$\beta _\eta $
. The linear form
![]() $\beta _\eta $
is not identically zero (as a consequence of [Reference Gelfand and KaždanGK72], [Reference JacquetJac10, Proposition 5] and [Reference KemarskyKem15]) and
$\beta _\eta $
is not identically zero (as a consequence of [Reference Gelfand and KaždanGK72], [Reference JacquetJac10, Proposition 5] and [Reference KemarskyKem15]) and
![]() $Z^{RS}(0)$
is nonzero if and only if
$Z^{RS}(0)$
is nonzero if and only if
![]() $L(\frac 12,\Pi _\lambda )\not =0$
(as follows from the work Jacquet, Piatetski-Shapiro and Shalika [Reference Jacquet, Piatetskii-Shapiro and ShalikaJPSS83], [Reference JacquetJac04]). Since by Theorem 4.2.8.1, we have
$L(\frac 12,\Pi _\lambda )\not =0$
(as follows from the work Jacquet, Piatetski-Shapiro and Shalika [Reference Jacquet, Piatetskii-Shapiro and ShalikaJPSS83], [Reference JacquetJac04]). Since by Theorem 4.2.8.1, we have
![]() $I_{\Pi _\lambda }=I_{P,\pi }(\lambda )$
, we deduce that
$I_{\Pi _\lambda }=I_{P,\pi }(\lambda )$
, we deduce that
![]() $I_{P,\pi }(\lambda )$
is nonzero if and only if
$I_{P,\pi }(\lambda )$
is nonzero if and only if
![]() $L(\frac 12,\Pi _\lambda )\not =0$
.
$L(\frac 12,\Pi _\lambda )\not =0$
.
Let us consider
![]() $h\in \mathcal {H}$
, a parabolic subgroup
$h\in \mathcal {H}$
, a parabolic subgroup
![]() $P_h=M_{h}N_{P_h}$
of
$P_h=M_{h}N_{P_h}$
of
![]() $U_h$
and a cuspidal subrepresentation
$U_h$
and a cuspidal subrepresentation
![]() $\sigma $
of
$\sigma $
of
![]() $M_h$
. Let
$M_h$
. Let
![]() $\mathcal {A}_{P_h,\sigma _h}(U_h)\subset \mathcal {A}_{P_h}(U_h)$
be the space of forms
$\mathcal {A}_{P_h,\sigma _h}(U_h)\subset \mathcal {A}_{P_h}(U_h)$
be the space of forms
![]() $\varphi \in \mathcal {A}_{P}(G)$
such that
$\varphi \in \mathcal {A}_{P}(G)$
such that
belongs to the space of
![]() $\sigma $
for every
$\sigma $
for every
![]() $g\in G(\mathbb {A})$
. By a variation on §3.5.5, we define for
$g\in G(\mathbb {A})$
. By a variation on §3.5.5, we define for
![]() $\mu \in \mathfrak {a}_{M_h}^*$
the relative character
$\mu \in \mathfrak {a}_{M_h}^*$
the relative character
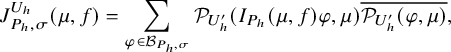 $$ \begin{align*} J_{P_h,\sigma}^{U_h}(\mu, f)=\sum_{\varphi\in \mathcal{B}_{P_h,\sigma}} \mathcal{P}_{U^{\prime}_h}(I_{P_h}(\mu,f)\varphi,\mu)\overline{ \mathcal{P}_{U^{\prime}_h}(\varphi,\mu) }, \end{align*} $$
$$ \begin{align*} J_{P_h,\sigma}^{U_h}(\mu, f)=\sum_{\varphi\in \mathcal{B}_{P_h,\sigma}} \mathcal{P}_{U^{\prime}_h}(I_{P_h}(\mu,f)\varphi,\mu)\overline{ \mathcal{P}_{U^{\prime}_h}(\varphi,\mu) }, \end{align*} $$
where
![]() $\mathcal {B}_{P_h,\sigma }$
is a K-basis of
$\mathcal {B}_{P_h,\sigma }$
is a K-basis of
![]() $\mathcal {A}_{P_h,\sigma _h}(U_h)$
; that is, it is the union over of
$\mathcal {A}_{P_h,\sigma _h}(U_h)$
; that is, it is the union over of
![]() $\tau \in \hat K_h$
of orthonormal bases
$\tau \in \hat K_h$
of orthonormal bases
![]() $\mathcal {B}_{P_h,\sigma ,\tau }$
for the Petersson inner product of the finite dimensional subspaces
$\mathcal {B}_{P_h,\sigma ,\tau }$
for the Petersson inner product of the finite dimensional subspaces
![]() $\mathcal {A}_{P_h,\sigma }(U_h,\tau )$
of functions in
$\mathcal {A}_{P_h,\sigma }(U_h,\tau )$
of functions in
![]() $\mathcal {A}_{P_h,\sigma }(U_h)$
which transform under
$\mathcal {A}_{P_h,\sigma }(U_h)$
which transform under
![]() $K_h$
according to
$K_h$
according to
![]() $\tau $
.
$\tau $
.
Let us assume that
![]() $\Pi $
is the weak base change of
$\Pi $
is the weak base change of
![]() $(P_h, \sigma )$
. Then we have the map
$(P_h, \sigma )$
. Then we have the map
![]() $bc:a_M^{L,*}\to \mathfrak {a}_{M_h}^*$
; see (7.1.5.1). It is clear that the distribution
$bc:a_M^{L,*}\to \mathfrak {a}_{M_h}^*$
; see (7.1.5.1). It is clear that the distribution
![]() $J_{P_h,\sigma }^h(bc(\lambda ))$
is nonzero if and only if the period integral
$J_{P_h,\sigma }^h(bc(\lambda ))$
is nonzero if and only if the period integral
![]() $\mathcal {P}_{U^{\prime }_h}(\cdot ,bc(\lambda ))$
induces a nonzero linear form on the space of
$\mathcal {P}_{U^{\prime }_h}(\cdot ,bc(\lambda ))$
induces a nonzero linear form on the space of
![]() $\sigma $
. Then Theorem 1.2.3.1 reduces to the equivalence between the two assertions:
$\sigma $
. Then Theorem 1.2.3.1 reduces to the equivalence between the two assertions:
-
(A) The distribution
 $I_{P,\pi }(\lambda )$
is nonzero.
$I_{P,\pi }(\lambda )$
is nonzero. -
(B) There exist
 $h\in \mathcal {H}$
, a parabolic subgroup
$h\in \mathcal {H}$
, a parabolic subgroup
 $P_h=M_{h}N_{P_h}$
of
$P_h=M_{h}N_{P_h}$
of
 $U_h$
and a cuspidal subrepresentation
$U_h$
and a cuspidal subrepresentation
 $\sigma $
of
$\sigma $
of
 $M_h$
such that
$M_h$
such that
 $\Pi $
is the weak base change of
$\Pi $
is the weak base change of
 $(P_h, \sigma )$
and
$(P_h, \sigma )$
and
 $J_{P_h,\sigma }^h(bc(\lambda ),f) \not =0$
.
$J_{P_h,\sigma }^h(bc(\lambda ),f) \not =0$
.
7.2.2 Proof of
 $(A)\Rightarrow (B)$
$(A)\Rightarrow (B)$
Let
![]() $S_0$
be the finite set of §7.1.2 such that
$S_0$
be the finite set of §7.1.2 such that
![]() $I_\Pi $
is not identically zero on
$I_\Pi $
is not identically zero on
![]() $\mathcal {S}^\circ (G(\mathbb {A}))$
. Then by results of [Reference XueXue19] towards the archimedean transfert and the existence of p-adic transfer of [Reference ZhangZha14b], we see that there exist functions f and
$\mathcal {S}^\circ (G(\mathbb {A}))$
. Then by results of [Reference XueXue19] towards the archimedean transfert and the existence of p-adic transfer of [Reference ZhangZha14b], we see that there exist functions f and
![]() $f^h$
for
$f^h$
for
![]() $h\in \mathcal {H}^\circ $
satisfying the hypotheses of Theorem 7.1.6.1 and such that
$h\in \mathcal {H}^\circ $
satisfying the hypotheses of Theorem 7.1.6.1 and such that
![]() $I_{P,\pi }(\lambda ,f)\not =0$
. Then
$I_{P,\pi }(\lambda ,f)\not =0$
. Then
![]() $(B)$
follows from (7.1.6.1).
$(B)$
follows from (7.1.6.1).
7.2.3 Proof of
 $(B) \Rightarrow (A)$
$(B) \Rightarrow (A)$
We may choose the set
![]() $S_0$
so that there exist
$S_0$
so that there exist
![]() $h_0\in \mathcal {H}^\circ $
, a parabolic subgroup
$h_0\in \mathcal {H}^\circ $
, a parabolic subgroup
![]() $P_{h_0}=M_{h_0}N_{P_{h_0}}\subset U_{h_0}$
, a cuspidal subrepresentation
$P_{h_0}=M_{h_0}N_{P_{h_0}}\subset U_{h_0}$
, a cuspidal subrepresentation
![]() $\sigma _0$
of
$\sigma _0$
of
![]() $M_{h_0}(\mathbb {A})$
and a function
$M_{h_0}(\mathbb {A})$
and a function
![]() $\xi \in \mathcal {S}^\circ (U_{h_0}(\mathbb {A}))$
such that
$\xi \in \mathcal {S}^\circ (U_{h_0}(\mathbb {A}))$
such that
-
• the class of
 $(M_{h_0},\sigma _0)$
belongs to
$(M_{h_0},\sigma _0)$
belongs to
 $\mathfrak {X}_\Pi ^{h_0}$
;
$\mathfrak {X}_\Pi ^{h_0}$
; -
•
 $J_{P_{h_0},\sigma _0}^{h_0}(bc_{}(\lambda ),\xi ) \not =0$
.
$J_{P_{h_0},\sigma _0}^{h_0}(bc_{}(\lambda ),\xi ) \not =0$
.
We set
![]() $f_0^{h_0}=\xi *\xi ^\vee $
, where
$f_0^{h_0}=\xi *\xi ^\vee $
, where
![]() $\xi ^\vee (g)=\overline {\xi (g^{-1})}$
. Then (see [Reference ZhangZha14b, p. 993]) we have
$\xi ^\vee (g)=\overline {\xi (g^{-1})}$
. Then (see [Reference ZhangZha14b, p. 993]) we have
![]() $J_{P,\sigma }^{h_0}(bc(\lambda ),f^{h_0}_0)\geqslant 0$
for all pairs
$J_{P,\sigma }^{h_0}(bc(\lambda ),f^{h_0}_0)\geqslant 0$
for all pairs
![]() $(P,\sigma )$
whose class belongs to
$(P,\sigma )$
whose class belongs to
![]() $\mathfrak {X}_\Pi ^{h_0}$
. Moreover,
$\mathfrak {X}_\Pi ^{h_0}$
. Moreover,
![]() $J_{P_{h_0},\sigma _0}^{h_0}(bc_{h_0}(\lambda ),f^{h_0}_0)>0$
. For any
$J_{P_{h_0},\sigma _0}^{h_0}(bc_{h_0}(\lambda ),f^{h_0}_0)>0$
. For any
![]() $h\in \mathcal {H}^\circ $
such that
$h\in \mathcal {H}^\circ $
such that
![]() $h\not =h_0$
, we set
$h\not =h_0$
, we set
![]() $f^h_0=0$
. Up to enlarging
$f^h_0=0$
. Up to enlarging
![]() $S_0$
, we may and shall assume that the family
$S_0$
, we may and shall assume that the family
![]() $(f^h_0)_{h\in \mathcal {H}^\circ }$
satisfies conditions 2 and 5 of Theorem 7.1.6.1. The left-hand side of (7.1.6.1) for the family
$(f^h_0)_{h\in \mathcal {H}^\circ }$
satisfies conditions 2 and 5 of Theorem 7.1.6.1. The left-hand side of (7.1.6.1) for the family
![]() $(f^h_0)_{h\in \mathcal {H}^\circ }$
is nonzero. By the existence of transfer in [Reference ZhangZha14b] and the results towards archimedean transfer in [Reference XueXue19], we can find test functions
$(f^h_0)_{h\in \mathcal {H}^\circ }$
is nonzero. By the existence of transfer in [Reference ZhangZha14b] and the results towards archimedean transfer in [Reference XueXue19], we can find test functions
![]() $f\in \mathcal {S}^\circ (G(\mathbb {A}))$
and
$f\in \mathcal {S}^\circ (G(\mathbb {A}))$
and
![]() $f^h\in \mathcal {S}^\circ (U_h(\mathbb {A}))$
, for
$f^h\in \mathcal {S}^\circ (U_h(\mathbb {A}))$
, for
![]() $h\in \mathcal {H}^\circ $
, satisfying all the conditions of Theorem 7.1.6.1 and such that the left-hand side of (7.1.6.1) is nonzero. Assertion (A) is then clear.
$h\in \mathcal {H}^\circ $
, satisfying all the conditions of Theorem 7.1.6.1 and such that the left-hand side of (7.1.6.1) is nonzero. Assertion (A) is then clear.
7.3 Proof of Theorem 1.2.4.1
7.3.1
Let
![]() $h\in \mathcal {H}$
. Let
$h\in \mathcal {H}$
. Let
![]() $P=M_PN_P$
be a parabolic subgroup of
$P=M_PN_P$
be a parabolic subgroup of
![]() $U_h$
and
$U_h$
and
![]() $\sigma $
be a cuspidal automorphic subrepresentation of
$\sigma $
be a cuspidal automorphic subrepresentation of
![]() $M_P(\mathbb {A})$
which is tempered everywhere. Then the group
$M_P(\mathbb {A})$
which is tempered everywhere. Then the group
![]() $\operatorname {\mathrm {Res}}_{E/F}(P\times _F E)$
obtained by extension to E and restriction of scalars to F can be identified to a parabolic subgroup
$\operatorname {\mathrm {Res}}_{E/F}(P\times _F E)$
obtained by extension to E and restriction of scalars to F can be identified to a parabolic subgroup
![]() $Q=M_QN_Q$
of G. Then by [Reference MokMok15], [Reference Kaletha, Minguez, Shin and WhiteKMSW],
$Q=M_QN_Q$
of G. Then by [Reference MokMok15], [Reference Kaletha, Minguez, Shin and WhiteKMSW],
![]() $\sigma $
admits a strong base-change
$\sigma $
admits a strong base-change
![]() $\pi $
to
$\pi $
to
![]() $M_Q$
; namely, for every place v of F, the local base-change of
$M_Q$
; namely, for every place v of F, the local base-change of
![]() $\sigma _{v}$
(defined in [Reference MokMok15] and [Reference Kaletha, Minguez, Shin and WhiteKMSW]) coincides with
$\sigma _{v}$
(defined in [Reference MokMok15] and [Reference Kaletha, Minguez, Shin and WhiteKMSW]) coincides with
![]() $\pi _v$
. Let
$\pi _v$
. Let
![]() $\Pi =\operatorname {\mathrm {Ind}}_Q^G(\pi )$
. It follows that
$\Pi =\operatorname {\mathrm {Ind}}_Q^G(\pi )$
. It follows that
![]() $\pi $
and
$\pi $
and
![]() $\Pi $
are also tempered everywhere. We assume that
$\Pi $
are also tempered everywhere. We assume that
![]() $\Pi $
is a H-regular hermitian Arthur parameter. As in §1.1.3, we shall not distinguish in the notation the spaces
$\Pi $
is a H-regular hermitian Arthur parameter. As in §1.1.3, we shall not distinguish in the notation the spaces
![]() $\mathfrak {a}_\Pi ^*$
and
$\mathfrak {a}_\Pi ^*$
and
![]() $\mathfrak {a}_P^*$
. Let
$\mathfrak {a}_P^*$
. Let
![]() $\lambda \in i\mathfrak {a}_\Pi ^*$
.
$\lambda \in i\mathfrak {a}_\Pi ^*$
.
We choose a finite set of places
![]() $S_0$
as in §7.1.2 such that
$S_0$
as in §7.1.2 such that
![]() $h\in \mathcal {H}^\circ $
and
$h\in \mathcal {H}^\circ $
and
![]() $\sigma $
as well as the additive character
$\sigma $
as well as the additive character
![]() $\psi '$
used to normalize local Haar measures in §2.1.8 are unramified outside of
$\psi '$
used to normalize local Haar measures in §2.1.8 are unramified outside of
![]() $S_0$
.
$S_0$
.
We have a decomposition
![]() $\sigma =\otimes _{v\in V_F}\sigma _v$
. Let
$\sigma =\otimes _{v\in V_F}\sigma _v$
. Let
![]() $\Sigma _{\lambda ,v}$
be the full induced representation
$\Sigma _{\lambda ,v}$
be the full induced representation
![]() $\operatorname {\mathrm {Ind}}_{P(F_v)}^{U_h(F_v)}(\sigma _v\otimes \lambda )$
. Let
$\operatorname {\mathrm {Ind}}_{P(F_v)}^{U_h(F_v)}(\sigma _v\otimes \lambda )$
. Let
![]() $v\in V_F$
. We define a distribution
$v\in V_F$
. We define a distribution
![]() $J_{\Sigma _{\lambda ,v}}$
on
$J_{\Sigma _{\lambda ,v}}$
on
![]() $\mathcal {S}(U_{h}(F_v))$
by
$\mathcal {S}(U_{h}(F_v))$
by
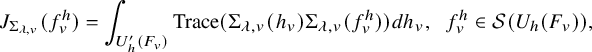 $$ \begin{align*} J_{\Sigma_{\lambda,v}}(f^{h}_v)=\int_{U^{\prime}_{h}(F_v)} \mathrm{Trace}(\Sigma_{\lambda,v}(h_v)\Sigma_{\lambda,v}(f^{h}_v)) dh_v,\;\; f^{h}_v\in \mathcal{S}(U_{h}(F_v)), \end{align*} $$
$$ \begin{align*} J_{\Sigma_{\lambda,v}}(f^{h}_v)=\int_{U^{\prime}_{h}(F_v)} \mathrm{Trace}(\Sigma_{\lambda,v}(h_v)\Sigma_{\lambda,v}(f^{h}_v)) dh_v,\;\; f^{h}_v\in \mathcal{S}(U_{h}(F_v)), \end{align*} $$
where
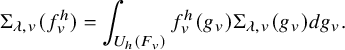 $$ \begin{align*} \Sigma_{\lambda,v}(f^{h}_v)=\int_{U_{h}(F_v)} f^{h}_v(g_v) \Sigma_{\lambda,v}(g_v)dg_v. \end{align*} $$
$$ \begin{align*} \Sigma_{\lambda,v}(f^{h}_v)=\int_{U_{h}(F_v)} f^{h}_v(g_v) \Sigma_{\lambda,v}(g_v)dg_v. \end{align*} $$
By [Reference HarrisHar14], since the representations
![]() $\Sigma _{\lambda ,v}$
are all tempered, the expression defining
$\Sigma _{\lambda ,v}$
are all tempered, the expression defining
![]() $J_{\Sigma _{\lambda ,v}}$
is absolutely convergent, and for every
$J_{\Sigma _{\lambda ,v}}$
is absolutely convergent, and for every
![]() $v\notin S_0$
, we have
$v\notin S_0$
, we have
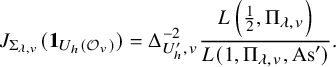 $$ \begin{align*}J_{\Sigma_{\lambda,v}}(\mathbf{1}_{U_{h}(\mathcal{O}_v)})=\Delta_{U^{\prime}_{h},v}^{-2} \frac{L\left(\frac12,\Pi_{\lambda,v}\right)}{L(1,\Pi_{\lambda,v},\mathrm{As}')}.\end{align*} $$
$$ \begin{align*}J_{\Sigma_{\lambda,v}}(\mathbf{1}_{U_{h}(\mathcal{O}_v)})=\Delta_{U^{\prime}_{h},v}^{-2} \frac{L\left(\frac12,\Pi_{\lambda,v}\right)}{L(1,\Pi_{\lambda,v},\mathrm{As}')}.\end{align*} $$
If there exists a place
![]() $v\in S_0$
such that
$v\in S_0$
such that
![]() $\sigma _{v}$
does not support any nonzero continuous
$\sigma _{v}$
does not support any nonzero continuous
![]() $U^{\prime }_{h}(F_v)$
-invariant functional, both sides of (1.2.4.1) in Theorem 1.2.4.1 are clearly automatically zero. So we shall assume that for every
$U^{\prime }_{h}(F_v)$
-invariant functional, both sides of (1.2.4.1) in Theorem 1.2.4.1 are clearly automatically zero. So we shall assume that for every
![]() $v\in S_0$
, the local representation
$v\in S_0$
, the local representation
![]() $\sigma _{v}$
supports a nonzero continuous
$\sigma _{v}$
supports a nonzero continuous
![]() $U^{\prime }_{h}(F_v)$
-invariant functional. Then the semi-local distribution
$U^{\prime }_{h}(F_v)$
-invariant functional. Then the semi-local distribution
![]() $\prod _{v\in S_0} J_{\Sigma _{\lambda , v}}(f_v^{h})$
does not vanish identically by [Reference Beuzart-PlessisBP20, theorem 8.2.1]. According to our choice of local measure, Theorem 1.2.4.1 is then equivalent to the following assertion: for all factorizable test function
$\prod _{v\in S_0} J_{\Sigma _{\lambda , v}}(f_v^{h})$
does not vanish identically by [Reference Beuzart-PlessisBP20, theorem 8.2.1]. According to our choice of local measure, Theorem 1.2.4.1 is then equivalent to the following assertion: for all factorizable test function
![]() $f^{h}\in \mathcal {S}(U_{h_0}(\mathbb {A}))$
of the form
$f^{h}\in \mathcal {S}(U_{h_0}(\mathbb {A}))$
of the form
![]() $f^{h}=(\Delta _{U^{\prime }_{h}}^{S_0})^2\prod _{v\in S_0} f^{h}_v\times \prod _{v\notin S_0} \mathbf {1}_{U_{h}(\mathcal {O}_v)}$
, we have
$f^{h}=(\Delta _{U^{\prime }_{h}}^{S_0})^2\prod _{v\in S_0} f^{h}_v\times \prod _{v\notin S_0} \mathbf {1}_{U_{h}(\mathcal {O}_v)}$
, we have
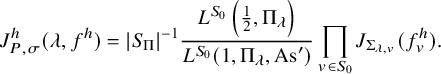 $$ \begin{align} J^{h}_{P,\sigma}(\lambda,f^{h})=\lvert S_\Pi\rvert^{-1} \frac{L^{S_0}\left(\frac12,\Pi_\lambda\right)}{L^{S_0}(1,\Pi_\lambda,\mathrm{As}')}\prod_{v\in S_0} J_{\Sigma_{\lambda, v}}(f_v^{h}). \end{align} $$
$$ \begin{align} J^{h}_{P,\sigma}(\lambda,f^{h})=\lvert S_\Pi\rvert^{-1} \frac{L^{S_0}\left(\frac12,\Pi_\lambda\right)}{L^{S_0}(1,\Pi_\lambda,\mathrm{As}')}\prod_{v\in S_0} J_{\Sigma_{\lambda, v}}(f_v^{h}). \end{align} $$
7.3.2
By Theorem 4.2.8.1 and the definition of
![]() $I_{\Pi _\lambda }$
there, for every factorizable test function
$I_{\Pi _\lambda }$
there, for every factorizable test function
![]() $f\in \mathcal {S}(G(\mathbb {A}))$
of the form
$f\in \mathcal {S}(G(\mathbb {A}))$
of the form
![]() $f=\Delta _H^{S_0,*}\Delta _{G'}^{S_0,*}\prod _{v\in S_0} f_v \times \prod _{v\notin S_0} \mathbf {1}_{G(\mathcal {O}_v)}$
, we have
$f=\Delta _H^{S_0,*}\Delta _{G'}^{S_0,*}\prod _{v\in S_0} f_v \times \prod _{v\notin S_0} \mathbf {1}_{G(\mathcal {O}_v)}$
, we have
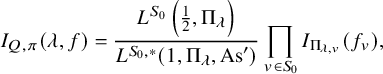 $$ \begin{align} I_{Q,\pi}(\lambda,f)=\frac{L^{S_0}\left(\frac12,\Pi_\lambda\right) }{ L^{S_0,*}(1,\Pi_\lambda,\mathrm{As}') } \prod_{v\in S_0} I_{\Pi_{\lambda,v}}(f_v), \end{align} $$
$$ \begin{align} I_{Q,\pi}(\lambda,f)=\frac{L^{S_0}\left(\frac12,\Pi_\lambda\right) }{ L^{S_0,*}(1,\Pi_\lambda,\mathrm{As}') } \prod_{v\in S_0} I_{\Pi_{\lambda,v}}(f_v), \end{align} $$
where for for every place
![]() $v\in S_0$
, we introduce the local relative character
$v\in S_0$
, we introduce the local relative character
![]() $I_{\Pi _{\lambda ,v}}$
defined by
$I_{\Pi _{\lambda ,v}}$
defined by
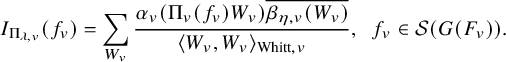 $$ \begin{align*} I_{\Pi_{\lambda,v}}(f_v)=\sum_{W_v} \frac{\alpha_v(\Pi_v(f_v)W_v) \overline{\beta_{\eta,v}(W_v)}}{\langle W_v,W_v\rangle_{\mathrm{Whitt}, v}},\;\; f_v\in \mathcal{S}(G(F_v)). \end{align*} $$
$$ \begin{align*} I_{\Pi_{\lambda,v}}(f_v)=\sum_{W_v} \frac{\alpha_v(\Pi_v(f_v)W_v) \overline{\beta_{\eta,v}(W_v)}}{\langle W_v,W_v\rangle_{\mathrm{Whitt}, v}},\;\; f_v\in \mathcal{S}(G(F_v)). \end{align*} $$
Here, the sum runs over a
![]() $K_v$
-basis of the Whittaker model
$K_v$
-basis of the Whittaker model
![]() $\mathcal {W}(\Pi _{\lambda ,v},\psi _{N,v})$
, and
$\mathcal {W}(\Pi _{\lambda ,v},\psi _{N,v})$
, and
![]() $\lambda _v$
,
$\lambda _v$
,
![]() $\beta _{\eta ,v}$
,
$\beta _{\eta ,v}$
,
![]() $\langle .,.\rangle _{\mathrm {Whitt},v}$
are given by
$\langle .,.\rangle _{\mathrm {Whitt},v}$
are given by
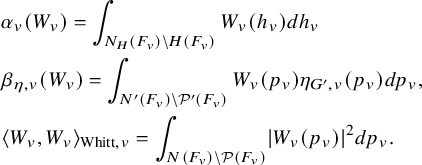 $$ \begin{align*} & \alpha_v(W_v)=\int_{N_H(F_v)\backslash H(F_v)} W_v(h_v)dh_v \\ & \beta_{\eta,v}(W_v)=\int_{N'(F_v)\backslash \mathcal{P}'(F_v)} W_v(p_v) \eta_{G',v}(p_v) dp_v, \\ & \langle W_v,W_v\rangle_{\mathrm{Whitt},v}=\int_{N(F_v)\backslash \mathcal{P}(F_v)} \lvert W_v(p_v)\rvert^2 dp_v. \end{align*} $$
$$ \begin{align*} & \alpha_v(W_v)=\int_{N_H(F_v)\backslash H(F_v)} W_v(h_v)dh_v \\ & \beta_{\eta,v}(W_v)=\int_{N'(F_v)\backslash \mathcal{P}'(F_v)} W_v(p_v) \eta_{G',v}(p_v) dp_v, \\ & \langle W_v,W_v\rangle_{\mathrm{Whitt},v}=\int_{N(F_v)\backslash \mathcal{P}(F_v)} \lvert W_v(p_v)\rvert^2 dp_v. \end{align*} $$
The above expressions, especially
![]() $\alpha _v(W_v)$
, are all absolutely convergent due to the fact that
$\alpha _v(W_v)$
, are all absolutely convergent due to the fact that
![]() $\Pi _{\lambda ,v}$
is tempered (see [Reference Jacquet, Piatetskii-Shapiro and ShalikaJPSS83, Proposition 8.4]). The above definition implicitly depends on the choice of an additive character
$\Pi _{\lambda ,v}$
is tempered (see [Reference Jacquet, Piatetskii-Shapiro and ShalikaJPSS83, Proposition 8.4]). The above definition implicitly depends on the choice of an additive character
![]() $\psi $
of
$\psi $
of
![]() $\mathbb {A}_E/E$
trivial on
$\mathbb {A}_E/E$
trivial on
![]() $\mathbb {A}$
which, up to enlarging
$\mathbb {A}$
which, up to enlarging
![]() $S_0$
, we may assume to be unramified outside of
$S_0$
, we may assume to be unramified outside of
![]() $S_0$
.
$S_0$
.
7.3.3
Let
![]() $f^{h}$
be a test function as in (7.3.1.1). Since both sides of (7.3.1.1) are continuous functionals in
$f^{h}$
be a test function as in (7.3.1.1). Since both sides of (7.3.1.1) are continuous functionals in
![]() $f^{h}_v$
for
$f^{h}_v$
for
![]() $v\in S_0$
, we may assume that the function
$v\in S_0$
, we may assume that the function
![]() $f^{h}_v$
admits a transfer
$f^{h}_v$
admits a transfer
![]() $f_v\in \mathcal {S}(G(F_v))$
for every
$f_v\in \mathcal {S}(G(F_v))$
for every
![]() $v\in S_0$
using results of [Reference XueXue19] and [Reference ZhangZha14b]. Moreover, by the results of those references, we may also assume that for every
$v\in S_0$
using results of [Reference XueXue19] and [Reference ZhangZha14b]. Moreover, by the results of those references, we may also assume that for every
![]() $h'\in \mathcal {H}^\circ $
with
$h'\in \mathcal {H}^\circ $
with
![]() $h'\neq h$
, the zero function on
$h'\neq h$
, the zero function on
![]() $U_{h'}(F_{S_0})$
is a transfer of
$U_{h'}(F_{S_0})$
is a transfer of
![]() $f_{S_0}=\prod _{v\in S_0} f_v$
. We set
$f_{S_0}=\prod _{v\in S_0} f_v$
. We set
![]() $f=\Delta _H^{S_0,*}\Delta _{G'}^{S_0,*}f_{S_0} \times \prod _{v\notin S_0} \mathbf {1}_{G(\mathcal {O}_v)}$
. Then, setting
$f=\Delta _H^{S_0,*}\Delta _{G'}^{S_0,*}f_{S_0} \times \prod _{v\notin S_0} \mathbf {1}_{G(\mathcal {O}_v)}$
. Then, setting
![]() $f^{h'}=0$
for every
$f^{h'}=0$
for every
![]() $h'\in \mathcal {H}^\circ \setminus \{h \}$
, the functions f and
$h'\in \mathcal {H}^\circ \setminus \{h \}$
, the functions f and
![]() $(f^{h'})_{h'\in \mathcal {H}^\circ }$
satisfy the assumptions of Theorem 7.1.6.1. Therefore, we have
$(f^{h'})_{h'\in \mathcal {H}^\circ }$
satisfy the assumptions of Theorem 7.1.6.1. Therefore, we have
7.3.4
By the local Gan-Gross-Prasad Conjecture [Reference Beuzart-PlessisBP20], the classification of cuspidal automorphic representations of
![]() $U_{h}$
in terms of local L-packets [Reference MokMok15], [Reference Kaletha, Minguez, Shin and WhiteKMSW], all the terms in the definition of
$U_{h}$
in terms of local L-packets [Reference MokMok15], [Reference Kaletha, Minguez, Shin and WhiteKMSW], all the terms in the definition of
![]() $J_{\Pi }^{h}(\lambda ,f^{h})$
(see (7.1.5.2)) vanish except possibly
$J_{\Pi }^{h}(\lambda ,f^{h})$
(see (7.1.5.2)) vanish except possibly
![]() $J_{P,\sigma }^{h}(\lambda , f^{h})$
. So (7.3.3.1) reduces to
$J_{P,\sigma }^{h}(\lambda , f^{h})$
. So (7.3.3.1) reduces to
By [Reference Beuzart-PlessisBP21, Theorem 5.4.1] and since
![]() $\Pi _v$
is the local base-change of
$\Pi _v$
is the local base-change of
![]() $\sigma _{v}$
, there are explicit constants
$\sigma _{v}$
, there are explicit constants
![]() $\kappa _v\in \mathbb {C}^\times $
for
$\kappa _v\in \mathbb {C}^\times $
for
![]() $v\in S_0$
satisfying
$v\in S_0$
satisfying
![]() $\prod _{v\in S_0} \kappa _v=1$
and such that
$\prod _{v\in S_0} \kappa _v=1$
and such that
for every
![]() $v\in S_0$
. Now (7.3.1.1) results from the combination of (7.3.4.1), the factorization (7.3.2.1) and the local comparison (7.3.4.2).
$v\in S_0$
. Now (7.3.1.1) results from the combination of (7.3.4.1), the factorization (7.3.2.1) and the local comparison (7.3.4.2).
8 Application to the Gan-Gross-Prasad and Ichino-Ikeda conjectures for Bessel periods
8.1 Groups
8.1.1 Notations
They are as in Sections 2, 3 and 4. In particular,
![]() $E/F$
is a quadratic extension of number fields. For every place v of F, we set
$E/F$
is a quadratic extension of number fields. For every place v of F, we set
![]() $E_v=F_v\otimes _F E$
and we let
$E_v=F_v\otimes _F E$
and we let
![]() $\mathcal {O}_{E_v}$
be the ‘ring of integers’ in the quadratic étale extension
$\mathcal {O}_{E_v}$
be the ‘ring of integers’ in the quadratic étale extension
![]() $E_v$
of
$E_v$
of
![]() $F_v$
. We denote by
$F_v$
. We denote by
![]() $\mathbb {A}_E=\prod _v^{\prime } E_v$
the ring of adeles of E. We fix a nontrivial character
$\mathbb {A}_E=\prod _v^{\prime } E_v$
the ring of adeles of E. We fix a nontrivial character
![]() $\psi : \mathbb {A}_E/E\to \mathbb {C}^\times $
that is trivial on
$\psi : \mathbb {A}_E/E\to \mathbb {C}^\times $
that is trivial on
![]() $\mathbb {A}$
. We also set (see §2.1.7)
$\mathbb {A}$
. We also set (see §2.1.7)
If V is a finite dimensional vector space over F, we also fix a height
![]() $\lVert .\rVert _{V_{\mathbb {A}}}: V_{\mathbb {A}}=V\otimes _F \mathbb {A}\to \mathbb {R}_{\geqslant 1}$
as in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, §2.4.2], and for every place v of F, we denote by
$\lVert .\rVert _{V_{\mathbb {A}}}: V_{\mathbb {A}}=V\otimes _F \mathbb {A}\to \mathbb {R}_{\geqslant 1}$
as in [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, §2.4.2], and for every place v of F, we denote by
![]() $\lVert .\rVert _{V_v}$
the restriction of
$\lVert .\rVert _{V_v}$
the restriction of
![]() $\lVert .\rVert _{V_{\mathbb {A}}}$
to
$\lVert .\rVert _{V_{\mathbb {A}}}$
to
![]() $V_v:=V\otimes _F F_v$
. We will also write
$V_v:=V\otimes _F F_v$
. We will also write
![]() $\mathcal {S}(V_v)$
for the usual Schwartz-Bruhat space on the vector space
$\mathcal {S}(V_v)$
for the usual Schwartz-Bruhat space on the vector space
![]() $V_v$
(i.e., the usual Schwartz space if v is Archimedean or the space of compactly supported locally constant functions when v is non-Archimedean).
$V_v$
(i.e., the usual Schwartz space if v is Archimedean or the space of compactly supported locally constant functions when v is non-Archimedean).
Recall also, that for every integer
![]() $n\geqslant 0$
,
$n\geqslant 0$
,
![]() $\mathcal {H}_n$
stands for the set of isomorphism classes of Hermitian forms of rank n for the extension
$\mathcal {H}_n$
stands for the set of isomorphism classes of Hermitian forms of rank n for the extension
![]() $E/F$
. For each
$E/F$
. For each
![]() $h\in \mathcal {H}_n$
, we denote by
$h\in \mathcal {H}_n$
, we denote by
![]() $U(h)$
the corresponding unitary group. We also fix, as in 3.1, some Hermitian form of rank one
$U(h)$
the corresponding unitary group. We also fix, as in 3.1, some Hermitian form of rank one
![]() $h_0\in \mathcal {H}_1$
.
$h_0\in \mathcal {H}_1$
.
8.1.2 Linear groups
For every
![]() $k\geqslant 0$
, we set
$k\geqslant 0$
, we set
![]() $G_k=\operatorname {\mathrm {Res}}_{E/F}\mathrm {GL}_{k,E}$
equipped with the pair
$G_k=\operatorname {\mathrm {Res}}_{E/F}\mathrm {GL}_{k,E}$
equipped with the pair
![]() $(B_k,T_k)$
as in §4.1.1. Let
$(B_k,T_k)$
as in §4.1.1. Let
![]() $N_k\subset B_k$
be the unipotent radical of
$N_k\subset B_k$
be the unipotent radical of
![]() $ B_k$
. We define two generic characters
$ B_k$
. We define two generic characters
![]() $\psi _k,\psi _{-k}:[N_k]\to \mathbb {C}^\times $
by
$\psi _k,\psi _{-k}:[N_k]\to \mathbb {C}^\times $
by
 $$ \begin{align*} \psi_{k}(u)=\psi \left(\sum_{i=1}^{k-1}u_{i,i+1}\right). \end{align*} $$
$$ \begin{align*} \psi_{k}(u)=\psi \left(\sum_{i=1}^{k-1}u_{i,i+1}\right). \end{align*} $$
 $$ \begin{align*} \psi_{-k}(u)=\psi \left(-\sum_{i=1}^{k-1}u_{i,i+1} \right),\;\; u\in [N_k]. \end{align*} $$
$$ \begin{align*} \psi_{-k}(u)=\psi \left(-\sum_{i=1}^{k-1}u_{i,i+1} \right),\;\; u\in [N_k]. \end{align*} $$
We also let
![]() $P_k\subset G_k$
be the mirabolic subgroup consisting of matrices with last row
$P_k\subset G_k$
be the mirabolic subgroup consisting of matrices with last row
![]() $(0,\ldots ,0,1)$
and
$(0,\ldots ,0,1)$
and
![]() $K_k=\prod _{v}K_{k,v}$
be the standard maximal compact subgroup of
$K_k=\prod _{v}K_{k,v}$
be the standard maximal compact subgroup of
![]() $G_k(\mathbb {A})$
.
$G_k(\mathbb {A})$
.
8.1.3 Unitary groups
We define the Hermitian form
![]() $h_s\in \mathcal {H}_2$
by
$h_s\in \mathcal {H}_2$
by
![]() $h_s=h_0\oplus -h_0$
. We also fix a basis
$h_s=h_0\oplus -h_0$
. We also fix a basis
![]() $(x,y)$
of
$(x,y)$
of
![]() $E^2$
consisting of isotropic vectors for
$E^2$
consisting of isotropic vectors for
![]() $h_s$
(i.e.
$h_s$
(i.e.
![]() $h_s(x,x)=h_s(y,y)=0$
) such that
$h_s(x,x)=h_s(y,y)=0$
) such that
![]() $h_s(x,y)=1$
, and we set
$h_s(x,y)=1$
, and we set
![]() $X=Ex$
,
$X=Ex$
,
![]() $Y=Ey$
.
$Y=Ey$
.
We fix once and for all two positive integers
![]() $n\geqslant m$
of the same parity. Thus,
$n\geqslant m$
of the same parity. Thus,
![]() $n=m+2r$
for some
$n=m+2r$
for some
![]() $r\geqslant 0$
. Let
$r\geqslant 0$
. Let
![]() $h_m\in \mathcal {H}_m$
. We set
$h_m\in \mathcal {H}_m$
. We set
![]() $h_{m+1}=h_m\oplus h_0$
,
$h_{m+1}=h_m\oplus h_0$
,
![]() $h_n=h_s^{\oplus r}\oplus h_m$
,
$h_n=h_s^{\oplus r}\oplus h_m$
,
![]() $h_{n+1}=h_n\oplus h_0=h_s^{\oplus r}\oplus h_{m+1}$
and
$h_{n+1}=h_n\oplus h_0=h_s^{\oplus r}\oplus h_{m+1}$
and
Note that we have natural inclusions
![]() $U_m\hookrightarrow U_{m+1}\hookrightarrow U_n\hookrightarrow U_{n+1}$
. We also define the following products:
$U_m\hookrightarrow U_{m+1}\hookrightarrow U_n\hookrightarrow U_{n+1}$
. We also define the following products:
For every
![]() $0\leqslant i\leqslant r$
, we set
$0\leqslant i\leqslant r$
, we set
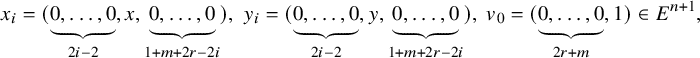 $$ \begin{align*}x_i=(\underbrace{0,\ldots,0}_{2i-2},x,\underbrace{0,\ldots,0}_{1+m+2r-2i}),\; y_i=(\underbrace{0,\ldots,0}_{2i-2},y,\underbrace{0,\ldots,0}_{1+m+2r-2i}),\; v_0=(\underbrace{0,\ldots,0}_{2r+m},1)\in E^{n+1},\end{align*} $$
$$ \begin{align*}x_i=(\underbrace{0,\ldots,0}_{2i-2},x,\underbrace{0,\ldots,0}_{1+m+2r-2i}),\; y_i=(\underbrace{0,\ldots,0}_{2i-2},y,\underbrace{0,\ldots,0}_{1+m+2r-2i}),\; v_0=(\underbrace{0,\ldots,0}_{2r+m},1)\in E^{n+1},\end{align*} $$
and we define the subvector spaces
![]() $X_i=\langle x_1,\ldots ,x_i\rangle $
and
$X_i=\langle x_1,\ldots ,x_i\rangle $
and
![]() $Y_i=\langle y_1,\ldots ,y_i\rangle $
of
$Y_i=\langle y_1,\ldots ,y_i\rangle $
of
![]() $E^{n+1}$
spanned by
$E^{n+1}$
spanned by
![]() $(x_1,\ldots ,x_i)$
and
$(x_1,\ldots ,x_i)$
and
![]() $(y_1,\ldots ,y_i)$
, respectively. Then,
$(y_1,\ldots ,y_i)$
, respectively. Then,
![]() $0=X_0\subsetneq X_1\ldots \subsetneq X_r$
is a flag of
$0=X_0\subsetneq X_1\ldots \subsetneq X_r$
is a flag of
![]() $h_{n+1}$
-isotropic subspaces, and we let
$h_{n+1}$
-isotropic subspaces, and we let
![]() $P\subset U_{n+1}$
be the parabolic subgroup stabilizing it. Let N be the unipotent radical of P. We define a character
$P\subset U_{n+1}$
be the parabolic subgroup stabilizing it. Let N be the unipotent radical of P. We define a character
![]() $\psi _N:[N]\to \mathbb {C}^\times $
by
$\psi _N:[N]\to \mathbb {C}^\times $
by
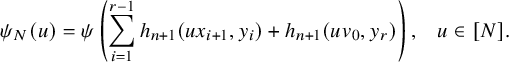 $$ \begin{align*}\psi_N(u)=\psi\left(\sum_{i=1}^{r-1} h_{n+1}(ux_{i+1},y_i)+h_{n+1}(uv_0,y_r) \right),\;\;\; u\in [N].\end{align*} $$
$$ \begin{align*}\psi_N(u)=\psi\left(\sum_{i=1}^{r-1} h_{n+1}(ux_{i+1},y_i)+h_{n+1}(uv_0,y_r) \right),\;\;\; u\in [N].\end{align*} $$
The subgroup
![]() $U_m\subset U_{n+1}$
normalizes N, and
$U_m\subset U_{n+1}$
normalizes N, and
![]() $\psi _N$
is invariant by
$\psi _N$
is invariant by
![]() $U_m(\mathbb {A})$
-conjugation. We define the following three subgroups of the respective groups in (8.1.3.1):
$U_m(\mathbb {A})$
-conjugation. We define the following three subgroups of the respective groups in (8.1.3.1):
where the embedding
![]() $\mathcal {B}\subset \mathcal {G}$
is the product of the inclusion
$\mathcal {B}\subset \mathcal {G}$
is the product of the inclusion
![]() $\mathcal {B}\subset U_{n+1}$
and the natural projection
$\mathcal {B}\subset U_{n+1}$
and the natural projection
![]() $\mathcal {B}\to U_m$
, whereas the embeddings
$\mathcal {B}\to U_m$
, whereas the embeddings
![]() $U'\subset U$
,
$U'\subset U$
,
![]() $\widetilde {U}'\subset \widetilde {U}$
are the diagonal ones. We also let
$\widetilde {U}'\subset \widetilde {U}$
are the diagonal ones. We also let
![]() $\psi _{\mathcal {B}}: [\mathcal {B}]\to \mathbb {C}^\times $
be the character that coincides with
$\psi _{\mathcal {B}}: [\mathcal {B}]\to \mathbb {C}^\times $
be the character that coincides with
![]() $\psi _N$
on
$\psi _N$
on
![]() $[N]$
and is trivial on
$[N]$
and is trivial on
![]() $[U_m]$
.
$[U_m]$
.
We will also need some auxiliary parabolic subgroups. First, we let
![]() $P'=P\cap U_n$
be the stabilizer of the flag
$P'=P\cap U_n$
be the stabilizer of the flag
![]() $X_0\subsetneq \ldots \subsetneq X_r$
in
$X_0\subsetneq \ldots \subsetneq X_r$
in
![]() $U_n$
. We also let
$U_n$
. We also let
![]() $Q_{n+1}\subset U_{n+1}$
(resp.
$Q_{n+1}\subset U_{n+1}$
(resp.
![]() $Q_n\subset U_n$
) be the parabolic subgroup stabilizing the
$Q_n\subset U_n$
) be the parabolic subgroup stabilizing the
![]() $h_{n+1}$
-isotropic (resp.
$h_{n+1}$
-isotropic (resp.
![]() $h_n$
-isotropic) subspace
$h_n$
-isotropic) subspace
![]() $X_r$
and we denote by
$X_r$
and we denote by
![]() $V_{n+1}$
(resp.
$V_{n+1}$
(resp.
![]() $V_n$
) its unipotent radical.
$V_n$
) its unipotent radical.
Using the basis
![]() $(x_1,\ldots ,x_r)$
of
$(x_1,\ldots ,x_r)$
of
![]() $X_r$
, we will identify
$X_r$
, we will identify
![]() $G_r$
as the subgroup of elements in both
$G_r$
as the subgroup of elements in both
![]() $U_n$
and
$U_n$
and
![]() $U_{n+1}$
that stabilize the two isotropic subspaces
$U_{n+1}$
that stabilize the two isotropic subspaces
![]() $X_r$
,
$X_r$
,
![]() $Y_r$
and act trivially on the orthogonal complement
$Y_r$
and act trivially on the orthogonal complement
![]() $(X_r\oplus Y_r)^\perp $
. We then have a semi-direct decomposition
$(X_r\oplus Y_r)^\perp $
. We then have a semi-direct decomposition
We also let
![]() $L_n\subset Q_n$
be the Levi factor of
$L_n\subset Q_n$
be the Levi factor of
![]() $Q_n$
stabilizing
$Q_n$
stabilizing
![]() $Y_r$
. We have
$Y_r$
. We have
We will also use the natural identification
![]() $a_{Q_n}^*\simeq a_{G_r}^*\simeq \mathbb {C}$
sending
$a_{Q_n}^*\simeq a_{G_r}^*\simeq \mathbb {C}$
sending
![]() $s\in \mathbb {C}$
to the unramified character
$s\in \mathbb {C}$
to the unramified character
![]() $(g_r,h)\in L_n(\mathbb {A})\mapsto \lvert \det (g_r)\rvert _{\mathbb {A}_E}^s$
. Similarly, for any representation
$(g_r,h)\in L_n(\mathbb {A})\mapsto \lvert \det (g_r)\rvert _{\mathbb {A}_E}^s$
. Similarly, for any representation
![]() $\tau $
of
$\tau $
of
![]() $L_n(\mathbb {A})$
, we will denote by
$L_n(\mathbb {A})$
, we will denote by
![]() $\tau _s$
the twist of
$\tau _s$
the twist of
![]() $\tau $
by this character. Also, once we have fixed suitable maximal compact subgroups below giving rise to a Harish-Chandra map
$\tau $
by this character. Also, once we have fixed suitable maximal compact subgroups below giving rise to a Harish-Chandra map
![]() $H_{Q_n}:U_n(\mathbb {A})\to a_{Q_n}$
, for each
$H_{Q_n}:U_n(\mathbb {A})\to a_{Q_n}$
, for each
![]() $\phi _n\in I_{Q_n}^{U_n}(\tau )$
and
$\phi _n\in I_{Q_n}^{U_n}(\tau )$
and
![]() $s\in \mathbb {C}$
, we will denote by
$s\in \mathbb {C}$
, we will denote by
![]() $\phi _{n,s}\in I_{Q_n}^{U_n}(\tau _s)$
the section given by
$\phi _{n,s}\in I_{Q_n}^{U_n}(\tau _s)$
the section given by
![]() $g\mapsto \exp (s\langle \det ,H_{Q_n}(g)\rangle )\phi _n(g)$
. This applies in particular to
$g\mapsto \exp (s\langle \det ,H_{Q_n}(g)\rangle )\phi _n(g)$
. This applies in particular to
![]() $\phi _n\in \mathcal {A}_{Q_n}(U_n)$
, and we will write
$\phi _n\in \mathcal {A}_{Q_n}(U_n)$
, and we will write
![]() $E_{Q_n}^{U_n}(\phi _n,s)$
for the Eisenstein series
$E_{Q_n}^{U_n}(\phi _n,s)$
for the Eisenstein series
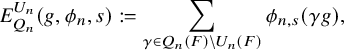 $$ \begin{align*}E_{Q_n}^{U_n}(g,\phi_n,s):=\sum_{\gamma\in Q_n(F)\backslash U_n(F)} \phi_{n,s}(\gamma g),\end{align*} $$
$$ \begin{align*}E_{Q_n}^{U_n}(g,\phi_n,s):=\sum_{\gamma\in Q_n(F)\backslash U_n(F)} \phi_{n,s}(\gamma g),\end{align*} $$
which converges absolutely when
![]() $\Re (s)$
is large enough.
$\Re (s)$
is large enough.
We also set
![]() $Q=Q_n\times U_{n+1}$
(a maximal parabolic subgroup of U) and
$Q=Q_n\times U_{n+1}$
(a maximal parabolic subgroup of U) and
(a Levi factor of Q). We define the following subgroup of L:
as well as the character
![]() $\psi ^L_{\mathcal {B}}=\psi _{-r}\boxtimes \psi _{\mathcal {B}}$
of
$\psi ^L_{\mathcal {B}}=\psi _{-r}\boxtimes \psi _{\mathcal {B}}$
of
![]() $[\mathcal {B}^L]$
. We also set
$[\mathcal {B}^L]$
. We also set
We fix a finite set S of places of F containing the Archimedean places as well a the places dividing
![]() $2$
and such that the character
$2$
and such that the character
![]() $\psi $
and the Hermitian form
$\psi $
and the Hermitian form
![]() $h_m$
are both unramified outside S (i.e., there exists a lattice
$h_m$
are both unramified outside S (i.e., there exists a lattice
![]() $\Lambda _m\subset E^m$
such that
$\Lambda _m\subset E^m$
such that
![]() $\Lambda _{m,v}:=\Lambda _m\otimes _{\mathcal {O}_E} \mathcal {O}_{E_v}$
is self-dual with respect to
$\Lambda _{m,v}:=\Lambda _m\otimes _{\mathcal {O}_E} \mathcal {O}_{E_v}$
is self-dual with respect to
![]() $h_m$
for every
$h_m$
for every
![]() $v\notin S$
). Then, the same holds for the lattices
$v\notin S$
). Then, the same holds for the lattices
![]() $\Lambda _{m+1}=\Lambda _{m}\oplus \mathcal {O}_E$
,
$\Lambda _{m+1}=\Lambda _{m}\oplus \mathcal {O}_E$
,
![]() $\Lambda _n=\mathcal {O}_E^{\oplus 2r}\oplus \Lambda _m$
and
$\Lambda _n=\mathcal {O}_E^{\oplus 2r}\oplus \Lambda _m$
and
![]() $\Lambda _{n+1}=\Lambda _n\oplus \mathcal {O}_E$
with respect to the Hermitian forms
$\Lambda _{n+1}=\Lambda _n\oplus \mathcal {O}_E$
with respect to the Hermitian forms
![]() $h_{m+1}$
,
$h_{m+1}$
,
![]() $h_n$
and
$h_n$
and
![]() $h_{n+1}$
, respectively.
$h_{n+1}$
, respectively.
For
![]() $\ell \in \{m,m+1,n,n+1 \}$
, we fix a maximal compact subgroup
$\ell \in \{m,m+1,n,n+1 \}$
, we fix a maximal compact subgroup
![]() $K^U_{\ell }=\prod _v K^U_{\ell ,v}\subset U_{\ell }(\mathbb {A})$
such that for every
$K^U_{\ell }=\prod _v K^U_{\ell ,v}\subset U_{\ell }(\mathbb {A})$
such that for every
![]() $v\notin S$
,
$v\notin S$
,
![]() $K^U_{\ell ,v}$
is the stabilizer of the lattice
$K^U_{\ell ,v}$
is the stabilizer of the lattice
![]() $\Lambda _{\ell }\otimes _{\mathcal {O}_E} \mathcal {O}_{E_v}$
.
$\Lambda _{\ell }\otimes _{\mathcal {O}_E} \mathcal {O}_{E_v}$
.
8.2 Measures
8.2.1
For every linear algebraic group
![]() $\mathbb {G}$
defined over F, we have equipped
$\mathbb {G}$
defined over F, we have equipped
![]() $\mathbb {G}(\mathbb {A})$
with its (left) Tamagawa measure
$\mathbb {G}(\mathbb {A})$
with its (left) Tamagawa measure
![]() $dg$
; see §2.1.8. Also, for each
$dg$
; see §2.1.8. Also, for each
![]() $\mathbb {G}\in \{U_m,U_n,U_{n+1},U_{n+2}, G_r, V_n \}$
, we fix a factorization
$\mathbb {G}\in \{U_m,U_n,U_{n+1},U_{n+2}, G_r, V_n \}$
, we fix a factorization
![]() $dg=\prod _v dg_v$
into local Haar measures giving
$dg=\prod _v dg_v$
into local Haar measures giving
![]() $\mathbb {G}(\mathcal {O}_v)$
measure one for almost all v. In the case where
$\mathbb {G}(\mathcal {O}_v)$
measure one for almost all v. In the case where
![]() $\mathbb {G}=N_k$
, it will be convenient to fix more precisely the local measures as follows: for every place v of F, let
$\mathbb {G}=N_k$
, it will be convenient to fix more precisely the local measures as follows: for every place v of F, let
![]() $d_{\psi _v}x_v$
be the Haar measure on
$d_{\psi _v}x_v$
be the Haar measure on
![]() $E_v$
that is self-dual with respect to
$E_v$
that is self-dual with respect to
![]() $\psi _v$
. Then we equip
$\psi _v$
. Then we equip
![]() $N_k(F_v)$
with the product measure
$N_k(F_v)$
with the product measure
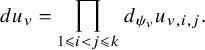 $$ \begin{align*}du_v=\prod_{1\leqslant i<j\leqslant k} d_{\psi_v} u_{v,i,j}.\end{align*} $$
$$ \begin{align*}du_v=\prod_{1\leqslant i<j\leqslant k} d_{\psi_v} u_{v,i,j}.\end{align*} $$
It is well known, and easy to check, that
![]() $du=\prod _v du_v$
is indeed the global Tamagawa measure on
$du=\prod _v du_v$
is indeed the global Tamagawa measure on
![]() $N_k(\mathbb {A})$
(i.e., it gives
$N_k(\mathbb {A})$
(i.e., it gives
![]() $[N_k]$
volume one).
$[N_k]$
volume one).
Similarly, for every v, there is another natural measure on
![]() $G_k(F_v)=\mathrm {GL}_k(E_v)$
defined by
$G_k(F_v)=\mathrm {GL}_k(E_v)$
defined by
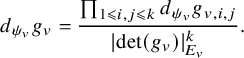 $$ \begin{align*}d_{\psi_v}g_v=\frac{\prod_{1\leqslant i,j\leqslant k} d_{\psi_v} g_{v,i,j}}{\lvert \det(g_v)\rvert_{E_v}^k}.\end{align*} $$
$$ \begin{align*}d_{\psi_v}g_v=\frac{\prod_{1\leqslant i,j\leqslant k} d_{\psi_v} g_{v,i,j}}{\lvert \det(g_v)\rvert_{E_v}^k}.\end{align*} $$
We will denote by
![]() $\nu (G_{k,v})\in \mathbb {R}_{>0}$
the quotient
$\nu (G_{k,v})\in \mathbb {R}_{>0}$
the quotient
![]() $dg_v(d_{\psi _v}g_v)^{-1}$
between the Haar measure we have fixed on
$dg_v(d_{\psi _v}g_v)^{-1}$
between the Haar measure we have fixed on
![]() $G_r(F_v)$
and the above one. Set
$G_r(F_v)$
and the above one. Set
 $$ \begin{align*}\Delta^*_{G_k}=\zeta^*_E(1)\prod_{i=2}^k \zeta_{E}(i),\end{align*} $$
$$ \begin{align*}\Delta^*_{G_k}=\zeta^*_E(1)\prod_{i=2}^k \zeta_{E}(i),\end{align*} $$
where
![]() $\zeta _E(s)$
denotes the completed Dedekind Zeta function of E and
$\zeta _E(s)$
denotes the completed Dedekind Zeta function of E and
![]() $\zeta _E^*(1)$
its residue at
$\zeta _E^*(1)$
its residue at
![]() $s=1$
. Similarly for every place v (resp. every finite set T of places), we set
$s=1$
. Similarly for every place v (resp. every finite set T of places), we set
 $$ \begin{align*}\Delta_{G_k,v}=\prod_{i=1}^k \zeta_{E_v}(i) \;\;\; (\mbox{resp. } \Delta^{T,*}_{G_k}=\zeta^{T,*}_E(1)\prod_{i=2}^k \zeta^T_{E}(i)),\end{align*} $$
$$ \begin{align*}\Delta_{G_k,v}=\prod_{i=1}^k \zeta_{E_v}(i) \;\;\; (\mbox{resp. } \Delta^{T,*}_{G_k}=\zeta^{T,*}_E(1)\prod_{i=2}^k \zeta^T_{E}(i)),\end{align*} $$
where
![]() $\zeta _{E_v}$
denotes the local Eulerian factorFootnote
1
of
$\zeta _{E_v}$
denotes the local Eulerian factorFootnote
1
of
![]() $\zeta _E$
at v (resp.
$\zeta _E$
at v (resp.
![]() $\zeta ^T_E(s)$
denotes the corresponding partial Dedekind zeta function and
$\zeta ^T_E(s)$
denotes the corresponding partial Dedekind zeta function and
![]() $\zeta ^{T,*}_E(1)$
is its residue at
$\zeta ^{T,*}_E(1)$
is its residue at
![]() $s=1$
). Then, for every non-Archimedean v where
$s=1$
). Then, for every non-Archimedean v where
![]() $\psi _v$
is unramified, we have
$\psi _v$
is unramified, we have
and the global Tamagawa measure on
![]() $G_k(\mathbb {A})$
is, by definition,
$G_k(\mathbb {A})$
is, by definition,
In particular, it follows that if T is a sufficiently large finite set of places, we have
![]() $\nu (G_{k,v})=\Delta _{G_k,v}$
for
$\nu (G_{k,v})=\Delta _{G_k,v}$
for
![]() $v\notin T$
and
$v\notin T$
and
8.2.2
Finally, we record the following Fourier inversion formula: for every
![]() $f\in C_c^\infty (P_{k+1}(F_v))$
setting
$f\in C_c^\infty (P_{k+1}(F_v))$
setting
 $$ \begin{align*}W_f(g_1,g_2)=\int_{N_{k+1}(F_v)} f(g_1^{-1}u_vg_2) \psi_{k+1}(u_v) du_v,\;\;\; g_1,g_2\in P_{k+1}(F_v),\end{align*} $$
$$ \begin{align*}W_f(g_1,g_2)=\int_{N_{k+1}(F_v)} f(g_1^{-1}u_vg_2) \psi_{k+1}(u_v) du_v,\;\;\; g_1,g_2\in P_{k+1}(F_v),\end{align*} $$
we have
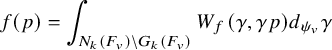 $$ \begin{align*} f(p)=\int_{N_k(F_v)\backslash G_k(F_v)} W_f(\gamma,\gamma p) d_{\psi_v}\gamma \end{align*} $$
$$ \begin{align*} f(p)=\int_{N_k(F_v)\backslash G_k(F_v)} W_f(\gamma,\gamma p) d_{\psi_v}\gamma \end{align*} $$
for every
![]() $p\in P_{k+1}(F_v)$
, where
$p\in P_{k+1}(F_v)$
, where
![]() $d_{\psi _v}\gamma $
denotes the quotient of the Haar measure
$d_{\psi _v}\gamma $
denotes the quotient of the Haar measure
![]() $d_{\psi _v}g_v$
on
$d_{\psi _v}g_v$
on
![]() $G_k(F_v)$
by the Haar measure
$G_k(F_v)$
by the Haar measure
![]() $du_v=d_{\psi _v}u_v$
on
$du_v=d_{\psi _v}u_v$
on
![]() $N_k(F_v)$
. In particular, replacing
$N_k(F_v)$
. In particular, replacing
![]() $d_{\psi _v}\gamma $
by the quotient measure
$d_{\psi _v}\gamma $
by the quotient measure
![]() $d\gamma $
of
$d\gamma $
of
![]() $dg_v$
by
$dg_v$
by
![]() $du_v$
, we obtain the following renormalized inversion formula:
$du_v$
, we obtain the following renormalized inversion formula:
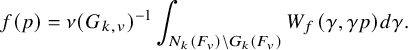 $$ \begin{align} f(p)=\nu(G_{k,v})^{-1}\int_{N_k(F_v)\backslash G_k(F_v)} W_f(\gamma,\gamma p) d\gamma. \end{align} $$
$$ \begin{align} f(p)=\nu(G_{k,v})^{-1}\int_{N_k(F_v)\backslash G_k(F_v)} W_f(\gamma,\gamma p) d\gamma. \end{align} $$
8.3 Global periods
8.3.1
We define the Whittaker period on
![]() $G_r$
as the linear form
$G_r$
as the linear form
(Note the minus sign.)
8.3.2
Under extra assumptions ensuring absolute convergence (e.g., cuspidality), we will consider the following global Bessel period for
![]() $\phi \in \mathcal {A}([\mathcal {G}])$
(resp.
$\phi \in \mathcal {A}([\mathcal {G}])$
(resp.
![]() $\phi \in \mathcal {A}([U])$
):
$\phi \in \mathcal {A}([U])$
):
For example, it is readily seen that the period
![]() $\mathcal {P}_{U'}(\phi )$
is absolutely convergent for
$\mathcal {P}_{U'}(\phi )$
is absolutely convergent for
![]() $\phi =\phi _n\otimes \phi _{n+1}$
, where
$\phi =\phi _n\otimes \phi _{n+1}$
, where
![]() $\phi _n\in \mathcal {A}([U_n])$
and
$\phi _n\in \mathcal {A}([U_n])$
and
![]() $\phi _{n+1}\in \mathcal {A}_{cusp}([U_{n+1}])$
.
$\phi _{n+1}\in \mathcal {A}_{cusp}([U_{n+1}])$
.
8.3.3
Again provided it is convergent, for
![]() $\phi \in \mathcal {A}([L])$
, we define the mixed Whittaker-Bessel period
$\phi \in \mathcal {A}([L])$
, we define the mixed Whittaker-Bessel period
For example, this period is absolutely convergent when
![]() $\phi =\phi _r\otimes \phi '$
where
$\phi =\phi _r\otimes \phi '$
where
![]() $\phi _r\in \mathcal {A}([G_r])$
and
$\phi _r\in \mathcal {A}([G_r])$
and
![]() $\phi '\in \mathcal {A}_{cusp}([\mathcal {G}])$
, in which case we have
$\phi '\in \mathcal {A}_{cusp}([\mathcal {G}])$
, in which case we have
8.4 Local Bessel periods
8.4.1
Let v be a place of F. For every connected reductive group
![]() $\mathbb {G}$
defined over
$\mathbb {G}$
defined over
![]() $F_v$
, we let
$F_v$
, we let
![]() $\mathcal {C}^w(\mathbb {G}(F_v))$
be the space of tempered functions on
$\mathcal {C}^w(\mathbb {G}(F_v))$
be the space of tempered functions on
![]() $\mathbb {G}(F_v)$
as defined in [Reference Beuzart-PlessisBP20, §1.5] (where it is called the weak Harish-Chandra Schwartz space). Since we will need it, let us recall quickly its definition. Let
$\mathbb {G}(F_v)$
as defined in [Reference Beuzart-PlessisBP20, §1.5] (where it is called the weak Harish-Chandra Schwartz space). Since we will need it, let us recall quickly its definition. Let
![]() $\Xi ^{\mathbb {G}}$
Harish-Chandra special spherical function on
$\Xi ^{\mathbb {G}}$
Harish-Chandra special spherical function on
![]() $\mathbb {G}(F_v)$
, which, strictly speaking, depends on the choice of a maximal compact subgroup
$\mathbb {G}(F_v)$
, which, strictly speaking, depends on the choice of a maximal compact subgroup
![]() $\mathbb {K}_v\subset \mathbb {G}(F_v)$
(such a choice has already been made for all the groups we will have to consider). For each
$\mathbb {K}_v\subset \mathbb {G}(F_v)$
(such a choice has already been made for all the groups we will have to consider). For each
![]() $d>0$
, we let
$d>0$
, we let
![]() $\mathcal {C}^w_d(\mathbb {G}(F_v))$
be the space of functions
$\mathcal {C}^w_d(\mathbb {G}(F_v))$
be the space of functions
![]() $f:\mathbb {G}(F_v)\to \mathbb {C}$
such that:
$f:\mathbb {G}(F_v)\to \mathbb {C}$
such that:
-
• If v is non-Archimedean, f is biinvariant by a compact-open subgroup and we have
 $$ \begin{align*}\lvert f(g)\rvert\ll \Xi^{\mathbb{G}}(g)\sigma(g)^d, \mbox{ for } g\in \mathbb{G}(F_v);\end{align*} $$
$$ \begin{align*}\lvert f(g)\rvert\ll \Xi^{\mathbb{G}}(g)\sigma(g)^d, \mbox{ for } g\in \mathbb{G}(F_v);\end{align*} $$
-
• If v is Archimedean, f is
 $C^\infty $
and for every
$C^\infty $
and for every
 $X,Y\in \mathcal {U}(\operatorname {\mathrm {Lie}}(\mathbb {G}(F_v)))$
,
$X,Y\in \mathcal {U}(\operatorname {\mathrm {Lie}}(\mathbb {G}(F_v)))$
,  $$ \begin{align*}\lvert (L(X)R(Y)f)(g)\rvert\ll_{X,Y} \Xi^{\mathbb{G}}(g)\sigma(g)^d, \mbox{ for } g\in \mathbb{G}(F_v).\end{align*} $$
$$ \begin{align*}\lvert (L(X)R(Y)f)(g)\rvert\ll_{X,Y} \Xi^{\mathbb{G}}(g)\sigma(g)^d, \mbox{ for } g\in \mathbb{G}(F_v).\end{align*} $$
When v is Archimedean,
![]() $\mathcal {C}^w_d(\mathbb {G}(F_v))$
is naturally a Fréchet space, whereas if v is non-Archimedean,
$\mathcal {C}^w_d(\mathbb {G}(F_v))$
is naturally a Fréchet space, whereas if v is non-Archimedean,
![]() $\mathcal {C}^w_d(\mathbb {G}(F_v))$
is a strict LF space. By definition, the space of tempered functions is
$\mathcal {C}^w_d(\mathbb {G}(F_v))$
is a strict LF space. By definition, the space of tempered functions is
![]() $\mathcal {C}^w(\mathbb {G}(F_v))=\bigcup _{d>0} \mathcal {C}^w_d(\mathbb {G}(F_v))$
. It is equipped with the direct limit locally convex topology, and it contains
$\mathcal {C}^w(\mathbb {G}(F_v))=\bigcup _{d>0} \mathcal {C}^w_d(\mathbb {G}(F_v))$
. It is equipped with the direct limit locally convex topology, and it contains
![]() $C_c^\infty (\mathbb {G}(F_v))$
as a dense subspace. (However, note that
$C_c^\infty (\mathbb {G}(F_v))$
as a dense subspace. (However, note that
![]() $C_c^\infty (\mathbb {G}(F_v))$
is not dense in
$C_c^\infty (\mathbb {G}(F_v))$
is not dense in
![]() $\mathcal {C}^w_d(\mathbb {G}(F_v))$
for any
$\mathcal {C}^w_d(\mathbb {G}(F_v))$
for any
![]() $d>0$
.)
$d>0$
.)
8.4.2
By definition, the local period
![]() $\mathcal {P}_{U',v}$
is the linear form
$\mathcal {P}_{U',v}$
is the linear form
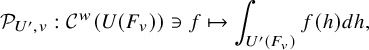 $$ \begin{align*}\mathcal{P}_{U',v}:\mathcal{C}^w(U(F_v))\ni f\mapsto \int_{U'(F_v)} f(h)dh,\end{align*} $$
$$ \begin{align*}\mathcal{P}_{U',v}:\mathcal{C}^w(U(F_v))\ni f\mapsto \int_{U'(F_v)} f(h)dh,\end{align*} $$
the integral being absolutely convergent by [Reference Beuzart-PlessisBP20, Lemma 6.5.1(i)].
Moreover, it is shown in [Reference Beuzart-PlessisBP20, Proposition 7.1.1] that the linear form
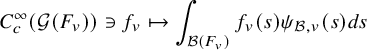 $$ \begin{align*}C_c^\infty(\mathcal{G}(F_v))\ni f_v\mapsto \int_{\mathcal{B}(F_v)} f_v(s) \psi_{\mathcal{B},v}(s) ds\end{align*} $$
$$ \begin{align*}C_c^\infty(\mathcal{G}(F_v))\ni f_v\mapsto \int_{\mathcal{B}(F_v)} f_v(s) \psi_{\mathcal{B},v}(s) ds\end{align*} $$
extends by continuity to
![]() $\mathcal {C}^w(\mathcal {G}(F_v))$
. We denote this unique continuous extension by
$\mathcal {C}^w(\mathcal {G}(F_v))$
. We denote this unique continuous extension by
![]() $\mathcal {P}_{\mathcal {B},\psi _{\mathcal {B}},v}$
and call it the local Bessel period.
$\mathcal {P}_{\mathcal {B},\psi _{\mathcal {B}},v}$
and call it the local Bessel period.
A similar argument shows that the linear forms
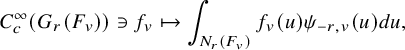 $$ \begin{align*}C_c^\infty(G_r(F_v))\ni f_v\mapsto \int_{N_r(F_v)} f_v(u) \psi_{-r,v}(u) du,\end{align*} $$
$$ \begin{align*}C_c^\infty(G_r(F_v))\ni f_v\mapsto \int_{N_r(F_v)} f_v(u) \psi_{-r,v}(u) du,\end{align*} $$
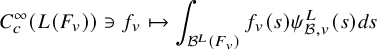 $$ \begin{align*}C_c^\infty(L(F_v))\ni f_v\mapsto \int_{\mathcal{B}^L(F_v)} f_v(s) \psi^L_{\mathcal{B},v}(s) ds\end{align*} $$
$$ \begin{align*}C_c^\infty(L(F_v))\ni f_v\mapsto \int_{\mathcal{B}^L(F_v)} f_v(s) \psi^L_{\mathcal{B},v}(s) ds\end{align*} $$
extend by continuity to
![]() $\mathcal {C}^w(G_r(F_v))$
and
$\mathcal {C}^w(G_r(F_v))$
and
![]() $\mathcal {C}^w(L(F_v))$
, respectively. We denote these unique continuous extensions by
$\mathcal {C}^w(L(F_v))$
, respectively. We denote these unique continuous extensions by
![]() $\mathcal {P}_{N_r,\psi _{-r},v}$
,
$\mathcal {P}_{N_r,\psi _{-r},v}$
,
![]() $\mathcal {P}_{\mathcal {B}^L,\psi ^L_{\mathcal {B}},v}$
and call them the local Whittaker period and Whittaker-Bessel period, respectively.
$\mathcal {P}_{\mathcal {B}^L,\psi ^L_{\mathcal {B}},v}$
and call them the local Whittaker period and Whittaker-Bessel period, respectively.
8.4.3
Let
![]() $(\mathbb {G},\mathbb {H})\in \{(U,U'),(\mathcal {G},(\mathcal {B},\psi _{\mathcal {B}})),(L,(\mathcal {B}^L,\psi ^L_{\mathcal {B}})), (G_r,(N_r,\psi _{-r})) \}$
. Then, for any tempered irreducible representation
$(\mathbb {G},\mathbb {H})\in \{(U,U'),(\mathcal {G},(\mathcal {B},\psi _{\mathcal {B}})),(L,(\mathcal {B}^L,\psi ^L_{\mathcal {B}})), (G_r,(N_r,\psi _{-r})) \}$
. Then, for any tempered irreducible representation
![]() $\sigma _v$
of
$\sigma _v$
of
![]() $\mathbb {G}(F_v)$
equipped with an invariant inner product
$\mathbb {G}(F_v)$
equipped with an invariant inner product
![]() $(\cdot ,\cdot )_v$
and vectors
$(\cdot ,\cdot )_v$
and vectors
![]() $\phi _v,\phi ^{\prime }_v\in \sigma _v$
, the matrix coefficient
$\phi _v,\phi ^{\prime }_v\in \sigma _v$
, the matrix coefficient
belongs to
![]() $\mathcal {C}^w(\mathbb {G}(F_v))$
. We set
$\mathcal {C}^w(\mathbb {G}(F_v))$
. We set
8.5 Relation between global periods
8.5.1
Proposition 8.5.1.1. Let
![]() $\phi _n\in \mathcal {A}_{Q_n}(U_n)$
and
$\phi _n\in \mathcal {A}_{Q_n}(U_n)$
and
![]() $\phi _{n+1}\in \mathcal {A}_{cusp}(U_{n+1})$
. Then, there exists
$\phi _{n+1}\in \mathcal {A}_{cusp}(U_{n+1})$
. Then, there exists
![]() $c>0$
such that for
$c>0$
such that for
![]() $s\in \mathcal {H}_{>c}$
, we have the identity
$s\in \mathcal {H}_{>c}$
, we have the identity
where the right expression is absolutely convergent.
Proof. For
![]() $\Re (s)$
sufficiently large, we have
$\Re (s)$
sufficiently large, we have
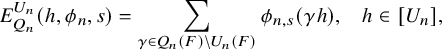 $$ \begin{align*}E_{Q_n}^{U_n}(h,\phi_n,s)=\sum_{\gamma\in Q_n(F)\backslash U_n(F)} \phi_{n,s}(\gamma h),\;\;\; h\in [U_n],\end{align*} $$
$$ \begin{align*}E_{Q_n}^{U_n}(h,\phi_n,s)=\sum_{\gamma\in Q_n(F)\backslash U_n(F)} \phi_{n,s}(\gamma h),\;\;\; h\in [U_n],\end{align*} $$
so that (the resulting expression being absolutely convergent by cuspidality of
![]() $\phi _{n+1}$
)
$\phi _{n+1}$
)
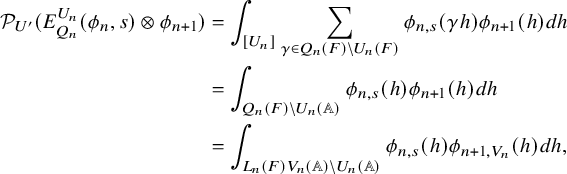 $$ \begin{align} \mathcal{P}_{U'}(E_{Q_n}^{U_n}(\phi_n,s)\otimes \phi_{n+1}) & =\int_{[U_n]} \sum_{\gamma\in Q_n(F)\backslash U_n(F)} \phi_{n,s}(\gamma h) \phi_{n+1}(h) dh \\ \nonumber & =\int_{Q_n(F)\backslash U_n(\mathbb{A})} \phi_{n,s}(h) \phi_{n+1}(h) dh \\ \nonumber & =\int_{L_n(F)V_n(\mathbb{A})\backslash U_n(\mathbb{A})} \phi_{n,s}(h) \phi_{n+1,V_n}(h) dh, \end{align} $$
$$ \begin{align} \mathcal{P}_{U'}(E_{Q_n}^{U_n}(\phi_n,s)\otimes \phi_{n+1}) & =\int_{[U_n]} \sum_{\gamma\in Q_n(F)\backslash U_n(F)} \phi_{n,s}(\gamma h) \phi_{n+1}(h) dh \\ \nonumber & =\int_{Q_n(F)\backslash U_n(\mathbb{A})} \phi_{n,s}(h) \phi_{n+1}(h) dh \\ \nonumber & =\int_{L_n(F)V_n(\mathbb{A})\backslash U_n(\mathbb{A})} \phi_{n,s}(h) \phi_{n+1,V_n}(h) dh, \end{align} $$
where
We claim that we have a Fourier expansion
for every
![]() $h\in U_{n+1}(\mathbb {A})$
where we have set
$h\in U_{n+1}(\mathbb {A})$
where we have set
Indeed, the subgroup
![]() $G_r N$
of
$G_r N$
of
![]() $U_{n+1}$
contains
$U_{n+1}$
contains
![]() $V_n$
as a normal subgroup, and the quotient
$V_n$
as a normal subgroup, and the quotient
![]() $G_r N/V_n$
can be identified with the mirabolic subgroup
$G_r N/V_n$
can be identified with the mirabolic subgroup
![]() $P_{r+1}$
of
$P_{r+1}$
of
![]() $G_{r+1}$
via restriction to the subspace
$G_{r+1}$
via restriction to the subspace
![]() $\langle x_1,\ldots ,x_r,x_{r+1}\rangle $
, where we have set
$\langle x_1,\ldots ,x_r,x_{r+1}\rangle $
, where we have set
![]() $x_{r+1}=v_0$
. It readily follows from the cuspidality of
$x_{r+1}=v_0$
. It readily follows from the cuspidality of
![]() $\phi _{n+1}$
that for any
$\phi _{n+1}$
that for any
![]() $h\in U_{n+1}(\mathbb {A})$
, the function
$h\in U_{n+1}(\mathbb {A})$
, the function
![]() $p\in [P_{r+1}]\mapsto \phi _{n+1,V_n}(ph)$
is cuspidal in the sense of [Reference CogdellCog08, §1.1] and therefore by loc. cit. that we have the Fourier expansion (8.5.1.2).
$p\in [P_{r+1}]\mapsto \phi _{n+1,V_n}(ph)$
is cuspidal in the sense of [Reference CogdellCog08, §1.1] and therefore by loc. cit. that we have the Fourier expansion (8.5.1.2).
Replacing
![]() $\phi _{n+1,V_n}$
by its Fourier expansion (8.5.1.2) in (8.5.1.1), we formally obtain (remembering the decomposition (8.1.3.3) for
$\phi _{n+1,V_n}$
by its Fourier expansion (8.5.1.2) in (8.5.1.1), we formally obtain (remembering the decomposition (8.1.3.3) for
![]() $L_n$
)
$L_n$
)
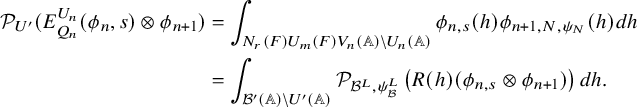 $$\begin{align*}\begin{aligned} \mathcal{P}_{U'}(E_{Q_n}^{U_n}(\phi_n,s)\otimes \phi_{n+1}) & =\int_{N_r(F)U_m(F)V_n(\mathbb{A})\backslash U_n(\mathbb{A})} \phi_{n,s}(h) \phi_{n+1,N,\psi_N}(h) dh \\ & =\int_{\mathcal{B}'(\mathbb{A})\backslash U'(\mathbb{A})} \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}}}\left(R(h)(\phi_{n,s}\otimes \phi_{n+1})\right) dh. \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} \mathcal{P}_{U'}(E_{Q_n}^{U_n}(\phi_n,s)\otimes \phi_{n+1}) & =\int_{N_r(F)U_m(F)V_n(\mathbb{A})\backslash U_n(\mathbb{A})} \phi_{n,s}(h) \phi_{n+1,N,\psi_N}(h) dh \\ & =\int_{\mathcal{B}'(\mathbb{A})\backslash U'(\mathbb{A})} \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}}}\left(R(h)(\phi_{n,s}\otimes \phi_{n+1})\right) dh. \end{aligned}\end{align*}$$
To justify this formal computation, it remains to check that the integral
converges for
![]() $\Re (s)$
sufficiently large. This can be rewritten as
$\Re (s)$
sufficiently large. This can be rewritten as
Thus, as
![]() $P'(\mathbb {A})\backslash U'(\mathbb {A})$
is compact, it suffices to check the convergence of
$P'(\mathbb {A})\backslash U'(\mathbb {A})$
is compact, it suffices to check the convergence of
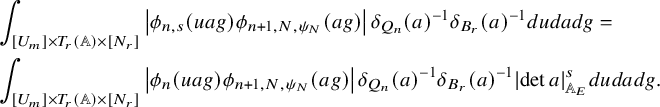 $$\begin{align*}\begin{aligned} & \int_{[U_m]\times T_r(\mathbb{A})\times [N_r]} \left\lvert\phi_{n,s}(uag) \phi_{n+1,N,\psi_N}(ag) \right\rvert \delta_{Q_n}(a)^{-1}\delta_{B_r}(a)^{-1} dudadg= \\ & \int_{[U_m]\times T_r(\mathbb{A})\times [N_r]} \left\lvert\phi_{n}(uag) \phi_{n+1,N,\psi_N}(ag) \right\rvert \delta_{Q_n}(a)^{-1}\delta_{B_r}(a)^{-1} \lvert \det a\rvert_{\mathbb{A}_E}^s dudadg. \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} & \int_{[U_m]\times T_r(\mathbb{A})\times [N_r]} \left\lvert\phi_{n,s}(uag) \phi_{n+1,N,\psi_N}(ag) \right\rvert \delta_{Q_n}(a)^{-1}\delta_{B_r}(a)^{-1} dudadg= \\ & \int_{[U_m]\times T_r(\mathbb{A})\times [N_r]} \left\lvert\phi_{n}(uag) \phi_{n+1,N,\psi_N}(ag) \right\rvert \delta_{Q_n}(a)^{-1}\delta_{B_r}(a)^{-1} \lvert \det a\rvert_{\mathbb{A}_E}^s dudadg. \end{aligned}\end{align*}$$
Let us embed
![]() $T_r(\mathbb {A})$
into
$T_r(\mathbb {A})$
into
![]() $\mathbb {A}_E^r$
in the natural way. Then, by [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Lemma 2.6.1.1] and since
$\mathbb {A}_E^r$
in the natural way. Then, by [Reference Beuzart-Plessis, Chaudouard and ZydorBPCZ22, Lemma 2.6.1.1] and since
![]() $\phi _{n+1}$
is cuspidal, for every
$\phi _{n+1}$
is cuspidal, for every
![]() $R>0$
, we have
$R>0$
, we have
Moreover, since
![]() $\phi _n$
is of moderate growth, we can find
$\phi _n$
is of moderate growth, we can find
![]() $D>0$
such that
$D>0$
such that
Combining (8.5.1.3) with (8.5.1.4), we are eventually reduced to the following readily checked property: for every s large enough, there exists
![]() $R>0$
such that the integral
$R>0$
such that the integral
converges.
8.6 Relations between local periods
8.6.1
Let v be a place of F and let
![]() $\tau $
,
$\tau $
,
![]() $\sigma _{m}$
,
$\sigma _{m}$
,
![]() $\sigma _{n+1}$
be irreducible representations of
$\sigma _{n+1}$
be irreducible representations of
![]() $G_r(F_v)$
,
$G_r(F_v)$
,
![]() $U_m(F_v)$
and
$U_m(F_v)$
and
![]() $U_{n+1}(F_v)$
, respectively. We set
$U_{n+1}(F_v)$
, respectively. We set
![]() $\sigma =\sigma _{m}\boxtimes \sigma _{n+1}$
(an irreducible representation of
$\sigma =\sigma _{m}\boxtimes \sigma _{n+1}$
(an irreducible representation of
![]() $\mathcal {G}(F_v)=U_m(F_v)\times U_{n+1}(F_v)$
). Let
$\mathcal {G}(F_v)=U_m(F_v)\times U_{n+1}(F_v)$
). Let
By multiplicity one results [Reference Aizenbud, Gourevitch, Rallis and SchiffmannARS10], [Reference Gan, Gross and PrasadGGP12, Corollary 15.3], [Reference Jiang, Sun and ZhuJSZ10],
![]() $\mathcal {L}$
factors as
$\mathcal {L}$
factors as
![]() $\mathcal {L}=\mathcal {L}^W\otimes \mathcal {L}^B$
, where
$\mathcal {L}=\mathcal {L}^W\otimes \mathcal {L}^B$
, where
![]() $\mathcal {L}^W\in \operatorname {\mathrm {Hom}}_{N_r(F_v)}(\tau ,\psi _{-r,v})$
and
$\mathcal {L}^W\in \operatorname {\mathrm {Hom}}_{N_r(F_v)}(\tau ,\psi _{-r,v})$
and
![]() $\mathcal {L}^B\in \operatorname {\mathrm {Hom}}_{\mathcal {B}(F_v)}(\sigma ,\psi _{\mathcal {B},v})$
.
$\mathcal {L}^B\in \operatorname {\mathrm {Hom}}_{\mathcal {B}(F_v)}(\sigma ,\psi _{\mathcal {B},v})$
.
For every
![]() $s\in \mathbb {C}$
, we set
$s\in \mathbb {C}$
, we set
![]() $\tau _s=\tau \lvert \det \rvert _{E_v}^s$
and we denote by
$\tau _s=\tau \lvert \det \rvert _{E_v}^s$
and we denote by
![]() $I_{Q_n(F_v)}^{U_n(F_v)}(\tau _s \boxtimes \sigma _{m})$
the normalized parabolic induction of
$I_{Q_n(F_v)}^{U_n(F_v)}(\tau _s \boxtimes \sigma _{m})$
the normalized parabolic induction of
![]() $\tau _s \boxtimes \sigma _{m}$
to
$\tau _s \boxtimes \sigma _{m}$
to
![]() $U_n(F_v)$
.
$U_n(F_v)$
.
Proposition 8.6.1.1. There exists
![]() $c\in \mathbb {R}$
such that the functional
$c\in \mathbb {R}$
such that the functional
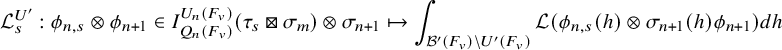 $$ \begin{align*}\mathcal{L}_s^{U'}: \phi_{n,s}\otimes \phi_{n+1}\in I_{Q_n(F_v)}^{U_n(F_v)}(\tau_s \boxtimes \sigma_{m})\otimes \sigma_{n+1}\mapsto \int_{\mathcal{B}'(F_v)\backslash U'(F_v)} \mathcal{L}(\phi_{n,s}(h)\otimes \sigma_{n+1}(h)\phi_{n+1}) dh\end{align*} $$
$$ \begin{align*}\mathcal{L}_s^{U'}: \phi_{n,s}\otimes \phi_{n+1}\in I_{Q_n(F_v)}^{U_n(F_v)}(\tau_s \boxtimes \sigma_{m})\otimes \sigma_{n+1}\mapsto \int_{\mathcal{B}'(F_v)\backslash U'(F_v)} \mathcal{L}(\phi_{n,s}(h)\otimes \sigma_{n+1}(h)\phi_{n+1}) dh\end{align*} $$
converges absolutely for
![]() $s\in \mathcal {H}_{>c}$
. If, moreover, both
$s\in \mathcal {H}_{>c}$
. If, moreover, both
![]() $\sigma $
and
$\sigma $
and
![]() $\tau $
are tempered, we may take
$\tau $
are tempered, we may take
![]() $c=-1/2$
. Furthermore, for s with sufficiently large real part, the following assertions are equivalent:
$c=-1/2$
. Furthermore, for s with sufficiently large real part, the following assertions are equivalent:
-
1. There exist
 $\phi _{\tau }\in \tau $
,
$\phi _{\tau }\in \tau $
,
 $\phi _m\in \sigma _{m}$
and
$\phi _m\in \sigma _{m}$
and
 $\phi _{n+1}\in \sigma _{n+1}$
such that
$\phi _{n+1}\in \sigma _{n+1}$
such that
 $\mathcal {L}(\phi _{\tau }\otimes \phi _m\otimes \phi _{n+1})\neq 0$
;
$\mathcal {L}(\phi _{\tau }\otimes \phi _m\otimes \phi _{n+1})\neq 0$
; -
2. There exist
 $\phi _{n,s}\in I_{Q_n(F_v)}^{U_n(F_v)}(\tau _s\boxtimes \sigma _{m})$
and
$\phi _{n,s}\in I_{Q_n(F_v)}^{U_n(F_v)}(\tau _s\boxtimes \sigma _{m})$
and
 $\phi _{n+1}\in \sigma _{n+1}$
such that
$\phi _{n+1}\in \sigma _{n+1}$
such that
 $\mathcal {L}_s^{U'}(\phi _{n,s}\otimes \phi _{n+1})\neq 0$
.
$\mathcal {L}_s^{U'}(\phi _{n,s}\otimes \phi _{n+1})\neq 0$
.
Proof. Since
![]() $P'=T_r\mathcal {B}'$
is a parabolic subgroup of
$P'=T_r\mathcal {B}'$
is a parabolic subgroup of
![]() $U'$
, it suffices to check the convergence of the integral
$U'$
, it suffices to check the convergence of the integral
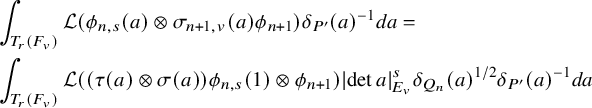 $$\begin{align*}\begin{aligned} & \int_{T_r(F_v)} \mathcal{L}(\phi_{n,s}(a)\otimes \sigma_{n+1,v}(a)\phi_{n+1}) \delta_{P'}(a)^{-1}da= \\ & \int_{T_r(F_v)} \mathcal{L}((\tau(a)\otimes \sigma(a))\phi_{n,s}(1)\otimes \phi_{n+1}) \lvert \det a\rvert_{E_v}^s\delta_{Q_n}(a)^{1/2}\delta_{P'}(a)^{-1}da \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} & \int_{T_r(F_v)} \mathcal{L}(\phi_{n,s}(a)\otimes \sigma_{n+1,v}(a)\phi_{n+1}) \delta_{P'}(a)^{-1}da= \\ & \int_{T_r(F_v)} \mathcal{L}((\tau(a)\otimes \sigma(a))\phi_{n,s}(1)\otimes \phi_{n+1}) \lvert \det a\rvert_{E_v}^s\delta_{Q_n}(a)^{1/2}\delta_{P'}(a)^{-1}da \end{aligned}\end{align*}$$
for
![]() $\Re (s)\gg 0$
.
$\Re (s)\gg 0$
.
Lemma 8.6.1.2. There exists
![]() $D>0$
such that for every
$D>0$
such that for every
![]() $\phi \in \tau \boxtimes \sigma $
and
$\phi \in \tau \boxtimes \sigma $
and
![]() $R>0$
, we have
$R>0$
, we have
If, moreover,
![]() $\sigma $
and
$\sigma $
and
![]() $\tau $
are tempered, for every
$\tau $
are tempered, for every
![]() $\phi \in \tau \boxtimes \sigma $
and
$\phi \in \tau \boxtimes \sigma $
and
![]() $R>0$
, we have
$R>0$
, we have
Proof. It suffices to prove the lemma when
![]() $\phi $
is a pure tensor (i.e., it is of the form
$\phi $
is a pure tensor (i.e., it is of the form
![]() $\phi =\phi _\tau \otimes \phi _m\otimes \phi _{n+1}$
, where
$\phi =\phi _\tau \otimes \phi _m\otimes \phi _{n+1}$
, where
![]() $\phi _\tau \in \tau $
,
$\phi _\tau \in \tau $
,
![]() $\phi _m\in \sigma _{m}$
and
$\phi _m\in \sigma _{m}$
and
![]() $\phi _{n+1}\in \sigma _{n+1}$
). Indeed, in the case where v is non-Archimedean, every vector in
$\phi _{n+1}\in \sigma _{n+1}$
). Indeed, in the case where v is non-Archimedean, every vector in
![]() $\tau \boxtimes \sigma $
is a sum of pure tensors, whereas if v is Archimedean, the claimed inequalities would automatically extend from the algebraic tensor product to the completed tensor product by the Banach-Steinhaus theorem (see, for example, [Reference TrèvesTrè67, Theorem 34.1]).
$\tau \boxtimes \sigma $
is a sum of pure tensors, whereas if v is Archimedean, the claimed inequalities would automatically extend from the algebraic tensor product to the completed tensor product by the Banach-Steinhaus theorem (see, for example, [Reference TrèvesTrè67, Theorem 34.1]).
Using the equality
![]() $\mathcal {L}=\mathcal {L}^W\otimes \mathcal {L}^B$
, we are therefore reduced to show the existence of
$\mathcal {L}=\mathcal {L}^W\otimes \mathcal {L}^B$
, we are therefore reduced to show the existence of
![]() $D>0$
such that for every
$D>0$
such that for every
![]() $R>0$
(resp. that when
$R>0$
(resp. that when
![]() $\tau $
,
$\tau $
,
![]() $\sigma $
are tempered for every
$\sigma $
are tempered for every
![]() $R>0$
), we have
$R>0$
), we have
and
for
![]() $a\in T_r(F_v)$
.
$a\in T_r(F_v)$
.
The estimates (8.6.1.3) and (8.6.1.4) can be established along the same lines as Lemma B.2.1 and Lemma 7.3.1 (i) of [Reference Beuzart-PlessisBP20], respectively. More precisely, in the tempered case, (8.6.1.3) is a direct application of Lemma B.2.1 of loc.cit. The same inequality for general representations (and for a suitable D) is a consequence of the continuity of
![]() $\mathcal {L}^W$
when v is Archimedean, whereas, for v non-Archimedean, by the same argument as in [Reference Beuzart-PlessisBP20, Lemma B.2.1], we can bound the function
$\mathcal {L}^W$
when v is Archimedean, whereas, for v non-Archimedean, by the same argument as in [Reference Beuzart-PlessisBP20, Lemma B.2.1], we can bound the function
![]() $a\in T_r(F_v)\mapsto \left \lvert \mathcal {L}^W(\tau (a)\phi _\tau )\right \rvert $
by a matrix coefficient of
$a\in T_r(F_v)\mapsto \left \lvert \mathcal {L}^W(\tau (a)\phi _\tau )\right \rvert $
by a matrix coefficient of
![]() $\tau _v$
which is in turn essentially bounded by
$\tau _v$
which is in turn essentially bounded by
![]() $\lVert a\rVert ^D$
for some
$\lVert a\rVert ^D$
for some
![]() $D>0$
.
$D>0$
.
As for (8.6.1.4), we first note that
for every
![]() $(a,X)\in T_r(F_v)\times \operatorname {\mathrm {Lie}}(\mathcal {B}(F_v))$
. Furthermore, when v is Archimedean, differentiating the above identities yields
$(a,X)\in T_r(F_v)\times \operatorname {\mathrm {Lie}}(\mathcal {B}(F_v))$
. Furthermore, when v is Archimedean, differentiating the above identities yields
where
![]() $d\psi _{\mathcal {B},v}: Lie(\mathcal {B}(F_v))\to \mathbb {C}$
denotes the differential of
$d\psi _{\mathcal {B},v}: Lie(\mathcal {B}(F_v))\to \mathbb {C}$
denotes the differential of
![]() $\psi _{\mathcal {B},v}$
at
$\psi _{\mathcal {B},v}$
at
![]() $1$
. From (8.6.1.6), we deduce that for every linear form
$1$
. From (8.6.1.6), we deduce that for every linear form
![]() $\lambda : E_v^r\to F_v$
, there exists
$\lambda : E_v^r\to F_v$
, there exists
![]() $X_\lambda \in Lie(\mathcal {B}(F_v))$
such that
$X_\lambda \in Lie(\mathcal {B}(F_v))$
such that
for every
![]() $a\in T_r(F_v)$
. Similarly, when v is non-Archimedean, we deduce from (8.6.1.5) and the smoothness of
$a\in T_r(F_v)$
. Similarly, when v is non-Archimedean, we deduce from (8.6.1.5) and the smoothness of
![]() $\phi _{n+1}$
the existence of
$\phi _{n+1}$
the existence of
![]() $C>0$
such that
$C>0$
such that
![]() $\mathcal {L}^B(\phi _m\otimes \sigma _{n+1}(a)\phi _{n+1})=0$
unless
$\mathcal {L}^B(\phi _m\otimes \sigma _{n+1}(a)\phi _{n+1})=0$
unless
![]() $\lVert a\rVert _{E_v^r}\leqslant C$
. Combining these two facts, we are now reduced to show the existence of
$\lVert a\rVert _{E_v^r}\leqslant C$
. Combining these two facts, we are now reduced to show the existence of
![]() $D>0$
such that (resp. that for
$D>0$
such that (resp. that for
![]() $\sigma $
tempered we have)
$\sigma $
tempered we have)
for
![]() $a\in T_r(F_v)$
. The case where
$a\in T_r(F_v)$
. The case where
![]() $\sigma $
is tempered is a direct application of [Reference Beuzart-PlessisBP20, Lemma 7.3.1(i)], whereas the case of a general representation follows from continuity of
$\sigma $
is tempered is a direct application of [Reference Beuzart-PlessisBP20, Lemma 7.3.1(i)], whereas the case of a general representation follows from continuity of
![]() $\mathcal {L}^B$
in the Archimedean case or an argument similar to that of loc. cit. to show that
$\mathcal {L}^B$
in the Archimedean case or an argument similar to that of loc. cit. to show that
![]() $a\mapsto \mathcal {L}^B(\phi _m\otimes \sigma _{n+1}(a)\phi _{n+1})$
is bounded by a matrix coefficient of
$a\mapsto \mathcal {L}^B(\phi _m\otimes \sigma _{n+1}(a)\phi _{n+1})$
is bounded by a matrix coefficient of
![]() $\sigma $
in the non-Archimedean case.
$\sigma $
in the non-Archimedean case.
By the lemma, and since there exists
![]() $d>0$
such that (see [Reference WaldspurgerWal03, Lemme II.1.1])
$d>0$
such that (see [Reference WaldspurgerWal03, Lemme II.1.1])
the convergence part of the proposition reduces to the two following readily checked facts:
-
• Let
 $D>0$
. Then, we can find
$D>0$
. Then, we can find
 $c>0$
such that for every
$c>0$
such that for every
 $s>c$
and for suitable
$s>c$
and for suitable
 $R>0$
, the integral converges;
$R>0$
, the integral converges; $$ \begin{align*}\int_{T_r(F_v)} \lVert a \rVert^D \lVert a\rVert_{E_v^r}^{-R} \lvert \det a\rvert_{E_v}^s \delta_{Q_n}(a)^{1/2} \delta_{P'}(a)^{-1} da\end{align*} $$
$$ \begin{align*}\int_{T_r(F_v)} \lVert a \rVert^D \lVert a\rVert_{E_v^r}^{-R} \lvert \det a\rvert_{E_v}^s \delta_{Q_n}(a)^{1/2} \delta_{P'}(a)^{-1} da\end{align*} $$
-
• For every
 $s>-1/2$
, we can find
$s>-1/2$
, we can find
 $R>0$
such that the integral converges.
$R>0$
such that the integral converges. $$\begin{align*}\begin{aligned} & \int_{T_r(F_v)} \lVert a\rVert_{E_v^r}^{-R} \lvert \det a\rvert_{E_v}^s \delta_{B_r}(a)^{1/2}\delta_P(a)^{1/2}\delta_{Q_n}(a)^{1/2} \delta_{P'}(a)^{-1} \sigma(a)^dda= \\ & \int_{T_r(F_v)} \lVert a\rVert_{E_v^r}^{-R} \lvert \det a\rvert_{E_v}^{s+1/2} \sigma(a)^dda \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} & \int_{T_r(F_v)} \lVert a\rVert_{E_v^r}^{-R} \lvert \det a\rvert_{E_v}^s \delta_{B_r}(a)^{1/2}\delta_P(a)^{1/2}\delta_{Q_n}(a)^{1/2} \delta_{P'}(a)^{-1} \sigma(a)^dda= \\ & \int_{T_r(F_v)} \lVert a\rVert_{E_v^r}^{-R} \lvert \det a\rvert_{E_v}^{s+1/2} \sigma(a)^dda \end{aligned}\end{align*}$$
The implication
![]() $2.\Rightarrow 1.$
is clear from the definition of
$2.\Rightarrow 1.$
is clear from the definition of
![]() $\mathcal {L}_s^{U'}$
. Let us show the converse. Thus, we assume that
$\mathcal {L}_s^{U'}$
. Let us show the converse. Thus, we assume that
![]() $\mathcal {L}$
is not identically zero, and we aim to prove that the same holds for
$\mathcal {L}$
is not identically zero, and we aim to prove that the same holds for
![]() $\mathcal {L}_s^{U'}$
for
$\mathcal {L}_s^{U'}$
for
![]() $\Re (s)\gg 0$
. First, by the equality
$\Re (s)\gg 0$
. First, by the equality
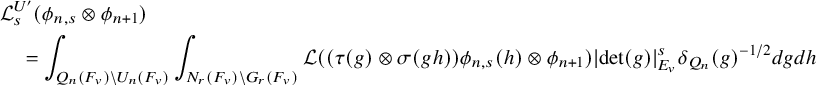 $$ \begin{align*} & \mathcal{L}_s^{U'}(\phi_{n,s}\otimes \phi_{n+1}) \\ & \quad =\int_{Q_n(F_v)\backslash U_n(F_v)} \int_{N_r(F_v)\backslash G_r(F_v)} \mathcal{L}((\tau(g)\otimes \sigma(gh))\phi_{n,s}(h)\otimes \phi_{n+1}) \lvert \det(g)\rvert_{E_v}^s\delta_{Q_n}(g)^{-1/2}dgdh\end{align*} $$
$$ \begin{align*} & \mathcal{L}_s^{U'}(\phi_{n,s}\otimes \phi_{n+1}) \\ & \quad =\int_{Q_n(F_v)\backslash U_n(F_v)} \int_{N_r(F_v)\backslash G_r(F_v)} \mathcal{L}((\tau(g)\otimes \sigma(gh))\phi_{n,s}(h)\otimes \phi_{n+1}) \lvert \det(g)\rvert_{E_v}^s\delta_{Q_n}(g)^{-1/2}dgdh\end{align*} $$
and since the space of
![]() $I_{Q_n(F_v)}^{U_n(F_v)}(\tau _{s}\boxtimes \sigma _{m})$
is stable by multiplication by functions in
$I_{Q_n(F_v)}^{U_n(F_v)}(\tau _{s}\boxtimes \sigma _{m})$
is stable by multiplication by functions in
![]() $C^\infty (Q_n(F_v)\backslash U_n(F_v))$
, it suffices to show the existence
$C^\infty (Q_n(F_v)\backslash U_n(F_v))$
, it suffices to show the existence
![]() $\phi _\tau \in \tau $
,
$\phi _\tau \in \tau $
,
![]() $\phi _m\in \sigma _{m}$
and
$\phi _m\in \sigma _{m}$
and
![]() $\phi _{n+1}\in \sigma _{n+1}$
such that
$\phi _{n+1}\in \sigma _{n+1}$
such that
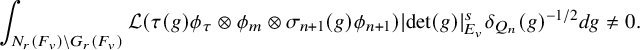 $$ \begin{align*}\displaystyle\int_{N_r(F_v)\backslash G_r(F_v)} \mathcal{L}(\tau(g)\phi_\tau\otimes \phi_m\otimes \sigma_{n+1}(g)\phi_{n+1}) \lvert \det(g)\rvert_{E_v}^s\delta_{Q_n}(g)^{-1/2}dg\neq 0.\end{align*} $$
$$ \begin{align*}\displaystyle\int_{N_r(F_v)\backslash G_r(F_v)} \mathcal{L}(\tau(g)\phi_\tau\otimes \phi_m\otimes \sigma_{n+1}(g)\phi_{n+1}) \lvert \det(g)\rvert_{E_v}^s\delta_{Q_n}(g)^{-1/2}dg\neq 0.\end{align*} $$
Let
![]() $f\in \mathcal {S}(V_{n+1}(F_v))$
,
$f\in \mathcal {S}(V_{n+1}(F_v))$
,
![]() $g\in G_r(F_v)$
,
$g\in G_r(F_v)$
,
![]() $\phi _m\in \sigma _m$
and
$\phi _m\in \sigma _m$
and
![]() $\phi _{n+1}\in \sigma _{n+1}$
. From the equivariance property of
$\phi _{n+1}\in \sigma _{n+1}$
. From the equivariance property of
![]() $\mathcal {L}^B$
, we deduce
$\mathcal {L}^B$
, we deduce
where for
![]() $y\in Y_r(F_v)$
, we have set
$y\in Y_r(F_v)$
, we have set
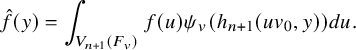 $$ \begin{align*}\hat{f}(y)=\int_{V_{n+1}(F_v)} f(u) \psi_v(h_{n+1}(uv_0,y))du.\end{align*} $$
$$ \begin{align*}\hat{f}(y)=\int_{V_{n+1}(F_v)} f(u) \psi_v(h_{n+1}(uv_0,y))du.\end{align*} $$
By the theory of Fourier transform,
![]() $f\mapsto \hat {f}$
induces a surjective map
$f\mapsto \hat {f}$
induces a surjective map
![]() $\mathcal {S}(V_{n+1}(F_v))\to \mathcal {S}(Y_r(F_v))$
, whereas the map
$\mathcal {S}(V_{n+1}(F_v))\to \mathcal {S}(Y_r(F_v))$
, whereas the map
![]() $g\mapsto g^* y_r$
induces an embedding
$g\mapsto g^* y_r$
induces an embedding
![]() $\mathcal {S}(P_r(F_v)\backslash G_r(F_v))\hookrightarrow \mathcal {S}(Y_r(F_v))$
(where we recall that
$\mathcal {S}(P_r(F_v)\backslash G_r(F_v))\hookrightarrow \mathcal {S}(Y_r(F_v))$
(where we recall that
![]() $P_r$
denotes the mirabolic subgroup of
$P_r$
denotes the mirabolic subgroup of
![]() $G_r$
). Consequently, it suffices to prove the existence of
$G_r$
). Consequently, it suffices to prove the existence of
![]() $\phi _\tau \in \tau $
,
$\phi _\tau \in \tau $
,
![]() $\phi _m\in \sigma _{m}$
,
$\phi _m\in \sigma _{m}$
,
![]() $\phi _{n+1}\in \sigma _{n+1}$
and
$\phi _{n+1}\in \sigma _{n+1}$
and
![]() $f\in \mathcal {S}(P_r(F_v)\backslash G_r(F_v))$
such that
$f\in \mathcal {S}(P_r(F_v)\backslash G_r(F_v))$
such that
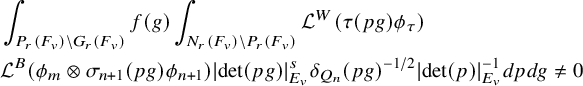 $$\begin{align*}\begin{aligned} & \int_{P_r(F_v)\backslash G_r(F_v)} f(g) \int_{N_r(F_v)\backslash P_r(F_v)} \mathcal{L}^W(\tau(pg)\phi_\tau) \\ & \mathcal{L}^B(\phi_m\otimes \sigma_{n+1}(pg)\phi_{n+1}) \lvert \det(pg)\rvert_{E_v}^{s} \delta_{Q_n}(pg)^{-1/2} \lvert \det(p)\rvert_{E_v}^{-1} dpdg\neq 0 \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} & \int_{P_r(F_v)\backslash G_r(F_v)} f(g) \int_{N_r(F_v)\backslash P_r(F_v)} \mathcal{L}^W(\tau(pg)\phi_\tau) \\ & \mathcal{L}^B(\phi_m\otimes \sigma_{n+1}(pg)\phi_{n+1}) \lvert \det(pg)\rvert_{E_v}^{s} \delta_{Q_n}(pg)^{-1/2} \lvert \det(p)\rvert_{E_v}^{-1} dpdg\neq 0 \end{aligned}\end{align*}$$
or, equivalently, the existence of
![]() $\phi _\tau \in \tau $
,
$\phi _\tau \in \tau $
,
![]() $\phi _m\in \sigma _{m}$
,
$\phi _m\in \sigma _{m}$
,
![]() $\phi _{n+1}\in \sigma _{n+1}$
such that
$\phi _{n+1}\in \sigma _{n+1}$
such that
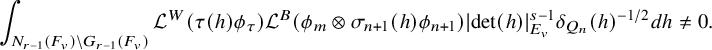 $$ \begin{align*}\int_{N_{r-1}(F_v)\backslash G_{r-1}(F_v)} \mathcal{L}^W(\tau(h)\phi_\tau)\mathcal{L}^B(\phi_m\otimes \sigma_{n+1}(h)\phi_{n+1}) \lvert \det(h)\rvert_{E_v}^{s-1} \delta_{Q_n}(h)^{-1/2} dh\neq 0.\end{align*} $$
$$ \begin{align*}\int_{N_{r-1}(F_v)\backslash G_{r-1}(F_v)} \mathcal{L}^W(\tau(h)\phi_\tau)\mathcal{L}^B(\phi_m\otimes \sigma_{n+1}(h)\phi_{n+1}) \lvert \det(h)\rvert_{E_v}^{s-1} \delta_{Q_n}(h)^{-1/2} dh\neq 0.\end{align*} $$
By [Reference Gelfand and KajdanGK75, Theorem 6] and [Reference KemarskyKem15, Theorem 1], for every
![]() $f\in C_c^\infty (N_{r-1}(F_v)\backslash G_{r-1}(F_v))$
, we can find
$f\in C_c^\infty (N_{r-1}(F_v)\backslash G_{r-1}(F_v))$
, we can find
![]() $\phi _\tau \in \tau $
such that
$\phi _\tau \in \tau $
such that
![]() $\mathcal {L}^W(\tau (h)\phi _\tau )=f(h)$
for
$\mathcal {L}^W(\tau (h)\phi _\tau )=f(h)$
for
![]() $h\in G_{r-1}(F_v)$
, and from this, the claim follows readily from the nonvanishing of
$h\in G_{r-1}(F_v)$
, and from this, the claim follows readily from the nonvanishing of
![]() $\mathcal {L}^B$
.
$\mathcal {L}^B$
.
8.6.2
Proposition 8.6.2.1. Assume that
![]() $\sigma $
and
$\sigma $
and
![]() $\tau $
are tempered. Then, for every
$\tau $
are tempered. Then, for every
![]() $\phi _n,\phi ^{\prime }_n\in I_{Q_n(F_v)}^{U_n(F_v)}(\tau \boxtimes \sigma _{m})$
and
$\phi _n,\phi ^{\prime }_n\in I_{Q_n(F_v)}^{U_n(F_v)}(\tau \boxtimes \sigma _{m})$
and
![]() $\phi _{n+1},\phi _{n+1}'\in \sigma _{n+1}$
, we have
$\phi _{n+1},\phi _{n+1}'\in \sigma _{n+1}$
, we have
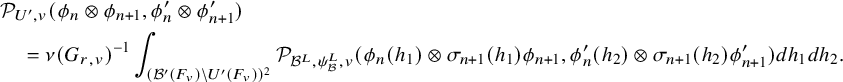 $$ \begin{align} & \mathcal{P}_{U',v}(\phi_n\otimes \phi_{n+1},\phi^{\prime}_n\otimes \phi^{\prime}_{n+1}) \\ \nonumber & \quad =\nu(G_{r,v})^{-1}\int_{(\mathcal{B}'(F_v)\backslash U'(F_v))^2} \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}},v}(\phi_n(h_1)\otimes \sigma_{n+1}(h_1)\phi_{n+1},\phi^{\prime}_n(h_2)\otimes \sigma_{n+1}(h_2)\phi^{\prime}_{n+1}) dh_1dh_2. \end{align} $$
$$ \begin{align} & \mathcal{P}_{U',v}(\phi_n\otimes \phi_{n+1},\phi^{\prime}_n\otimes \phi^{\prime}_{n+1}) \\ \nonumber & \quad =\nu(G_{r,v})^{-1}\int_{(\mathcal{B}'(F_v)\backslash U'(F_v))^2} \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}},v}(\phi_n(h_1)\otimes \sigma_{n+1}(h_1)\phi_{n+1},\phi^{\prime}_n(h_2)\otimes \sigma_{n+1}(h_2)\phi^{\prime}_{n+1}) dh_1dh_2. \end{align} $$
Proof. By definition of the local period
![]() $\mathcal {P}_{U',v}$
and of the invariant inner product on
$\mathcal {P}_{U',v}$
and of the invariant inner product on
![]() $I_{Q_n(F_v)}^{U_n(F_v)}(\tau \boxtimes \sigma _{m})$
, we have
$I_{Q_n(F_v)}^{U_n(F_v)}(\tau \boxtimes \sigma _{m})$
, we have
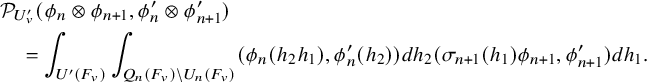 $$ \begin{align} & \mathcal{P}_{U^{\prime}_v}(\phi_n\otimes \phi_{n+1},\phi^{\prime}_n\otimes \phi^{\prime}_{n+1}) \\ \nonumber & \quad = \int_{U'(F_v)}\int_{Q_n(F_v)\backslash U_n(F_v)} (\phi_n(h_2h_1),\phi^{\prime}_n(h_2)) dh_2 (\sigma_{n+1}(h_1)\phi_{n+1},\phi^{\prime}_{n+1})dh_1. \end{align} $$
$$ \begin{align} & \mathcal{P}_{U^{\prime}_v}(\phi_n\otimes \phi_{n+1},\phi^{\prime}_n\otimes \phi^{\prime}_{n+1}) \\ \nonumber & \quad = \int_{U'(F_v)}\int_{Q_n(F_v)\backslash U_n(F_v)} (\phi_n(h_2h_1),\phi^{\prime}_n(h_2)) dh_2 (\sigma_{n+1}(h_1)\phi_{n+1},\phi^{\prime}_{n+1})dh_1. \end{align} $$
The above double integral is absolutely convergent. Indeed, from [Reference Cowling, Haagerup and HoweCHH88, Theorem 2] and [Reference WaldspurgerWal03, Lemme II.1.6], we have
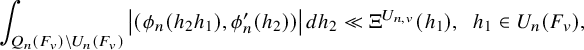 $$ \begin{align*}\int_{Q_n(F_v)\backslash U_n(F_v)} \left\lvert (\phi_n(h_2h_1),\phi^{\prime}_n(h_2))\right\rvert dh_2 \ll \Xi^{U_{n,v}}(h_1),\;\; h_1\in U_n(F_v),\end{align*} $$
$$ \begin{align*}\int_{Q_n(F_v)\backslash U_n(F_v)} \left\lvert (\phi_n(h_2h_1),\phi^{\prime}_n(h_2))\right\rvert dh_2 \ll \Xi^{U_{n,v}}(h_1),\;\; h_1\in U_n(F_v),\end{align*} $$
and
![]() $(\sigma _{n+1}(h_1)\phi _{n+1},\phi ^{\prime }_{n+1})\ll \Xi ^{U_{n+1,v}}(h_1)$
, whereas
$(\sigma _{n+1}(h_1)\phi _{n+1},\phi ^{\prime }_{n+1})\ll \Xi ^{U_{n+1,v}}(h_1)$
, whereas
![]() $\Xi ^{U_v}=\Xi ^{U_{n,v}}\Xi ^{U_{n+1,v}}$
is integrable on
$\Xi ^{U_v}=\Xi ^{U_{n,v}}\Xi ^{U_{n+1,v}}$
is integrable on
![]() $U'(F_v)$
([Reference Beuzart-PlessisBP20, Lemme 6.5.1(i)]).
$U'(F_v)$
([Reference Beuzart-PlessisBP20, Lemme 6.5.1(i)]).
For the next lemma, we set
![]() $Q':=Q_n$
that we consider as a subgroup of
$Q':=Q_n$
that we consider as a subgroup of
![]() $G_r\times \mathcal {G}=L_n\times U_{n+1}$
via the product of the natural surjection
$G_r\times \mathcal {G}=L_n\times U_{n+1}$
via the product of the natural surjection
![]() $Q_n\twoheadrightarrow L_n$
and inclusion
$Q_n\twoheadrightarrow L_n$
and inclusion
![]() $Q_n\subset U_{n+1}$
.
$Q_n\subset U_{n+1}$
.
Lemma 8.6.2.2. For every
![]() $f\in \mathcal {C}^w(G_r(F_v)\times \mathcal {G}(F_v))$
, we have the identity
$f\in \mathcal {C}^w(G_r(F_v)\times \mathcal {G}(F_v))$
, we have the identity
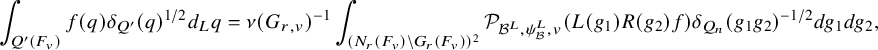 $$ \begin{align} \int_{Q'(F_v)} f(q) \delta_{Q'}(q)^{1/2}d_Lq=\nu(G_{r,v})^{-1}\int_{(N_r(F_v)\backslash G_r(F_v))^2} \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}},v}(L(g_1)R(g_2)f) \delta_{Q_n}(g_1g_2)^{-1/2}dg_1dg_2, \end{align} $$
$$ \begin{align} \int_{Q'(F_v)} f(q) \delta_{Q'}(q)^{1/2}d_Lq=\nu(G_{r,v})^{-1}\int_{(N_r(F_v)\backslash G_r(F_v))^2} \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}},v}(L(g_1)R(g_2)f) \delta_{Q_n}(g_1g_2)^{-1/2}dg_1dg_2, \end{align} $$
where both sides are absolutely convergent.
Indeed, assuming the lemma for the moment, from (8.6.2.2), we obtain
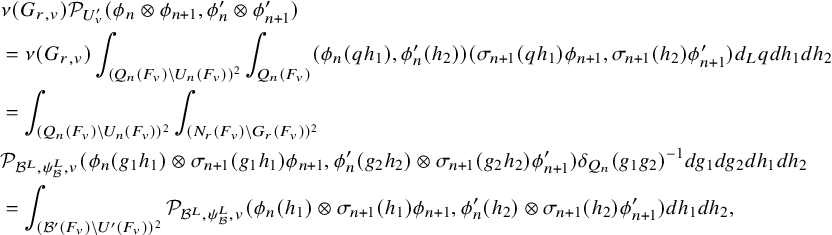 $$\begin{align*}\begin{aligned} & \nu(G_{r,v})\mathcal{P}_{U^{\prime}_v}(\phi_n\otimes \phi_{n+1},\phi^{\prime}_n\otimes \phi^{\prime}_{n+1}) \\ & =\nu(G_{r,v})\int_{(Q_n(F_v)\backslash U_n(F_v))^2} \int_{Q_n(F_v)} (\phi_n(qh_1),\phi^{\prime}_n(h_2)) (\sigma_{n+1}(qh_1)\phi_{n+1},\sigma_{n+1}(h_2)\phi^{\prime}_{n+1})d_Lq dh_1dh_2 \\ & =\int_{(Q_n(F_v)\backslash U_n(F_v))^2} \int_{(N_r(F_v)\backslash G_r(F_v))^2} \\ & \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}},v}(\phi_n(g_1h_1)\otimes \sigma_{n+1}(g_1h_1)\phi_{n+1} ,\phi^{\prime}_n(g_2h_2)\otimes \sigma_{n+1}(g_2h_2)\phi^{\prime}_{n+1}) \delta_{Q_n}(g_1g_2)^{-1}dg_1dg_2 dh_1dh_2 \\ & =\int_{(\mathcal{B}'(F_v)\backslash U'(F_v))^2} \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}},v}(\phi_n(h_1)\otimes \sigma_{n+1}(h_1)\phi_{n+1},\phi^{\prime}_n(h_2)\otimes \sigma_{n+1}(h_2)\phi^{\prime}_{n+1}) dh_1dh_2, \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} & \nu(G_{r,v})\mathcal{P}_{U^{\prime}_v}(\phi_n\otimes \phi_{n+1},\phi^{\prime}_n\otimes \phi^{\prime}_{n+1}) \\ & =\nu(G_{r,v})\int_{(Q_n(F_v)\backslash U_n(F_v))^2} \int_{Q_n(F_v)} (\phi_n(qh_1),\phi^{\prime}_n(h_2)) (\sigma_{n+1}(qh_1)\phi_{n+1},\sigma_{n+1}(h_2)\phi^{\prime}_{n+1})d_Lq dh_1dh_2 \\ & =\int_{(Q_n(F_v)\backslash U_n(F_v))^2} \int_{(N_r(F_v)\backslash G_r(F_v))^2} \\ & \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}},v}(\phi_n(g_1h_1)\otimes \sigma_{n+1}(g_1h_1)\phi_{n+1} ,\phi^{\prime}_n(g_2h_2)\otimes \sigma_{n+1}(g_2h_2)\phi^{\prime}_{n+1}) \delta_{Q_n}(g_1g_2)^{-1}dg_1dg_2 dh_1dh_2 \\ & =\int_{(\mathcal{B}'(F_v)\backslash U'(F_v))^2} \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}},v}(\phi_n(h_1)\otimes \sigma_{n+1}(h_1)\phi_{n+1},\phi^{\prime}_n(h_2)\otimes \sigma_{n+1}(h_2)\phi^{\prime}_{n+1}) dh_1dh_2, \end{aligned}\end{align*}$$
where in the second equality, we have applied the lemma thanks to the fact that the function
belongs to
![]() $\mathcal {C}^w(G_r(F_v)\times \mathcal {G}(F_v))$
and the proposition is therefore established.
$\mathcal {C}^w(G_r(F_v)\times \mathcal {G}(F_v))$
and the proposition is therefore established.
Proof. (of Lemma 8.6.2.2). First, we check that both sides are convergent and define continuous functionals on
![]() $\mathcal {C}^w(G_r(F_v)\times \mathcal {G}(F_v))$
.
$\mathcal {C}^w(G_r(F_v)\times \mathcal {G}(F_v))$
.
For the left-hand side, we can use the identity ([Reference WaldspurgerWal03, Lemme II.1.6])
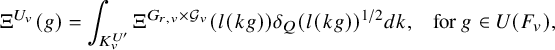 $$ \begin{align*}\Xi^{U_v}(g)=\int_{K^{U'}_{v}} \Xi^{G_{r,v}\times \mathcal{G}_v}(l(kg)) \delta_{Q}(l(kg))^{1/2}dk,\;\; \mbox{ for } g\in U(F_v),\end{align*} $$
$$ \begin{align*}\Xi^{U_v}(g)=\int_{K^{U'}_{v}} \Xi^{G_{r,v}\times \mathcal{G}_v}(l(kg)) \delta_{Q}(l(kg))^{1/2}dk,\;\; \mbox{ for } g\in U(F_v),\end{align*} $$
where, for
![]() $g\in U(F_v)$
,
$g\in U(F_v)$
,
![]() $l(g)$
denotes any element in
$l(g)$
denotes any element in
![]() $L(F_v)=G_r(F_v)\times \mathcal {G}(F_v)$
such that
$L(F_v)=G_r(F_v)\times \mathcal {G}(F_v)$
such that
![]() $l(g)^{-1}g\in (V_n(F_v)\times 1)K^U_{v}$
, which in turn implies
$l(g)^{-1}g\in (V_n(F_v)\times 1)K^U_{v}$
, which in turn implies
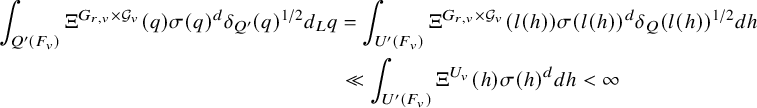 $$\begin{align*}\begin{aligned} \int_{Q'(F_v)} \Xi^{G_{r,v}\times \mathcal{G}_v}(q) \sigma(q)^d \delta_{Q'}(q)^{1/2}d_Lq & =\int_{U'(F_v)} \Xi^{G_{r,v}\times \mathcal{G}_v}(l(h)) \sigma(l(h))^d \delta_{Q}(l(h))^{1/2} dh \\ & \ll \int_{U'(F_v)} \Xi^{U_v}(h) \sigma(h)^d dh<\infty \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} \int_{Q'(F_v)} \Xi^{G_{r,v}\times \mathcal{G}_v}(q) \sigma(q)^d \delta_{Q'}(q)^{1/2}d_Lq & =\int_{U'(F_v)} \Xi^{G_{r,v}\times \mathcal{G}_v}(l(h)) \sigma(l(h))^d \delta_{Q}(l(h))^{1/2} dh \\ & \ll \int_{U'(F_v)} \Xi^{U_v}(h) \sigma(h)^d dh<\infty \end{aligned}\end{align*}$$
for every
![]() $d>0$
.
$d>0$
.
For the right-hand side, as in the proof of Proposition 8.6.1.1, it suffices to show for every
![]() $d>0$
the existence of
$d>0$
the existence of
![]() $d'>0$
as well as a continuous semi-norm
$d'>0$
as well as a continuous semi-norm
![]() $\nu _d$
on
$\nu _d$
on
![]() $\mathcal {C}^w_d(G_r(F_v)\times \mathcal {G}(F_v))$
such that
$\mathcal {C}^w_d(G_r(F_v)\times \mathcal {G}(F_v))$
such that
for
![]() $f\in \mathcal {C}^w_d(G_r(F_v)\times \mathcal {G}(F_v))$
and
$f\in \mathcal {C}^w_d(G_r(F_v)\times \mathcal {G}(F_v))$
and
![]() $a_1,a_2\in T_r(F_v)$
. Such an inequality can be proved along the same lines as [Reference Beuzart-PlessisBP20, Lemma 7.3.1(ii)].
$a_1,a_2\in T_r(F_v)$
. Such an inequality can be proved along the same lines as [Reference Beuzart-PlessisBP20, Lemma 7.3.1(ii)].
Now that we know that both sides of (8.6.2.3) define continuous functionals on
![]() $\mathcal {C}^w(G_r(F_v)\times \mathcal {G}(F_v))$
, by density it suffices to check the claimed identity for
$\mathcal {C}^w(G_r(F_v)\times \mathcal {G}(F_v))$
, by density it suffices to check the claimed identity for
![]() $f=f_1\otimes f_2\in C_c^\infty (G_r(F_v))\otimes C_c^\infty (\mathcal {G}(F_v))$
. The subgroup
$f=f_1\otimes f_2\in C_c^\infty (G_r(F_v))\otimes C_c^\infty (\mathcal {G}(F_v))$
. The subgroup
![]() $G_r\mathcal {B}$
of
$G_r\mathcal {B}$
of
![]() $U_{n+1}$
contains
$U_{n+1}$
contains
![]() $U_m\ltimes V_n$
as a normal subgroup, and we may define a function
$U_m\ltimes V_n$
as a normal subgroup, and we may define a function
![]() $f_3\in C_c^\infty (G_r(F_v)\mathcal {B}(F_v)/U_m(F_v)V_n(F_v))$
by
$f_3\in C_c^\infty (G_r(F_v)\mathcal {B}(F_v)/U_m(F_v)V_n(F_v))$
by
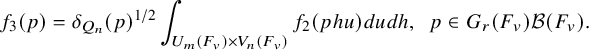 $$ \begin{align*}f_3(p)=\delta_{Q_n}(p)^{1/2}\int_{U_m(F_v)\times V_n(F_v)} f_2(phu) dudh,\;\; p\in G_r(F_v)\mathcal{B}(F_v).\end{align*} $$
$$ \begin{align*}f_3(p)=\delta_{Q_n}(p)^{1/2}\int_{U_m(F_v)\times V_n(F_v)} f_2(phu) dudh,\;\; p\in G_r(F_v)\mathcal{B}(F_v).\end{align*} $$
Moreover, restriction to the susbpace
![]() $\langle x_1,\ldots ,x_{r+1}\rangle $
, where we have again set
$\langle x_1,\ldots ,x_{r+1}\rangle $
, where we have again set
![]() $x_{r+1}=v_0$
, induces an identification
$x_{r+1}=v_0$
, induces an identification
![]() $G_r\mathcal {B}/U_mV_n\simeq P_{r+1}$
. Seeing
$G_r\mathcal {B}/U_mV_n\simeq P_{r+1}$
. Seeing
![]() $f_3$
as a test function on
$f_3$
as a test function on
![]() $P_{r+1}(F_v)$
in this way, the identity of the lemma becomes
$P_{r+1}(F_v)$
in this way, the identity of the lemma becomes
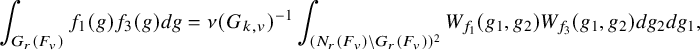 $$ \begin{align} \int_{G_r(F_v)} f_1(g)f_3(g) dg=\nu(G_{k,v})^{-1}\int_{(N_r(F_v)\backslash G_r(F_v))^2} W_{f_1}(g_1,g_2) W_{f_3}(g_1,g_2) dg_2dg_1, \end{align} $$
$$ \begin{align} \int_{G_r(F_v)} f_1(g)f_3(g) dg=\nu(G_{k,v})^{-1}\int_{(N_r(F_v)\backslash G_r(F_v))^2} W_{f_1}(g_1,g_2) W_{f_3}(g_1,g_2) dg_2dg_1, \end{align} $$
where we have set
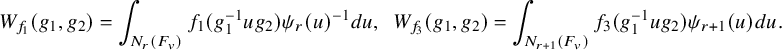 $$ \begin{align*}W_{f_1}(g_1,g_2)=\int_{N_r(F_v)} f_1(g_1^{-1}u g_2) \psi_r(u)^{-1}du,\;\; W_{f_3}(g_1,g_2)=\int_{N_{r+1}(F_v)} f_3(g_1^{-1}ug_2)\psi_{r+1}(u) du.\end{align*} $$
$$ \begin{align*}W_{f_1}(g_1,g_2)=\int_{N_r(F_v)} f_1(g_1^{-1}u g_2) \psi_r(u)^{-1}du,\;\; W_{f_3}(g_1,g_2)=\int_{N_{r+1}(F_v)} f_3(g_1^{-1}ug_2)\psi_{r+1}(u) du.\end{align*} $$
But (8.6.2.5) is now a direct consequence of the Fourier inversion formula (8.2.2.1).
8.7 Unramified computation
8.7.1
We continue with the setting of the previous subsection assuming, moreover, that
![]() $v\notin S$
and the representations
$v\notin S$
and the representations
![]() $\tau $
,
$\tau $
,
![]() $\sigma _{m}$
,
$\sigma _{m}$
,
![]() $\sigma _{n+1}$
are unramified in the sense that
$\sigma _{n+1}$
are unramified in the sense that
![]() $\tau ^{K_{r,v}}\neq 0$
,
$\tau ^{K_{r,v}}\neq 0$
,
![]() $\sigma _m^{K^U_{m,v}}\neq 0$
and
$\sigma _m^{K^U_{m,v}}\neq 0$
and
![]() $\sigma _{n+1}^{K^U_{n+1,v}}\neq 0$
. Note that this implies
$\sigma _{n+1}^{K^U_{n+1,v}}\neq 0$
. Note that this implies
![]() $I_{Q_n(F_v)}^{U_n(F_v)}(\tau _s\boxtimes \sigma _{m})^{K^U_{n,v}}\neq 0$
(i.e.,
$I_{Q_n(F_v)}^{U_n(F_v)}(\tau _s\boxtimes \sigma _{m})^{K^U_{n,v}}\neq 0$
(i.e.,
![]() $I_{Q_n(F_v)}^{U_n(F_v)}(\tau _s\boxtimes \sigma _{m})$
is also unramified).
$I_{Q_n(F_v)}^{U_n(F_v)}(\tau _s\boxtimes \sigma _{m})$
is also unramified).
8.7.2
Proposition 8.7.2.1. For
![]() $\Re (s)$
sufficiently large,
$\Re (s)$
sufficiently large,
![]() $\phi ^\circ _{n,s}\in I_{Q_n(F_v)}^{U_n(F_v)}(\tau _s\boxtimes \sigma _{m})^{K^U_{n,v}}$
and
$\phi ^\circ _{n,s}\in I_{Q_n(F_v)}^{U_n(F_v)}(\tau _s\boxtimes \sigma _{m})^{K^U_{n,v}}$
and
![]() $\phi ^\circ _{n+1}\in \sigma _{n+1}^{K^U_{n+1,v}}$
, we have
$\phi ^\circ _{n+1}\in \sigma _{n+1}^{K^U_{n+1,v}}$
, we have
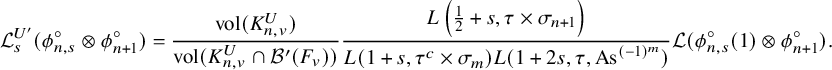 $$ \begin{align} \mathcal{L}_s^{U'}(\phi^\circ_{n,s}\otimes \phi^\circ_{n+1}) &= \frac{\operatorname{\mathrm{vol}}(K^U_{n,v})}{\operatorname{\mathrm{vol}}(K^U_{n,v}\cap \mathcal{B}'(F_v))}\frac{L\left(\frac{1}{2}+s,\tau\times \sigma_{n+1}\right)}{L(1+s,\tau^c\times \sigma_{m})L(1+2s,\tau,\mathrm{As}^{(-1)^m})}\mathcal{L}(\phi^\circ_{n,s}(1)\otimes \phi^\circ_{n+1}). \end{align} $$
$$ \begin{align} \mathcal{L}_s^{U'}(\phi^\circ_{n,s}\otimes \phi^\circ_{n+1}) &= \frac{\operatorname{\mathrm{vol}}(K^U_{n,v})}{\operatorname{\mathrm{vol}}(K^U_{n,v}\cap \mathcal{B}'(F_v))}\frac{L\left(\frac{1}{2}+s,\tau\times \sigma_{n+1}\right)}{L(1+s,\tau^c\times \sigma_{m})L(1+2s,\tau,\mathrm{As}^{(-1)^m})}\mathcal{L}(\phi^\circ_{n,s}(1)\otimes \phi^\circ_{n+1}). \end{align} $$
Proof. Let
![]() $\phi ^\circ _\tau \in \tau ^{K_{r,v}}$
and
$\phi ^\circ _\tau \in \tau ^{K_{r,v}}$
and
![]() $\phi _{m}^\circ \in \sigma _m^{K^U_{m,v}}$
be such that
$\phi _{m}^\circ \in \sigma _m^{K^U_{m,v}}$
be such that
![]() $\phi _n^\circ (1)= \phi ^\circ _\tau \otimes \phi _{m}^\circ $
. Recall the factorization
$\phi _n^\circ (1)= \phi ^\circ _\tau \otimes \phi _{m}^\circ $
. Recall the factorization
![]() $\mathcal {L}=\mathcal {L}^W\otimes \mathcal {L}^B$
. Up to scaling, we may assume, without loss of generality, that
$\mathcal {L}=\mathcal {L}^W\otimes \mathcal {L}^B$
. Up to scaling, we may assume, without loss of generality, that
Let
![]() $P'=P\cap U'\subset U'$
be the parabolic subgroup stabilizing the flag
$P'=P\cap U'\subset U'$
be the parabolic subgroup stabilizing the flag
Then, we have
![]() $P'=\mathcal {B}'\rtimes T_r$
and from the Iwasawa decomposition
$P'=\mathcal {B}'\rtimes T_r$
and from the Iwasawa decomposition
![]() $U'(F_v)=P'(F_v)K_{n,v}^{U}$
, we obtain
$U'(F_v)=P'(F_v)K_{n,v}^{U}$
, we obtain
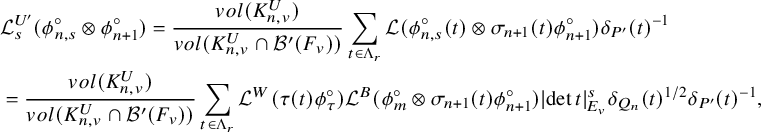 $$ \begin{align} & \mathcal{L}_s^{U'}(\phi_{n,s}^\circ\otimes \phi_{n+1}^\circ) =\frac{vol(K_{n,v}^U)}{vol(K_{n,v}^U\cap \mathcal{B}'(F_v))} \sum_{t\in \Lambda_r} \mathcal{L}(\phi_{n,s}^\circ(t)\otimes \sigma_{n+1}(t)\phi_{n+1}^\circ) \delta_{P'}(t)^{-1} \\ \nonumber & =\frac{vol(K_{n,v}^U)}{vol(K_{n,v}^U\cap \mathcal{B}'(F_v))} \sum_{t\in \Lambda_r} \mathcal{L}^W(\tau(t)\phi_{\tau}^\circ) \mathcal{L}^B(\phi_{m}^\circ\otimes \sigma_{n+1}(t)\phi_{n+1}^\circ) \lvert \det t\rvert_{E_v}^s \delta_{Q_n}(t)^{1/2}\delta_{P'}(t)^{-1}, \end{align} $$
$$ \begin{align} & \mathcal{L}_s^{U'}(\phi_{n,s}^\circ\otimes \phi_{n+1}^\circ) =\frac{vol(K_{n,v}^U)}{vol(K_{n,v}^U\cap \mathcal{B}'(F_v))} \sum_{t\in \Lambda_r} \mathcal{L}(\phi_{n,s}^\circ(t)\otimes \sigma_{n+1}(t)\phi_{n+1}^\circ) \delta_{P'}(t)^{-1} \\ \nonumber & =\frac{vol(K_{n,v}^U)}{vol(K_{n,v}^U\cap \mathcal{B}'(F_v))} \sum_{t\in \Lambda_r} \mathcal{L}^W(\tau(t)\phi_{\tau}^\circ) \mathcal{L}^B(\phi_{m}^\circ\otimes \sigma_{n+1}(t)\phi_{n+1}^\circ) \lvert \det t\rvert_{E_v}^s \delta_{Q_n}(t)^{1/2}\delta_{P'}(t)^{-1}, \end{align} $$
where we have set
![]() $\Lambda _r=T_r(F_v)/T_r(\mathcal {O}_v)$
, which we will identify with the cocharacter lattice
$\Lambda _r=T_r(F_v)/T_r(\mathcal {O}_v)$
, which we will identify with the cocharacter lattice
![]() $X_*(T_{r,v})$
via the map
$X_*(T_{r,v})$
via the map
![]() $\lambda \mapsto \lambda (\varpi _F)$
. Let
$\lambda \mapsto \lambda (\varpi _F)$
. Let
![]() $\Lambda _r^+\subset \Lambda _r$
be the cone of dominant cocharacters with respect to
$\Lambda _r^+\subset \Lambda _r$
be the cone of dominant cocharacters with respect to
![]() $B_r$
and
$B_r$
and
![]() $\Lambda _r^{++}\subset \Lambda _r^+$
the subcone of cocharacters that are moreover dominant with respect to
$\Lambda _r^{++}\subset \Lambda _r^+$
the subcone of cocharacters that are moreover dominant with respect to
![]() $B_{r+1}$
through the embedding
$B_{r+1}$
through the embedding
 $g\in G_r\mapsto \begin {pmatrix} g & \\ & 1 \end {pmatrix}\in G_{r+1}$
. To lighten the computations a bit, we will assume from now on that the local measures at v have been chosen such that
$g\in G_r\mapsto \begin {pmatrix} g & \\ & 1 \end {pmatrix}\in G_{r+1}$
. To lighten the computations a bit, we will assume from now on that the local measures at v have been chosen such that
![]() $vol(K_{n,v}^U)=vol(K_{n,v}^U\cap \mathcal {B}'(F_v))=1$
.
$vol(K_{n,v}^U)=vol(K_{n,v}^U\cap \mathcal {B}'(F_v))=1$
.
Before proceeding, it will be convenient to introduce some notation pertaining to complex dual groups:
-
• For
 $\ell \in \{m,m+1,n+1\}$
, we identify the dual group
$\ell \in \{m,m+1,n+1\}$
, we identify the dual group
 $\widehat {U}_\ell $
of
$\widehat {U}_\ell $
of
 $U_\ell $
(resp.
$U_\ell $
(resp.
 $\widehat {G}_r$
of
$\widehat {G}_r$
of
 $G_r$
) with
$G_r$
) with
 $\mathrm {GL}_\ell (\mathbb {C})$
(resp.
$\mathrm {GL}_\ell (\mathbb {C})$
(resp.
 $\mathrm {GL}_r(\mathbb {C})\times \mathrm {GL}_r(\mathbb {C})$
) equipped with its standard pinning. Its L-group can be written where the Galois action is given by
$\mathrm {GL}_r(\mathbb {C})\times \mathrm {GL}_r(\mathbb {C})$
) equipped with its standard pinning. Its L-group can be written where the Galois action is given by $$ \begin{align*}{}^L U_\ell=\mathrm{GL}_\ell(\mathbb{C})\rtimes \operatorname{\mathrm{Gal}}(E/F) \;\; (\mbox{resp. } {}^L G_r=(\mathrm{GL}_r(\mathbb{C})\times \mathrm{GL}_r(\mathbb{C}))\rtimes \operatorname{\mathrm{Gal}}(E/F)),\end{align*} $$
$$ \begin{align*}{}^L U_\ell=\mathrm{GL}_\ell(\mathbb{C})\rtimes \operatorname{\mathrm{Gal}}(E/F) \;\; (\mbox{resp. } {}^L G_r=(\mathrm{GL}_r(\mathbb{C})\times \mathrm{GL}_r(\mathbb{C}))\rtimes \operatorname{\mathrm{Gal}}(E/F)),\end{align*} $$
 $c(g)=g^\star $
(resp.
$c(g)=g^\star $
(resp.
 $c(g_1,g_2)=(g_2,g_1)$
), where the involution
$c(g_1,g_2)=(g_2,g_1)$
), where the involution
 $g\in \mathrm {GL}_\ell (\mathbb {C})\mapsto g^\star $
is We will also denote by
$g\in \mathrm {GL}_\ell (\mathbb {C})\mapsto g^\star $
is We will also denote by $$ \begin{align*}g^\star=J_\ell {}^t g^{-1} J_\ell^{-1},\;\;\; J_\ell=\begin{pmatrix} & & 1 \\ & \unicode{x22F0} & \\ (-1)^{\ell-1} & & \end{pmatrix}.\end{align*} $$
$$ \begin{align*}g^\star=J_\ell {}^t g^{-1} J_\ell^{-1},\;\;\; J_\ell=\begin{pmatrix} & & 1 \\ & \unicode{x22F0} & \\ (-1)^{\ell-1} & & \end{pmatrix}.\end{align*} $$
 $S\mapsto S^\star $
the automorphism of
$S\mapsto S^\star $
the automorphism of
 ${}^L G_r$
which is the identity on
${}^L G_r$
which is the identity on
 $\operatorname {\mathrm {Gal}}(E/F)$
and given by
$\operatorname {\mathrm {Gal}}(E/F)$
and given by
 $(g_1,g_2)\mapsto (g_2^\star , g_1^\star )$
on
$(g_1,g_2)\mapsto (g_2^\star , g_1^\star )$
on
 $\widehat {G}_r$
.
$\widehat {G}_r$
.
-
• We will write
 $(\widehat {T}_r,\widehat {B}_r)$
for the standard Borel pair in
$(\widehat {T}_r,\widehat {B}_r)$
for the standard Borel pair in
 $\widehat {G}_r$
and
$\widehat {G}_r$
and
 $(\widehat {T}^U_\ell ,\widehat {B}_\ell ^U)$
for that in
$(\widehat {T}^U_\ell ,\widehat {B}_\ell ^U)$
for that in
 $\widehat {U}_\ell $
. The corresponding semi-direct products with
$\widehat {U}_\ell $
. The corresponding semi-direct products with
 $\operatorname {\mathrm {Gal}}(E/F)$
will be denoted
$\operatorname {\mathrm {Gal}}(E/F)$
will be denoted  $$ \begin{align*}{}^L T_r=\widehat{T}_r\rtimes \operatorname{\mathrm{Gal}}(E/F),\; {}^L B_r=\widehat{B}_r\rtimes \operatorname{\mathrm{Gal}}(E/F),\; {}^L T^U_\ell=\widehat{T}^U_\ell\rtimes \operatorname{\mathrm{Gal}}(E/F),\; {}^L B^U_\ell=\widehat{B}^U_\ell\rtimes \operatorname{\mathrm{Gal}}(E/F).\end{align*} $$
$$ \begin{align*}{}^L T_r=\widehat{T}_r\rtimes \operatorname{\mathrm{Gal}}(E/F),\; {}^L B_r=\widehat{B}_r\rtimes \operatorname{\mathrm{Gal}}(E/F),\; {}^L T^U_\ell=\widehat{T}^U_\ell\rtimes \operatorname{\mathrm{Gal}}(E/F),\; {}^L B^U_\ell=\widehat{B}^U_\ell\rtimes \operatorname{\mathrm{Gal}}(E/F).\end{align*} $$
-
• The dual groups of
 $\mathcal {G}$
,
$\mathcal {G}$
,
 $\widetilde {U}$
are and writing
$\widetilde {U}$
are and writing $$ \begin{align*}\widehat{\mathcal{G}}=\widehat{U}_m\times \widehat{U}_{n+1},\; \widehat{\widetilde{U}}=\widehat{U}_m\times \widehat{U}_{m+1},\end{align*} $$
$$ \begin{align*}\widehat{\mathcal{G}}=\widehat{U}_m\times \widehat{U}_{n+1},\; \widehat{\widetilde{U}}=\widehat{U}_m\times \widehat{U}_{m+1},\end{align*} $$
 $\times _\Gamma $
for the fibered products over
$\times _\Gamma $
for the fibered products over
 $\operatorname {\mathrm {Gal}}(E/F)$
, their L-groups are respectively. We let
$\operatorname {\mathrm {Gal}}(E/F)$
, their L-groups are respectively. We let $$ \begin{align*}{}^L \mathcal{G}={}^L U_m\times_\Gamma {}^L U_{n+1},\; {}^L \widetilde{U}={}^L U_m\times_\Gamma {}^L U_{m+1},\end{align*} $$
$$ \begin{align*}{}^L \mathcal{G}={}^L U_m\times_\Gamma {}^L U_{n+1},\; {}^L \widetilde{U}={}^L U_m\times_\Gamma {}^L U_{m+1},\end{align*} $$
 $\widehat {B}=\widehat {B}^U_m\times \widehat {B}^U_{n+1}$
,
$\widehat {B}=\widehat {B}^U_m\times \widehat {B}^U_{n+1}$
,
 $\widehat {T}=\widehat {T}^U_m\times \widehat {T}^U_{n+1}$
(resp.
$\widehat {T}=\widehat {T}^U_m\times \widehat {T}^U_{n+1}$
(resp.
 $\widehat {\widetilde {B}}=\widehat {B}^U_m\times \widehat {B}^U_{m+1}$
,
$\widehat {\widetilde {B}}=\widehat {B}^U_m\times \widehat {B}^U_{m+1}$
,
 $\widehat {\widetilde {T}}=\widehat {T}^U_m\times \widehat {T}^U_{m+1}$
) be the standard Borel and maximal torus in
$\widehat {\widetilde {T}}=\widehat {T}^U_m\times \widehat {T}^U_{m+1}$
) be the standard Borel and maximal torus in
 $\widehat {\mathcal {G}}$
(resp. in
$\widehat {\mathcal {G}}$
(resp. in
 $\widehat {\widetilde {U}}$
). We also write
$\widehat {\widetilde {U}}$
). We also write  $$ \begin{align*}{}^L T=\widehat{T}\rtimes \operatorname{\mathrm{Gal}}(E/F),\; {}^L \widetilde{T}=\widehat{\widetilde{T}}\rtimes \operatorname{\mathrm{Gal}}(E/F).\end{align*} $$
$$ \begin{align*}{}^L T=\widehat{T}\rtimes \operatorname{\mathrm{Gal}}(E/F),\; {}^L \widetilde{T}=\widehat{\widetilde{T}}\rtimes \operatorname{\mathrm{Gal}}(E/F).\end{align*} $$
-
• The parabolic subgroup
 $Q_{n+1}\subset U_{n+1}$
stabilizing the isotropic subspace
$Q_{n+1}\subset U_{n+1}$
stabilizing the isotropic subspace
 $X_r$
corresponds to a standard parabolic subgroup
$X_r$
corresponds to a standard parabolic subgroup
 $\widehat {Q}_{n+1}$
of
$\widehat {Q}_{n+1}$
of
 $\widehat {U}_{n+1}$
with standard Levi The corresponding L-group
$\widehat {U}_{n+1}$
with standard Levi The corresponding L-group $$ \begin{align*}\widehat{L}_{n+1}=\begin{pmatrix} \mathrm{GL}_r(\mathbb{C}) & & \\ & \mathrm{GL}_{m+1}(\mathbb{C}) & \\ & & \mathrm{GL}_r(\mathbb{C}) \end{pmatrix}.\end{align*} $$
$$ \begin{align*}\widehat{L}_{n+1}=\begin{pmatrix} \mathrm{GL}_r(\mathbb{C}) & & \\ & \mathrm{GL}_{m+1}(\mathbb{C}) & \\ & & \mathrm{GL}_r(\mathbb{C}) \end{pmatrix}.\end{align*} $$
 ${}^L L_{n+1}=\widehat {L}_{n+1}\rtimes \operatorname {\mathrm {Gal}}(E/F)$
is isomorphic to
${}^L L_{n+1}=\widehat {L}_{n+1}\rtimes \operatorname {\mathrm {Gal}}(E/F)$
is isomorphic to
 ${}^L G_r\times _\Gamma {}^L U_{m+1}$
via the map which is the identity on
${}^L G_r\times _\Gamma {}^L U_{m+1}$
via the map which is the identity on
 $\operatorname {\mathrm {Gal}}(E/F)$
and on
$\operatorname {\mathrm {Gal}}(E/F)$
and on $$ \begin{align*}\begin{pmatrix} g^{(1)}_r & & \\ & g_{m+1} & \\ & & g_r^{(2)}\end{pmatrix}\mapsto ((g_r^{(1)},g_r^{(2)\star}),g_{m+1})\end{align*} $$
$$ \begin{align*}\begin{pmatrix} g^{(1)}_r & & \\ & g_{m+1} & \\ & & g_r^{(2)}\end{pmatrix}\mapsto ((g_r^{(1)},g_r^{(2)\star}),g_{m+1})\end{align*} $$
 $\widehat {L}_{n+1}$
. For
$\widehat {L}_{n+1}$
. For
 $S\in {}^L L_{n+1}$
, we denote by
$S\in {}^L L_{n+1}$
, we denote by
 $(S^{(r)}, S^{(m+1)})\in {}^L G_r\times _\Gamma {}^L U_{m+1}$
its image by this isomorphism.
$(S^{(r)}, S^{(m+1)})\in {}^L G_r\times _\Gamma {}^L U_{m+1}$
its image by this isomorphism.
-
• It will also be convenient to use the parabolic subgroup
 $\mathcal {Q}=U_m\times Q_{n+1}$
of
$\mathcal {Q}=U_m\times Q_{n+1}$
of
 $\mathcal {G}$
. We set
$\mathcal {G}$
. We set
 $\widehat {\mathcal {Q}}=\widehat {U}_m\times \widehat {Q}_{n+1}$
,
$\widehat {\mathcal {Q}}=\widehat {U}_m\times \widehat {Q}_{n+1}$
,
 $\widehat {\mathcal {L}}=\widehat {U}_m\times \widehat {L}_{n+1}$
and
$\widehat {\mathcal {L}}=\widehat {U}_m\times \widehat {L}_{n+1}$
and
 ${}^L \mathcal {L}=\widehat {\mathcal {L}}\rtimes \operatorname {\mathrm {Gal}}(E/F)$
. There are two natural decompositions and for
${}^L \mathcal {L}=\widehat {\mathcal {L}}\rtimes \operatorname {\mathrm {Gal}}(E/F)$
. There are two natural decompositions and for $$ \begin{align*}{}^L \mathcal{L}={}^L U_m\times_{\Gamma}{}^L L_{n+1} \mbox{ and } {}^L \mathcal{L}={}^L \widetilde{U}\times_\Gamma {}^L G_r,\end{align*} $$
$$ \begin{align*}{}^L \mathcal{L}={}^L U_m\times_{\Gamma}{}^L L_{n+1} \mbox{ and } {}^L \mathcal{L}={}^L \widetilde{U}\times_\Gamma {}^L G_r,\end{align*} $$
 $S\in {}^L \mathcal {L}$
, we will denote by
$S\in {}^L \mathcal {L}$
, we will denote by
 $(S_m,S_{n+1})$
and
$(S_m,S_{n+1})$
and
 $(\widetilde {S}, S_{n+1}^{(r)})$
the corresponding respective decompositions of S.
$(\widetilde {S}, S_{n+1}^{(r)})$
the corresponding respective decompositions of S.
-
• For every complex Lie group
 ${}^L \mathbb {G}$
with a subgroup
${}^L \mathbb {G}$
with a subgroup
 ${}^L \mathbb {Q}$
and respective identity components
${}^L \mathbb {Q}$
and respective identity components
 $\widehat {\mathbb {G}}$
,
$\widehat {\mathbb {G}}$
,
 $\widehat {\mathbb {Q}}$
, we set
$\widehat {\mathbb {Q}}$
, we set  $$ \begin{align*}D_{\widehat{\mathbb{G}}/\widehat{\mathbb{Q}}}(S)=\det(1-Ad(S)\mid Lie(\widehat{\mathbb{G}})/Lie(\widehat{\mathbb{Q}})), \mbox{ for } S\in {}^L \mathbb{Q}.\end{align*} $$
$$ \begin{align*}D_{\widehat{\mathbb{G}}/\widehat{\mathbb{Q}}}(S)=\det(1-Ad(S)\mid Lie(\widehat{\mathbb{G}})/Lie(\widehat{\mathbb{Q}})), \mbox{ for } S\in {}^L \mathbb{Q}.\end{align*} $$
-
• For
 $\mathbb {G}\in \{G_r,U_\ell , \mathcal {G}, \mathcal {L}, L_{n+1}, T_r, T^U_\ell , T \}$
, we denote by
$\mathbb {G}\in \{G_r,U_\ell , \mathcal {G}, \mathcal {L}, L_{n+1}, T_r, T^U_\ell , T \}$
, we denote by
 ${}^L \mathbb {G}_v$
the L-group of
${}^L \mathbb {G}_v$
the L-group of
 $\mathbb {G}_v=\mathbb {G}\times _F F_v$
that is Also, for
$\mathbb {G}_v=\mathbb {G}\times _F F_v$
that is Also, for $$ \begin{align*}{}^L \mathbb{G}_{v} =\left\{\begin{array}{ll} {}^L \mathbb{G} & \mbox{ if } v \mbox{ is inert in } E; \\ \widehat{\mathbb{G}} & \mbox{ if } v \mbox{ splits in } E. \end{array} \right.\end{align*} $$
$$ \begin{align*}{}^L \mathbb{G}_{v} =\left\{\begin{array}{ll} {}^L \mathbb{G} & \mbox{ if } v \mbox{ is inert in } E; \\ \widehat{\mathbb{G}} & \mbox{ if } v \mbox{ splits in } E. \end{array} \right.\end{align*} $$
 $\mathbb {G}\in \{G_r,U_\ell , \mathcal {G}, \mathcal {L}, L_{n+1}\}$
, we write
$\mathbb {G}\in \{G_r,U_\ell , \mathcal {G}, \mathcal {L}, L_{n+1}\}$
, we write
 $W(\mathbb {G}_v)$
for the Weyl group
$W(\mathbb {G}_v)$
for the Weyl group
 $Norm_{\widehat {\mathbb {G}}}({}^L \mathbb {T}_v)/\widehat {\mathbb {T}}$
, where
$Norm_{\widehat {\mathbb {G}}}({}^L \mathbb {T}_v)/\widehat {\mathbb {T}}$
, where
 $\widehat {\mathbb {T}}\subset \widehat {\mathbb {G}}$
is the standard maximal torus.
$\widehat {\mathbb {T}}\subset \widehat {\mathbb {G}}$
is the standard maximal torus.
-
• The choice of the Borel pair
 $(T_r,B_r)$
allows to identify
$(T_r,B_r)$
allows to identify
 $\Lambda _r$
with the group of characters of
$\Lambda _r$
with the group of characters of
 ${}^L T_{r,v}$
that are trivial on
${}^L T_{r,v}$
that are trivial on
 $\operatorname {\mathrm {Gal}}(E/F)$
, and we will denote by
$\operatorname {\mathrm {Gal}}(E/F)$
, and we will denote by
 $\Lambda _r\ni t\mapsto \chi _t$
this identification. For
$\Lambda _r\ni t\mapsto \chi _t$
this identification. For
 $t\in \Lambda _r^+$
, we write
$t\in \Lambda _r^+$
, we write
 $ch_t$
for the character of the irreducible representation of
$ch_t$
for the character of the irreducible representation of
 ${}^L G_r$
with highest weight
${}^L G_r$
with highest weight
 $\chi _t$
(see Appendix A).
$\chi _t$
(see Appendix A). -
• For
 $k,\ell \in \mathbb {N}$
, we define the representation
$k,\ell \in \mathbb {N}$
, we define the representation  $$ \begin{align*}{}^L(G_k\times G_\ell)={}^LG_k\times_\Gamma {}^L G_\ell\to \mathrm{GL}(\mathbb{C}^k\otimes \mathbb{C}^\ell\oplus \mathbb{C}^k\otimes \mathbb{C}^\ell)\end{align*} $$
which sends
$$ \begin{align*}{}^L(G_k\times G_\ell)={}^LG_k\times_\Gamma {}^L G_\ell\to \mathrm{GL}(\mathbb{C}^k\otimes \mathbb{C}^\ell\oplus \mathbb{C}^k\otimes \mathbb{C}^\ell)\end{align*} $$
which sends $$ \begin{align*}(S_k,S_\ell)\mapsto S_k\overset{\mathrm{I}}{\otimes} S_\ell,\end{align*} $$
$$ \begin{align*}(S_k,S_\ell)\mapsto S_k\overset{\mathrm{I}}{\otimes} S_\ell,\end{align*} $$
 $((g_k^{(1)},g_k^{(2)}),(g^{(1)}_\ell ,g_\ell ^{(2)}))\in \widehat {G_k}\times \widehat {G_\ell }$
to
$((g_k^{(1)},g_k^{(2)}),(g^{(1)}_\ell ,g_\ell ^{(2)}))\in \widehat {G_k}\times \widehat {G_\ell }$
to
 $g_k^{(1)}\otimes g_\ell ^{(1)}\oplus g_k^{(2)}\otimes g_\ell ^{(2)}$
and
$g_k^{(1)}\otimes g_\ell ^{(1)}\oplus g_k^{(2)}\otimes g_\ell ^{(2)}$
and
 $c\in \operatorname {\mathrm {Gal}}(E/F)$
to the operator
$c\in \operatorname {\mathrm {Gal}}(E/F)$
to the operator
 $\iota $
that swaps the two copies of
$\iota $
that swaps the two copies of
 $\mathbb {C}^k\otimes \mathbb {C}^\ell $
.
$\mathbb {C}^k\otimes \mathbb {C}^\ell $
.
-
• Composing this representation with the embeddings
 ${}^L U_i\to {}^L G_i$
,
${}^L U_i\to {}^L G_i$
,
 $g\in \widehat {U}_i\mapsto (g,g^\star )$
, (
$g\in \widehat {U}_i\mapsto (g,g^\star )$
, (
 $i=k,\ell $
), we obtain representations and
$i=k,\ell $
), we obtain representations and $$ \begin{align*}{}^L(U_k\times G_\ell)\to \mathrm{GL}(\mathbb{C}^k\otimes \mathbb{C}^\ell\oplus \mathbb{C}^k\otimes \mathbb{C}^\ell)\end{align*} $$
that for simplicity we will also denote by the symbol
$$ \begin{align*}{}^L(U_k\times G_\ell)\to \mathrm{GL}(\mathbb{C}^k\otimes \mathbb{C}^\ell\oplus \mathbb{C}^k\otimes \mathbb{C}^\ell)\end{align*} $$
that for simplicity we will also denote by the symbol $$ \begin{align*}{}^L(U_k\times U_\ell)\to \mathrm{GL}(\mathbb{C}^k\otimes \mathbb{C}^\ell\oplus \mathbb{C}^k\otimes \mathbb{C}^\ell)\end{align*} $$
$$ \begin{align*}{}^L(U_k\times U_\ell)\to \mathrm{GL}(\mathbb{C}^k\otimes \mathbb{C}^\ell\oplus \mathbb{C}^k\otimes \mathbb{C}^\ell)\end{align*} $$
 $\overset {\mathrm {I}}{\otimes }$
.
$\overset {\mathrm {I}}{\otimes }$
.
-
• In particular, we have two representations
 $$ \begin{align*}\mathcal{R}: {}^L \mathcal{G}={}^L(U_m\times U_{n+1})\to \mathrm{GL}(\mathbb{C}^m\otimes \mathbb{C}^{n+1}\oplus \mathbb{C}^m\otimes \mathbb{C}^{n+1}),\; (S_m,S_{n+1})\mapsto S_m \overset{\mathrm{I}}{\otimes} S_{n+1}\end{align*} $$
that we will denote by
$$ \begin{align*}\mathcal{R}: {}^L \mathcal{G}={}^L(U_m\times U_{n+1})\to \mathrm{GL}(\mathbb{C}^m\otimes \mathbb{C}^{n+1}\oplus \mathbb{C}^m\otimes \mathbb{C}^{n+1}),\; (S_m,S_{n+1})\mapsto S_m \overset{\mathrm{I}}{\otimes} S_{n+1}\end{align*} $$
that we will denote by $$ \begin{align*}\widetilde{\mathcal{R}}: {}^L \widetilde{U}={}^L(U_m\times U_{m+1})\to \mathrm{GL}(\mathbb{C}^m\otimes \mathbb{C}^{m+1}\oplus \mathbb{C}^m\otimes \mathbb{C}^{m+1}),\; (S_m,S_{m+1})\mapsto S_m \overset{\mathrm{I}}{\otimes} S_{m+1}\end{align*} $$
$$ \begin{align*}\widetilde{\mathcal{R}}: {}^L \widetilde{U}={}^L(U_m\times U_{m+1})\to \mathrm{GL}(\mathbb{C}^m\otimes \mathbb{C}^{m+1}\oplus \mathbb{C}^m\otimes \mathbb{C}^{m+1}),\; (S_m,S_{m+1})\mapsto S_m \overset{\mathrm{I}}{\otimes} S_{m+1}\end{align*} $$
 $\mathcal {R}$
and
$\mathcal {R}$
and
 $\widetilde {\mathcal {R}}$
, respectively. The subspace
$\widetilde {\mathcal {R}}$
, respectively. The subspace  $$ \begin{align*}V_-:=\left\langle (e_i\otimes e_j,0) \mid \substack{1\leqslant i\leqslant m \\ 1\leqslant j\leqslant n+1 \\ i+j> m+r+1}\right\rangle\oplus \left\langle (0,e_i\otimes e_j) \mid \substack{1\leqslant i\leqslant m \\ 1\leqslant j\leqslant n+1 \\ i+j> m+r+1}\right\rangle\end{align*} $$
where we denote by
$$ \begin{align*}V_-:=\left\langle (e_i\otimes e_j,0) \mid \substack{1\leqslant i\leqslant m \\ 1\leqslant j\leqslant n+1 \\ i+j> m+r+1}\right\rangle\oplus \left\langle (0,e_i\otimes e_j) \mid \substack{1\leqslant i\leqslant m \\ 1\leqslant j\leqslant n+1 \\ i+j> m+r+1}\right\rangle\end{align*} $$
where we denote by $$ \begin{align*}\left(\mbox{resp. } \widetilde{V}_-:=\left\langle (e_i\otimes e_j,0) \mid \substack{1\leqslant i\leqslant m \\ 1\leqslant j\leqslant m+1 \\ i+j> m+1}\right\rangle\oplus \left\langle (0,e_i\otimes e_j) \mid \substack{1\leqslant i\leqslant m \\ 1\leqslant j\leqslant m+1 \\ i+j> m+1}\right\rangle \right),\end{align*} $$
$$ \begin{align*}\left(\mbox{resp. } \widetilde{V}_-:=\left\langle (e_i\otimes e_j,0) \mid \substack{1\leqslant i\leqslant m \\ 1\leqslant j\leqslant m+1 \\ i+j> m+1}\right\rangle\oplus \left\langle (0,e_i\otimes e_j) \mid \substack{1\leqslant i\leqslant m \\ 1\leqslant j\leqslant m+1 \\ i+j> m+1}\right\rangle \right),\end{align*} $$
 $(e_i)_{i=1}^k$
the standard basis of
$(e_i)_{i=1}^k$
the standard basis of
 $\mathbb {C}^k$
for any k, is stable by
$\mathbb {C}^k$
for any k, is stable by
 ${}^L T$
(resp. by
${}^L T$
(resp. by
 ${}^L \widetilde {T}$
), and we set
${}^L \widetilde {T}$
), and we set
 $\mathcal {R}_-(S):=\mathcal {R}(S)\mid _{V_-}$
(resp.
$\mathcal {R}_-(S):=\mathcal {R}(S)\mid _{V_-}$
(resp.
 $\widetilde {\mathcal {R}}_-(\widetilde {S}):=\widetilde {\mathcal {R}}(\widetilde {S})_{\mid \widetilde {V}_-}$
) for
$\widetilde {\mathcal {R}}_-(\widetilde {S}):=\widetilde {\mathcal {R}}(\widetilde {S})_{\mid \widetilde {V}_-}$
) for
 $S\in {}^L T$
(resp.
$S\in {}^L T$
(resp.
 $\widetilde {S}\in {}^L \widetilde {T}$
).
$\widetilde {S}\in {}^L \widetilde {T}$
).
-
• We will also denote by
 $\mathrm {As}_m$
the representation given by
$\mathrm {As}_m$
the representation given by $$ \begin{align*}\mathrm{As}_m: {}^L G_r\to \mathrm{GL}(\mathbb{C}^r\otimes \mathbb{C}^r)\end{align*} $$
$$ \begin{align*}\mathrm{As}_m: {}^L G_r\to \mathrm{GL}(\mathbb{C}^r\otimes \mathbb{C}^r)\end{align*} $$
 $\mathrm {As}_m(g^{(1)},g^{(2)})=g^{(1)}\otimes g^{(2)}$
for
$\mathrm {As}_m(g^{(1)},g^{(2)})=g^{(1)}\otimes g^{(2)}$
for
 $(g^{(1)},g^{(2)})\in \widehat {G}_r$
and
$(g^{(1)},g^{(2)})\in \widehat {G}_r$
and
 $\mathrm {As}_m(c)=(-1)^m s$
, where
$\mathrm {As}_m(c)=(-1)^m s$
, where
 $s: \mathbb {C}^r\otimes \mathbb {C}^r\to \mathbb {C}^r\otimes \mathbb {C}^r$
is defined by
$s: \mathbb {C}^r\otimes \mathbb {C}^r\to \mathbb {C}^r\otimes \mathbb {C}^r$
is defined by
 $s(u\otimes v)=v\otimes u$
for
$s(u\otimes v)=v\otimes u$
for
 $u,v\in \mathbb {C}^r$
.
$u,v\in \mathbb {C}^r$
.
-
• The Satake parameters of the unramified representations
 $\tau $
,
$\tau $
,
 $\sigma _m$
,
$\sigma _m$
,
 $\sigma _{n+1}$
will be denoted by
$\sigma _{n+1}$
will be denoted by
 $S_\tau $
,
$S_\tau $
,
 $S_m$
and
$S_m$
and
 $S_{n+1}$
, respectively. These are semisimple conjugacy classes in
$S_{n+1}$
, respectively. These are semisimple conjugacy classes in
 ${}^L G_r$
,
${}^L G_r$
,
 ${}^L U_m$
and
${}^L U_m$
and
 ${}^L U_{n+1}$
, and to simplify some arguments, we will choose representatives of them in
${}^L U_{n+1}$
, and to simplify some arguments, we will choose representatives of them in
 ${}^L T_r$
,
${}^L T_r$
,
 ${}^L T_m^U$
and
${}^L T_m^U$
and
 ${}^L T_{n+1}^U$
, respectively. Thus, denoting by
${}^L T_{n+1}^U$
, respectively. Thus, denoting by
 $Frob_v\in \operatorname {\mathrm {Gal}}(E/F)$
the Frobenius at v, we have We will also write
$Frob_v\in \operatorname {\mathrm {Gal}}(E/F)$
the Frobenius at v, we have We will also write $$ \begin{align*}S_\tau\in \widehat{T}_r Frob_v,\;\; S_m\in \widehat{T}^U_m Frob_v \; \mbox{ and }\; S_{n+1}\in \widehat{T}^U_{n+1}Frob_v.\end{align*} $$
$$ \begin{align*}S_\tau\in \widehat{T}_r Frob_v,\;\; S_m\in \widehat{T}^U_m Frob_v \; \mbox{ and }\; S_{n+1}\in \widehat{T}^U_{n+1}Frob_v.\end{align*} $$
 $S=(S_m,S_{n+1})\in {}^L T$
for the Satake parameter of
$S=(S_m,S_{n+1})\in {}^L T$
for the Satake parameter of
 $\sigma =\sigma _m\boxtimes \sigma _{n+1}$
.
$\sigma =\sigma _m\boxtimes \sigma _{n+1}$
.
By Shintani and Casselman-Shalika’s formula [Reference ShintaniShi76] [Reference Casselman and ShalikaCS80], we have
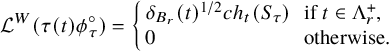 $$ \begin{align} \mathcal{L}^W(\tau(t)\phi_{\tau}^\circ)=\left\{\begin{array}{ll} \delta_{B_r}(t)^{1/2} ch_t(S_\tau) & \mbox{ if } t\in \Lambda_r^+, \\ 0 & \mbox{ otherwise.} \end{array} \right. \end{align} $$
$$ \begin{align} \mathcal{L}^W(\tau(t)\phi_{\tau}^\circ)=\left\{\begin{array}{ll} \delta_{B_r}(t)^{1/2} ch_t(S_\tau) & \mbox{ if } t\in \Lambda_r^+, \\ 0 & \mbox{ otherwise.} \end{array} \right. \end{align} $$
Moreover, according to the formulas given in [Reference KhouryKho08, Theorem 11.4], [Reference LiuLiu16, Proposition 6.4] and [Reference ZhangZha18], when
![]() $S\in {}^L T$
is regular, we have
$S\in {}^L T$
is regular, we have
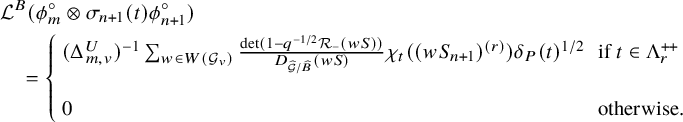 $$ \begin{align} & \mathcal{L}^B(\phi_{m}^\circ\otimes \sigma_{n+1}(t)\phi_{n+1}^\circ) \\ \nonumber & \quad = \left\{\begin{array}{ll} (\Delta_{m,v}^U)^{-1} \sum_{w\in W(\mathcal{G}_v)} \frac{\det(1-q^{-1/2} \mathcal{R}_-(wS))}{D_{\widehat{\mathcal{G}}/\widehat{B}}(wS)} \chi_{t}((wS_{n+1})^{(r)}) \delta_P(t)^{1/2} & \mbox{ if } t\in \Lambda_r^{++} \\ \\ 0 & \mbox{ otherwise.} \end{array} \right. \end{align} $$
$$ \begin{align} & \mathcal{L}^B(\phi_{m}^\circ\otimes \sigma_{n+1}(t)\phi_{n+1}^\circ) \\ \nonumber & \quad = \left\{\begin{array}{ll} (\Delta_{m,v}^U)^{-1} \sum_{w\in W(\mathcal{G}_v)} \frac{\det(1-q^{-1/2} \mathcal{R}_-(wS))}{D_{\widehat{\mathcal{G}}/\widehat{B}}(wS)} \chi_{t}((wS_{n+1})^{(r)}) \delta_P(t)^{1/2} & \mbox{ if } t\in \Lambda_r^{++} \\ \\ 0 & \mbox{ otherwise.} \end{array} \right. \end{align} $$
Moreover, the above sum over
![]() $W(\mathcal {G}_v)$
extends to a regular function on
$W(\mathcal {G}_v)$
extends to a regular function on
![]() ${}^L T$
, and the formula is still valid when we interpret the right-hand side in terms of this extension. We will now prove the formula of the proposition assuming that S is regular but, as it is an identity between rational functions, the extension to the non-regular case will follow.
${}^L T$
, and the formula is still valid when we interpret the right-hand side in terms of this extension. We will now prove the formula of the proposition assuming that S is regular but, as it is an identity between rational functions, the extension to the non-regular case will follow.
Lemma 8.7.2.2. For
![]() $t\in \Lambda _r^{++}$
, we have
$t\in \Lambda _r^{++}$
, we have
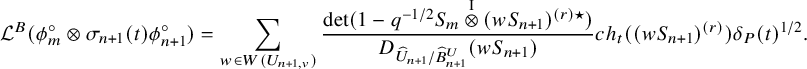 $$ \begin{align} \mathcal{L}^B(\phi_{m}^\circ\otimes \sigma_{n+1}(t)\phi_{n+1}^\circ)= \sum_{w\in W(U_{n+1,v})} \frac{\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})}{D_{\widehat{U}_{n+1}/\widehat{B}^U_{n+1}}(wS_{n+1})} ch_t((wS_{n+1})^{(r)}) \delta_P(t)^{1/2}. \end{align} $$
$$ \begin{align} \mathcal{L}^B(\phi_{m}^\circ\otimes \sigma_{n+1}(t)\phi_{n+1}^\circ)= \sum_{w\in W(U_{n+1,v})} \frac{\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})}{D_{\widehat{U}_{n+1}/\widehat{B}^U_{n+1}}(wS_{n+1})} ch_t((wS_{n+1})^{(r)}) \delta_P(t)^{1/2}. \end{align} $$
Proof. First, we note that the function
is invariant under the action of
![]() $W(L_{n+1,v})$
. Combining this with the identity (see Corollary A.0.2.2)
$W(L_{n+1,v})$
. Combining this with the identity (see Corollary A.0.2.2)
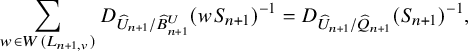 $$ \begin{align*}\sum_{w\in W(L_{n+1,v})} D_{\widehat{U}_{n+1}/\widehat{B}^U_{n+1}}(wS_{n+1})^{-1}=D_{\widehat{U}_{n+1}/\widehat{Q}_{n+1}}(S_{n+1})^{-1},\end{align*} $$
$$ \begin{align*}\sum_{w\in W(L_{n+1,v})} D_{\widehat{U}_{n+1}/\widehat{B}^U_{n+1}}(wS_{n+1})^{-1}=D_{\widehat{U}_{n+1}/\widehat{Q}_{n+1}}(S_{n+1})^{-1},\end{align*} $$
we see that the right-hand side of (8.7.2.5) can be rewritten as
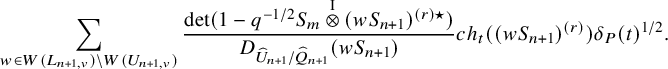 $$ \begin{align*}\sum_{w\in W(L_{n+1,v})\backslash W(U_{n+1,v})} \frac{\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})}{D_{\widehat{U}_{n+1}/\widehat{Q}_{n+1}}(wS_{n+1})} ch_t((wS_{n+1})^{(r)}) \delta_P(t)^{1/2}.\end{align*} $$
$$ \begin{align*}\sum_{w\in W(L_{n+1,v})\backslash W(U_{n+1,v})} \frac{\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})}{D_{\widehat{U}_{n+1}/\widehat{Q}_{n+1}}(wS_{n+1})} ch_t((wS_{n+1})^{(r)}) \delta_P(t)^{1/2}.\end{align*} $$
The natural projection
![]() $W(\mathcal {G}_v)\to W(U_{n+1,v})$
induces a bijection
$W(\mathcal {G}_v)\to W(U_{n+1,v})$
induces a bijection
and thus by (8.7.2.4), we just need to establish, for every regular
![]() $S=(S_m,S_{n+1})\in {}^L T$
and
$S=(S_m,S_{n+1})\in {}^L T$
and
![]() $t\in \Lambda _r$
, the identity
$t\in \Lambda _r$
, the identity
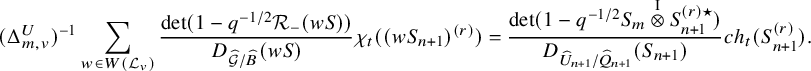 $$ \begin{align} (\Delta_{m,v}^U)^{-1} \sum_{w\in W(\mathcal{L}_v)} \frac{\det(1-q^{-1/2} \mathcal{R}_-(wS))}{D_{\widehat{\mathcal{G}}/\widehat{B}}(wS)} \chi_{t}((wS_{n+1})^{(r)})=\frac{\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} S_{n+1}^{(r)\star})}{D_{\widehat{U}_{n+1}/\widehat{Q}_{n+1}}(S_{n+1})} ch_t(S_{n+1}^{(r)}). \end{align} $$
$$ \begin{align} (\Delta_{m,v}^U)^{-1} \sum_{w\in W(\mathcal{L}_v)} \frac{\det(1-q^{-1/2} \mathcal{R}_-(wS))}{D_{\widehat{\mathcal{G}}/\widehat{B}}(wS)} \chi_{t}((wS_{n+1})^{(r)})=\frac{\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} S_{n+1}^{(r)\star})}{D_{\widehat{U}_{n+1}/\widehat{Q}_{n+1}}(S_{n+1})} ch_t(S_{n+1}^{(r)}). \end{align} $$
We have decompositions
and
This leads to the following expression for the left-hand side of (8.7.2.6):
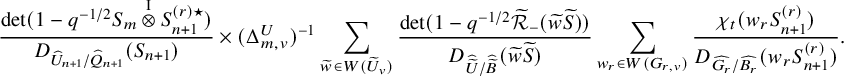 $$\begin{align*}\begin{aligned} & \frac{\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} S_{n+1}^{(r)\star})}{D_{\widehat{U}_{n+1}/\widehat{Q}_{n+1}}(S_{n+1})} \times (\Delta_{m,v}^U)^{-1} \sum_{\widetilde{w}\in W(\widetilde{U}_v)} \frac{\det(1-q^{-1/2} \widetilde{\mathcal{R}}_-(\widetilde{w}\widetilde{S}))}{D_{\widehat{\widetilde{U}}/\widehat{\widetilde{B}}}(\widetilde{w}\widetilde{S})} \sum_{w_r\in W(G_{r,v})} \frac{\chi_{t}(w_rS_{n+1}^{(r)})}{D_{\widehat{G_r}/\widehat{B_r}}(w_rS_{n+1}^{(r)})}. \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} & \frac{\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} S_{n+1}^{(r)\star})}{D_{\widehat{U}_{n+1}/\widehat{Q}_{n+1}}(S_{n+1})} \times (\Delta_{m,v}^U)^{-1} \sum_{\widetilde{w}\in W(\widetilde{U}_v)} \frac{\det(1-q^{-1/2} \widetilde{\mathcal{R}}_-(\widetilde{w}\widetilde{S}))}{D_{\widehat{\widetilde{U}}/\widehat{\widetilde{B}}}(\widetilde{w}\widetilde{S})} \sum_{w_r\in W(G_{r,v})} \frac{\chi_{t}(w_rS_{n+1}^{(r)})}{D_{\widehat{G_r}/\widehat{B_r}}(w_rS_{n+1}^{(r)})}. \end{aligned}\end{align*}$$
Furthermore, Weyl’s character formula implies (see Proposition A.0.2.1)
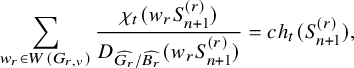 $$ \begin{align*}\sum_{w_r\in W(G_{r,v})} \frac{\chi_{t}(w_rS_{n+1}^{(r)})}{D_{\widehat{G_r}/\widehat{B_r}}(w_rS_{n+1}^{(r)})}=ch_t(S_{n+1}^{(r)}),\end{align*} $$
$$ \begin{align*}\sum_{w_r\in W(G_{r,v})} \frac{\chi_{t}(w_rS_{n+1}^{(r)})}{D_{\widehat{G_r}/\widehat{B_r}}(w_rS_{n+1}^{(r)})}=ch_t(S_{n+1}^{(r)}),\end{align*} $$
while, according to [Reference LiuLiu16, Proposition 6.4], we have
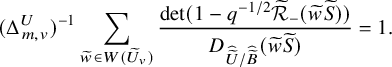 $$ \begin{align*}(\Delta_{m,v}^U)^{-1} \sum_{\widetilde{w}\in W(\widetilde{U}_v)} \frac{\det(1-q^{-1/2} \widetilde{\mathcal{R}}_-(\widetilde{w}\widetilde{S}))}{D_{\widehat{\widetilde{U}}/\widehat{\widetilde{B}}}(\widetilde{w}\widetilde{S})}=1.\end{align*} $$
$$ \begin{align*}(\Delta_{m,v}^U)^{-1} \sum_{\widetilde{w}\in W(\widetilde{U}_v)} \frac{\det(1-q^{-1/2} \widetilde{\mathcal{R}}_-(\widetilde{w}\widetilde{S}))}{D_{\widehat{\widetilde{U}}/\widehat{\widetilde{B}}}(\widetilde{w}\widetilde{S})}=1.\end{align*} $$
This shows the formula (8.7.2.6) and ends the proof of the lemma.
The next lemma is a consequence of the Cauchy identity [Reference BumpBum04, Theorem 43.3].
Lemma 8.7.2.3. Let
![]() $S_1,S_2\in \widehat {T_{r}}Frob_v$
. Then, for
$S_1,S_2\in \widehat {T_{r}}Frob_v$
. Then, for
![]() $\Re (s)$
sufficiently large, we have
$\Re (s)$
sufficiently large, we have
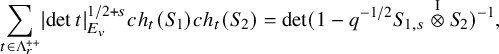 $$ \begin{align*}\sum_{t\in \Lambda_r^{++}} \lvert \det t\rvert_{E_v}^{1/2+s}ch_t(S_{1}) ch_t(S_2) =\det(1-q^{-1/2} S_{1,s}\overset{\mathrm{I}}{\otimes} S_{2})^{-1},\end{align*} $$
$$ \begin{align*}\sum_{t\in \Lambda_r^{++}} \lvert \det t\rvert_{E_v}^{1/2+s}ch_t(S_{1}) ch_t(S_2) =\det(1-q^{-1/2} S_{1,s}\overset{\mathrm{I}}{\otimes} S_{2})^{-1},\end{align*} $$
where we have set
![]() $S_{1,s}:=q^{-s}S_1$
$S_{1,s}:=q^{-s}S_1$
Combining the two above lemmas with (8.7.2.2), (8.7.2.3) as well as the identity
we obtain
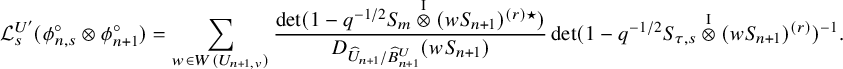 $$ \begin{align} \mathcal{L}_s^{U'}(\phi_{n,s}^\circ\otimes \phi_{n+1}^\circ) =\sum_{w\in W(U_{n+1,v})} \frac{\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})}{D_{\widehat{U}_{n+1}/\widehat{B}^U_{n+1}}(wS_{n+1})} \det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)})^{-1}. \end{align} $$
$$ \begin{align} \mathcal{L}_s^{U'}(\phi_{n,s}^\circ\otimes \phi_{n+1}^\circ) =\sum_{w\in W(U_{n+1,v})} \frac{\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})}{D_{\widehat{U}_{n+1}/\widehat{B}^U_{n+1}}(wS_{n+1})} \det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)})^{-1}. \end{align} $$
For every
![]() $w\in W(U_{n+1,v})$
, we have the identity
$w\in W(U_{n+1,v})$
, we have the identity
It follows that
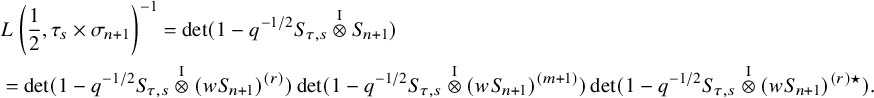 $$ \begin{align*} & L\left(\frac{1}{2},\tau_s\times \sigma_{n+1}\right)^{-1}=\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} S_{n+1}) \\ & =\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)})\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(m+1)})\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star}). \end{align*} $$
$$ \begin{align*} & L\left(\frac{1}{2},\tau_s\times \sigma_{n+1}\right)^{-1}=\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} S_{n+1}) \\ & =\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)})\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(m+1)})\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star}). \end{align*} $$
Thus, (8.7.2.7) can be rewritten as
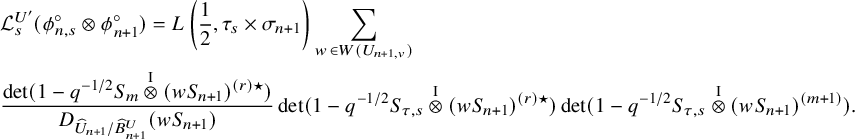 $$ \begin{align*} & \mathcal{L}_s^{U'}(\phi_{n,s}^\circ\otimes \phi_{n+1}^\circ) = L\left(\frac{1}{2},\tau_s\times \sigma_{n+1}\right) \sum_{w\in W(U_{n+1,v})}\\ \nonumber & \frac{\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})}{D_{\widehat{U}_{n+1}/\widehat{B}^U_{n+1}}(wS_{n+1})} \det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(m+1)}). \end{align*} $$
$$ \begin{align*} & \mathcal{L}_s^{U'}(\phi_{n,s}^\circ\otimes \phi_{n+1}^\circ) = L\left(\frac{1}{2},\tau_s\times \sigma_{n+1}\right) \sum_{w\in W(U_{n+1,v})}\\ \nonumber & \frac{\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})}{D_{\widehat{U}_{n+1}/\widehat{B}^U_{n+1}}(wS_{n+1})} \det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(m+1)}). \end{align*} $$
Since we have
we see that the proposition is now reduced to the equality
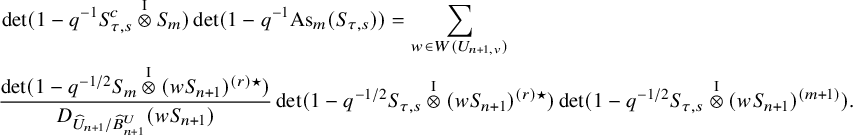 $$ \begin{align} & \det(1-q^{-1}S^c_{\tau,s}\overset{\mathrm{I}}{\otimes} S_m)\det(1-q^{-1}\mathrm{As}_m(S_{\tau,s}))=\sum_{w\in W(U_{n+1,v})} \\ \nonumber & \frac{\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})}{D_{\widehat{U}_{n+1}/\widehat{B}^U_{n+1}}(wS_{n+1})} \det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(m+1)}). \end{align} $$
$$ \begin{align} & \det(1-q^{-1}S^c_{\tau,s}\overset{\mathrm{I}}{\otimes} S_m)\det(1-q^{-1}\mathrm{As}_m(S_{\tau,s}))=\sum_{w\in W(U_{n+1,v})} \\ \nonumber & \frac{\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})}{D_{\widehat{U}_{n+1}/\widehat{B}^U_{n+1}}(wS_{n+1})} \det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(m+1)}). \end{align} $$
To prove the above identity, we first show that the right-hand side of (8.7.2.8) considered as a function of the regular element
![]() $S_{n+1}\in \widehat {T}_{n+1}^U Frob_v$
is constant. For this, we first note that the function
$S_{n+1}\in \widehat {T}_{n+1}^U Frob_v$
is constant. For this, we first note that the function
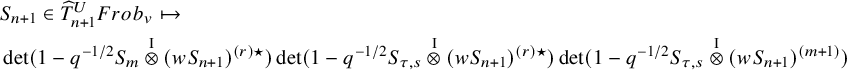 $$ \begin{align*} & S_{n+1}\in \widehat{T}_{n+1}^U Frob_v\mapsto \\ &\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(m+1)}) \end{align*} $$
$$ \begin{align*} & S_{n+1}\in \widehat{T}_{n+1}^U Frob_v\mapsto \\ &\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(m+1)}) \end{align*} $$
is (the restriction of) a linear combination of characters of
![]() ${}^L T_{n+1}^U$
. Thus, by Proposition A.0.2.1, it suffices to check that for every character
${}^L T_{n+1}^U$
. Thus, by Proposition A.0.2.1, it suffices to check that for every character
![]() $\chi $
appearing in this linear combination the sum
$\chi $
appearing in this linear combination the sum
![]() $\rho +\chi \mid _{\widehat {T}_{n+1}^U}$
, where
$\rho +\chi \mid _{\widehat {T}_{n+1}^U}$
, where
![]() $\rho \in X^*(\widehat {T}_{n+1}^U)$
stands for the half-sum of positive roots (with respect to
$\rho \in X^*(\widehat {T}_{n+1}^U)$
stands for the half-sum of positive roots (with respect to
![]() $\widehat {B}_{n+1}^U$
), is either singular or conjugate, under the full Weyl group of
$\widehat {B}_{n+1}^U$
), is either singular or conjugate, under the full Weyl group of
![]() $(\widehat {U}_{n+1},\widehat {T}_{n+1}^U)$
, to
$(\widehat {U}_{n+1},\widehat {T}_{n+1}^U)$
, to
![]() $\rho $
. Let
$\rho $
. Let
![]() $\chi $
be such a character. Using the natural isomorphism
$\chi $
be such a character. Using the natural isomorphism
![]() $X^*(\widehat {T}_{n+1}^U)\simeq \mathbb {Z}^{n+1}$
, we have
$X^*(\widehat {T}_{n+1}^U)\simeq \mathbb {Z}^{n+1}$
, we have
![]() $\chi \mid _{\widehat {T}_{n+1}^U}=(\lambda _1,\ldots ,\lambda _{n+1})$
, where the
$\chi \mid _{\widehat {T}_{n+1}^U}=(\lambda _1,\ldots ,\lambda _{n+1})$
, where the
![]() $\lambda _i$
’s are integers satisfying
$\lambda _i$
’s are integers satisfying
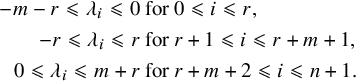 $$ \begin{align*} -m-r\leqslant \lambda_i\leqslant 0 &\text{ for } 0\leqslant i\leqslant r,\;\\ -r\leqslant \lambda_i\leqslant r &\text{ for } r+1\leqslant i\leqslant r+m+1,\; \\ 0\leqslant \lambda_i\leqslant m+r &\text{ for } r+m+2\leqslant i\leqslant n+1. \end{align*} $$
$$ \begin{align*} -m-r\leqslant \lambda_i\leqslant 0 &\text{ for } 0\leqslant i\leqslant r,\;\\ -r\leqslant \lambda_i\leqslant r &\text{ for } r+1\leqslant i\leqslant r+m+1,\; \\ 0\leqslant \lambda_i\leqslant m+r &\text{ for } r+m+2\leqslant i\leqslant n+1. \end{align*} $$
Furthermore, we have
![]() $\rho =(\frac {n}{2},\frac {n-2}{2},\ldots , -\frac {n}{2})$
, and from the above inequality, we see that the coordinates of
$\rho =(\frac {n}{2},\frac {n-2}{2},\ldots , -\frac {n}{2})$
, and from the above inequality, we see that the coordinates of
![]() $\rho +\chi \mid _{\widehat {T}_{n+1}^U}$
are all integers or half-integers between
$\rho +\chi \mid _{\widehat {T}_{n+1}^U}$
are all integers or half-integers between
![]() $-\frac {n}{2}$
and
$-\frac {n}{2}$
and
![]() $\frac {n}{2}$
. The claim about
$\frac {n}{2}$
. The claim about
![]() $\chi \mid _{\widehat {T}_{n+1}^U}+\rho $
readily follows, and we therefore deduce that the right-hand side of (8.7.2.8) is indeed independent of
$\chi \mid _{\widehat {T}_{n+1}^U}+\rho $
readily follows, and we therefore deduce that the right-hand side of (8.7.2.8) is indeed independent of
![]() $S_{n+1}$
.
$S_{n+1}$
.
Let
![]() $A,B\in \mathrm {GL}_r(\mathbb {C})$
be such that
$A,B\in \mathrm {GL}_r(\mathbb {C})$
be such that
![]() $S_{\tau ,s}=(A,B)Frob_v$
. Then, plugging
$S_{\tau ,s}=(A,B)Frob_v$
. Then, plugging
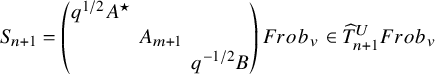 $$ \begin{align*}S_{n+1}=\begin{pmatrix}q^{1/2}A^\star & & \\ & A_{m+1} & \\ & & q^{-1/2} B \end{pmatrix} Frob_v\in \widehat{T}_{n+1}^U Frob_v\end{align*} $$
$$ \begin{align*}S_{n+1}=\begin{pmatrix}q^{1/2}A^\star & & \\ & A_{m+1} & \\ & & q^{-1/2} B \end{pmatrix} Frob_v\in \widehat{T}_{n+1}^U Frob_v\end{align*} $$
in the right-hand side of (8.7.2.8), where the matrix
![]() $A_{m+1}\in \mathrm {GL}_{m+1}(\mathbb {C})$
is chosen such that
$A_{m+1}\in \mathrm {GL}_{m+1}(\mathbb {C})$
is chosen such that
![]() $S_{n+1}$
is regular, the term indexed by
$S_{n+1}$
is regular, the term indexed by
![]() $w\in W(U_{n+1,v})$
is nonzero only when
$w\in W(U_{n+1,v})$
is nonzero only when
![]() $w\in W(L_{n+1,v})$
. It follows that this sum equals
$w\in W(L_{n+1,v})$
. It follows that this sum equals
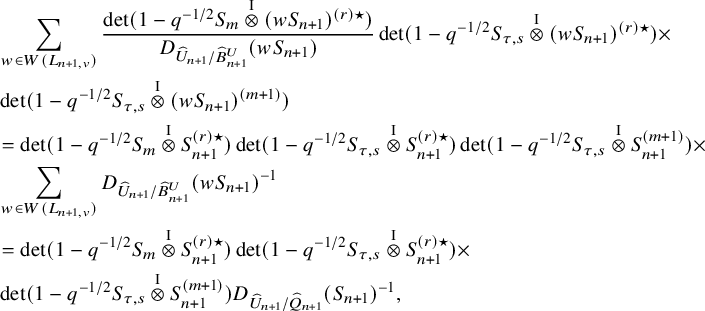 $$ \begin{align*} & \sum_{w\in W(L_{n+1,v})} \frac{\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})}{D_{\widehat{U}_{n+1}/\widehat{B}^U_{n+1}}(wS_{n+1})} \det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})\times\\ &\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(m+1)}) \\ &=\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} S_{n+1}^{(r)\star})\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} S_{n+1}^{(r)\star})\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} S_{n+1}^{(m+1)}) \times\\ &\sum_{w\in W(L_{n+1,v})} D_{\widehat{U}_{n+1}/\widehat{B}^U_{n+1}}(wS_{n+1})^{-1} \\ & =\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} S_{n+1}^{(r)\star})\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} S_{n+1}^{(r)\star})\times\\ &\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} S_{n+1}^{(m+1)}) D_{\widehat{U}_{n+1}/\widehat{Q}_{n+1}}(S_{n+1})^{-1}, \end{align*} $$
$$ \begin{align*} & \sum_{w\in W(L_{n+1,v})} \frac{\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})}{D_{\widehat{U}_{n+1}/\widehat{B}^U_{n+1}}(wS_{n+1})} \det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(r)\star})\times\\ &\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} (wS_{n+1})^{(m+1)}) \\ &=\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} S_{n+1}^{(r)\star})\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} S_{n+1}^{(r)\star})\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} S_{n+1}^{(m+1)}) \times\\ &\sum_{w\in W(L_{n+1,v})} D_{\widehat{U}_{n+1}/\widehat{B}^U_{n+1}}(wS_{n+1})^{-1} \\ & =\det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} S_{n+1}^{(r)\star})\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} S_{n+1}^{(r)\star})\times\\ &\det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} S_{n+1}^{(m+1)}) D_{\widehat{U}_{n+1}/\widehat{Q}_{n+1}}(S_{n+1})^{-1}, \end{align*} $$
where the last equality follows from Corollary A.0.2.2. By direct computation, we have
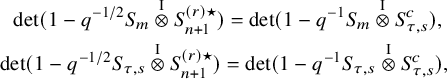 $$ \begin{align*} \det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} S_{n+1}^{(r)\star})=\det(1-q^{-1}S_m\overset{\mathrm{I}}{\otimes} S_{\tau,s}^c),\; \\ \det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} S_{n+1}^{(r)\star})=\det(1-q^{-1} S_{\tau,s}\overset{\mathrm{I}}{\otimes} S_{\tau,s}^c), \end{align*} $$
$$ \begin{align*} \det(1-q^{-1/2} S_m\overset{\mathrm{I}}{\otimes} S_{n+1}^{(r)\star})=\det(1-q^{-1}S_m\overset{\mathrm{I}}{\otimes} S_{\tau,s}^c),\; \\ \det(1-q^{-1/2} S_{\tau,s}\overset{\mathrm{I}}{\otimes} S_{n+1}^{(r)\star})=\det(1-q^{-1} S_{\tau,s}\overset{\mathrm{I}}{\otimes} S_{\tau,s}^c), \end{align*} $$
where we have set
![]() $S_{m+1}=A_{m+1}Frob_v\in \widehat {T}_{m+1}^U Frob_v$
. Since
$S_{m+1}=A_{m+1}Frob_v\in \widehat {T}_{m+1}^U Frob_v$
. Since
![]() $S_{\tau ,s}\overset {\mathrm {I}}{\otimes } S_{\tau ,s}^c=\mathrm {As}_m(S_{\tau ,s})\oplus \mathrm {As}_{m+1}(S_{\tau ,s})$
, this concludes the proof of (8.7.2.8) and therefore of the proposition.
$S_{\tau ,s}\overset {\mathrm {I}}{\otimes } S_{\tau ,s}^c=\mathrm {As}_m(S_{\tau ,s})\oplus \mathrm {As}_{m+1}(S_{\tau ,s})$
, this concludes the proof of (8.7.2.8) and therefore of the proposition.
8.8 Reduction to the corank one case
8.8.1
In this subsection, we let
-
•
 $\sigma _m$
and
$\sigma _m$
and
 $\sigma _{n+1}$
be cuspidal automorphic representations of
$\sigma _{n+1}$
be cuspidal automorphic representations of
 $U_m(\mathbb {A})$
and
$U_m(\mathbb {A})$
and
 $U_{n+1}(\mathbb {A})$
, respectively;
$U_{n+1}(\mathbb {A})$
, respectively; -
•
 $\tau $
be an irreducible automorphic representation of
$\tau $
be an irreducible automorphic representation of
 $G_r(\mathbb {A})$
that is induced from a unitary cuspidal representation, meaning that there exist a parabolic subgroup
$G_r(\mathbb {A})$
that is induced from a unitary cuspidal representation, meaning that there exist a parabolic subgroup
 $R=MN_R\subset G_r$
as well as a unitary cuspidal automorphic representation
$R=MN_R\subset G_r$
as well as a unitary cuspidal automorphic representation
 $\kappa $
of
$\kappa $
of
 $M(\mathbb {A})$
such that
$M(\mathbb {A})$
such that  $$ \begin{align*}\tau=\{E_R^{G_r}(\phi,0)\mid \phi\in I_{R(\mathbb{A})}^{G_r(\mathbb{A})}(\kappa) \}.\end{align*} $$
$$ \begin{align*}\tau=\{E_R^{G_r}(\phi,0)\mid \phi\in I_{R(\mathbb{A})}^{G_r(\mathbb{A})}(\kappa) \}.\end{align*} $$
Moreover, we henceforth identify
![]() $\mathcal {A}_{Q_n,\tau \boxtimes \sigma _m}(U_n)$
with the parabolic induction
$\mathcal {A}_{Q_n,\tau \boxtimes \sigma _m}(U_n)$
with the parabolic induction
![]() $\sigma _n:=I_{Q_n(\mathbb {A})}^{U_n(\mathbb {A})}(\tau \boxtimes \sigma _m)$
so that for
$\sigma _n:=I_{Q_n(\mathbb {A})}^{U_n(\mathbb {A})}(\tau \boxtimes \sigma _m)$
so that for
![]() $\phi _n \in \sigma _n$
and any
$\phi _n \in \sigma _n$
and any
![]() $s\in \mathbb {C}$
, we have
$s\in \mathbb {C}$
, we have
![]() $\phi _{n,s}\in \sigma _{n,s}:=I_{Q_n(\mathbb {A})}^{U_n(\mathbb {A})}(\tau _s\boxtimes \sigma _m)$
. Then, by Proposition 8.5.1.1 and Proposition 8.7.2.1, for
$\phi _{n,s}\in \sigma _{n,s}:=I_{Q_n(\mathbb {A})}^{U_n(\mathbb {A})}(\tau _s\boxtimes \sigma _m)$
. Then, by Proposition 8.5.1.1 and Proposition 8.7.2.1, for
![]() $\phi _n\in \sigma _n$
and
$\phi _n\in \sigma _n$
and
![]() $\phi _{n+1}\in \sigma _{n+1}$
, we have
$\phi _{n+1}\in \sigma _{n+1}$
, we have
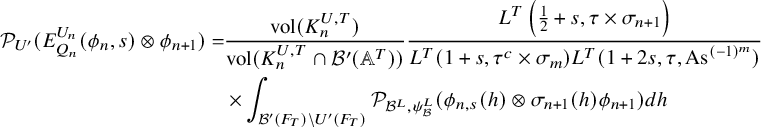 $$ \begin{align} \mathcal{P}_{U'}(E_{Q_n}^{U_n}(\phi_n,s)\otimes \phi_{n+1})= & \frac{\operatorname{\mathrm{vol}}(K_n^{U,T})}{\operatorname{\mathrm{vol}}(K_n^{U,T}\cap \mathcal{B}'(\mathbb{A}^T))}\frac{L^T\left(\frac{1}{2}+s,\tau\times \sigma_{n+1}\right)}{L^T(1+s,\tau^c\times \sigma_m) L^T(1+2s,\tau,\mathrm{As}^{(-1)^m})} \\ \nonumber & \times \int_{\mathcal{B}'(F_T)\backslash U'(F_T)} \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}}}(\phi_{n,s}(h)\otimes \sigma_{n+1}(h)\phi_{n+1})dh \end{align} $$
$$ \begin{align} \mathcal{P}_{U'}(E_{Q_n}^{U_n}(\phi_n,s)\otimes \phi_{n+1})= & \frac{\operatorname{\mathrm{vol}}(K_n^{U,T})}{\operatorname{\mathrm{vol}}(K_n^{U,T}\cap \mathcal{B}'(\mathbb{A}^T))}\frac{L^T\left(\frac{1}{2}+s,\tau\times \sigma_{n+1}\right)}{L^T(1+s,\tau^c\times \sigma_m) L^T(1+2s,\tau,\mathrm{As}^{(-1)^m})} \\ \nonumber & \times \int_{\mathcal{B}'(F_T)\backslash U'(F_T)} \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}}}(\phi_{n,s}(h)\otimes \sigma_{n+1}(h)\phi_{n+1})dh \end{align} $$
for
![]() $\Re (s)\gg 0$
and where
$\Re (s)\gg 0$
and where
![]() $T\supset S$
is any sufficiently large finite set of places such that
$T\supset S$
is any sufficiently large finite set of places such that
![]() $\phi _n$
is
$\phi _n$
is
![]() $K_n^{U,T}$
-invariant and
$K_n^{U,T}$
-invariant and
![]() $\phi _{n+1}$
is
$\phi _{n+1}$
is
![]() $K_{n+1}^{U,T}$
-invariant.
$K_{n+1}^{U,T}$
-invariant.
8.8.2
Proposition 8.8.2.1. The following are equivalent:
-
1. There exist
 $\phi _m\in \sigma _m$
and
$\phi _m\in \sigma _m$
and
 $\phi _{n+1}\in \sigma _{n+1}$
such that
$\phi _{n+1}\in \sigma _{n+1}$
such that
 $\mathcal {P}_{\mathcal {B},\psi _{\mathcal {B}}}(\phi _m\otimes \phi _{n+1})\neq 0$
;
$\mathcal {P}_{\mathcal {B},\psi _{\mathcal {B}}}(\phi _m\otimes \phi _{n+1})\neq 0$
; -
2. There exist
 $\phi _n\in \sigma _n$
,
$\phi _n\in \sigma _n$
,
 $\phi _{n+1}\in \sigma _{n+1}$
and
$\phi _{n+1}\in \sigma _{n+1}$
and
 $s\in \mathbb {C}$
such that
$s\in \mathbb {C}$
such that
 $E_{Q_n}^{U_n}(\phi _n,.)$
has no pole at s and
$E_{Q_n}^{U_n}(\phi _n,.)$
has no pole at s and
 $\mathcal {P}_{U'}(E_{Q_n}^{U_n}(\phi _n,s)\otimes \phi _{n+1})\neq 0$
.
$\mathcal {P}_{U'}(E_{Q_n}^{U_n}(\phi _n,s)\otimes \phi _{n+1})\neq 0$
.
Proof. First, we remark that since there exists
![]() $\phi _{\tau }\in \tau $
whose Whittaker period
$\phi _{\tau }\in \tau $
whose Whittaker period
![]() $\int _{[N_r]} \phi _{\tau }(u)\psi _{-r}(u)du$
is nonzero, assertion 1 is equivalent to the nonvanishing of
$\int _{[N_r]} \phi _{\tau }(u)\psi _{-r}(u)du$
is nonzero, assertion 1 is equivalent to the nonvanishing of
![]() $\mathcal {P}_{\mathcal {B}^L,\psi ^L_{\mathcal {B}}}$
on
$\mathcal {P}_{\mathcal {B}^L,\psi ^L_{\mathcal {B}}}$
on
![]() $\tau \boxtimes \sigma _m\boxtimes \sigma _{n+1}$
. Then, the equivalence
$\tau \boxtimes \sigma _m\boxtimes \sigma _{n+1}$
. Then, the equivalence
![]() $2.\Leftrightarrow 1.$
follows from (8.8.1.1) and the last part of Proposition 8.6.1.1.
$2.\Leftrightarrow 1.$
follows from (8.8.1.1) and the last part of Proposition 8.6.1.1.
8.8.3
Choose isomorphisms
![]() $\tau \simeq \bigotimes _v^{\prime } \tau _v$
,
$\tau \simeq \bigotimes _v^{\prime } \tau _v$
,
![]() $\sigma _m\simeq \bigotimes _v^{\prime } \sigma _{m,v}$
and
$\sigma _m\simeq \bigotimes _v^{\prime } \sigma _{m,v}$
and
![]() $\sigma _{n+1}\simeq \bigotimes ^{\prime }_v \sigma _{n+1,v}$
. This induces an isomorphism
$\sigma _{n+1}\simeq \bigotimes ^{\prime }_v \sigma _{n+1,v}$
. This induces an isomorphism
![]() $\sigma _n\simeq \bigotimes _v^{\prime } \sigma _{n,v}$
, where
$\sigma _n\simeq \bigotimes _v^{\prime } \sigma _{n,v}$
, where
![]() $\sigma _{n,v}:= I_{Q_n(F_v)}^{U_n(F_v)}(\tau _v\boxtimes \sigma _{m,v})$
. We assume henceforth that for every place v, the representations
$\sigma _{n,v}:= I_{Q_n(F_v)}^{U_n(F_v)}(\tau _v\boxtimes \sigma _{m,v})$
. We assume henceforth that for every place v, the representations
![]() $\tau _v$
,
$\tau _v$
,
![]() $\sigma _{m,v}$
and
$\sigma _{m,v}$
and
![]() $\sigma _{n+1,v}$
are all tempered. Let
$\sigma _{n+1,v}$
are all tempered. Let
![]() $\phi _\tau \in \tau $
,
$\phi _\tau \in \tau $
,
![]() $\phi _m\in \sigma _m$
,
$\phi _m\in \sigma _m$
,
![]() $\phi _n\in \sigma _n$
and
$\phi _n\in \sigma _n$
and
![]() $\phi _{n+1}\in \sigma _{n+1}$
be factorizable vectors – that is,
$\phi _{n+1}\in \sigma _{n+1}$
be factorizable vectors – that is,
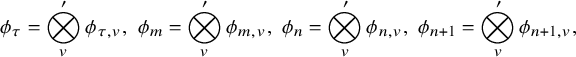 $$ \begin{align*}\phi_\tau=\bigotimes_v^{\prime} \phi_{\tau,v},\; \phi_m=\bigotimes^{\prime}_v \phi_{m,v},\; \phi_n=\bigotimes_v^{\prime} \phi_{n,v},\; \phi_{n+1}=\bigotimes_v^{\prime} \phi_{n+1,v},\end{align*} $$
$$ \begin{align*}\phi_\tau=\bigotimes_v^{\prime} \phi_{\tau,v},\; \phi_m=\bigotimes^{\prime}_v \phi_{m,v},\; \phi_n=\bigotimes_v^{\prime} \phi_{n,v},\; \phi_{n+1}=\bigotimes_v^{\prime} \phi_{n+1,v},\end{align*} $$
where
![]() $\phi _{\tau ,v}\in \tau _v$
,
$\phi _{\tau ,v}\in \tau _v$
,
![]() $\phi _{m,v}\in \sigma _{m,v}$
,
$\phi _{m,v}\in \sigma _{m,v}$
,
![]() $\phi _{n,v}\in \sigma _{n,v}$
and
$\phi _{n,v}\in \sigma _{n,v}$
and
![]() $\phi _{n+1,v}\in \sigma _{n+1,v}$
.
$\phi _{n+1,v}\in \sigma _{n+1,v}$
.
We equip
![]() $\sigma _m$
,
$\sigma _m$
,
![]() $\sigma _{n+1}$
,
$\sigma _{n+1}$
,
![]() $\tau $
and
$\tau $
and
![]() $\sigma _n$
with invariant inner products as follows:
$\sigma _n$
with invariant inner products as follows:
-
• We endow
 $\sigma _m$
,
$\sigma _m$
,
 $\sigma _{n+1}$
with the Petersson inner products
$\sigma _{n+1}$
with the Petersson inner products
 $\langle .,.\rangle _{Pet}$
(i.e., the
$\langle .,.\rangle _{Pet}$
(i.e., the
 $L^2$
inner products with respect to the Tamagawa measures on
$L^2$
inner products with respect to the Tamagawa measures on
 $[U_m]$
and
$[U_m]$
and
 $[U_{n+1}]$
, respectively).
$[U_{n+1}]$
, respectively). -
• On
 $\tau $
, we put the inner product defined by for
$\tau $
, we put the inner product defined by for $$ \begin{align*}\langle E_R^{G_r}(\phi,0), E_R^{G_r}(\phi',0)\rangle_\tau=\int_{R(\mathbb{A})\backslash G_r(\mathbb{A})} \int_{[M]^1} \phi(mg) \overline{\phi'(mg)} dm dg\end{align*} $$
$$ \begin{align*}\langle E_R^{G_r}(\phi,0), E_R^{G_r}(\phi',0)\rangle_\tau=\int_{R(\mathbb{A})\backslash G_r(\mathbb{A})} \int_{[M]^1} \phi(mg) \overline{\phi'(mg)} dm dg\end{align*} $$
 $\phi ,\phi '\in I_{R(\mathbb {A})}^{G_r(\mathbb {A})}(\kappa )$
.
$\phi ,\phi '\in I_{R(\mathbb {A})}^{G_r(\mathbb {A})}(\kappa )$
.
-
•
 $\sigma _n$
is equipped with the inner product induced from that on
$\sigma _n$
is equipped with the inner product induced from that on
 $\tau \boxtimes \sigma _m$
, here denoted
$\tau \boxtimes \sigma _m$
, here denoted
 $\langle .,.\rangle _{\tau \boxtimes \sigma _m}$
; that is,
$\langle .,.\rangle _{\tau \boxtimes \sigma _m}$
; that is,  $$ \begin{align*}\langle \phi,\phi'\rangle_{\sigma_n}=\int_{Q_n(\mathbb{A})\backslash U_n(\mathbb{A})} \langle \phi(g),\phi'(g)\rangle_{\tau\boxtimes \sigma_m} dg,\mbox{ for } \phi,\phi'\in \sigma_n.\end{align*} $$
$$ \begin{align*}\langle \phi,\phi'\rangle_{\sigma_n}=\int_{Q_n(\mathbb{A})\backslash U_n(\mathbb{A})} \langle \phi(g),\phi'(g)\rangle_{\tau\boxtimes \sigma_m} dg,\mbox{ for } \phi,\phi'\in \sigma_n.\end{align*} $$
We also fix factorizations of these inner products on
![]() $\sigma _{m}$
,
$\sigma _{m}$
,
![]() $\sigma _{n+1}$
,
$\sigma _{n+1}$
,
![]() $\tau $
and
$\tau $
and
![]() $\sigma _n$
into local invariant inner products. Following Section 8.4, this allows to define, for every place v of F, local periods
$\sigma _n$
into local invariant inner products. Following Section 8.4, this allows to define, for every place v of F, local periods
![]() $\mathcal {P}_{U',v}$
,
$\mathcal {P}_{U',v}$
,
![]() $\mathcal {P}_{\mathcal {B},\psi _{\mathcal {B}},v}$
,
$\mathcal {P}_{\mathcal {B},\psi _{\mathcal {B}},v}$
,
![]() $\mathcal {P}_{N_r,\psi _{-r},v}$
and
$\mathcal {P}_{N_r,\psi _{-r},v}$
and
![]() $\mathcal {P}_{\mathcal {B}^L,\psi ^L_{\mathcal {B}},v}$
on
$\mathcal {P}_{\mathcal {B}^L,\psi ^L_{\mathcal {B}},v}$
on
![]() $\sigma _{n,v}\boxtimes \sigma _{n+1,v}$
,
$\sigma _{n,v}\boxtimes \sigma _{n+1,v}$
,
![]() $\sigma _{m,v}\boxtimes \sigma _{n,v}$
,
$\sigma _{m,v}\boxtimes \sigma _{n,v}$
,
![]() $\tau _v$
and
$\tau _v$
and
![]() $\tau _v\boxtimes \sigma _{m,v}\boxtimes \sigma _{n+1,v}$
, respectively. Furthermore, for almost all v, we have
$\tau _v\boxtimes \sigma _{m,v}\boxtimes \sigma _{n+1,v}$
, respectively. Furthermore, for almost all v, we have
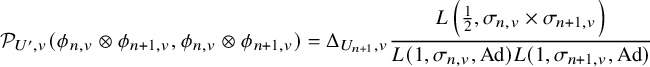 $$\begin{align*}\begin{aligned} \mathcal{P}_{U',v}(\phi_{n,v}\otimes \phi_{n+1,v},\phi_{n,v}\otimes \phi_{n+1,v})=\Delta_{U_{n+1},v} \frac{L\left(\frac{1}{2},\sigma_{n,v}\times \sigma_{n+1,v}\right)}{L(1,\sigma_{n,v},\operatorname{\mathrm{Ad}})L(1,\sigma_{n+1,v},\operatorname{\mathrm{Ad}})} \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} \mathcal{P}_{U',v}(\phi_{n,v}\otimes \phi_{n+1,v},\phi_{n,v}\otimes \phi_{n+1,v})=\Delta_{U_{n+1},v} \frac{L\left(\frac{1}{2},\sigma_{n,v}\times \sigma_{n+1,v}\right)}{L(1,\sigma_{n,v},\operatorname{\mathrm{Ad}})L(1,\sigma_{n+1,v},\operatorname{\mathrm{Ad}})} \end{aligned}\end{align*}$$
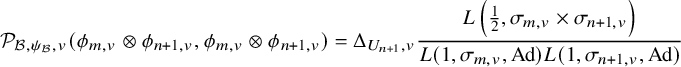 $$ \begin{align*} \mathcal{P}_{\mathcal{B},\psi_{\mathcal{B}},v}(\phi_{m,v}\otimes \phi_{n+1,v},\phi_{m,v}\otimes \phi_{n+1,v})=\Delta_{U_{n+1},v} \frac{L\left(\frac{1}{2},\sigma_{m,v}\times \sigma_{n+1,v}\right)}{L(1,\sigma_{m,v},\operatorname{\mathrm{Ad}})L(1,\sigma_{n+1,v},\operatorname{\mathrm{Ad}})} \end{align*} $$
$$ \begin{align*} \mathcal{P}_{\mathcal{B},\psi_{\mathcal{B}},v}(\phi_{m,v}\otimes \phi_{n+1,v},\phi_{m,v}\otimes \phi_{n+1,v})=\Delta_{U_{n+1},v} \frac{L\left(\frac{1}{2},\sigma_{m,v}\times \sigma_{n+1,v}\right)}{L(1,\sigma_{m,v},\operatorname{\mathrm{Ad}})L(1,\sigma_{n+1,v},\operatorname{\mathrm{Ad}})} \end{align*} $$
where we have set
![]() $\Delta _{U_{n+1},v}=\prod _{i=1}^{n+1} L(i,\eta _{E/F,v}^i)$
and
$\Delta _{U_{n+1},v}=\prod _{i=1}^{n+1} L(i,\eta _{E/F,v}^i)$
and
![]() $\Delta _{G_r,v}=\prod _{i=1}^r \zeta _{E_v}(i)$
. Note that the last two equalities above imply that
$\Delta _{G_r,v}=\prod _{i=1}^r \zeta _{E_v}(i)$
. Note that the last two equalities above imply that
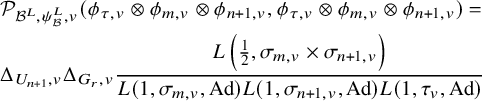 $$\begin{align*}\begin{aligned} & \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}},v}(\phi_{\tau,v}\otimes \phi_{m,v}\otimes \phi_{n+1,v},\phi_{\tau,v}\otimes \phi_{m,v}\otimes \phi_{n+1,v})= \\ & \Delta_{U_{n+1},v} \Delta_{G_r,v} \frac{L\left(\frac{1}{2},\sigma_{m,v}\times \sigma_{n+1,v}\right)}{L(1,\sigma_{m,v},\operatorname{\mathrm{Ad}})L(1,\sigma_{n+1,v},\operatorname{\mathrm{Ad}})L(1,\tau_{v},\operatorname{\mathrm{Ad}})} \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} & \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}},v}(\phi_{\tau,v}\otimes \phi_{m,v}\otimes \phi_{n+1,v},\phi_{\tau,v}\otimes \phi_{m,v}\otimes \phi_{n+1,v})= \\ & \Delta_{U_{n+1},v} \Delta_{G_r,v} \frac{L\left(\frac{1}{2},\sigma_{m,v}\times \sigma_{n+1,v}\right)}{L(1,\sigma_{m,v},\operatorname{\mathrm{Ad}})L(1,\sigma_{n+1,v},\operatorname{\mathrm{Ad}})L(1,\tau_{v},\operatorname{\mathrm{Ad}})} \end{aligned}\end{align*}$$
for almost all v. Given all these identities, it makes sense to define
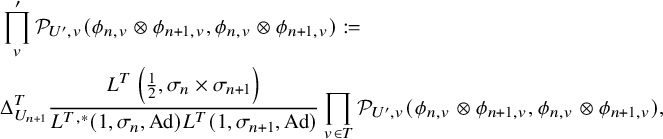 $$\begin{align*}\begin{aligned} & \prod_v^{\prime} \mathcal{P}_{U',v}(\phi_{n,v}\otimes \phi_{n+1,v},\phi_{n,v}\otimes \phi_{n+1,v}):= \\ & \Delta^T_{U_{n+1}} \frac{L^T\left(\frac{1}{2},\sigma_{n}\times \sigma_{n+1}\right)}{L^{T,*}(1,\sigma_{n},\operatorname{\mathrm{Ad}})L^T(1,\sigma_{n+1},\operatorname{\mathrm{Ad}})} \prod_{v\in T} \mathcal{P}_{U',v}(\phi_{n,v}\otimes \phi_{n+1,v},\phi_{n,v}\otimes \phi_{n+1,v}), \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} & \prod_v^{\prime} \mathcal{P}_{U',v}(\phi_{n,v}\otimes \phi_{n+1,v},\phi_{n,v}\otimes \phi_{n+1,v}):= \\ & \Delta^T_{U_{n+1}} \frac{L^T\left(\frac{1}{2},\sigma_{n}\times \sigma_{n+1}\right)}{L^{T,*}(1,\sigma_{n},\operatorname{\mathrm{Ad}})L^T(1,\sigma_{n+1},\operatorname{\mathrm{Ad}})} \prod_{v\in T} \mathcal{P}_{U',v}(\phi_{n,v}\otimes \phi_{n+1,v},\phi_{n,v}\otimes \phi_{n+1,v}), \end{aligned}\end{align*}$$
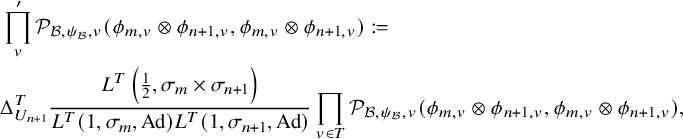 $$\begin{align*}\begin{aligned} & \prod_v^{\prime}\mathcal{P}_{\mathcal{B},\psi_{\mathcal{B}},v}(\phi_{m,v}\otimes \phi_{n+1,v},\phi_{m,v}\otimes \phi_{n+1,v}):= \\ & \Delta^T_{U_{n+1}} \frac{L^T\left(\frac{1}{2},\sigma_{m}\times \sigma_{n+1}\right)}{L^T(1,\sigma_{m},\operatorname{\mathrm{Ad}})L^T(1,\sigma_{n+1},\operatorname{\mathrm{Ad}})}\prod_{v\in T} \mathcal{P}_{\mathcal{B},\psi_{\mathcal{B}},v}(\phi_{m,v}\otimes \phi_{n+1,v},\phi_{m,v}\otimes \phi_{n+1,v}), \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} & \prod_v^{\prime}\mathcal{P}_{\mathcal{B},\psi_{\mathcal{B}},v}(\phi_{m,v}\otimes \phi_{n+1,v},\phi_{m,v}\otimes \phi_{n+1,v}):= \\ & \Delta^T_{U_{n+1}} \frac{L^T\left(\frac{1}{2},\sigma_{m}\times \sigma_{n+1}\right)}{L^T(1,\sigma_{m},\operatorname{\mathrm{Ad}})L^T(1,\sigma_{n+1},\operatorname{\mathrm{Ad}})}\prod_{v\in T} \mathcal{P}_{\mathcal{B},\psi_{\mathcal{B}},v}(\phi_{m,v}\otimes \phi_{n+1,v},\phi_{m,v}\otimes \phi_{n+1,v}), \end{aligned}\end{align*}$$
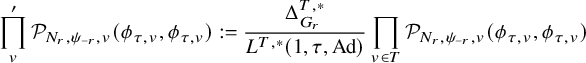 $$ \begin{align*} \prod_v^{\prime}\mathcal{P}_{N_r,\psi_{-r},v}(\phi_{\tau,v},\phi_{\tau,v}):=\frac{\Delta^{T,*}_{G_r}}{L^{T,*}(1,\tau,\operatorname{\mathrm{Ad}})}\prod_{v\in T} \mathcal{P}_{N_r,\psi_{-r},v}(\phi_{\tau,v},\phi_{\tau,v}) \end{align*} $$
$$ \begin{align*} \prod_v^{\prime}\mathcal{P}_{N_r,\psi_{-r},v}(\phi_{\tau,v},\phi_{\tau,v}):=\frac{\Delta^{T,*}_{G_r}}{L^{T,*}(1,\tau,\operatorname{\mathrm{Ad}})}\prod_{v\in T} \mathcal{P}_{N_r,\psi_{-r},v}(\phi_{\tau,v},\phi_{\tau,v}) \end{align*} $$
for any sufficiently large finite set T of places where we have set
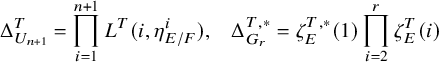 $$ \begin{align*}\Delta^T_{U_{n+1}}=\prod_{i=1}^{n+1} L^T(i,\eta_{E/F}^i),\;\;\; \Delta^{T,*}_{G_r}=\zeta_E^{T,*}(1)\prod_{i=2}^r \zeta_E^T(i)\end{align*} $$
$$ \begin{align*}\Delta^T_{U_{n+1}}=\prod_{i=1}^{n+1} L^T(i,\eta_{E/F}^i),\;\;\; \Delta^{T,*}_{G_r}=\zeta_E^{T,*}(1)\prod_{i=2}^r \zeta_E^T(i)\end{align*} $$
and
![]() $L^{T,*}(1,\sigma _{n},\operatorname {\mathrm {Ad}})$
,
$L^{T,*}(1,\sigma _{n},\operatorname {\mathrm {Ad}})$
,
![]() $L^{T,*}(1,\tau ,\operatorname {\mathrm {Ad}})$
stand for the regularized values
$L^{T,*}(1,\tau ,\operatorname {\mathrm {Ad}})$
stand for the regularized values
with
![]() $a=\dim (A_M)$
, respectively. We define similarly
$a=\dim (A_M)$
, respectively. We define similarly
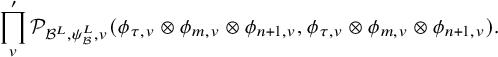 $$ \begin{align*}\prod_v^{\prime} \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}},v}(\phi_{\tau,v}\otimes \phi_{m,v}\otimes \phi_{n+1,v},\phi_{\tau,v}\otimes \phi_{m,v}\otimes \phi_{n+1,v}).\end{align*} $$
$$ \begin{align*}\prod_v^{\prime} \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}},v}(\phi_{\tau,v}\otimes \phi_{m,v}\otimes \phi_{n+1,v},\phi_{\tau,v}\otimes \phi_{m,v}\otimes \phi_{n+1,v}).\end{align*} $$
Of course, the previous discussion applies verbatim when we replace
![]() $\tau $
and
$\tau $
and
![]() $\sigma _n$
by
$\sigma _n$
by
![]() $\tau _s$
and
$\tau _s$
and
![]() $\sigma _{n,s}$
for every
$\sigma _{n,s}$
for every
![]() $s\in i\mathbb {R}$
.
$s\in i\mathbb {R}$
.
Proposition 8.8.3.1. Let
![]() $c\in \mathbb {C}$
and assume that for every factorizable vectors
$c\in \mathbb {C}$
and assume that for every factorizable vectors
![]() $\phi _n\in \sigma _n$
,
$\phi _n\in \sigma _n$
,
![]() $\phi _{n+1}\in \sigma _{n+1}$
and every
$\phi _{n+1}\in \sigma _{n+1}$
and every
![]() $s\in i\mathbb {R}$
, we have
$s\in i\mathbb {R}$
, we have
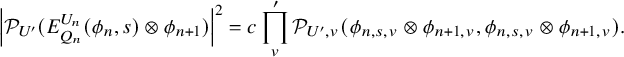 $$ \begin{align*}\left\lvert \mathcal{P}_{U'}(E_{Q_n}^{U_n}(\phi_n,s)\otimes \phi_{n+1})\right\rvert^2=c \prod_v^{\prime} \mathcal{P}_{U',v}(\phi_{n,s,v}\otimes \phi_{n+1,v},\phi_{n,s,v}\otimes \phi_{n+1,v}).\end{align*} $$
$$ \begin{align*}\left\lvert \mathcal{P}_{U'}(E_{Q_n}^{U_n}(\phi_n,s)\otimes \phi_{n+1})\right\rvert^2=c \prod_v^{\prime} \mathcal{P}_{U',v}(\phi_{n,s,v}\otimes \phi_{n+1,v},\phi_{n,s,v}\otimes \phi_{n+1,v}).\end{align*} $$
Then, for every factorizable vectors
![]() $\phi _m\in \sigma _m$
and
$\phi _m\in \sigma _m$
and
![]() $\phi _{n+1}\in \sigma _{n+1}$
, we have
$\phi _{n+1}\in \sigma _{n+1}$
, we have
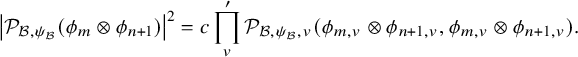 $$ \begin{align*}\left\lvert \mathcal{P}_{\mathcal{B},\psi_{\mathcal{B}}}(\phi_m\otimes \phi_{n+1})\right\rvert^2=c \prod_v^{\prime} \mathcal{P}_{\mathcal{B},\psi_{\mathcal{B}},v}(\phi_{m,v}\otimes \phi_{n+1,v},\phi_{m,v}\otimes \phi_{n+1,v}).\end{align*} $$
$$ \begin{align*}\left\lvert \mathcal{P}_{\mathcal{B},\psi_{\mathcal{B}}}(\phi_m\otimes \phi_{n+1})\right\rvert^2=c \prod_v^{\prime} \mathcal{P}_{\mathcal{B},\psi_{\mathcal{B}},v}(\phi_{m,v}\otimes \phi_{n+1,v},\phi_{m,v}\otimes \phi_{n+1,v}).\end{align*} $$
Proof. Let
![]() $\phi _n\in \sigma _n$
and
$\phi _n\in \sigma _n$
and
![]() $\phi _{n+1}\in \sigma _{n+1}$
be factorizable vectors and let T be a finite set of places of F that we will assume throughout to be sufficiently large. By (8.8.1.1), we have
$\phi _{n+1}\in \sigma _{n+1}$
be factorizable vectors and let T be a finite set of places of F that we will assume throughout to be sufficiently large. By (8.8.1.1), we have
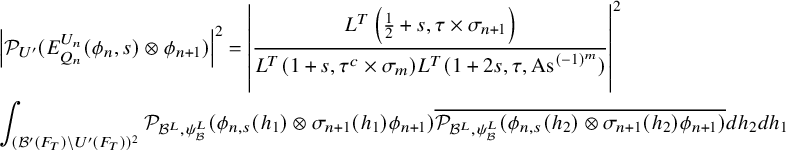 $$ \begin{align} & \left\lvert \mathcal{P}_{U'}(E_{Q_n}^{U_n}(\phi_n,s)\otimes \phi_{n+1})\right\rvert^2= \left\lvert \frac{L^T\left(\frac{1}{2}+s,\tau\times \sigma_{n+1}\right)}{L^T(1+s,\tau^c\times \sigma_m) L^T(1+2s,\tau,\mathrm{As}^{(-1)^m})}\right\rvert^2 \\ \nonumber & \int_{(\mathcal{B}'(F_T)\backslash U'(F_T))^2} \mathcal{P}_{\mathcal{B}^L,\psi_{\mathcal{B}}^L}(\phi_{n,s}(h_1)\otimes \sigma_{n+1}(h_1)\phi_{n+1}) \overline{\mathcal{P}_{\mathcal{B}^L,\psi_{\mathcal{B}}^L}(\phi_{n,s}(h_2)\otimes \sigma_{n+1}(h_2)\phi_{n+1})} dh_2dh_1 \end{align} $$
$$ \begin{align} & \left\lvert \mathcal{P}_{U'}(E_{Q_n}^{U_n}(\phi_n,s)\otimes \phi_{n+1})\right\rvert^2= \left\lvert \frac{L^T\left(\frac{1}{2}+s,\tau\times \sigma_{n+1}\right)}{L^T(1+s,\tau^c\times \sigma_m) L^T(1+2s,\tau,\mathrm{As}^{(-1)^m})}\right\rvert^2 \\ \nonumber & \int_{(\mathcal{B}'(F_T)\backslash U'(F_T))^2} \mathcal{P}_{\mathcal{B}^L,\psi_{\mathcal{B}}^L}(\phi_{n,s}(h_1)\otimes \sigma_{n+1}(h_1)\phi_{n+1}) \overline{\mathcal{P}_{\mathcal{B}^L,\psi_{\mathcal{B}}^L}(\phi_{n,s}(h_2)\otimes \sigma_{n+1}(h_2)\phi_{n+1})} dh_2dh_1 \end{align} $$
for
![]() $s\in i\mathbb {R}$
. However, from the hypothesis, Proposition 8.6.2.1 and (8.2.1.1), we obtain
$s\in i\mathbb {R}$
. However, from the hypothesis, Proposition 8.6.2.1 and (8.2.1.1), we obtain
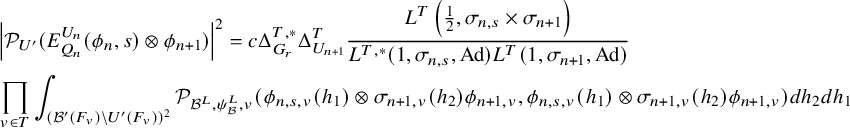 $$ \begin{align} & \left\lvert \mathcal{P}_{U'}(E_{Q_n}^{U_n}(\phi_n,s)\otimes \phi_{n+1})\right\rvert^2=c \Delta^{T,*}_{G_r}\Delta_{U_{n+1}}^T \frac{L^T\left(\frac{1}{2},\sigma_{n,s}\times \sigma_{n+1}\right)}{L^{T,*}(1,\sigma_{n,s},\operatorname{\mathrm{Ad}})L^T(1,\sigma_{n+1},\operatorname{\mathrm{Ad}})} \\ \nonumber & \prod_{v\in T} \int_{(\mathcal{B}'(F_v)\backslash U'(F_v))^2} \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}},v}(\phi_{n,s,v}(h_1)\otimes \sigma_{n+1,v}(h_2)\phi_{n+1,v},\phi_{n,s,v}(h_1)\otimes \sigma_{n+1,v}(h_2)\phi_{n+1,v} ) dh_2dh_1 \end{align} $$
$$ \begin{align} & \left\lvert \mathcal{P}_{U'}(E_{Q_n}^{U_n}(\phi_n,s)\otimes \phi_{n+1})\right\rvert^2=c \Delta^{T,*}_{G_r}\Delta_{U_{n+1}}^T \frac{L^T\left(\frac{1}{2},\sigma_{n,s}\times \sigma_{n+1}\right)}{L^{T,*}(1,\sigma_{n,s},\operatorname{\mathrm{Ad}})L^T(1,\sigma_{n+1},\operatorname{\mathrm{Ad}})} \\ \nonumber & \prod_{v\in T} \int_{(\mathcal{B}'(F_v)\backslash U'(F_v))^2} \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}},v}(\phi_{n,s,v}(h_1)\otimes \sigma_{n+1,v}(h_2)\phi_{n+1,v},\phi_{n,s,v}(h_1)\otimes \sigma_{n+1,v}(h_2)\phi_{n+1,v} ) dh_2dh_1 \end{align} $$
for
![]() $s\in i\mathbb {R}$
. From (8.8.3.1), (8.8.3.2), the last part of Proposition 8.6.1.1 as well as the identity of partial L-functions for
$s\in i\mathbb {R}$
. From (8.8.3.1), (8.8.3.2), the last part of Proposition 8.6.1.1 as well as the identity of partial L-functions for
![]() $s\in i\mathbb {R}$
$s\in i\mathbb {R}$
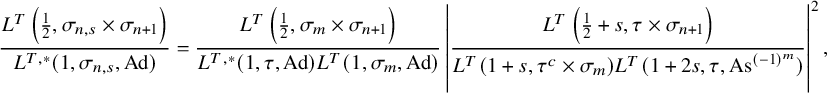 $$ \begin{align*}\frac{L^T\left(\frac{1}{2},\sigma_{n,s}\times \sigma_{n+1}\right)}{L^{T,*}(1,\sigma_{n,s},\operatorname{\mathrm{Ad}})}=\frac{L^T \left(\frac{1}{2},\sigma_{m}\times \sigma_{n+1} \right)}{L^{T,*}(1,\tau,\operatorname{\mathrm{Ad}})L^{T}(1,\sigma_{m},\operatorname{\mathrm{Ad}})} \left\lvert \frac{L^T\left(\frac{1}{2}+s,\tau\times \sigma_{n+1}\right)}{L^T(1+s,\tau^c\times \sigma_m) L^T(1+2s,\tau,\mathrm{As}^{(-1)^m})}\right\rvert^2,\end{align*} $$
$$ \begin{align*}\frac{L^T\left(\frac{1}{2},\sigma_{n,s}\times \sigma_{n+1}\right)}{L^{T,*}(1,\sigma_{n,s},\operatorname{\mathrm{Ad}})}=\frac{L^T \left(\frac{1}{2},\sigma_{m}\times \sigma_{n+1} \right)}{L^{T,*}(1,\tau,\operatorname{\mathrm{Ad}})L^{T}(1,\sigma_{m},\operatorname{\mathrm{Ad}})} \left\lvert \frac{L^T\left(\frac{1}{2}+s,\tau\times \sigma_{n+1}\right)}{L^T(1+s,\tau^c\times \sigma_m) L^T(1+2s,\tau,\mathrm{As}^{(-1)^m})}\right\rvert^2,\end{align*} $$
we deduce the equality
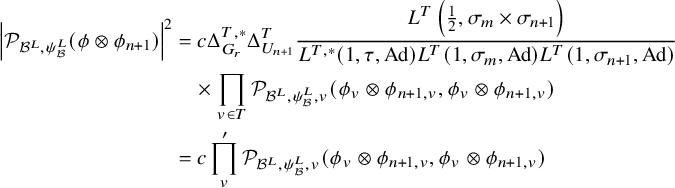 $$ \begin{align} \left\lvert \mathcal{P}_{\mathcal{B}^L,\psi_{\mathcal{B}}^L}(\phi\otimes \phi_{n+1})\right\rvert^2 &= c\Delta^{T,*}_{G_r}\Delta_{U_{n+1}}^T \frac{L^T \left(\frac{1}{2},\sigma_{m}\times \sigma_{n+1} \right)}{L^{T,*}(1,\tau,\operatorname{\mathrm{Ad}})L^{T}(1,\sigma_{m},\operatorname{\mathrm{Ad}})L^T(1,\sigma_{n+1},\operatorname{\mathrm{Ad}})} \\ \nonumber & \quad\times \prod_{v\in T} \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}},v}(\phi_v\otimes \phi_{n+1,v},\phi_{v}\otimes \phi_{n+1,v} ) \\ \nonumber & =c\prod_v^{\prime} \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}},v}(\phi_v\otimes \phi_{n+1,v},\phi_{v}\otimes \phi_{n+1,v} ) \end{align} $$
$$ \begin{align} \left\lvert \mathcal{P}_{\mathcal{B}^L,\psi_{\mathcal{B}}^L}(\phi\otimes \phi_{n+1})\right\rvert^2 &= c\Delta^{T,*}_{G_r}\Delta_{U_{n+1}}^T \frac{L^T \left(\frac{1}{2},\sigma_{m}\times \sigma_{n+1} \right)}{L^{T,*}(1,\tau,\operatorname{\mathrm{Ad}})L^{T}(1,\sigma_{m},\operatorname{\mathrm{Ad}})L^T(1,\sigma_{n+1},\operatorname{\mathrm{Ad}})} \\ \nonumber & \quad\times \prod_{v\in T} \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}},v}(\phi_v\otimes \phi_{n+1,v},\phi_{v}\otimes \phi_{n+1,v} ) \\ \nonumber & =c\prod_v^{\prime} \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}},v}(\phi_v\otimes \phi_{n+1,v},\phi_{v}\otimes \phi_{n+1,v} ) \end{align} $$
for every factorizable vector
![]() $\phi =\bigotimes _v^{\prime } \phi _v\in \tau \boxtimes \sigma _m$
. Furthermore, for
$\phi =\bigotimes _v^{\prime } \phi _v\in \tau \boxtimes \sigma _m$
. Furthermore, for
![]() $\phi _\tau \in \tau $
and
$\phi _\tau \in \tau $
and
![]() $\phi _m\in \sigma _m$
two factorizable vectors, we have
$\phi _m\in \sigma _m$
two factorizable vectors, we have
and
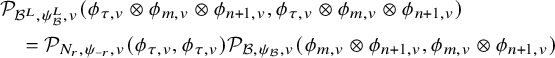 $$ \begin{align*} & \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}},v}(\phi_{\tau,v}\otimes \phi_{m,v}\otimes \phi_{n+1,v},\phi_{\tau,v}\otimes \phi_{m,v}\otimes \phi_{n+1,v} )\\ &\quad =\mathcal{P}_{N_r,\psi_{-r},v}(\phi_{\tau,v},\phi_{\tau,v}) \mathcal{P}_{\mathcal{B},\psi_{\mathcal{B}},v}(\phi_{m,v}\otimes \phi_{n+1,v},\phi_{m,v}\otimes \phi_{n+1,v} )\end{align*} $$
$$ \begin{align*} & \mathcal{P}_{\mathcal{B}^L,\psi^L_{\mathcal{B}},v}(\phi_{\tau,v}\otimes \phi_{m,v}\otimes \phi_{n+1,v},\phi_{\tau,v}\otimes \phi_{m,v}\otimes \phi_{n+1,v} )\\ &\quad =\mathcal{P}_{N_r,\psi_{-r},v}(\phi_{\tau,v},\phi_{\tau,v}) \mathcal{P}_{\mathcal{B},\psi_{\mathcal{B}},v}(\phi_{m,v}\otimes \phi_{n+1,v},\phi_{m,v}\otimes \phi_{n+1,v} )\end{align*} $$
for every place v as well as the identity (cf. [Reference Feigon, Lapid and OffenFLO12, Eq. (11.3)])
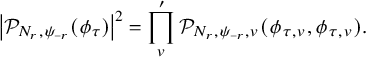 $$ \begin{align} \left\lvert \mathcal{P}_{N_r,\psi_{-r}}(\phi_\tau)\right\rvert^2=\prod_v^{\prime} \mathcal{P}_{N_r,\psi_{-r},v}(\phi_{\tau,v},\phi_{\tau,v}). \end{align} $$
$$ \begin{align} \left\lvert \mathcal{P}_{N_r,\psi_{-r}}(\phi_\tau)\right\rvert^2=\prod_v^{\prime} \mathcal{P}_{N_r,\psi_{-r},v}(\phi_{\tau,v},\phi_{\tau,v}). \end{align} $$
The proposition can now be deduced by dividing the identity (8.8.3.4) by (8.8.3.3). Note that such a deduction is valid as the Whittaker period
![]() $\mathcal {P}_{N_r,\psi _{-r}}$
is known to be nonzero on
$\mathcal {P}_{N_r,\psi _{-r}}$
is known to be nonzero on
![]() $\tau $
.
$\tau $
.
A Weyl character formula for non-connected groups
A.0.1
Let
![]() $\widehat {G}$
be a connected complex reductive group,
$\widehat {G}$
be a connected complex reductive group,
![]() $\widehat {B}\subset \widehat {G}$
be a Borel subgroup and
$\widehat {B}\subset \widehat {G}$
be a Borel subgroup and
![]() $\widehat {T}\subset \widehat {B}$
be a maximal torus. Let
$\widehat {T}\subset \widehat {B}$
be a maximal torus. Let
![]() $\Gamma $
be a cyclic finite group acting on
$\Gamma $
be a cyclic finite group acting on
![]() $\widehat {G}$
by holomorphic automorphisms preserving the Borel pair
$\widehat {G}$
by holomorphic automorphisms preserving the Borel pair
![]() $(\widehat {B},\widehat {T})$
. Set
$(\widehat {B},\widehat {T})$
. Set
![]() ${}^L G=\widehat {G}\rtimes \Gamma $
,
${}^L G=\widehat {G}\rtimes \Gamma $
,
![]() ${}^L T=\widehat {T}\rtimes \Gamma $
and
${}^L T=\widehat {T}\rtimes \Gamma $
and
![]() ${}^L B=\widehat {B}\rtimes \Gamma $
. We say that an element
${}^L B=\widehat {B}\rtimes \Gamma $
. We say that an element
![]() $S\in {}^L T$
is regular if the neutral component of its centralizer is contained in
$S\in {}^L T$
is regular if the neutral component of its centralizer is contained in
![]() $\widehat {T}$
.
$\widehat {T}$
.
Let
![]() $X^*(\widehat {T})$
be the group of algebraic characters of
$X^*(\widehat {T})$
be the group of algebraic characters of
![]() $\widehat {T}$
and
$\widehat {T}$
and
![]() $X^*(\widehat {T})^+\subset X^*(\widehat {T})$
be the subset of dominant elements (with respect to the chosen Borel
$X^*(\widehat {T})^+\subset X^*(\widehat {T})$
be the subset of dominant elements (with respect to the chosen Borel
![]() $\widehat {B}$
). For every
$\widehat {B}$
). For every
![]() $\chi \in X^*(\widehat {T})^+$
, we denote by
$\chi \in X^*(\widehat {T})^+$
, we denote by
![]() $(\pi _\chi , V_\chi )$
an algebraic irreducible representation of
$(\pi _\chi , V_\chi )$
an algebraic irreducible representation of
![]() $\widehat {G}$
with highest weight
$\widehat {G}$
with highest weight
![]() $\chi $
(it is unique up to isomorphism). Note that the subgroup of
$\chi $
(it is unique up to isomorphism). Note that the subgroup of
![]() $\Gamma $
-invariant characters
$\Gamma $
-invariant characters
![]() $X^*(\widehat {T})^\Gamma $
can be identified with the set of algebraic characters
$X^*(\widehat {T})^\Gamma $
can be identified with the set of algebraic characters
![]() ${}^L T\to \mathbb {C}^\times $
that are trivial on
${}^L T\to \mathbb {C}^\times $
that are trivial on
![]() $\Gamma $
. Moreover, for every
$\Gamma $
. Moreover, for every
![]() $\chi \in X^*(\widehat {T})^+\cap X^*(\widehat {T})^\Gamma $
, the representation
$\chi \in X^*(\widehat {T})^+\cap X^*(\widehat {T})^\Gamma $
, the representation
![]() $(\pi _\chi ,V_\chi )$
can be extended in a unique way to a representation of
$(\pi _\chi ,V_\chi )$
can be extended in a unique way to a representation of
![]() ${}^L G$
such that
${}^L G$
such that
![]() $\Gamma $
acts trivially on the line of highest weight vectors. We shall denote by
$\Gamma $
acts trivially on the line of highest weight vectors. We shall denote by
![]() $ch_\chi $
the character of that representation of
$ch_\chi $
the character of that representation of
![]() ${}^L G$
(i.e.,
${}^L G$
(i.e.,
![]() $ch_\chi (S)=\mathrm {Tr} \pi _\chi (S)$
for
$ch_\chi (S)=\mathrm {Tr} \pi _\chi (S)$
for
![]() $S\in {}^L G$
).
$S\in {}^L G$
).
A.0.2
Let
![]() $\widehat {W}=\operatorname {\mathrm {Norm}}_{\widehat {G}}(\widehat {T})/\widehat {T}$
be the Weyl group of
$\widehat {W}=\operatorname {\mathrm {Norm}}_{\widehat {G}}(\widehat {T})/\widehat {T}$
be the Weyl group of
![]() $\widehat {T}$
in
$\widehat {T}$
in
![]() $\widehat {G}$
. Then,
$\widehat {G}$
. Then,
![]() $\Gamma $
acts in a natural way on
$\Gamma $
acts in a natural way on
![]() $\widehat {W}$
and the subgroup of fixed points
$\widehat {W}$
and the subgroup of fixed points
![]() $\widehat {W}^\Gamma $
can be identified with
$\widehat {W}^\Gamma $
can be identified with
![]() $W=\operatorname {\mathrm {Norm}}_{\widehat {G}}({}^L T)/\widehat {T}$
. Let
$W=\operatorname {\mathrm {Norm}}_{\widehat {G}}({}^L T)/\widehat {T}$
. Let
![]() $\rho \in \frac {1}{2}X^*(\widehat {T})$
be the half-sum of the positive roots with respect to
$\rho \in \frac {1}{2}X^*(\widehat {T})$
be the half-sum of the positive roots with respect to
![]() $\widehat {B}$
. The dot action of
$\widehat {B}$
. The dot action of
![]() $\widehat {W}$
on
$\widehat {W}$
on
![]() $X^*(\widehat {T})$
is defined by
$X^*(\widehat {T})$
is defined by
For
![]() $\chi \in X^*(\widehat {T})$
, we recall the following alternative. Either
$\chi \in X^*(\widehat {T})$
, we recall the following alternative. Either
-
•
 $\chi +\rho $
is singular (i.e., there exists a coroot
$\chi +\rho $
is singular (i.e., there exists a coroot
 $\alpha ^\vee $
such that
$\alpha ^\vee $
such that
 $\langle \alpha ^\vee , \chi +\rho \rangle =0$
);
$\langle \alpha ^\vee , \chi +\rho \rangle =0$
); -
• or there exists a unique
 $w_\chi \in \widehat {W}$
such that
$w_\chi \in \widehat {W}$
such that
 $w_\chi \cdot \chi \in X^*(\widehat {T})^+$
.
$w_\chi \cdot \chi \in X^*(\widehat {T})^+$
.
Note that, by unicity, for
![]() $\chi \in X^*(\widehat {T})^\Gamma $
such that
$\chi \in X^*(\widehat {T})^\Gamma $
such that
![]() $\chi +\rho $
is nonsingular, we have
$\chi +\rho $
is nonsingular, we have
![]() $w_\chi \in W$
.
$w_\chi \in W$
.
For every standard parabolic subgroup
![]() $\widehat {B}\subset \widehat {Q}\subset \widehat {G}$
that is
$\widehat {B}\subset \widehat {Q}\subset \widehat {G}$
that is
![]() $\Gamma $
-stable, we set
$\Gamma $
-stable, we set
for
![]() $S\in {}^LT$
.
$S\in {}^LT$
.
Proposition A.0.2.1. Let
![]() $F\in \Gamma $
be a generator and
$F\in \Gamma $
be a generator and
![]() $\chi \in X^*(\widehat {T})^\Gamma $
. Then
$\chi \in X^*(\widehat {T})^\Gamma $
. Then
-
1. If
 $\chi +\rho $
is singular, we have for every regular
$\chi +\rho $
is singular, we have for every regular $$ \begin{align*}\sum_{w\in W} \frac{\chi(wS)}{D_{\widehat{G}/\widehat{B}}(wS)}=0\end{align*} $$
$$ \begin{align*}\sum_{w\in W} \frac{\chi(wS)}{D_{\widehat{G}/\widehat{B}}(wS)}=0\end{align*} $$
 $S\in {}^L T$
.
$S\in {}^L T$
.
-
2. If
 $\chi +\rho $
is nonsingular, setting
$\chi +\rho $
is nonsingular, setting
 $\chi ^+=w_\chi \cdot \chi $
, there exists a root of unity
$\chi ^+=w_\chi \cdot \chi $
, there exists a root of unity
 $\epsilon _\chi \in \mathbb {C}^\times $
such that for every regular
$\epsilon _\chi \in \mathbb {C}^\times $
such that for every regular $$ \begin{align*}\sum_{w\in W} \frac{\chi(wS)}{D_{\widehat{G}/\widehat{B}}(wS)}=\epsilon_\chi ch_{\chi^+}(S)\end{align*} $$
$$ \begin{align*}\sum_{w\in W} \frac{\chi(wS)}{D_{\widehat{G}/\widehat{B}}(wS)}=\epsilon_\chi ch_{\chi^+}(S)\end{align*} $$
 $S\in \widehat {T} F$
. Moreover, if
$S\in \widehat {T} F$
. Moreover, if
 $\chi $
is dominant, we have
$\chi $
is dominant, we have
 $\epsilon _\chi =1$
.
$\epsilon _\chi =1$
.
Proof. Let
![]() $X=\widehat {G}/\widehat {B}$
be the flag variety of
$X=\widehat {G}/\widehat {B}$
be the flag variety of
![]() $\widehat {G}$
. The action of
$\widehat {G}$
. The action of
![]() $\widehat {G}$
on X naturally extends to
$\widehat {G}$
on X naturally extends to
![]() ${}^L G$
(e.g., because we can also write
${}^L G$
(e.g., because we can also write
![]() $X={}^L G/{}^L B$
). Let
$X={}^L G/{}^L B$
). Let
![]() $\mathcal {L}_\chi $
be the
$\mathcal {L}_\chi $
be the
![]() ${}^L G$
-equivariant line bundle on X such that the action of
${}^L G$
-equivariant line bundle on X such that the action of
![]() ${}^LB$
on the fiber above
${}^LB$
on the fiber above
![]() $1\in X$
is given by
$1\in X$
is given by
![]() $\chi $
. Then, by the Borel-Weil-Bott theorem, we have
$\chi $
. Then, by the Borel-Weil-Bott theorem, we have
-
• If
 $\chi +\rho $
is singular,
$\chi +\rho $
is singular,
 $H^i(X,\mathcal {L}_\chi )=0$
for
$H^i(X,\mathcal {L}_\chi )=0$
for
 $i\geqslant 0$
,
$i\geqslant 0$
, -
• otherwise (i.e., if
 $\chi +\rho $
is nonsingular), there exists a unique
$\chi +\rho $
is nonsingular), there exists a unique
 $i\geqslant 0$
such that
$i\geqslant 0$
such that
 $H^i(X,\mathcal {L}_\chi )\neq 0$
and, moreover,
$H^i(X,\mathcal {L}_\chi )\neq 0$
and, moreover,
 $H^i(X,\mathcal {L}_\chi )\simeq V_{\chi ^+}$
as
$H^i(X,\mathcal {L}_\chi )\simeq V_{\chi ^+}$
as
 $\widehat {G}$
-modules.
$\widehat {G}$
-modules.
Let
![]() $S\in \widehat {T} F$
be regular. We apply Atiyah-Bott fixed point theorem [Reference Atiyah and BottAB68, Theorem 4.12] to the action of S on the pair
$S\in \widehat {T} F$
be regular. We apply Atiyah-Bott fixed point theorem [Reference Atiyah and BottAB68, Theorem 4.12] to the action of S on the pair
![]() $(X,\mathcal {L}_\chi )$
. First, note that the set of fixed points of S in X is precisely the image of the natural embedding
$(X,\mathcal {L}_\chi )$
. First, note that the set of fixed points of S in X is precisely the image of the natural embedding
![]() $W\subset X$
. Moreover, for
$W\subset X$
. Moreover, for
![]() $w\in W$
, the action of S on the fiber
$w\in W$
, the action of S on the fiber
![]() $(\mathcal {L}_\chi )_w$
(resp. on the tangent space
$(\mathcal {L}_\chi )_w$
(resp. on the tangent space
![]() $T_wX$
identified in a natural way with
$T_wX$
identified in a natural way with
![]() $Lie(\widehat {G})/Lie(\widehat {B})$
) is the multiplication by
$Lie(\widehat {G})/Lie(\widehat {B})$
) is the multiplication by
![]() $\chi (w^{-1}S)$
(resp. the adjoint operator
$\chi (w^{-1}S)$
(resp. the adjoint operator
![]() $Ad(w^{-1}S)$
). Given this as well as the above description of the cohomology groups of
$Ad(w^{-1}S)$
). Given this as well as the above description of the cohomology groups of
![]() $\mathcal {L}_\chi $
, the Atiyah-Bott fixed point theorem implies directly the proposition when
$\mathcal {L}_\chi $
, the Atiyah-Bott fixed point theorem implies directly the proposition when
![]() $\chi +\rho $
is singular, whereas in the nonsingular, case it gives
$\chi +\rho $
is singular, whereas in the nonsingular, case it gives
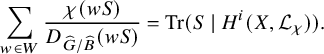 $$ \begin{align*}\sum_{w\in W} \frac{\chi(wS)}{D_{\widehat{G}/\widehat{B}}(wS)}=\mathrm{Tr}(S\mid H^i(X,\mathcal{L}_\chi)).\end{align*} $$
$$ \begin{align*}\sum_{w\in W} \frac{\chi(wS)}{D_{\widehat{G}/\widehat{B}}(wS)}=\mathrm{Tr}(S\mid H^i(X,\mathcal{L}_\chi)).\end{align*} $$
However, since
![]() $H^i(X,\mathcal {L}_\chi )\simeq V_{\chi ^+}$
as
$H^i(X,\mathcal {L}_\chi )\simeq V_{\chi ^+}$
as
![]() $\widehat {G}$
-modules and
$\widehat {G}$
-modules and
![]() $V_{\chi ^+}$
is irreducible, we see that
$V_{\chi ^+}$
is irreducible, we see that
![]() $H^i(X,\mathcal {L}_\chi )$
is isomorphic as a
$H^i(X,\mathcal {L}_\chi )$
is isomorphic as a
![]() ${}^L G$
-representation to a twist of
${}^L G$
-representation to a twist of
![]() $V_{\chi ^+}$
by a character of
$V_{\chi ^+}$
by a character of
![]() $\Gamma $
. Denoting by
$\Gamma $
. Denoting by
![]() $\epsilon _\chi $
the value of this character on F, we obtain the second formula of the proposition.
$\epsilon _\chi $
the value of this character on F, we obtain the second formula of the proposition.
Corollary A.0.2.2. Let
![]() $\widehat {Q}\subset \widehat {G}$
be a
$\widehat {Q}\subset \widehat {G}$
be a
![]() $\Gamma $
-stable standard parabolic subgroup. Let
$\Gamma $
-stable standard parabolic subgroup. Let
![]() $\widehat {L}\subset \widehat {Q}$
be the unique Levi component containing
$\widehat {L}\subset \widehat {Q}$
be the unique Levi component containing
![]() $\widehat {T}$
and set
$\widehat {T}$
and set
![]() $W^L=\operatorname {\mathrm {Norm}}_{{}^L L}(\widehat {T})/\widehat {T}\subset W$
, where we have set
$W^L=\operatorname {\mathrm {Norm}}_{{}^L L}(\widehat {T})/\widehat {T}\subset W$
, where we have set
![]() ${}^L L=\widehat {L}\rtimes \Gamma $
. Then, we have
${}^L L=\widehat {L}\rtimes \Gamma $
. Then, we have
for every regular
![]() $S\in {}^L T$
.
$S\in {}^L T$
.
Proof. Note that
for
![]() $S\in {}^L T$
, where we have set
$S\in {}^L T$
, where we have set
![]() $\widehat {B}_L=\widehat {B}\cap \widehat {L}$
. The corollary now follows readily from the previous proposition applied to the trivial character and
$\widehat {B}_L=\widehat {B}\cap \widehat {L}$
. The corollary now follows readily from the previous proposition applied to the trivial character and
![]() ${}^L L$
instead of
${}^L L$
instead of
![]() ${}^L G$
.
${}^L G$
.
Acknowledgements
We thank Paul Boisseau for pointing out an inaccuracy in the statement of Proposition 8.7.2.1 in a previous version of the paper. The work of first named author was funded by the European Union ERC Consolidator Grant, RELANTRA, project number 101044930. Views and opinions expressed are, however, those of the authors only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them.
The second named author would like to thank Michał Zydor, who was initially part of the project and with whom he has had many fruitful discussions over the last years on some of the topics covered in the article. He also thanks the Institut universitaire de France (IUF) for its support.
Competing interest
The authors have no competing interests to declare.