Hostname: page-component-76fb5796d-zzh7m Total loading time: 0 Render date: 2024-04-25T10:38:27.177Z Has data issue: false hasContentIssue false
  • English
  • Français

THE LOGARITHMICALLY AVERAGED CHOWLA AND ELLIOTT CONJECTURES FOR TWO-POINT CORRELATIONS

Part of: Multiplicative number theory

Published online by Cambridge University Press:  27 September 2016

TERENCE TAO
TERENCE TAO*
Affiliation:
Department of Mathematics, UCLA, 405 Hilgard Ave, Los Angeles, CA 90095, USA; tao@math.ucla.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $\unicode[STIX]{x1D706}$ denote the Liouville function. The Chowla conjecture, in the two-point correlation case, asserts that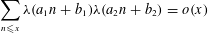

$$\begin{eqnarray}\mathop{\sum }_{n\leqslant x}\unicode[STIX]{x1D706}(a_{1}n+b_{1})\unicode[STIX]{x1D706}(a_{2}n+b_{2})=o(x)\end{eqnarray}$$
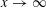as $x\rightarrow \infty$, for any fixed natural numbers $a_{1},a_{2}$ and nonnegative integer 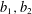$b_{1},b_{2}$ with 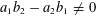$a_{1}b_{2}-a_{2}b_{1}\neq 0$. In this paper we establish the logarithmically averaged version
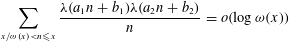$$\begin{eqnarray}\mathop{\sum }_{x/\unicode[STIX]{x1D714}(x)<n\leqslant x}\frac{\unicode[STIX]{x1D706}(a_{1}n+b_{1})\unicode[STIX]{x1D706}(a_{2}n+b_{2})}{n}=o(\log \unicode[STIX]{x1D714}(x))\end{eqnarray}$$
 of the Chowla conjecture as $x\rightarrow \infty$, where $1\leqslant \unicode[STIX]{x1D714}(x)\leqslant x$ is an arbitrary function of $x$ that goes to infinity as $x\rightarrow \infty$, thus breaking the ‘parity barrier’ for this problem. Our main tools are the multiplicativity of the Liouville function at small primes, a recent result of Matomäki, Radziwiłł, and the author on the averages of modulated multiplicative functions in short intervals, concentration of measure inequalities, the Hardy–Littlewood circle method combined with a restriction theorem for the primes, and a novel ‘entropy decrement argument’. Most of these ingredients are also available (in principle, at least) for the higher order correlations, with the main missing ingredient being the need to control short sums of multiplicative functions modulated by local nilsequences. Our arguments also extend to more general bounded multiplicative functions than the Liouville function $\unicode[STIX]{x1D706}$, leading to a logarithmically averaged version of the Elliott conjecture in the two-point case. In a subsequent paper we will use this version of the Elliott conjecture to affirmatively settle the Erdős discrepancy problem.

MSC classification

Primary: 11N37: Asymptotic results on arithmetic functions
Type
Research Article
Information
Forum of Mathematics, Pi , Volume 4 , 2016 , e8
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2016

References

El Abdalaoui, H., Kulaga-Przymus, J., Lemańczyk, M. and de la Rue, T., ‘The Chowla and the Sarnak conjectures from ergodic theory point of view’. Preprint, 2014, arXiv:1410.1673.Google Scholar
Billingsley, P., Ergodic Theory and Information, (Robert E. Krieger Publishing Co., Huntington, NY, 1978). Reprint of the 1965 original.Google Scholar
Chowla, S., The Riemann Hypothesis and Hilbert’s Tenth Problem, (Gordon and Breach, New York, 1965).Google Scholar
Elliott, P. D. T. A., ‘On the correlation of multiplicative functions’, Notas Soc. Mat. Chile, Notas de la Sociedad de Matemática de Chile 11 (1992), 1–11.Google Scholar
Erdős, P., ‘Some unsolved problems’, Michigan Math. J. 4 (1957), 299–300.Google Scholar
Frantzikinatkis, N., ‘An averaged Chowla and Elliott conjecture along independent polynomials’. Preprint, 2016, arXiv:1606.08420.CrossRefGoogle Scholar
Frantzikinatkis, N. and Host, B., ‘Higher order Fourier analysis of multiplicative functions and applications’. Preprint, 2014, arXiv:1403.0945.Google Scholar
Frantzikinakis, N. and Host, B., ‘Asymptotics for multilinear averages of multiplicative functions’, Math. Proc. Cambridge Philos. Soc. 161(1) (2016), 87–101.CrossRefGoogle Scholar
Frantzikinakis, N., Host, B. and Kra, B., ‘Multiple recurrence and convergence for sequences related to the prime numbers’, J. Reine Angew. Math. 611 (2007), 131–144.Google Scholar
Friedlander, J. and Iwaniec, H., ‘The polynomial X 2 + Y 4 captures its primes’, Ann. of Math. (2) 148(3) (1998), 945–1040.CrossRefGoogle Scholar
Friedlander, J. and Iwaniec, H., Opera de Cribro, American Mathematical Society Colloquium Publications, 57 (American Mathematical Society, Providence, RI, 2010).CrossRefGoogle Scholar
Granville, A. and Soundararajan, K., ‘Decay of mean values of multiplicative functions’, Canad. J. Math. 55(6) (2003), 1191–1230.CrossRefGoogle Scholar
Green, B. and Tao, T., ‘Restriction theory of the Selberg sieve, with applications’, J. Théor. Nombres Bordeaux 18(1) (2006), 147–182.Google Scholar
Green, B. and Tao, T., ‘Linear equations in primes’, Ann. of Math. (2) 171(3) (2010), 1753–1850.Google Scholar
Green, B., Tao, T. and Ziegler, T., ‘An inverse theorem for the Gowers U s+1[N]-norm’, Ann. of Math. (2) 176(2) (2012), 1231–1372.Google Scholar
Harman, G., Pintz, J. and Wolke, D., ‘A note on the Möbius and Liouville functions’, Studia Sci. Math. Hungar. 20(1–4) (1985), 295–299.Google Scholar
Hildebrand, A., ‘On consecutive values of the Liouville function’, Enseign. Math. (2) 32(3–4) (1986), 219–226.Google Scholar
Hoeffding, W., ‘Probability inequalities for sums of bounded random variables’, J. Amer. Stat. Assoc. 58 (1963), 13–30.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory, American Mathematical Society Colloquium Publications, 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Klurman, O., ‘Correlations of multiplicative functions and applications’. Preprint, 2016, arXiv:1603.084533.Google Scholar
Matomäki, K. and Radziwiłł, M., ‘Multiplicative functions in short intervals’, Ann. of Math. (2) 183(3) (2016), 1015–1056.Google Scholar
Matomäki, K. and Radziwiłł, M., ‘A note on the Liouville function in short intervals’. Preprint, 2015, arXiv:1502.02374.Google Scholar
Matomäki, K., Radziwiłł, M. and Tao, T., ‘An averaged form of Chowla’s conjecture’, Algebra Number Theory 9 (2015), 2167–2196.CrossRefGoogle Scholar
Matomäki, K., Radziwiłł, M. and Tao, T., ‘Sign patterns of the Möbius and Liouville functions’, Forum Math. Sigma 4 (2016), e14, 44 pp.CrossRefGoogle Scholar
Montgomery, H., Ten lectures on the interface between analytic number theory and harmonic analysis, CBMS Regional Conference Series in Mathematics, 84 (American Mathematical Society, Providence, RI, 1994). Published for the Conference Board of the Mathematical Sciences, Washington, DC.CrossRefGoogle Scholar
Moser, R. and Tardos, G., ‘A constructive proof of the general Lovász local lemma’, J. ACM 57(2) (2010), Art. 11, 15 pp.Google Scholar
Polymath, D. H. J., ‘The Erdős discrepancy problem’, michaelnielsen.org/polymath1/index.php?title=The_Erd%C5%91s_discrepancy_problem.Google Scholar
Sarnak, P., ‘Three lectures on the Möbius function randomness and dynamics’, 2010, publications.ias.edu/sarnak/paper/506.Google Scholar
Tao, T., ‘The ergodic and combinatorial approaches to Szemerédi’s theorem’, inAdditive Combinatorics, CRM Proc. Lecture Notes, 43 (American Mathematical Society, Providence, RI, 2007), 145–193.Google Scholar
Tao, T., ‘The Erdős discrepancy problem’, Discrete Anal. 1 (2016), 29 pp.Google Scholar
Tao, T., ‘Equivalence of the logarithmically averaged Chowla and Sarnak conjectures’. Preprint, 2016, arXiv:1605.04628.Google Scholar
Tenenbaum, G., Introduction to Analytic and Probabilistic Number Theory, Cambridge Studies in Advanced Mathematics, 46 (Cambridge University Press, Cambridge, 1995). Translated from the second French edition (1995) by C. B. Thomas.Google Scholar
Wooley, T. and Ziegler, T., ‘Multiple recurrence and convergence along the primes’, Amer. J. Math. 134(6) (2012), 1705–1732.CrossRefGoogle Scholar