Article contents
A BILINEAR RUBIO DE FRANCIA INEQUALITY FOR ARBITRARY SQUARES
Published online by Cambridge University Press: 19 September 2016
Abstract
We prove the boundedness of a smooth bilinear Rubio de Francia operator associated with an arbitrary collection of squares (with sides parallel to the axes) in the frequency plane 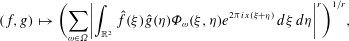 $$\begin{eqnarray}(f,g)\mapsto \biggl(\mathop{\sum }_{\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}}\biggl|\int _{\mathbb{R}^{2}}\hat{f}(\unicode[STIX]{x1D709}){\hat{g}}(\unicode[STIX]{x1D702})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D714}}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})e^{2\unicode[STIX]{x1D70B}ix(\unicode[STIX]{x1D709}+\unicode[STIX]{x1D702})}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\biggr|^{r}\biggr)^{1/r},\end{eqnarray}$$
$$\begin{eqnarray}(f,g)\mapsto \biggl(\mathop{\sum }_{\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}}\biggl|\int _{\mathbb{R}^{2}}\hat{f}(\unicode[STIX]{x1D709}){\hat{g}}(\unicode[STIX]{x1D702})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D714}}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})e^{2\unicode[STIX]{x1D70B}ix(\unicode[STIX]{x1D709}+\unicode[STIX]{x1D702})}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\biggr|^{r}\biggr)^{1/r},\end{eqnarray}$$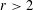 $r>2$ . More exactly, we show that the above operator maps
$r>2$ . More exactly, we show that the above operator maps 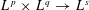 $L^{p}\times L^{q}\rightarrow L^{s}$ whenever
$L^{p}\times L^{q}\rightarrow L^{s}$ whenever 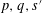 $p,q,s^{\prime }$ are in the ‘local
$p,q,s^{\prime }$ are in the ‘local 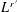 $L^{r^{\prime }}$ ’ range, that is,
$L^{r^{\prime }}$ ’ range, that is, 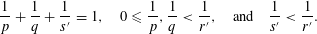 $$\begin{eqnarray}\frac{1}{p}+\frac{1}{q}+\frac{1}{s^{\prime }}=1,\quad 0\leqslant \frac{1}{p},\frac{1}{q}<\frac{1}{r^{\prime }},\quad \text{and}\quad \frac{1}{s^{\prime }}<\frac{1}{r^{\prime }}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{p}+\frac{1}{q}+\frac{1}{s^{\prime }}=1,\quad 0\leqslant \frac{1}{p},\frac{1}{q}<\frac{1}{r^{\prime }},\quad \text{and}\quad \frac{1}{s^{\prime }}<\frac{1}{r^{\prime }}.\end{eqnarray}$$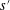 $s^{\prime }$ , which correspond to quasi-Banach spaces
$s^{\prime }$ , which correspond to quasi-Banach spaces 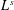 $L^{s}$ .
$L^{s}$ .
MSC classification
Information
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2016
References
- 2
- Cited by


