Hostname: page-component-76c49bb84f-zv2rg Total loading time: 0 Render date: 2025-07-08T13:10:50.164Z Has data issue: false hasContentIssue false
  • English
  • Français

Smoothness of solutions of a convolution equation of restricted type on the sphere

Part of: Miscellaneous topics in calculus of variations and optimal control Partial differential equations Harmonic analysis in several variables

Published online by Cambridge University Press:  07 April 2021

Diogo Oliveira e Silva  and
René Quilodrán
Diogo Oliveira e Silva
Affiliation:
School of Mathematics, University of Birmingham, Edgbaston, B15 2TT, England; E-mail: d.oliveiraesilva@bham.ac.uk
René Quilodrán
Affiliation:
Santiago, Chile; E-mail: rquilodr@dim.uchile.cl

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 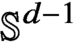$\mathbb {S}^{d-1}$ denote the unit sphere in Euclidean space $\mathbb {R}^d$, 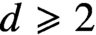$d\geq 2$, equipped with surface measure 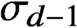$\sigma _{d-1}$. An instance of our main result concerns the regularity of solutions of the convolution equation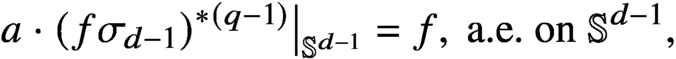

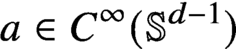$$\begin{align*}a\cdot(f\sigma_{d-1})^{\ast {(q-1)}}\big\vert_{\mathbb{S}^{d-1}}=f,\text{ a.e. on }\mathbb{S}^{d-1}, \end{align*}$$
where $a\in C^\infty (\mathbb {S}^{d-1})$, 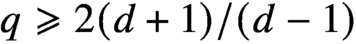$q\geq 2(d+1)/(d-1)$ is an integer, and the only a priori assumption is 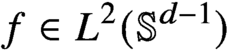$f\in L^2(\mathbb {S}^{d-1})$. We prove that any such solution belongs to the class 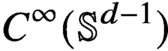$C^\infty (\mathbb {S}^{d-1})$. In particular, we show that all critical points associated with the sharp form of the corresponding adjoint Fourier restriction inequality on 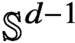$\mathbb {S}^{d-1}$ are 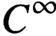$C^\infty $-smooth. This extends previous work of Christ and Shao [4] to arbitrary dimensions and general even exponents and plays a key role in the companion paper [24].

MSC classification

Primary: 49N60: Regularity of solutions
Secondary: 35B38: Critical points 42B37: Harmonic analysis and PDE

Information

Type
Analysis
Information
Forum of Mathematics, Sigma , Volume 9 , 2021 , e12
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Carneiro, E. and Oliveira e Silva, D., ‘Some sharp restriction inequalities on the sphere’, Int. Math. Res. Not. IMRN 2015(17) (2015), 8233–8267.CrossRefGoogle Scholar
Christ, M. and Quilodrán, R., ‘Gaussians rarely extremize adjoint Fourier restriction inequalities for paraboloids’, Proc. Amer. Math. Soc. 142(3) (2014), 887–896.CrossRefGoogle Scholar
Christ, M. and Shao, S., ‘Existence of extremals for a Fourier restriction inequality’, Anal. PDE 5(2) (2012), 261–312.CrossRefGoogle Scholar
Christ, M. and Shao, S., ‘On the extremizers of an adjoint Fourier restriction inequality’, Adv. Math. 230(3) (2012), 957–977.CrossRefGoogle Scholar
Colzani, L., ‘Lipschitz spaces on compact rank one symmetric spaces’, in Harmonic Analysis (Cortona, 1982), Lecture Notes in Mathematics, Vol. 992 (Springer, Berlin, 1983), 139–160.Google Scholar
Dai, F. and Xu, Y., ‘Moduli of smoothness and approximation on the unit sphere and the unit ball’, Adv. Math. 224(4) (2010), 1233–1310.CrossRefGoogle Scholar
Dai, F. and Xu, Y., ‘Polynomial approximation in Sobolev spaces on the unit sphere and the unit ball’, J. Approx. Theory 163(10) (2011), 1400–1418.CrossRefGoogle Scholar
Dai, F. and Xu, Y., Approximation Theory and Harmonic Analysis on Spheres and Balls, Springer Monographs in Mathematics (Springer, New York, 2013).CrossRefGoogle Scholar
Fanelli, L., Vega, L. and Visciglia, N., ‘On the existence of maximizers for a family of restriction theorems’, Bull. Lond. Math. Soc. 43(4) (2011), 811–817.CrossRefGoogle Scholar
Foschi, D., On the Regularity of Multilinear Forms Associated to the Wave Equation (PhD Dissertation, Princeton University, 2000).Google Scholar
Foschi, D., ‘Global maximizers for the sphere adjoint Fourier restriction inequality’, J. Funct. Anal. 268 (2015), 690–702.CrossRefGoogle Scholar
Foschi, D. and Oliveira e Silva, D., ‘Some recent progress on sharp Fourier restriction theory’, Anal. Math. 43(2) (2017), 241–265.CrossRefGoogle Scholar
Frank, R., Lieb, E. H. and Sabin, J., ‘Maximizers for the Stein-Tomas inequality’, Geom. Funct. Anal. 26 (2016), no. 4, 1095–1134.CrossRefGoogle Scholar
Grafakos, L., Modern Fourier Analysis, third ed., Graduate Texts in Mathematics, Vol. 250 (Springer, New York, 2014).Google Scholar
Greenwald, H. C., ‘Lipschitz spaces on the surface of the unit sphere in Euclidean $\text{n}$-space’, Pacific J. Math. 50 (1974), 63–80.CrossRefGoogle Scholar
Greenwald, H. C., ‘Lipschitz spaces of distributions on the surface of unit sphere in Euclidean $\text{n}$-space’, Pacific J. Math. 70(1) (1977), 163–176.CrossRefGoogle Scholar
Hall, B., Lie Groups, Lie Algebras, and Representations. An Elementary Introduction, second ed., Graduate Texts in Mathematics, Vol. 222 (Springer-Verlag, New York, 2015).Google Scholar
Hebey, E., Nonlinear Analysis on Manifolds: Sobolev Spaces and Inequalities, Courant Lecture Notes in Mathematics, Vol. 5 (New York University, Courant Institute of Mathematical Sciences, New York; American Mathematical Society, Providence, RI, 1999).Google Scholar
Herz, C. S., ‘Lipschitz spaces and Bernstein’s theorem on absolutely convergent Fourier transforms’, J. Math. Mech. 18 (1968–69), 283–323.Google Scholar
Hörmander, L., ‘Hypoelliptic second order differential equations’, Acta Math. 119 (1967), 147–171.CrossRefGoogle Scholar
Jurdjevic, V. and Sussmann, H. J., ‘Control systems on Lie groups’, J. Differ. Equ. 12 (1972), 313–329.CrossRefGoogle Scholar
Lions, J.-L. and Magenes, E., Non-homogeneous Boundary Value Problems and Applications: Vol. I. Die Grundlehren der mathematischen Wissenschaften [Comprehensive Studies in Mathematics], Band 181 (Springer-Verlag, New York, 1972). Translated from the French by Kenneth, P..Google Scholar
Lizorkin, P.I. and Rustamov, KH. P., ‘Nikol’skiĭ-Besov spaces on the sphere in connection with approximation theory’, Proc. Steklov Inst. Math. 204 (1994), 149–172.Google Scholar
Oliveira e Silva, D. and Quilodrán, R., ‘Global maximizers for adjoint Fourier restriction inequalities on low dimensional spheres’, J. Funct. Anal. 280(7) (2021) 108825, https://doi.org/10.1016/j.jfa.2020.108825.CrossRefGoogle Scholar
Shao, S., ‘On existence of extremizers for the Tomas-Stein inequality for $\mathbb{S}^{1}$’, J. Funct. Anal. 270 (2016), 3996–4038.CrossRefGoogle Scholar
Shao, S., ‘On smoothness of extremizers of the Tomas-Stein inequality for $\mathbb{S}^{1}$’, Preprint (2016), arXiv:1601.07119v3.CrossRefGoogle Scholar
Stein, E. M., Singular Integrals and Differentiability of Functions (Princeton University Press, Princeton, NJ, 1970).Google Scholar
Stein, E. M., Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals (Princeton University Press, Princeton, NJ, 1993).Google Scholar
Tomas, P., ‘A restriction theorem for the Fourier transform’, Bull. Amer. Math. Soc. 81(2) (1975), 477–478.CrossRefGoogle Scholar
Triebel, H., Theory of Function Spaces II, Monographs in Mathematics, Vol. 84 (Birkhäuser Verlag, Basel, Switzerland, 1992).Google Scholar