We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 10 June 2016
Let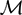 
$\mathcal{M}$ and G denote, respectively, the maximal operator and the geometric maximal operator associated with the dyadic lattice on 
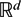$\mathbb{R}^d$.
(i) We prove that for any 0 < p < ∞, any weight w on 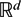$\mathbb{R}^d$ and any measurable f on 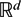$\mathbb{R}^d$, we have Fefferman–Stein-type estimate
For each p, the constant e1/p is the best possible.
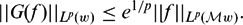$$\begin{equation*}
||G(f)||_{L^p(w)}\leq e^{1/p}||f||_{L^p(\mathcal{M}w)}.
\end{equation*}
$$
(ii) We show that for any weight w on $\mathbb{R}^d$ and any measurable f on $\mathbb{R}^d$,
and prove that the constant e is optimal.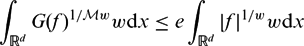
$$\begin{equation*}
\int_{\mathbb{R}^d} G(f)^{1/\mathcal{M}w}w\mbox{d}x\leq e\int_{\mathbb{R}^d} |f|^{1/w}w\mbox{d}x
\end{equation*}
$$
$\mathbb{R}^n$
, Studia Math.
144
(1) (2001), 1–37.CrossRefGoogle Scholar
You have
Access
