Contents
Research Article
Factoring absolutely summing operators through Hilbert-Schmidt operators
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 131-135
-
- Article
-
- You have access
- Export citation
On projective Hjelmslev planes of level n
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 257-261
-
- Article
-
- You have access
- Export citation
Equational bases for subvarieties of double MS-algebras
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-16
-
- Article
-
- You have access
- Export citation
The non-abelian tensor product of groups and related constructions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 17-29
-
- Article
-
- You have access
- Export citation
Another proof of a result of N. J. Kalton, E. Saab and P. Saab on the Dieudonné property in C(K, E)
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 137-140
-
- Article
-
- You have access
- Export citation
Relation modules of amalgamated free products and HNN extensions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 263-270
-
- Article
-
- You have access
- Export citation
Small amplitude capillary-gravity waves in a channel of finite depth
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 142-160
-
- Article
-
- You have access
- Export citation
Coordinates for analytic operator algebras
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 31-47
-
- Article
-
- You have access
- Export citation
A Proof of some identities of Ramanujan using modular forms
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 271-295
-
- Article
-
- You have access
- Export citation
A Counterexample in the theory of derivations
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 161-163
-
- Article
-
- You have access
- Export citation
x4 + dx2y2 + y2= z2: Some cases with only trivial solutions—and a solution Euler missed
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 297-307
-
- Article
-
- You have access
- Export citation
Dunford-Pettis and strongly Dunford-Pettis operators on L1(μ)
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 49-57
-
- Article
-
- You have access
- Export citation
Some remarks on quasi-uniform spaces
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 309-320
-
- Article
-
- You have access
- Export citation
A remark on the essential spectra of quasi-similar dominant contractions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 165-168
-
- Article
-
- You have access
- Export citation
On weak approximation and convexification in weighted spaces of vector-valued continuous functions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 59-64
-
- Article
-
- You have access
- Export citation
Supersoluble groups of automorphisms of compact Riemann surfaces
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 321-327
-
- Article
-
- You have access
- Export citation
On formulae of Macbeath and Hussein
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 65-70
-
- Article
-
- You have access
- Export citation
A note on the positive Schur property
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 169-172
-
- Article
-
- You have access
- Export citation
Soluble Groups with Finite Wielandt length
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 329-334
-
- Article
-
- You have access
- Export citation
A result on hermitian operators
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 71-72
-
- Article
-
- You have access
- Export citation

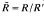 = R/R', the abelianized normal subgroup
= R/R', the abelianized normal subgroup 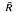 is called the relation module determined by the presentation (1). For a detailed discussion of this subject we refer to Gruenberg [
is called the relation module determined by the presentation (1). For a detailed discussion of this subject we refer to Gruenberg [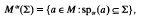
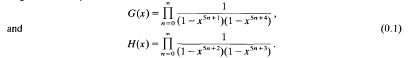
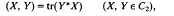
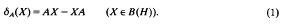
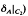 have been extensively studied (for example [1–3]). In [1], Fuad Kittaneh proved the following result.
have been extensively studied (for example [1–3]). In [1], Fuad Kittaneh proved the following result.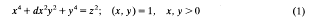
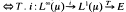 is compact, where
is compact, where 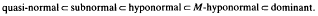
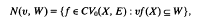
 of finite groups let
of finite groups let