Contents
Research Article
On residually transcendental valued function fields of conics
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 137-145
-
- Article
-
- You have access
- Export citation
A class of groups rich in finite quotients
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 263-274
-
- Article
-
- You have access
- Export citation
On the generators of elementary subgroups of general linear groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-10
-
- Article
-
- You have access
- Export citation
On linear recurrence sequences with polynomial coefficients
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 147-155
-
- Article
-
- You have access
- Export citation
Semigroup-graded rings with finite support
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 11-18
-
- Article
-
- You have access
- Export citation
Finite groups of outer automorphisms of free groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 275-282
-
- Article
-
- You have access
- Export citation
Prime ideals of quantized Weyl algebras
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 283-297
-
- Article
-
- You have access
- Export citation
Perfect Pell Powers
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 19-20
-
- Article
-
- You have access
- Export citation
On the theorem of Wójcik
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 157-162
-
- Article
-
- You have access
- Export citation
Finite co-Dedekindian groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 163-169
-
- Article
-
- You have access
- Export citation
A problem of Hooley in Diophantine approximation
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 299-308
-
- Article
-
- You have access
- Export citation
Equality of essential spectra of quasisimilar operators with property (δ)
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 21-28
-
- Article
-
- You have access
- Export citation
Normal structure and fixed point property
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 29-37
-
- Article
-
- You have access
- Export citation
An extension of the Kegel–Wielandt theorem to locally finite groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 171-176
-
- Article
-
- You have access
- Export citation
Spectra of conjugated ideals in group algebras of abelian groups of finite rank and control theorems
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 309-320
-
- Article
-
- You have access
- Export citation
Primary decompositions over domains
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 321-326
-
- Article
-
- You have access
- Export citation
Boundaries of nonpositively curved groups of the form G × ℤn
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 177-189
-
- Article
-
- You have access
- Export citation
Orders in power semigroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 39-47
-
- Article
-
- You have access
- Export citation
Khinchin's inequality for operators
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 327-336
-
- Article
-
- You have access
- Export citation
A simple proof of Noether's theorem
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 49-51
-
- Article
-
- You have access
- Export citation
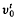 on the subfield
on the subfield 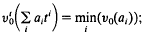 (ii)
(ii) 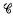 (which includes
(which includes 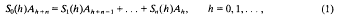
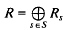 be an
be an 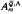 which arises from the work of Maltsiniotis [10] on noncommutative differential calculus. This algebra has been studied from the point of view of noncommutative ring theory by various authors including Alev and Dumas [1], the second author [9], Cauchon [3], and Goodearl and Lenagan [5]. In [9], it is shown that
which arises from the work of Maltsiniotis [10] on noncommutative differential calculus. This algebra has been studied from the point of view of noncommutative ring theory by various authors including Alev and Dumas [1], the second author [9], Cauchon [3], and Goodearl and Lenagan [5]. In [9], it is shown that 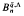 obtained on inverting these elements is simple of Krull and global dimension
obtained on inverting these elements is simple of Krull and global dimension 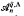 . This algebra has more symmetric defining relations than those of
. This algebra has more symmetric defining relations than those of 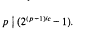
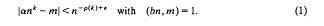
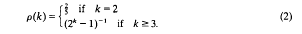
 the annihilator of
the annihilator of 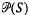 is given by
is given by 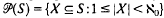 with multiplication
with multiplication 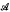 be either a
be either a 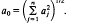 .
.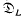 is a free
is a free 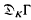 -module where Γ=Gal(
-module where Γ=Gal(