Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-28T19:28:09.625Z Has data issue: false hasContentIssue false
  • English
  • Français

Tessellation-valued processes that are generated by cell division

Part of: Geometric probability and stochastic geometry Markov processes

Published online by Cambridge University Press:  01 November 2023

Servet Martínez  and
Werner Nagel
Servet Martínez*
Affiliation:
Universidad de Chile
Werner Nagel*
Affiliation:
Friedrich-Schiller-Universität Jena
*
*Postal address: Universidad de Chile, Departamento Ingeniería Matemática and Centro Modelamiento Matemático, UMI 2807 CNRS, Casilla 170-3, Correo 3, Santiago, Chile. Email: smartine@dim.uchile.cl
**Postal address: Friedrich-Schiller-Universität Jena, Institut für Mathematik, Ernst-Abbe-Platz 2, 07743 Jena, Germany. Email: werner.nagel@uni-jena.de
Get access Rights & Permissions [Opens in a new window]

Abstract

Processes of random tessellations of the Euclidean space 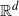$\mathbb{R}^d$, 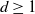$d\geq 1$, are considered that are generated by subsequent division of their cells. Such processes are characterized by the laws of the life times of the cells until their division and by the laws for the random hyperplanes that divide the cells at the end of their life times. The STIT (STable with respect to ITerations) tessellation processes are a reference model. In the present paper a generalization concerning the life time distributions is introduced, a sufficient condition for the existence of such cell division tessellation processes is provided, and a construction is described. In particular, for the case that the random dividing hyperplanes have a Mondrian distribution—which means that all cells of the tessellations are cuboids—it is shown that the intrinsic volumes, except the Euler characteristic, can be used as the parameter for the exponential life time distribution of the cells.

Keywords

Stochastic geometrystochastic process of random tessellationsSTIT tessellationcrack patternMondrian modelfragmentation

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry
Secondary: 60J25: Continuous-time Markov processes on general state spaces 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Type
Original Article
Information
Journal of Applied Probability , First View , pp. 1 - 19
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bertoin, J. (2006). Random Fragmentation and Coagulation Processes (Cambridge Studies in Adv. Math. 102). Cambridge University Press.Google Scholar
Boulogne, F., Giorgiutti-Dauphiné, F. and Pauchard, L. (2015). Surface patterns in drying films of silica colloidal dispersions. Soft Matter 11, 102–108.CrossRefGoogle ScholarPubMed
Cowan, R. (2010). New classes of random tessellations arising from iterative division of cells. Adv. Appl. Prob. 42, 26–47.CrossRefGoogle Scholar
Georgii, H.-O., Schreiber, T. and Thäle, C. (2015). Branching random tessellations with interaction: A thermodynamic view. Ann. Prob. 43, 1892–1943.CrossRefGoogle Scholar
Hafver, A. et al. (2014). Classification of fracture patterns by heterogeneity and topology. Europhys. Lett, 105, 56004.CrossRefGoogle Scholar
Halmos, P. (1970). Measure Theory. Springer, New York.Google Scholar
Kallenberg, O. (2021). Foundations of Modern Probability, 3rd edn. Springer, New York.CrossRefGoogle Scholar
Klain, D. A. and Rota, G.-C. (1997). Introduction to Geometric Probability. Cambridge University Press.Google Scholar
Last, G. and Penrose, M. (2018). Lectures on the Poisson Process (Institute of Math. Statist. Textbooks 7). Cambridge University Press.Google Scholar
León, R. (2023). Code for crack pattern simulation. Available at https://github.com/rleonphd/crackPattern.git.Google Scholar
León, R., Montero, E. and Nagel, W. (2023). Parameter optimization on a tessellation model for crack pattern simulation. Submitted.Google Scholar
León, R., Nagel, W., Ohser, J. and Arscott, S. (2020). Modeling crack patterns by modified STIT tessellations. Image Anal. Stereol. 39, 33–46.CrossRefGoogle Scholar
Martínez, S. and Nagel, W. (2012). Ergodic description of STIT tessellations. Stochastics 84, 113–134.CrossRefGoogle Scholar
Martínez, S. and Nagel, W. (2014). STIT tessellations have trivial tail $\sigma$ -algebra. Adv. Appl. Prob. 46, 643–660.CrossRefGoogle Scholar
Martínez, S. and Nagel, W. (2016). The $\beta$ -mixing rate of STIT tessellations. Stochastics 88, 396–414.CrossRefGoogle Scholar
Martnez, S. and Nagel, W. (2018). Regenerative processes for Poisson zero polytopes. Adv. Appl. Prob. 50, 1217–1226.CrossRefGoogle Scholar
Mecke, J., Nagel, W. and Weiss, V. (2007). Length distributions of edges in planar stationary and isotropic STIT tessellations. Izv. Nats. Akad. Nauk Armenii Mat. 42, 39–60.Google Scholar
Mecke, J., Nagel, W. and Weiss, V. (2008). A global construction of homogeneous random planar tessellations that are stable under iteration. Stochastics 80, 51–67.CrossRefGoogle Scholar
Nagel, W. and Biehler, E. (2015). Consistency of constructions for cell division processes. Adv. Appl. Prob. 47, 640–651.CrossRefGoogle Scholar
Nagel, W., Mecke, J., Ohser, J. and Weiß, V. (2008). A tessellation model for crack patterns on surfaces. Image Anal. Stereol. 27, 73–78.CrossRefGoogle Scholar
Nagel, W. and Weiß, V. (2005). Crack STIT tessellations: Characterization of stationary random tessellations stable with respect to iteration. Adv. Appl. Prob. 37, 859–883.CrossRefGoogle Scholar
Nagel, W. and Weiß, V. (2008). Mean values for homogeneous STIT tessellations in 3D. Image Anal. Stereol. 27, 29–37.CrossRefGoogle Scholar
Nandakishore, P. and Goehring, L. (2016). Crack patterns over uneven substrates. Soft Matter 12, 2233–2492.CrossRefGoogle ScholarPubMed
O’Reilly, E. and Tran, N. M. (2022). Stochastic geometry to generalize the Mondrian process. SIAM J. Math. Data Sci. 4, 531–552.CrossRefGoogle Scholar
Schneider, R. and Weil, W. (2008). Stochastic and Integral Geometry. Springer, Berlin.CrossRefGoogle Scholar
Schreiber, T. and Thäle, C. (2012). Second-order theory for iteration stable tessellations. Prob. Math. Statist. 32, 281–300.Google Scholar
Schreiber, T. and Thäle, C. (2013). Geometry of iteration stable tessellations: Connection with Poisson hyperplanes. Bernoulli 19, 1637–1654.CrossRefGoogle Scholar
Schreiber, T. and Thäle, C. (2013). Limit theorems for iteration stable tessellations. Ann. Prob. 41, 2261–2278.CrossRefGoogle Scholar
Schreiber, T. and Thäle, C. (2013). Shape-driven nested Markov tessellations. Stochastics 85, 510–531.CrossRefGoogle Scholar
Seghir, R. and Arscott, S. (2015). Controlled mud-crack patterning and self-organized cracking of polydimethylsiloxane elastomer surfaces. Sci. Rep. 5, 14787–14802.CrossRefGoogle Scholar
Xia, Z. and Hutchinson, J. (2000). Crack patterns in thin films. J. Mech. Phys. Solids 48, 1107–1131.CrossRefGoogle Scholar