Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Alberello, Alberto
and
Iafrati, Alessandro
2019.
The Velocity Field Underneath a Breaking Rogue Wave: Laboratory Experiments Versus Numerical Simulations.
Fluids,
Vol. 4,
Issue. 2,
p.
68.
Craciunescu, Constantin Cosmin
and
Christou, Marios
2020.
Wave breaking energy dissipation in long-crested focused wave groups based on JONSWAP spectra.
Applied Ocean Research,
Vol. 99,
Issue. ,
p.
102144.
Kanehira, T.
McAllister, M.L.
Draycott, S.
Nakashima, T.
Taniguchi, N.
Ingram, D.M.
van den Bremer, T.S.
and
Mutsuda, H.
2021.
Highly directionally spread, overturning breaking waves modelled with Smoothed Particle Hydrodynamics: A case study involving the Draupner wave.
Ocean Modelling,
Vol. 164,
Issue. ,
p.
101822.
Sinnis, James T.
Grare, Laurent
Lenain, Luc
and
Pizzo, Nick
2021.
Laboratory studies of the role of bandwidth in surface transport and energy dissipation of deep-water breaking waves.
Journal of Fluid Mechanics,
Vol. 927,
Issue. ,
Gándara, Tomás
Barrio, Ernesto Castillo Del
Cruchaga, Marcela
and
Baiges, Joan
2021.
Experimental and numerical modeling of a sloshing problem in a stepped based rectangular tank.
Physics of Fluids,
Vol. 33,
Issue. 3,
Khait, Anatoliy
and
Ma, Zhihua
2021.
On an eddy viscosity model for energetic deep-water surface gravity wave breaking.
Journal of Fluid Mechanics,
Vol. 929,
Issue. ,
Li, Yuzhu
and
Fuhrman, David R.
2022.
Computational Fluid Dynamics Simulation of Deep-Water Wave Instabilities Involving Wave Breaking.
Journal of Offshore Mechanics and Arctic Engineering,
Vol. 144,
Issue. 2,
Deike, Luc
2022.
Mass Transfer at the Ocean–Atmosphere Interface: The Role of Wave Breaking, Droplets, and Bubbles.
Annual Review of Fluid Mechanics,
Vol. 54,
Issue. 1,
p.
191.
Mostert, W.
Popinet, S.
and
Deike, L.
2022.
High-resolution direct simulation of deep water breaking waves: transition to turbulence, bubbles and droplets production.
Journal of Fluid Mechanics,
Vol. 942,
Issue. ,
Di Giorgio, Simone
Pirozzoli, Sergio
and
Iafrati, Alessandro
2022.
On coherent vortical structures in wave breaking.
Journal of Fluid Mechanics,
Vol. 947,
Issue. ,
Liu, Shuo
Wang, Hui
Bayeul-Lainé, Annie-Claude
Li, Cheng
Katz, Joseph
and
Coutier-Delgosha, Olivier
2023.
Wave statistics and energy dissipation of shallow-water breaking waves in a tank with a level bottom.
Journal of Fluid Mechanics,
Vol. 975,
Issue. ,
Boettger, Daniel G.
Keating, Shane R.
Banner, Michael L.
Morison, Russel P.
and
Barthélémy, Xavier
2023.
An energetic signature for breaking inception in surface gravity waves.
Journal of Fluid Mechanics,
Vol. 959,
Issue. ,
Zhang, Jiu-ming
Zou, Li
Sun, Tie-zhi
Yu, Zong-bing
and
Wang, Hao
2023.
Discussion on the extended form of internal solitary wave models between two typical stratification systems.
Journal of Hydrodynamics,
Vol. 35,
Issue. 1,
p.
155.
Zhang, Jiuming
Zou, Li
Sun, Tiezhi
Ma, Xinyu
and
Wang, Hao
2024.
Non-Boussinesq effect on the internal solitary wave propagation under a Lagrangian-like description for various pycnocline thickness conditions.
Physica D: Nonlinear Phenomena,
Vol. 458,
Issue. ,
p.
134007.
Dinesh Kumar, E
Sannasiraj, S A
and
Sundar, V
2024.
Lattice Boltzmann simulation of breaking waves.
Fluid Dynamics Research,
Vol. 56,
Issue. 3,
p.
035503.
Hao, Xuanting
2024.
Quantifying Bioluminescent Light Intensity in Breaking Waves Using Numerical Simulations.
Geophysical Research Letters,
Vol. 51,
Issue. 20,
Boettger, Daniel G.
Keating, Shane R.
Banner, Michael L.
Morison, Russel P.
and
Barthélémy, Xavier
2024.
Energetic inception of breaking in surface gravity waves under wind forcing.
Physical Review Fluids,
Vol. 9,
Issue. 5,
Durap, Ahmet
2025.
Thresholds and trends in wave steepness: A data-driven study of coastal wave breaking risk.
Marine Science and Technology Bulletin,
Vol. 14,
Issue. 2,
p.
80.
Zhang, Chengzhao
and
Buldakov, Eugeny
2025.
Evaluating RANS and LES turbulence models in hybrid wave modelling of breaking waves.
Frontiers in Marine Science,
Vol. 12,
Issue. ,
He, Yanli
Gao, Zhe
Wang, Lei
Li, Jinxuan
and
Dong, Guohai
2025.
Experimental investigation of the impact of directional distribution on the geometric characteristics of focused waves in finite water depth.
Physics of Fluids,
Vol. 37,
Issue. 2,
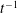 $t^{-1}$.
$t^{-1}$.

