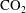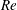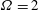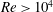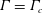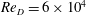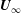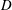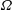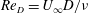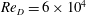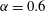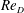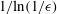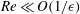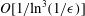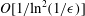Contents
JFM Papers
From a steady plume to periodic puffs during confined carbon dioxide dissolution
-
- Published online by Cambridge University Press:
- 20 September 2018, pp. 1-27
-
- Article
- Export citation
Particle fountains in a confined environment
-
- Published online by Cambridge University Press:
- 14 September 2018, pp. 28-42
-
- Article
- Export citation
Complex dynamics in a stratified lid-driven square cavity flow
-
- Published online by Cambridge University Press:
- 20 September 2018, pp. 43-66
-
- Article
- Export citation
From electrodiffusion theory to the electrohydrodynamics of leaky dielectrics through the weak electrolyte limit
-
- Published online by Cambridge University Press:
- 14 September 2018, pp. 67-130
-
- Article
- Export citation
Aerofoil broadband noise reductions through double-wavelength leading-edge serrations: a new control concept
-
- Published online by Cambridge University Press:
- 14 September 2018, pp. 131-151
-
- Article
- Export citation
Newly identified principle for aerodynamic heating in hypersonic flows
-
- Published online by Cambridge University Press:
- 14 September 2018, pp. 152-180
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Marangoni-enhanced capillary wetting in surfactant-driven superspreading
-
- Published online by Cambridge University Press:
- 14 September 2018, pp. 181-209
-
- Article
- Export citation
Two-dimensional pulse dynamics and the formation of bound states on electrified falling films
-
- Published online by Cambridge University Press:
- 14 September 2018, pp. 210-235
-
- Article
- Export citation
Control of flow around a cylinder by rotary oscillations at a high subcritical Reynolds number
-
- Published online by Cambridge University Press:
- 18 September 2018, pp. 236-266
-
- Article
- Export citation
Breaking of modulated wave groups: kinematics and energy dissipation processes
-
- Published online by Cambridge University Press:
- 18 September 2018, pp. 267-298
-
- Article
- Export citation
Vortex sheet roll-up revisited
-
- Published online by Cambridge University Press:
- 18 September 2018, pp. 299-321
-
- Article
- Export citation
Particle paths in nonlinear Schrödinger models in the presence of linear shear currents
-
- Published online by Cambridge University Press:
- 18 September 2018, pp. 322-350
-
- Article
- Export citation
The impact of dynamic roughness elements on marginally separated boundary layers
-
- Published online by Cambridge University Press:
- 19 September 2018, pp. 351-370
-
- Article
- Export citation
Large-eddy simulation of flow over a rotating cylinder: the lift crisis at
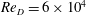 $Re_{D}=6\times 10^{4}$
$Re_{D}=6\times 10^{4}$
-
- Published online by Cambridge University Press:
- 19 September 2018, pp. 371-407
-
- Article
- Export citation
On viscous propulsion in active transversely isotropic media
-
- Published online by Cambridge University Press:
- 19 September 2018, pp. 408-420
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A higher-order slender-body theory for axisymmetric flow past a particle at moderate Reynolds number
-
- Published online by Cambridge University Press:
- 19 September 2018, pp. 421-444
-
- Article
- Export citation
Oblique waves in steady supersonic flows of Bethe–Zel’dovich–Thompson fluids
-
- Published online by Cambridge University Press:
- 19 September 2018, pp. 445-468
-
- Article
- Export citation
Modal analysis of the wake past a marine propeller
-
- Published online by Cambridge University Press:
- 19 September 2018, pp. 469-502
-
- Article
- Export citation
Propagation, proppant transport and the evolution of transport properties of hydraulic fractures
-
- Published online by Cambridge University Press:
- 19 September 2018, pp. 503-534
-
- Article
- Export citation
Hydrodynamic interactions between aerosol particles in the transition regime
-
- Published online by Cambridge University Press:
- 19 September 2018, pp. 535-553
-
- Article
- Export citation