Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Plesniak, Michael W.
and
Bulusu, Kartik V.
2016.
Morphology of Secondary Flows in a Curved Pipe With Pulsatile Inflow.
Journal of Fluids Engineering,
Vol. 138,
Issue. 10,
Burshtein, Noa
Zografos, Konstantinos
Shen, Amy Q.
Poole, Robert J.
and
Haward, Simon J.
2017.
Inertioelastic Flow Instability at a Stagnation Point.
Physical Review X,
Vol. 7,
Issue. 4,
Chen, Kevin K.
Rowley, Clarence W.
and
Stone, Howard A.
2017.
Vortex breakdown, linear global instability and sensitivity of pipe bifurcation flows.
Journal of Fluid Mechanics,
Vol. 815,
Issue. ,
p.
257.
Ault, Jesse T.
Rallabandi, Bhargav
Shardt, Orest
Chen, Kevin K.
and
Stone, Howard A.
2017.
Entry and exit flows in curved pipes.
Journal of Fluid Mechanics,
Vol. 815,
Issue. ,
p.
570.
Bulusu, Kartik V.
and
Plesniak, Michael W.
2018.
Insights on arterial secondary flow structures and vortex dynamics gained using the MRV technique.
International Journal of Heat and Fluid Flow,
Vol. 73,
Issue. ,
p.
143.
Burshtein, Noa
Shen, Amy Q.
and
Haward, Simon J.
2019.
Controlled symmetry breaking and vortex dynamics in intersecting flows.
Physics of Fluids,
Vol. 31,
Issue. 3,
Wang, Jietuo
Dalla Barba, Federico
and
Picano, Francesco
2021.
Direct numerical simulation of an evaporating turbulent diluted jet-spray at moderate reynolds number.
International Journal of Multiphase Flow,
Vol. 137,
Issue. ,
p.
103567.
Hamami Bissor (Abir), E.
Magnini, M.
Ullmann, A.
and
Brauner, N.
2021.
Numerical investigation of gas-liquid hydrodynamics during trapped-liquid displacement from low sections of high-pressure gas pipelines.
Journal of Natural Gas Science and Engineering,
Vol. 95,
Issue. ,
p.
104185.
Abraham, Aliza
He, Ruichen
Shao, Siyao
Kumar, S. Santosh
Wang, Changchang
Guo, Buyu
Trifonov, Maximilian
Placucci, Rafael Grazzini
Willis, Mele
and
Hong, Jiarong
2021.
Risk assessment and mitigation of airborne disease transmission in orchestral wind instrument performance.
Journal of Aerosol Science,
Vol. 157,
Issue. ,
p.
105797.
Chaudhury, Kaustav
Banerjee, Chandranath
and
Urankar, Swapnil
2021.
Estimation of characteristic vortex structures in complex flow.
Journal of Turbulence,
Vol. 22,
Issue. 9,
p.
517.
Kim, Minyoung
and
Borhan, Ali
2023.
Critical conditions for development of a second pair of Dean vortices in curved microfluidic channels.
Physical Review E,
Vol. 107,
Issue. 5,
Chorin, Paul
Boned, Antoine
Sebilleau, Julien
Colin, Catherine
Schoele-Schulz, Olaf
Picchi, Nicola
Schwarz, Christian
Toth, Balazs
and
Mangini, Daniele
2023.
Conception of a compact flow boiling loop for the International Space Station- First results in parabolic flights.
Comptes Rendus. Mécanique,
Vol. 351,
Issue. S2,
p.
199.
Vasa, Adarsh
and
Chaudhury, Kaustav
2023.
The vortex structures of the mean turbulent flow field in a 90-degree bend pipe.
European Journal of Mechanics - B/Fluids,
Vol. 98,
Issue. ,
p.
21.
Yin, Guang
Ong, Muk Chen
and
Zhang, Puyang
2023.
Numerical investigations of pipe flow downstream a flow conditioner with bundle of tubes.
Engineering Applications of Computational Fluid Mechanics,
Vol. 17,
Issue. 1,
Fang, Zixuan
Li, Yongjiang
Zhang, Dingwei
Liu, Xiaokang
Li, Jingxuan
Yang, Lijun
and
Fu, Qingfei
2023.
Pressure oscillation and vortex in an asymmetric T-junction.
Acta Astronautica,
Vol. 213,
Issue. ,
p.
320.
Spasov, G.H.
Rossi, R.
Vanossi, A.
Cottini, C.
and
Benassi, A.
2024.
A critical analysis of the CFD-DEM simulation of pharmaceutical aerosols deposition in upper intra-thoracic airways: Considerations on air flow.
Computers in Biology and Medicine,
Vol. 170,
Issue. ,
p.
107948.
Liang, ZHAO
Tianlai, ZHANG
Ziyang, XU
Jiang, HUANG
Xiang, LIU
Leilei, XU
and
Wei, TANG
2025.
Flow and heat transfer characteristics of low water content jet fuel in U-bend tubes: A numerical study using LES and DPM approaches.
Applied Thermal Engineering,
Vol. 258,
Issue. ,
p.
124682.
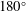 $180^{\circ }$ curved pipe that exits into a straight outlet. The flow is studied for a range of Reynolds numbers and pipe-to-curvature radius ratios. Velocity, pressure and vorticity fields are calculated to visualize the downstream decay process. Transition ‘decay’ lengths are calculated using the norm of the velocity perturbation from the Hagen–Poiseuille velocity profile, the wall-averaged shear stress, the integral of the magnitude of the vorticity, and the maximum value of the
$180^{\circ }$ curved pipe that exits into a straight outlet. The flow is studied for a range of Reynolds numbers and pipe-to-curvature radius ratios. Velocity, pressure and vorticity fields are calculated to visualize the downstream decay process. Transition ‘decay’ lengths are calculated using the norm of the velocity perturbation from the Hagen–Poiseuille velocity profile, the wall-averaged shear stress, the integral of the magnitude of the vorticity, and the maximum value of the 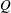 $Q$ -criterion on a cross-section. Transition lengths to the fully developed Poiseuille distribution are found to have a linear dependence on the Reynolds number with no noticeable dependence on the pipe-to-curvature radius ratio, despite the flow’s dependence on both parameters. This linear dependence of Reynolds number on the transition length is explained by linearizing the Navier–Stokes equations about the Poiseuille flow, using the form of the fully developed Dean flow as an initial condition, and using appropriate scaling arguments. We extend our results by comparing this flow recovery downstream of a curved pipe to the flow recovery in the downstream outlets of a T-junction flow. Specifically, we compare the transition lengths between these flows and document how the transition lengths depend on the Reynolds number.
$Q$ -criterion on a cross-section. Transition lengths to the fully developed Poiseuille distribution are found to have a linear dependence on the Reynolds number with no noticeable dependence on the pipe-to-curvature radius ratio, despite the flow’s dependence on both parameters. This linear dependence of Reynolds number on the transition length is explained by linearizing the Navier–Stokes equations about the Poiseuille flow, using the form of the fully developed Dean flow as an initial condition, and using appropriate scaling arguments. We extend our results by comparing this flow recovery downstream of a curved pipe to the flow recovery in the downstream outlets of a T-junction flow. Specifically, we compare the transition lengths between these flows and document how the transition lengths depend on the Reynolds number.

