We consider the long-time (many revolutions) behaviour of an axisymmetric isolated anticyclonic vortex of constant density which floats inside a large ambient linear-stratified fluid rotating with constant  ${\it\Omega}$ . We have developed a closed simple model for the prediction of the vertical thickness to diameter aspect ratio
${\it\Omega}$ . We have developed a closed simple model for the prediction of the vertical thickness to diameter aspect ratio  ${\it\alpha}$ (and actually the shape) and internal angular velocity
${\it\alpha}$ (and actually the shape) and internal angular velocity 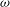 ${\it\omega}$ , relative to the ambient, as functions of time
${\it\omega}$ , relative to the ambient, as functions of time  $t$ . (In our model
$t$ . (In our model 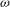 ${\it\omega}$ is scaled with
${\it\omega}$ is scaled with 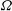 ${\it\Omega}$ ; the literature sometimes uses the Rossby number
${\it\Omega}$ ; the literature sometimes uses the Rossby number  $Ro={\it\omega}/2$ .) This model is an extension of the model of Aubert et al. (J. Fluid Mech., vol. 706, 2012, pp. 34–45) and Hassanzadeh et al. (J. Fluid Mech., vol. 706, 2012, pp. 46–57), which derived the connection between
$Ro={\it\omega}/2$ .) This model is an extension of the model of Aubert et al. (J. Fluid Mech., vol. 706, 2012, pp. 34–45) and Hassanzadeh et al. (J. Fluid Mech., vol. 706, 2012, pp. 46–57), which derived the connection between  ${\it\alpha}$ and
${\it\alpha}$ and 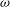 ${\it\omega}$ , for prescribed
${\it\omega}$ , for prescribed 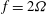 $f=2{\it\Omega}$ and buoyancy frequency of the ambient
$f=2{\it\Omega}$ and buoyancy frequency of the ambient 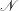 $\mathscr{N}$ . This work adds the balance of angular momentum and resolves the spin-up process of the vortex, which were not accounted for in the previous model. The Ekman number
$\mathscr{N}$ . This work adds the balance of angular momentum and resolves the spin-up process of the vortex, which were not accounted for in the previous model. The Ekman number 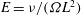 $E={\it\nu}/({\it\Omega}L^{2})$ now enters into the formulation; here
$E={\it\nu}/({\it\Omega}L^{2})$ now enters into the formulation; here  ${\it\nu}$ is the coefficient of kinematic viscosity and
${\it\nu}$ is the coefficient of kinematic viscosity and 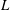 $L$ is the half-height of the vortex, roughly (a sharper definition is given in the paper). The model can be applied to cases of both fixed-volume and injection-sustained vortices.
$L$ is the half-height of the vortex, roughly (a sharper definition is given in the paper). The model can be applied to cases of both fixed-volume and injection-sustained vortices.
The often-cited aspect ratio 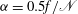 ${\it\alpha}=0.5f/\mathscr{N}$ corresponds to
${\it\alpha}=0.5f/\mathscr{N}$ corresponds to 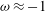 ${\it\omega}\approx -1$ , which is a plausible initial condition for typical systems. We show that the continuous ‘decay’ of
${\it\omega}\approx -1$ , which is a plausible initial condition for typical systems. We show that the continuous ‘decay’ of  ${\it\alpha}$ from that value over many revolutions of the system is indeed governed by the spin-up effect which reduces
${\it\alpha}$ from that value over many revolutions of the system is indeed governed by the spin-up effect which reduces 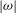 $|{\it\omega}|$ , but with significant differences to the classical spin-up of a fluid in a closed solid container. The spin-up shear torque decays with time because the thickness of the boundary shear layer increases. The layer starts as a double Ekman layer (between two fluids) but it quite quickly expands due to stratification effects, and later due to viscous diffusion. This prolongs the spin-up somewhat beyond the classical
$|{\it\omega}|$ , but with significant differences to the classical spin-up of a fluid in a closed solid container. The spin-up shear torque decays with time because the thickness of the boundary shear layer increases. The layer starts as a double Ekman layer (between two fluids) but it quite quickly expands due to stratification effects, and later due to viscous diffusion. This prolongs the spin-up somewhat beyond the classical 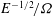 $E^{-1/2}/{\it\Omega}$ time interval. Moreover, when
$E^{-1/2}/{\it\Omega}$ time interval. Moreover, when 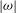 $|{\it\omega}|$ becomes small, the momentum of angular inertia of the vortex increases like
$|{\it\omega}|$ becomes small, the momentum of angular inertia of the vortex increases like 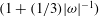 $(1+(1/3)|{\it\omega}|^{-1})$ ; this further hinders the spin-up, and prolongs the process.
$(1+(1/3)|{\it\omega}|^{-1})$ ; this further hinders the spin-up, and prolongs the process.
Comparisons of the prediction of the model with previously published experimental and Navier–Stokes simulation data were performed for four cases. In three cases the agreement is good. In one case, the model predicts a much faster decay than the observed one; we have suggested a plausible explanation for this discrepancy.