Article contents
Drops and bubbles in wedges
Published online by Cambridge University Press: 06 May 2014
Abstract
We investigate experimentally the spontaneous motion of drops and bubbles confined between two plates forming a narrow wedge. Such discoidal objects migrate under the gradient in interfacial energy induced by the non-homogeneous confinement. The resulting capillary driving force is balanced by viscous resistance. The viscous friction on a drop bridging parallel plates is estimated by measuring its sliding velocity under gravity. The viscous forces are the sum of two contributions, from the bulk of the liquid and from contact lines, the relative strength of which depends on the drop size and velocity and the physical properties of the liquid. The balance of capillarity and viscosity quantitatively explains the dynamics of spontaneous migration of a drop in a wedge. Close the tip of the wedge, bulk dissipation dominates and the migrating velocity of drops is constant and independent of drop volume. The distance between the drop and the tip of the wedge is thus linear with time  $t$ ,
$t$ , 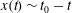 $x(t) \sim t_0-t$ , where
$x(t) \sim t_0-t$ , where 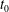 $t_0$ is the time at which the drop reaches the tip of the wedge. Far away from the apex, contact lines dominate the friction, the motion is accelerated toward the tip of the wedge and velocities are higher for larger drops. In this regime, it is shown that
$t_0$ is the time at which the drop reaches the tip of the wedge. Far away from the apex, contact lines dominate the friction, the motion is accelerated toward the tip of the wedge and velocities are higher for larger drops. In this regime, it is shown that  $x(t) \sim (t_0-t)^{4/13}$ . The position and time of the crossover between the two dissipation regimes are used to write a dimensionless equation of motion. Plotted in rescaled variables, all experimental trajectories collapse to the prediction of our model. In contrast to drops, gas bubbles in a liquid-filled wedge behave as non-wetting objects. They thus escape the confinement of the wedge to reduce their surface area. The physical mechanisms involved are similar for drops and bubbles, so that the forces acting have the same mathematical structures in both cases, except for the sign of the capillary driving force and a numerical factor. We thus predict and show experimentally that the trajectories of drops and bubbles obey the same equation of motion, except for a change in the sign of
$x(t) \sim (t_0-t)^{4/13}$ . The position and time of the crossover between the two dissipation regimes are used to write a dimensionless equation of motion. Plotted in rescaled variables, all experimental trajectories collapse to the prediction of our model. In contrast to drops, gas bubbles in a liquid-filled wedge behave as non-wetting objects. They thus escape the confinement of the wedge to reduce their surface area. The physical mechanisms involved are similar for drops and bubbles, so that the forces acting have the same mathematical structures in both cases, except for the sign of the capillary driving force and a numerical factor. We thus predict and show experimentally that the trajectories of drops and bubbles obey the same equation of motion, except for a change in the sign of 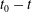 $t_0-t$ .
$t_0-t$ .
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 62
- Cited by

