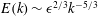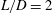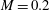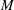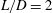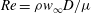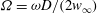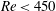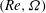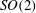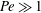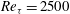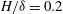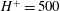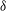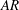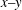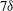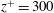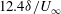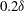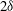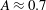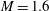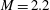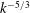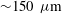Contents
Focus on Fluids
Drag kings: characterizing large-scale flows in cycling aerodynamics
-
- Published online by Cambridge University Press:
- 28 April 2014, pp. 1-4
-
- Article
-
- You have access
- Export citation
Papers
Flow topology in the wake of a cyclist and its effect on aerodynamic drag
-
- Published online by Cambridge University Press:
- 28 April 2014, pp. 5-35
-
- Article
- Export citation
Effect of mean and fluctuating pressure gradients on boundary layer turbulence
-
- Published online by Cambridge University Press:
- 28 April 2014, pp. 36-84
-
- Article
- Export citation
Turbulent mixing driven by spherical implosions. Part 1. Flow description and mixing-layer growth
-
- Published online by Cambridge University Press:
- 28 April 2014, pp. 85-112
-
- Article
- Export citation
Turbulent mixing driven by spherical implosions. Part 2. Turbulence statistics
-
- Published online by Cambridge University Press:
- 28 April 2014, pp. 113-142
-
- Article
- Export citation
Bulldozing of granular material
-
- Published online by Cambridge University Press:
- 28 April 2014, pp. 143-174
-
- Article
- Export citation
An exact representation of the nonlinear triad interaction terms in spectral space
-
- Published online by Cambridge University Press:
- 28 April 2014, pp. 175-188
-
- Article
- Export citation
Three-dimensional instabilities over a rectangular open cavity: from linear stability analysis to experimentation
-
- Published online by Cambridge University Press:
- 28 April 2014, pp. 189-220
-
- Article
- Export citation
Nonlinear and dispersive free surface waves propagating over fluids with weak vertical and horizontal density variation
-
- Published online by Cambridge University Press:
- 28 April 2014, pp. 221-240
-
- Article
- Export citation
Optimal mixing in two-dimensional plane Poiseuille flow at finite Péclet number
-
- Published online by Cambridge University Press:
- 28 April 2014, pp. 241-277
-
- Article
- Export citation
Reduced-order representation of near-wall structures in the late transitional boundary layer
-
- Published online by Cambridge University Press:
- 28 April 2014, pp. 278-301
-
- Article
- Export citation
Global stability analysis of the axisymmetric wake past a spinning bullet-shaped body
-
- Published online by Cambridge University Press:
- 29 April 2014, pp. 302-327
-
- Article
- Export citation
The detrimental effect of hydrodynamic interactions on the process of Brownian flocculation in shear flow
-
- Published online by Cambridge University Press:
- 29 April 2014, pp. 328-349
-
- Article
- Export citation
Oscillatory rarefied gas flow inside rectangular cavities
-
- Published online by Cambridge University Press:
- 29 April 2014, pp. 350-367
-
- Article
- Export citation
Perturbing vortex packets in a turbulent boundary layer
-
- Published online by Cambridge University Press:
- 29 April 2014, pp. 368-398
-
- Article
- Export citation
Coherence decay and its impact on sound radiation by wavepackets
-
- Published online by Cambridge University Press:
- 29 April 2014, pp. 399-415
-
- Article
- Export citation
Nonlinear wave run-up in bays of arbitrary cross-section: generalization of the Carrier–Greenspan approach
-
- Published online by Cambridge University Press:
- 30 April 2014, pp. 416-432
-
- Article
- Export citation
Wavelet-based adaptive simulations of three-dimensional flow past a square cylinder
-
- Published online by Cambridge University Press:
- 30 April 2014, pp. 433-456
-
- Article
- Export citation
An experimental investigation of the turbulent mixing transition in the Richtmyer–Meshkov instability
-
- Published online by Cambridge University Press:
- 01 May 2014, pp. 457-487
-
- Article
- Export citation
Non-spherical osmotic motor: chemical sailing
-
- Published online by Cambridge University Press:
- 01 May 2014, pp. 488-520
-
- Article
- Export citation