Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Reese, Daniel
Oakley, Jason
Navarro-Nunez, Alonso
Rothamer, David
Weber, Chris
and
Bonazza, Riccardo
2014.
Simultaneous concentration and velocity field measurements in a shock-accelerated mixing layer.
Experiments in Fluids,
Vol. 55,
Issue. 10,
Tritschler, V. K.
Zubel, M.
Hickel, S.
and
Adams, N. A.
2014.
Evolution of length scales and statistics of Richtmyer-Meshkov instability from direct numerical simulations.
Physical Review E,
Vol. 90,
Issue. 6,
Tritschler, V. K.
Olson, B. J.
Lele, S. K.
Hickel, S.
Hu, X. Y.
and
Adams, N. A.
2014.
On the Richtmyer–Meshkov instability evolving from a deterministic multimode planar interface.
Journal of Fluid Mechanics,
Vol. 755,
Issue. ,
p.
429.
Orlicz, G. C.
Balasubramanian, Sridhar
Vorobieff, P.
and
Prestridge, K. P.
2015.
Mixing transition in a shocked variable-density flow.
Physics of Fluids,
Vol. 27,
Issue. 11,
Wilson, B. M.
Mejia-Alvarez, R.
and
Prestridge, K. P.
2016.
Single-Interface Richtmyer–Meshkov Turbulent Mixing at the Los Alamos Vertical Shock Tube.
Journal of Fluids Engineering,
Vol. 138,
Issue. 7,
Gao, Fujie
Zhang, Yousheng
He, Zhiwei
and
Tian, Baolin
2016.
Formula for growth rate of mixing width applied to Richtmyer-Meshkov instability.
Physics of Fluids,
Vol. 28,
Issue. 11,
Mikaelian, Karnig O.
2016.
Oscillations of a standing shock wave generated by the Richtmyer-Meshkov instability.
Physical Review Fluids,
Vol. 1,
Issue. 3,
Zou, Liyong
Liu, Jinhong
Liao, Shenfei
Zheng, Xianxu
Zhai, Zhigang
and
Luo, Xisheng
2017.
Richtmyer-Meshkov instability of a flat interface subjected to a rippled shock wave.
Physical Review E,
Vol. 95,
Issue. 1,
Zhou, Ye
2017.
Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. II.
Physics Reports,
Vol. 723-725,
Issue. ,
p.
1.
Bonazza, R.
2017.
30th International Symposium on Shock Waves 1.
p.
23.
Olmstead, Dell
Wayne, Patrick
Yoo, Jae-Hwun
Kumar, Sanjay
Truman, C. Randall
and
Vorobieff, Peter
2017.
Experimental study of shock-accelerated inclined heavy gas cylinder.
Experiments in Fluids,
Vol. 58,
Issue. 6,
Di Stefano, C. A.
Rasmus, A. M.
Doss, F. W.
Flippo, K. A.
Hager, J. D.
Kline, J. L.
and
Bradley, P. A.
2017.
Multimode instability evolution driven by strong, high-energy-density shocks in a rarefaction-reflected geometry.
Physics of Plasmas,
Vol. 24,
Issue. 5,
Mohaghar, Mohammad
Carter, John
Musci, Benjamin
Reilly, David
McFarland, Jacob
and
Ranjan, Devesh
2017.
Evaluation of turbulent mixing transition in a shock-driven variable-density flow.
Journal of Fluid Mechanics,
Vol. 831,
Issue. ,
p.
779.
Zhou, Ye
2017.
Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. I.
Physics Reports,
Vol. 720-722,
Issue. ,
p.
1.
Zeng, Wei-Gang
Pan, Jian-Hua
Sun, Yu-Tao
and
Ren, Yu-Xin
2018.
Turbulent mixing and energy transfer of reshocked heavy gas curtain.
Physics of Fluids,
Vol. 30,
Issue. 6,
Zeng, Wei-Gang
Pan, Jian-Hua
Ren, Yu-Xin
and
Sun, Yu-Tao
2018.
Numerical study on the turbulent mixing of planar shock-accelerated triangular heavy gases interface.
Acta Mechanica Sinica,
Vol. 34,
Issue. 5,
p.
855.
Reese, Daniel T.
Ames, Alex M.
Noble, Chris D.
Oakley, Jason G.
Rothamer, David A.
and
Bonazza, Riccardo
2018.
Simultaneous direct measurements of concentration and velocity in the Richtmyer–Meshkov instability.
Journal of Fluid Mechanics,
Vol. 849,
Issue. ,
p.
541.
Zhou, Ye
Clark, Timothy T.
Clark, Daniel S.
Gail Glendinning, S.
Aaron Skinner, M.
Huntington, Channing M.
Hurricane, Omar A.
Dimits, Andris M.
and
Remington, Bruce A.
2019.
Turbulent mixing and transition criteria of flows induced by hydrodynamic instabilities.
Physics of Plasmas,
Vol. 26,
Issue. 8,
Thornber, B.
Griffond, J.
Bigdelou, P.
Boureima, I.
Ramaprabhu, P.
Schilling, O.
and
Williams, R. J. R.
2019.
Turbulent transport and mixing in the multimode narrowband Richtmyer-Meshkov instability.
Physics of Fluids,
Vol. 31,
Issue. 9,
Wong, Man Long
Livescu, Daniel
and
Lele, Sanjiva K.
2019.
High-resolution Navier-Stokes simulations of Richtmyer-Meshkov instability with reshock.
Physical Review Fluids,
Vol. 4,
Issue. 10,
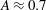 $A\approx 0.7$ ). The interface is created without the use of a membrane by first setting up a flat, gravitationally stable stagnation plane, where the gases are injected from the ends of the shock tube and exit through horizontal slots at the interface location. Following this, the interface is perturbed by injecting gas within the plane of the interface. Perturbations form in the lower portion of this layer due to the shear between this injected stream and the surrounding gas. This shear layer serves as a statistically repeatable broadband initial condition to the RMI. The interface is accelerated by either a
$A\approx 0.7$ ). The interface is created without the use of a membrane by first setting up a flat, gravitationally stable stagnation plane, where the gases are injected from the ends of the shock tube and exit through horizontal slots at the interface location. Following this, the interface is perturbed by injecting gas within the plane of the interface. Perturbations form in the lower portion of this layer due to the shear between this injected stream and the surrounding gas. This shear layer serves as a statistically repeatable broadband initial condition to the RMI. The interface is accelerated by either a 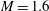 $M= 1.6 $ or
$M= 1.6 $ or 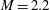 $M= 2.2 $ planar shock wave, and the development of the ensuing mixing layer is investigated using planar laser-induced fluorescence (PLIF). The PLIF images are processed to reveal the light-gas mole fraction by accounting for laser absorption and laser-steering effects. The images suggest a transition to turbulent mixing occurring during the experiment. An analysis of the mole-fraction distribution confirms this transition, showing the gases begin to homogenize at later times. The scalar variance energy spectra exhibits a near
$M= 2.2 $ planar shock wave, and the development of the ensuing mixing layer is investigated using planar laser-induced fluorescence (PLIF). The PLIF images are processed to reveal the light-gas mole fraction by accounting for laser absorption and laser-steering effects. The images suggest a transition to turbulent mixing occurring during the experiment. An analysis of the mole-fraction distribution confirms this transition, showing the gases begin to homogenize at later times. The scalar variance energy spectra exhibits a near 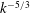 $k^{-5/3}$ inertial range, providing further evidence for turbulent mixing. Measurements of the Batchelor and Taylor microscales are made from the mole-fraction images, giving
$k^{-5/3}$ inertial range, providing further evidence for turbulent mixing. Measurements of the Batchelor and Taylor microscales are made from the mole-fraction images, giving 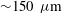 ${\sim }150\ \mu \mathrm{m}$ and 4 mm, respectively, by the latest times. The ratio of these scales implies an outer-scale Reynolds number of
${\sim }150\ \mu \mathrm{m}$ and 4 mm, respectively, by the latest times. The ratio of these scales implies an outer-scale Reynolds number of 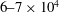 $6\text {--}7\times 10^4$ .
$6\text {--}7\times 10^4$ .
