Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Eglit, M. E.
and
Yakubenko, A. E.
2016.
Effect of the bottom material capture and the non-Newtonian rheology on the dynamics of turbulent downslope flows.
Fluid Dynamics,
Vol. 51,
Issue. 3,
p.
299.
Bates, B.M.
and
Ancey, C.
2017.
The dam-break problem for eroding viscoplastic fluids.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 243,
Issue. ,
p.
64.
Ancey, Christophe
and
Bates, Belinda M.
2017.
Stokes’ third problem for Herschel–Bulkley fluids.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 243,
Issue. ,
p.
27.
Larcher, Michele
Prati, Anna
and
Fraccarollo, Luigi
2018.
Particle entrainment in unsteady-uniform granular avalanches.
Physical Review Fluids,
Vol. 3,
Issue. 12,
Faug, T.
Turnbull, B.
and
Gauer, P.
2018.
Looking Beyond the Powder/Dense Flow Avalanche Dichotomy.
Journal of Geophysical Research: Earth Surface,
Vol. 123,
Issue. 6,
p.
1183.
Rauter, Matthias
Kofler, Andreas
Huber, Andreas
and
Fellin, Wolfgang
2018.
faSavageHutterFOAM 1.0: depth-integrated simulation of dense snow avalanches on natural terrain with OpenFOAM.
Geoscientific Model Development,
Vol. 11,
Issue. 7,
p.
2923.
Issler, Dieter
Gauer, Peter
Schaer, Mark
and
Keller, Stefan
2019.
Inferences on Mixed Snow Avalanches from Field Observations.
Geosciences,
Vol. 10,
Issue. 1,
p.
2.
Vanneste, Maarten
Løvholt, Finn
Issler, Dieter
Liu, Zhongqiang
Boylan, Noel
and
Kim, Jihwan
2019.
A Novel Quasi-3D Landslide Dynamics Model: From Theory to Applications and Risk Assessment.
Issler, Dieter
2020.
Comments on “On a Continuum Model for Avalanche Flow and Its Simplified Variants” by S. S. Grigorian and A. V. Ostroumov.
Geosciences,
Vol. 10,
Issue. 3,
p.
96.
Pudasaini, Shiva P.
and
Fischer, Jan-Thomas
2020.
A mechanical erosion model for two-phase mass flows.
International Journal of Multiphase Flow,
Vol. 132,
Issue. ,
p.
103416.
Nikooei, Mohammad
and
Manzari, Mehrdad T.
2020.
Studying effect of entrainment on dynamics of debris flows using numerical simulation.
Computers & Geosciences,
Vol. 134,
Issue. ,
p.
104337.
Eglit, Margarita
Yakubenko, Alexander
and
Zayko, Julia
2020.
A Review of Russian Snow Avalanche Models—From Analytical Solutions to Novel 3D Models.
Geosciences,
Vol. 10,
Issue. 2,
p.
77.
Vicari, Hervé
Tran, Quoc Anh
Nordal, Steinar
and
Thakur, Vikas
2022.
MPM modelling of debris flow entrainment and interaction with an upstream flexible barrier.
Landslides,
Vol. 19,
Issue. 9,
p.
2101.
TANABE, Takahiro
and
SHIMIZU, Hiroyuki
2022.
Introduction of avalanche dynamics simulator "faSavageHutterFOAM".
Journal of the Japanese Society of Snow and Ice,
Vol. 84,
Issue. 4,
p.
297.
Li, Xingyue
Sovilla, Betty
Ligneau, Camille
Jiang, Chenfanfu
and
Gaume, Johan
2022.
Different erosion and entrainment mechanisms in snow avalanches.
Mechanics Research Communications,
Vol. 124,
Issue. ,
p.
103914.
Pope, Ed L.
Cartigny, Matthieu J. B.
Clare, Michael A.
Talling, Peter J.
Lintern, D. Gwyn
Vellinga, Age
Hage, Sophie
Açikalin, Sanem
Bailey, Lewis
Chapplow, Natasha
Chen, Ye
Eggenhuisen, Joris T.
Hendry, Alison
Heerema, Catharina J.
Heijnen, Maarten S.
Hubbard, Stephen M.
Hunt, James E.
McGhee, Claire
Parsons, Daniel R.
Simmons, Stephen M.
Stacey, Cooper D.
and
Vendettuoli, Daniela
2022.
First source-to-sink monitoring shows dense head controls sediment flux and runout in turbidity currents.
Science Advances,
Vol. 8,
Issue. 20,
Pastor, Manuel
Tayyebi, Saeid M.
Stickle, Miguel M.
Molinos, Miguel
Yague, Angel
Manzanal, Diego
and
Navas, Pedro
2022.
An Arbitrary Lagrangian Eulerian (ALE) finite difference (FD)‐SPH depth integrated model for pore pressure evolution on landslides over erodible terrains.
International Journal for Numerical and Analytical Methods in Geomechanics,
Vol. 46,
Issue. 6,
p.
1127.
Løvholt, Finn
Esclasans, Roger Urgeles
Harbitz, Carl Bonnevie
Vanneste, Maarten
and
Carlton, Brian
2022.
Treatise on Geomorphology.
p.
919.
SHIMIZU, Hiroyuki
2022.
Applicability of numerical two-layer depth-averaged models for pyroclastic density currents to powder snow avalanches: Toward developing a unified model for powder snow avalanches and pyroclastic density currents.
Journal of the Japanese Society of Snow and Ice,
Vol. 84,
Issue. 4,
p.
323.
Xia, Xilin
Jarsve, Kristine Thorkildsen
Dijkstra, Tom
Liang, Qiuhua
Meng, Xingmin
and
Chen, Guan
2023.
An integrated hydrodynamic model for runoff-generated debris flows with novel formulation of bed erosion and deposition.
Engineering Geology,
Vol. 326,
Issue. ,
p.
107310.
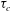 ${\it\tau}_{c}$ , and erosion along the bottom surface of the flow; frontal entrainment is neglected here. The brittleness assumption implies that the shear stress at the bed surface cannot exceed
${\it\tau}_{c}$ , and erosion along the bottom surface of the flow; frontal entrainment is neglected here. The brittleness assumption implies that the shear stress at the bed surface cannot exceed 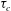 ${\it\tau}_{c}$ . For quasi-stationary flows in a simplified setting, analytic solutions are found for Bingham and frictional–collisional (FC) fluids. Extending this theory to non-stationary flows requires some assumptions for the velocity profile. For the Bingham fluid, the profile of a ‘proxy’ quasi-stationary eroding flow is used; the rheological parameters are chosen to match the instantaneous velocity and shear-layer depth of the non-stationary flow. For the FC fluid, a two-parameter family of functions that closely match the profiles obtained in depth-resolved numerical simulations is assumed; the boundary conditions determine the instantaneous parameter values and allow computation of the erosion rate. Preliminary tests with the FC erosion formula incorporated in a simple slab model indicate that the non-stationary erosion formula matches the depth-resolved simulations asymptotically, but differs in the start-up phase. The non-stationary erosion formulae are valid only up to a limit velocity (and to a limit flow depth if there is Coulomb friction). This appears to mark the transition to another erosion regime – to be described by a different model – where chunks of bed material are intermittently ripped out and gradually entrained into the flow.
${\it\tau}_{c}$ . For quasi-stationary flows in a simplified setting, analytic solutions are found for Bingham and frictional–collisional (FC) fluids. Extending this theory to non-stationary flows requires some assumptions for the velocity profile. For the Bingham fluid, the profile of a ‘proxy’ quasi-stationary eroding flow is used; the rheological parameters are chosen to match the instantaneous velocity and shear-layer depth of the non-stationary flow. For the FC fluid, a two-parameter family of functions that closely match the profiles obtained in depth-resolved numerical simulations is assumed; the boundary conditions determine the instantaneous parameter values and allow computation of the erosion rate. Preliminary tests with the FC erosion formula incorporated in a simple slab model indicate that the non-stationary erosion formula matches the depth-resolved simulations asymptotically, but differs in the start-up phase. The non-stationary erosion formulae are valid only up to a limit velocity (and to a limit flow depth if there is Coulomb friction). This appears to mark the transition to another erosion regime – to be described by a different model – where chunks of bed material are intermittently ripped out and gradually entrained into the flow.

