A novel approach to the study of the kinematics and dynamics of turbulent flows is presented. The method involves tracking in time coherent structures, and provides all of the information required to characterize eddies from birth to death. Spatially and temporally well-resolved DNSs of channel data at 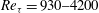 $\mathit{Re}_{{\it\tau}}=930{-}4200$ are used to analyse the evolution of three-dimensional sweeps, ejections (Lozano-Durán et al., J. Fluid Mech., vol. 694, 2012, pp. 100–130) and clusters of vortices (del Álamo et al., J. Fluid Mech., vol. 561, 2006, pp. 329–358). The results show that most of the eddies remain small and do not last for long times, but that some become large, attach to the wall and extend across the logarithmic layer. The latter are geometrically and temporally self-similar, with lifetimes proportional to their size (or distance from the wall), and their dynamics is controlled by the mean shear near their centre of gravity. They are responsible for most of the total momentum transfer. Their origin, eventual disappearance, and history are investigated and characterized, including their advection velocity at different wall distances and the temporal evolution of their size. Reinforcing previous results, the symmetry found between sweeps and ejections supports the idea that they are not independent structures, but different manifestations of larger quasi-streamwise rollers in which they are embedded. Spatially localized direct and inverse cascades are respectively associated with the splitting and merging of individual structures, as in the models of Richardson (Proc. R. Soc. Lond. A, vol. 97(686), 1920, pp. 354–373) or Obukhov (Izv. Akad. Nauk USSR, Ser. Geogr. Geofiz., vol. 5(4), 1941, pp. 453–466). It is found that the direct cascade predominates, but that both directions are roughly comparable. Most of the merged or split fragments have sizes of the order of a few Kolmogorov viscous units, but a substantial fraction of the growth and decay of the larger eddies is due to a self-similar inertial process in which eddies merge and split in fragments spanning a wide range of scales.
$\mathit{Re}_{{\it\tau}}=930{-}4200$ are used to analyse the evolution of three-dimensional sweeps, ejections (Lozano-Durán et al., J. Fluid Mech., vol. 694, 2012, pp. 100–130) and clusters of vortices (del Álamo et al., J. Fluid Mech., vol. 561, 2006, pp. 329–358). The results show that most of the eddies remain small and do not last for long times, but that some become large, attach to the wall and extend across the logarithmic layer. The latter are geometrically and temporally self-similar, with lifetimes proportional to their size (or distance from the wall), and their dynamics is controlled by the mean shear near their centre of gravity. They are responsible for most of the total momentum transfer. Their origin, eventual disappearance, and history are investigated and characterized, including their advection velocity at different wall distances and the temporal evolution of their size. Reinforcing previous results, the symmetry found between sweeps and ejections supports the idea that they are not independent structures, but different manifestations of larger quasi-streamwise rollers in which they are embedded. Spatially localized direct and inverse cascades are respectively associated with the splitting and merging of individual structures, as in the models of Richardson (Proc. R. Soc. Lond. A, vol. 97(686), 1920, pp. 354–373) or Obukhov (Izv. Akad. Nauk USSR, Ser. Geogr. Geofiz., vol. 5(4), 1941, pp. 453–466). It is found that the direct cascade predominates, but that both directions are roughly comparable. Most of the merged or split fragments have sizes of the order of a few Kolmogorov viscous units, but a substantial fraction of the growth and decay of the larger eddies is due to a self-similar inertial process in which eddies merge and split in fragments spanning a wide range of scales.