Article contents
Experimental investigation of transitional flow in a toroidal pipe
Published online by Cambridge University Press: 13 December 2013
Abstract
The flow instability and further transition to turbulence in a toroidal pipe (torus) with curvature ratio (tube-to-coiling diameter) 0.049 is investigated experimentally. The flow inside the toroidal pipe is driven by a steel sphere fitted to the inner pipe diameter. The sphere is moved with constant azimuthal velocity from outside the torus by a moving magnet. The experiment is designed to investigate curved pipe flow by optical measurement techniques. Using stereoscopic particle image velocimetry, laser Doppler velocimetry and pressure drop measurements, the flow is measured for Reynolds numbers ranging from 1000 to 15 000. Time- and space-resolved velocity fields are obtained and analysed. The steady axisymmetric basic flow is strongly influenced by centrifugal effects. On an increase of the Reynolds number we find a sequence of bifurcations. For 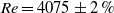 $\mathit{Re}= 4075\pm 2\hspace{0.167em} \% $ a supercritical bifurcation to an oscillatory flow is found in which waves travel in the streamwise direction with a phase velocity slightly faster than the mean flow. The oscillatory flow is superseded by a presumably quasi-periodic flow at a further increase of the Reynolds number before turbulence sets in. The results are found to be compatible, in general, with earlier experimental and numerical investigations on transition to turbulence in helical and curved pipes. However, important aspects of the bifurcation scenario differ considerably.
$\mathit{Re}= 4075\pm 2\hspace{0.167em} \% $ a supercritical bifurcation to an oscillatory flow is found in which waves travel in the streamwise direction with a phase velocity slightly faster than the mean flow. The oscillatory flow is superseded by a presumably quasi-periodic flow at a further increase of the Reynolds number before turbulence sets in. The results are found to be compatible, in general, with earlier experimental and numerical investigations on transition to turbulence in helical and curved pipes. However, important aspects of the bifurcation scenario differ considerably.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
Kühnen et al. supplementary movie
Movie of a short section of the toroidal pipe from above at Re = 4350. The camera is following the flow with the velocity of the driving sphere, i.e. practically the bulk velocity of the flow.
- 28
- Cited by

