Published online by Cambridge University Press: 29 April 2014
We analyze the global linear stability of the axisymmetric flow around a spinning bullet-shaped body of length-to-diameter ratio 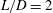 $L/D=2$ , as a function of the Reynolds number,
$L/D=2$ , as a function of the Reynolds number, 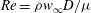 $Re=\rho w_{\infty } D /\mu $ , and of the rotation parameter
$Re=\rho w_{\infty } D /\mu $ , and of the rotation parameter 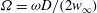 $\varOmega =\omega D/(2 w_{\infty })$ , in the ranges
$\varOmega =\omega D/(2 w_{\infty })$ , in the ranges 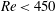 $Re<450$ and
$Re<450$ and 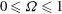 $0\leq \varOmega \leq 1$ . Here,
$0\leq \varOmega \leq 1$ . Here, 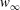 $w_{\infty }$ and
$w_{\infty }$ and 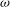 $\omega $ are the free-stream and the body rotation velocities respectively, and
$\omega $ are the free-stream and the body rotation velocities respectively, and 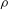 $\rho $ and
$\rho $ and 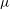 $\mu $ are the fluid density and viscosity. The two-dimensional eigenvalue problem (EVP) is solved numerically to find the spectrum of complex eigenvalues and their associated eigenfunctions, allowing us to explain the different bifurcations from the axisymmetric state observed in previous numerical studies. Our results reveal that, for the parameter ranges investigated herein, three global eigenmodes, denoted low-frequency (LF), medium-frequency (MF) and high-frequency (HF) modes, become unstable in different regions of the
$\mu $ are the fluid density and viscosity. The two-dimensional eigenvalue problem (EVP) is solved numerically to find the spectrum of complex eigenvalues and their associated eigenfunctions, allowing us to explain the different bifurcations from the axisymmetric state observed in previous numerical studies. Our results reveal that, for the parameter ranges investigated herein, three global eigenmodes, denoted low-frequency (LF), medium-frequency (MF) and high-frequency (HF) modes, become unstable in different regions of the 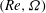 $(Re,\varOmega )$ -parameter plane. We provide precise computations of the corresponding neutral curves, that divide the
$(Re,\varOmega )$ -parameter plane. We provide precise computations of the corresponding neutral curves, that divide the 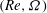 $(Re,\varOmega )$ -plane into four different regions: the stable axisymmetric flow prevails for small enough values of
$(Re,\varOmega )$ -plane into four different regions: the stable axisymmetric flow prevails for small enough values of 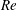 $Re$ and
$Re$ and 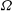 $\varOmega $ , while three different frozen states, where the wake structures co-rotate with the body at different angular velocities, take place as a consequence of the destabilization of the LF, MF and HF modes. Several direct numerical simulations (DNS) of the nonlinear state associated with the MF mode, identified here for the first time, are also reported to complement the linear stability results. Finally, we point out the important fact that, since the axisymmetric base flow is
$\varOmega $ , while three different frozen states, where the wake structures co-rotate with the body at different angular velocities, take place as a consequence of the destabilization of the LF, MF and HF modes. Several direct numerical simulations (DNS) of the nonlinear state associated with the MF mode, identified here for the first time, are also reported to complement the linear stability results. Finally, we point out the important fact that, since the axisymmetric base flow is 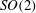 $SO(2)$ -symmetric, the theory of equivariant bifurcations implies that the weakly nonlinear regimes that emerge close to criticality must necessarily take the form of rotating-wave states. These states, previously referred to as frozen wakes in the literature, are thus shown to result from the base-flow symmetry.
$SO(2)$ -symmetric, the theory of equivariant bifurcations implies that the weakly nonlinear regimes that emerge close to criticality must necessarily take the form of rotating-wave states. These states, previously referred to as frozen wakes in the literature, are thus shown to result from the base-flow symmetry.