Hostname: page-component-5db58dd55d-smskv Total loading time: 0 Render date: 2026-06-04T11:40:24.475Z Has data issue: false hasContentIssue false
  • English
  • Français

A local analysis of the axisymmetric Navier–Stokes flow near a saddle point and no-slip flat boundary

Published online by Cambridge University Press:  04 April 2016

P.-Y. Hsu ,
H. Notsu  and
T. Yoneda
P.-Y. Hsu*
Affiliation:
Graduate School of Mathematical Sciences, University of Tokyo, 3-8-1 Komaba, Meguro-ku, Tokyo 153-8914, Japan
H. Notsu
Affiliation:
Waseda Institute for Advanced Study, Waseda University, 3-4-1 Ohkubo, Shinjuku-ku, Tokyo 169-8555, Japan
T. Yoneda
Affiliation:
Department of Mathematics, Tokyo Institute of Technology, Meguro-ku, Tokyo 152-8551, Japan
*
†Email address for correspondence: pyhsu@ms.u-tokyo.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

Tornadoes are one type of violent flow phenomenon and occur in many places in the world. There are many research methods that aim to reduce the loss of human lives and material damage caused by tornadoes. One effective method is numerical simulation such as that in Ishihara et al. (J. Wind Engng Ind. Aerodyn., vol. 99, 2011, pp. 239–248). The swirling structure of the Navier–Stokes flow is significant for both the mathematical analysis and numerical simulations of tornadoes. In this paper, we try to clarify the swirling structure. More precisely, we performed numerical computations on axisymmetric Navier–Stokes flows with a no-slip flat boundary. We compared a hyperbolic flow with swirl and one without swirl, and observed that the following phenomenon occurs only in the swirl case: the distance between the point with the maximum magnitude of velocity 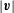$|\boldsymbol{v}|$ and the $z$ -axis changed drastically at a specific time (which we call the turning point). Besides, an ‘increasing velocity phenomenon’ occurred near the boundary, and the maximum value of 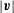$|\boldsymbol{v}|$ was obtained near the axis of symmetry and the boundary when the time was close to the turning point in the swirl case.

JFM classification

Mathematical Foundations: Mathematical Foundations

Information

Type
Papers
Information
Journal of Fluid Mechanics , Volume 794 , 10 May 2016 , pp. 444 - 459
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bourgain, J. & Li, D. 2015a Strong ill-posedness of the incompressible Euler equations in borderline Sobolev spaces. Invent. Math. 201, 97–157.Google Scholar
Bourgain, J. & Li, D. 2015b Strong illposedness of the incompressible Euler equation in integer $C^{m}$ spaces. Geom. Funct. Anal. 25, 1–86.CrossRefGoogle Scholar
Caffarelli, L., Kohn, R. & Nirenberg, L. 1982 Partial regularity of suitable weak solutions of the Navier–Stokes equations. Commun. Pure Appl. Maths 35, 771–831.Google Scholar
Chan, C.-H. & Yoneda, T. 2012 On possible isolated blow-up phenomena and regularity criterion of the 3D Navier–Stokes equation along the streamlines. Meth. Appl. Anal. 19, 211–242.Google Scholar
Chen, C.-C., Strain, R. M., Tsai, T.-P. & Yau, H.-T. 2009 Lower bounds on the blow-up rate of the axisymmetric Navier–Stokes equations. II. Commun. Part. Diff. Equ. 34, 203–232.Google Scholar
Choi, K., Hou, T., Kiselev, A., Luo, G., Sverak, V. & Yao, Y.2014 On the finite-time blowup of a 1D model for the 3D axisymmetric Euler equations. Preprint, arXiv:1407.4776.Google Scholar
Constantin, P. & Fefferman, C. 1993 Direction of vorticity and the problem of global regularity for the Navier–Stokes equations. Indiana Univ. Math. J. 42, 775–789.CrossRefGoogle Scholar
Elgindi, T. & Masmoudi, N.2014 $L^{\infty }$ ill-posedness for a class of equations arising in hydrodynamics. Preprint, arXiv:1405.2478 [math.AP].Google Scholar
Escauriaza, L., Seregin, G. A. & Sverak, V. 2003 $L_{3,\infty }$ -solutions of Navier–Stokes equations and backward uniqueness. Usp. Mat. Nauk 58, 3–44.Google Scholar
Giga, Y., Hsu, P.-Y. & Maekawa, Y. 2014 A Liouville theorem for the planar Navier–Stokes equations with the no-slip boundary condition and its application to a geometric regularity criterion. Commun. Part. Diff. Equ. 39 (10), 1906–1935.Google Scholar
Hopf, E. 1951 Uber die Anfangswertaufgabe fur die hydrodynamischen Grundgleichungen. Math. Nachr. 4, 213–231.Google Scholar
Ishihara, T. & Liu, Z. 2014 Numerical study on dynamics of a tornado-like vortex with touching down by using the LES turbulent model. Wind Struct. 19, 89–111.CrossRefGoogle Scholar
Ishihara, T., Oh, S. & Tokuyama, Y. 2011 Numerical study on flow fields of tornado-like vortices using the LES turbulence model. J. Wind Engng Ind. Aerodyn. 99, 239–248.CrossRefGoogle Scholar
Itoh, T., Miura, H. & Yoneda, T.2014 Remark on single exponential bound of the vorticity gradient for the two-dimensional Euler flow around a corner. J. Math. Fluid Mech. (in press).Google Scholar
Kang, K. 2004 Regularity of axially symmetric flows in a half-space in three dimensions. SIAM J. Math. Anal. 35, 1636–1643.Google Scholar
Kiselev, A. & Sverak, V. 2014 Small scale creation for solutions of the incompressible two dimensional Euler equation. Ann. Maths 180, 1205–1220.CrossRefGoogle Scholar
Kiselev, A. & Zlatos, A. 2015 Blow up for the 2D Euler equation on some bounded domains. J. Differ. Equ. 259 (7), 3490–3494.Google Scholar
Koch, G., Nadirashvili, N., Seregin, G. & Sverak, V. 2009 Liouville theorems for the Navier–Stokes equations and applications. Acta Math. 203 (1), 83–105.Google Scholar
Ladyzhenskaya, O. A. 1967 Uniqueness and smoothness of generalized solutions of Navier–Stokes equations. Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 5, 169–185.Google Scholar
Ladyzhenskaya, O. A. 1968 On the unique global solvability to the Cauchy problem for the Navier–Stokes equations in the presence of the axial symmetry. Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 7, 155–177.Google Scholar
Leray, J. 1934 Sur le mouvement d’un liquide visqueux emplissant l’espace. Acta Math. 63, 193–248.CrossRefGoogle Scholar
Luo, G. & Hou, T. Y. 2014 Potentially singular solutions of the 3D incompressible Euler equations. Proc. Natl Acad. Sci. USA 111 (36), 12968–12973.Google Scholar
Nolan, D. S. 2012 Three-dimensional instabilities in tornado-like vortices with secondary circulations. J. Fluid Mech. 711, 61–100.CrossRefGoogle Scholar
Notsu, H. 2008 Numerical computations of cavity flow problems by a pressure stabilized characteristic-curve finite element scheme. Trans. Japan. Soc. Comput. Engng Sci. 2008, 20080032.Google Scholar
Notsu, H. & Tabata, M. 2008 A combined finite element scheme with a pressure stabilization and a characteristic-curve method for the Navier–Stokes equations (in Japanese). Trans. Japan. Soc. Ind. Appl. Maths No. 18, 427–445.Google Scholar
Notsu, H. & Tabata, M. 2015a Error estimates of a pressure-stabilized characteristics finite element scheme for the Oseen equations. J. Sci. Comput. 65, 940–955.CrossRefGoogle Scholar
Notsu, H. & Tabata, M. 2015b Error estimates of a stabilized Lagrange–Galerkin scheme for the Navier–Stokes equations. ESAIM: Proc. M2AN 50, 361–380.Google Scholar
Prodi, G. 1959 Un teorema di unicita per le equazioni di Navier–Stokes. Ann. Mat. Pura Appl. 48, 173–182.Google Scholar
Serrin, J. 1963 The initial value problem for the Navier–Stokes equations. In Nonlinear Problems (Proc. Symp., Madison, WI), University of Wisconsin Press.Google Scholar
Ukhovskii, M. R. & Iudovich, V. I. 1968 Axially symmetric flows of ideal and viscous fluids filling the whole space. Z. Angew. Math. Mech. 32, 52–61.Google Scholar
Wan, J. W. L. & Ding, X.2005 Physically-based simulation of tornadoes. In Proceedings of the Second International Conference on Virtual Reality Interaction and Physical Simulation, ISTI-CNR, Pisa, Italy.Google Scholar
Xu, X.2014 Fast growth of the vorticity gradient in symmetric smooth domains for 2D incompressible ideal flow. J. Math. Anal. Appl. (in press); doi:10.1016/j.jmaa.2016.02.066.CrossRefGoogle Scholar