Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-12-01T07:54:11.788Z Has data issue: false hasContentIssue false
  • English
  • Français

Mean turbulence statistics in boundary layers over high-porosity foams

Published online by Cambridge University Press:  21 February 2018

Christoph Efstathiou  and
Mitul Luhar Open the ORCID record for Mitul Luhar [Opens in a new window]
Christoph Efstathiou
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA 90089, USA
Mitul Luhar*
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA 90089, USA
*
†Email address for correspondence: luhar@usc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper reports turbulent boundary layer measurements made over open-cell reticulated foams with varying pore size and thickness, but constant porosity (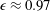$\unicode[STIX]{x1D716}\approx 0.97$). The foams were flush-mounted into a cutout on a flat plate. A laser Doppler velocimeter (LDV) was used to measure mean streamwise velocity and turbulence intensity immediately upstream of the porous section, and at multiple measurement stations along the porous substrate. The friction Reynolds number upstream of the porous section was 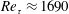$Re_{\unicode[STIX]{x1D70F}}\approx 1690$. For all but the thickest foam tested, the internal boundary layer was fully developed by 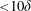${<}10\unicode[STIX]{x1D6FF}$ downstream from the porous transition, where $\unicode[STIX]{x1D6FF}$ is the boundary layer thickness. Fully developed mean velocity profiles showed the presence of a substantial slip velocity at the porous interface (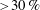${>}30\,\%$ of the free-stream velocity) and a mean velocity deficit relative to the canonical smooth-wall profile further from the wall. While the magnitude of the mean velocity deficit increased with average pore size, the slip velocity remained approximately constant. Fits to the mean velocity profile suggest that the logarithmic region is shifted relative to a smooth wall, and that this shift increases with pore size until it becomes comparable to substrate thickness 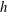$h$. For all foams, the turbulence intensity was found to be elevated further into the boundary layer to 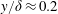$y/\unicode[STIX]{x1D6FF}\approx 0.2$. An outer peak in intensity was also evident for the largest pore sizes. Velocity spectra indicate that this outer peak is associated with large-scale structures resembling Kelvin–Helmholtz vortices that have streamwise length scale 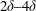$2\unicode[STIX]{x1D6FF}{-}4\unicode[STIX]{x1D6FF}$. Skewness profiles suggest that these large-scale structures may have an amplitude-modulating effect on the interfacial turbulence.

JFM classification

Low-Reynolds-number flows: Porous media Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 841 , 25 April 2018 , pp. 351 - 379
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A. & Luxton, R. E. 1971 The response of a turbulent boundary layer to a step change in surface roughness part 1. Smooth to rough. J. Fluid Mech. 48 (4), 721–761.CrossRefGoogle Scholar
Battiato, I. 2012 Self-similarity in coupled Brinkman/Navier–Stokes flows. J. Fluid Mech. 699, 94–114.Google Scholar
Belcher, S. E., Jerram, N. & Hunt, J. C. R. 2003 Adjustment of a turbulent boundary layer to a canopy of roughness elements. J. Fluid Mech. 488, 369–398.CrossRefGoogle Scholar
Breugem, W. P., Boersma, B. J. & Uittenbogaard, R. E. 2006 The influence of wall permeability on turbulent channel flow. J. Fluid Mech. 562, 35–72.CrossRefGoogle Scholar
Chandesris, M., d’Hueppe, A., Mathieu, B., Jamet, D. & Goyeau, B. 2013 Direct numerical simulation of turbulent heat transfer in a fluid-porous domain. Phys. Fluids 25 (12), 125110.CrossRefGoogle Scholar
De Graaff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.Google Scholar
De Graaff, D. B. & Eaton, J. K. 2001 A high-resolution laser Doppler anemometer: design, qualification, and uncertainty. Exp. Fluids 30 (5), 522–530.CrossRefGoogle Scholar
Detert, M., Nikora, V. & Jirka, G. H. 2010 Synoptic velocity and pressure fields at the water–sediment interface of streambeds. J. Fluid Mech. 660, 55–86.Google Scholar
Durst, F., Melling, A. & Whitelaw, J. H.1976 Principles and practice of laser-Doppler anemometry. NASA STI/Recon Tech. Rep. A 76.Google Scholar
Duvvuri, S. & McKeon, B. J. 2015 Triadic scale interactions in a turbulent boundary layer. J. Fluid Mech. 767, R4.Google Scholar
Favier, J., Dauptain, A., Basso, D. & Bottaro, A. 2009 Passive separation control using a self-adaptive hairy coating. J. Fluid Mech. 627, 451–483.Google Scholar
Finnigan, J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32 (1), 519–571.CrossRefGoogle Scholar
Ghisalberti, M. 2009 Obstructed shear flows: similarities across systems and scales. J. Fluid Mech. 641, 51–61.Google Scholar
Herrin, J. L. & Dutton, J. C. 1993 An investigation of LDV velocity bias correction techniques for high-speed separated flows. Exp. Fluids 15 (4), 354–363.Google Scholar
Ho, C.-M. & Huerre, P. 1984 Perturbed free shear layers. Annu. Rev. Fluid Mech. 16 (1), 365–422.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Itoh, M., Tamano, S., Iguchi, R., Yokota, K., Akino, N., Hino, R. & Kubo, S. 2006 Turbulent drag reduction by the seal fur surface. Phys. Fluids 18 (6), 065102.Google Scholar
Jackson, P. S. 1981 On the displacement height in the logarithmic velocity profile. J. Fluid Mech. 111, 15–25.CrossRefGoogle Scholar
Jacobi, I. & McKeon, B. J. 2011 New perspectives on the impulsive roughness-perturbation of a turbulent boundary layer. J. Fluid Mech. 677, 179–203.CrossRefGoogle Scholar
Jaworski, J. W. & Peake, N. 2013 Aerodynamic noise from a poroelastic edge with implications for the silent flight of owls. J. Fluid Mech. 723, 456–479.CrossRefGoogle Scholar
Jimenez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.Google Scholar
Jimenez, J., Uhlmann, M., Pinelli, A. & Kawahara, G. 2001 Turbulent shear flow over active and passive porous surfaces. J. Fluid Mech. 442, 89–117.CrossRefGoogle Scholar
Jovic, S. & Driver, D. M.1994 Backward-facing step measurements at low Reynolds number, $Re_{h}=5000$ . NASA STI/Recon Tech. Rep. N 94.Google Scholar
Kim, T., Blois, G., Best, J. & Christensen, K. T. 2016 Experimental study of a coarse-gravel river bed: Elucidating the nearwall and pore-space turbulent flow physics. In River Flow 2016, pp. 950–955. CRC Press.Google Scholar
Kong, F. & Schetz, J. 1982 Turbulent boundary layer over porous surfaces with different surface geometries. In 20th Aerospace Sciences Meeting (Orlando, FL), p. 30. American Institute of Aeronautics and Astronautics.Google Scholar
Kuwata, Y. & Suga, K. 2016 Lattice Boltzmann direct numerical simulation of interface turbulence over porous and rough walls. Intl J. Heat Fluid Flow 61 (Part A), 145–157; tSFP9 Special Issue.CrossRefGoogle Scholar
Kuwata, Y. & Suga, K. 2017 Direct numerical simulation of turbulence over anisotropic porous media. J. Fluid Mech. 831, 41–71.Google Scholar
Le, H., Moin, P. & Kim, J. 1997 Direct numerical simulation of turbulent flow over a backward-facing step. J. Fluid Mech. 330, 349–374.Google Scholar
Luhar, M., Rominger, J. & Nepf, H. 2008 Interaction between flow, transport and vegetation spatial structure. Environ. Fluid Mech. 8 (5), 423–439.Google Scholar
Mahjoob, S. & Vafai, K. 2008 A synthesis of fluid and thermal transport models for metal foam heat exchangers. Intl J. Heat Mass Transfer 51 (15), 3701–3711.CrossRefGoogle Scholar
Manes, C., Poggi, D. & Ridolfi, L. 2011 Turbulent boundary layers over permeable walls: scaling and near-wall structure. J. Fluid Mech. 687, 141–170.CrossRefGoogle Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 Predictive model for wall-bounded turbulent flow. Science 329 (5988), 193–196.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
Mathis, R., Marusic, I., Chernyshenko, S. I. & Hutchins, N. 2013 Estimating wall-shear-stress fluctuations given an outer region input. J. Fluid Mech. 715, 163.CrossRefGoogle Scholar
Mathis, R., Marusic, I., Hutchins, N. & Sreenivasan, K. R. 2011 The relationship between the velocity skewness and the amplitude modulation of the small scale by the large scale in turbulent boundary layers. Phys. Fluids 23 (12), 121702.Google Scholar
McLaughlin, D. K. & Tiederman, W. G. 1973 Biasing correction for individual realization of laser anemometer measurements in turbulent flows. Phys. Fluids 16 (12), 2082–2088.Google Scholar
Motlagh, S. Y. & Taghizadeh, S. 2016 POD analysis of low Reynolds turbulent porous channel flow. Intl J. Heat Fluid Flow 61 (Part B), 665–676.CrossRefGoogle Scholar
Nepf, H. M. 2012 Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 44, 123–142.Google Scholar
Parikh, P. G.2011 Passive removal of suction air for laminar flow control, and associated systems and methods. US Patent 7 866 609.Google Scholar
Patel, V. C. 1965 Calibration of the preston tube and limitations on its use in pressure gradients. J. Fluid Mech. 23 (1), 185–208.Google Scholar
Pathikonda, G. & Christensen, K. T. 2017 Inner–outer interactions in a turbulent boundary layer overlying complex roughness. Phys. Rev. Fluids 2 (4), 044603.Google Scholar
Poggi, D., Porporato, A., Ridolfi, L., Albertson, J. D. & Katul, G. G. 2004 The effect of vegetation density on canopy sub-layer turbulence. Boundary-Layer Meteorol. 111 (3), 565–587.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.Google Scholar
Rosti, M. E., Cortelezzi, L. & Quadrio, M. 2015 Direct numerical simulation of turbulent channel flow over porous walls. J. Fluid Mech. 784, 396–442.Google Scholar
Ruff, J. F. & Gelhar, L. W. 1972 Turbulent shear flow in porous boundary. J. Engng Mech. ASCE 504 (98), 975.Google Scholar
Schlatter, P. & Örlü, R. 2010 Quantifying the interaction between large and small scales in wall-bounded turbulent flows: a note of caution. Phys. Fluids 22 (5), 051704.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.CrossRefGoogle Scholar
Schultz, M. P. & Flack, K. A. 2007 The rough-wall turbulent boundary layer from the hydraulically smooth to the fully rough regime. J. Fluid Mech. 580, 381–405.CrossRefGoogle Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High–Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Suga, K., Matsumura, Y., Ashitaka, Y., Tominaga, S. & Kaneda, M. 2010 Effects of wall permeability on turbulence. Intl J. Heat Fluid Flow 31 (6), 974–984.CrossRefGoogle Scholar
White, B. L. & Nepf, H. M. 2007 Shear instability and coherent structures in shallow flow adjacent to a porous layer. J. Fluid Mech. 593, 1–32.CrossRefGoogle Scholar
Zagni, A. F. E. & Smith, K. V. H. 1976 Channel flow over permeable beds of graded spheres. J. Hydraul. Div. ASCE 102 (2), 207–222.Google Scholar